1. Background and Summary
The Collatz conjecture is a mathematical conjecture that was first proposed by Lothar Collatz in 1937. Collatz conjecture is also known as 3X + 1 problem, which states simply: Take any positive integer number x. If x is even, divide it by 2 to get x/2. If x is odd, multiply it by 3 and add 1 to get 3 × x + 1. Repeat the process again and again. The Collatz conjecture is that no matter what the starting number (i.e., x) is taken, the process will always eventually reach 1.
Original dynamics is from the starting number to 1. In contrast, reduced dynamics is from the starting number to the first number that is less than the starting number. We propose studying reduced dynamics [
1] because it is more primitive—it is the component (building block) of original dynamics. Indeed, reduced dynamics presents inner regulations such as period that does not exist in original dynamics. We find that 3 ×
x + 1 is always even and is always followed by
x/2. Thus, 3 ×
x + 1 and
x/2 can be combined together as (3 ×
x + 1)/2. Because the computation for Collatz conjecture is either 3 ×
x + 1 or
x/2, we use “I” to denote (3 ×
x + 1)/2 and “O” to denote
x/2. Intuitively, if all positive integers can return to an integer that smaller than it, then it will finally return 1. Indeed, we proposed the reduced Collatz conjecture and proved it is equivalent to Collatz conjecture formally in another paper [
1]. We can prove that if reduced dynamics for all positive integers exist, then original dynamics for all positive integers exist. Inverse direction is also guaranteed. Here, we assume reduced dynamics for 1 is (3 ×
x + 1)/2 and
x/2, i.e., “IO”.
Reduced dynamics for some integers are trivial. For example, reduced dynamics for an even integer is “O”, as after x/2 the transformed number is less than the starting number. Besides, reduced dynamics for odd integers has the form 4k + 1 is “IO”. It can be proved as follows; suppose starting integer is x, and x is 4k + 1 (k is a natural number). Thus, (3 × x + 1)/2 occurs. After (3 × x + 1)/2, x is (12k + 3 + 1)/2, which is 6k + 2. Thus, x/2 occurs. After x/2, transformed number is 3k + 1, which is less than 4k + 1. Thus, reduced dynamics is obtained and is “IO”. Furthermore, for including special case when x equals 1, we intentionally assume the reduced dynamics for 1 is “IO”. In the following, we only concentrate on reduced dynamics for odd with 4k + 3.
To prove the reduced Collatz conjecture, i.e., to prove all positive integers has reduced dynamics, we study the properties in reduced dynamics. We designed a computer program that can output reduced dynamics for odd integers with 4
k + 3, e.g., [3, 99999999]. Outputting (reduced) dynamics for much larger integers are also possible. The source code in C is txpo9.c [
2]. There are five options in arguments for more flexible output. Those data can reveal the properties of reduced dynamics. The most important are ratio and period. We observed and discovered that the ratio, which is the count of
x/2 over the count of (3 ×
x + 1)/2, is bounded by a constant value, ln(1.5)/ln(2). We prove mathematically that the ratio of reduced dynamics is larger than
λ = ln(1.5)/ln(2) ≈ 0.58496250 formally in another paper [
3]. Those data outputted by txpo9.c can be used to verify this bound. The data shows that our analysis on the bound of ratio is correct. Indeed, we also derive the equation on the count of
x/2 and the count of (3 ×
x + 1)/2 for any reduced dynamics. That is,
CntO(c) = ceil(CntI(c) ×
λ) where
ceil(x) returns the minimal integer that is not less than
x;
λ equals ln(1.5)/ln(2)
; c is any reduced dynamics in terms of “I” and “O” with length larger than 1;
CntO(c) is a function returns the count of “O” in inputting string denoted as
c; and
CntI(c) is a function returns the count of “I” in inputting string denoted as
c. For example, “O” is a reduced dynamics for even, it is trivial and listed aside. “IO” is reduced dynamics for odd with 4
k + 1, we can check the equation as follows
It is worth to note that the bound can help us generate all valid reduced dynamics by algorithm, instead of selecting a positive number to compute its reduced dynamics. Besides, we also discover that the period of reduced dynamics does exist. That is, if the reduced dynamics of
x is a sequence consisting of “I” and “O” with length
L, then the reduced dynamics of
x + 2
L equals the reduced dynamics of
x. We also prove it mathematically in another paper [
4]. This period can also be observed and verified in the data file that is outputted by the program txpo9.c. Note that, for the better vision in computer program output, we use “-” to represent “I” (i.e., the computation of (3 ×
x + 1)/2) and “0” to represent “O” (i.e., the computation of
x/2).
Currently, the largest integer being verified for Collatz conjecture is ~2
60 [
5,
6]. To verify whether extremely large integers such as 2
100000 − 1 can return 1, we designed a new algorithm [
7] to compute 3 ×
x + 1, which is
O(lnx). This dedicated algorithm can change numerical computation into bit or Boolean computation, hence original dynamics for an extremely large integer without upper bound can be computed. By this algorithm, we thus design novel computer program that can output original dynamics for extremely large integers without upper-bound such as 2
100000 − 1, which is the largest integer being verified until now. The source code in C is txpo15.c [
8]. The bit length of extremely large integer can be set up by “macro” (named MAXLEN) in source code. The program can output the original dynamics (called CODE) of a starting integer in terms of “-” presenting (3 ×
x + 1)/2 and “0” presenting
x/2. This data can be used for verifying whether an extremely large number can go to 1 finally. Note that, there is no upper bound for extremely large starting integer; all is a timing issue. We just use desktop PC (Intel Core i5-6500 3.2 GHz) to compute the results for ~15 days.
After we study the ratio for reduced dynamics, we continue to study the ratio for original dynamics, especially for extremely large integers asymptotically. We designed a computer program that can randomly generate extremely large integers and output their original dynamics. The source code is txpo10b.c [
9]. The bit length of integers can be defined by “macro” (named MAXLEN) in source code. The number of randomly generated integers can be set by inputting argument. The program can output the original dynamics of a starting integer in terms of “-” presenting (3 ×
x + 1)/2 and “0” presenting
x/2. This data can be used for observing the relation between the count of “-” and the count of “0”. By analyzing outputting data, we discover that the ratio, which is the count of “-” over the count of “0”, is 1 asymptotically with the grow of starting integer.
We further study a reverse problem: Given a reduced dynamics or partial dynamics, can we compute a residue class that presents those dynamics? We designed a dedicated algorithm that takes as input a dynamics with length t consists of “I” or “O” that can output a residue class who presents this dynamics in the first
t transformations. We thus designed a computer program that can output a reside class by inputting a reduced dynamics or partial dynamics. That is, inputting
c∈{I,O}L, CntO(s) ≤ ceil(CntI(s) × λ),
λ = ln(1.5)/ln(2) = 0.58469250,
s = Substr(c,1,i), I = 1, 2, …,
L, where
CntO(s) returns the count of “O” in string denoted as
s;
CntI(s) returns the count of “I” in string denoted as
s;
ceil(x) returns the minimal integer that is not less than
x;
Substr(c,1,i) returns the first
i characters in terms of “I” or “O” (i.e., substring) in string denoted as
c. In other words, the dynamics is above of or cutting ratio line in our proposed Collatz graph (i.e., Figure 2). Note that the algorithm is quit lightweight and designed from our formal proof of Partition Theorem [
10]; we prove that all natural numbers are partitioned regularly corresponding to ongoing dynamics. Given any natural number
x that equals
i module
2t (
i is an odd integer), the first
t transformations in terms of “I” or “O” can be determined and identical with the first
t transformations of
i. Once current value after
t (
t is greater or equal to 2) transformations of “I” or “O”, is less than
x, then reduced dynamics of
x is obtained. Otherwise, the residue class of
x (namely,
i module 2
t) can be partitioned into two halves (namely,
i module 2
t + 1 and
i + 2
t module 2
t + 1), and either half presents “I” or “O” in intermediately forthcoming (
t + 1)-th transformation.
The Collatz conjecture seems to be extremely hard and advances are few although it is out for more than 80 years. L. Colussi [
11] proposed Collatz function
R(x) = (3 ×
x + 1)/
2h where
h is the highest power of 2 that divides 3 ×
x + 1. They explore some properties of convergence classes (i.e., the set of odd positive integers) denoted as
Gk such that
Rk(x) = 1. The longest progressions for initial starting numbers of less than 10 billion and 100 quadrillion are calculated by G.T. Leavens [
12] and R.E. Crandall [
13], respectively. I. Krasikov and J.C. Lagarias proved that the number of integers finally reaching one in the interval [1,
x] is at least proportional to
x 0.84 [
14].
2. Data Description
The format of txpo9-c3-3-9999999 (with file size 140 MB) is listed in
Table 1. More integers can be computed, e.g., txpo9-c3-3-99999999 (with file size 1.5 GB), by changing inputting arguments.
For more examples in details, we illustrate some lines in the data files.
3 11 2 2 1.0000000 --00
7 111 4 3 0.7500000 ---0-00
11 1011 3 2 0.6666667 --0-0
15 1111 4 3 0.7500000 ----000
19 10011 2 2 1.0000000 --00
23 10111 3 2 0.6666667 ---00
27 11011 37 22 0.5945946 --0-----0-0--0---0----0-00---0--0------00----000-0-0-000-00
31 11111 35 21 0.6000000 -----0-0--0---0----0-00---0--0------00----000-0-0-000-00
35 100011 2 2 1.0000000 --00
39 100111 5 3 0.6000000 ---0--00
43 101011 3 2 0.6666667 --0-0
47 101111 34 20 0.5882353 ----0-0--0---0----0-00---0--0------00----000-0-0-000-0
51 110011 2 2 1.0000000 --00
55 110111 3 2 0.6666667 ---00
59 111011 4 3 0.7500000 --0--00
63 111111 34 20 0.5882353 ------000--0---0----0-00---0--0------00----000-0-0-000
….
Those are reduced dynamics, but the source code can be changed to output original dynamics. The meaning of data column is identical.
Table 2 lists data columns in file named CODE that is outputted by txpo15.exe for original dynamics of an extremely large integer.
For example, the CODE file for starting integer that equals 2100 − 1 is as follows:
----------------------------------------------------------------------------------------------------0000-00---00-000--0--000-000--0000-0--00---00-0---00-0---0---0-00---0-0---0000--00-0-00---0-0000---00-----0-00-0000-000--000-000---0-00-00-0--00------0-----00---0-0-0000-0--000-0----0-00000---000-0-0000-0------00--00-00---0-0-00000-0-0000-0----00-----00--0--0-000000--0--0000-00-00---00--0--0--000-0----0------0----00-0000---0---0-00--0---000-00000-00-----0--0--0-0---0--0------000-00---00-0-0-0---0-00-0000-00---0-0-0--00-00-00-0--0-00-0000------0---00--0000-----0-0-0-0----00-0--0-0----0--000------0-00--0---00-00-0-00---0--00--0-000-000-0-----00-----0---0--0-0-0-000--0--000000--000--0-0--0-0-0-00----0--00-0-0--0---000000---0000--0-00----0-0-0--000-0000-0--0------0--000-0--00-00-0-00-0---0-0-00-00-000-----00-----00---0-0-00000000----0000-0------0--0-0-0-0----0-0-0-00-0-0--0--00-00-0000-0--0--0-00-0--000000-0-00-00-0000---0000-000
528 409 0.7746212
We can check whether extremely large integer can return 1 finally, as well as the count of “-”, the count of “0”, and the ratio between the count of “0” over the count of “-”.
There is only one column in the data file that is ratio, which is the count of “0” over the count of “-” in original dynamics.
For example, the first 20 lines in generated file txpo10b-len100-try5000 by txpo10b.exe is as follows.
0.9958678
1.0360360
1.2907802
1.1111112
1.0516431
0.9225589
0.9426523
1.0514019
1.0042194
0.9166667
0.9918367
0.9958848
1.0041841
1.0264317
1.1396648
1.0265486
0.9456522
1.0265486
1.0084746
0.8750000
….
There are 5000 randomly generated starting integers, thus there are 5000 lines in this data file. Note that we can also output the details on original dynamics for each sample by turn on the printing option in source code, but as we need further compute average and variation so those details are omitted and option is commented.
By using comp4.exe, the average and variation of those 5000 ratios can be computed.
For example, just run comp4.exe with data file.
comp4.exe txpo10b-len100-try5000
The results of the above are as follows.
1.0184816 0.0095717
For another example,
comp4.exe txpo10b-len1000-try40000
1.0018520 0.0008443
Note that as the starting integers (samples) are randomly generated, the results are usually not same. Here we use randomly generated integers because enumerating all such large integer is impossible and unnecessary in a proper short running time.
The major output of the program is a residue class whose reduced dynamics is inputting argument or the first t transforms are inputting argument with length t.
For example,
txpo25.exe IIOO > txpo25-IIOO
The last line of the file is as follows.
“Main: final
i = 3, module is 16, i.e., RD[
x in [
3]_{16}] = IIOO. “
txpo25.exe IIIIOOO > txpo25-IIIIOOO
The last line of the file is as follows.
“Main: final
i = 15, module is 128, i.e., RD[
x in [
15]_{128}] = IIIIOOO.”
txpo25.exe IIO > txpo25-IIO
The last line of the file is as follows.
“Main: final
i = 3, module is 8, i.e., DYNM[
x in [
3]_{8},3] = IIO.”
We also output the intermediate computation results for whole procedure, which can be as a reference, although the last line is of the most importance.
3. Methods
Dataset I: Exploring Properties in Reduced Dynamics ([
2])
Step 1: txpo9.c. It is source code in C that can be compiled into an executable program by any C compiler. It is ANSI C code, thus it can be complied for either Windows or Linux platform.
Step 2: Compile txpo9.c to generate txpo9.exe. txpo9.exe is an executable program, and can be executed in any DOS command shell in Windows (if compiled for Windows platform) and computing results (as generated files) will be obtained.
Step 3: Run txpo9.exe, which has five options (as the first argument).
(1) Output reduced dynamics of a specific integer, which can be set in the source code before compiling, e.g., we can set the integer as 210000 − 1, which has a form like 11…11 where the bit length is 10000 and all bits are 1. The MAXLEN of bit length is 80,040 due to inner memory constraint. Note that, inner memory constraint can be broken by out file manipulation, which is provided in txpo15.c.
E.g., txpo9.exe 1 > txpo9-c1 //210000 − 1 c: choice p: pow()
(2) Output reduced dynamics of a specific decimal integer, which is inputted as an argument.
E.g., txpo9.exe 2 703 > txpo9-c2-703 //703
txpo9.exe 2 8088063 > txpo9-c2-8088063 //8088063
(3) Output reduced dynamics of a specific decimal integers in a rang, which are inputted as two arguments.
E.g., txpo9.exe 3 3 1000000 > txpo9-c3-3-1000000 //[3, 1000000]
(4) Output reduced dynamics of large decimal integers in a range, which are inputted as two arguments for exponents.
E.g., txpo9.exe 4 6 8 > txpo9-c4-p106-p108 //[106 + 3, 108]
txpo9.exe 4 8 9 > txpo9-c4-p108-p109 //[108 + 3, 109]
(5) Output reduced dynamics of extremely large decimal integer that is ~1018. Eighteen can be modified to others in source codes. If it is larger, then the waiting time will be more.
E.g., txpo9.exe 5 > txpo9-c5 //[1018 + 3, 16 × 1018]
Note that the source code can be changed to output original dynamics easily by replacing main loop to as follows: “while (strlen(current_x)!=1)”, because the final integer in original dynamics is 1 that is represented by a string with length 1.
Dataset II: Verifying Whether Extremely Large Integer Guarantees Collatz Conjecture (Can Return to 1 Finally) ([
8])
Step 1: Configuring following code in source code of txpo15.c, which is a “macro” in C as follows:
#define MAXLEN 100//the maximal bit length, e.g., 100, 1000, 10000, 100000, and 1000000.
txpo15.c. It is source code in C that can be compiled into an executable program by any C compiler. It is ANSI C code, thus it can be complied for either Windows or Linux platform.
Step 2: Compile txpo15.c to generate txpo15.exe.
txpo15.exe is an executable program, and can be executed in any DOS command shell in Windows (if compiled for Windows platform) and computing results (as generated files) will be obtained.
Step 3: Run txpo15.exe, generating following data.
CODE. The file is generated by running the program (i.e., txpo15.exe), and it stores dynamics data in terms of “-” presenting (3X + 1)/2 and “0” presenting x/2. The counts on the number of “-” and “0” are also included in the file.
input_start. The file is generated by running the program, and it stores tested starting integer that is determined by 2MAXLEN − 1, e.g., 2100000 − 1.
DYNAMICS. The file is generated by running the program, which records all intermediate results (transformed integers), after occurring either (3X + 1)/2 or x/2, from the starting integer to 1. Note that, we suggest to stop outputting this file JUST for saving time; it can be used for check the results for small starting integers such as less then 230 − 1.
Dataset III: Exploring the Ratio Between the Count of x/2 and the Count of (3 × x + 1)/2 in Original Dynamics for Extremely Large Starting Integers Asymptotically ([
9])
Step 1: Configuring following code in source code of txpo10b.c, which is a “macro” in C as follows.
#define MAXLEN 100//the maximal bit length, e.g., 100, 1000, 80,000.
txpo10b.c is source code in C that can be compiled into an executable program by any C compiler. It is ANSI C code, thus it can be complied for either Windows or Linux platform.
Step 2: Compile txpo10b.c, generate txpo10b.exe.
txpo10b.exe is an executable program, and can be executed in any DOS command shell in Windows (if compiled for Windows platform) and computing results (as generated files) will be obtained.
Step 3: Run txpo10b.exe by inputting argument that specifying the number of randomly generated integers.
For example, If MAXLEN is 2000 that specifies the bit length of randomly generated integers, and inputting argument is 4000 that specifies the number of randomly generated integers, then use following command:
tpxo10b.exe 4000 > tpxo10b-len2000-try4000
The data file named tpxo10b-len2000-try4000 will be generated.
Step 4: Compile comp4.c to generate comp4.exe.
Step 5: Run comp4.exe to compute the average and variation of ratios for samples.
For example, to get the average and variation of ratios for 4000 samples in above data file, just do
comp4.exe tpxo10b-len2000-try4000.
Then, the average and variation of ratios that is count of “-’’ over count of “0’’ for 4000 samples will be displayed.
Dataset IV: Exploring the Inverse Mapping from a Dynamics to a Residue Class—Inputting a Reduced Dynamics or Partial Dynamics and Outputting a Residue Class ([
16])
Step 1: txpo25.c is source code in C that can be compiled into an executable program by any C compiler. It is ANSI C code, thus it can be complied for either Windows or Linux platform.
Step 2: Compile txpo25.c, generate txpo25.exe.
txpo25.exe is an executable program, and can be executed in any DOS command shell in Windows (if compiled for Windows platform) and computing results (as generated files) will be obtained.
Step 3: Run txpo25.exe by inputting argument that specifying a reduced dynamics or a partial dynamics.
tpxo25.exe IIOO > tpxo25-IIOO
tpxo25.exe II > tpxo25-II
tpxo25.exe O > tpxo25-O
4. Code Availability
txpo9.c ([
2]). It is source code in C that can be compiled into an executable program by any C compiler. It is ANSI C code, thus it can be complied for either Windows or Linux platform.
This code can output reduced dynamics for a range of integers such as [3, 99999999]. The range is inputted as two arguments.
txpo15.c ([
8]). It is source code in C that can be compiled into an executable program by any C compiler. It is ANSI C code, thus it can be complied for either Windows or Linux platform.
This code generates original dynamics for extremely large integers without upper-bound, e.g., 2100000 − 1. The bit length of integers can be specified by “macro” definition for MAXLEN in the source code.
txpo10b.c ([
9]). It is source code in C that can be compiled into an executable program by any C compiler. It is ANSI C code, thus it can be complied for either Windows or Linux platform.
This code outputs original dynamics of many randomly generated integers (also call samples). The number of randomly samples is specified by inputting argument of the program. The bit length of randomly generated integers can be specified by Marco definition for MAXLEN in the source code.
txpo25.c ([
16]). It is source code in C that can be compiled into an executable program by any C compiler. It is ANSI C code, thus it can be complied for either Windows or Linux platform.
This program can takes as input a reduced dynamic or partial dynamics consists of “I” or “O” with length L, and outputs a residue class whose first L transformations are inputting.
It creates a one-to-one mapping between residue class and dynamics.
5. Technical Validation
The reduced dynamics in txpo9-c3-3-9999999 can be manually verified.
For example, the 2nd line in the file is as follows
7 111 4 3 0.7500000 ---0-00
It can be manually computed by 7 -> 11 -> 17 -> 26 -> 13 -> 20 -> 10 -> 5. 5 is less than 7, thus ends. Here we combine 3 × x + 1 and x/2 together as it always occurs in both.
We can also randomly choose one line in the data file to verify its soundness manually.
Note that in source code txpo9.c we can see that if there is a ratio that is not larger λ = ln(1.5)/ln(2) = 0.58496250, the program will output an alert. More specifically, the source code in txpo9.c is as follows.
if (ratio<=0.58496250)
{
printf("\n\n\n------Alert!------\n\n\n");
exit(0);
} |
By searching “Alert” in txpo9-c3-3-99999999 (e.g., grep or any string search function in a text edit tool), we can find that there exists no “Alert” in the file, which means all ratios are larger than 0.58496250. It thus verified that in [3, 9999999] all odds with 4k + 3 guarantee this bound. The ratios for even and odd wit 4k + 1 are trivial, because the reduced dynamics for even is trivial, i.e., “O”, and the reduced for odds with 4k + 1 is also trivial, i.e., “IO”. Together with ratio = 1/0 for even and ratio = 1/1 for 4k + 1.
Indeed, we formally prove this observation in another paper.
Besides, we prove the period of reduced dynamics in another paper, which can be observed in the reduced dynamics data file with the name such as txpo9-c3-3-99999999. The period is 2L, L is the length of reduced dynamics.
For example, reduced dynamics for 7 is the 2nd line in the file as follows
The length is 4 + 3 = 7. Thus, the period is 2
7 = 128. That is, reduced dynamics of 7 + 128 = 135 is identical with 7 and is ---0-00 too. It can be checked by the 34th line in the file as follows
Similarly, reduced dynamics of 135+128 = 263 is the same as 135, which can be checked by the 66th line in the file as follows
Note that, L is also the total count of x/2 that includes the count of “0” presenting x/2 and the count of “-” presenting (3 × x +1)/2.
We can choose 24 − 1=16 − 1=15 to verify the correctness of the program.
The CODE file outputted by txpo15.exe is as follows
It can be manually verified by 15 -> 23 -> 35 -> 53 -> 80 -> 40 -> 20 -> 10 -> 5 -> 8 -> 4 -> 2 ->1.
The original dynamics is right.
The count of “-” is 5 and the count of “0” is 7. Thus, the ratio is 7/5 =1.4.
By the program txpo15.exe, we can verify that even extremely large integers can also return to 1 finally. For example, by outputted file CODE of txpo15.exe that includes “macro” definition for MAXLEN 100000, we can verify that 2100000 − 1 can return to 1 after 481603 times of “-” (i.e., (3 × x + 1)/2) and 381720 times of “0” (i.e., x/2). The ratio, which is the count of x/2 over the count of (3 × x + 1)/2, is 0.7926030.
More results are listed in
Table 3. In the table,
U is the count of
3 ×
x + 1, which equals the count of “-”.
D − U is
D (i.e., the count of
x/2) minus
U (i.e., the count of 3 ×
x + 1), which indeed equals the count of “0”. MAXLEN is the bit length of starting integer, which is also Marco in C source code. Ratio is
(D − U)/U that is the count of “0” over the count of “-”.
We can generate 10 samples by txpo10b.exe 10 > txpo10b-len100-try10.
Then, manually compute the average and variance of these 10 ratios.
For the verification of generated ratios, we can modify the source code to output the original dynamics, recompile the source code, execute the program, and verify the original dynamics manually.
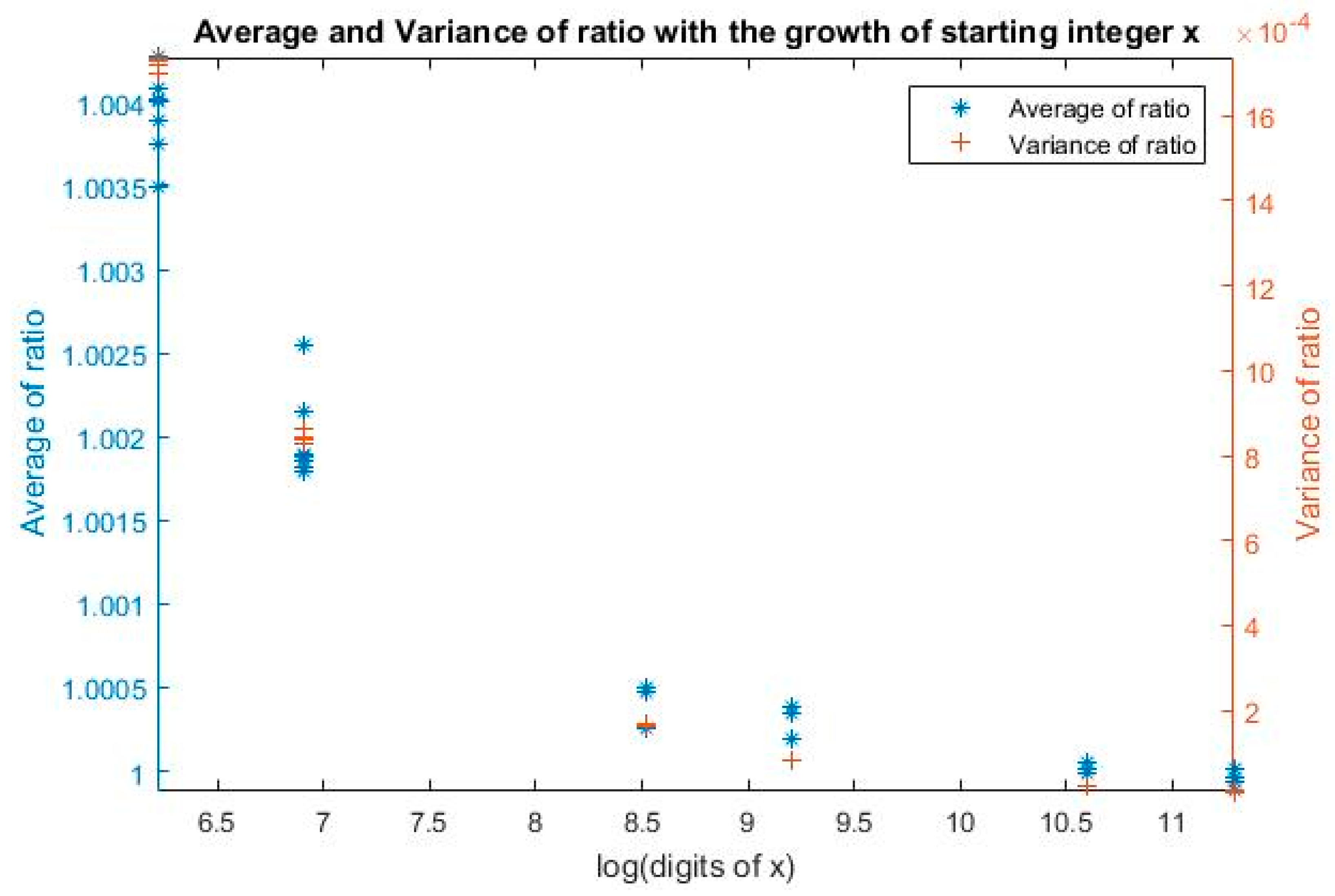
It would be better if the number of samples are larger. We observe that the ratio—the count of
x/2 over the count of (3 ×
x + 1)/2 in original dynamics—asymptotically approaches 1, with the growth of starting integer. It can be observed that average of ratio approaches 1 and variance approaches to 0. More results are listed in
Table 4.
The results can also be depicted in
Figure 1.
The correctness of the outputted residue class can be verified manually or by data file txpo9-c3-3-99999999 that presents the reduced dynamics, and partial dynamics can also be verified in them.
Indeed, we prove Partition Theorem in another paper [
10]. The partition can be observed in the following reduced dynamics graph. Given any natural number
x, that is,
i module 2
t (
i is an odd integer), the first t transformations in terms of I or O can be determined and identical with the first t transformations of
i. Once current value after
t (
t is greater or equal to 2) transformations of I or O, is less than
x, then reduced dynamics of
x is obtained. Otherwise, the residue class of
x (namely,
i module 2
t) can be partitioned into two halves (namely, i module 2
t + 1 and
i + 2
t module 2
t + 1), and either half presents I or O in intermediately forthcoming (
t + 1)-
th transformation.
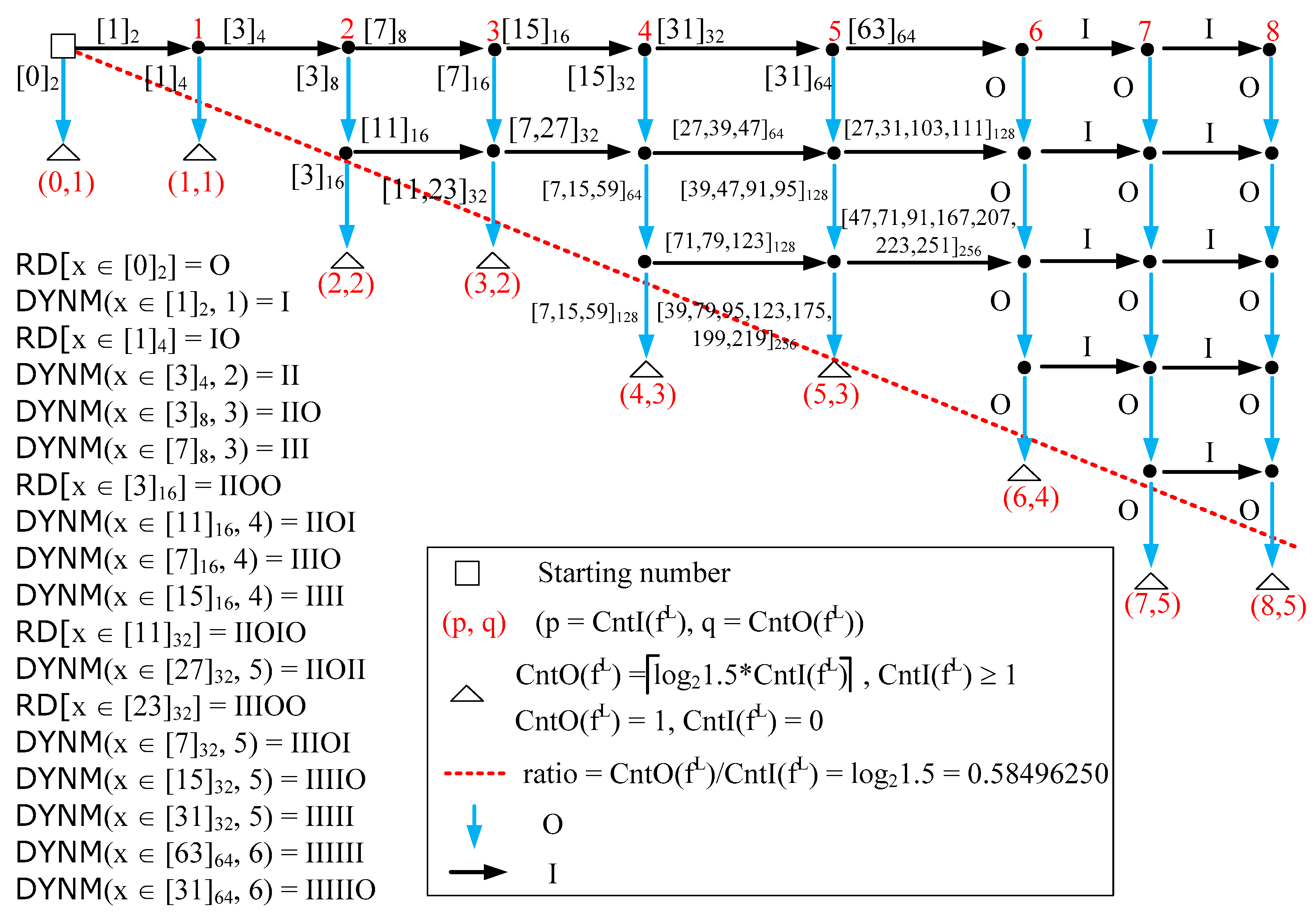
Here we propose to present reduced dynamics as a graph (tree) for better understanding (see
Figure 2), in which there are two types of edges such as I or O. I is represented by black right arrow and O is represented by blue down arrow. Squares represent the starting integer and triangles represent the first transformed integer that is less than starting integer. Thus, a path from square to triangle will be a reduced dynamics. Each edge has a label related to a residue class. RD[
x] represents reduced dynamics of
x. DYNM(
x,
t) represents the first t transforms of
x, in terms of I or O. (
p,
q) is the count of “I” and the count of “O”, respectively. In all reduced dynamics,
q = 1 when
p = 0.
q =
ceil(
λ ×
p) when
p ≥ 1 where
λ = ln(1.5)/ln(2). The slope of ratio line (in red) is λ = ln(1.5)/ln(2) = 0.58496250. All reduced dynamics cuts ration line in the last edge. Above ration line is a partial dynamics. Given a reduced dynamics or a partial dynamics, a residue class can be computed by txpo25.exe. From this graph, we can also observe the partition is regular in half for each edge with the path prolonging.
By this graph, we can easily verify the outputting residue class of txpo25.exe.
For example, txpo25.exe IIOO > txpo25-IIOO. The outputting residue is
x in [
3]
16 (i.e., residue class that is 3 module 16). We can verify whether this reside class is correct or incorrect according to txpo9-c3-3-99999999.
The first line of the file is as follows.
3 11 2 2 1.0000000 --00
3 + 16 = 19. The 5th line of the file is as follows.
19 10011 2 2 1.0000000 --00
Similarly, 35 100011 2 2 1.0000000 --00; 51 110011 2 2 1.0000000 --00.
6. Conclusions
In this paper, we describe the data for studying Collatz dynamics that may result in the final proof of Collatz conjecture. The data come from the output of computer programs, and the source code of the computer programs are also described. Some laws on Collatz reduced dynamics can be observed in the data, and those laws reveal critical properties in the computation such as ratio, period, and residue classes. The results in this paper may also providing heuristics for exploring other mathematical problems in multiple folders such as linear dynamics system, discrete dynamics system, and complexity system.