A High Resolution Dataset of Drought Indices for Spain
Abstract
:1. Introduction
2. Dataset Description
3. Material and Methods
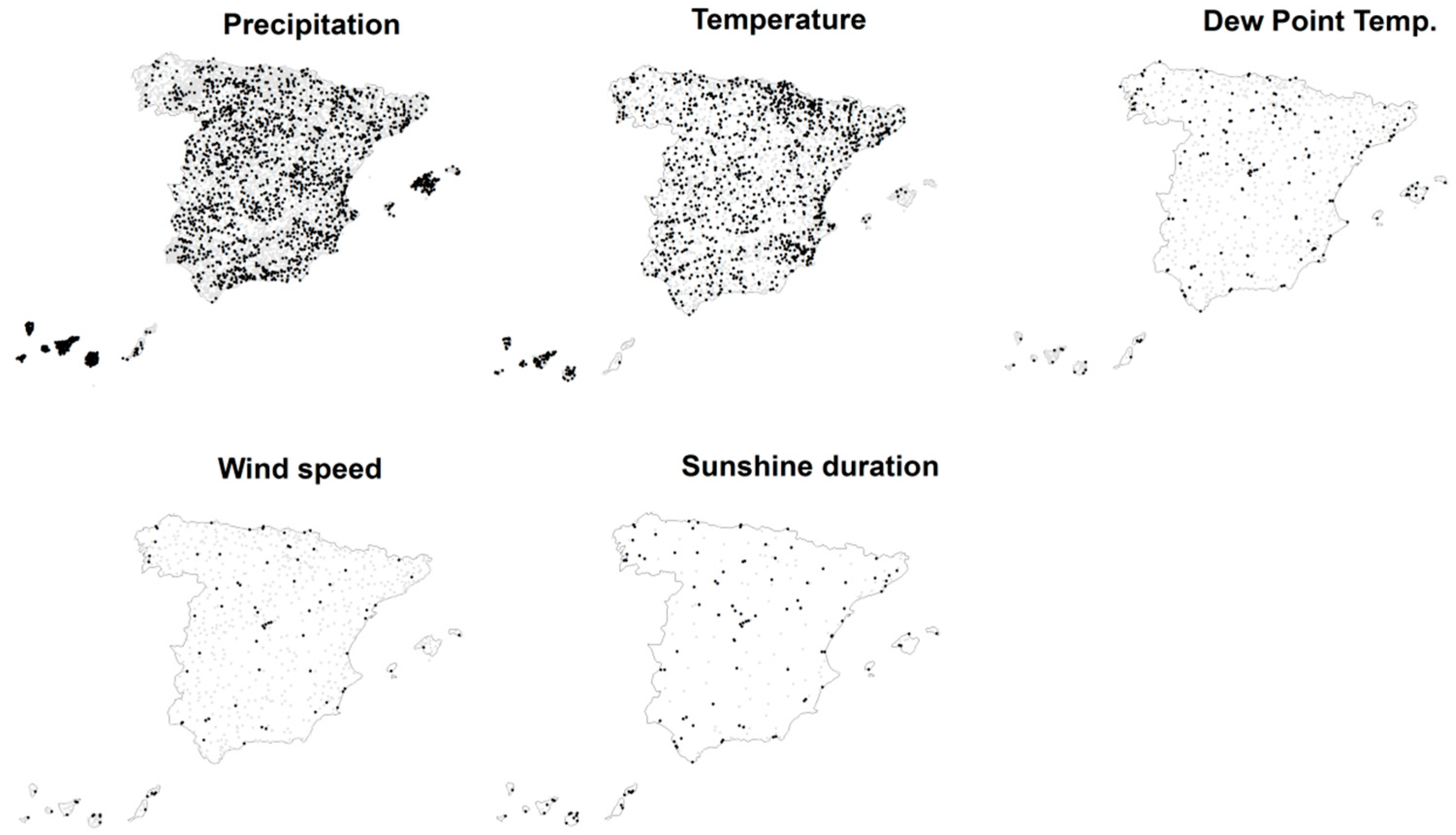
3.1. Data Acquisition and Processing
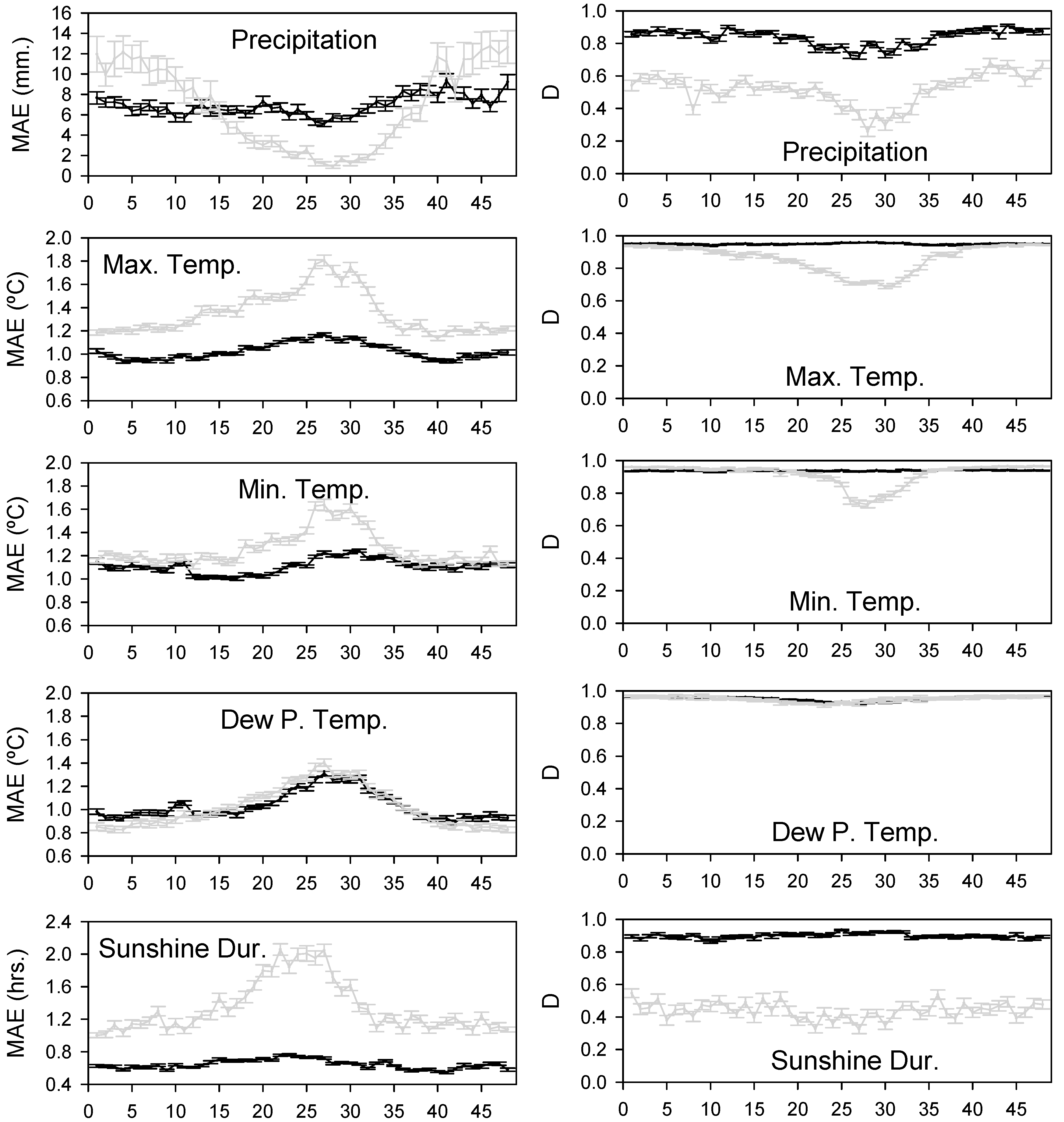
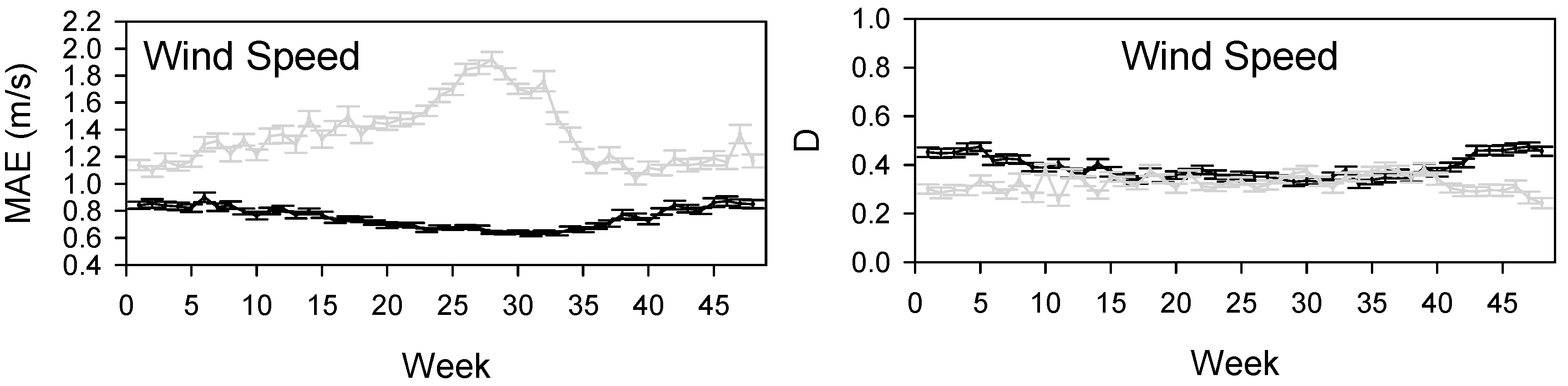
3.2. Climate Gridding and Evaluation
3.3. Calculation of the Reference Evapotranspiration
3.4. Drought Index Calculation
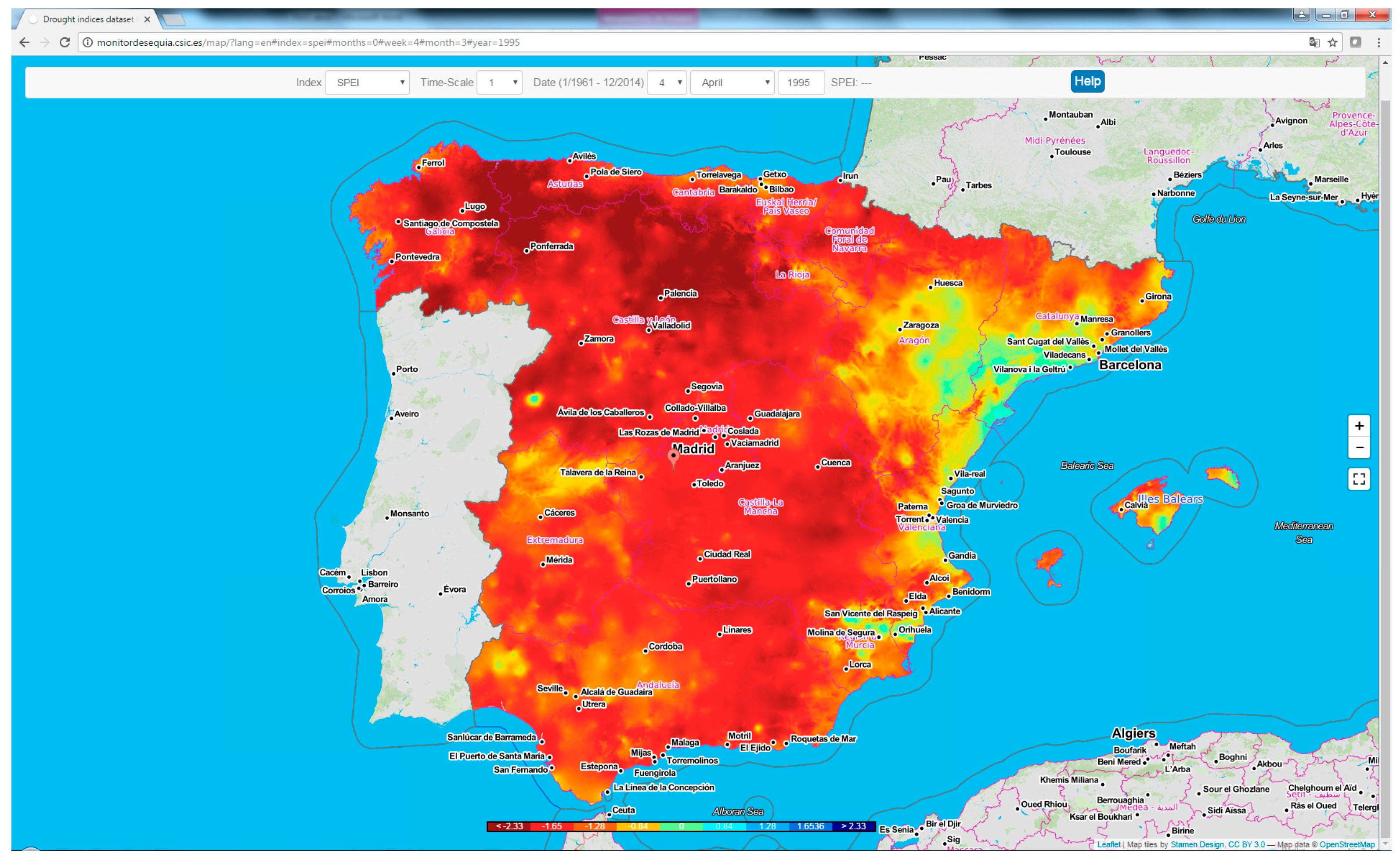
4. Data Use and Application
5. Dataset Availability
Acknowledgements
Author contribution
Conflicts of Interest
References
- Lal, R. Soil degradation by erosion. Land Degrad. Dev. 2001, 12, 519–539. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Tucker, C.J.; Ba, M.B. Desertification, drought and surface vegetation: An example from the west African Sahel. Bull. Am. Meteorol. Soc. 1998, 79, 815–829. [Google Scholar] [CrossRef]
- Pickup, G. Desertification and climate change—The Australian perspective. Clim. Res. 1998, 11, 51–63. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought as a natural hazard: Concepts and definitions. In Drought: A Global Assessment; Routledge: Abingdon, UK, 2000; Volume 1, pp. 3–18. [Google Scholar]
- Cook, B.I.; Miller, R.L.; Seager, R. Amplification of the North American "Dust Bowl" drought through human-induced land degradation. Proc. Natl. Acad. Sci. USA 2009, 106, 4997–5001. [Google Scholar] [CrossRef] [PubMed]
- Vicente-Serrano, S.M.; Zouber, A.; Lasanta, T.; Pueyo, Y. Dryness is accelerating degradation of vulnerable shrublands in semiarid Mediterranean environments. Ecol. Monogr. 2012, 82, 407–428. [Google Scholar] [CrossRef]
- Wilhite, D.A. Drought Assessment, Management and Planning: Theory and Case Studies; Kluwer Academic Publishers: Boston, MA, USA, 1993. [Google Scholar]
- Svoboda, M.; LeCompte, D.; Hayes, M.; Heim, R.; Gleason, K.; Angel, J.; Rippey, B.; Tinker, R.; Palecki, M.; Stooksbury, D.; et al. The drought monitor. Bull. Am. Meteorol. Soc. 2002, 83, 1181–1190. [Google Scholar]
- Heim, R.R., Jr. A review of twentieth-century drought indices used in the United States. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1165. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- McKee, T.B.N.; Doesken, J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multi-scalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index—SPEI. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Cuadrat, J.M. North Atlantic Oscillation control of droughts in Northeast of Spain: Evaluation since A.D. 1600. Clim. Change 2007, 85, 357–379. [Google Scholar] [CrossRef]
- Domínguez-Castro, F.; Ribera, P.; García-Herrera, R.; Cuadrat, J.M.; Moreno, J.M. Assessing extreme droughts in Spain during 1750–1850 from rogation ceremonies. Clim. Past 2012, 8, 705–722. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Spatial and temporal analysis of droughts in the Iberian Peninsula (1910–2000). Hydrol. Sci. J. 2006, 51, 83–97. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Spatial and temporal evolution of precipitation droughts in Spain in the last century. In Adverse Weather in Spain; Martínez, C.C.-L., Rodríguez, F.V., Eds.; WCRP Spanish Committee: Madrid, Spain, 2013; pp. 283–296. [Google Scholar]
- Maia, R.; Vicente-Serrano, S.M. Drought Planning and Management in the Iberian Peninsula. In Drought and Water Crises: Science, Technology and Management Issues; Wilhite, D., Pulwarty, R.S., Eds.; CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Lorenzo-Lacruz, J.; Vicente-Serrano, S.M.; González-Hidalgo, J.C.; López-Moreno, J.I.; Cortesi, N. Hydrological drought response to meteorological drought at various time scales in the Iberian Peninsula. Clim. Res. 2013, 58, 117–131. [Google Scholar] [CrossRef]
- Carnicer, J.; Coll, M.; Ninyerola, M.; Pons, X.; Sánchez, G.; Peñuelas, J. Widespread crown condition decline, food web disruption, and amplified tree mortality with increased climate change type drought. Proc. Natl. Acad. Sci. USA 2011, 108, 1474–1478. [Google Scholar] [CrossRef] [PubMed]
- Camarero, J.J.; Gazol, A.; Sangüesa-Barreda, G.; Oliva, J.; Vicente-Serrano, S.M. To die or not to die: Early warnings of tree dieback in response to a severe drought. J. Ecol. 2015, 103, 44–57. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Evaluating the Impact of Drought Using Remote Sensing In a Mediterranean, Semi-Arid Region. Nat. Hazard. 2007, 40, 173–208. [Google Scholar] [CrossRef]
- Páscoa, P.; Gouveia, C.M.; Russo, A.; Trigo, R.M. The role of drought on wheat yield interannual variability in the Iberian Peninsula from 1929 to 2012. Int. J. Biometeorol. 2017, 61, 439–451. [Google Scholar] [CrossRef] [PubMed]
- Tomas-Burguera, M.; Jimenez, A.; Luna, M.Y.; Morata, A.; Vicente-Serrano, S.M.; González-Hidalgo, J.C.; Beguería, S. Control de Calidad de Siete Variables del Banco Nacional de Datos de AEMET; Olcina Cantos, J., Rico Amorós, A.M., Moltó Mantero, E., Eds.; Universidad de Alicante: Alicante, Spain, 2016; pp. 407–415. [Google Scholar]
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Borrough, P.A.; McDonnell, R.A. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Phillips, D.L.; Dolph, J.; Marks, D. A comparison of geostatistical procedures for spatial analysis of precipitation in mountainous terrain. Agric. Meteorol. 1992, 58, 119–141. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. FAO 1998, 300, D05109. [Google Scholar]
- Itenfisu, D.; Elliott, R. L.; Allen, R.G.; Walter, I.A. Comparison of Reference Evapotranspiration Calculations across a Range of Climates. In Proceedings of the 4th National Irrigation Symposium, Phoenix, AZ, USA, 14–16 November 2000; pp. 216–227. [Google Scholar]
- López-Urrea, R.; Martín de Santa Olalla, F.; Fabeiro, C.; Moratalla, A. Testing evapotranspiration equations using lysimeter observations in a semiarid climate. Agric. Water Manag. 2006, 85, 15–26. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating Palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- World Meteorological Organization. Standardized Precipitation Index User Guide. Available online: http://www.wamis.org/agm/pubs/SPI/WMO_1090_EN.pdf (accessed on 27 June 2017).
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized Precipitation Evapotranspiration Index (SPEI) revisited: Parameter fitting, evapotranspiration models, kernel weighting, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Ma, M.; Ren, L.; Yuan, F.; Jiang, S.; Liu, Y.; Kong, H.; Gong, L. A new standardized Palmer drought index for hydro-meteorological use. Hydrol. Process. 2014, 28, 5645–5661. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S. Comment on “Candidate Distributions for Climatological Drought Indices (SPI and SPEI)” by James H. Stagge et al. Int. J. Clim. 2016, 36, 2120–2131. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.J.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef] [PubMed]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Change 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Dracup, J.A.; Lee, K.S.; Paulson, E.G. On the Statistical Characteristics of Drought Events. Water Resour. Res. 1980, 16, 289–296. [Google Scholar] [CrossRef]
- Santos, J.F.; Portela, M.M.; Pulido-Calvo, I. Regional Frequency Analysis of Droughts in Portugal. Water Resour. Manag. 2011, 25, 3537–3558. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; Gimeno, L.; Eklundh, L.; Giuliani, G.; Weston, D.; El Kenawy, A.; López-Moreno, J.I.; Nieto, R.; Ayenew, T.; et al. Challenges for drought mitigation in Africa: The potential use of geospatial data and drought information systems. Appl. Geogr. 2012, 34, 471–486. [Google Scholar] [CrossRef]
- Merlin, M.; Perot, T.; Perret, S.; Korboulewsky, N.; Vallet, P. Effects of stand composition and tree size on resistance and resilience to drought in sessile oak and Scots pine. For. Ecol. Manag. 2015, 339, 22–33. [Google Scholar] [CrossRef]
- Greenwood, S.; Ruiz-Benito, P.; Martínez-Vilalta, J.; Lloret, F.; Kitzberger, T.; Allen, C.D.; Fensham, R.; Laughlin, D.C.; Kattge, J.; Bönisch, G.; et al. Tree mortality across biomes is promoted by drought intensity, lower wood density and higher specific leaf area. Ecol. Lett. 2017, 20, 539–553. [Google Scholar] [CrossRef] [PubMed]
- Zipper, S.C.; Qiu, J.; Kucharik, C.J. Drought effects on US maize and soybean production: Spatiotemporal patterns and historical changes. Environ. Res. Lett. 2016, 11, 094021. [Google Scholar] [CrossRef]
- Turco, M.; Levin, N.; Tessler, N.; Saaroni, H. Recent changes and relations among drought, vegetation and wildfires in the Eastern Mediterranean: The case of Israel. Glob. Planet. Change 2017, 151, 28–35. [Google Scholar] [CrossRef]
- Russo, A.; Gouveia, C.M.; Páscoa, P.; DaCamara, C.C.; Sousa, P.M.; Trigo, R.M. Assessing the role of drought events on wildfires in the Iberian Peninsula. Agric. For. Meteorol. 2017, 237, 50–59. [Google Scholar] [CrossRef]
- Ivits, E.; Horion, S.; Fensholt, R.; Cherlet, M. Drought footprint on European ecosystems between 1999 and 2010 assessed by remotely sensed vegetation phenology and productivity. Glob. Change Biol. 2014, 20, 581–593. [Google Scholar] [CrossRef] [PubMed]
- Vicente-Serrano, S.M.; Cabello, D.; Tomás-Burguera, M.; Martín-Hernández, N.; Beguería, S.; Azorin-Molina, C.; Kenawy, K.E. Drought variability and land degradation in semiarid regions: Assessment using remote sensing data and drought indices (1982–2011). Remote Sens. 2015, 7, 4391–4423. [Google Scholar] [CrossRef]
- Symeonakis, E.; Calvo-Cases, A.; Arnau-Rosalen, E. Land use change and land degradation in southeastern Mediterranean Spain. Environ. Manag. 2007, 40, 80–94. [Google Scholar] [CrossRef] [PubMed]
- Contador, J.F.L.; Schnabel, S.; Gómez Gutiérrez, A.; Pulido Fernández, M. Mapping sensitivity to land degradation in Extremadura, SW Spain. Land Degrad. Dev. 2009, 20, 129–144. [Google Scholar] [CrossRef]
- Del Barrio, G.; Puigdefabregas, J.; Sanjuan, M.E.; Stellmes, M.; Ruiz, A. Assessment and monitoring of land condition in the Iberian Peninsula, 1989–2000. Remote Sens. Environ. 2010, 114, 1817–1832. [Google Scholar] [CrossRef]
- Gouveia, C.M.; Páscoa, P.; Russo, A.; Trigo, R.M. Land degradation trend assessment over Iberia during 1982–2012. Cuad. Investig. Geogr. 2016, 42, 89–112. [Google Scholar] [CrossRef]
- Martínez-Valderrama, J.; Ibáñez, J.; Del Barrio, G.; Sanjuán, M.E.; Alcalá, F.J.; Martínez-Vicente, S.; Ruiz, A.; Puigdefábregas, J. Present and future of desertification in Spain: Implementation of a surveillance system to prevent land degradation. Sci. Total Environ. 2016, 563, 169–178. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vicente-Serrano, S.M.; Tomas-Burguera, M.; Beguería, S.; Reig, F.; Latorre, B.; Peña-Gallardo, M.; Luna, M.Y.; Morata, A.; González-Hidalgo, J.C. A High Resolution Dataset of Drought Indices for Spain. Data 2017, 2, 22. https://doi.org/10.3390/data2030022
Vicente-Serrano SM, Tomas-Burguera M, Beguería S, Reig F, Latorre B, Peña-Gallardo M, Luna MY, Morata A, González-Hidalgo JC. A High Resolution Dataset of Drought Indices for Spain. Data. 2017; 2(3):22. https://doi.org/10.3390/data2030022
Chicago/Turabian StyleVicente-Serrano, Sergio M., Miquel Tomas-Burguera, Santiago Beguería, Fergus Reig, Borja Latorre, Marina Peña-Gallardo, M. Yolanda Luna, Ana Morata, and José C. González-Hidalgo. 2017. "A High Resolution Dataset of Drought Indices for Spain" Data 2, no. 3: 22. https://doi.org/10.3390/data2030022
APA StyleVicente-Serrano, S. M., Tomas-Burguera, M., Beguería, S., Reig, F., Latorre, B., Peña-Gallardo, M., Luna, M. Y., Morata, A., & González-Hidalgo, J. C. (2017). A High Resolution Dataset of Drought Indices for Spain. Data, 2(3), 22. https://doi.org/10.3390/data2030022






