Abstract
An event is an occurrence that takes place at a specific time and location that can be either weather-related (snowfall), social (crime), natural (earthquake), political (political unrest), or medical (pandemic) in nature. These events do not belong to the “normal” or “usual” spectrum and result in a change in a given situation; thus, their prediction would be very beneficial, both in terms of timely response to them and for their prevention, for example, the prevention of traffic accidents. However, this is currently challenging for researchers, who are called upon to manage and analyze a huge volume of data in order to design applications for predicting events using artificial intelligence and high computing power. Although significant progress has been made in this area, the heterogeneity in the input data that a forecasting application needs to process—in terms of their nature (spatial, temporal, and semantic)—and the corresponding complex dependencies between them constitute the greatest challenge for researchers. For this reason, the initial forecasting applications process data for specific situations, in terms of number and characteristics, while, at the same time, having the possibility to respond to different situations, e.g., an application that predicts a pandemic can also predict a central phenomenon, simply by using different data types. In this work, we present the forecasting applications that have been designed to date. We also present a model for predicting traffic accidents using categorical logic, creating a Knowledge Base using the Resolution algorithm as a proof of concept. We study and analyze all possible scenarios that arise under different conditions. Finally, we implement the traffic accident prediction model using the Prolog language with the corresponding Queries in JPL.
1. Introduction
An event has a specific identity; that is, it involves a specific human activity or the environment. It can be weather-related, social, or medical, and it takes place at a specific time and location. A set of events can be related to a long-term situation, such as the course of business, medical care, political stability, etc. The study of events has a spectrum throughout human life and the environment. There has been particular interest in studying events in recent decades, particularly in terms of their detection and prediction [1]. Predicting events can have enormous benefits. By predicting events, a person can act promptly and effectively to manage a difficult situation and take necessary preventive measures, such as dealing with and avoiding a traffic accident, illness, crime, or even a threat to one’s home [2]. Until a few years ago, the mere thought of predicting events was prohibitive because of the heterogeneity in and interrelationship between events and their various causes, as well as the resources that researchers had at their disposal [3]. However, in the last decade, because of the progress in artificial intelligence and the development of computing power and big data, researchers can now predict events from big data using various methodologies. By studying previous events, they can now design models that can predict future events through observation of the characteristics of past events and, with the valuable help of machine learning and spatiotemporal data mining, extract the patterns within. Spatiotemporal data differ from the spatial data on which computational approaches are developed because the sources of these data have been available for many decades and have dynamic characteristics since they are constantly modified in real time. Spatiotemporal data include trajectory data, reference point data, Raster data, and spatiotemporal event-type data (which we will use in this study) [4,5]. Several problems arise when predicting events by studying and analyzing big data. The following are the most important:
- (1)
- An event depends on time, space, and its nature, intensity, and duration. With each change in these heterogeneous but interdependent parameters, a different event arises. Because of the variety of results/events, determining the label of each result requires automatic methods, which introduce errors during the coding of events; thus, we cannot guarantee the quality of the label. It is difficult to determine the criteria by which a prediction can be characterized as false or true (valid or not) [6].
- (2)
- Because of the interdependence of events, most of the time, one event indirectly or directly affects another or is the cause of another. Consequently, many and complex dependencies appear between the predicted events during the forecasting process, creating a problem in terms of examining and evaluating these correlations [7,8].
Event prediction requires the study and analysis of data on past events to derive the desired predictions; however, events are dynamic and are constantly changing, making monitoring them in a training model problematic; for example, a disease can spread to affect 20% of a population at one point in time, and then, very soon after, cover 70% of the population [9]. Consequently, the distribution of input data, as well as their sources, dynamically changes in real time. This requires trained learning models to be constantly upgraded and updated, which costs both time and money. Additional weaknesses include the prediction of rare events, the inability to recover lost input data, the inability to make long-term predictions, the inability to separate useful from scattered and irrelevant input data, and the management of uncertainty during prediction. To address the challenges associated with event prediction, researchers have conducted targeted experiments using specific and controlled input data. These experiments aim to isolate and better understand the complexities inherent in predictive modeling [10]. In recent years, substantial research has been devoted to overcoming these obstacles, both in refining the methodologies used for event prediction and expanding their practical applications.
Despite this progress, event prediction remains in its infancy compared to other scientific domains. Most techniques developed thus far are limited in scope, having been tailored to narrowly defined datasets and conditions. This specificity significantly constrains their generalizability and broader applicability.
One of the core challenges lies in the sensitivity of prediction outcomes to variations in input data—particularly in terms of accuracy and the timing of data acquisition. Even minor deviations in these parameters can produce significantly different results, hindering efforts to establish standardized forecasting methodologies. The absence of widely accepted benchmarks or identified bottlenecks further impedes progress, leaving the field fragmented and underdeveloped.
This study aims to systematically document the existing approaches to event prediction using big data, with a particular emphasis on spatiotemporal (st) data. We begin by categorizing predictive methods based on the nature of the problems they address and the primary data dimension they prioritize—namely, time, location, or semantics. These categories are then compared to highlight the strengths and limitations of each.
The resulting classification is intended to support researchers in selecting the most suitable forecasting techniques for specific use cases and to help define the levels of reporting and abstraction that future applications might require. We also propose a framework for standardizing the evaluation of forecasting methods, acknowledging the wide variability in prediction outcomes that depend on when, where, and under what conditions input data are collected [11].
Finally, this study presents a case study focused on traffic accident prediction, formulated under the following conditions:
“A driver is operating a vehicle on a roadway while under the influence of a significant amount of alcohol—exceeding the legal blood alcohol concentration limit of 0.25%. The environmental conditions are adverse, characterized by heavy rainfall at a rate of 50 mm/s. The route the driver intends to follow includes a sharp turn. Furthermore, the journey takes place during late-night hours (between 12:00 a.m. and 5:00 a.m.), resulting in low visibility due to darkness. Compounding these risks, the driver is traveling at a high speed, exceeding 100 km/h. The event predicted—and demonstrated in this study—is the occurrence of a traffic accident under these combined conditions. It is important to note that the threshold values assigned to the variables (e.g., alcohol level, rainfall intensity, speed) are indicative and may be adjusted to reflect the specific requirements of different scenarios or environments, depending on the problem under investigation”.
To enable the prediction of traffic accidents, this study employs categorical logic to construct a knowledge base, which is then evaluated using the Resolution algorithm. All potential scenarios that may emerge from the predicted situation are systematically examined by varying the values of the relevant descriptive variables. The predicted event scenario is subsequently implemented in a Prolog program, with associated queries executed through the Java-Prolog Library (JPL). This represents a novel approach that, to the best of our knowledge, has not yet been explored in prior research.
This study is structured as follows. Section 2 reviews the relevant literature in the field of event prediction. Section 3 explores various domains where forecasting techniques have been applied. Section 4 delves into specific methodologies for event prediction, while Section 5 introduces categorical logic as a formal framework for modeling such problems. In Section 6, we present the proposed traffic accident prediction model. We begin by formulating the problem using categorical logic and constructing a corresponding knowledge base (Section 6.1). We then demonstrate the logical validity of the predicted event using the Resolution algorithm (Section 6.2). To explore the model’s robustness, we extract all possible scenarios by varying the input variables across their full range of combinations (Section 6.3). The implementation phase follows in Section 6.4, where the knowledge base is encoded in the Prolog programming language. Section 6.5 outlines the execution of related queries using the Java-Prolog Library (JPL) to facilitate user interaction through a dynamic interface. Finally, Section 7 discusses open challenges and outlines future directions for research in event prediction. This study concludes with a summary of findings related to traffic accident forecasting, including a brief overview of the real-time application we developed. This application utilizes a live-updated map interface to feed variable values into the knowledge base, enabling continuous prediction updates under actual driving conditions.
2. Related Research
This section identifies and discusses three major categories of research related to event prediction using big data. These categories are defined by (i) the methods employed for detecting events, (ii) the nature and structure of the input data used in predictive models, and (iii) the types of outcomes targeted, often specific to particular application domains [12].
Early research primarily concentrated on event detection, which involves identifying historical or ongoing events rather than forecasting future occurrences. The objective of detection is to extract recurring patterns, identify anomalies, and group related observations [13]. For example, many modern applications utilize interactive maps to detect and log extreme or unusual events in real time [14]. Over the past decade, significant advancements have been made in this area, especially in fields such as social media analysis, where event detection techniques are used to uncover emergent patterns and disruptions [15].
In predictive modeling, the analysis process must adapt continuously to fluctuations in input data and changes in the associated dependent variable. This dependent variable, or target, can take the form of a scalar value, a vector, or a structured object—representing anything from economic activity or geographic regions to emotional sentiment. Notably, the target does not always pertain to future states; rather, its type determines the analytical approach. Depending on the nature of the prediction, outputs may be structured temporally, spatially, or semantically. These dimensions help to classify the predictive models and their use in various applications.
In parallel, several methods have been developed specifically for spatiotemporal event prediction, incorporating temporally and spatially dependent variables to improve predictive accuracy [16,17].
Considerable research attention has focused on domain-specific event forecasting. These include social phenomena, such as civil unrest; environmental conditions, like droughts and floods; renewable energy trends, including the forecasting of peak solar or wind prices at specific locations; and business-critical events, such as organizational failures or bankruptcies [18]. Despite growing interest, researchers face persistent and often complex challenges in modeling such events because of the dynamic, multidimensional nature of the data involved.
2.1. Time, Location, and Semantics Prediction
To predict future events by specifying their time, location, and semantic characteristics, researchers have developed a range of techniques. These approaches generally fall into three categories, i.e., (i) system-based, (ii) model-based, and (iii) tensor-based methods, which are more specifically defined as follows:
- System-based techniques rely on integrated systems that employ fusion methods to forecast future events using human-derived predictive inputs. One of the primary challenges in these approaches is the considerable variability in individual predictive abilities, which often stems from differences in cognitive background and domain expertise. To mitigate this, some systems group participants based on similar competencies and then aggregate their predictions to improve overall accuracy. An alternative system-based method involves synthesizing inputs from multiple individual predictors. In this framework, contributors assign a confidence value to each prediction—typically represented as a virtual “coupon”—which quantifies their certainty regarding the outcome. These predictions are then traded in a simulated market environment where participants “buy” or “sell” outcomes. This mechanism incentivizes accurate predictions by rewarding correct outcomes and penalizing incorrect ones, thereby reinforcing reliability and accountability. Some system-based approaches are specifically designed to detect “programmed” future events—those that are anticipated based on identifiable trends or indicators extracted from structured or unstructured data sources, such as social media content or online news. These methods often leverage natural language processing (NLP) and are typically implemented through a four-stage pipeline. Stage 1 involves content filtering, where texts related to the target event are selected using either supervised methods (e.g., text classifiers) or unsupervised techniques (e.g., keyword-based filtering). Stage 2 focuses on time expression identification, which entails detecting future-oriented temporal references in the text using linguistic rules or NLP parsing tools. Stage 3 extracts future reference expressions, which serve as the core indicators of potential upcoming events. These expressions are identified using regular expressions or classification algorithms. Stage 4 addresses location identification, which is particularly challenging because of the inconsistency and noise in spatial references. To improve precision, geocoding techniques are employed. Spatial data may be drawn from article metadata, author information, or contextual clues, and the spatial scope is refined either through geometric boundaries or by logically merging similar location expressions to reduce redundancy and error [19,20,21].
- Model-based approaches rely on predictive systems that integrate and compile multiple models to forecast future events. These systems are capable of determining not only the time, location, and semantic context of an event but also its frequency and type. A prominent example is the EMBERS system [22], which operates primarily in the digital domain and analyzes diverse data sources to anticipate civil unrest and other events of interest. EMBERS has demonstrated high levels of both prediction accuracy and recall, thereby enhancing user trust in its outputs. The methodology underpinning such systems typically begins with the independent evaluation of each predictive model, emphasizing accuracy regardless of recall. Once all candidate models are generated, their outputs are combined using fusion techniques—such as Bayesian fusion—to exploit their complementary strengths. This fusion process significantly improves recall, enabling the system to detect a broader range of potential outcomes. An illustrative example of this approach is the Cardon system, which also leverages multiple predictive models and combines their outputs to improve both the reliability and comprehensiveness of event prediction [23,24,25].
- Tensor-based approaches represent data as multidimensional arrays—or tensors—that encode information across three primary dimensions: time, location, and semantics. These tensors are then decomposed into lower-order matrices, each of which captures latent patterns or unresolved relationships within a specific dimension. This decomposition facilitates the extraction of meaningful features from complex, high-dimensional data. To enable forecasting, the original tensor is extended to cover future time intervals using various extrapolation techniques. One such method involves extending the time dimension by multiplying it with matrices representing other contextual dimensions, thereby generating a new tensor that projects into the future. An alternative approach introduces blank entries—corresponding to future values—into the initial tensor. These missing values are then estimated using tensor completion or integration techniques, ultimately producing predictions that reflect plausible future events [26].
2.2. Event Prediction Evaluation
Event prediction evaluation seeks to determine whether the set of predicted events, denoted as Y′, accurately corresponds to and represents the actual set of observed events, Y. The evaluation techniques typically produce outputs in the form of entities characterized by multiple attributes, such as time, location, and type. However, before a meaningful assessment of a prediction model’s performance can be made, it is essential to establish prediction pairs—each consisting of a predicted event and its corresponding real-world counterpart. These pairs must be carefully labeled and matched to ensure that both prediction accuracy and error rates are reliably measured and interpreted [27,28,29].
2.3. The Techniques That Researchers Have Followed to Date
Assignment of Predicted to Real Events:
(i) One common method for aligning predicted events with actual occurrences is prefix matching. In this approach, a predicted event is considered a match to a real event when there is a high degree of similarity across key characteristics, particularly time and location. This method typically assumes that each predicted event corresponds to a single real event that occurs at a specific point in time and space. For example, a predicted event scheduled for 23 September 2025 (time/t) in Heraklion (location/l) would only be matched to a real event that actually takes place on that exact date and in that specific location [30].
(ii) Optimized matching, when a prediction cannot perfectly match any real event, the link is established between the predicted event and the real one that most closely resembles it in terms of characteristic similarity, with a corresponding degree of inaccuracy and a reduction in the technique’s overall precision. The comparison between characteristics is performed using either Euclidean distance or another appropriate metric to measure the distance between the attributes of the compared events. After these distances are calculated, the pair with the smallest distance across characteristics is selected. For example, if a predicted event is “at 10 a.m., on 20 September 2025” (t), “Heraklion, Crete, Greece” (l), “flood” (semantics/s), and the two actual events are (1) “at 10 a.m. on 20 September 2025” (t), “Heraklion, Crete, Greece” (l), “snowfall” (s), and (2) “20 September 2025” (t), “Heraklion, Crete, Greece” (l), “strike” (semantics), then the matching will be made with the most similar of the two actual events—namely, the first one [13].
However, researchers today commonly adopt the optimized matching technique to establish pairs between predicted and actual events, enabling subsequent comparison to evaluate the performance quality of the event prediction method.
The effectiveness of a prediction technique is assessed using two key indicators: (1) goodness of matching, which measures the percentage of predicted events that have been successfully matched with actual events [31], and (2) qualitative correspondence, which assesses how closely each predicted event aligns with its corresponding actual event among the established pairs [32].
2.4. Event Forecasting Techniques
Event forecasting techniques can be categorized into distinct types and subtypes, depending on the nature of the output produced by the forecasting method. This output is typically defined by three key dimensions: time, location, and the semantic nature of the predicted event. Forecasting methods are further classified according to their primary objective—whether the aim is to predict the timing, location, nature of the event, or some combination of these factors. The corresponding techniques applied in each case are presented in the following subsections.
2.4.1. Time Forecasting Techniques
Time forecasting techniques aim to determine the precise moment at which an event will occur [11]. These techniques are categorized as follows:
- Event Forecasting: This method focuses on determining whether a specific event will occur within a given time frame. If the event is predicted to occur, it is labeled as a positive class; if not, it falls under the negative class. This approach effectively constitutes a binary classification of future events.
- Anomaly Detection: This technique involves identifying anomalies in historical data to learn the characteristics of typical, or “normal,” patterns—those under which an event is not expected to occur. The distance of a new event’s data from these normal patterns is then measured; a significant deviation suggests the potential occurrence of a future event [33].
- Discrete Time Prediction: In addition to predicting whether an event will occur, this approach aims to estimate the approximate time of occurrence [34]. Time is initially segmented into discrete intervals (e.g., hours, days, months), and the goal is to identify the interval during which the event is most likely to happen. These methods are further divided into the following approaches:
- ○
- Direct approaches, which estimate the specific interval or ordinal scale (e.g., immediate, short-term, or long-term future) during which the event may occur. This is typically achieved using regression or ordinal regression techniques to determine either exact time boundaries or ranked time categories.
- ○
- Indirect approaches, which first align the input data temporally and then apply autoregressive models to historical time series in order to forecast future time series. Once these future sequences are predicted, the presence of events is detected using methods such as burst detection, change detection, or supervised learning. In supervised techniques, researchers infer future event patterns based on historical observations, with or without labeled data. If no time series is available, labeled training data can still be used to extract the relevant predictive patterns.
- Continuous Time Prediction: This method addresses the challenges of forecasting events on a continuous time scale. The primary difficulty lies in achieving the required time resolution, which often demands extremely high computational power. Moreover, the process is highly sensitive to the precision of time prediction, making it difficult and time-consuming, particularly during model training and synchronization phases [35].
To mitigate these challenges, researchers have proposed simplified modeling approaches, including the following:
- Simple Regression [36];
- Point Process Models [37].
2.4.2. Location Prediction Techniques
Location prediction techniques aim to determine the geographic position where an event is likely to occur. The predicted location can be represented in two primary forms: raster-based or point-based.
When the event is expected to occur over a broad spatial extent—such as a general region rather than a specific coordinate—the output is typically represented as a raster. A raster is a spatial grid composed of individual cells, each corresponding to a portion of the target area. This format is particularly useful for forecasting events with diffuse or large-scale spatial characteristics.
Conversely, when the event is localized and confined to a very small area—such as at discrete points or network nodes—the forecast output is defined as a point. This point-based representation is more appropriate for predicting events with precise geographic locations [38].
2.4.3. Semantic Prediction Techniques
Semantic prediction focuses not on determining when or where an event will occur but rather on forecasting its description, subject, or other semantic attributes. In these approaches, the goal is to predict the nature or category of an event—its meaning—rather than its temporal or spatial dimensions.
Unlike time or location prediction methods that often rely on numerical input, semantic prediction methods may utilize a variety of data formats, including symbolic representations and natural language text. As a result, the choice of technique is closely tied to the nature of the input data.
Three primary data types are commonly used in semantic prediction:
- Rule-based data, where prediction is driven by association mining or the identification of logical patterns derived from historical data. These rules capture relationships that help anticipate future events based on past occurrences.
- Sequential data, in which events are assumed to follow a temporal chain or order. By analyzing these sequences, it becomes possible to predict future events by extending the logical progression of prior occurrences.
- Graph-based data, which build on sequential modeling by representing event relationships as graphs. This approach captures complex dependencies and interconnections among events by modeling them as nodes and edges within a structured graph [39].
2.4.4. Multifaceted Prediction Techniques
Multifaceted prediction refers to forecasting approaches that simultaneously consider multiple dimensions of an event—specifically, its time, location, and semantic content. These methods aim to provide a more comprehensive understanding of future events by integrating all relevant aspects of their occurrence.
There are three primary approaches within this framework, based on how these dimensions are weighted and combined:
- One approach treats time and semantics as equally significant predictive factors.
- Another approach emphasizes time and location.
- The most comprehensive approach considers time, location, and semantics together, offering a fully integrated prediction model [40,41,42].
3. Fields in Which Event Prediction Techniques Are Applied
Event prediction techniques are now applied across a wide range of domains. In healthcare, they are used to forecast the onset and spread of diseases, particularly in the context of epidemics. In multimedia analysis, data from video, audio, or text sources are employed to predict actions in sports events or to anticipate future news developments. In the field of human mobility and transportation, these techniques help forecast both individual and group movements [43,44].
Additionally, event prediction has demonstrated high accuracy in political forecasting, including the prediction of social unrest and conflicts, primarily by leveraging data from social media platforms. In environmental applications, it is used to anticipate natural disasters, such as floods or earthquakes. In the business sector, prediction models are utilized to identify potential bankruptcies and to forecast consumer purchasing behavior within specific populations [45]. Moreover, these techniques are applied in security and public safety contexts to predict delinquent behavior, such as robbery, crime, or even terrorist attacks [27,46].
4. Event Prediction Problem
An event is defined as an occurrence that takes place at a specific time and location and is characterized by a distinct semantic identity—for example, a traffic accident. Formally, an event can be represented as:
where t denotes the time of the event, l represents the location, and s describes the semantic nature or type of the event. The location l can be specified at various levels of granularity: it may refer to a broad area, such as a neighborhood or city, or to an exact point defined by geographic coordinates. Similarly, the time parameter t can be expressed as either a precise timestamp or a broader time interval, for example, a 24-hour period. The semantic parameter s may encompass any descriptive characteristic that helps define the nature of the event. Using this modeling framework, an example event might be expressed as “1:00 p.m. on 12 May 2024” (t), “Heraklion, Crete, Greece” (l), “heavy rain” (s)—where the values represent time, location, and semantics, respectively. In an event prediction system, the inputs used to forecast such events are referred to as indicators (denoted as X). These indicators contain various types of information relevant to the potential occurrence of an event. However, not all inputs are equally useful; in addition to critical predictive features, some may include irrelevant or noisy information [47]. This relationship is typically formalized as:
In this context, let L represent the location, T the time, and F a set of features or information attributes that are unrelated to time or location. If we define the current moment as tnow and distinguish between past and future times, we can denote:
Thus, the event prediction problem can be formulated as follows. Given a set of event indicators:
and a corresponding set of historical event data Y0:
the goal of event prediction is to derive a set of forecasted future events, denoted as Yˆ. This formulation defines prediction as the process of generating future event instances Yˆ based on prior indicator data and historical event records:
such that for each predicted future event yˆ = (t, l, s) ∈ Yˆ, where t > tnow.
y = (t, l, s)
X ⊆ T × L × F
T − ≡ {t |t ≤ tnow, t ∈ T} and T+ ≡ {t |t > tnow, t ∈ T}.
X ⊆ T − × L × F
Y0 ⊆ T − × L × S,
Yˆ ⊆ T + × L × S,
It is important to note that different prediction methods assign varying levels of emphasis to the three core parameters—time, location, and semantic nature—depending on the specific requirements of the forecasting problem. For instance, in modeling the progression of an individual’s illness, the location of the patient may be of minimal or no relevance, whereas the duration and severity of the illness are critical factors [48]. In contrast, when predicting the spread of an infectious disease, the location becomes a primary variable of concern, with time and semantics playing a comparatively lesser role.
As a result, the evaluation criteria used across forecasting methods differ significantly. This variation stems from the distinct weighting assigned to each parameter—time, place, and nature of the event—in alignment with the goals of the specific application domain.
To effectively represent both temporal and spatial aspects—along with a variety of additional characteristics that accompany forecasted events—researchers increasingly turn to categorical logic. This approach offers a more abstract and algebraic representation of knowledge, closely aligned with human reasoning, in contrast to traditional classical logic, which tends to be rigid and strictly defined [49].
5. Categorical Logic in the Service of Event Prediction
Categorical logic, as the name implies, is a form of logic developed within the framework of category theory. It is a branch of algebraic logic, offering a structured and abstract representation of logical reasoning. At its core, categorical logic captures the way humans intuitively approach and interpret the world, but within an algebraic formalism.
Much like algebraic logic encodes propositional logic—whether classical, intuitionistic, or otherwise—through structures such as Lindenbaum–Tarski algebras (e.g., Boolean algebras, Heyting algebras), categorical logic generalizes this concept to first-order and higher-order logics. These logics are encoded in categories equipped with additional structural properties, such as Boolean categories and Heyting categories. From a technical standpoint, categorical logic can be seen as a generalization of the algebraic encoding of propositional logic, extending it into more expressive logical systems.
Unlike propositional logic, categorical logic goes beyond mere predicates to also express relations between predicates, particularly in the form of functions. A key distinction lies in its incorporation of quantifiers—the existential quantifier (∃) and the universal quantifier (∀). The existential quantifier asserts the existence of an object satisfying a certain condition, while the universal quantifier asserts that a condition holds for all objects within the domain of discourse.
In the context of prediction modeling, categorical logic consists of facts that define the properties of objects, which are the central entities in a prediction problem. For example, in the context of traffic accident prediction, these objects might include the driver(X), the road(Y), time(T), the vehicle speed (Tax), and the rain condition (B). The logic also includes rules or predicates that express properties or relationships between these objects—such as heavy_rain(B), if B > “value”.
Categorical logic enables connections to other foundational concepts, such as intuitive reasoning, recursive functions, and completeness theorems for various logical systems. More than just a technical tool, categorical logic provides a framework that reveals fundamental properties and conceptual insights about the structures it encodes. Many results derived from categorical techniques carry meaningful philosophical implications, offering a deeper understanding of logic beyond classical formalisms.
While categorical logic is firmly grounded in mathematics, its abstraction, flexibility, and intuitive alignment with human reasoning make it a particularly powerful tool for modeling and predicting real-world events. Researchers increasingly apply it to describe and reason about future events, establishing their logical existence using mechanisms such as the Resolution algorithm [1,49,50,51].
The next section presents a case study of future event prediction—specifically, a traffic accident—first formulated in natural language and then translated into categorical logic, followed by a formal proof of the event’s existence using the Resolution algorithm.
6. Problem Statement
Today, traffic accidents remain a leading cause of injury and death worldwide, often resulting from human error, adverse weather conditions, or other environmental factors. In countries such as Greece, the situation is particularly severe, with a significant number of fatalities each year—many involving young drivers. Despite growing awareness and legislative efforts, the number of traffic-related deaths remains alarmingly high.
Computer Science, through advancements in predictive learning and event forecasting, offers promising tools to help address this critical public health issue. Predictive models can be developed to anticipate the likelihood of traffic accidents, thereby enabling timely interventions that may help prevent them altogether.
Although driving under the influence of alcohol, speeding, and other reckless behaviors are prohibited by law, these regulations are not always observed. This disregard for traffic laws endangers not only the drivers themselves but also others on the road. In Greece, the high rate of fatalities among young drivers under the influence of alcohol is one of the country’s most pressing safety concerns.
While authorities have implemented various countermeasures—including increased police patrols, stricter fines, license revocation, and public awareness campaigns delivered through schools, television, news media, and social networks—the problem persists. These efforts, though important, are not always sufficient to prevent tragic outcomes, especially when drivers are incapable of making rational decisions in critical moments.
In this context, science—particularly data-driven methods and intelligent systems—can play a vital role. By supporting decision-making in real time, predictive systems can act when the driver cannot, enhancing safety for all road users.
This paper proposes the development of a traffic accident prediction model designed not only to forecast the likelihood of an accident but also to actively encourage safer driving behavior. The system aims to warn drivers about imminent dangers and promote preventive action, ultimately contributing to the reduction of accidents and saving lives.
The problem statement is as follows:
“Consider a scenario (Problem 1) in which a driver X is operating a vehicle A on a roadway Y, traveling at a speed Tax at a given time T. The overall risk associated with the journey is influenced by several factors. One such factor is the configuration of the road itself, particularly whether it includes sharp turns, denoted as Ap_str, which increase the likelihood of losing control. Additionally, the specific route chosen by the driver may introduce varying degrees of difficulty or danger. Weather conditions also play a crucial role; for example, heavy rainfall can create slippery surfaces, significantly compromising vehicle stability and braking capability. The driver’s sobriety further affects safety, as heavy alcohol consumption can impair decision-making, reduce situational awareness, and slow reflexes—all of which are critical for safe driving. Moreover, if the driver is traveling at high speed (e.g., ≥100 km/h), the severity and probability of an accident increase substantially. This risk is compounded if the journey takes place at night, where reduced visibility due to darkness further impairs the driver’s ability to perceive hazards in time. Taken together, these conditions form a high-risk environment that can potentially result in a traffic accident (at).”
In this study, we aim to address the problem of traffic accident prediction by employing categorical logic and constructing a dedicated knowledge base [51] (see Section 6.1). We will demonstrate the existence of the predicted event—a traffic accident—through formal proof using the Resolution algorithm [52] (Section 6.2). Subsequently, we generate and analyze all possible scenarios that may arise from the initial problem by assigning different values to each of the variables that define the context, exploring every possible combination (Section 6.3).
In addition, we implement this predictive framework using the Prolog programming language (Section 6.4) and integrate it with a user interface via the Java-Prolog Library (JPL) (Section 6.5). To the best of our knowledge, this integrated and logic-based approach to traffic accident prediction has not been previously undertaken in the existing research.
6.1. Knowledge Base
A verbal description (text format) of the real-world driving conditions outlined in Problem 1 is provided below. These conditions are formally represented through a set of predicates within the corresponding knowledge base:
“A driver (driver(X)) is driving a car (car(A), driving(X,A)) on a road (road(Y)) under the influence of a large amount of alcohol (alcohol(Al), Al >= 1, the alcohol, the amount of alcohol is Al and the limit in the human body is 0.25%). The driver has bad driving behavior (bdb(X,Al)), the weather conditions are bad, it is raining heavily (rain(B), heavy_rain(B), B >= 50, with B the amount of rain, is 50 mm/s of rain) and the road is slippery (sl(Y,B)). On the route that the driver wishes to follow, there is a turn (turn(F)), a sharp turn (sharp_turn(As), where As = ‘yes’ means yes, there is a sharp turn, so the turn F is a sharp turn, is(F,As), and have(Y,F,As), the road Y has a sharp turn), it is late at night (time(T), night(T), if T >= 0 and T =< 5, time is between 0 a.m. and 5 a.m.), so it is dark and the driver’s visibility is reduced (rv(X,T)). Finally, the driver is running with high speed (speed(Tax) with Tax >= 100, the speed is over 100 km/h, so the driver is running: run(X,Tax)). The limits of the values given to the variables are indicative and can be changed on a case-by-case basis to satisfy the conditions of another environment, depending on the problem that the user is called upon to face. The predicted event, which we wish to prove in this work, is that a traffic accident will occur (at(X,Y,A,F,As,Tax,B,Al,T))”.
Then, the extraction of facts and predicates is carried out.
The events include the following:
1. driver(X) (some driver);
2. road(Y) (some road);
3. car(A) (some car);
4. speed(Tax) (some speed);
5. time(T) (at some time);
6. turn(F) (some turn);
7. sharp_turn(As) (is sharp);
8. alcohol(Al) (amount of alcohol);
9. rain(B) (some rain);
10. Tax>=100 (high speed);
11. B>=50 (large amount of rain);
12. As=‘yes’ (is sharp);
13. Al>=1 (large amount of alcohol);
14. T>=0, T=<55 (time interval between 0 and 5 in the morning).
The rules are as follows: “Every driver X, drives a car A” (rule formulation in natural language).
driver(X),car(A) → driving(X,A) (rule formulation in categorical logic).
Using Morgan’s rule ¬(P^Q) ↔ ¬P ˅ ¬Q and the equivalence P → Q ↔ ¬P˅Q
¬driver(X)˅¬car(A)˅driving(X,A) (normal disjunctive form, where “^” is the logical and, “˅” is the logical or, “→” is the implication, “↔” is the equivalence, and ” ¬” is the logical not);
\+driver(X);\+car(A);driving(X,A) (rule execution in Prolog, where “\+” is the logical not, “;” is the logical or, “,” is the logical and, and “:-” is the implication).
- “All drivers drive at some speed, and if this speed is high, then the driver is running”:
driver(X),speed(Tax),Tax>=0 → running(X,Tax);
¬driver(X)˅¬speed(Tax)˅¬(Tax>=100)˅ running(X,Tax);
\+driver(X);\+speed(Tax);\+(Tax>=100); running(X,Tax).
- 2.
- “Between 0 and 5 a.m., it is night”:
time(T),T>=0,T=<5 → night(T);
¬time(T)˅¬(T>=0T=<5)˅night(T);
\+time(T);\+(T>=0T=<5);night(T).
- 3.
- “A turn F is sharp”:
turn(F),sharp_turn(As),As=‘yes’ → is(F,As);
¬turn(F)˅¬sharp_turn(As)˅¬(As=‘yes’)˅is(F,As);
\+turn(F);\+sharp_turn(As);\+(As=‘yes’);is(F,As).
- 4.
- “A Y road has a turn F and is sharp (As=‘yes’)”:
road(Y),turn(F),is(F,As) → have(Y,F,As);
¬road(Y)˅¬turn(F)˅¬is(F,As)˅have(Y,F,As);
\+road(Y);\+turn(F);\+is(F,As);have(Y,F,As).
- 5.
- “A driver X has consumed a large amount of alcohol (Al>=1) and has bad driving behavior (bdb)”:
driver(X),alcohol(Al),Al>=1 → bdb(X,Al);
¬driver(X)˅¬alcohol(Al)˅¬(Al>=1)˅bdb(X,Al);
\+driver(X);\+alcohol(Al);\+(Al>=1);bdb(X,Al).
- 6.
- “There is rain (rain), and it is heavy (heavy_rain with B>=50)”:
rain(B),B>=50 → heavy_rain(B);
¬rain(B)˅¬(B>=50)˅heavy_rain(B);
\+rain(B);\+(B>=50);heavy_rain(B).
- 7.
- “There is reduced visibility (rv) due to night (night)”:
driver(X),night(T) → rv(X,T);
¬driver(X)˅¬night(T)˅rv(X,T);
\+driver(X);\+night(T);rv(X,T).
- 8.
- “There is slipperiness (sl) on the road Y due to heavy rain (heavy_rain)”:
road(Y),heavy_rain(B) → sl(Y,B);
¬road(Y)˅¬heavy_rain(B)˅sl(Y,B);
\+road(Y);\+heavy_rain(B);sl(Y,B).
- 9.
- “When a driver X is driving a car A with bad driving behavior (bdb) and there is a sharp turn (have(Y,F,As)) on the road Y, with slipperiness (sl) and reduced visibility (rv), and, at the same time, the driver is running (running) at high speed (Tax>=100), the result is to cause a traffic accident accident(at())”:
driving(X,A),bdb(X,Al),have(Y,F,As),sl(Y,B),rv(X,T),running(X,Tax),Tax>=100,B>=50,Al>=1,T>=0,T=<5,As=‘yes’→at(X,Y,A,F,As,Tax,B,Al,T);
¬driving(X,A)˅¬bdb(X,Al)˅¬have(Y,F,As)˅¬sl(Y,B)˅¬rv(X,T)˅¬running(X,Tax)˅¬(Tax>=100)˅¬(B>=50)˅¬(Al>=1)˅¬(T>=0^T=<5) ˅¬(As=‘yes’)˅at(X,Y,A,F,As,Tax,B,Al,T);
\+driving(X,A);\+bdb(X,Al);\+have(Y,F,As);\+sl(Y,B);\+rv(X,T);\+running(X,Tax);\+(Tax>=100);\+(B>=50);\+(Al>=1);\+(T>=0,T=<5);at(X,Y,A,F,As,Tax,B,Al,T).
- 10.
- “No accident will occur”:
¬at(X,Y,A,F,As,Tax,B,Al,T);
\+at(X,Y,A,F,As,Tax,B,Al,T).
(Based on this sentence, with the method of atopy, through the Resolution algorithm, we will be led to the conclusion that an accident will occur.)
Although the knowledge base is represented using categorical logic, we do not explicitly use quantifiers. This is because all variables in the predicates are implicitly universally quantified. As such, the need for explicit quantifiers is eliminated, either through variable substitution or because the logic inherently assumes universal applicability. Below, we present two representative examples.
Rule 15 is stated as follows:
“Every driver X drives a car A” (rule formulation in natural language).
In predicate logic, this is expressed as follows:
∀X∀A(driver(X),car(A) → driving(X,A)).
The variables X and A are both universal, so they are eliminated, resulting in the following:
driver(X),car(A) →driving(X,A)
With the equivalence P→Q ↔ ¬P˅Q, and using the de Morgan rule ¬(P^Q) ↔ ¬P ˅¬Q, we then have the following:
¬(driver(X) ^ car(A)) ^driving(X,A)
or
¬driver(X) ˅ ¬car(A)˅driving(X,A).
And in an executable Prolog rule,
\+driver(X);\+car(A);driving(X,A).
But, rule 16 is stated as follows:
“All drivers drive at some speed, and if this speed is high, then the driver is running”, that is,
∀X∃Tax(driver(X),speed(Tax),Tax>=0→ running(X,Tax)).
For each X, there are some Tax, or in algebraic form
f(X)=Tax or X1=Tax.
Then, by substitution, we are led to the following relation:
driver(X),speed(X1),X1>=0 → running(X,X1),
which is equivalent to
driver(X),speed(Tax),Tax>=0 → running(X,Tax).
And based on the equivalence rule P → Q ↔ ¬P˅Q, we then have the following:
¬driver(X) ^¬speed(Tax)^¬(Tax>=100)˅running(X,Tax);
\+driver(X),\+speed(Tax),\+(Tax>=100); running(X,Tax).
6.2. Resolution Algorithm
In mathematical logic and automated theorem proving, the Resolution algorithm is a fundamental inference rule used to derive logical conclusions. It serves as the basis for a complete proof technique by refutation, applicable to both categorical logic and first-order logic. In the context of categorical logic, systematic application of the Resolution rule provides a decision procedure for determining the unsatisfiability of a formula, effectively solving the complement of the Boolean satisfiability problem.
The Resolution algorithm is considered one of the most robust inference mechanisms in categorical logic. It operates by generating a new clause that is logically implied by two existing clauses containing complementary literals. A literal is defined as a predicate, a rule, or the negation of a predicate. Two literals are complementary when one is the negation of the other—for example, driver(X) and ¬driver(X), where one negates the assertion of the other [52].
The Resolution algorithm (Figure 1) functions by combining logical sentences and systematically eliminating complementary predicates, meaning predicates, and their corresponding negations. This process introduces minimal changes to the original sentences and aims to establish the satisfiability of the knowledge base. In this way, the algorithm provides a means to validate a hypothesized event by demonstrating that the assumption of the opposite event leads to a logical contradiction.
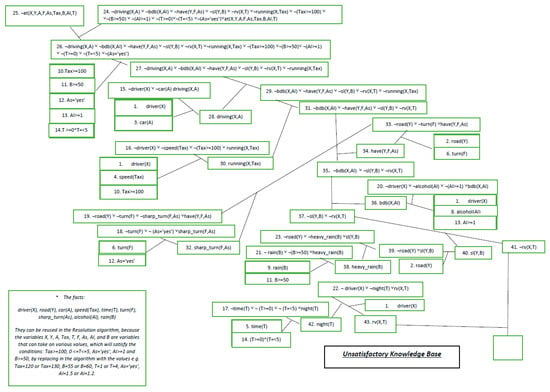
Figure 1.
The Resolution algorithm in traffic accident prediction.
In the context of this study, the algorithm is applied using abductive reasoning. We introduce, into the knowledge base, the negation of the predicted event, specifically that a traffic accident will not occur. The algorithm then tests whether this negated assumption is logically consistent with the remaining facts and rules. If it leads to an unsatisfiable knowledge base, the contradiction confirms that the negation is false.
As a result, we are able to prove that a traffic accident will occur under the specified conditions, which are described using variables such as Al, B, As, and others. The resulting contradiction provides formal evidence that the prediction is valid.
6.3. All Possible Scenarios
The following scenarios are generated by assigning different values to the variables that define the problem (Figure 2):
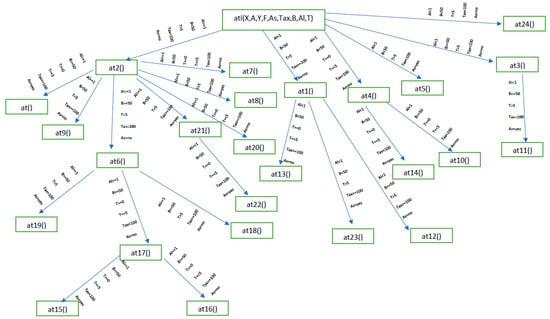
Figure 2.
Flowchart of script execution with all possible values that the variables can take. The edges of the shape contain the values of the variables, and the nodes contain the scenarios resulting from these values.
1. The driver is drunk, there is heavy rain that causes slipperiness on the road, and it is dark because it is night; therefore, there is reduced visibility. On the route, there is a sharp turn, and the driver is running at a speed of over 100 km/h. Consequently, there is a high certainty of an accident (at()).
The following message is sent to the driver:
“Caution: Risk of accident!” (at()).
2. The driver is sober, the weather conditions are good, it is daytime, there is no sharp turn on the route, but the vehicle’s speed is high, over 100 km/h.
The following message is sent to the driver:
“Caution: The driver is driving too fast!” (at1()).
3. The driver is drunk, the weather conditions are good, it is daytime, there is no sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: You have consumed a large amount of alcohol; it would be better not to drive” (at2()).
4. The driver is sober, and the weather conditions are bad, with heavy rain causing slipperiness on the road. It is daytime, there is no sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: There is slipperiness on the road due to heavy rain” (at3()).
5. The driver is sober, the weather conditions are good, and it is nighttime, so visibility is reduced. There is no sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: Reduced visibility due to night, darkness prevails” (at4()).
6. The driver is sober, the weather conditions are good, it is daytime, there is a sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: On the road, there is a sharp turn” (at5()).
7. The driver is drunk, the weather conditions are good, it is daytime, there is a sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk and there is a sharp turn on the road” (at6()).
8. The driver is drunk, the weather conditions are good, it is night, there is no sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk and there is reduced visibility due to the night” (at7()).
9. The driver is drunk, the weather conditions are good, it is daytime, there is a sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk, and there is a sharp turn” (at8()).
10. The driver is drunk, the weather conditions are good, it is daytime, there is no sharp turn on the route, but the vehicle speed is high, above 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk and driving too fast, reduce speed” (at9()).
11. The driver is sober, and the weather conditions are bad, where heavy rain is causing a slippery road. It is night, and darkness prevails, which reduces visibility for the driver. There is no sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: The road is slippery, and there is reduced visibility” (at10()).
12. The driver is sober, and the weather conditions, where heavy rain is causing a slippery road. It is daytime, there is a sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: The road is slippery, and there is a sharp turn” (at11()).
13. The driver is sober, and the weather conditions are bad, where heavy rain is causing a slippery road. It is daytime, and there is no sharp turn on the route, but the vehicle speed is high, above 100 km/h.
The following message is sent to the driver:
“Caution: The road is slippery, and you are running” (at12()).
14. The driver is sober, the weather conditions are good, and it is night, so visibility is limited. There is no sharp turn on the route, and the vehicle speed is high, above 100 km/h.
The following message is sent to the driver:
“Caution: There is reduced visibility, and the driver is driving too fast!” (at13()).
15. The driver is sober, the weather conditions are good, and it is night; therefore, there is limited visibility. There is a sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: There is reduced visibility, and there is a sharp turn on the route” (at14()).
16. The driver is drunk, the weather conditions are bad, and it is slippery on the road. It is night; therefore, there is limited visibility. There is a sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: There is reduced visibility and a slippery road; there is a sharp turn ahead, and you are drunk” (at15()).
17. The driver is drunk, the weather conditions are bad, and, therefore, the road is slippery. It is night; therefore, there is limited visibility. There is no sharp turn ahead, and the vehicle speed is high, above 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk. There is a slippery road, reduced visibility, and the driver is driving too fast” (at16()).
18. The driver is drunk, the weather conditions are bad, and, therefore, the road is slippery. It is night; therefore, there is limited visibility. There is no sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk, there is reduced visibility, and a slippery road” (at17()).
19. The driver is drunk, the weather conditions are bad, and, therefore, the road is slippery. It is daytime, there is no sharp turn on the route, and the vehicle speed is high, above 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk, there is a slippery road, and the driver is driving too fast” (at18()).
20. The driver is drunk, the weather conditions are bad, and, therefore, the road is slippery. It is daytime, there is a sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk, there is a slippery road, and a sharp turn follows” (at19()).
21. The driver is drunk, the weather conditions are good, and it is night; therefore, there is limited visibility. There is no sharp turn on the route, and the vehicle speed is high, above 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk, there is reduced visibility, and the driver is driving too fast” (at20()).
22. The driver is drunk, the weather conditions are good, it is daytime, there is a sharp turn on the route, and the vehicle speed is high, above 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk, there is a sharp turn on the road, and the driver is driving too fast” (at21()).
23. The driver is drunk, the weather conditions are good, and it is night; therefore, there is limited visibility. There is a sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Caution: The driver is drunk, there is reduced visibility, and there is a sharp turn on the route” (at22()).
24. The driver is sober, the weather conditions are good, it is daytime, there is a sharp turn on the route, and the vehicle speed is high, above 100 km/h.
The following message is sent to the driver:
“Caution: The driver is driving too fast, and there is a sharp turn on the route” (at23()).
25. The driver is sober, the weather conditions are good, it is daytime, there is no sharp turn on the route, and the vehicle speed is low, below 100 km/h.
The following message is sent to the driver:
“Have a good and safe trip” (at24()).
6.4. Knowledge Base Implementation Using Prolog
Prolog is a logic programming language with foundational roots in artificial intelligence, automated theorem proving, and computational linguistics. It is based on first-order logic, a formal system of reasoning, and differs from many conventional programming languages in that it is primarily declarative. In Prolog, a program consists of facts and rules that define relationships among objects relevant to a given problem. Computation in Prolog begins by executing a query against this knowledge base.
As one of the earliest logic programming languages, Prolog remains the most widely used to this day, supported by numerous free and open-source implementations. It has been applied in diverse domains, including theorem proving, expert systems, term rewriting, type systems, and automated system design [53].
Prolog is a general-purpose, Turing-complete programming language that is particularly well suited for applications involving intelligent knowledge processing. In the context of this study, Problem 1 and its various scenarios are represented using a corresponding Prolog knowledge base. The translation of this logic into Prolog syntax is presented below.
6.5. The Queries That Result Using JPL
In this implementation, "accident" refers to the Prolog module developed to represent the program described above. The resulting queries are as follows:
For example (Figure 3), if the driver is operating a vehicle at night between 12:00 a.m. and 5:00 a.m., and the selected route includes a sharp turn, executing the code will produce the following output (Figure 4):

Figure 3.
Query at JPL, outputting a message to the user depending on the input values received from the knowledge base, which relate to the driver’s status and the driving environment.

Figure 4.
An example of the output of a scenario (where Tax < 100, T >= 0, T <= 5, As = “yes”, B < 50, Al < 1, which mean “the driver is not speeding, the driver is driving at night, the route the driver wishes to take has a sharp turn, it is not raining heavily, and the driver is sober”, with the following output message: “CAUTION: there is reduced visibility, and there is a sharp turn on the road”/script 15 is executed (at14())).
7. Stages of Implementation of the Application
The implementation of the application was carried out through the following steps:
- Docker Setup and Map Data Configuration: Docker Machine [54] was installed, and the greece_latest.pdf file was extracted from Geofabrik [55] to allow the Open-Source Routing Machine (OSRM) [56] to operate locally via localhost:5000. This setup enabled the extraction of routes selected by the user through map interactions.
- Interactive Map Creation: A dynamic map was created using the Leaflet platform [55], featuring real-time updates of the user’s current coordinates through the Geolocation API [57].
- Variable Input Collection: Every 5 seconds, values for the system variables were fetched from the local server and injected into the map using the fetch method.
- Knowledge Base Generation and Update: The variable values displayed on the map were written to a .pl file, which serves as the Prolog knowledge base. This file was automatically updated every 5 seconds to reflect current inputs.
- Query Execution and User Feedback: Queries were executed by importing data from the knowledge base and returning context-aware messages to the user. This entire process, including feedback generation, was refreshed every 5 seconds (Figure 5).
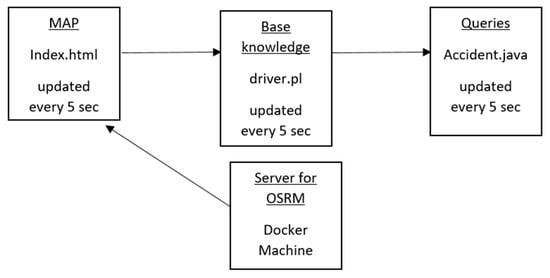 Figure 5. Implementation stages.
Figure 5. Implementation stages.
7.1. Real-Time Application Performance
The application was tested using both historical traffic accident data, where it demonstrated a high level of accuracy, and live-streaming data, where it achieved satisfactory performance.
Minor deviations were observed in the input values, primarily because of inconsistencies from the weather API [56]. However, these small discrepancies did not significantly affect the system’s output. For instance, the API might report a rainfall value of 1 mm when no precipitation occurs in reality—this is considered noise. Nonetheless, since the threshold for triggering a rain-related alert was set considerably higher, such minor deviations did not influence the conclusions drawn. For the rainfall and vehicle speed variables, deviations of up to ±2 were observed, which remained within acceptable limits and had no impact on the overall results. No deviations were noted for time and road curvature (sharp turns). In the case of alcohol consumption, the variation was also minimal and did not affect the accuracy of the system’s predictions.
If real-time values for key variables, such as rainfall or time, are not received, the system defaults these inputs to zero and proceeds with the evaluation, producing a corresponding result. However, an exception is made for the alcohol consumption variable. If this value is not received, the system does not proceed, as alcohol consumption is considered the most critical parameter in the prediction framework.
7.2. System Scalability and Complexity
The proposed model is designed to be expandable in two primary ways:
- Adaptive Vehicle Behavior Based on System Output: The system can be extended to dynamically influence vehicle behavior in response to specific driver conditions. For instance, if the driver is identified as being under the influence of alcohol, the vehicle can be fully immobilized, regardless of the safety of the route (e.g., even if there are no sharp turns or hazardous weather conditions). In contrast, if the driver is sober but exceeding the speed limit, the system could impose a maximum speed cap (e.g., 100 km/h) to mitigate risk. The complexity of this mechanism can be expressed as O1(1) × O2(1), where O1(1) refers to the computational complexity of the driver status evaluation and O2(1) corresponds to the complexity of the vehicle control algorithm.
- Multi-Driver Monitoring and City-Wide Risk Detection: The application could also be expanded to support multi-driver input and monitoring across a city. This would enable the system to generate warnings based on unsafe driving behaviors observed in any participating vehicle. Additionally, it could provide real-time alerts to drivers who share or intersect the same route.
For example, if Driver A is traveling along a route and another vehicle—Driver B—is approaching from the opposite direction but has erroneously entered Driver A’s lane, the system would detect the risk of collision. In response, it would immediately notify Driver A, along with all other nearby drivers in the affected lane, allowing them to take timely evasive actions. The complexity of this multi-driver coordination system would be O(n), where n represents the number of drivers currently connected to the application.
8. Comparison of the Application with Others in Machine Learning
To date, numerous approaches have been developed for predicting future events, most of which rely on machine learning techniques. In the following section, we present a comparative analysis between our proposed algorithm and two of the most widely used machine learning algorithms for event prediction—specifically in the context of traffic accident forecasting.
8.1. Bernoulli Naïve Bayesian Classifier (NBC)
One of the fundamental algorithms in machine learning is the Bernoulli Naïve Bayes classifier [4]. This algorithm is grounded in Bayes’ theorem, which estimates the probability of an event occurring based on historical data associated with that event. It operates under the assumption that all input features, or conditions, are independent of one another. This simplification is what gives the algorithm the label "naïve." The Bernoulli Naïve Bayes classifier is particularly effective for binary classification problems and provides one of two possible outputs: 1, indicating that the event is predicted to occur, or 0, indicating that it is not.
Bayes’ theorem is stated as follows:
P(A|B) = ((P(B|A) ∗ P(A))/P(B))
Let us define A as the desired future event to be predicted and B as the set of conditions or features that describe the relevant driving environment. Then, we define the following:
P(A|B): the probability of A occurring, given B;
P(B|A): the probability of B occurring, given A;
P(A): the probability of A occurring, regardless of B;
P(B): the probability of B occurring, regardless of A.
For example, the probability of a driver getting into an accident, under certain bad driving conditions, based on the Bayes algorithm, will be as follows:
P(A): the probability of a driver getting into an accident (generally);
P(B|A): the probability of bad driving conditions, given that a driver has gotten into an accident;
P(B): the probability of bad driving conditions existing.
Based on this formulation, we can compute the conditional probability P(A∣B), which represents the likelihood of a traffic accident occurring given the presence of adverse driving conditions. This probability can be estimated with relatively high accuracy.
The Bernoulli Naïve Bayes algorithm assumes that all input features are independent of one another. In the context of traffic accident prediction, this assumption is generally acceptable because the conditions involved, such as poor driving behavior, slippery roads, reduced visibility, high speed, and sharp turns, can reasonably be treated as independent variables. As a result, the algorithm is capable of delivering strong performance under these circumstances.
However, a significant limitation of the Bernoulli Naïve Bayes algorithm, compared to our proposed approach, is the large volume of training data required to achieve high performance. The algorithm typically reaches a classification accuracy of approximately 84 percent but requires substantial computing power and extensive data to be trained effectively.
8.2. Logistic Regression (LR)
Regression analysis is a method used to model relationships between variables. It estimates the probability of a predicted value for a future event by determining the value of a dependent variable (output) based on one or more independent variables (input values) that influence the prediction.
Logistic regression is a specific form of regression where the dependent variable is binary, taking on the value of 1 if the predicted event occurs or 0 if it does not. The model relies on historical datasets containing various values for the independent variables, along with observed outcomes for the dependent variable, marked as either 0 or 1.
During training, the algorithm uses these data to adjust the weights of its decision function. This process allows the system, often supported by neural networks, to learn the underlying patterns in the data. Once trained, the model can reliably determine whether a future event is likely to occur or not based on new input values.
The logistic function is defined as follows:
In this context (Figure 6), P(accident) represents the probability that a traffic accident will occur. This probability takes a value between 0 and 1. The variables x1, x2, …, xk are the independent variables that describe the conditions relevant to the problem. For the scenario under study, these variables include factors such as heavy rain, high speed, nighttime driving, alcohol consumption, and sharp turns along the route. Each of these variables is binary, with a value of 1 indicating that the condition is present and 0 indicating that it is not. For example, if there is heavy rain, the variable for rain is assigned a value of 1; if the driver is speeding, the high speed variable is also assigned a value of 1.
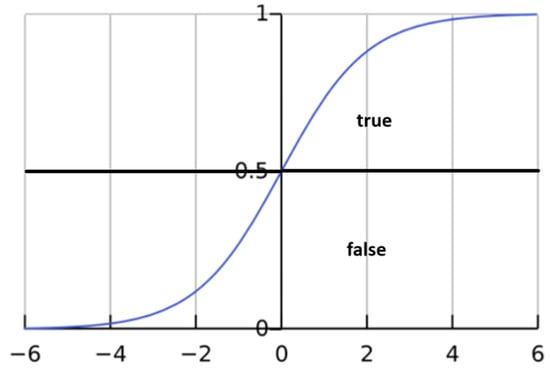
Figure 6.
Logistic function.
The parameters b1, b2, …, b3 are the weights assigned to each independent variable. These weights are learned by the neural network during the training phase, using a dataset of historical examples. The training process adjusts the weights to reflect the relative importance of each variable in determining the outcome. Variables that have a stronger influence on the occurrence of an accident receive higher weights.
For instance, in the scenario analyzed in this study, the variable indicating alcohol consumption is expected to receive the highest weight. When this variable has a value of 1, indicating that the driver has consumed alcohol, the probability of an accident increases significantly. The variable for vehicle speed is also expected to receive a high weight, as it is another major contributing factor to the risk of a traffic accident.
If the probability calculated using the model exceeds 0.5 (Figure 7), the system concludes that the event will occur—in this case, a traffic accident is predicted. Conversely, if the probability is less than 0.5, the model concludes that the event will not occur, meaning that no traffic accident is expected to happen in the scenario under analysis [57].
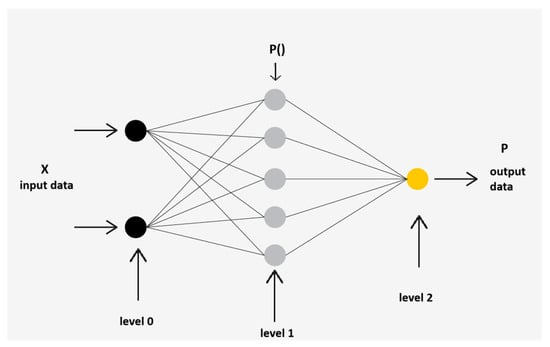
Figure 7.
Machine learning with a neural network, where x is the input values and y is the output values, with each node executing the logistic function (the black nodes are inputs and the yellow node is the output)
While the accuracy of this algorithm is generally high, a major limitation is the substantial amount of historical training data and computational power required to build and maintain the model. This contrasts with our proposed prediction framework, which is designed to operate effectively with fewer data requirements and lower computational complexity.
9. Open Challenges—Future Research
Despite significant progress in event prediction research over the past decade, many challenges and open questions remain. Considerable effort continues to be devoted to improving predictive accuracy through advanced machine learning techniques, including neural networks and ensemble models. However, one persistent obstacle is the complexity of these models, which often makes them difficult for non-expert users to understand and apply effectively. This limits their adoption among professionals who rely on artificial intelligence systems with embedded predictive capabilities. In such contexts, the inability to interpret model outputs clearly can hinder both the proper use of these systems and timely decision-making, particularly when the goal is to prevent accidents or mitigate disasters.
Another limitation is the quality of the input data. In many cases, predictions are derived from noisy or unreliable sources, such as social media feeds. Low-quality data can compromise the integrity of the forecast, leading to inaccurate or misleading conclusions. Furthermore, some forecasting systems attempt to model the real world through comprehensive data representations but struggle with the sheer volume and variability in the incoming data. This challenge often introduces significant deviations between predicted and actual outcomes. On the other hand, there are systems capable of handling large-scale data inputs efficiently, but these may fall short in accurately modeling the real-world dynamics that underlie the events.
As a result, there is an increasing need to integrate both approaches: systems capable of managing vast datasets and those focused on precise world modeling. Such integration may lead to the development of more effective and reliable forecasting tools.
For researchers, it is important not only to predict whether a future event will occur but also to anticipate the evolution of ongoing events, such as the progression of an epidemic. However, achieving desired outcomes in such cases often depends on implementing targeted interventions and meeting specific preconditions. Defining these measures is complex, as they must account for dynamic, real-time, and often unpredictable everyday conditions.
A related area of investigation involves predicting non-real or hypothetical events, including those with very low probabilities of occurrence. This type of forecasting, based on atypical or abstract conditions, enables the identification of events that may seem unlikely but are still possible under specific scenarios. This approach was adopted in our traffic accident prediction study to explore and validate future risk conditions.
Another technique relevant to this field is cluster analysis, where sets of actions or behaviors are grouped as input data to improve pattern recognition within the system.
Despite promising results in areas such as epidemiology, research in this domain is still in an early stage. The value of a prediction depends on several factors, including the accuracy of the time and location, the detail and clarity of the event description, and the intensity or severity of the event itself. Continued efforts to optimize forecasting systems are essential to achieving high-performance models capable of producing reliable and actionable predictions.
10. Conclusions
This research presents a comprehensive overview of the progress and development of event prediction systems over the past ten years. It focuses specifically on predicting traffic accidents and generating customized messages for users based on real-time conditions. The ultimate goal is to help prevent accidents that are often caused by factors such as alcohol consumption, excessive speed, poor visibility, slippery road surfaces, and dangerous road features, like sharp turns.
In this study, we modeled the traffic accident prediction problem using categorical logic. We constructed a knowledge base representing the predicted event and demonstrated its logical validity through the Resolution algorithm. We then explored all possible scenarios derived from the initial problem by assigning different values to each variable and evaluating every possible combination. This process allowed us to generate a comprehensive set of user-facing messages that indicate whether driving conditions are safe or unsafe.
The knowledge base was implemented in the Prolog programming language, and queries were executed through JPL to establish an interactive interface with the user. The final application was built on a real-time map interface created using the Leaflet platform [55]. This interface included live weather updates through the weather API platform [56,57,58,59,60], using the appropriate weather key to retrieve current data. The map also displayed the user’s current location, updated every five seconds, and allowed users to define their route either by searching or by clicking directly on the map.
As the route is updated, the knowledge base is also refreshed in real time, incorporating key variables such as time, rainfall levels, vehicle speed, road curvature, and alcohol level. Alcohol intake is monitored using an integrated sensor. Based on the current data, the system continuously evaluates driving conditions and provides timely messages to the user about whether movement is safe or potentially dangerous. The objective is to predict and prevent traffic accidents by enabling informed and proactive driving decisions.
Despite the progress made in the field of event prediction, the domain remains open and faces many unresolved challenges. Accurately predicting events like traffic accidents requires further advancements in data quality, model precision, and interpretability. Future systems must achieve high accuracy in determining not only the occurrence but also the exact time, location, nature, and intensity of such events.
Author Contributions
Methodology, E.K. and G.V.; software, E.K.; validation, G.V.; resources, E.K.; writing—original draft, E.K., G.V. and N.P.; writing—review and editing, N.P.; supervision, N.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, L. Event prediction in the big data era: A systematic survey. ACM Comput. Surv. (CSUR) 2021, 54, 1–37. [Google Scholar] [CrossRef]
- Kucharavy, D.; de Guio, R. Problems of forecast. In Proceedings of the ETRIA TRIZ Future 2005, Graz, Austria, 16–18 November 2005. [Google Scholar]
- Koutsaki, E.; Vardakis, G.; Papadakis, N. Spatiotemporal data mining problems and methods. Analytics 2023, 2, 485–508. [Google Scholar] [CrossRef]
- Murphy, K.P. Naive bayes classifiers. Univ. Br. Columbia 2006, 18, 1–8. [Google Scholar]
- Xu, X. Adaptive intrusion detection based on machine learning: Feature extraction, classifier construction and sequential pattern prediction. Int. J. Web Serv. Pract. 2006, 2, 49–58. [Google Scholar]
- Yu, M.; Bambacus, M.; Cervone, G.; Clarke, K.; Duffy, D.; Huang, Q.; Li, J.; Li, W.; Li, Z.; Liu, Q.; et al. Spatiotemporal event detection: A review. Int. J. Digit. Earth 2020, 13, 1339–1365. [Google Scholar] [CrossRef]
- Gouarir, A.; Martínez-Arellano, G.; Terrazas, G.; Benardos, P.; Ratchev, S. In-process tool wear prediction system based on machine learning techniques and force analysis. Procedia CIRP 2018, 77, 501–504. [Google Scholar] [CrossRef]
- Vardakis, G.; Tsamis, G.; Koutsaki, E.; Haridimos, K.; Papadakis, N. Smart home: Deep learning as a method for machine learning in recognition of face, silhouette and human activity in the service of a safe home. Electronics 2022, 11, 1622. [Google Scholar] [CrossRef]
- Balsamo, S.; Di Marco, A.; Inverardi, P.; Simeoni, M. Model-based performance prediction in software development: A survey. IEEE Trans. Softw. Eng. 2004, 30, 295–310. [Google Scholar] [CrossRef]
- Fanaee-T, H.; João, G. Tensor-based anomaly detection: An interdisciplinary survey. Knowl. Based Syst. 2016, 98, 130–147. [Google Scholar] [CrossRef]
- Park, S.Y.; Park, J.E.; Kim, H.; Park, S.H. Review of statistical methods for evaluating the performance of survival or other time-to-event prediction models (from conventional to deep learning approaches). Korean J. Radiol. 2021, 22, 1697–1707. [Google Scholar] [CrossRef]
- Agrawal, J.; Diao, Y.; Gyllstrom, D.; Immerman, N. Efficient pattern matching over event streams. In SIGMOD ‘08, Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 9–12 June 2008; Association for Computing Machinery: New York, NY, USA, 2008. [Google Scholar]
- Özdogan, U.; Roland, N.H. Optimization of well placement with a history matching approach. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. [Google Scholar]
- Bognár, L.; Fauszt, T. Factors and conditions that affect the goodness of machine learning models for predicting the success of learning. Comput. Educ. Artif. Intell. 2022, 3, 100100. [Google Scholar] [CrossRef]
- Cantril, H. The prediction of social events. J. Abnorm. Soc. Psychol. 1938, 33, 364. [Google Scholar] [CrossRef]
- Liu, W.; Luo, W.; Lian, D.; Gao, S. Future frame prediction for anomaly detection—A new baseline. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Suresh, K.; Severn, C.; Ghosh, D. Survival prediction models: An introduction to discrete-time modeling. BMC Med. Res. Methodol. 2022, 22, 207. [Google Scholar] [CrossRef] [PubMed]
- Tutz, G.; Schmid, M. Modeling Discrete Time-to-Event Data; Springer: New York, NY, USA, 2016. [Google Scholar]
- Krzywinski, M.; Altman, N. Multiple linear regression: When multiple variables are associated with a response, the interpretation of a prediction equation is seldom simple. Nat. Methods 2015, 12, 1103–1105. [Google Scholar] [CrossRef]
- Al-Amoudi, A.; Zhang, L. Application of radial basis function networks for solar-array modelling and maximum power-point prediction. IEE Proc. Gener. Transm. Distrib. 2000, 147, 310–316. [Google Scholar] [CrossRef]
- Zheng, X.; Han, J.; Sun, A. A survey of location prediction on twitter. IEEE Trans. Knowl. Data Eng. 2018, 30, 1652–1671. [Google Scholar] [CrossRef]
- Wohlfarth, T.; Ichise, R. Semantic and event-based approach for link prediction. In Proceedings of the International Conference on Practical Aspects of Knowledge Management, Yokohama, Japan, 22–23 November 2008. [Google Scholar]
- George, S.; Santra, A.K. Traffic prediction using multifaceted techniques: A survey. Wirel. Pers. Commun. 2020, 115, 1047–1106. [Google Scholar] [CrossRef]
- Mehrmolaei, S.; Keyvanpourr, M.R. A brief survey on event prediction methods in time series. In Artificial Intelligence Perspectives and Applications, Proceedings of the 4th Computer Science On-line Conference 2015 (CSOC2015), Online, 27–30 April 2015; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Molaei, S.M.; Keyvanpour, M.R. An analytical review for event prediction system on time series. In Proceedings of the 2015 2nd International Conference on Pattern Recognition and Image Analysis (IPRIA), Rasht, Iran, 11–12 March 2015. [Google Scholar]
- Brown, R.G. Smoothing, Forecasting and Prediction of Discrete Time Series; Courier Corporation: Chelmsford, MA, USA, 2004. [Google Scholar]
- Micci-Barreca, D. A preprocessing scheme for high-cardinality categorical attributes in classification and prediction problems. ACM SIGKDD Explor. Newsl. 2001, 3, 27–32. [Google Scholar] [CrossRef]
- Copeland, D.E. Theories of categorical reasoning and extended syllogisms. Think. Reason. 2006, 12, 379–412. [Google Scholar] [CrossRef]
- Lambek, J.; Scott, P.J. Introduction to Higher-Order Categorical Logic; Cambridge University Press: Cambridge, UK, 1988; Volume 7. [Google Scholar]
- Moser, W.; Adlassnig, K.-P. Consistency checking of binary categorical relationships in a medical knowledge base. Artif. Intell. Med. 1992, 4, 389–407. [Google Scholar] [CrossRef]
- Bachmair, L.; Ganzinger, H. Resolution Theorem Proving. Handb. Autom. Reason. 2001, 1. [Google Scholar] [CrossRef]
- Tanyi, E.B.; Linkens, D.A.; Bennett, S. The use of Prolog in the implementation of a Knowledge-based Environment for Modelling and Simulation (KEMS). Trans. Inst. Meas. Control 1993, 15, 248–259. [Google Scholar] [CrossRef]
- Adhikari, B.; Xu, X.; Ramakrishnan, N.; Prakash, B.A. Epideep: Exploiting embeddings for epidemic forecasting. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Al Boni, M.; Gerber, M.S. Area-specific crime prediction models. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016. [Google Scholar]
- Alaka, H.A.; Oyedele, L.O.; Owolabi, H.A.; Ajayi, S.O.; Bilal, M.; Akinade, O.O. Methodological approach of construction business failure prediction studies: A review. Constr. Manag. Econ. 2016, 34, 808–842. [Google Scholar] [CrossRef]
- Alevizos, E.; Artikis, A.; Paliouras, G. Event forecasting with pattern markov chains. In Proceedings of the 11th ACM International Conference on Distributed and Event-Based Systems, Barcelona, Spain, 19–23 June 2017; ACM Press: New York, NY, USA, 2017. [Google Scholar]
- Alevizos, E.; Artikis, A.; Paliouras, G. Wayeb: A tool for complex event forecasting. arXiv 2018, arXiv:1901.01826. [Google Scholar]
- Alevizos, E.; Skarlatidis, A.; Artikis, A.; Paliouras, G. Probabilistic complex event recognition: A survey. ACM Comput. Surv. (CSUR) 2017, 50, 1–31. [Google Scholar] [CrossRef]
- Allan, J.; Papka, R.; Lavrenko, V. On-line new event detection and tracking. In Proceedings of the 21st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Melbourne, Australia, 24–28 August 1998. [Google Scholar]
- Asher, J. Forecasting Ebola with a regression transmission model. Epidemics 2018, 22, 50–55. [Google Scholar] [CrossRef]
- Menzies, P.; Beebee, H. Counterfactual theories of causation. In Stanford Encyclopedia of Philosophy; Stanford University: Stanford, CA, USA, 2019. [Google Scholar]
- Muthiah, S.; Butler, P.; Khandpur, R.P.; Saraf, P.; Self, N.; Rozovskaya, A.; Zhao, L.; Cadena, J.; Lu, C.T.; Vullikanti, A.; et al. EMBERS at 4 years: Experiences operating an open source indicators forecasting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Ramdasi, S.S.; Mutha, G.R.; Marathe, N.V.; Patwardhan, M.A.; Raju, S.; Mulye, A.; Loknath, M.S. Study of Modal and Dynamic Behavior of Engine Coupled Systems for Design/Development of Range of Cardon Shafts, Couplings and Bed Plate Systems. SAE Technical Paper 2007. Available online: https://www.sae.org/publications/technical-papers/content/2007-26-052/ (accessed on 2 March 2025).
- Artikis, A.; Sergot, M.; Paliouras, G. An event calculus for event recognition. IEEE Trans. Knowl. Data Eng. 2014, 27, 895–908. [Google Scholar] [CrossRef]
- Nakajima, Y.; Ptaszynski, M.; Masui, F.; Hirotoshi, H. A prototype method for future event prediction based on future reference sentence extraction. In Proceedings of the Workshop on Linguistic and Cognitive Approaches to Dialogue Agents, Melbourne, Australia, 21 August 2017. [Google Scholar]
- Beven, K. Changing ideas in hydrology—The case of physically-based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Huang, Z.G.; Zhang, H.F.; Eisenberg, D.; Seager, T.P.; Lai, Y.C. Extreme events in multilayer, interdependent complex networks and control. Sci. Rep. 2015, 5, 17277. [Google Scholar] [CrossRef]
- Monroe, S.M. Major and minor life events as predictors of psychological distress: Further issues and findings. J. Behav. Med. 1983, 6, 189–205. [Google Scholar] [CrossRef]
- Ruta, D.; Gabrys, B. An overview of classifier fusion methods. Comput. Inf. Syst. 2000, 7, 1–10. [Google Scholar]
- Papadakis, N.; Petrakis, P.; Plexousakis, D.; Manifavas, C. A Solution to the Ramification Problem Expressed in Temporal Description Logics. Int. J. Semant. Comput. 2014, 8, 1–46. [Google Scholar] [CrossRef]
- Arias, M.; Arratia, A.; Xuriguera, R. Forecasting with twitter data. ACM Trans. Intell. Syst. Technol. (TIST) 2014, 5, 1–24. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, Q.; Ye, J.; Chen, F.; Lu, C.T.; Ramakrishnan, N. Multi-task learning for spatio-temporal event forecasting. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015. [Google Scholar]
- Vardakis, G.; Hatzivasilis, G.; Koutsaki, E.; Papadakis, N. Review of Smart-Home Security Using the Internet of Things. Electronics 2024, 13, 3343. [Google Scholar] [CrossRef]
- Sun, S.; Luo, C.; Chen, J. A review of natural language processing techniques for opinion mining systems. Inf. Fusion 2017, 36, 10–25. [Google Scholar] [CrossRef]
- Available online: https://leafletjs.com (accessed on 2 March 2025).
- Chowdhury, S.N.; Ray, A.; Mishra, A.; Ghosh, D. Extreme events in globally coupled chaotic maps. J. Phys. Complex. 2021, 2, 035021. [Google Scholar] [CrossRef]
- Chowdhury, S.N.; Majhi, S.; Ghosh, D. Distance dependent competitive interactions in a frustrated network of mobile agents. IEEE Trans. Netw. Sci. Eng. 2020, 7, 3159–3170. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Chowdhury, S.N.; Ray, A.; Dana, S.K.; Ghosh, D. Extreme events in dynamical systems and random walkers: A review. Phys. Rep. 2022, 966, 1–52. [Google Scholar] [CrossRef]
- Chowdhury, S.N.; Majhi, S.; Ozer, M.; Ghosh, D.; Perc, M. Synchronization to extreme events in moving agents. New J. Phys. 2019, 21, 073048. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).