1. Introduction
The World Health Organization estimates that approximately two billion people are infected with parasitic helminths worldwide [
1]. Helminths are parasitic worms that feed on a living host to gain nourishment and protection, while causing poor nutrient absorption, weakness and disease in the host. Soil-transmitted helminths cause most of the helminth infections and if an infected person or animal has defecated on soil, helminth eggs, that are present in their feces, contaminate the soil. People in developing countries, especially children who play in such contaminated soil, easily acquire helminth infection when worms, in the infective life cycle stage, penetrate human skin or are swallowed accidentally. These worms can cause several diseases, including severe pathologies of the intestine, liver, lungs, or brain. The use of 16S rRNA sequencing technologies to determine microbial community structure (taxa detected and their abundance; non-negative integers) of bacterial strains from such fecal specimens is becoming a popular method to study the impact of bacteria on human health and disease [
2,
3]. Even though next generation sequencing platforms have advanced microbiota profiling, several challenges remain. These include (1) sparseness of samples from which the microbiota data are acquired due to resource constraints, i.e., low coverage [
4]; (2) sparseness of data since many species are not detected, resulting in zero counts, i.e., low abundant taxa due to primer bias [
5]; and (3) the relatively recent development of automated methodologies for integrative analysis of human microbiota data, as it is a rapidly evolving and upcoming field of research, i.e., use of suboptimal tools [
6].
For studying the association between microbiota features and host phenotypes to deal with challenges of this domain, many statistical methods have been proposed which use sequence counts as microbiota data. These statistical analysis methods can be categorized into several approaches: (a) simple univariate methods and tests of diversity; (b) multivariate methods; and (c) model-selection methods [
7]. Univariate approaches ignore the multivariate and correlated nature of the taxa count and test each feature individually. These methods are considered to be effective when few taxa have strong effects on the host phenotype. White et al. use a non-parametric t-test based on permutation or a Fisher’s exact test for the sparse data to recognize organisms whose differential abundance is correlated with disease [
8]. In linear discriminant analysis (LDA) effect size (LEfSe), a univariate test (Welch’s tor Wilcoxon rank test) is used to assess the significance of each feature [
9]. First, LEFSe uses the Kruskal–Wallis (KW) ranksum test to estimate whether or not values in different classes are differentially distributed. Then, features violating the null hypothesis in the KW test are further analyzed using the paired Wilcoxon test between subclasses of data to test whether all pairwise comparisons between subclasses of classes are significantly compatible with the class level trend. Finally, the Latent Dirichlet Allocation (LDA) is used for ranking the relevant features. The resulting features are ranked according to the effect size with which they distinguish classes.
Multivariate methods calculate the association of the vector of multiple variables. In [
10,
11], different methods have been proposed to model variable abundances as drawn from a Dirichlet-multinomial, or a mixture of Dirichlet multinomials. Various non-parametric multivariate tests are based on pairwise distance measures that can be tree-unaware or tree-aware. Based on pairwise distances, various non-parametric multivariate tests can be conducted, such as the Mantel test and multivariate analysis of variance (MANOVA) [
12,
13,
14]. One example of a tree-aware method is UniFrac, which calculates distances between pairs of microbiota samples in the phylogenetic tree [
15].
A final category of methods for analyzing association between taxa abundances and host phenotypes consists of regression-based variable-selection methods, such as methods of the Partial Least Squares (PLS) family. PLS is a regression model that tries to find the direction in the observable variables (taxa) space that leads to the maximum multidimensional variance direction in the predicted variables (phenotype) space by projecting both types of variables to a new space [
16]. Even though PLS is originally designed for regression problems, it performs well for classification problems too [
17,
18]. Sparse PLS (sPLS) was proposed in [
19,
20] to add Lasso penalization combined with Singular Value Decomposition (SVD) computation into PLS in order to handle sparse data. By considering predicted variables as another dataset of observable variables, this method was initially designed to identify the subsets of correlated variables of two different types in a way that each step consists of both variable selection and modeling procedures [
21]. Sparse PLS Discriminant Analysis (sPLS-DA) is another method of the PLS-family which is an extension of sPLS to a supervised classification framework [
22]. For gaining classification ability, the predicted variables can be coded with dummy variables to indicate the class of each observation. The class of a test observation can be selected based on the distance measures such as, maximum distance, centroid, or Mahalanobis. Another framework that extends sPLS-DA for metagenomic discovery is called mixMC, which identifies significant discriminative observable variables for preparing interpretable outputs. The mixMC framework uses Principal Component Analysis (PCA) to visualize diversity patterns and sPLS-DA to find indicator species or determinant microbiota members discriminating habitats or body sites [
23].
While diversity tests and multivariate methods are usually used to determine whether there is an association between a set of taxa and the phenotype, univariate tests and model-selection methods extract these sets of features if the association exists. However, most of these methods model taxa as independent variables and ignore the phylogenetic relationship among them. Moreover, the regression-based variable-selection models, such as the PLS-family methods, assume multicollinearity between data. These methods also project the variables into a new space in order to satisfy their goals, such as predicting variables, dealing with data sparsity, or expanding visualization power. However, projecting features reduces the result interpretation, since the new features can only be approximately associated with the original feature set. Thus, interpretation and visualization in these methods are just limited to depicting samples in a two-dimensional space of projected components which allows manual subjective approximation of the association between the observable and predicted variables.
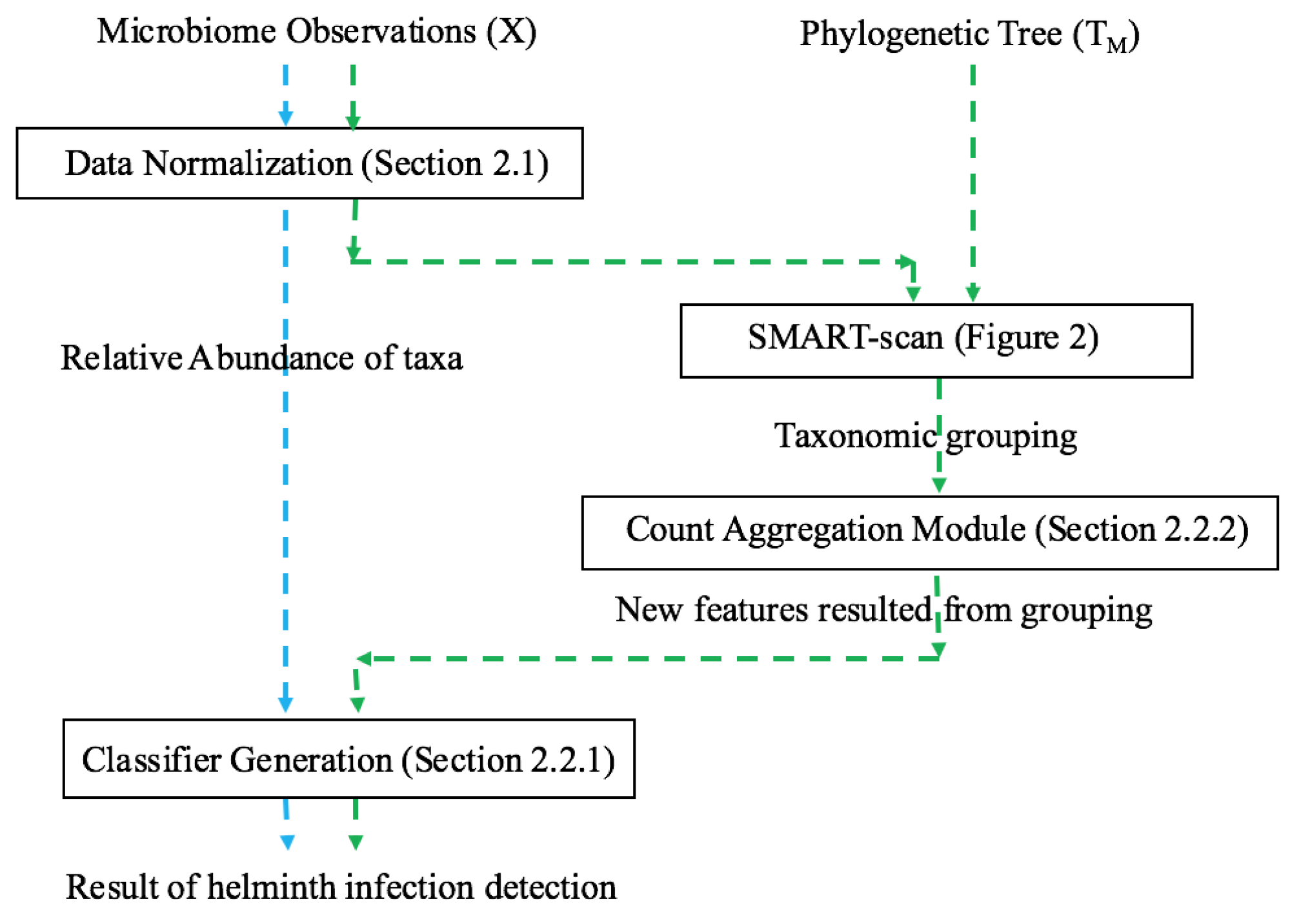
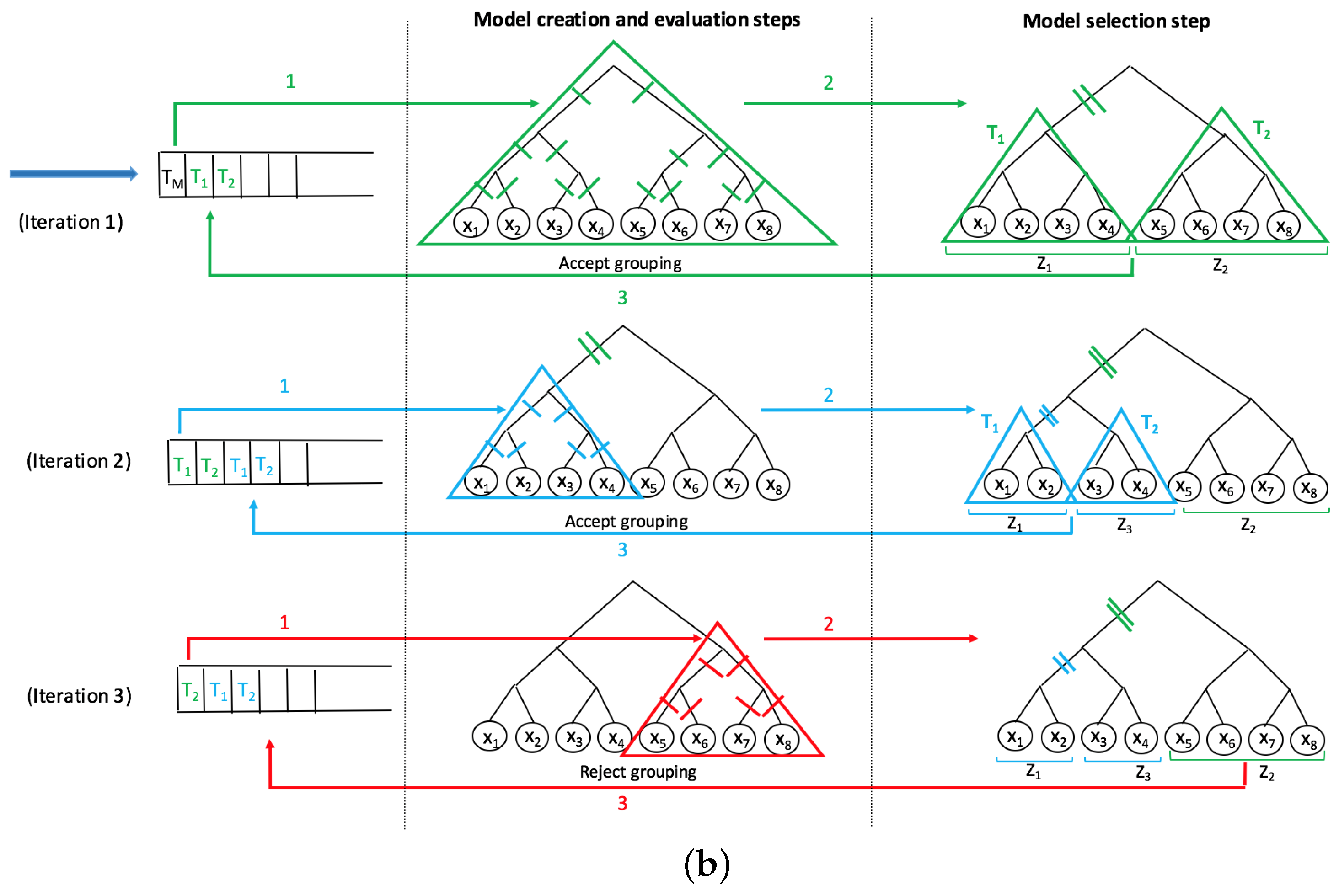
A recent innovative method, SMART-scan, for analyzing human microbiota data incorporates a taxonomic tree to increase modeling precision [
7]. This method deals with the shortcomings of previous workflows in the way that it uses the phylogenetic dependency among taxa to not only eliminate the uninformative variables, but also to group the functionally similar variables into separate sets of grouped data with underlying biological connectivity. The main advantage of this method is its highly interpretable results, as no projection method is used and the new groups contain the original taxa which can be easily visualized in the phylogenetic tree. The SMART-scan algorithm was tested on a simulated dataset and the gut microbiota of vervet monkeys under two different diets: normal and fatty diets. For the simulated data, the authors compare SMART-scan to other statistical methods: Single-Variable analysis (SVA), stepwise regression, LASSO used in [
24,
25], and classification and regression trees (CART) [
26]. The authors showed that SMART-scan has higher power than other statistical methods when there are group effects and its power drops if there is no group effect. For the vervet monkeys, they wanted to investigate the effects of a fatty diet on microbiota composition. They showed that the application of SMART-scan can reveal important features associated with groups and result in relevant parts of the phylogenetic tree associated with microbiota changes in response to diet, which otherwise would not have been detected by other non-tree aware approaches.
In this paper, we apply the SMART-scan algorithm to the analysis of two microbiota datasets acquired from 16s rRNA sequencing of stool specimens from global human populations with and without helminth infection. We believe that our paper is the first application of this automated phylogenetic clustering method to human microbiota datasets. Our long-term goal is to present an integrative biomarker discovery workflow that extracts robust, generalizable, and interpretable propositional rule patterns, showing the association between taxa and phenotypes. Previous workflows suffer from subjective interpretation and strong assumption of phylogenetic independency among taxa. Our workflow is designed to facilitate knowledge transfer from different but related microbiome datasets by phylogenetically-related functional mapping. In [
27], functional mapping was introduced for relating different sparse biomedical datasets obtained for the same classification task, in order to effectively transfer information for integrative biomarker discovery. Therein, clusters of functionally-similar features are extracted from gene expression knowledge bases, and used to map variables between the related datasets. Herein, our goal is to automatically extract such functional mappings for microbiota data. We have this general hypothesis that “applying SMART-scan to multiple microbiota datasets that share phylogenetically dependent features would not decrease the classification performance for helminth infection detection over using just a single dataset, while allowing for grouping of taxa and phenotype associations at a more general and robust level”. We test this hypothesis using two datasets of helminth microbiota as starting points, and then by learning classifiers with and without SMART-scan groupings to observe the changes in predictive performance measures. The rest of this paper is organized to present the methods, datasets, experiments, and results used to demonstrate the feasibility of this hypothesis. This demonstration of feasibility is the first step towards the longer-term goal of enhancing our in-house developed machine learning methods to transfer learning of the classification rules to the application of microbiota data via the use of these phylogenetic groupings.
4. Conclusions
In this paper, we showed that taxonomic modeling, using a recently published method called SMART-scan, improves classification performance of real-world human microbiota datasets. Particularly, we tested the improvements in the AUC, Specificity, Sensitivity, and Balanced Accuracy performance over 10 runs of 10-fold cross-validation of application of SMART-scan to aggregate bacterial groups detected in two global populations with and without helminth infection. By showing the achieved improvement, we proved our hypothesis that “applying SMART-scan on phylogenetically dependent microbiota datasets would result in clusters representing functional mapping for to identify the association between taxa and phenotypes for our helminth datasets.” We also showed that by adding the SMART-scan algorithm to our models, we increased model performance by dealing with the problem of data sparsity.
We also tried four different classifiers in our experiments: naive Bayes, support vector machines, multilayer perceptrons, and random forests, with all leading to statistically significantly improved AUCs, specificity, sensitivity, and Balanced accuracy with the SMART-scan module. Moreover, we observe a much greater performance gain for those classifiers that have feature independency assumptions [naive Bayes] and those which map the classification problem to a feature space [support vector machines]. As our future work, we are aiming to study classification models adaptable to the SMART-scan groupings. Advancing the models would result in precisely defining the microbial ecology underlying helminth infections and determining whether microbiota assemblages, after deworming, resemble the healthy microbiota state.