Regression Models for Description of Roasted Ground Coffee Powder Color Change during Secondary Shelf-Life as Related to Storage Conditions and Packaging Material
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ground Coffee Samples
2.2. Moisture Content
2.3. Ambient Conditions
2.4. Color Measurements
2.5. Nonlinear Regression Models
2.6. Linear Regression Models
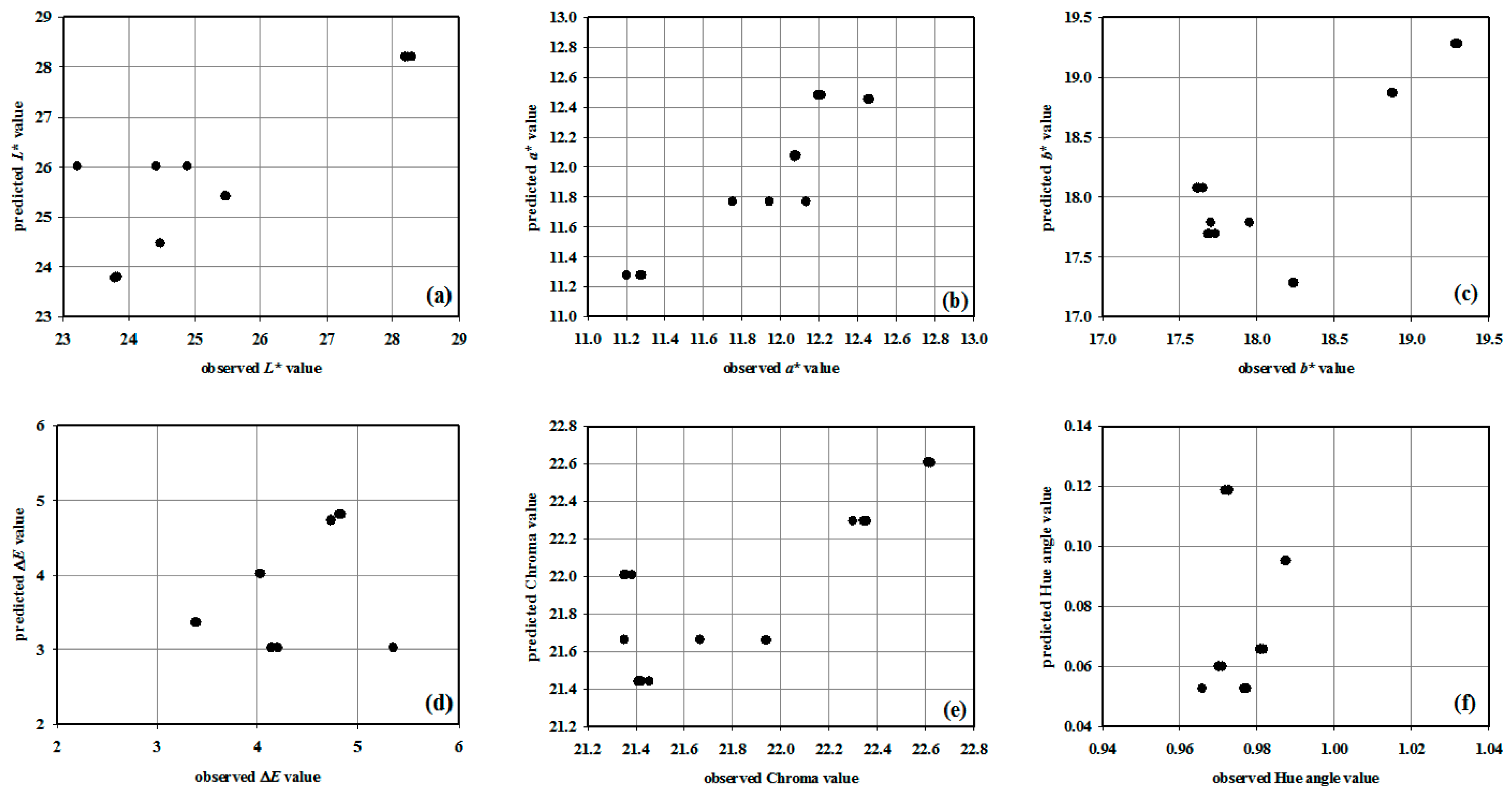
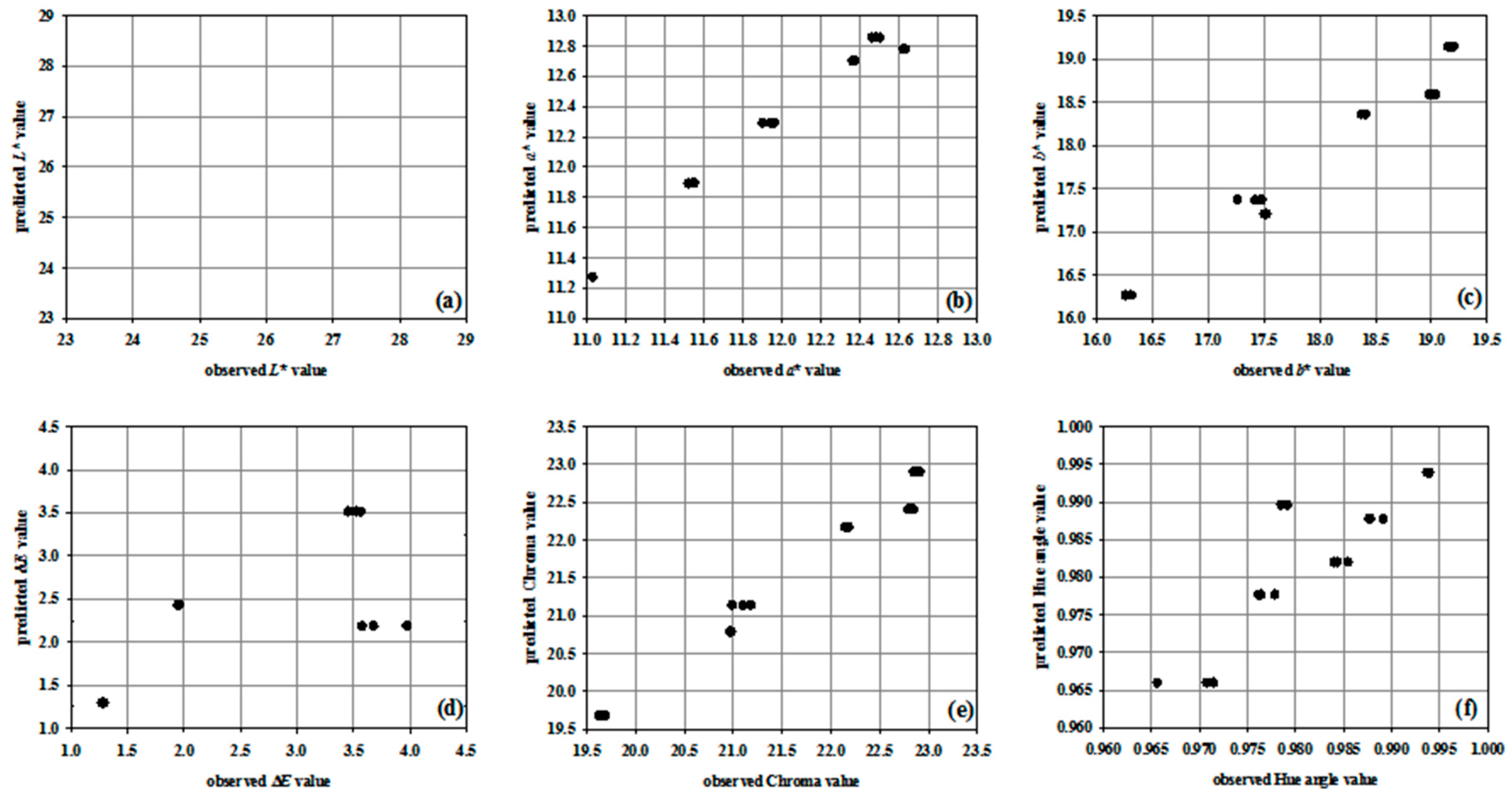
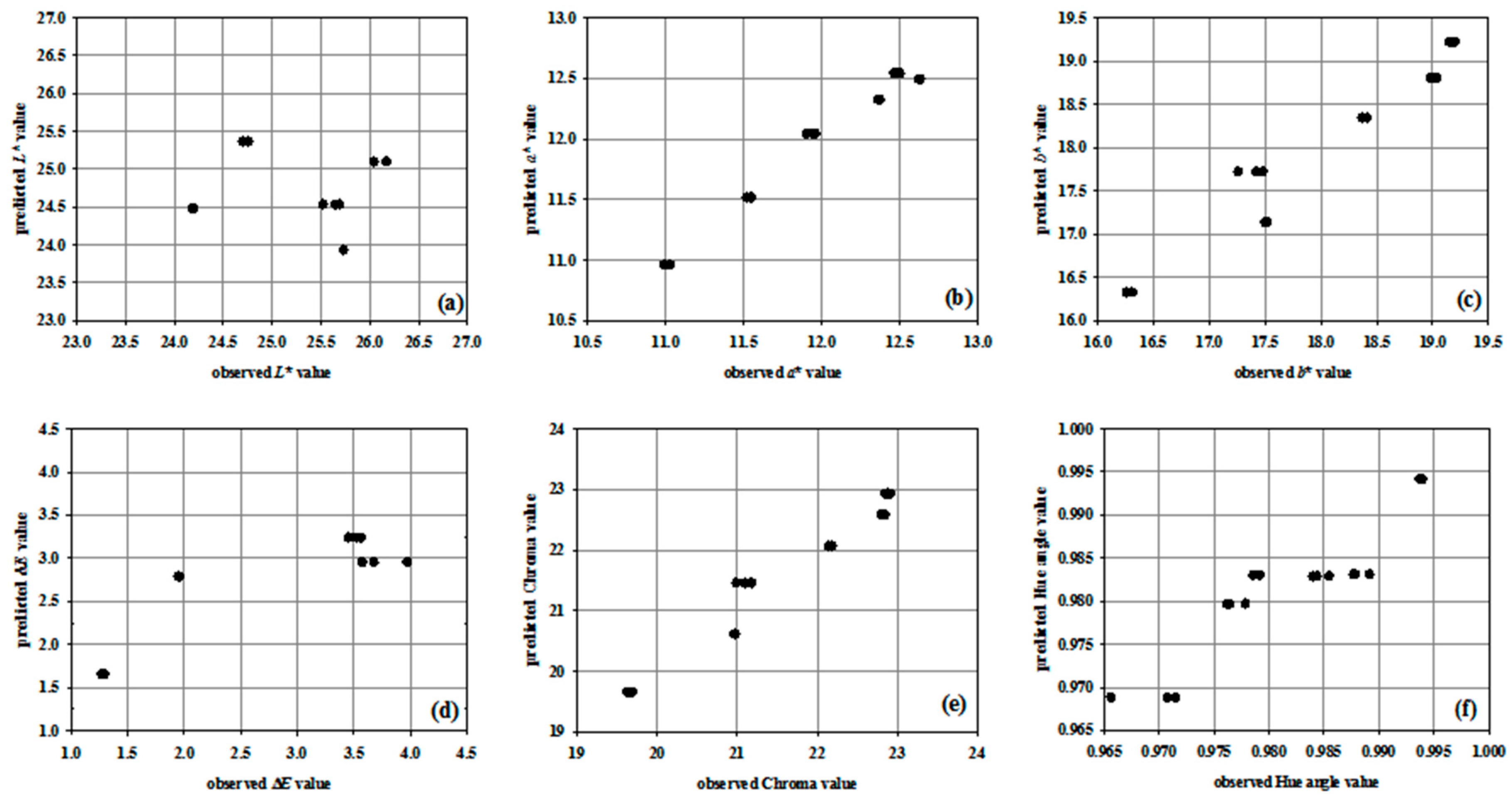
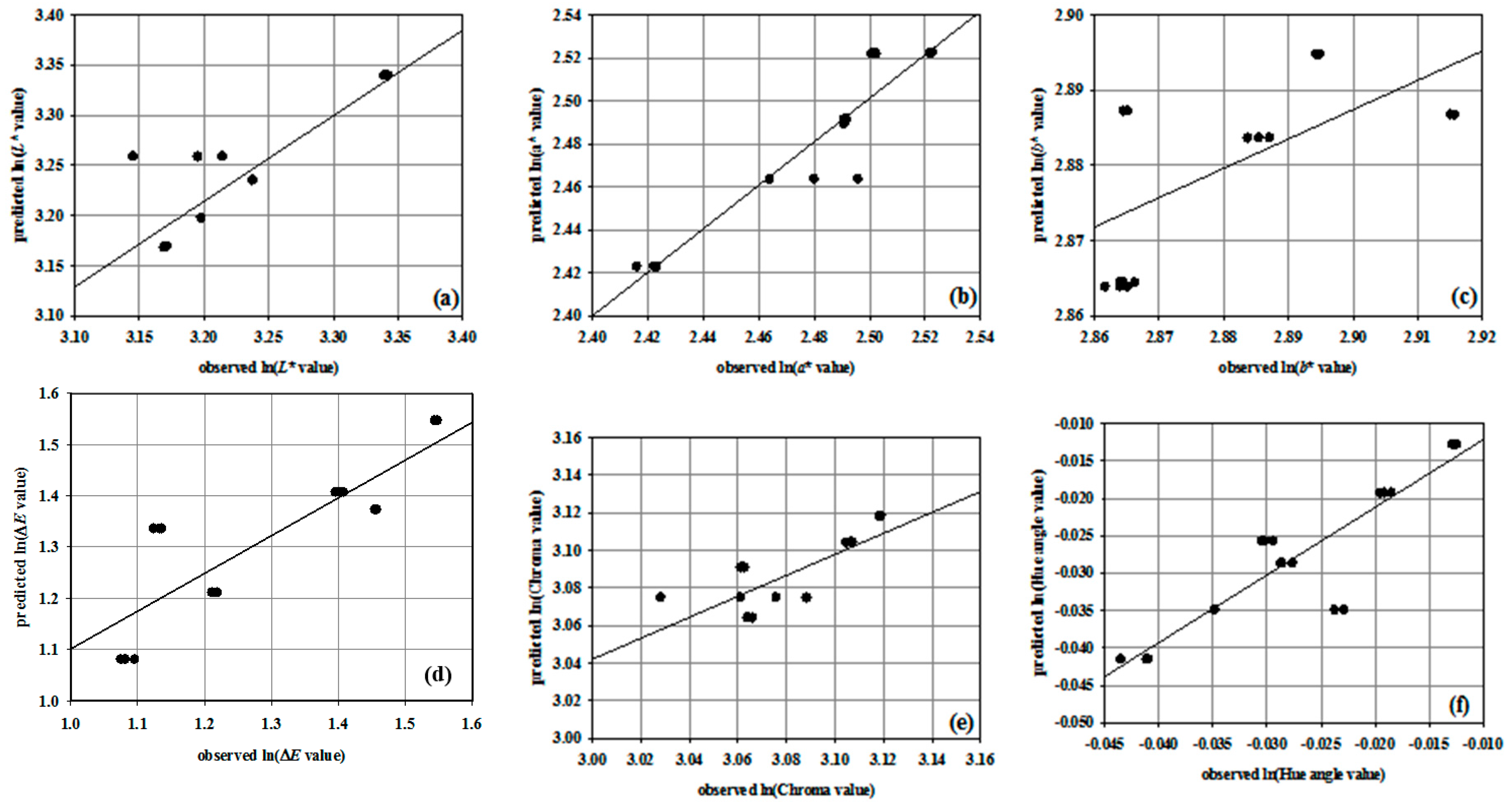
3. Results and Discussion
3.1. Experimental Data
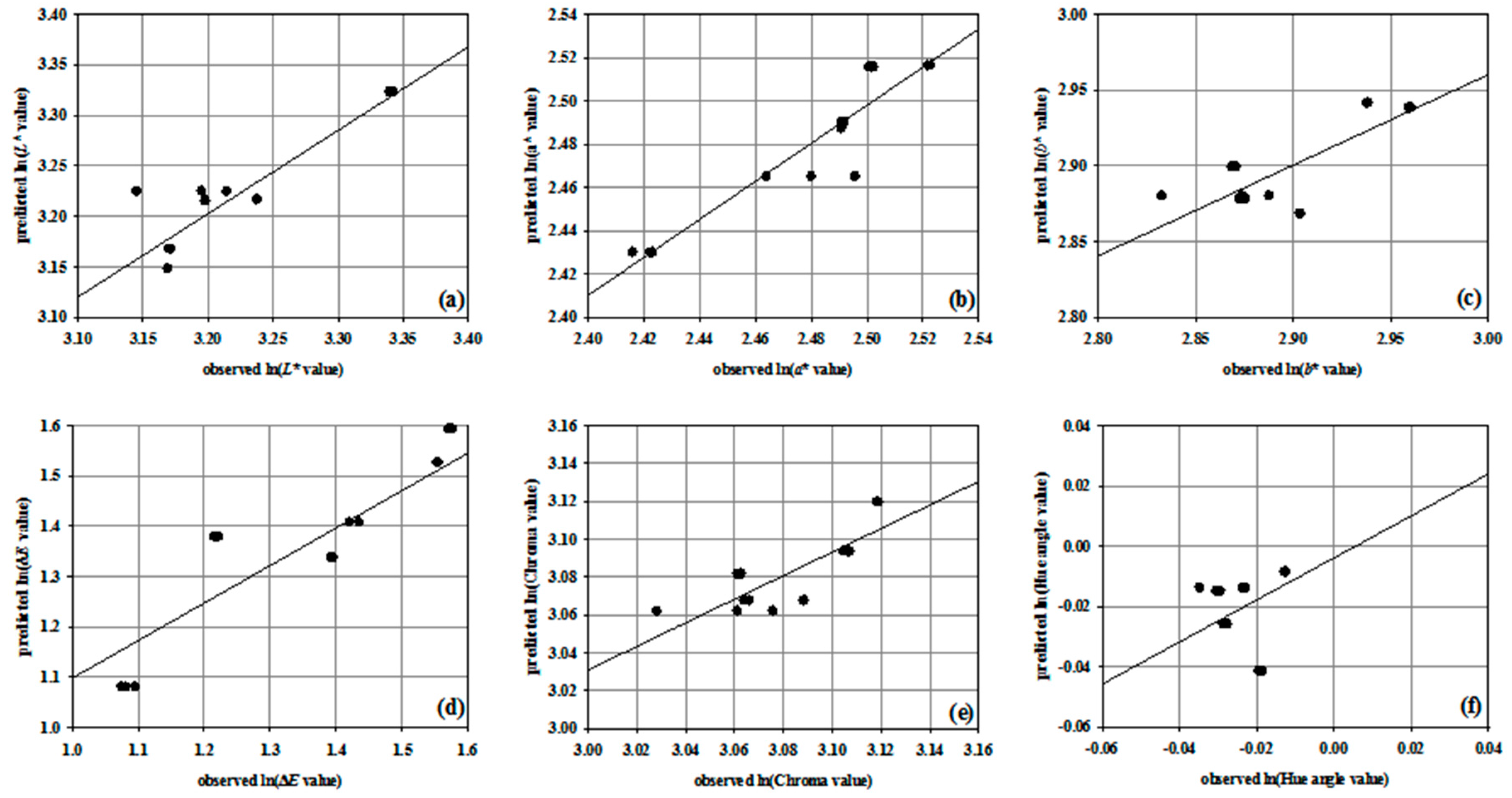
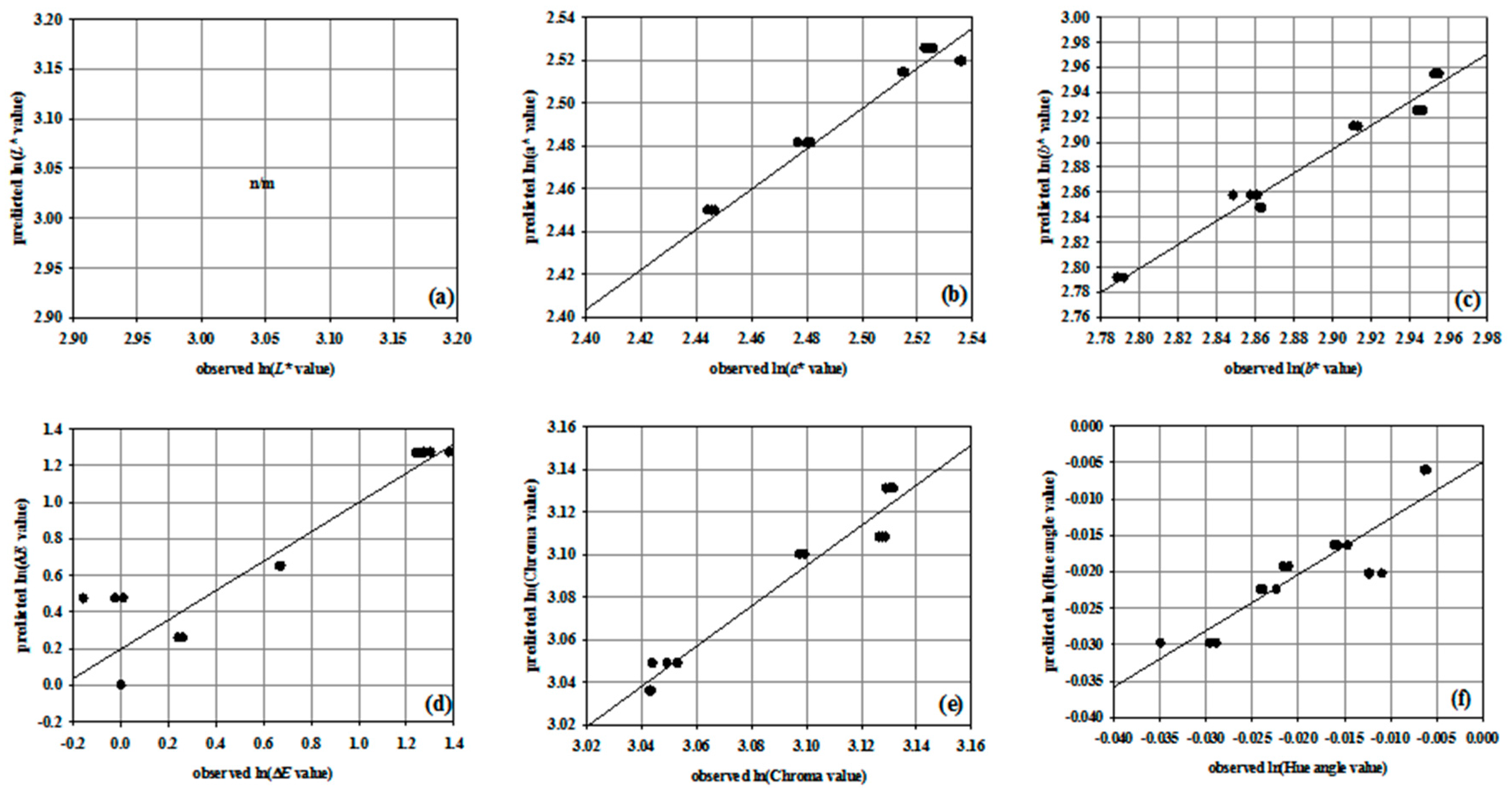
3.2. Non-Linear Regression Models
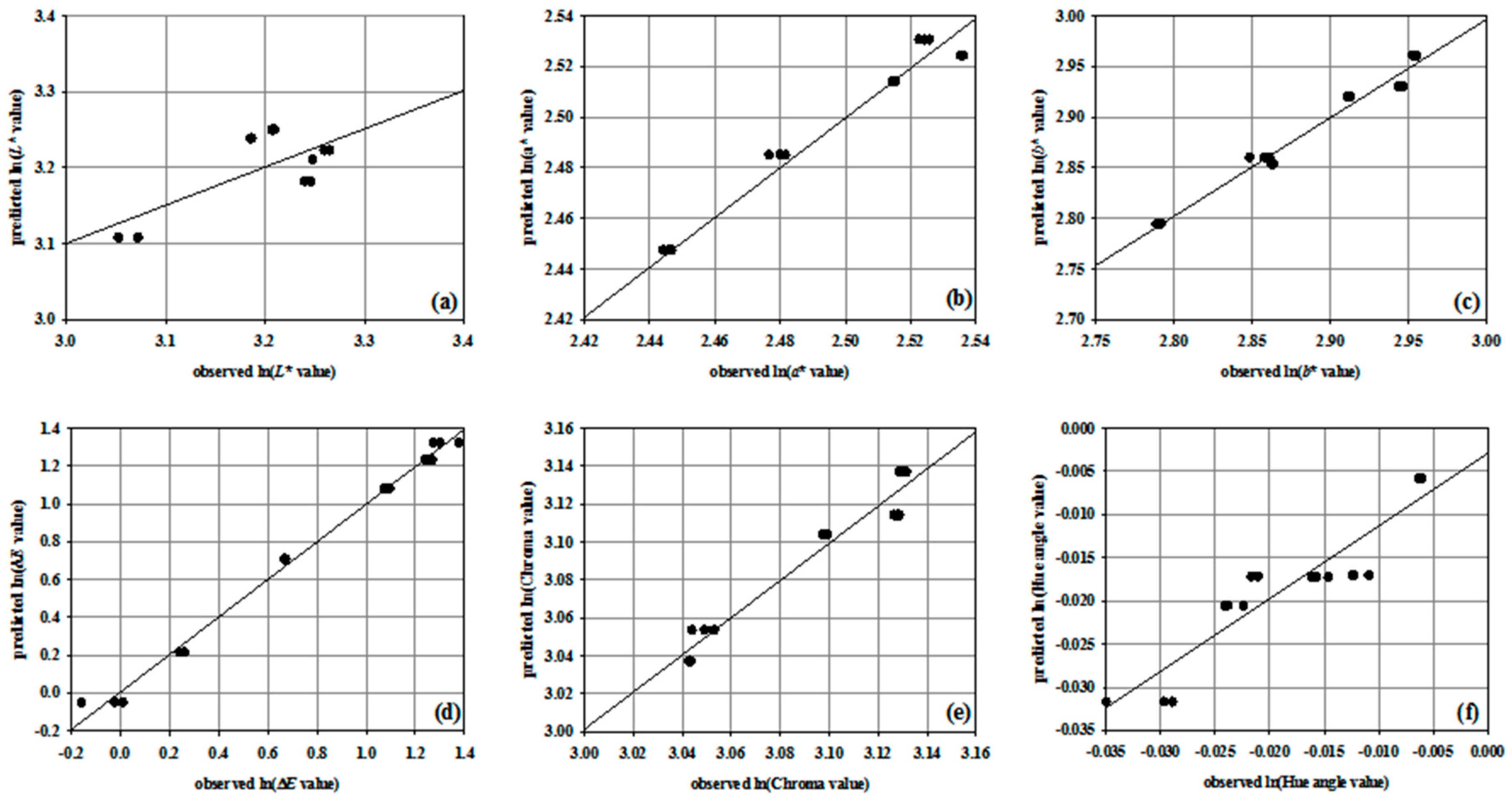
3.3. Linear Regression Models
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bae, J.H.; Park, J.H.; Im, S.S.; Song, D.K. Coffee and health. Integr. Med. Res. 2014, 3, 189–191. [Google Scholar] [CrossRef] [PubMed]
- Tajik, N.; Tajik, M.; Mack, I.; Enck, P. The potential effects of chlorogenic acid, the main phenolic components in coffee, on health: A comprehensive review of the literature. Eur. J. Nutr. 2017, 56, 2215–2244. [Google Scholar] [CrossRef] [PubMed]
- Franca, A.S.; Oliveira, L.S.; Mendonça, J.C.F.; Silva, X.A. Physical and chemical attributes of defective crude and roasted coffee beans. Food Chem. 2005, 90, 89–94. [Google Scholar] [CrossRef]
- Bicho, N.C.; Leitao, A.E.; Ramalho, J.C.; Lidon, F.C. Use of color parameters for roasted coffee assessment. Food Sci. Technol. (Campinas) 2012, 32, 436–442. [Google Scholar] [CrossRef]
- Anese, M.; Manzocco, L.; Nicoli, M.C. Modelling the secondary shelf life of ground roasted coffee. J. Agric. Food Chem. 2006, 54, 5571–5576. [Google Scholar] [CrossRef] [PubMed]
- Esteban-Diez, I.; Gonzalez-Saiz, J.M.; Pizzaro, C. Prediction of sensory properties of espresso from roasted coffee samples by near-infrared spectroscopy. Anal. Chim. Acta 2004, 525, 171–182. [Google Scholar] [CrossRef]
- Šimunac, D. Knjiga o Kavi. Grafen: Zagreb; Grafen: Zagreb, Croatia, 2004. (In Croatian) [Google Scholar]
- Demiray, E.; Thulek, Y.; Yilmaz, Y. Degradation kinetics of lycopene, β-carotene and ascorbic acid in tomatoes during hot air drying. LWT-Food Sci. Technol. 2013, 50, 172–176. [Google Scholar] [CrossRef]
- Topuz, A. A novel approach for color degradation kinetics of paprika as a function of water activity. LWT Food Sci. Technol. 2008, 41, 1672–1677. [Google Scholar] [CrossRef]
- Corzo, O.; Álvarez, C. Color change kinetics of mango at different maturity stages during air drying. J. Food Process. Preserv. 2012, 38, 208–517. [Google Scholar] [CrossRef]
- Shahabi, M.; Rafiee, S.; Mohtasebi, S.S.; Hosseinpour, S. Image analysis and green tea color change kinetics during thin-layer drying. Food Sci. Technol. Int. 2014, 20, 465–476. [Google Scholar] [CrossRef] [PubMed]
- Ochoa, M.R.; Kesseler, A.G.; De Michelis, A.; Mugridge, A.; Chaves, A.R. Kinetics of color change of raspberry, sweet (Prunus avium) and sour (Prunus cerasus) cherries preserves packed in glass containers: Light and room temperature effects. J. Food Eng. 2001, 49, 55–62. [Google Scholar] [CrossRef]
- Ren, K.; Tu, K.; Pan, L.; Chen, Y. Kinetic modelling of broccoli color changes during chilled storage. J. Food Process. Preserv. 2006, 30, 180–193. [Google Scholar] [CrossRef]
- Haugaard Sørensen, I.; Krag, J.; Pisecky, J.; Westergaard, V. Analytical Methods for Dry Milk Products; Niro Atomizer: Copenhagen, Denmark, 1978. [Google Scholar]
- McGuire, R.G. Reporting of objective color measurements. HortScience 1992, 27, 1254–1255. [Google Scholar]
- Serpen, A.; Gökmen, V. Evaluation of the Maillard reaction in potato crisps by acrylamide, antioxidant capacity and color. J. Food Comp. Anal. 2009, 22, 589–595. [Google Scholar] [CrossRef]
- Benković, M.; Belščak-Cvitanović, A.; Komes, D.; Bauman, I. Physical properties of non-agglomerated cocoa drink powder mixtures containing various types of sugars and sweeteners. Food Bioprocess Technol. 2013, 6, 1044–1058. [Google Scholar] [CrossRef]
- Maskan, M. Kinetics of color change of kiwifruits during hot air and microwave drying. J. Food Eng. 2001, 48, 169–175. [Google Scholar] [CrossRef]
- Duboz, R.; Versmisse, D.; Travers, M.; Ramat, E.; Shin, Y. Application of an evolutionary algorithm to the inverse parameter estimation of an individual-based model. Ecol. Model. 2010, 221, 840–849. [Google Scholar] [CrossRef]
- Cirilo, M.P.G.; Coelho, A.F.S.; Araujo, C.M.; Goncalves, F.R.B.; Nogueira, F.D.; Gloria, M.B.A. Profile and levels of bioactive amines in green and roasted coffee. Food Chem. 2003, 82, 397–402. [Google Scholar] [CrossRef]
- Sacchetti, G.; Di Mattia, C.; Pittia, P.; Mastrocola, D. Effect of roasting degree, equivalent thermal effect and coffee type on the radical scavenging activity of coffee brews and their phenolic fraction. J. Food Eng. 2009, 90, 74–80. [Google Scholar] [CrossRef]
- Kreuml, M.T.; Majchrzak, D.; Ploederl, B.; Koenig, J. Changes in sensory quality characteristics of coffee during storage. Food Sci. Nutr. 2014, 1, 267–272. [Google Scholar] [CrossRef] [PubMed]
- Rendon, M.Y.; Garcia Salva, T.; Bragagnolo, N. Impact of chemical changes on the sensory characteristics of coffee beans during storage. Food Chem. 2014, 147, 279–286. [Google Scholar] [CrossRef] [PubMed]
- Kallio, H.; Leino, M.; Koullias, K.; Kallio, S.; Kaitaranta, J. Headspace of roasted coffee as an indicator of storage time. Food Chem. 1990, 36, 135–148. [Google Scholar] [CrossRef]
- Marin, K.; Požrl, T.; Zlatić, E.; Plestenjak, A. A new aroma index to determine the aroma quality to roasted and ground coffee during storage. Food Technol. Biotechnol. 2008, 46, 442–447. [Google Scholar]
- Lampton, M. Damping-undamping strategies for the Levenberg-Marquart non-linear least-squares method. Comput. Phys. J. 1997, 11, 110–115. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least squares estimation of non-linear parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Cardelli, C.; Labudza, T.P. Application of Weibull hazard analysis to the determination of the shelf life of roasted and ground coffee. LWT-Food Sci. Technol. 2001, 34, 273–278. [Google Scholar] [CrossRef]
- Teunou, E.; Fitzpatrick, J.J. Effect of relative humidity and temperature on food powder flowability. J. Food Eng. 1999, 42, 109–116. [Google Scholar] [CrossRef]

| Sample | Parameter | Storage Time (Days) | |||||
|---|---|---|---|---|---|---|---|
| 30 | 60 | 90 | 120 | 150 | 180 | ||
| V1KMK | L* | 24.74 ± 0.03 | 25.62 ± 0.09 | 25.73 ± 0.00 | 21.45 ± 0.24 | 24.19 ± 0.01 | 26.13 ± 0.07 |
| a* | 12.48 ± 0.02 | 12.62 ± 0.01 | 12.37 ± 0.01 | 11.93 ± 0.03 | 11.54 ± 0.01 | 11.00 ± 0.02 | |
| b* | 19.18 ± 0.02 | 19.01 ± 0.03 | 18.40 ± 0.02 | 17.39 ± 0.11 | 17.51 ± 0.01 | 16.29 ± 0.03 | |
| ΔE | / | 0.91 ± 0.08 | 1.27 ± 0.01 | 3.78 ± 0.21 | 1.99 ± 0.01 | 3.52 ± 0.05 | |
| Chroma | 22.88 ± 0.03 | 22.82 ± 0.02 | 22.17 ± 0.02 | 21.09 ± 0.09 | 20.97 ± 0.01 | 19.66 ± 0.03 | |
| Hue | 0.99 ± 0.01 | 0.98 ± 0.00 | 0.98 ± 0.00 | 0.97 ± 0.00 | 0.99 ± 0.00 | 0.98 ± 0.00 | |
| Moisture content | 1.28 ± 0.01 | 1.46 ± 0.01 | 1.68 ± 0.02 | 1.82 ± 0.01 | 1.87 ± 0.01 | 1.97 ± 0.02 | |
| RH | 64 ± 1.00 | 32 ± 1.00 | 58 ± 1.00 | 45 ± 1.00 | 32 ± 1.00 | 20 ± 1.00 | |
| T | 18 ± 0.20 | 18 ± 0.20 | 17 ± 0.10 | 17 ± 0.20 | 15 ± 0.00 | 14 ± 0.00 | |
| L1KMK | L* | 28.23 ± 0.04 | 24.17 ± 0.85 | 25.46 ± 0.01 | 23.78 ± 0.00 | 24.48 ± 0.01 | 23.81 ± 0.02 |
| a* | 11.25 ± 0.04 | 11.94 ± 0.19 | 12.07 ± 0.00 | 12.20 ± 0.01 | 12.46 ± 0.01 | 12.08 ± 0.01 | |
| b* | 19.29 ± 0.01 | 17.55 ± 0.50 | 17.63 ± 0.02 | 18.23 ± 0.01 | 18.87 ± 0.01 | 17.70 ± 0.03 | |
| ΔE | / | 1.81 ± 0.68 | 1.76 ± 0.01 | 1.37 ± 0.00 | 0.40 ± 0.01 | 1.79 ± 0.01 | |
| Chroma | 22.33 ± 0.03 | 21.22 ± 0.51 | 21.36 ± 0.02 | 21.94 ± 0.00 | 22.61 ± 0.01 | 21.43 ± 0.02 | |
| Hue | 1.04 ± 0.00 | 0.97 ± 0.01 | 0.97 ± 0.00 | 0.98 ± 0.00 | 0.99 ± 0.00 | 0.97 ± 0.00 | |
| Moisture content | 1.01 ± 0.01 | 1.41 ± 0.01 | 1.66 ± 0.01 | 2.25 ± 0.01 | 2.21 ± 0.10 | 2.27 ± 0.02 | |
| RH | 58 ± 1.00 | 64 ± 1.00 | 53 ± 1.00 | 44 ± 1.00 | 28 ± 1.00 | 20 ± 1.00 | |
| T | 18 ± 0.00 | 18 ± 0.00 | 16 ± 0.20 | 16 ± 0.10 | 14 ± 0.10 | 20 ± 0.10 | |
| Parameter | Coefficient | R2 | Correlation Coefficient | Maximum Error | Mean Squared Error | Mean Absolute Error | |
|---|---|---|---|---|---|---|---|
| L* | b0 b1 b2 b3 | 40.590 −0.236 −0.028 −0.085 | 0.737 | 0.883 | 2.810 | 0.658 | 0.326 |
| a* | b0 b1 b2 b3 | 12.82 0.134 0.022 −0.075 | 0.842 | 0.934 | 0.360 | 0.022 | 0.084 |
| b* | b0 b1 b2 b3 | 64.140 −0.213 −0.107 −0.265 | 0.528 | 0.770 | 0.957 | 0.221 | 0.296 |
| ΔE | b0 b1 b2 b3 | 0.225 1.208 0.147 0.5442 | 0.611 | 0.817 | 2.325 | 1.115 | 0.596 |
| Chroma | b0 b1 b2 b3 | 43.780 −0.076 −0.038 −0.179 | 0.519 | 0.759 | 1.007 | 0.144 | 0.237 |
| Hue angle | b0 b1 b2 b3 | 1.925 −0.175 −0.780 −0.102 | 0.488 | 0.836 | 0.044 | 0.0003 | 0.009 |
| L* | a* | b* | ||||
| Parameter | Value | p-Value | Value | p-Value | Value | p-Value |
| b0 | 68.793 ± 18.421 † | 0.002 | 13.259 ± 1.541 † | 0 | 53.819 ± 13.173 † | 0.001 |
| b1 | −0.284 ± 0.038 † | 0 | 0.098 ± 0.017 † | 0 | −0.156 ± 0.036 † | 0 |
| b2 | −0.085 ± 0.027 † | 0.007 | 0.012 ± 0.012 | 0.305 | −0.084 ± 0.025 † | 0.004 |
| b3 | −0.192 ± 0.069 † | 0.015 | −0.071 ± 0.029 † | 0.031 | −0.242 ± 0.063 † | 0.002 |
| ΔE | Chroma | Hue Angle | ||||
| Parameter | Value | p-Value | Value | p-Value | Value | p-Value |
| b0 | 0.006 ± 0.017 | 0.741 | 47.904 ± 7.659 † | 0 | 1.567 ± 0.231 † | 0 |
| b1 | 1.865 ± 0.501 † | 0.002 | −0.080 ± 0.024 † | 0.004 | −0.117 ± 0.021 † | 0 |
| b2 | 0.519 ± 0.269 | 0.075 | −0.055 ± 0.016 † | 0.004 | −0.045 ± 0.015 † | 0.008 |
| b3 | 1.214 ± 0.713 | 0.111 | −0.190 ± 0.041 † | 0 | −0.081 ± 0.038 † | 0.048 |
| Parameter | Coefficient | R2 | Correlation Coefficient | Maximum Error | Mean Squared Error | Mean Absolute Error | |
|---|---|---|---|---|---|---|---|
| L* | b0 b1 b2 b3 | n/m n/m n/m n/m | n/m | n/m | n/m | n/m | n/m |
| a* | b0 b1 b2 b3 | 9.605 −0.016 0.123 −0.085 | 0.977 | 0.990 | 0.204 | 0.007 | 0.053 |
| b* | b0 b1 b2 b3 | 32.220 −0.181 0.157 −0.390 | 0.965 | 0.987 | 0.400 | 0.036 | 0.1257 |
| ΔE | b0 b1 b2 b3 | 0.011 4.580 −0.530 1.597 | 0.738 | 0.869 | 1.781 | 0.478 | 0.447 |
| Chroma | b0 b1 b2 b3 | 29.760 −0.128 0.145 −0.288 | 0.973 | 0.989 | 0.431 | 0.035 | 0.122 |
| Hue angle | b0 b1 b2 b3 | 2.301 −0.072 0.071 −0.386 | 0.642 | 0.856 | 0.011 | 0.000 | 0.003 |
| L* | a* | b* | ||||
| Parameter | Value | p-Value | Value | p-Value | Value | p-Value |
| b0 | 47.873 ± 72.388 | 0.519 | 6.274 ± 1.151 † | 0 | 13.940 ± 4.795 † | 0.011 |
| b1 | −0.262 ± 0.178 | 0.163 | −0.009 ± 0.020 | 0.671 | −0.142 ± 0.039 † | 0.003 |
| b2 | −0.066 ± 0.170 | 0.704 | 0.087 ± 0.019 † | 0 | 0.088 ± 0.038 † | 0.035 |
| b3 | −0.102 ± 0.786 | 0.898 | 0.114 ± 0.091 | 0.223 | −0.004 ± 0.174 | 0.983 |
| ΔE | Chroma | Hue Angle | ||||
| Parameter | Value | p-Value | Value | p-Value | Value | p-Value |
| b0 | 0.002 ± 0.002 | 0.889 | 13.165 ± 3.935 † | 0.005 | 1.676 ± 0.158 † | 0 |
| b1 | 7.818 ± 2.474 † | 0.007 | −0.096 ± 0.034 † | 0.013 | −0.077 ± 0.010 † | 0 |
| b2 | 0.342 ± 0.837 | 0.689 | 0.078 ± 0.033 † | 0.033 | 0.031 ± 0.009 † | 0.006 |
| b3 | 1.217 ± 3.081 | 0.699 | 0.089 ± 0.151 | 0.567 | −0.219 ± 0.045 † | 0 |
| Parameter | Coefficient | R2 | Correlation Coefficient | Maximum Error | Mean Squared Error | Mean Absolute Error | |
|---|---|---|---|---|---|---|---|
| L* | β0 β1 β2 β3 | 3.710 −0.237 −0.028 −0.087 | 0.714 | 0.874 | 0.114 | 0.001 | 0.013 |
| a* | β0 β1 β2 β3 | 2.590 0.119 0.018 −0.079 | 0.856 | 0.937 | 0.032 | 0.000 | 0.007 |
| b* | β0 β1 β2 β3 | 2.631 0.022 0.039 0.033 | 0.400 | 0.636 | 0.029 | 0.000 | 0.009 |
| ΔE | β0 β1 β2 β3 | 4.865 −0.606 −0.119 −0.978 | 0.724 | 0.859 | 0.212 | 0.008 | 0.051 |
| Chroma | β0 β1 β2 β3 | 3.791 −0.077 −0.039 −0.182 | 0.509 | 0.750 | 0.047 | 0.000 | 0.011 |
| Hue angle | β0 β1 β2 β3 | 0.100 0.020 −0.001 −0.047 | 0.561 | 0.806 | 0.012 | 0.000 | 0.002 |
| L* | a* | b* | ||||
| Parameter | Value | p-value | Value | p-Value | Value | p-Value |
| β0 | 4.202 ± 0.272 † | 0 | 2.568 ± 0.119 † | 0 | 3.980 ± 0.253 † | 0 |
| β1 | −0.275 ± 0.039 † | 0 | 0.102 ± 0.017 † | 0 | −0.152 ± 0.036 † | 0.001 |
| β2 | −0.081 ± 0.027 † | 0.009 | 0.014 ± 0.012 | 0.246 | −0.083 ± 0.025 † | 0.005 |
| β3 | −0.188 ± 0.069 † | 0.017 | −0.068 ± 0.030 † | 0.041 | −0.243 ± 0.063 † | 0.002 |
| ΔE | Chroma | Hue Angle | ||||
| Parameter | Value | p-Value | Value | p-Value | Value | p-Value |
| β0 | −1.784 ± 1.356 | 0.224 | 3.871 ± 0.164 † | 0 | 0.439 ± 0.148 † | 0.010 |
| β1 | 0.579 ± 0.319 | 0.097 | −0.079 ± 0.024 † | 0.005 | −0.116 ± 0.021 † | 0 |
| β2 | 0.153 ± 0.147 | 0.319 | −0.055 ± 0.016 † | 0.0045 | −0.044 ± 0.015 † | 0.011 |
| β3 | 0.816 ± 0.307 † | 0.022 | −0.191 ± 0.042 † | 0 | −0.081 ± 0.038 | 0.051 |
| Parameter | Coefficient | R2 | Correlation Coefficient | Maximum Error | Mean Squared Error | Mean Absolute Error | |
|---|---|---|---|---|---|---|---|
| L* | β0 β1 β2 β3 | n/m n/m n/m n/m | n/m | n/m | n/m | n/m | n/m |
| a* | β0 β1 β2 β3 | 2.272 −0.015 0.125 −0.090 | 0.979 | 0.991 | 0.016 | 0.000 | 0.004 |
| b* | β0 β1 β2 β3 | 3.471 −0.181 0.157 −0.389 | 0.967 | 0.987 | 0.021 | 0.000 | 0.007 |
| ΔE | β0 β1 β2 β3 | −28.13 2.801 −3.502 13.890 | 0.843 | 0.933 | 0.634 | 0.049 | 0.104 |
| Chroma | β0 β1 β2 β3 | 3.530 −0.124 0.157 −0.352 | 0.974 | 0.990 | 0.020 | 0.000 | 0.006 |
| Hue angle | β0 β1 β2 β3 | 0.340 −0.072 0.017 −0.138 | 0.786 | 0.892 | 0.009 | 0.000 | 0.002 |
| L* | a* | b* | ||||
| Parameter | Value | p-Value | Value | p-Value | Value | p-Value |
| β0 | 7.591 ± 1.343 † | 0 | 2.077 ± 0.174 † | 0 | 3.608 ± 0.257 † | 0 |
| β1 | −0.443 ± 0.148 † | 0.009 | −0.021 ± 0.019 | 0.287 | −0.185 ± 0.028 † | 0 |
| β2 | 0.254 ± 0.139 | 0.089 | 0.107 ± 0.018 † | 0 | 0.173 ± 0.027 † | 0 |
| β3 | −1.829 ± 0.639 † | 0.012 | 0.004 ± 0.083 | 0.958 | −0.457 ± 0.122 † | 0.002 |
| ΔE | Chroma | Hue Angle | ||||
| Parameter | Value | p-Value | Value | p-Value | Value | p-Value |
| β0 | −29.087 ± 1.412 † | 0 | 3.441 ± 0.215 † | 0 | 0.516 ± 0.094 | 0 |
| β1 | 6.174 ± 0.267 † | 0 | −0.135 ± 0.024 † | 0 | −0.077 ± 0.010 | 0 |
| β2 | −2.291 ± 0.143 † | 0 | 0.152 ± 0.022 † | 0 | 0.031 ± 0.009 | 0.006 |
| β3 | 12.501 ± 0.648 † | 0.022 | −0.313 ± 0.102 † | 0.008 | −0.219 ± 0.045 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benković, M.; Tušek, A.J. Regression Models for Description of Roasted Ground Coffee Powder Color Change during Secondary Shelf-Life as Related to Storage Conditions and Packaging Material. Beverages 2018, 4, 16. https://doi.org/10.3390/beverages4010016
Benković M, Tušek AJ. Regression Models for Description of Roasted Ground Coffee Powder Color Change during Secondary Shelf-Life as Related to Storage Conditions and Packaging Material. Beverages. 2018; 4(1):16. https://doi.org/10.3390/beverages4010016
Chicago/Turabian StyleBenković, Maja, and Ana Jurinjak Tušek. 2018. "Regression Models for Description of Roasted Ground Coffee Powder Color Change during Secondary Shelf-Life as Related to Storage Conditions and Packaging Material" Beverages 4, no. 1: 16. https://doi.org/10.3390/beverages4010016
APA StyleBenković, M., & Tušek, A. J. (2018). Regression Models for Description of Roasted Ground Coffee Powder Color Change during Secondary Shelf-Life as Related to Storage Conditions and Packaging Material. Beverages, 4(1), 16. https://doi.org/10.3390/beverages4010016






