Review of Biomechanical Studies and Finite Element Modeling of Sternal Closure Using Bio-Active Adhesives
Abstract
1. Introduction
2. Relevant Anatomy of Median Sternotomy
3. Modeling Sternal Closure
3.1. Sternal Closure Techniques: Wiring and Adhesives
3.1.1. Wiring
3.1.2. Adhesives
3.2. Finite Element Models
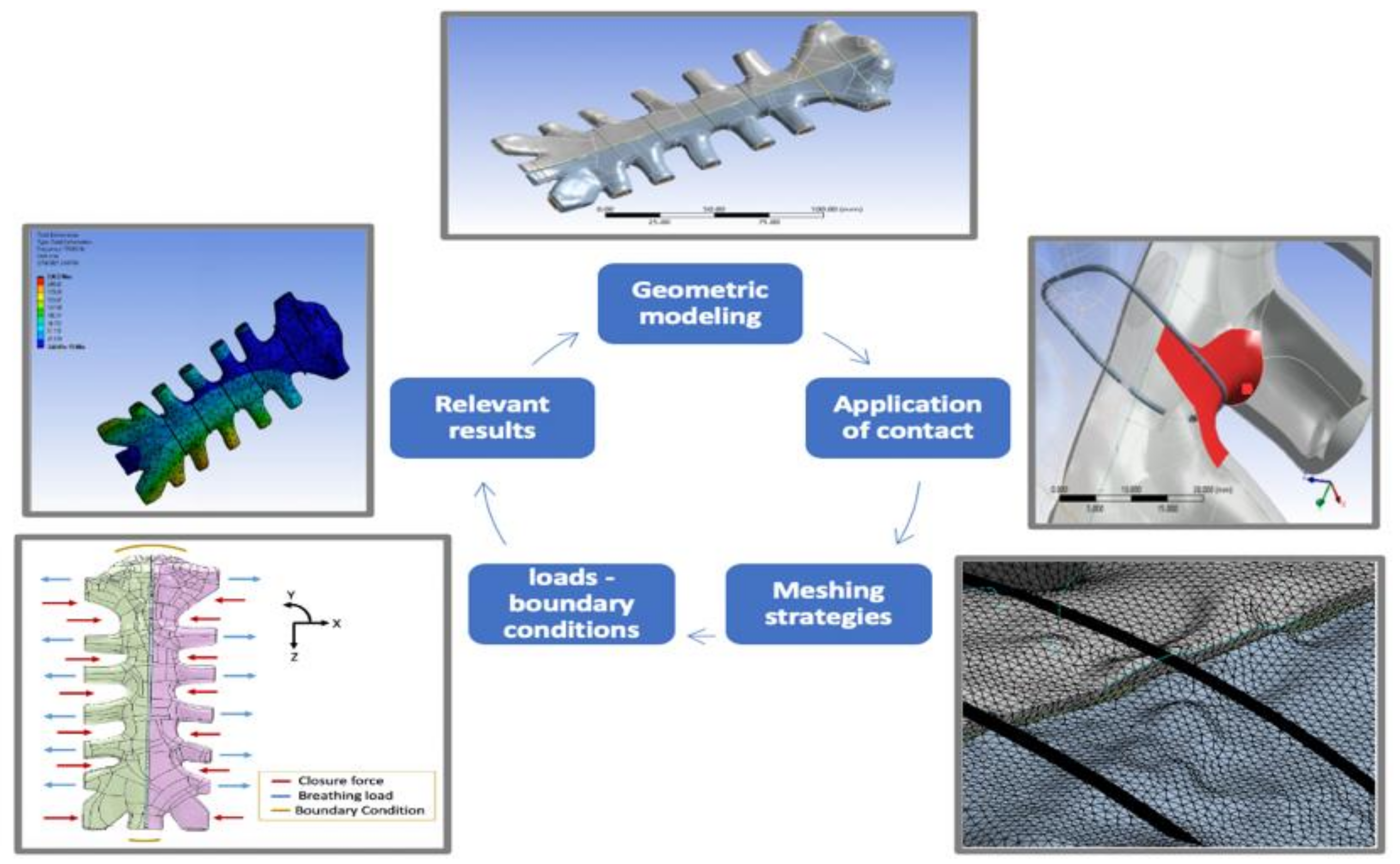
3.2.1. Geometric Modeling and Material Properties
3.2.2. Mesh Refinement and Mesh Sensitivity
3.2.3. Mesh Quality (Mesh Metrics)
3.2.4. High Order Meshing
3.2.5. Mesh Methods
3.2.6. Contact Surfaces
3.2.7. Applied Loads and Boundary Conditions
- (1)
- ‘c’ ends are fixed, ‘a’ ends are unconstrained, allowing movements in all directions;
- (2)
- ‘c’ ends are fixed, ‘b’ ends are constrained with the sternum by bonded contact;
- (3)
- ‘Tx = 0, Ry = Rz = 0′. Joints ‘a’ translation is constrained in x-axis and rotations are constrained in y and z axis;
- (4)
- ‘Ty = 0, Rx = Rz = 0′. Joints ‘a’ translation is constrained in y-axis and rotations are constrained in x and z axis;
- (5)
- ‘Tz = 0, Rx = Ry = 0′. Joints ‘a’ translation is constrained in z-axis and rotations are constrained in x and y axis;
- (6)
- ‘Tx = Ty = Tz = 0, Rx = Ry = Rz= 0′ the cartilage joints were set as fixed condition.
3.3. Numerical Solutions and Evaluation of Modeled Sternal Fixation Systems
3.4. Limitations of FEA in Studying Sternal Closure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mr, H.; Ramzi, P. Development of a Standardized Method for Comparing Biomechanical Properties of Various Sternal Closure Techniques. Master’s Thesis, The Faculty of California Polytechnic State University, San Luis Obispo, CA, USA, 2012. [Google Scholar]
- Awad, M.; Czer, L.; Mirocha, J.; Ruzza, A.; Rafiei, M.; Reich, H.; De Robertis, M.; Rihbany, K.; Pinzas, J.; Ramzy, D.; et al. Prior Sternotomy Increases the Mortality and Morbidity of Adult Heart Transplantation. Transplant. Proc. 2015, 47, 485–497. [Google Scholar] [CrossRef] [PubMed]
- Vestergaard, R.F.; Jensen, H.; Vind-Kezunovic, S.; Jakobsen, T.; Søballe, K.; Hasenkam, J.M. Bone healing after median sternotomy: A comparison of two hemostatic devices. J. Cardiothorac. Surg. 2010, 5, 117. [Google Scholar] [CrossRef] [PubMed]
- Dalton, M.L.; Connally, S.R.; Sealy, W.C. Julian’s reintroduction of Milton’s operation. Ann. Thorac. Surg. 1992, 53, 532. [Google Scholar] [CrossRef]
- Russo, M.J.; Gnezda, J.; Merlo, A.; Johnson, E.M.; Hashmi, M.; Raman, J. The Arrowhead Ministernotomy with Rigid Sternal Plate Fixation: A Minimally Invasive Approach for Surgery of the Ascending Aorta and Aortic Root. Minim. Invasive Surg. 2014, 2014, 681371. [Google Scholar] [CrossRef] [PubMed]
- Schiraldi, L.; Jabbour, G.; Centofanti, P.; Giordano, S.; Abdelnour, E.; Gonzalez, M.; Raffoul, W.; di Summa, P.G. Deep sternal wound infections: Evidence for prevention, treatment, and reconstructive surgery. Arch. Plast. Surg. 2019, 46, 291–302. [Google Scholar] [CrossRef]
- Ott, D.A.; Cooley, D.A.; Solis, R.T.; Harrison, C.B., III. Wound complications after median sternotomy: A study of 61 patients from a consecutive series of 9,279. Cardiovasc. Dis. 1980, 7, 104. [Google Scholar] [PubMed]
- Goodman, L.R.; Kay, H.R.; Teplick, S.K.; Mundth, E.D. Complications of median sternotomy: Computed tomographic evaluation. Am. J. Roentgenol. 1983, 141, 225–230. Available online: http://www.ajronline.org/content/141/2/225.full.pdf (accessed on 1 May 2012). [CrossRef]
- Benjamin, E.J.; Blaha, M.J.; Chiuve, S.E.; Chamberlain, A.M.; Chang, A.R.; Cheng, S.; Chiuve, S.E.; Cushman, M.; Delling, F.N.; Deo, R.; et al. Heart disease and stroke statistics—2018 update. Circulation 2018, 137, e475–e480. [Google Scholar] [CrossRef]
- Plass, A.; Grünenfelder, J.; Reuthebuch, O.; Vachenauer, R.; Gauer, J.-M.; Zünd, G.; Genoni, M. New Transverse Plate Fixation System for Complicated Sternal Wound Infection after Median Sternotomy. Ann. Thorac. Surg. 2007, 83, 1210–1212. [Google Scholar] [CrossRef]
- Sharma, R.; Puri, D.; Panigrahi, B.P.; Virdi, I.S. A modified parasternal wire technique for prevention and treatment of sternal dehiscence. Ann. Thorac. Surg. 2004, 77, 210–213. [Google Scholar] [CrossRef]
- Centofanti, P.; La Torre, M.; Barbato, L.; Verzini, A.; Patane, F.; di Summa, M. Sternal Closure Using Semirigid Fixation with Thermoreactive Clips. Soc. Thorac. Surg. 2002, 74, 943–945. [Google Scholar] [CrossRef]
- Sidhu, V.; Towler, M.R.; Papini, M. Measurement of Adhesion of Sternal Wires to a Novel Bioactive Glass-Based Adhesive. J. Funct. Biomater. 2019, 10, 37. [Google Scholar] [CrossRef] [PubMed]
- Baskett, R.J.; MacDougall, E.C.; Ross, D.B. Is mediastinitis a preventable complication? A 10-year review. Ann. Thorac. Surg. 1999, 67, 462–465. [Google Scholar] [CrossRef]
- Grapow, M.T.R.; Melly, L.F.; Eckstein, F.S.; Reuthebuch, O.T. A new cable-tie based sternal closure system: Description of the device, technique of implantation and first clinical evaluation. J. Cardiothorac. Surg. 2012, 7, 59. [Google Scholar] [CrossRef] [PubMed]
- Clarkin, O.; Boyd, D.; Towler, M. Strontium-based Glass Polyalkenoate Cements for Luting Applications in the Skeleton. J. Biomater. Appl. 2008, 24, 483–502. [Google Scholar] [CrossRef]
- Kobayashi, H.; Turner, A.S.; Seim, H.B., III; Kawamoto, T.; Bauer, T.W. Evaluation of a silica-containing bone graft substitute in a vertebral defect model. J. Biomed. Mater. Res. Part A Off. J. Soc. Biomater. Jpn. Soc. Biomater. Aust. Soc. Biomater. Korean Soc. Biomater. 2010, 92, 596–603. [Google Scholar] [CrossRef] [PubMed]
- Martini, F.; Nath, J.L.; Bartholomew, E.F. Fundamentals of Anatomy and Physiology; Cengage Learning: Boston, MA, USA, 2018; Volume 1. [Google Scholar]
- Baker, G.F.; Tortora, G.J.; Nostakos, N.P.A. Principles of Anatomy and Physiology. Am. J. Nurs. 1976, 76, 477. [Google Scholar] [CrossRef]
- Ellis, H.; Mahadevan, V. Clinical Anatomy: Applied Anatomy for Students and Junior Doctors; Wiley-Blackwell: Hoboken, NJ, USA, 2018. [Google Scholar]
- Keith, A. (1) A Treatise on Applied Anatomy (2) The Human Sternum (3) Der Gang des Menschen. Nature 1904, 71, 145–147. [Google Scholar] [CrossRef][Green Version]
- Graeber, G.M.; Nazim, M. The Anatomy of the Ribs and the Sternum and Their Relationship to Chest Wall Structure and Function. Thorac. Surg. Clin. 2007, 17, 473–489. [Google Scholar] [CrossRef]
- Dasika, U.K.; Trumble, D.R.; Magovern, A.J. Lower sternal reinforcement improves the stability of sternal closure. Ann. Thorac. Surg. 2003, 75, 1618–1621. [Google Scholar] [CrossRef]
- Stewart, T.D. Metamorphosis of the joints of the sternum in relation to age changes in other bones. Am. J. Phys. Anthropol. 1954, 12, 519–536. [Google Scholar] [CrossRef] [PubMed]
- Robicsek, F.; Fokin, A.; Cook, J.; Bhatia, D. Sternal Instability after Midline Sternotomy. Thorac. Cardiovasc. Surg. 2000, 48, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Elfström, A.; Grunditz, A. Evaluation of Sternum Closure Techniques Using Finite Element Analysis; The KTH Royal Institute of Technology: Flemingsberg, Stockholm, Sweden, 2013. [Google Scholar]
- Capek, L.; Henys, P.; Kalab, M.; Solfronk, P. Failure of sternal wires depends on the number of turns and plastic deformation: Combined experimental and computational approach. Interact. Cardiovasc. Thorac. Surg. 2018, 26, 777–782. [Google Scholar] [CrossRef] [PubMed]
- Losanoff, E.J.; Collier, A.D.; Wagner-Mann, C.C.; Richman, B.W.; Huff, H.; Hsieh, F.-H.; Diaz-Arias, A.; Jones, J.W. Biomechanical comparison of median sternotomy closures. Ann. Thorac. Surg. 2004, 77, 203–209. [Google Scholar] [CrossRef]
- Casha, A.R.; Camilleri, L.; Manché, A.; Gauci, M.; Magri, C.J.; Agius, A.; Yang, L. Effect of sternal wire twisting on sternotomy closure rigidity. Indian J. Thorac. Cardiovasc. Surg. 2017, 34, 25–30. [Google Scholar] [CrossRef]
- Shafi, A.M.A.; Abuelgasim, E.; Abuelgasim, B.; Iddawela, S.; Harky, A. Sternal closure with single compared with double or figure of 8 wires in obese patients following cardiac surgery: A systematic review and meta-analysis. J. Card. Surg. 2021, 36, 1072–1082. [Google Scholar] [CrossRef]
- Fedak, P.W.; Kolb, E.; Borsato, G.; Frohlich, D.E.; Kasatkin, A.; Narine, K.; Akkarapaka, N.; King, K.M. Kryptonite Bone Cement Prevents Pathologic Sternal Displacement. Ann. Thorac. Surg. 2010, 90, 979–985. [Google Scholar] [CrossRef]
- Fedak, P.W.; Kasatkin, A. Enhancing sternal closure using Kryptonite bone adhesive: Technical report. Surg. Innov. 2011, 18, NP8–NP11. [Google Scholar] [CrossRef]
- Subasi, O.; Oral, A.; Torabnia, S.; Erdogan, D.; Erdogan, M.B.; Lazoglu, I. In Silico Analysis of Elastomer-Coated Cerclage for Reducing Sternal Cut-Through in High-Risk Patients. J. Biomech. Eng. 2021, 143, 091007. [Google Scholar] [CrossRef]
- Jutley, R.S.; Watson, A.M.; Shepherd, D.E.T.; Hukins, D.W.L. Finite element analysis of stress around a sternum screw used to prevent sternal dehiscence after heart surgery. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2002, 216, 315–321. [Google Scholar] [CrossRef]
- Brown, R.; Esmore, D.; Lawson, C. Improved sternal fixation in the transsternal bilateral thoracotomy incision. J. Thorac. Cardiovasc. Surg. 1996, 112, 137–141. [Google Scholar] [CrossRef][Green Version]
- Stelly, M.M.; Rodning, C.B.; Stelly, T.C. Reduction in deep sternal wound infection with use of a peristernal cable-tie closure system: A retrospective case series. J. Cardiothorac. Surg. 2015, 10, 166. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kalush, S.L.; Bonchek, L.I. Peristernal Closure of Median Sternotomy Using Stainless Steel Bands. Ann. Thorac. Surg. 1976, 21, 172–173. [Google Scholar] [CrossRef]
- Alhalawani, A.M.; Towler, M.R. A review of sternal closure techniques. J. Biomater. Appl. 2013, 28, 483–497. [Google Scholar] [CrossRef]
- Casha, A.; Yang, L.; Kay, P.; Saleh, M.; Cooper, G. A biomechanical study of median sternotomy closure techniques1. Eur. J. Cardio-Thoracic Surg. 1999, 15, 365–369. [Google Scholar] [CrossRef]
- Karigyo, C.J.T.; Pesarini, A. A Simple Modification of the Conventional Figure-of-Eight Sternal Closure Technique. Braz. J. Cardiovasc. Surg. 2019, 34, 406–411. [Google Scholar] [CrossRef]
- De Cicco, G.; Tosi, D.; Crisci, R.; Bortolami, A.; Aquino, T.M.; Prencipe, A.; Di Matteo, G.; Benussi, S. Use of new cannulated screws for primary sternal closure in high risk patients for sternal dehiscence. J. Thorac. Dis. 2019, 11, 4538–4543. [Google Scholar] [CrossRef]
- Mehrvar, C.; Kuzyk, P.; Cohen, G.; Safir, O.; Zalzal, P.; Alhalawani, A.; Towler, M.R.; Papini, M. Novel adhesives for sternal fixation and stabilization: A biomechanical analysis. Clin. Biomech. 2019, 62, 66–71. [Google Scholar] [CrossRef]
- Mehrvar, C.; Kuzyk, P.; Shamlou, J.; Safir, O.; Zalzal, P.; Alhalawani, A.; Towler, M.R.; Papini, M. Novel adhesives for distal radius fixation: A biomechanical analysis. J. Mech. Behav. Biomed. Mater. 2019, 89, 99–106. [Google Scholar] [CrossRef]
- Uzun, I.; Keskin, C.; Güler, B. The sealing ability of novel Kryptonite adhesive bone cement as a retrograde filling material. J. Dent. Res. Dent. Clin. Dent. Prospect. 2016, 10, 189–193. [Google Scholar] [CrossRef]
- Lim, J.; Jariwala, A.; Wigderowitz, C.; Drew, T. The Use of Bone Adhesive for Fracture Fixation in Long Bones—A Biomechanical Study. Front. Biol. Life Sci. 2014, 2, 29–33. [Google Scholar] [CrossRef]
- Doumit, G.D.; Meisler, E.; Sidaoui, J.; Zins, J.E.; Papay, F.A. The Expansile Properties of Kryptonite Relating to Cranioplasty. J. Craniofacial Surg. 2014, 25, 880–883. [Google Scholar] [CrossRef] [PubMed]
- Pradeep, A.; Rangasamy, J.; Varma, P.K. Recent developments in controlling sternal wound infection after cardiac surgery and measures to enhance sternal healing. Med. Res. Rev. 2021, 41, 709–724. [Google Scholar] [CrossRef] [PubMed]
- Muehrcke, D.D.; Barberi, P.; Shimp, W.M. Calcium Phosphate Cements to Control Bleeding in Osteoporotic Sternums. Ann. Thorac. Surg. 2007, 84, 259–261. [Google Scholar] [CrossRef]
- Mehrvar, C.; Deignan, E.; Hurtig, M.; Cohen, G.; Zalzal, P.; Safir, O.; Alhalawani, A.; Papini, M.; Towler, M.R. In vivo analysis of a proprietary glass-based adhesive for sternal fixation and stabilization using rabbit and sheep models. J. Mater. Sci. Mater. Med. 2021, 32, 53. [Google Scholar] [CrossRef]
- Panagiotopouloou, V.C. Adhesives for Treatment of Bone Fractures: A Review of the State-of-The Art; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Chung, K.C.; Shauver, M.; Yin, H.; Kim, H.M.; Baser, O.; Birkmeyer, J.D. Variations in the Use of Internal Fixation for Distal Radial Fracture in the United States Medicare Population. J. Bone Jt. Surg. 2011, 93, 2154–2162. [Google Scholar] [CrossRef]
- Walls, A. Glass polyalkenoate (glass-ionomer) cements: A review. J. Dent. 1986, 14, 231–246. [Google Scholar] [CrossRef]
- Darling, M.; Hill, R. Novel polyalkenoate (glass-ionomer) dental cements based on zinc silicate glasses. Biomaterials 1994, 15, 299–306. [Google Scholar] [CrossRef]
- Inzana, J.A.; Olvera, D.; Fuller, S.M.; Kelly, J.P.; Graeve, O.A.; Schwarz, E.M.; Kates, S.L.; Awad, H.A. 3D printing of composite calcium phosphate and collagen scaffolds for bone regeneration. Biomaterials 2014, 35, 4026–4034. [Google Scholar] [CrossRef]
- Marx, D.; Yazdi, A.R.; Papini, M.; Towler, M. A review of the latest insights into the mechanism of action of strontium in bone. Bone Rep. 2020, 12, 100273. [Google Scholar] [CrossRef]
- Wren, A.; Boyd, D.; Towler, M.R. The processing, mechanical properties and bioactivity of strontium based glass polyalkenoate cements. J. Mater. Sci. Mater. Electron. 2008, 19, 1737–1743. [Google Scholar] [CrossRef] [PubMed]
- Lewis, G. Injectable bone cements for use in vertebroplasty and kyphoplasty: State-of-the-art review. J. Biomed. Mater. Res. Part B Appl. Biomater. 2006, 76, 456–468. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Skrzypiec, D.M.; Pollintine, P.; Adams, M.; Annesley-Williams, D.J.; Dolan, P. Mechanical efficacy of vertebroplasty: Influence of cement type, BMD, fracture severity, and disc degeneration. Bone 2007, 40, 1110–1119. [Google Scholar] [CrossRef] [PubMed]
- Sukumoda, E.; Nemoto, R.; Nozaki, K.; Omori, S.; Noda, M.; Sato, M.; Takita, M.; Miura, H. Increased Stress Concentration in Prosthesis, Adhesive Cement, and Periodontal Tissue with Zirconia RBFDPs by the Reduced Alveolar Bone Height. J. Prosthodont. 2021, 30, 617–624. [Google Scholar] [CrossRef] [PubMed]
- Khader, B.A.; Peel, S.A.F.; Towler, M.R. An Injectable Glass Polyalkenoate Cement Engineered for Fracture Fixation and Stabilization. J. Funct. Biomater. 2017, 8, 25. [Google Scholar] [CrossRef]
- Lieberman, I.H.; Togawa, D.; Kayanja, M.M. Vertebroplasty and kyphoplasty: Filler materials. Spine J. 2005, 5, S305–S316. [Google Scholar] [CrossRef]
- Pfeiffer, F.M. The Use of Finite Element Analysis to Enhance Research and Clinical Practice in Orthopedics. J. Knee Surg. 2016, 29, 149–158. [Google Scholar] [CrossRef]
- Tran, M.; Varzaly, J.A.; Chan, J.C.; Caplash, Y.; Worthington, M.G. Novel Sternal Reconstruction with Custom Three-Dimensional–Printed Titanium PoreStar Prosthesis. Innov. Technol. Tech. Cardiothorac. Vasc. Surg. 2018, 13, 309–311. [Google Scholar] [CrossRef]
- Zysset, P.K.; Dall’Ara, E.; Varga, P.; Pahr, D.H. Finite element analysis for prediction of bone strength. BoneKEy Rep. 2013, 2, 386. [Google Scholar] [CrossRef]
- Yalçın, M.; Kaya, B.; Laçin, N.; Arı, E. Three-Dimensional Finite Element Analysis of the Effect of Endosteal Implants with Different Macro Designs on Stress Distribution in Different Bone Qualities. Int. J. Oral Maxillofac. Implant. 2019, 34, e43–e50. [Google Scholar] [CrossRef]
- Dhatrak, P.; Shirsat, U.; Sumanth, S.; Deshmukh, V. Finite Element Analysis and Experimental Investigations on Stress Distribution of Dental Implants around Implant-Bone Interface. Mater. Today Proc. 2018, 5, 5641–5648. [Google Scholar] [CrossRef]
- Marcián, P.; Wolff, J.; Horáčková, L.; Kaiser, J.; Zikmund, T.; Borák, L. Micro finite element analysis of dental implants under different loading conditions. Comput. Biol. Med. 2018, 96, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Manić, M.; Stamenković, Z.; Mitković, M.; Stojković, M.; Shephard, D.E. Design of 3D model of customized anatomically adjusted implants. Facta Univ. Ser. Mech. Eng. 2015, 13, 269–282. [Google Scholar]
- Ni, M.; Niu, W.; Wong, D.W.-C.; Zeng, W.; Mei, J.; Zhang, M. Finite element analysis of locking plate and two types of intramedullary nails for treating mid-shaft clavicle fractures. Injury 2016, 47, 1618–1623. [Google Scholar] [CrossRef] [PubMed]
- Ricotta, J.J.; Pagan, J.; Xenos, M.; Alemu, Y.; Einav, S.; Bluestein, D. Cardiovascular disease management: The need for better diagnostics. Med Biol. Eng. Comput. 2008, 46, 1059–1068. [Google Scholar] [CrossRef]
- El Zahab, Z.; Divo, E.; Kassab, A. Minimisation of the wall shear stress gradients in bypass grafts anastomoses using meshless CFD and genetic algorithms optimisation. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 35–47. [Google Scholar] [CrossRef]
- Schimmer, C.; Özkur, M.; Hamouda, K.; Bensch, M.; Sommer, S.; Leyh, R. Closure of median sternotomy: An overview of different sternal closure techniques. Thorac. Cardiovasc. Surg. 2010, 58, V68. [Google Scholar] [CrossRef]
- Kwong, M. Investigation of hemodyanmics in the development of dissecting aneurysm within patient-specific dissecting aneurismal aortas using computational fluid dynamics (CFD) simulations. J. Biomech. 2010, 44, 827–836. [Google Scholar]
- Auricchio, F.; Di Loreto, M.; Sacco, E. Finite-element Analysis of a Stenotic Artery Revascularization Through a Stent Insertion. Comput. Methods Biomech. Biomed. Eng. 2001, 4, 249–263. [Google Scholar] [CrossRef]
- Selthofer, R.; Nikolić, V.; Mrcela, T.; Radić, R.; Leksan, I.; Rudez, I.; Selthofer, K. Morphometric analysis of the sternum. Coll. Antropol. 2006, 30, 43–47. [Google Scholar]
- Banichuk, N.V.; Barthold, F.J.; Falk, A.; Stein, E. Mesh refinement for shape optimization. Struct. Multidiscip. Optim. 1995, 9, 46–51. [Google Scholar] [CrossRef]
- Sundaram, S.; Feng, C. Finite element analysis of the human thorax. J. Biomech. 1977, 10, 505–516. [Google Scholar] [CrossRef]
- Abendschein, W.; Hyatt, G.W. Ultrasonics and selected physical properties of bone. Clin. Orthop. Relat. Res. 1970, 69, 294–301. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.B. A parallel algorithm for adaptive local refinement of tetrahedral meshes using bisection. Numer. Math. Theory Methods Appl. 2009, 2, 65–89. [Google Scholar]
- Lim, B.-Y.; Kim, Y.; Lee, C.S. Numerical investigation of the sternoclavicular joint modeling technique for improving the surgical treatment of pectus excavatum. Sci. Rep. 2020, 10, 7357. [Google Scholar] [CrossRef]
- Xiao, S.; Mo, F.; Yang, J.; Huang, J.; Xiao, Z.; Crandall, J.R. The influence of impact speed on chest injury outcome in whole body frontal sled impacts. Transp. 2021, 35, 669–678. [Google Scholar] [CrossRef]
- Fernández-Tena, A.; Marcos, A.C.; Agujetas, R.; Ferrera, C. Simulation of the human airways using virtual topology tools and meshing optimization. Biomech. Model. Mechanobiol. 2017, 17, 465–477. [Google Scholar] [CrossRef]
- Orhan, S.N.; Ozyazicioglu, M. Evaluation of sternum closure methods by means of a nonlinear finite element analysis. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2019, 233, 1282–1291. [Google Scholar] [CrossRef]
- More, S.T.; Bindu, R.S. Effect of mesh size on finite element analysis of plate structure. Int. J. Eng. Sci. Innovat. Technol. 2015, 4, 181–185. [Google Scholar]
- Cronin, D.S.; Bustamante, M.C.; Barker, J.; Singh, D.; Rafaels, K.A.; Bir, C. Assessment of Thorax Finite Element Model Response for Behind Armor Blunt Trauma Impact Loading Using an Epidemiological Database. J. Biomech. Eng. 2020, 143, 031007. [Google Scholar] [CrossRef]
- Kashan, J.S.; Ali, S.M. Modeling and simulation for mechanical behavior of modified biocomposite for scaffold application. Ingeniería Investig. 2019, 39, 63–75. [Google Scholar] [CrossRef]
- Burkhart, T.A.; Andrews, D.M.; Dunning, C.E. Finite element modeling mesh quality, energy balance and validation methods: A review with recommendations associated with the modeling of bone tissue. J. Biomech. 2013, 46, 1477–1488. [Google Scholar] [CrossRef] [PubMed]
- EngMorph. Warping Angle Calculation. Finite Element Method. 2015. Available online: https://www.engmorph.com/exmp-calc-warping-factor-angle (accessed on 2 August 2021).
- Fellipa, C. FEM Modeling: Mesh, Loads and BCs; University of Colorado: Boulder, CO, USA, 2012; Chapter 7; pp. 1–19. [Google Scholar]
- Knupp, P.M. Algebraic mesh quality metrics for unstructured initial meshes. Finite Elements Anal. Des. 2003, 39, 217–241. [Google Scholar] [CrossRef]
- Lebschy, C. Biomechanical Modelling of a Human Thorax Using the Finite Element Method. Ph.D. Thesis, Technische Universität Wien, Vienna, Austria, 2021. [Google Scholar]
- Deng, H.; Cheng, L.; To, A.C. Distortion energy-based topology optimization design of hyperelastic materials. Struct. Multidiscip. Optim. 2018, 59, 1895–1913. [Google Scholar] [CrossRef]
- Henke, S.F.; Shanbhag, S. Mesh sensitivity in peridynamic simulations. Comput. Phys. Commun. 2014, 185, 181–193. [Google Scholar] [CrossRef]
- Persson, P.-O.; Peraire, J. Curved Mesh Generation and Mesh Refinement using Lagrangian Solid Mechanics. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 949. [Google Scholar]
- Xiao, L.; Liu, P.; Liu, X.; Zhang, Z.; Wang, Y.; Yang, C.; Gui, W.; Chen, X.; Zhu, B. Sensitivity-based adaptive mesh refinement collocation method for dynamic optimization of chemical and biochemical processes. Bioprocess Biosyst. Eng. 2017, 40, 1375–1389. [Google Scholar] [CrossRef]
- Triyono, J.; Prabowo, A.R.; Sohn, J.M. Investigation of Meshing Strategy on Mechanical Behaviour of Hip Stem Implant Design Using FEA. Open Eng. 2020, 10, 769–775. [Google Scholar] [CrossRef]
- ANSYS. Meshing Advanced Techniques; ANSYS Inc.: Toronto, ON, Canada, 2017. [Google Scholar]
- ANSYS. ANSYS Mechanical Basic Structural Nonlinearities; ANSYS Inc.: Toronto, ON, Canada, 2017. [Google Scholar]
- ANSYS. Chapter 03: Advanced Contact. In ANSYS Training Manual; ANSYS Inc.: Toronto, ON, Canada, 2017. [Google Scholar]
- Cohen, C.D.J.; Griffin, L.V. A biomechanical comparison of three sternotomy closure techniques. Ann. Thorac. Surg. 2002, 73, 563–568. [Google Scholar] [CrossRef]
- Gunja, N.; Pai, S.; McMahon, N.L.; Dupak, E.L.; Lalikos, J.F.; Dunn, M.D.R.; Francalancia, M.D.N.; Pins, M.D.G.; Billiar, K.L. A biomechanical study of a rigid plating system for sternal fixation. In Proceedings of the IEEE 30th Annual Northeast Bioengineering Conference, Springfield, MA, USA, 17–18 April 2004; pp. 156–157. [Google Scholar]
- Saito, T.; Iguchi, A.; Sakurai, M.; Tabayashi, K. Biomechanical study of a Poly-L-Lactide (PLLA) sternal pin in sternal closure after cardiothoracic surgery. Ann. Thorac. Surg. 2004, 77, 684–687. [Google Scholar] [CrossRef]
- Orhan, S.N.; Ozyazicioglu, M.; Colak, A. A biomechanical study of 4 different sternum closure techniques under different deformation modes. Interact. Cardiovasc. Thorac. Surg. 2017, 25, 750–756. [Google Scholar] [CrossRef]
- Fawzy, H.; Alhodaib, N.; Mazer, C.D.; Harrington, A.; Latter, D.; Bonneau, D.; Errett, L.; Mahoney, J. Sternal plating for primary and secondary sternal closure; can it improve sternal stability? J. Cardiothorac. Surg. 2009, 4, 19. [Google Scholar] [CrossRef] [PubMed]
- Trumble, D.R.; McGregor, E.W.; Magovern, A.J. Validation of a bone analog model for studies of sternal closure. Ann. Thorac. Surg. 2002, 74, 739–744. [Google Scholar] [CrossRef]
- Bruhin, R.; Stock, U.A.; Drücker, J.-P.; Azhari, T.; Wippermann, J.; Albes, J.M.; Hintze, D.; Eckardt, S.; Könke, C.; Wahlers, T. Numerical Simulation Techniques to Study the Structural Response of the Human Chest Following Median Sternotomy. Ann. Thorac. Surg. 2005, 80, 623–630. [Google Scholar] [CrossRef] [PubMed]
- Onoda, N.; Ishikawa, T.; Yamada, N.; Okamura, T.; Tahara, H.; Inaba, M.; Takashima, T.; Sakate, Y.; Chung, K.H.-Y.S. Radioisotope-navigated video-assisted thoracoscopic operation for ectopic mediastinal parathyroid. Surgery 2002, 132, 17–19. [Google Scholar] [CrossRef] [PubMed]
- Alhalawani, A.; Mehrvar, C.; Stone, W.; Waldman, S.D.; Towler, M.R. A novel tantalum-containing bioglass. Part II. Development of a bioadhesive for sternal fixation and repair. Mater. Sci. Eng. C 2017, 71, 401–411. [Google Scholar] [CrossRef] [PubMed]

| Wire Closure Style | Modeled Illustration | The Significance of Wiring Style |
|---|---|---|
| Alternating Peristernal and Transsternal | 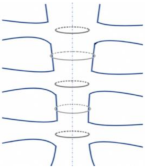 | It has been the best closure technique due to its superiority in mechanical stability and strength [27]. |
| Single Transsternal | 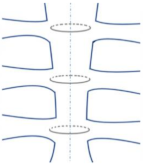 | The twisted free ends of the wire may penetrate the sternum (due to osteoporosis or other factors) when wire loops are installed trans-sternaly in weak bones [28,35]. |
| Single Peristernal | 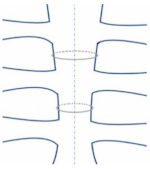 | Reduces risk of deep sternal wound infection by reinforcing the corpus sterni of the sternum [36] Safe for solid internal fixation [37]. Sternal stability was higher in single wire vs. figure of 8 wire in high-risk obese patients [38] |
| Figure-of-eight |  | Figure of eight wires are not superior to simple wires [38,39]. |
| Modified figure-of-eight | 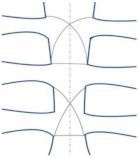 | Effective and safe method for limiting sternal dehiscence by limiting the penetration in the intercostal spaces [40] |
| Longitudinal parasternal | 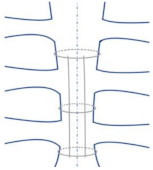 | Used for high-risk patients. Prevent sternal dehiscence and sternal wound complications [11]. |
| Criteria | Required Endpoints |
|---|---|
| Radiopacity [57] | High level of radiopacity to observe sternal displacements [36] |
| Nontoxic nature [61] | Safe to use inside a human body |
| Adhesive mechanical properties [16] | Sufficient strength to withstand the maximum forces imposed during leaning on one chest side or coughing. [16,57] |
| Aging mechanism of the cement [57] | Sufficient working time (6–10 min) and rapid setting time (maximum 15 min) |
| Biocompatibility [42] | It should be a bioactive material to avoid inflammation. |
| Viscosity [16] | Medium viscosity is required for injection and interpenetration of trabecular spaces. [16] |
| modulus of elasticity | Excessive damage occurs if the elastic limit is exceeded. [58] |
| Sternum Part | Modulus of Elasticity | Density | Poisson’s Ratio | Ultimate Tensile Strength UTS |
|---|---|---|---|---|
| Sternum and ribs [77] | (MPa) | ---- | 0.20 | 18,000 |
| Sternum [79] | 11.50 (GPa) | 0.30 | ---- | |
| Cortical bone Cancellous bone [34] | 15.25 (GPa) 1.12 (GPa) | ---- | 0.27 0.27 | ---- |
| Cortical bone Cancellous bone [80] | 11.50 (GPa) 0.04 (GPa) | ---- | ---- | ---- |
| Cortical bone Cancellous bone [81] | 10.18 (GPa) 0.04 (GPa) | 2000 1000 | 0.3 0.45 | 2.3 (GPa) 0.001 (GPa) |
| Mesh Metric | Constraint | Modeling Mesh Solution |
|---|---|---|
| Warp angle | Elements have more than 3 nodes | Add subdivisions to elements |
| Aspect ratio | Element has a symmetric shape 1 < (Max length/Min length) < 3 | Local mesh refinement |
| Skewness | Compression to ideal element | Improve surface meshing |
| Jacobian ratio | −1 < Jacobian determinant < 1 | Remeshing defected parts |
| Distortion | Occurs in hyperelastic material | Increase quality of the mesh |
| Pure Penalty | Augmented Lagrange | Normal Lagrange |
|---|---|---|
| Good convergence behavior | If penetration is too large, additional equilibrium needed | Chattering is present |
| Sensitive to the selection of normal contact stiffness. | Less sensitive to the selection of normal contact stiffness. | Not sensitive to the selection of normal contact stiffness. |
| Contact penetration is present and uncontrolled | Contact penetration is present and controlled | Penetration is almost near zero |
| Loading Type | Allowable Load (N) | Rupture Load (N) | Rupture Displacement (mm) |
|---|---|---|---|
| Lateral distraction | 1032.6 ± 120.4 | 1702.9 ± 327.3 | 6.28 ± 0.03 |
| Longitudinal shear | 579.79 ± 30.7 | 1458.16 ± 120.1 | 15.79 ± 0.05 |
| Torsion | 92.4 ± 6.44 | 955.1 ± 76.1 | 19.6 ± 0.00 |
| Load Values (N) | Closure Technique |
|---|---|
| 1457 | 3 steel bands + 4 steel wires |
| 1317 | 3 ZipFix bands + 4 steel wires |
| 1051 | conventional steel wire (7 steel wires) |
| 2380 | Additional wires at the manubrium and xiphoid |
| Reference | Load | Direction | Evaluation |
|---|---|---|---|
| Cohen and Griffin [100] | Breathing load Movement load | Anterior–posterior shear Aranial– caudal shear | Strength, stiffness, and post-yield analysis |
| Losanoff et al. [28] | Breathing load | Uniaxial test (0–800 N) Anterior–posterior and rostral–caudal | Lateral stress of the sternum |
| Gunja et al. [101] | Tensile test of sternum fixed with plates | Laterally pulled to a maximum load of 400 N | Sternal distraction between the two sternal halves |
| Saito et al. [102] | Shear stress | Anterior–posterior direction, and in a cranial–caudal direction | Displacement of sternal halves and fixation stability |
| Lim et al. [80] | External force of the raised pectus bar in the chest wall | Displacement and rotations around the sternoclavicular joint | Equivalent stress distribution on chest wall and anterior/posterior length of the chest wall |
| Orhan et al. [103] | Pre-loading types | Lateral distraction (1032.6 N), longitudinal shear (579.79), and torsion (92) | Rupture displacement |
| Orhan and Ozyazicioglu [83] | Lateral distraction loading | 2380 N | 2.0 mm displacement along the incision area |
| Fawzy et al. [104] | Intrathoracic pressure | Load increased gradually to reach longitudinal separation (2.0 mm) | Sternal stability |
| Type of 3D Modeling Study | The Designed Sternal Model | Wiring Closure Technique |
|---|---|---|
| Evaluate stress around a ster-num screw [34] | Block of sternum model | Stainless steel wire/screw |
| Evaluate closure of sternum at different processes [105] | Sternal model from Polyurethane foam | single-loop vs. figure-of-eight |
| Evaluate structural response of the median sternotomy [106] | Cadaveric sternal CT scans modeled as linear elastic material for the bone | single-loop vs. figure-of-eight |
| Evaluate three sternal closure techniques [83] | Sternal CT scans modeled as isotropic bilinear-elasto-plastic material | Steel bands, steel wires, and ZipFix bands. |
| Evaluate strength of sternal wire and rigidity of the sternotomy closure [95] | Steel sternal model | Changing the number of sternal wire twists (0–10). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Abassi, A.; Papini, M.; Towler, M. Review of Biomechanical Studies and Finite Element Modeling of Sternal Closure Using Bio-Active Adhesives. Bioengineering 2022, 9, 198. https://doi.org/10.3390/bioengineering9050198
Al-Abassi A, Papini M, Towler M. Review of Biomechanical Studies and Finite Element Modeling of Sternal Closure Using Bio-Active Adhesives. Bioengineering. 2022; 9(5):198. https://doi.org/10.3390/bioengineering9050198
Chicago/Turabian StyleAl-Abassi, Amatulraheem, Marcello Papini, and Mark Towler. 2022. "Review of Biomechanical Studies and Finite Element Modeling of Sternal Closure Using Bio-Active Adhesives" Bioengineering 9, no. 5: 198. https://doi.org/10.3390/bioengineering9050198
APA StyleAl-Abassi, A., Papini, M., & Towler, M. (2022). Review of Biomechanical Studies and Finite Element Modeling of Sternal Closure Using Bio-Active Adhesives. Bioengineering, 9(5), 198. https://doi.org/10.3390/bioengineering9050198





