Figure 1.
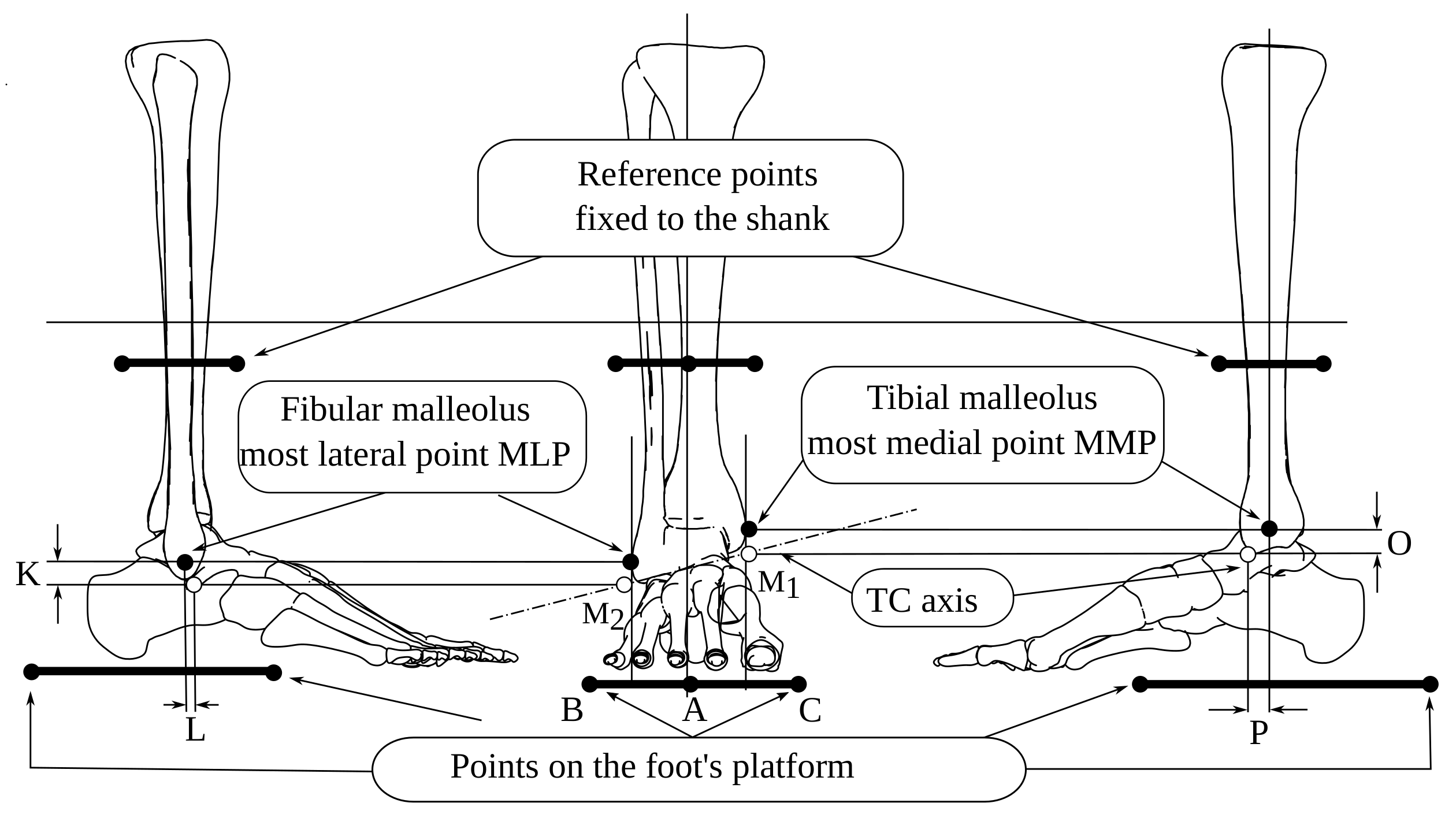
Reference points from anthropometric values K, L, O, and P.
Figure 1.
Reference points from anthropometric values K, L, O, and P.
Figure 2.
Q, W, and w distances from lateral and transverse views.
Figure 2.
Q, W, and w distances from lateral and transverse views.
Figure 3.
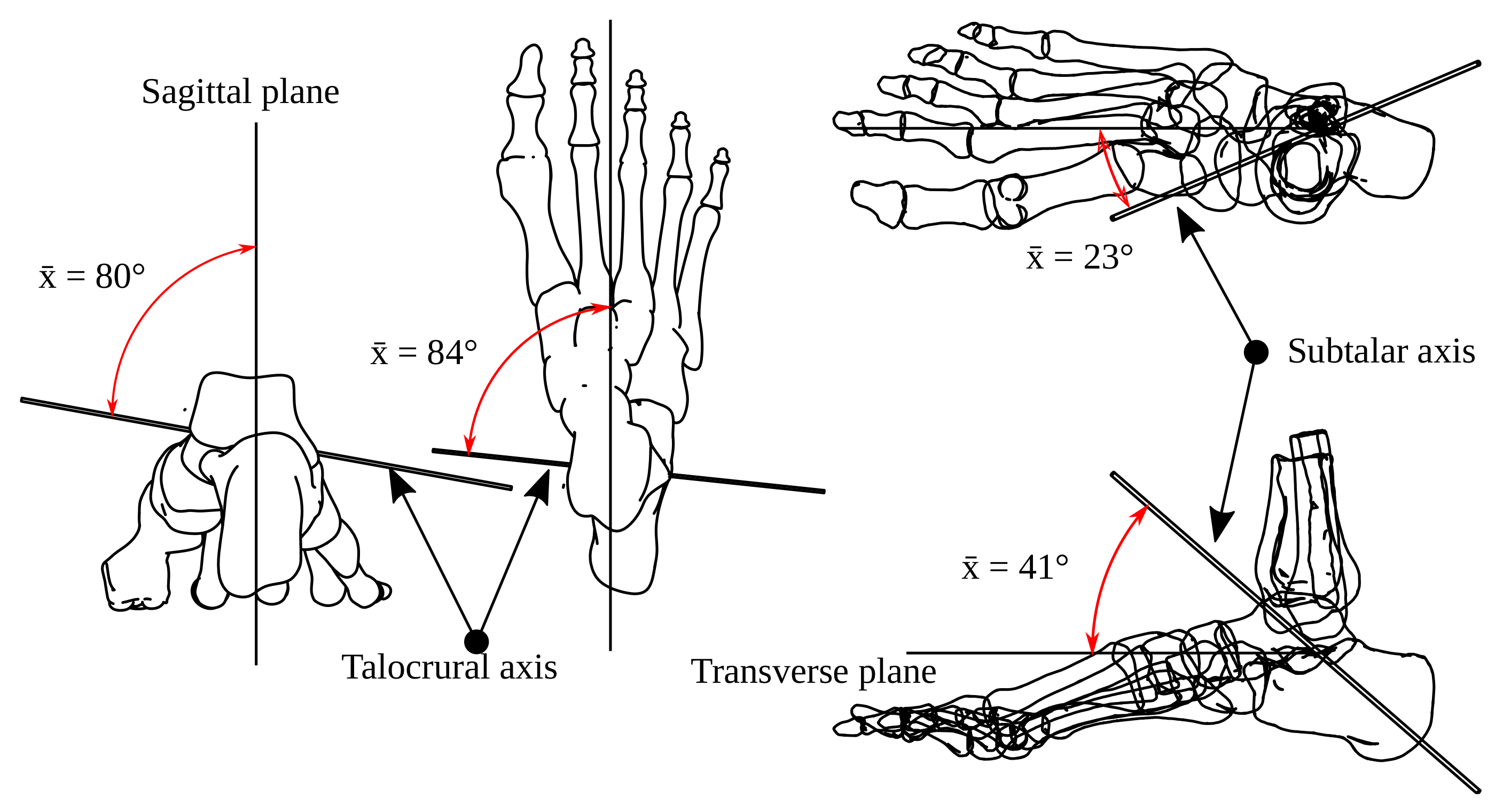
Mean relative position of the ST and TC axis.
Figure 3.
Mean relative position of the ST and TC axis.
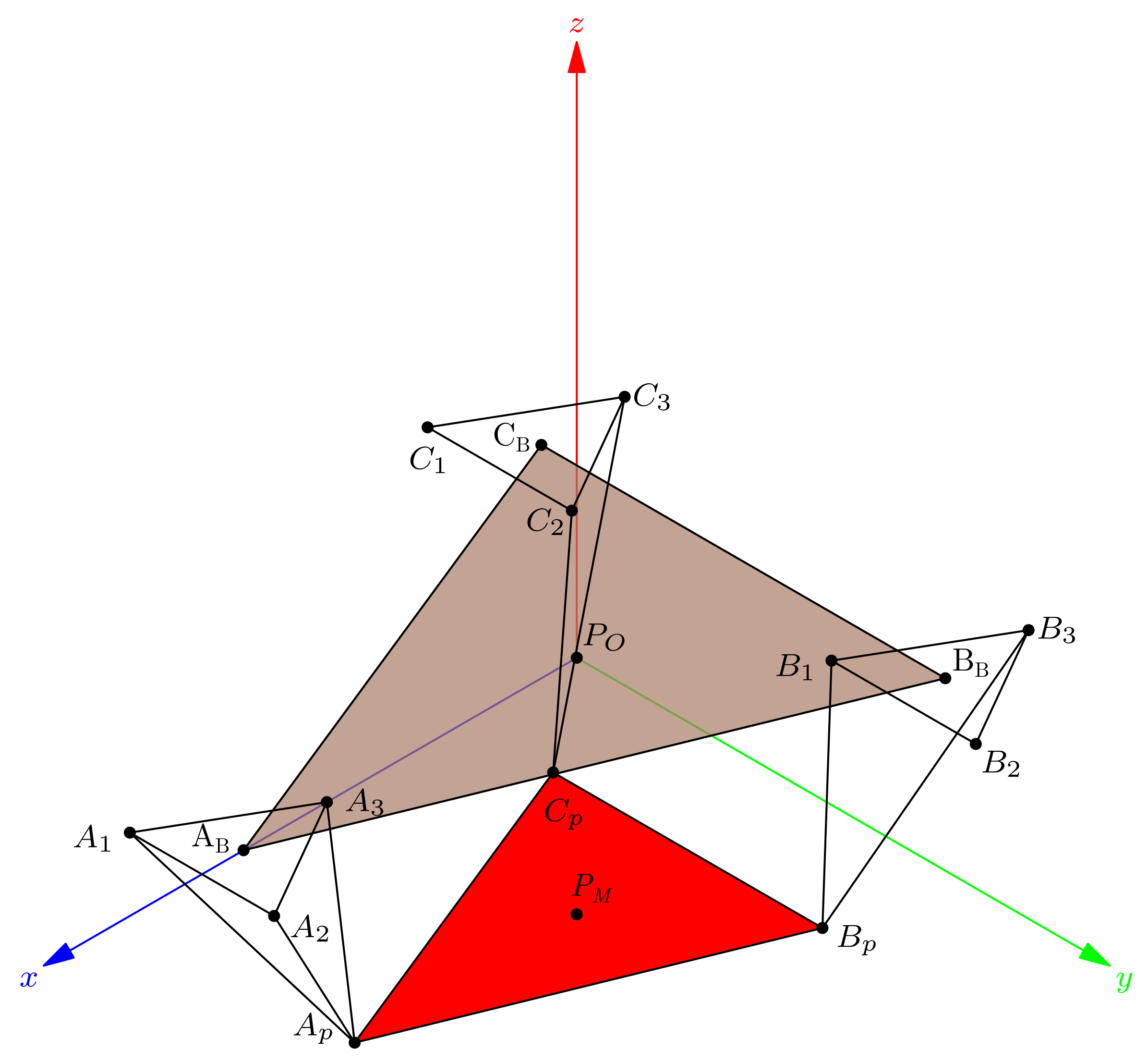
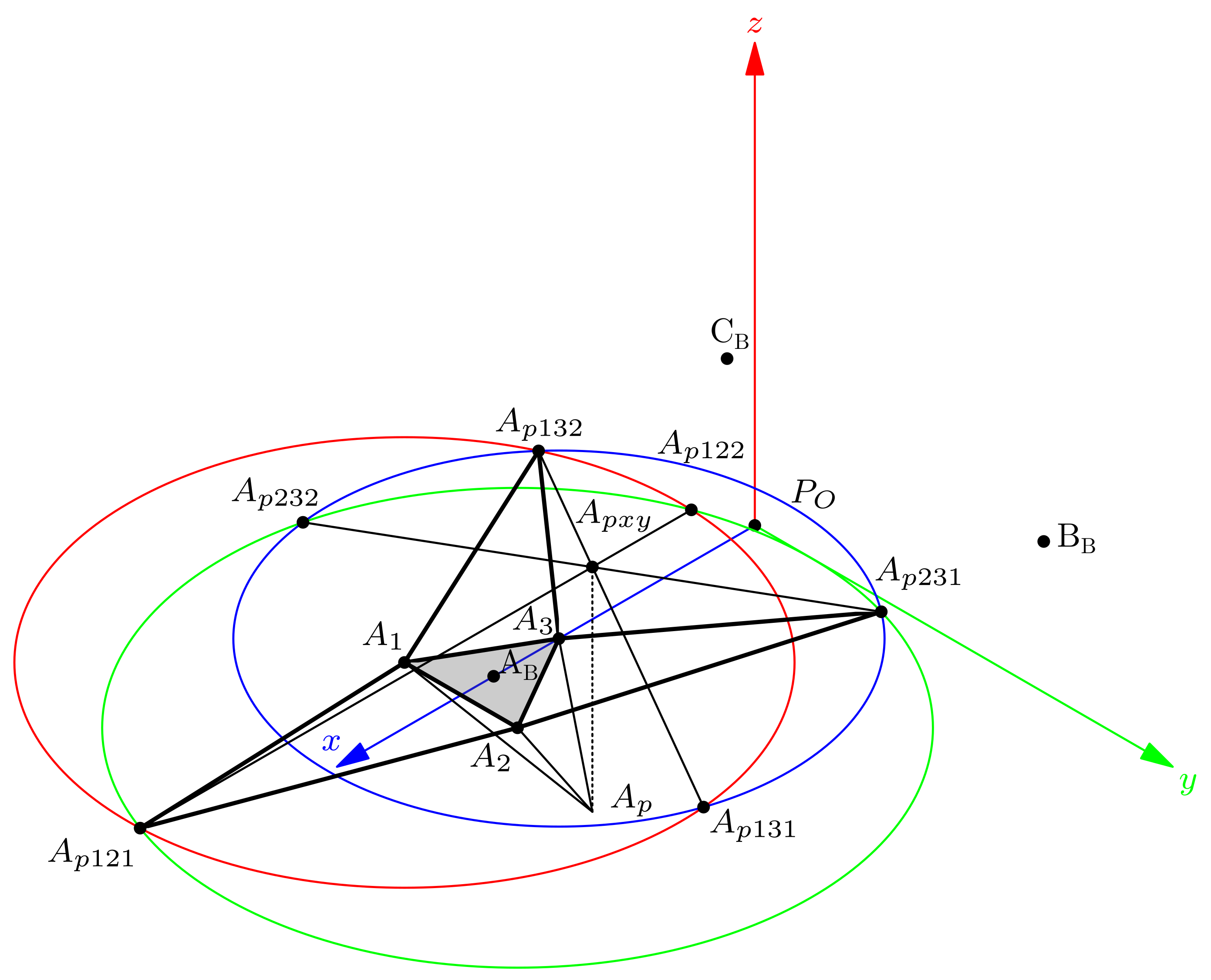
Figure 4.
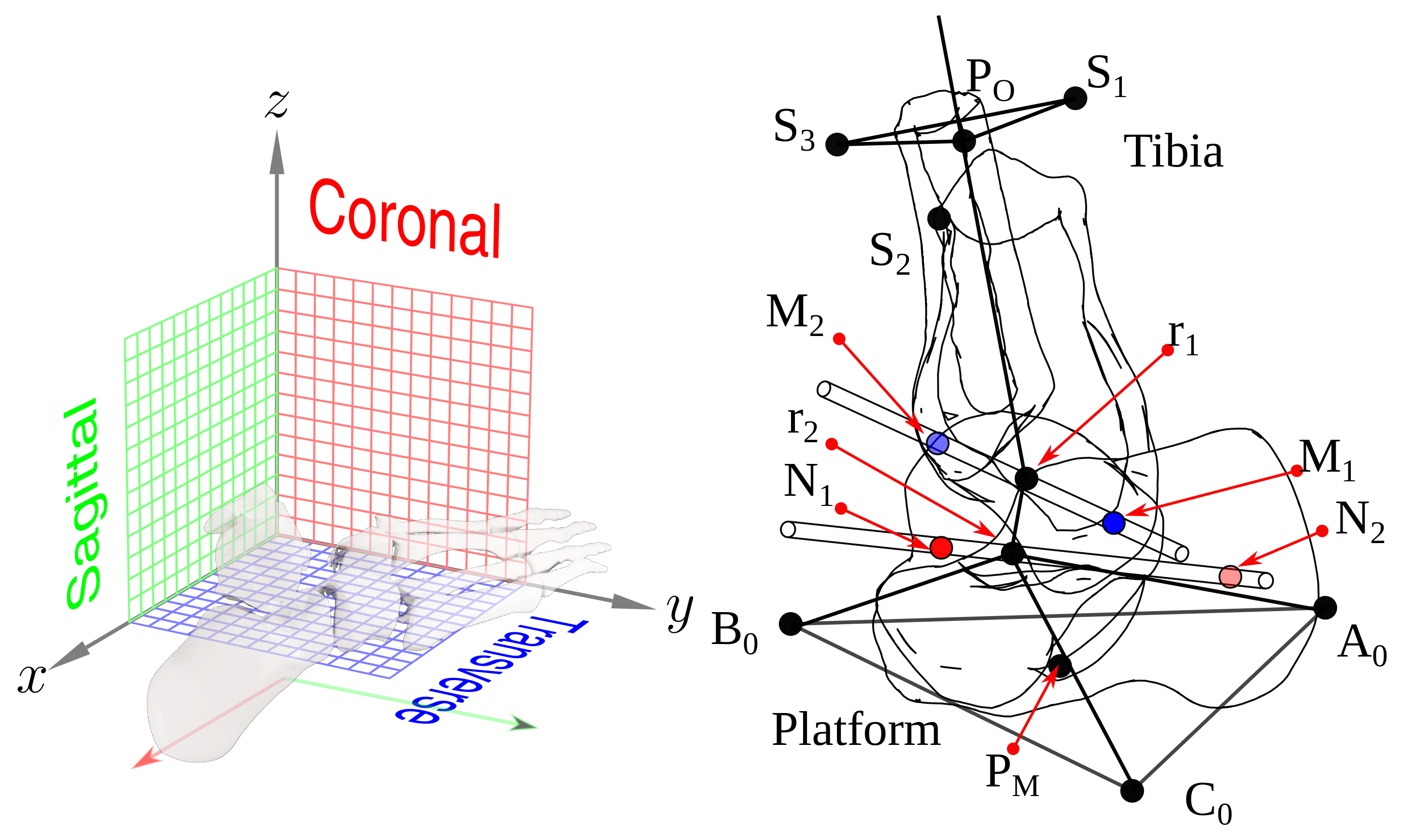
Planes, axes, and points of corresponding references.
Figure 4.
Planes, axes, and points of corresponding references.
Figure 5.
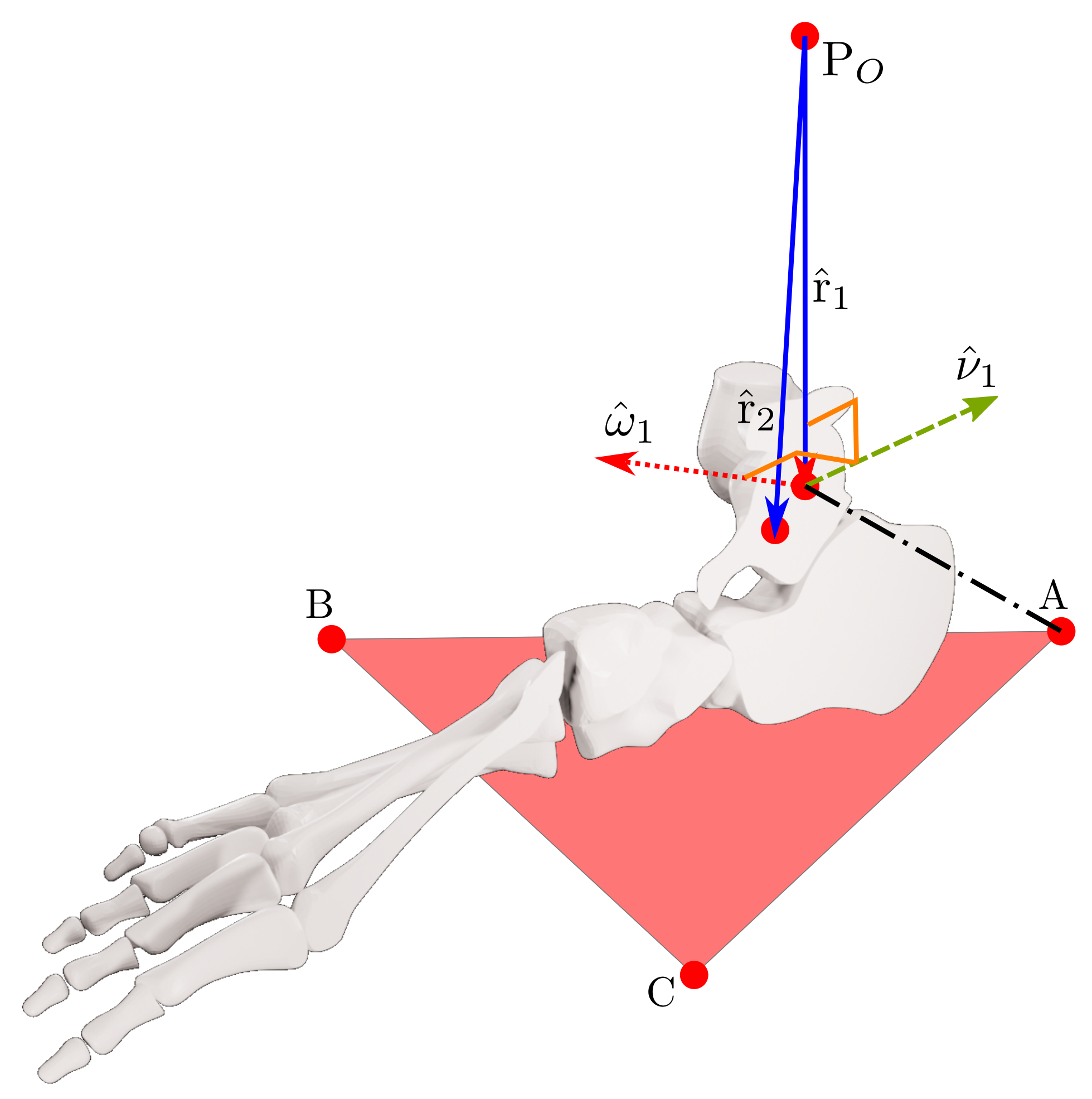
Vectors and points on the sagittal plane.
Figure 5.
Vectors and points on the sagittal plane.
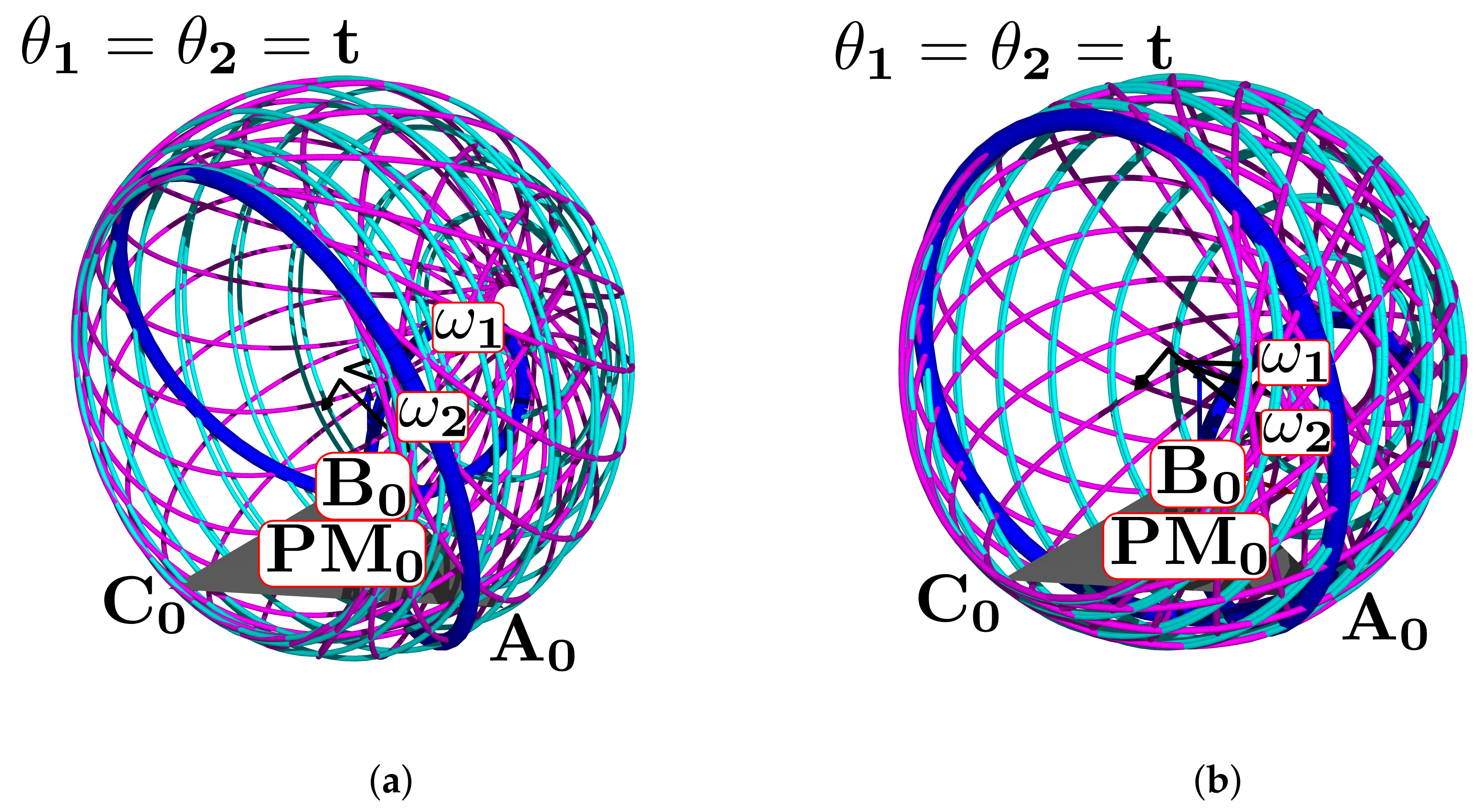
Figure 6.
Forward kinematics for (a) initial position and (b) and (c) .
Figure 6.
Forward kinematics for (a) initial position and (b) and (c) .
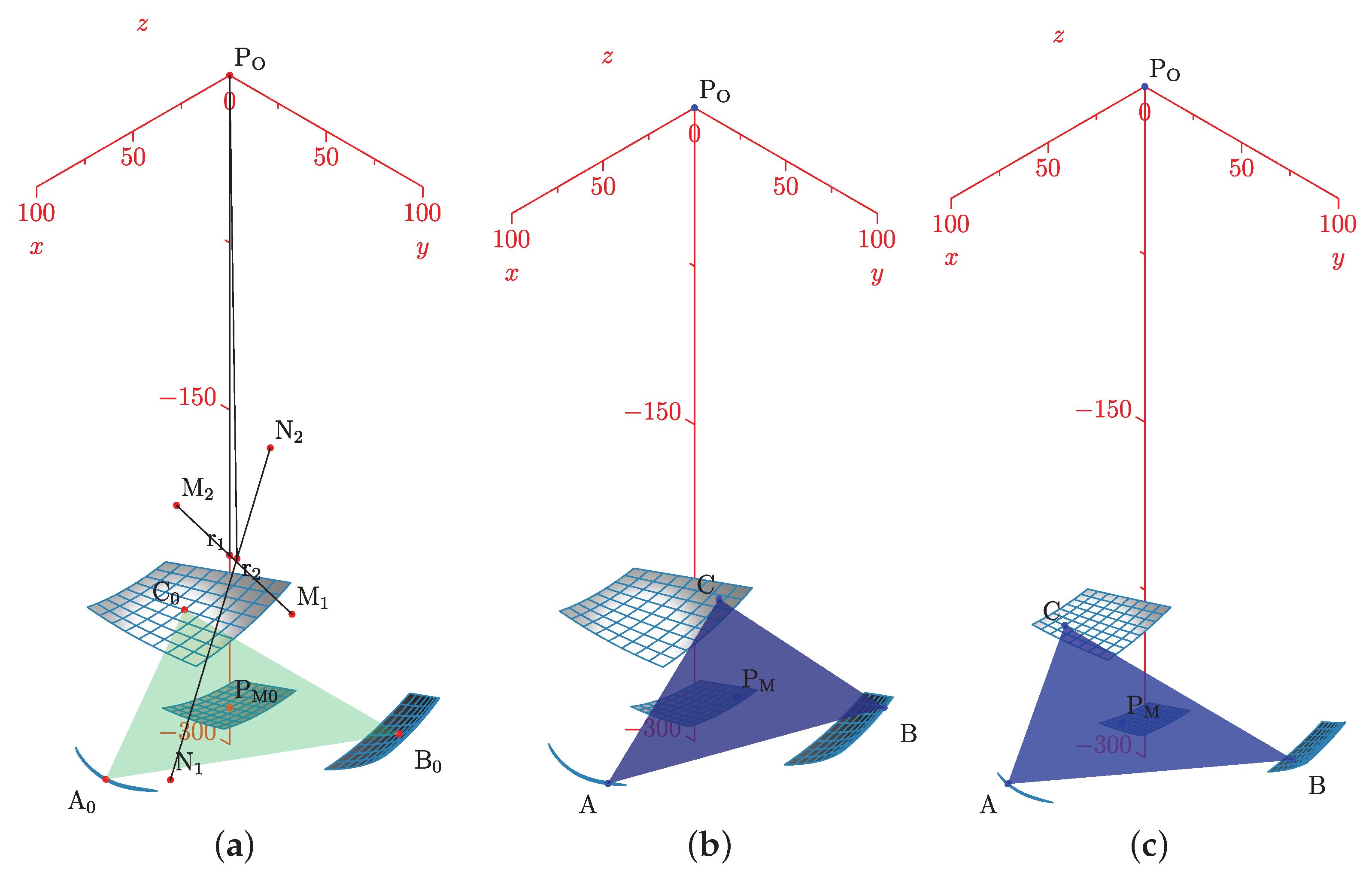
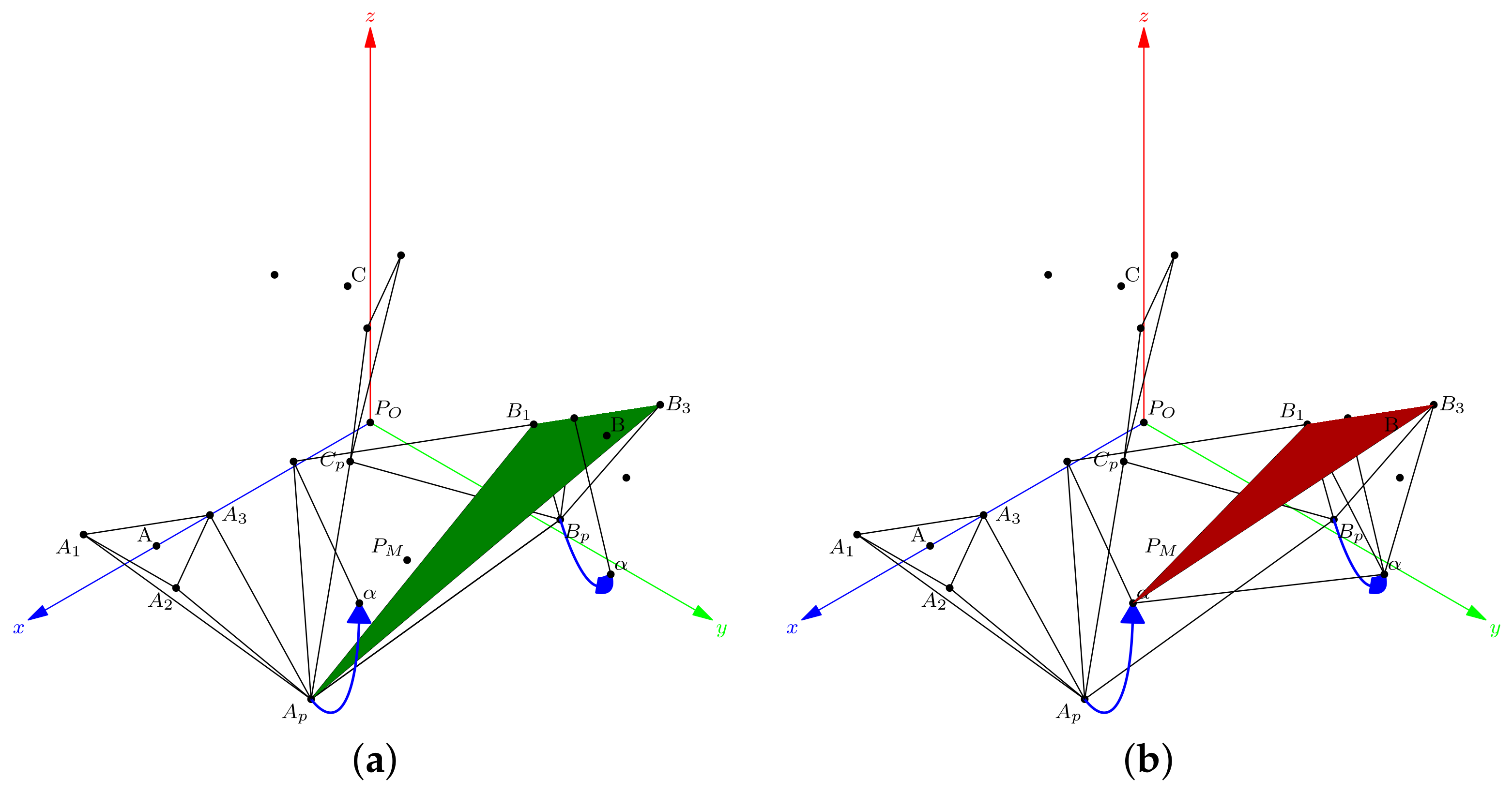
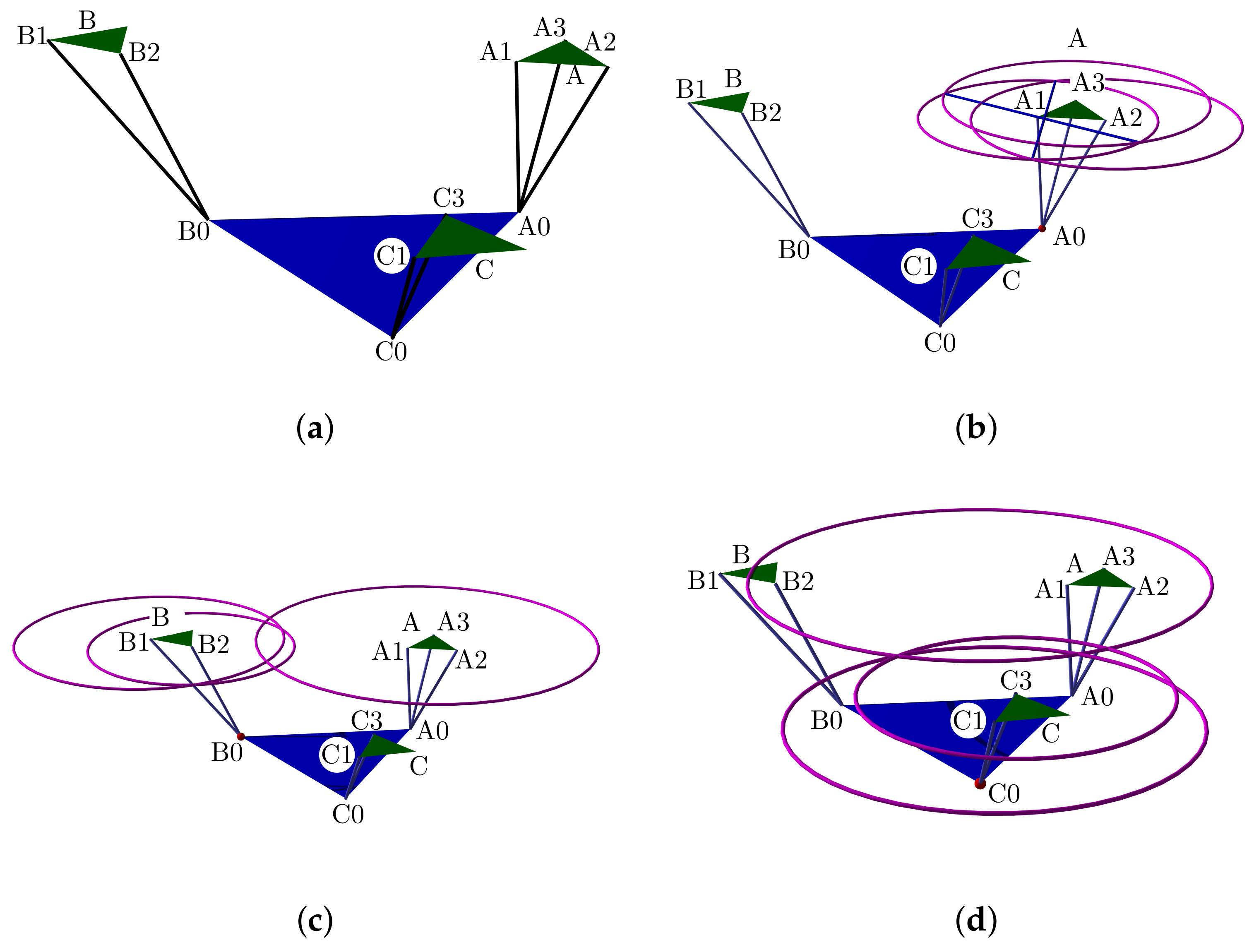
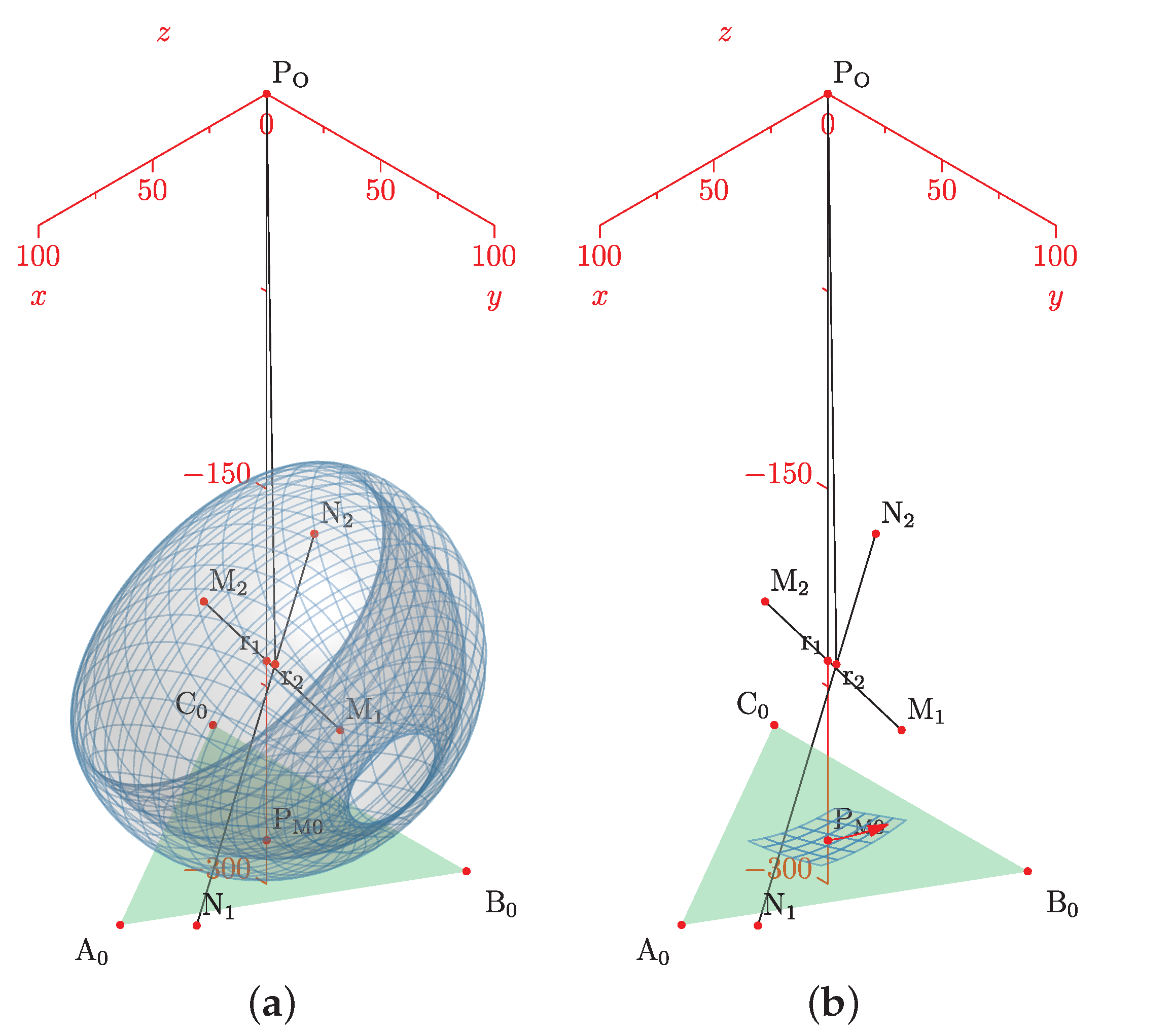
Figure 7.
Geometric design: (a) is the platform center, base, and ; and (b) platform vertices with talocrural and subtalar axis.
Figure 7.
Geometric design: (a) is the platform center, base, and ; and (b) platform vertices with talocrural and subtalar axis.
Figure 8.
Geometric design of the DWS arrays.
Figure 8.
Geometric design of the DWS arrays.
Figure 9.
Tetrahedron trilateration flowchart.
Figure 9.
Tetrahedron trilateration flowchart.
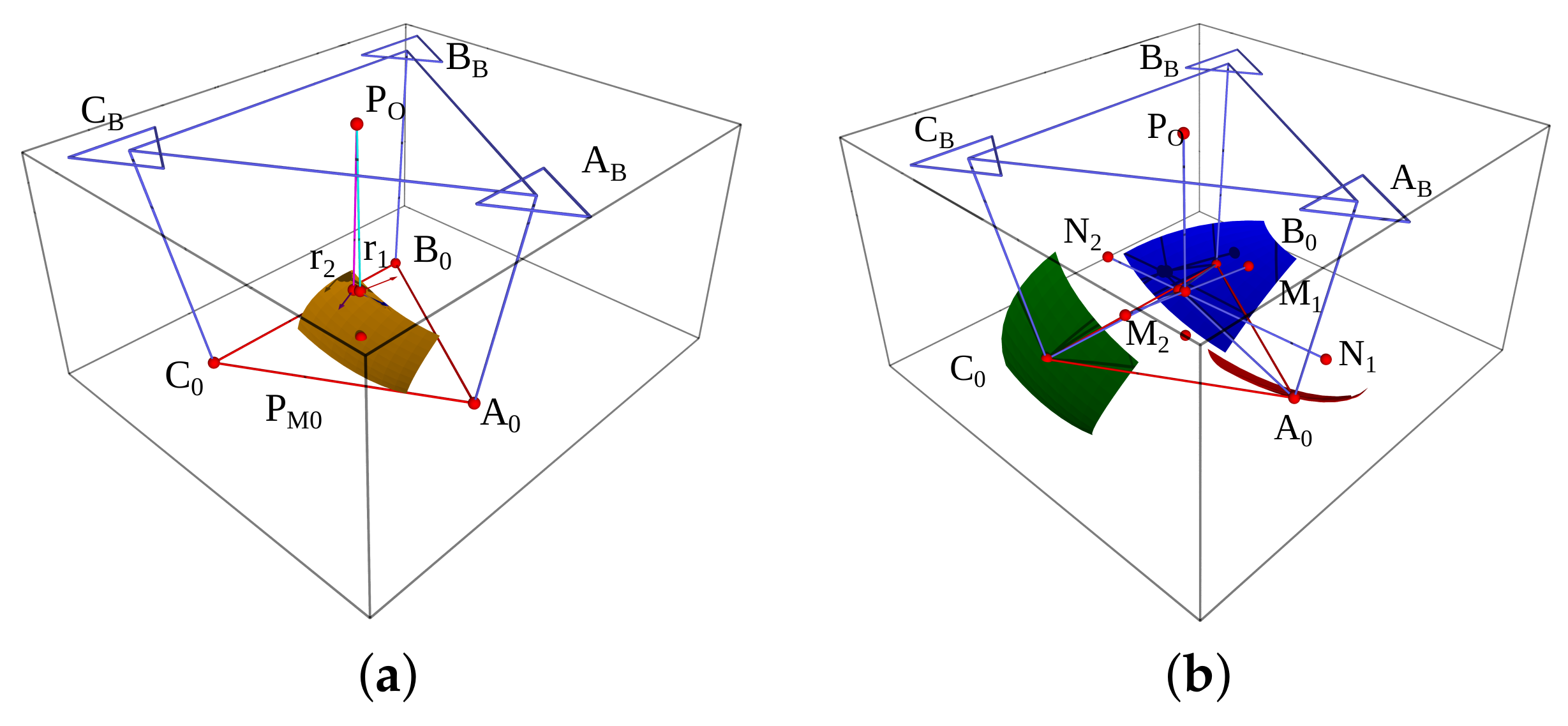
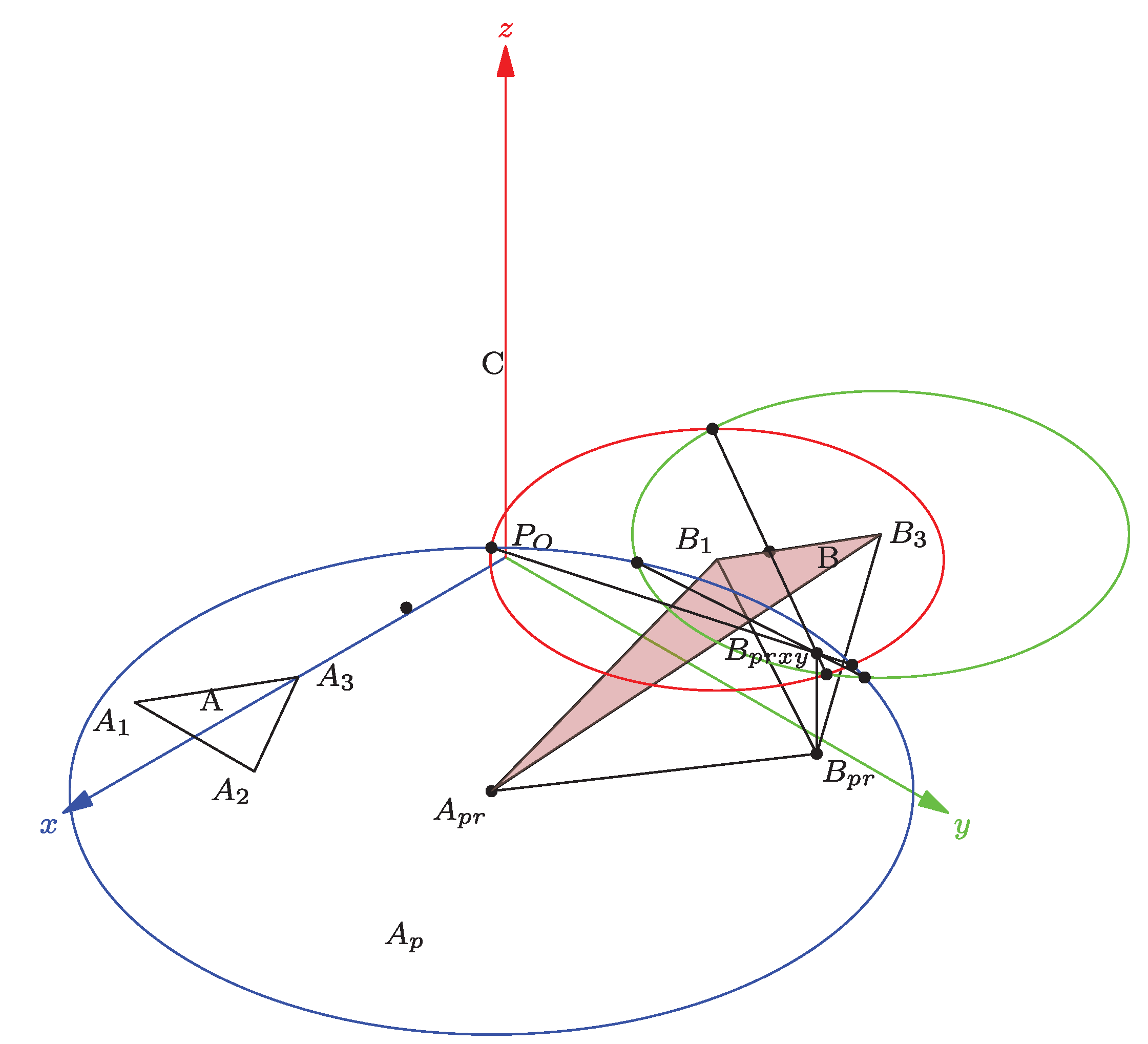
Figure 10.
Finding the apex .
Figure 10.
Finding the apex .
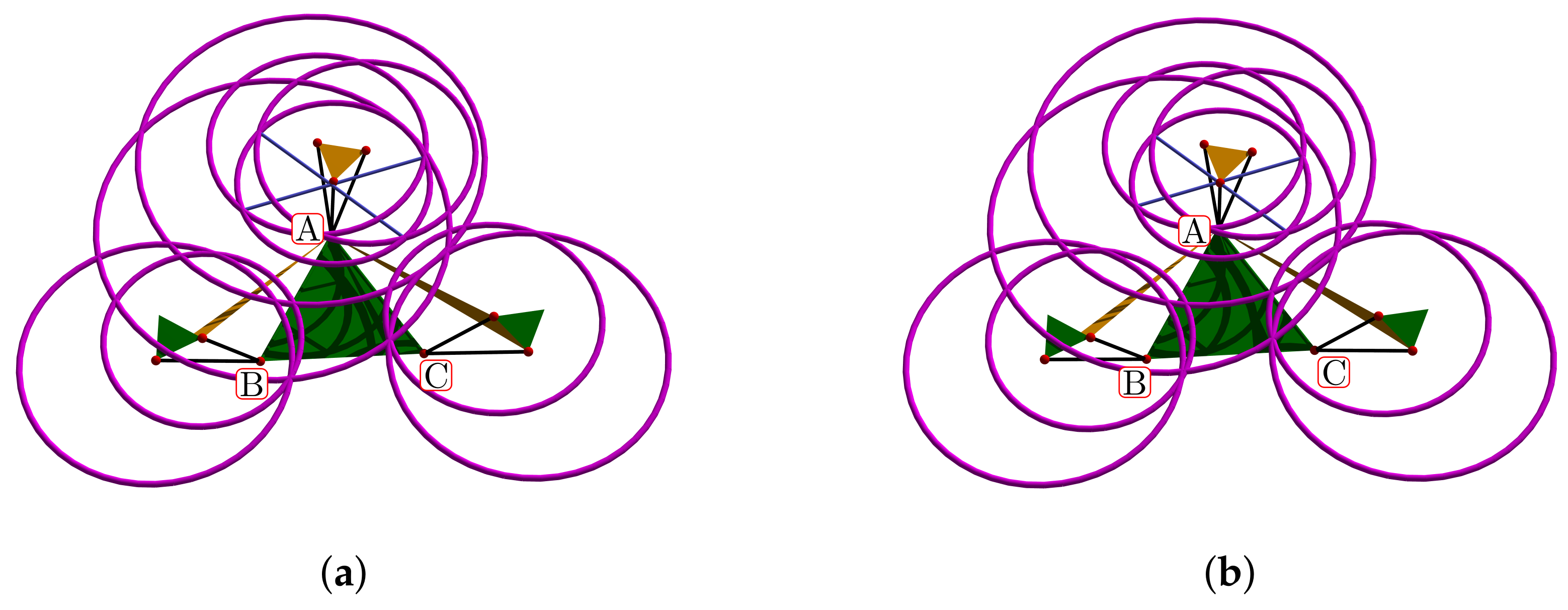
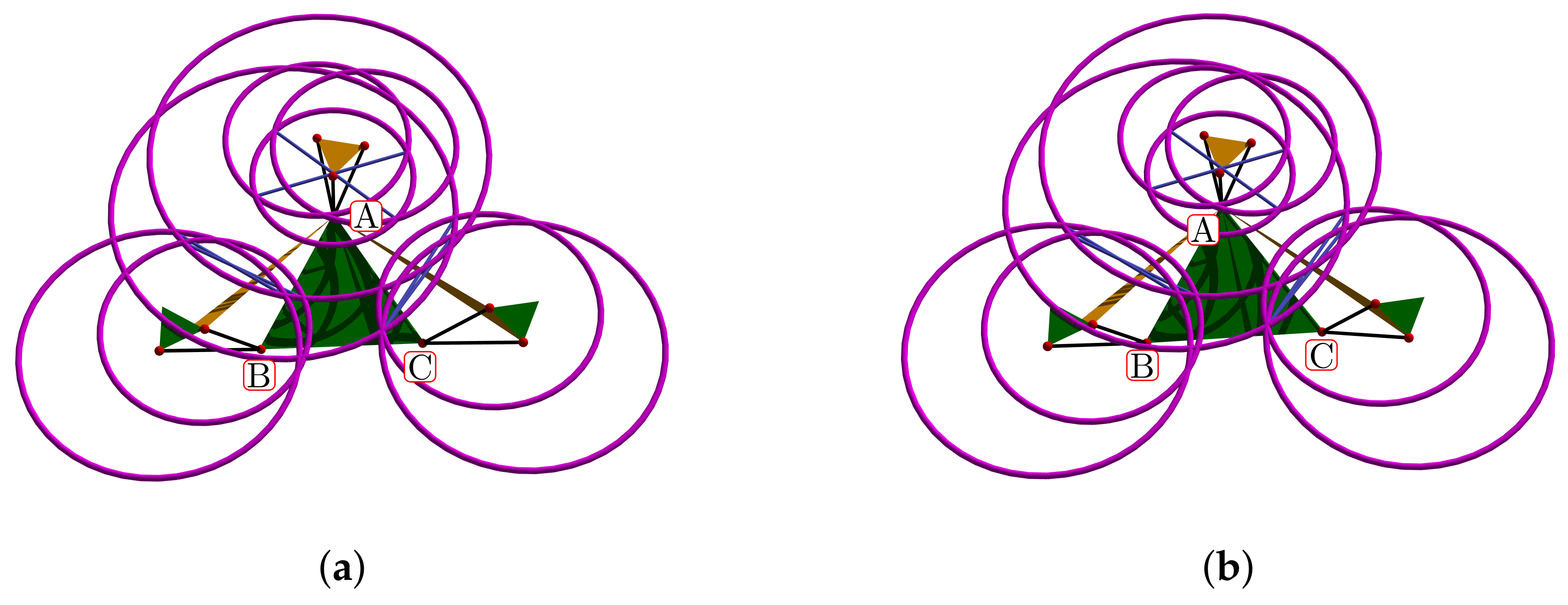
Figure 11.
Rotation of angle about the axis : (a) original tetrahedron, (b) rotated tetrahedron.
Figure 11.
Rotation of angle about the axis : (a) original tetrahedron, (b) rotated tetrahedron.
Figure 12.
Finding the apex .
Figure 12.
Finding the apex .
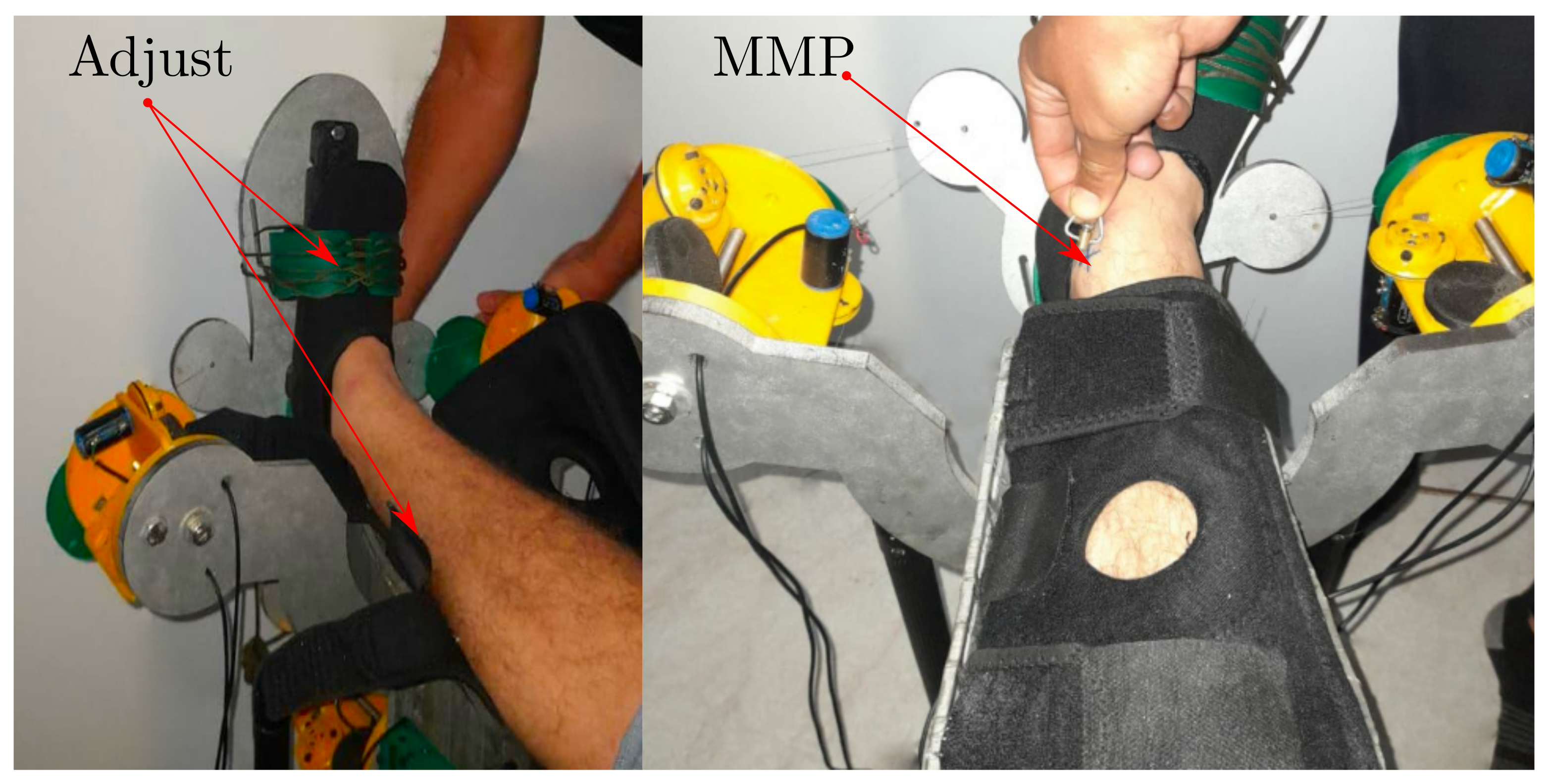
Figure 13.
Adjusting the foot, the shank and the Most Medial Point reference.
Figure 13.
Adjusting the foot, the shank and the Most Medial Point reference.
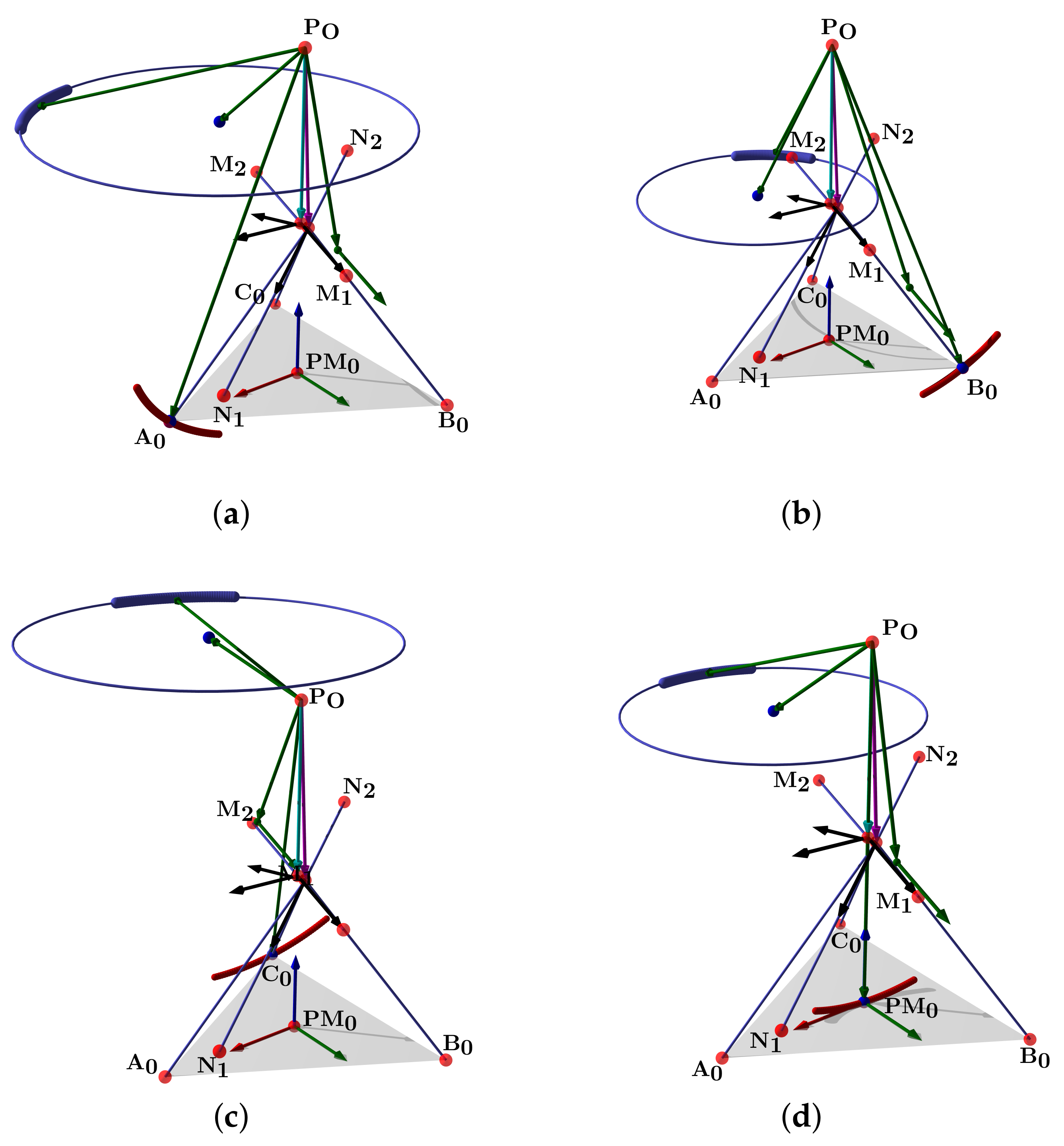
Figure 14.
Computed positions from sensor lengths at portable configuration: (a) the rest position, (b) apex A, (c) apex B, and (d) apex C.
Figure 14.
Computed positions from sensor lengths at portable configuration: (a) the rest position, (b) apex A, (c) apex B, and (d) apex C.
Figure 15.
Simulation of the platform central point with variations in the mean statistical values: (a) platform’s center point manifold, (b) manifold chart and a geodesic.
Figure 15.
Simulation of the platform central point with variations in the mean statistical values: (a) platform’s center point manifold, (b) manifold chart and a geodesic.
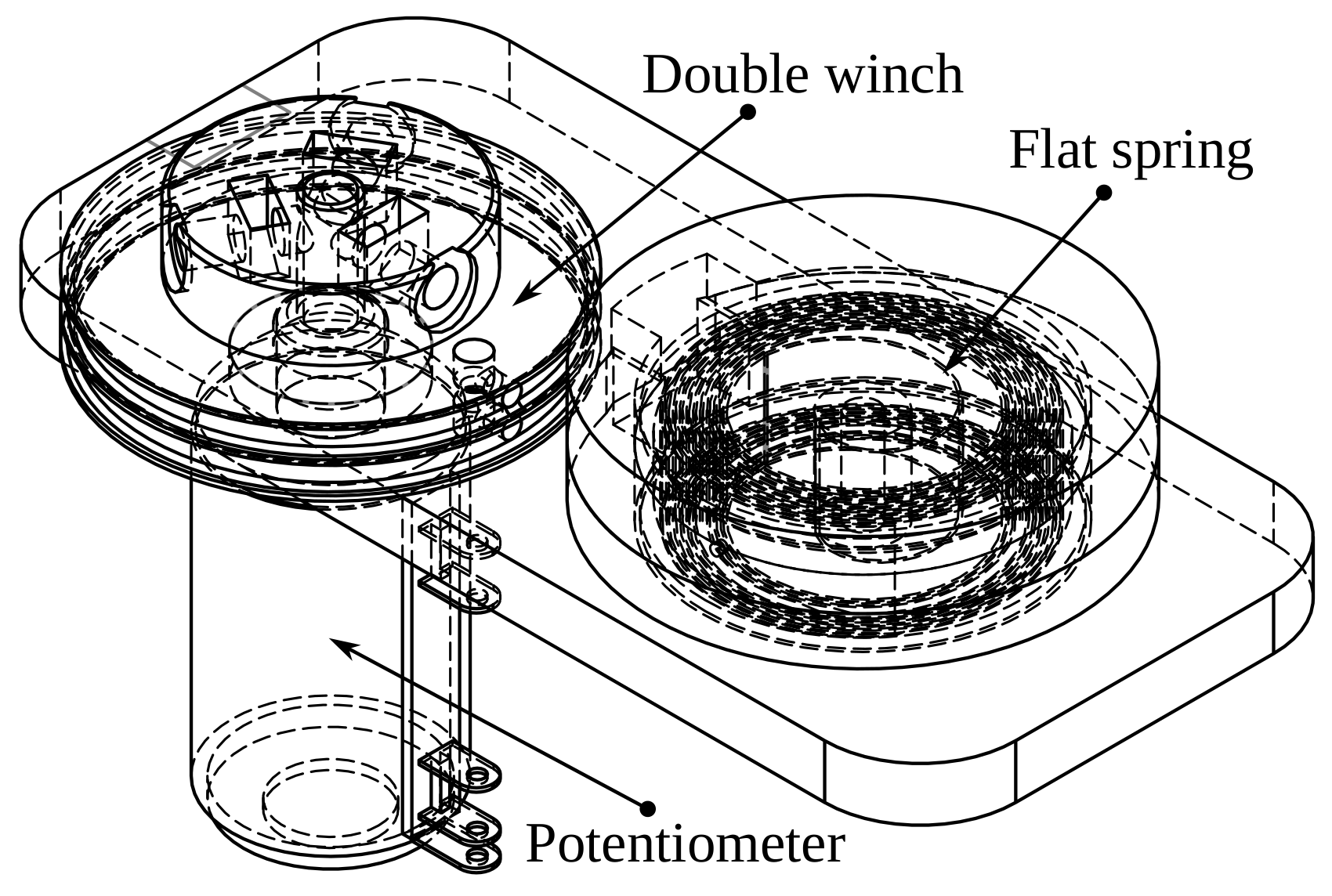
Figure 16.
Draw-wire sensor design.
Figure 16.
Draw-wire sensor design.
Figure 17.
Mechanical attachment: (a) calf support and (b) aluminum tube structure.
Figure 17.
Mechanical attachment: (a) calf support and (b) aluminum tube structure.
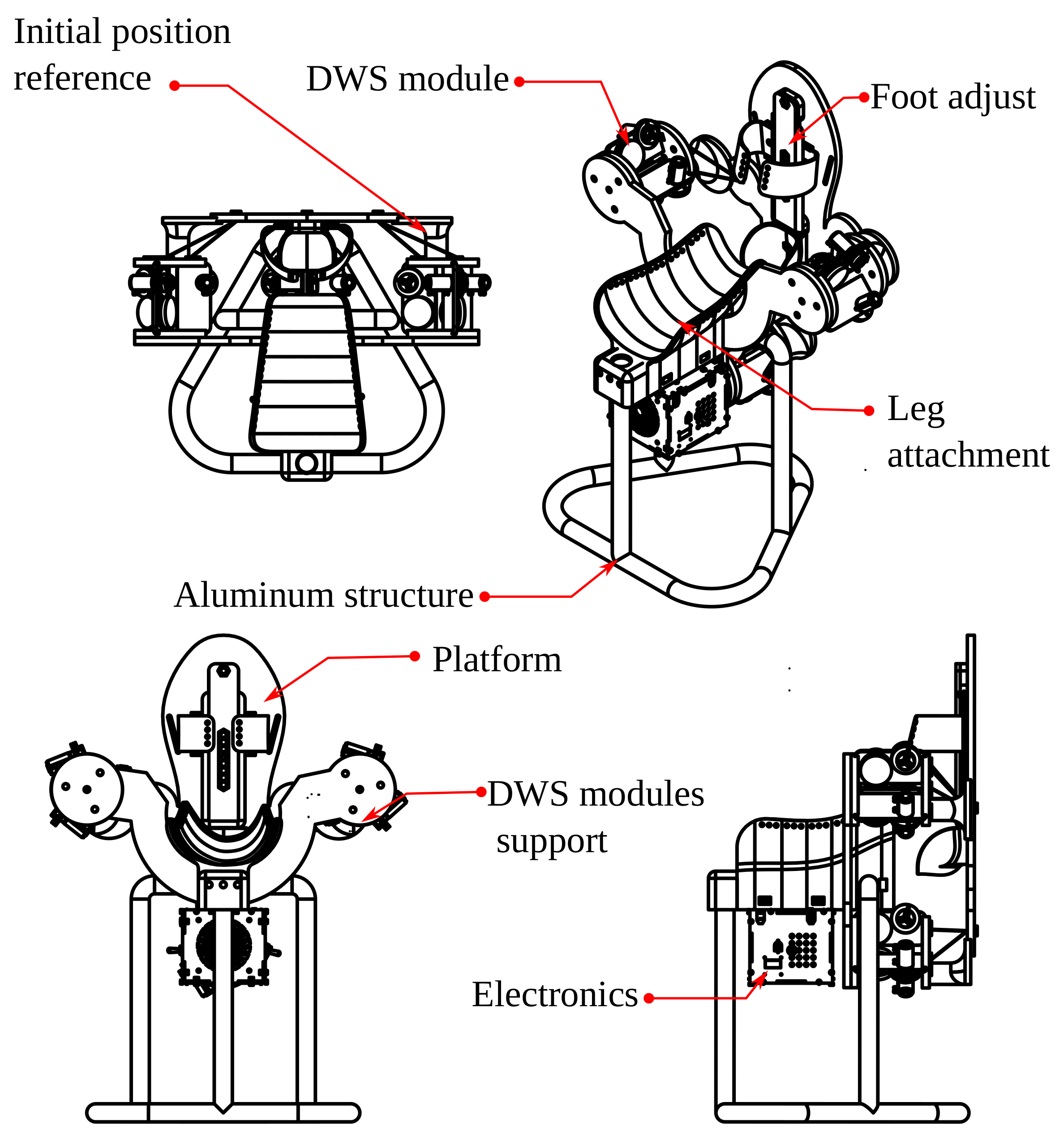
Figure 18.
Base and platform: (a) DWS modules support (b) platform with foot’s size adjustment.
Figure 18.
Base and platform: (a) DWS modules support (b) platform with foot’s size adjustment.
Figure 19.
Two Op. Amp. instrumentation amplifier.
Figure 19.
Two Op. Amp. instrumentation amplifier.
Figure 20.
Power system with backup, BMS, boost, and buck converters.
Figure 20.
Power system with backup, BMS, boost, and buck converters.
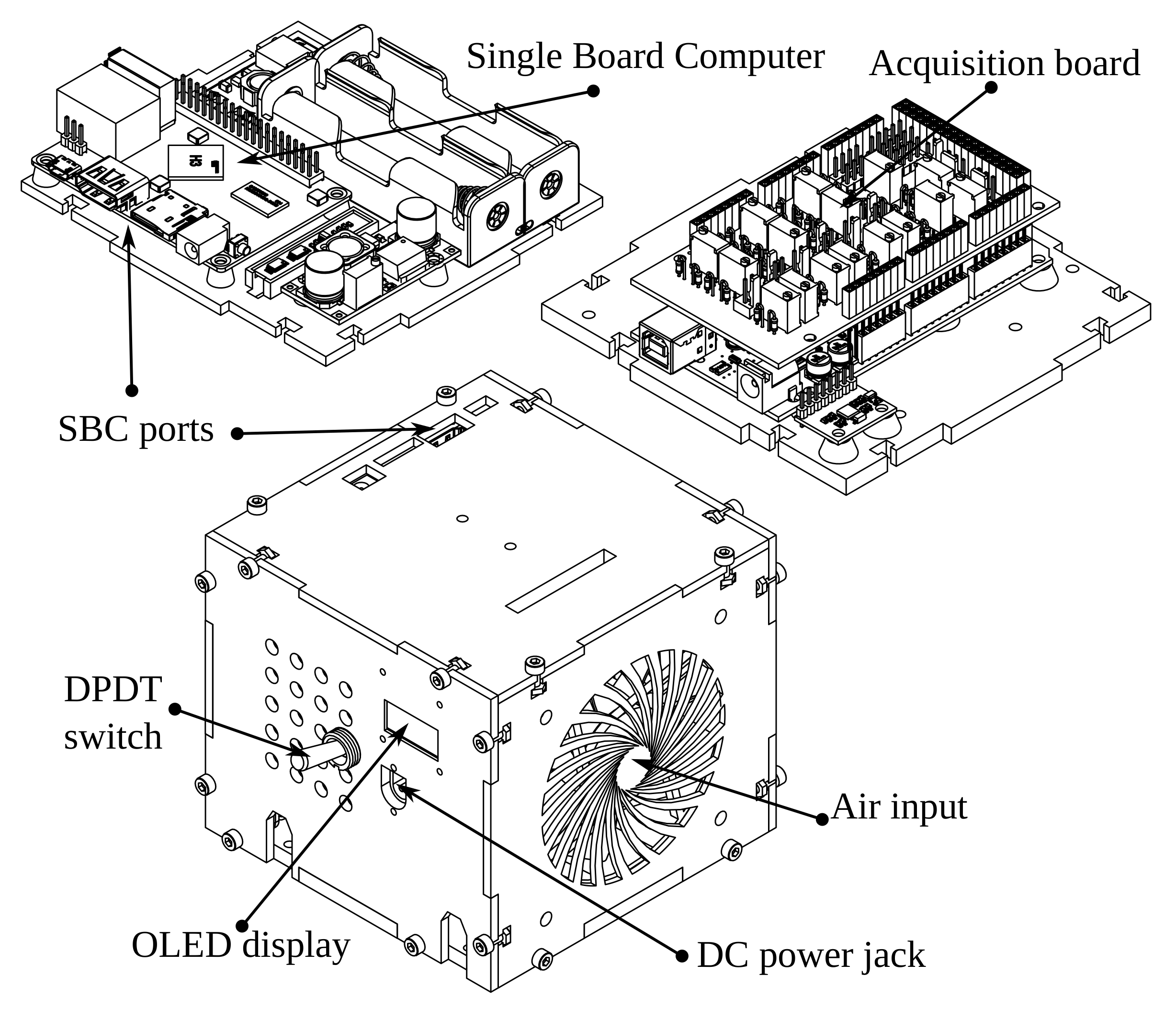
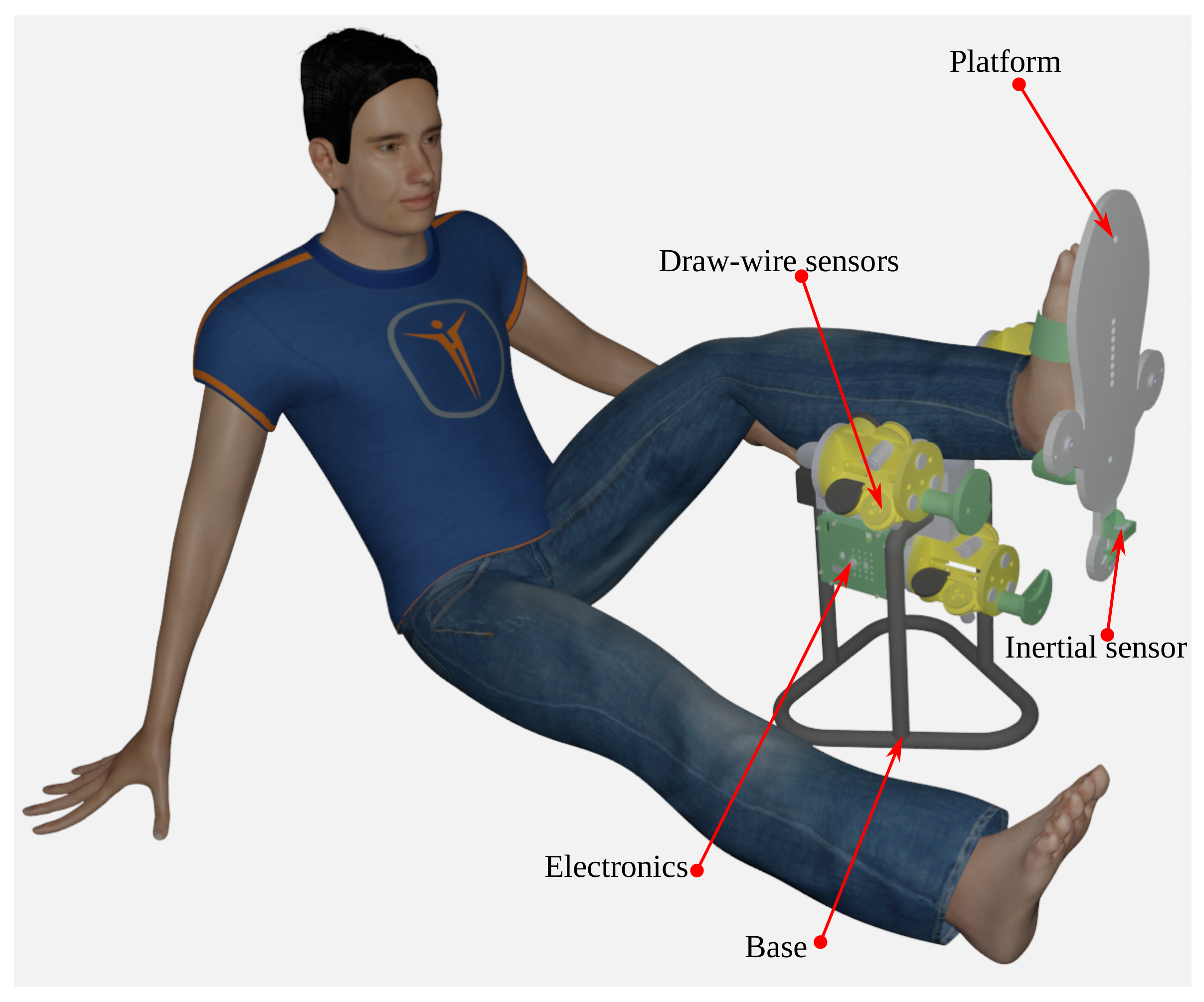
Figure 21.
Modular electronics casing.
Figure 21.
Modular electronics casing.
Figure 22.
Complete prototype.
Figure 22.
Complete prototype.
Figure 23.
Rendered image with a 175 cm height patient.
Figure 23.
Rendered image with a 175 cm height patient.
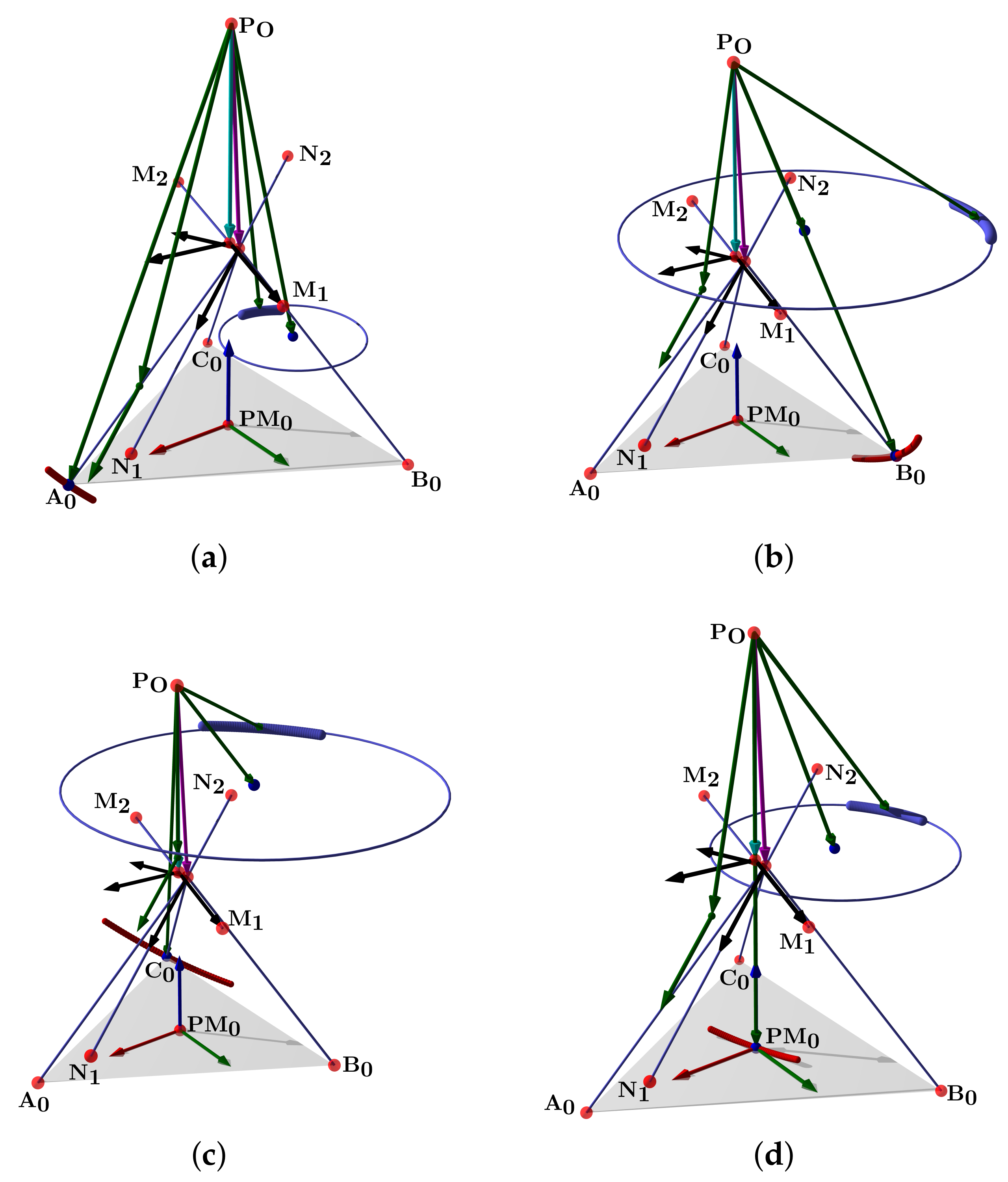
Figure 24.
Simulation of all points: (a) platform’s central point, (b) attachment a, (c) attachment b, and (d) attachment c.
Figure 24.
Simulation of all points: (a) platform’s central point, (b) attachment a, (c) attachment b, and (d) attachment c.
Figure 25.
Simulation of the platform central point with variations in the mean statistical values: (a) 10% below, and (b) 10% over.
Figure 25.
Simulation of the platform central point with variations in the mean statistical values: (a) 10% below, and (b) 10% over.
Figure 26.
Simulation of the platform’s attaching point A: (a) mean values plus 10%, (b) mean values minus 10%.
Figure 26.
Simulation of the platform’s attaching point A: (a) mean values plus 10%, (b) mean values minus 10%.
Figure 27.
Attaching point B simulation: (a) adding 10% to the statistic mean values, (b) subtracting 10%.
Figure 27.
Attaching point B simulation: (a) adding 10% to the statistic mean values, (b) subtracting 10%.
Figure 28.
Simulation results for C: (a) mean values plus 10%, (b) mean values minus 10%.
Figure 28.
Simulation results for C: (a) mean values plus 10%, (b) mean values minus 10%.
Figure 29.
Interactive simulation example: (a) sliders, (b) rendering.
Figure 29.
Interactive simulation example: (a) sliders, (b) rendering.
Figure 30.
Connections and electronics.
Figure 30.
Connections and electronics.
Figure 31.
Assembled structure.
Figure 31.
Assembled structure.
Figure 32.
Processing calibration interface.
Figure 32.
Processing calibration interface.
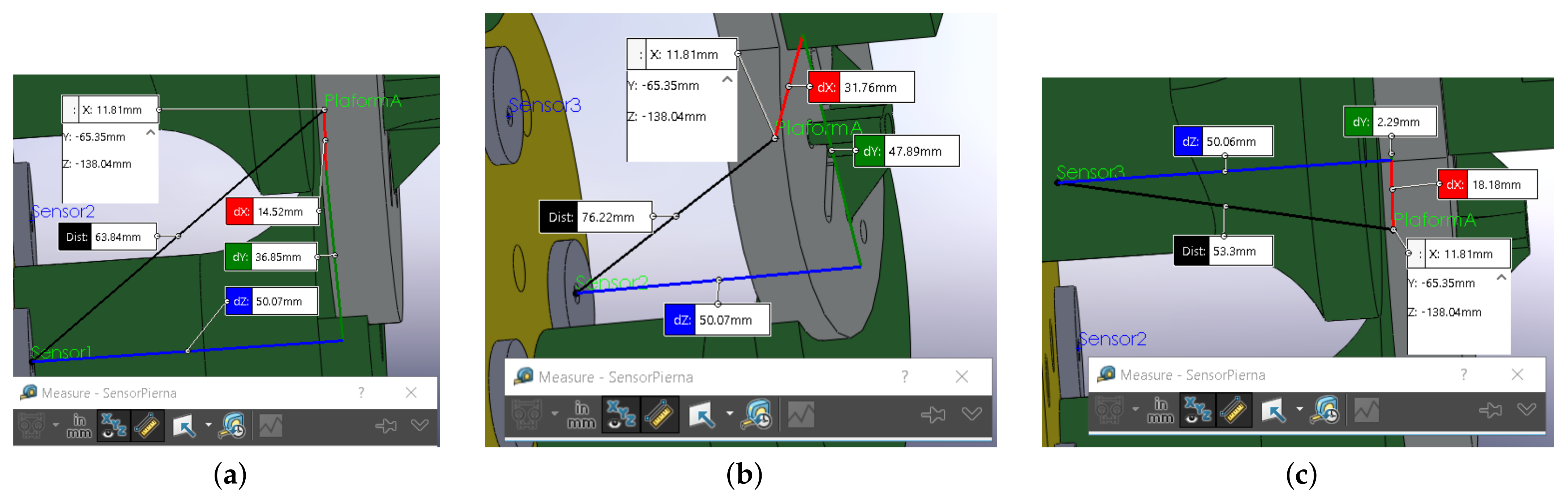
Figure 33.
Measuring in SolidWorks (2017–2018 Student Edition, Dassault Systèmes, Vélizy-Villacoublay, France)®: (a) sensor 1, (b) sensor 2, (c) sensor 3.
Figure 33.
Measuring in SolidWorks (2017–2018 Student Edition, Dassault Systèmes, Vélizy-Villacoublay, France)®: (a) sensor 1, (b) sensor 2, (c) sensor 3.
Figure 34.
First two trilateration results: (a) position 1, (b) position 2.
Figure 34.
First two trilateration results: (a) position 1, (b) position 2.
Figure 35.
Latest two trilateration results: (a) position 3, (b) position 4.
Figure 35.
Latest two trilateration results: (a) position 3, (b) position 4.
Figure 36.
TC axis circle fitting: (a) trajectory A, (b) trajectory B, (c) trajectory C, (d) trajectory PM.
Figure 36.
TC axis circle fitting: (a) trajectory A, (b) trajectory B, (c) trajectory C, (d) trajectory PM.
Figure 37.
ST axis circle fitting: (a) trajectory A, (b) trajectory B, (c) trajectory C, (d) trajectory PM.
Figure 37.
ST axis circle fitting: (a) trajectory A, (b) trajectory B, (c) trajectory C, (d) trajectory PM.
Figure 38.
Ankle joint manifold. (a) Manifold for PM, (b) chart with ankle axis coordinates.
Figure 38.
Ankle joint manifold. (a) Manifold for PM, (b) chart with ankle axis coordinates.
Figure 39.
Re-configurable cable-driven robot concept.
Figure 39.
Re-configurable cable-driven robot concept.
Table 1.
Mean values of anthropometric measurements.
Table 1.
Mean values of anthropometric measurements.
| Variable | K (cm) | L (cm) | O (cm) | P (cm) | Q (cm) | R = W/w |
|---|
| Mean | 1.2 cm | 1.1 cm | 1.6 cm | 1.0 cm | 0.5 cm | 0.54 cm |
Table 2.
Calibration results with digital measurements and real measurements.
Table 2.
Calibration results with digital measurements and real measurements.
| Measurements | l1M1 | l2M1 | l3M1 | l1M2 | l2M2 | l1M3 | l2M3 |
|---|
| BCD value | 239 | 330 | 246 | 265 | 177 | 252 | 242 |
| Vernier Caliper, cm | 8.0 cm | 5.3 cm | 6.9 cm | 13.0 cm | 8.4 cm | 7.8 cm | 11.5 cm |
Table 3.
Error compared with SolidWorks® measurements.
Table 3.
Error compared with SolidWorks® measurements.
| Measurements | l1M1 | l2M1 | l3M1 |
|---|
| Measured distance | 7.622 cm | 5.33 cm | 6.384 cm |
| Error in cm | 0.38 cm | −0.030 cm | 0.52 cm |
Table 4.
Sensor measurements in four different positions.
Table 4.
Sensor measurements in four different positions.
| Positions | l1M1 | l2M1 | l3M1 | l1M2 | l2M2 | l1M3 | l2M3 |
|---|
| Pos1., cm | 11.0 cm | 12.6 cm | 12.5 cm | 14.8 cm | 10.8 cm | 15.2 cm | 11.9 cm |
| Pos2., cm | 10.2 cm | 11.7 cm | 11.6 cm | 15.2 cm | 11.3 cm | 15.5 cm | 12.2 cm |
| Pos3., cm | 9.40 cm | 10.8 cm | 10.8 cm | 15.6 cm | 11.7 cm | 15.8 cm | 12.5 cm |
| Pos4., cm | 8.56 cm | 9.89 cm | 9.95 cm | 16.0 cm | 12.2 cm | 16.0 cm | 12.7 cm |
Table 5.
A, B and C coordinates computed from the four positions.
Table 5.
A, B and C coordinates computed from the four positions.
| Positions | A | B | C |
|---|
| Pos1., cm | (−11.7, −1.06, −11.0) cm | (6.11, −9.77, −8.76) cm | (5.54, 8.81, −9.35) cm |
| Pos2., cm | (−12.1, −0.93, −10.2) cm | (5.62, −9.92, −9.37) cm | (4.83, 9.46, −10.1) cm |
| Pos3., cm | (−12.4, −0.65, −9.39) cm | (5.27, −9.79, −9.68) cm | (4.94, 9.03, −10.2) cm |
| Pos4., cm | (−12.7, −0.48, −8.53) cm | (4.68, −10.0, −10.3) cm | (3.54, 10.7, −11.1) cm |
Table 6.
TC axis circle fitting.
Table 6.
TC axis circle fitting.
| Trajectory | Center | Direction | Radius |
|---|
| A | (0.08649, 2.138, −6.712) cm | (−0.089, −0.95, 0.31) | 7.666 |
| B | (0.5713, 5.531, −7.824) cm | (−0.089, −0.95, 0.31) | 5.246 cm |
| C | (−0.2442, −2.669, −5.315) cm | (−0.089, −0.95, 0.31) | 7.206 cm |
| PM | (0.1552, 1.642, −6.683) cm | (−0.089, −0.95, 0.31) | 5.375 cm |
Table 7.
ST axis circle fitting.
Table 7.
ST axis circle fitting.
| Trajectory | Center | Direction | Radius |
|---|
| A | (4.444, 1.825, −9.008) cm | (−0.75, −0.28, 0.60) | 2.428 cm |
| B | (1.757, 0.6768, −6.925) cm | (−0.75, −0.28, 0.60) | 6.567 cm |
| C | (0.1578, 0.1819, −5.807) cm | ((−0.75, −0.28, 0.60) | 6.935 cm |
| PM | (2.087, 0.8882, −7.281) cm | (−0.75, −0.28, 0.60) | 3.875 |
Table 8.
Axis estimation data.
Table 8.
Axis estimation data.
| Axis | Median Center | Median Normal | r | |
|---|
| TC | (1.92, 0.783, −7.10) cm | (−0.750, −0.280, 0.600) | (−0.174, 0.000, −5.43) cm | (−0.750, −0.280, 0.600) |
| ST | (0.121, 1.89, −6.70) cm | (−0.0890, −0.950, 0.310) | (−0.0562, 0.000, −6.08) cm | (−0.0890, −0.950, 0.310) |
Table 9.
Plucker line coordinates.
Table 9.
Plucker line coordinates.
| Axis | Plucker Line Coordinates |
|---|
| TC | [−0.750: −0.280: 0.600: −1.52: 4.17: 0.0487] |
| ST | [−0.0890: −0.950: 0.310: −5.78: 0.559: 0.0534] |