Learning Cephalometric Landmarks for Diagnostic Features Using Regression Trees
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Ensemble of Regression Trees
2.3. Transformations
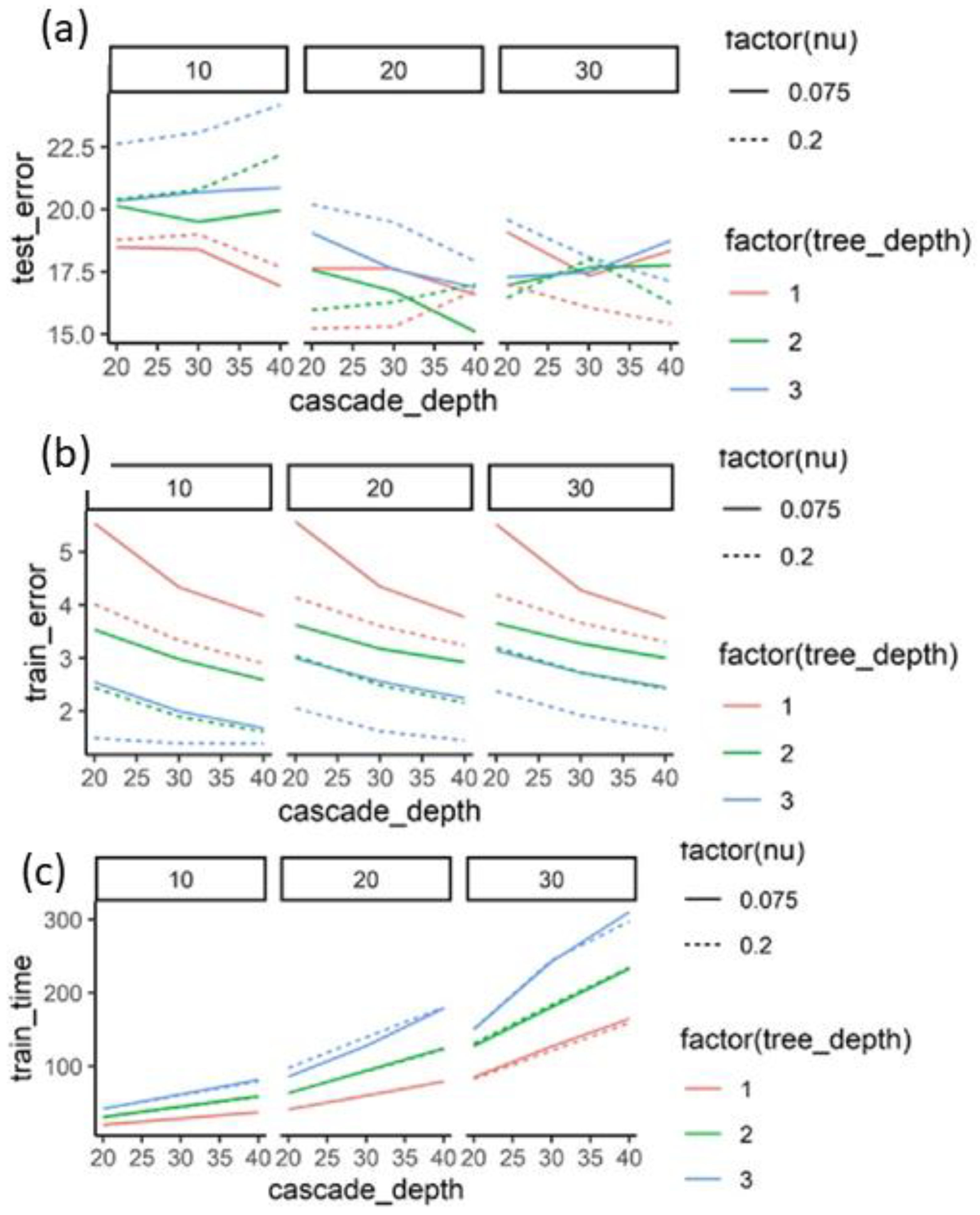
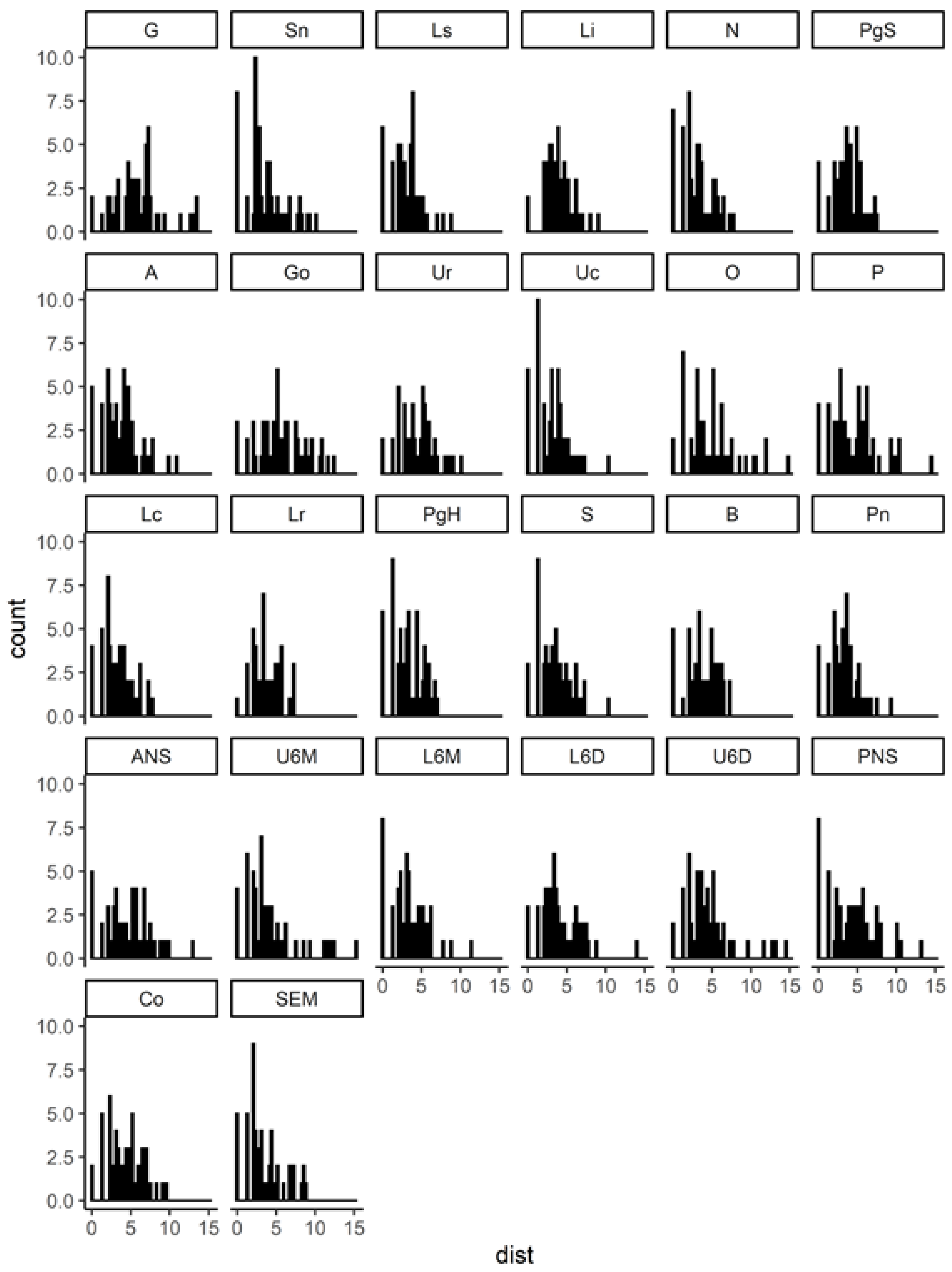
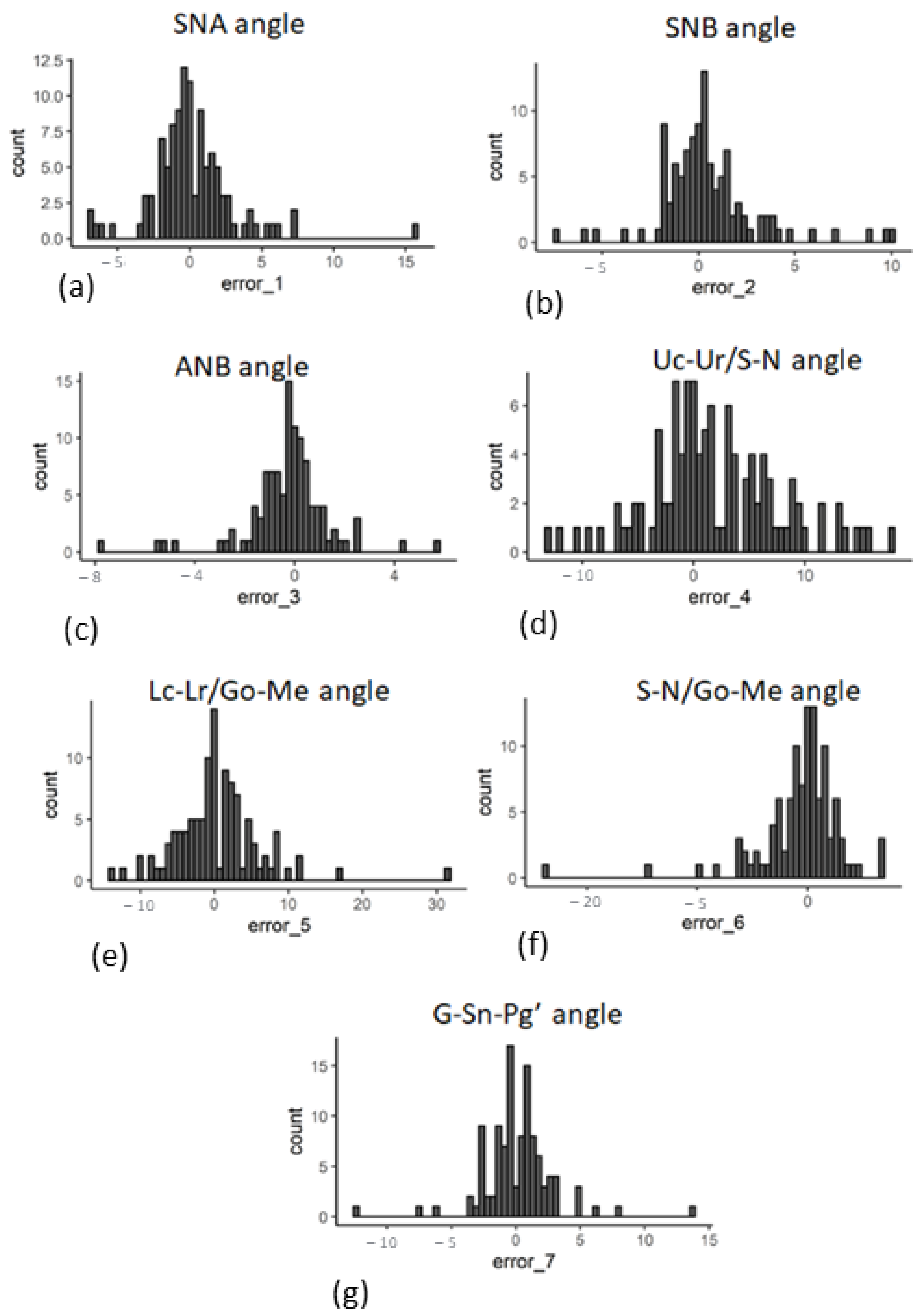
3. Results
3.1. Novelty Introduced by Data Augmentation Methods
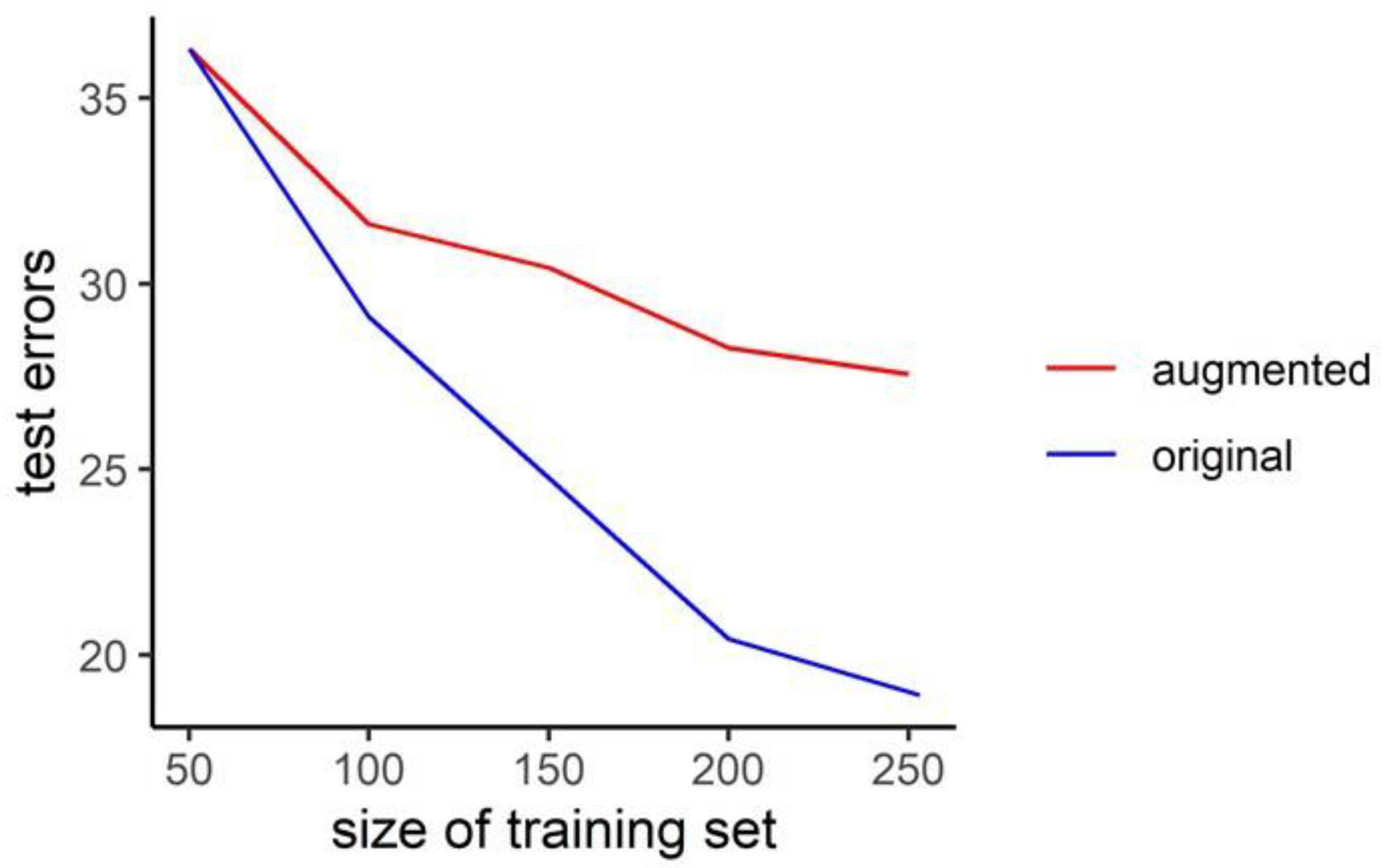
3.2. Performance Gains from Data Augmentation
4. Discussion
5. Conclusions
- Ensemble of regression tree proved to be a reliable approach for the automated identification of cephalometric landmarks.
- Augmentation methods could be used to artificially increase the training set size and consequently improve the performance of the machine learning model.
- Simple image transformations such as original, zoom, H-shift, W-shift, shear, and rotation worked well to introduce novelty to the model.
- The elastic transformation did not perform well as a method of augmentation for introducing novelty to the sample.
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Wang, C.W.; Huang, C.T.; Hsieh, M.C.; Li, C.H.; Chang, S.W.; Li, W.C.; Vandaele, R.; Marée, R.; Jodogne, S.; Geurts, P.; et al. Evaluation and Comparison of Anatomical Landmark Detection Methods for Cephalometric X-Ray Images: A Grand Challenge. IEEE Trans. Med. Imaging 2015, 34, 1890–1900. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.W.; Huang, C.T.; Lee, J.H.; Li, C.H.; Chang, S.W.; Siao, M.J.; Lai, T.M.; Ibragimov, B.; Vrtovec, T.; Ronneberger, O.; et al. A benchmark for comparison of dental radiography analysis algorithms. Med. Image Anal. 2016, 31, 63–76. [Google Scholar] [CrossRef]
- Lévy-Mandel, A.D.; Venetsanopoulos, A.N.; Tsotsos, J.K. Knowledge-based landmarking of cephalograms. Comput. Biomed. Res. 1986, 19, 282–309. [Google Scholar] [CrossRef]
- Cardillo, J.; Sid-Ahmed, M.A. An image processing system for locating craniofacial landmarks. IEEE Trans. Med. Imaging 1994, 13, 275–289. [Google Scholar] [CrossRef] [PubMed]
- Forsyth, D.B.; Shaw, W.C.; Richmond, S. Digital imaging of cephalometric radiography, Part 1: Advantages and limitations of digital imaging. Angle Orthod. 1996, 66, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Grau, V.; Alcañiz, M.; Juan, M.C.; Monserrat, C.; Knoll, C. Automatic localization of cephalometric Landmarks. J. Biomed. Inform. 2001, 34, 146–156. [Google Scholar] [CrossRef]
- Lindner, C.; Wang, C.W.; Huang, C.T.; Li, C.H.; Chang, S.W.; Cootes, T.F. Fully Automatic System for Accurate Localisation and Analysis of Cephalometric Landmarks in Lateral Cephalograms. Sci. Rep. 2016, 6, 33581, Erratum in: Sci. Rep. 2021, 11, 12049. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Li, J.; Zhang, Y.; Zou, B. Automatic Analysis of Lateral Cephalograms Based on Multiresolution Decision Tree Regression Voting. J. Healthc. Eng. 2018, 2018, 1797502. [Google Scholar] [CrossRef]
- Ibragimov, B.; Likar, B.; Pernuš, F.; Vrtovec, T. Shape representation for efficient landmark-based segmentation in 3-d. IEEE Trans. Med. Imaging 2014, 33, 861–874. [Google Scholar] [CrossRef]
- Ibragimov, B.; Likar, B.; FPernus, F.; Vrtovec, T. Automatic cephalometric X-ray landmark detection by applying game theory and random forests. In Proceedings ISBI International Symposium on Biomedical Imaging; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–8. [Google Scholar]
- Vandaele, R.; Aceto, J.; Muller, M.; Péronnet, F.; Debat, V.; Wang, C.W.; Huang, C.T.; Jodogne, S.; Martinive, P.; Geurts, P.; et al. Landmark detection in 2D bioimages for geometric morphometrics: A multi-resolution tree-based approach. Sci. Rep. 2018, 8, 538. [Google Scholar] [CrossRef] [PubMed]
- Oh, K.; Oh, I.S.; Le, V.N.T.; Lee, D.W. Deep Anatomical Context Feature Learning for Cephalometric Landmark Detection. IEEE J. Biomed. Health Inform. 2021, 25, 806–817. [Google Scholar] [CrossRef]
- Leonardi, R.; Giordano, D.; Maiorana, F.; Spampinato, C. Automatic cephalometric analysis. Angle Orthod. 2008, 78, 145–151. [Google Scholar] [CrossRef]
- Saad, A.A.; El-Bialy, A.; Kandil, A.H.; Sayed, A.A. Automatic cephalometric analysis using active appearance model and simulated annealing. In Proceedings of the International Conference on Graphics, Vision and Image Processing, Cairo, Egypt, 2005; pp. 19–21. [Google Scholar]
- Rudolph, D.J.; Sinclair, P.M.; Coggins, J.M. Automatic computerized radiographic identification of cephalometric landmarks. Am. J. Orthod. Dentofac. Orthop. 1998, 113, 173–179. [Google Scholar] [CrossRef]
- Kazemi, V.; Sullivan, J. One millisecond face alignment with an ensemble of regression trees. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1867–1874. [Google Scholar]
- King, D.E. Dlib-ml: A machine learning toolkit. J. Mach. Learn. Res. 2009, 10, 1755–1758. [Google Scholar]
- Van Rossum, G.; Drake, F.L., Jr. Python Reference Manual; Centrum voor Wiskunde en Informatica Amsterdam: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Barbosa, J.; Seo, W.K.; Kang, J. paraFaceTest: An ensemble of regression tree-based facial features extraction for efficient facial paralysis classification. BMC Med. Imaging 2019, 19, 30. [Google Scholar] [CrossRef] [PubMed]
- Belhumeur, P.N.; Jacobs, D.W.; Kriegman, D.J.; Kumar, N. Localizing parts of faces using a consensus of exemplars. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2930–2940. [Google Scholar] [CrossRef] [PubMed]
- Valle, R.; Buenaposada, J.M.; Valdés, A.; Baumela, L. A Deeply-Initialized Coarse-to-fine Ensemble of Regression Trees for Face Alignment. In Computer Vision—ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11218. [Google Scholar] [CrossRef]
- Lindner, C.; Bromiley, P.A.; Ionita, M.C.; Cootes, T.F. Robust and Accurate Shape Model Matching Using Random Forest Regression-Voting. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1862–1874. [Google Scholar] [CrossRef]
- Al Taki, A.; Yaqoub, S.; Hassan, M. Legan-burstone soft tissue profile values in a Circassian adult sample. J. Orthod. Sci. 2018, 7, 18. [Google Scholar] [CrossRef]
- Hwang, H.W.; Moon, J.H.; Kim, M.G.; Donatelli, R.E.; Lee, S.J. Evaluation of automated cephalometric analysis based on the latest deep learning method. Angle Orthod. 2021, 91, 329–335. [Google Scholar] [CrossRef]
- Jha, M.S. Cephalometric Evaluation Based on Steiner’s Analysis on Adults of Bihar. J. Pharm. Bioallied Sci. 2021, 13 (Suppl. 2), S1360–S1364. [Google Scholar] [CrossRef] [PubMed]
- Steiner, C.C. Cephalometrics for You and Me. Am. J. Orthod. 1953, 39, 729–755. [Google Scholar] [CrossRef]
- Hwang, H.W.; Park, J.H.; Moon, J.H.; Yu, Y.; Kim, H.; Her, S.B.; Srinivasan, G.; Aljanabi, M.N.A.; Donatelli, R.E.; Lee, S.J. Automated identification of cephalometric landmarks: Part 2-Might it be better than human? Angle Orthod. 2020, 90, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Park, J.H.; Hwang, H.W.; Moon, J.H.; Yu, Y.; Kim, H.; Her, S.B.; Srinivasan, G.; Aljanabi, M.N.A.; Donatelli, R.E.; Lee, S.J. Automated identification of cephalometric landmarks: Part 1-Comparisons between the latest deep-learning methods YOLOV3 and SSD. Angle Orthod. 2019, 89, 903–909. [Google Scholar] [CrossRef] [PubMed]
- Arık, S.Ö.; Ibragimov, B.; Xing, L. Fully automated quantitative cephalometry using convolutional neural networks. J. Med. Imaging 2017, 4, 014501. [Google Scholar] [CrossRef]
- Mehta, S.; Suahil, Y.; Nelson, J.; Upadhyay, M. Artificial Intelligence for radiographic image analysis. Sem. Orthod. 2021, 27, 109–120. [Google Scholar] [CrossRef]

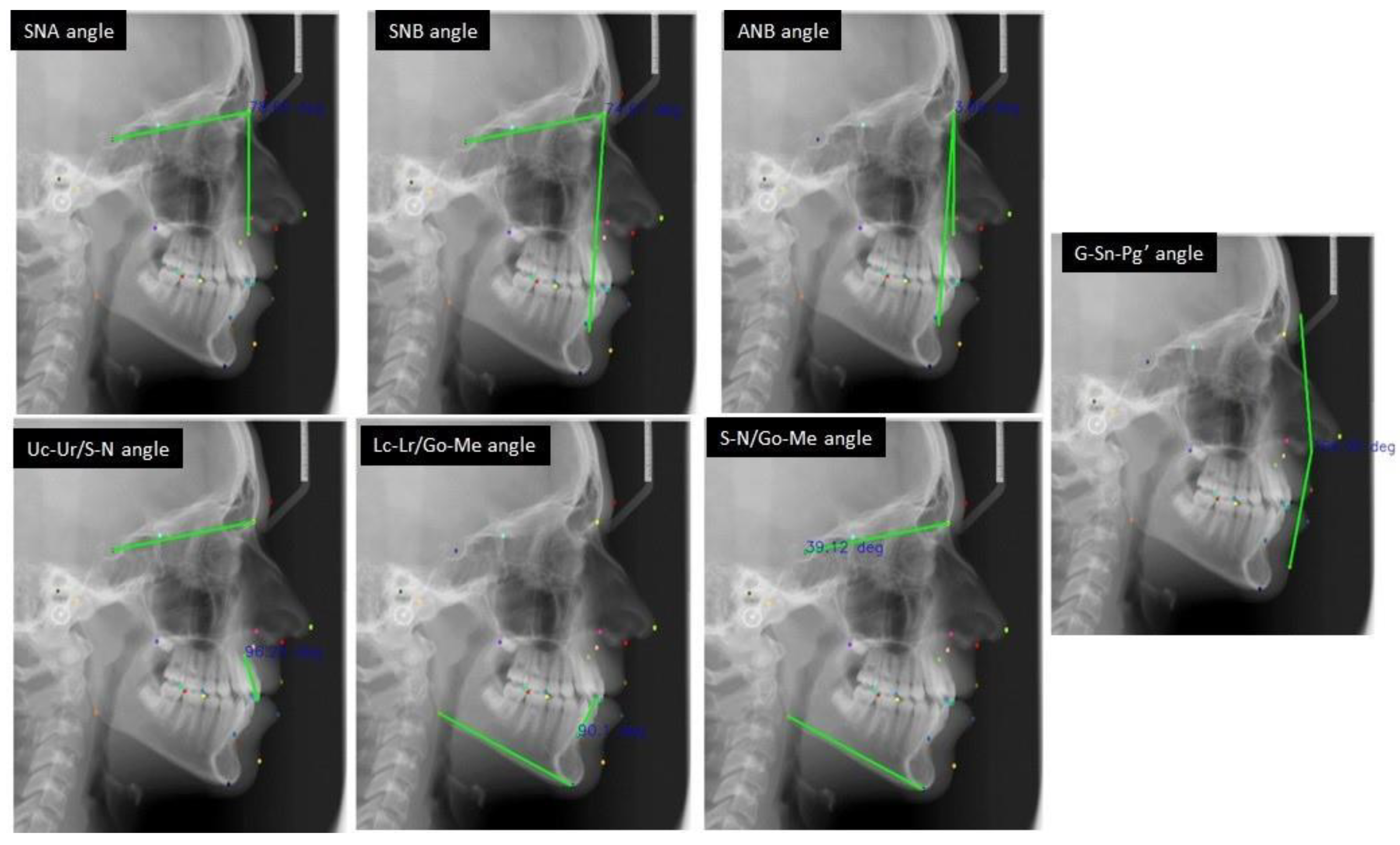


| Landmark | Description |
|---|---|
| S (Sella) | The geometric center point of the pituitary fossa. |
| P (Porion) | The most superior point on the external auditory meatus. |
| Go (Gonion) | Most posterior and inferior point on the curvature of the angle of the mandible. |
| N (Nasion) | The most anterior point on the frontonasal suture. |
| O (Orbitale) | The lowest point on the inferior rim of the orbit. |
| A (Point A) | The deepest point on the bony concavity between the ANS and supradentale. |
| B (Point b) | The deepest point on the bony concavity between the pogonion and infradentale. |
| Me (Menton) | The most inferior point on the hard tissue chin. |
| G (Glabella) | The most anterior point on the forehead. |
| Sn (Subnasale) | The junction of the nose and upper lip. |
| Ls (Labrale superius) | The most prominent point on the upper lip. |
| Li (Labrale inferius) | The most prominent point on the lower lip. |
| PgS (Soft tissue pogonion) | The most prominent point on the soft tissue chin. |
| Ur | The root tip of the upper incisor. |
| Uc | The crown tip of the upper incisor. |
| Lc | The crown tip of the lower incisor. |
| Lr | The root tip of the lower incisor. |
| ANS (Anterior nasal spine) | Anterior tip of the nasal spine. |
| PNS (Posterior nasal spine) | Posterior tip of the nasal spine. |
| U6M Upper first molar mesial tip | Most prominent point on the mesial cusp. |
| U6D Upper first molar distal tip | Most prominent point on the distal cusp. |
| L6M Lower first molar mesial tip | Most prominent point on the mesial cusp. |
| L6D Lower first molar distal tip | Most prominent point on the distal cusp. |
| SEM (Sphenoethmoidal point) | Intersection of the greater wing of sphenoid and the cranial floor. |
| Pn (Pronasale) | The most anterior point on the nose. |
| Co (Condylion) | The most superior and posterior point on the condylar head. |
| Parameter | Description |
|---|---|
| Nu | Weight given to new trees being successively added to the present ensemble. |
| Oversampling Amount | Number of times the same image is used for different regressors. |
| Cascade Depth | Total number of cascade stages. |
| Tree Depth | Depth of each regression tree in the ensembles. |
| Zoom | H-Shifted | W-Shifted | Shear | Rotate | Elastic |
|---|---|---|---|---|---|
| 10% | 50 pixels | 50 pixels | 10 deg | 10 deg | alpha = 100, sigma = 5, alpha_affine = 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suhail, S.; Harris, K.; Sinha, G.; Schmidt, M.; Durgekar, S.; Mehta, S.; Upadhyay, M. Learning Cephalometric Landmarks for Diagnostic Features Using Regression Trees. Bioengineering 2022, 9, 617. https://doi.org/10.3390/bioengineering9110617
Suhail S, Harris K, Sinha G, Schmidt M, Durgekar S, Mehta S, Upadhyay M. Learning Cephalometric Landmarks for Diagnostic Features Using Regression Trees. Bioengineering. 2022; 9(11):617. https://doi.org/10.3390/bioengineering9110617
Chicago/Turabian StyleSuhail, Sameera, Kayla Harris, Gaurav Sinha, Maayan Schmidt, Sujala Durgekar, Shivam Mehta, and Madhur Upadhyay. 2022. "Learning Cephalometric Landmarks for Diagnostic Features Using Regression Trees" Bioengineering 9, no. 11: 617. https://doi.org/10.3390/bioengineering9110617
APA StyleSuhail, S., Harris, K., Sinha, G., Schmidt, M., Durgekar, S., Mehta, S., & Upadhyay, M. (2022). Learning Cephalometric Landmarks for Diagnostic Features Using Regression Trees. Bioengineering, 9(11), 617. https://doi.org/10.3390/bioengineering9110617








