An Objective and Repeatable Sac Isolation Technique for Comparing Biomechanical Metrics in Abdominal Aortic Aneurysms
Abstract
1. Introduction
2. Materials and Methods
2.1. Clinical Dataset and Imaging Repository: De-Identified Sets of Clinical and Imaging
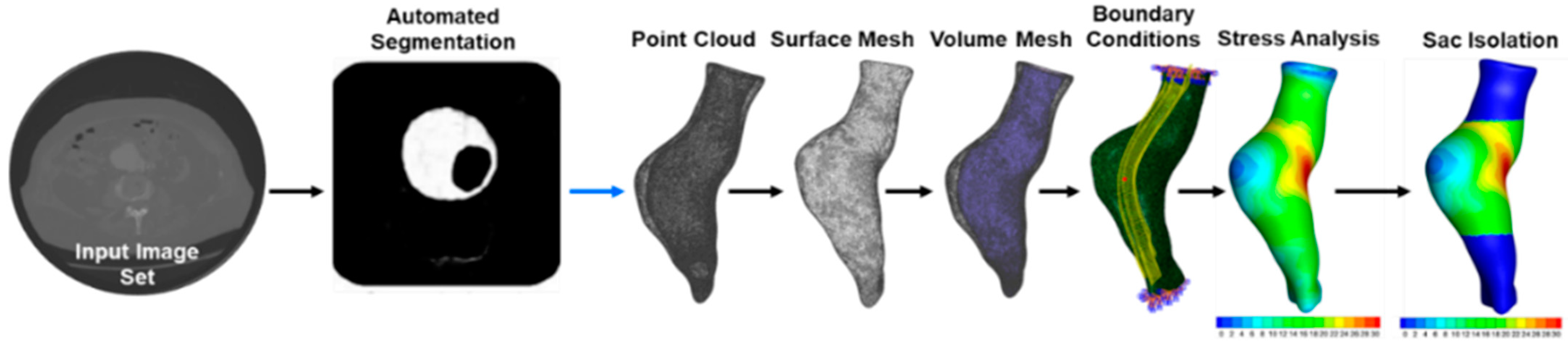
2.2. Image Segmentation of AAA from CT: Image Segmentation from CT Angiography
2.3. Finite Element Analysis
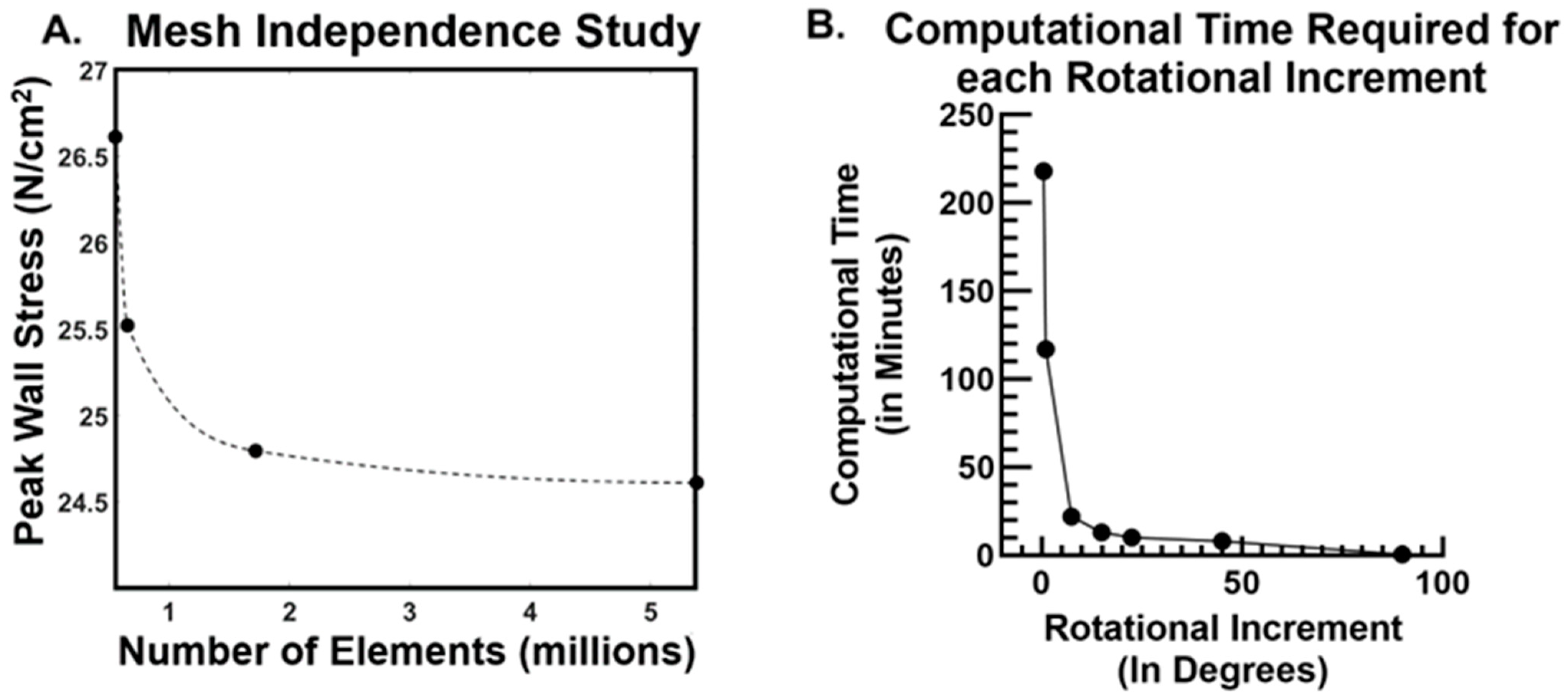
2.4. Mesh Independence Study and Mesh Quality Checks
2.5. Algorithmic Isolation of the Aneurysm Sac
2.6. Assessment of Computational Cost Dependence on Rotational Increment
2.7. Stress Calculations and Statistical Comparisons
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vorp, D.A. Biomechanics of abdominal aortic aneurysm. J. Biomech. 2007, 40, 1887–1902. [Google Scholar] [CrossRef] [PubMed]
- Holleman, J. Abdominal aortic aneurysm. Surg. Attend. Rounds 2015, 91, 345–357. [Google Scholar]
- Kontopodis, N.; Pantidis, D.; Dedes, A.; Daskalakis, N.; Ioannou, C.V. The—Not So—Solid 5.5 cm Threshold for Abdominal Aortic Aneurysm Repair: Facts, Misinterpretations, and Future Directions. Front. Surg. 2016, 3, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Darling, R.C.; Messina, C.R.; Brewster, D.C.; Ottinger, L.W. Autopsy study of unoperated abdominal aortic aneurysms. The case for early resection. Circulation 1997, 56, 161–164. [Google Scholar]
- Nicholls, S.C.; Gardner, J.B.; Meissner, M.H.; Johansen, K.H. Rupture in small abdominal aortic aneurysms. J. Vasc. Surg. 1998, 28, 884–888. [Google Scholar] [CrossRef]
- Vande Geest, J.P.; Di Martino, E.S.; Bohra, A.; Makaroun, M.S.; Vorp, D.A. A biomechanics-based rupture potential index for abdominal aortic aneurysm risk assessment: Demonstrative application. Ann. N. Y. Acad. Sci. 2006, 1085, 11–21. [Google Scholar] [CrossRef]
- Vande Geest, J.P.; Sacks, M.S.; Vorp, D.A. The effects of aneurysm on the biaxial mechanical behavior of human abdominal aorta. J. Biomech. 2006, 39, 1324–1334. [Google Scholar] [CrossRef] [PubMed]
- Vande Geest, J.P.; Schmidt, D.E.; Sacks, M.S.; Vorp, D.A. The effects of anisotropy on the stress analyses of patient-specific abdominal aortic aneurysms. Ann. Biomed. Eng. 2008, 36, 921–932. [Google Scholar] [CrossRef]
- Gasser, T.C.; Nchimi, A.; Swedenborg, J.; Roy, J.; Sakalihasan, N.; Böckler, D.; Hyhlik-Dürr, A. A novel strategy to translate the biomechanical rupture risk of abdominal aortic aneurysms to their equivalent diameter risk: Method and retrospective validation. Eur. J. Vasc. Endovasc. Surg. 2014, 47, 288–295. [Google Scholar] [CrossRef]
- Joldes, G.R.; Miller, K.; Wittek, A.; Forsythe, R.O.; Newby, D.E.; Doyle, B.J. BioPARR: A software system for estimating the rupture potential index for abdominal aortic aneurysms. Sci. Rep. 2017, 7, 4641. [Google Scholar] [CrossRef]
- Speelman, L.; Bosboom, E.M.H.; Schurink, G.W.H.; Hellenthal, F.A.M.V.I.; Buth, J.; Breeuwer, M.; Jacobs, M.J.; van de Vosse, F.N. Patient-Specific AAA Wall Stress Analysis: 99-Percentile Versus Peak Stress. Eur. J. Vasc. Endovasc. Surg. 2008, 36, 668–676. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Fillinger, M.F.; Marra, S.P.; Raghavan, M.L.; Kennedy, F.E. Prediction of rupture risk in abdominal aortic aneurysm during observation: Wall stress versus diameter. J. Vasc. Surg. 2003, 37, 724–732. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, M.L.; Fillinger, M.F.; Marra, S.P.; Naegelein, B.P.; Kennedy, F.E. Automated Methodology for Determination of Stress Distribution in Human Abdominal Aortic Aneurysm. J. Biomech. Eng. 2005, 127, 868. [Google Scholar] [CrossRef]
- Fillinger, M.F.; Raghavan, M.L.; Marra, S.P.; Cronenwett, J.L.; and Kennedy, F.E. In vivo analysis of mechanical wall stress and abdominal aortic aneurysm rupture risk. J. Vasc. Surg. 2002, 36, 589–597. [Google Scholar] [CrossRef] [PubMed]
- Chung, T.K.; da Silva, E.S.; Raghavan, S.M.L. Does elevated wall tension cause aortic aneurysm rupture? Investigation using a subject-specific heterogeneous model. J. Biomech. 2017, 64, 164–171. [Google Scholar] [CrossRef]
- Maier, A.; Gee, M.W.; Reeps, C.; Pongratz, J.; Eckstein, H.H.; Wall, W.A. A comparison of diameter, wall stress, and rupture potential index for abdominal aortic aneurysm rupture risk prediction. Ann. Biomed. Eng. 2010, 38, 3124–3134. [Google Scholar] [CrossRef]
- Truijers, M.; Pol, J.A.; SchultzeKool, L.J.; van Sterkenburg, S.M.; Fillinger, M.F.; Blankensteijn, J.D. Wall Stress Analysis in Small Asymptomatic, Symptomatic and Ruptured Abdominal Aortic Aneurysms. Eur. J. Vasc. Endovasc. Surg. 2007, 33, 401–407. [Google Scholar] [CrossRef]
- Raghavan, M.L.; Vorp, D.A. Toward a biomechanical tool to evaluate rupture potential of abdominal aortic aneurysm: Identification of a finite strain constitutive model and evaluation of its applicability. J. Biomech. 2000, 33, 475–482. [Google Scholar] [CrossRef]
- Wu, W.; Rengarajan, B.; Thirugnanasambandam, M.; Parikh, S.; Gomez, R.; De Oliviera, V.; Muluk, S.C.; Finol, E.A. Wall Stress and Geometry Measures in Electively Repaired Abdominal Aortic Aneurysms. Ann. Biomed. Eng. 2019, 47, 1611–1625. [Google Scholar] [CrossRef]
- Xiancheng, W.; Wei, L.; Bingyi, M.; He, J.; Jiang, Z.; Xu, W.; Ji, Z.; Hong, G.; Zhaomeng, S. Retina Blood Vessel Segmentation Using A U-Net Based Convolutional Neural Network. In Proceedings of the Procedia Computer Science: International Conference on Data Science (ICDS 2018), Beijing, China, 8–9 June 2018. [Google Scholar]
- Chung, T.K.; Liang, N.L.; Vorp, D.A. Artificial Intelligence Framework to Predict Wall Stress in Abdominal Aortic Aneurysm. Appl. Eng. Sci. 2022, 10, 100104. [Google Scholar] [CrossRef]
- Zhu, L.; Kukko, A.; Virtanen, J.-P.; Hyyppä, J.; Kaartinen, H.; Hyyppä, H.; Turppa, T. Multisource point clouds, point simplification and surface reconstruction. Remote Sens. 2019, 11, 2659. [Google Scholar] [CrossRef]
- Cignoni, P.; Montani, C.; Rocchini, C.; Scopigno, R.; Tarini, M. Preserving attribute values on simplified meshes by resampling detail textures. Vis. Comput. 1999, 15, 519–539. [Google Scholar] [CrossRef]
- Di Martino, E.S.; Vorp, D.A. Effect of variation in intraluminal thrombus constitutive properties on abdominal aortic aneurysm wall stress. Ann. Biomed. Eng. 2003, 31, 804–809. [Google Scholar] [CrossRef]
- Wang, D.H.J.; Makaroun, M.S.; Webster, M.W.; Vorp, D.A. Effect of intraluminal thrombus on wall stress in patient-specific models of abdominal aortic aneurysm. J. Vasc. Surg. 2002, 36, 598–604. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, M.L.; Ma, B.; Harbaugh, R.E. Quantified aneurysm shape and rupture risk. J. Neurosurg. 2005, 102, 355–362. [Google Scholar] [CrossRef] [PubMed]
- Larrabide, I.; Villa-Uriol, M.C.; Cárdenes, R.; Pozo, J.M.; Macho, J.; Roman, L.S.; Frangi, A.F. Three-dimensional morphological analysis of intracranial aneurysms: A fully automated method for aneurysm sac isolation and quantification. Med. Phys. 2011, 38, 2439–2449. [Google Scholar] [CrossRef]
- Piccinelli, M.; Steinman, D.A.; Hoi, Y.; Tong, F.; Veneziani, A.; Antiga, L. Automatic neck plane detection and 3D geometric characterization of aneurysmal sacs. Ann. Biomed. Eng. 2012, 40, 2188–2211. [Google Scholar] [CrossRef]
- Schanzer, A.; Greenberg, R.K.; Hevelone, N.; Robinson, W.P.; Eslami, M.H.; Goldberg, R.J.; Messina, L. Predictors of abdominal aortic aneurysm sac enlargement after endovascular repair. Circulation 2011, 123, 2848–2855. [Google Scholar] [CrossRef]
- Nakai, M.; Ikoma, A.; Sato, H.; Sato, M.; Nishimura, Y.; Okamura, Y. Risk factors associated with late aneurysmal sac expansion after endovascular abdominal aortic aneurysm repair. Diagn. Interv. Radiol. 2015, 21, 195–201. [Google Scholar] [CrossRef]
- Lalys, F.; Daoudal, A.; Gindre, J.; Göksu, C.; Lucas, A.; Kaladji, A. Influencing factors of sac shrinkage after endovascular aneurysm repair. J. Vasc. Surg. 2017, 65, 1830–1838. [Google Scholar] [CrossRef]
- Dingemans, S.A.; Jonker, F.H.; Moll, F.L.; van Herwaarden, J.A. Aneurysm sac enlargement after endovascular abdominal aortic aneurysm repair. Ann. Vasc. Surg. 2016, 31, 229–238. [Google Scholar] [CrossRef] [PubMed]
- Deery, S.E.; Ergul, E.A.; Schermerhorn, M.L.; Siracuse, J.J.; Schanzer, A.; Goodney, P.P.; Cambria, R.P.; Patel, V.I. Vascular Study Group of New England. Aneurysm sac expansion is independently associated with late mortality in patients treated with endovascular aneurysm repair. J. Vasc. Surg. 2018, 67, 157–164. [Google Scholar] [CrossRef] [PubMed]
- Raut, S.S.; Chandra, S.; Shum, J.; Finol, E.A. The Role of Geometric and Biomechanical Factors in Abdominal Aortic Aneurysm Rupture Risk Assessment. Ann. Biomed. Eng. 2013, 41, 1459–1477. [Google Scholar] [CrossRef] [PubMed]
- Pfaller, M.R.; Pham, J.; Verma, A.; Pegolotti, L.; Wilson, N.M.; Parker, D.W.; Yang, W.; Marsden, A.L. Automated Generation of 0D and 1D Reduced-Order Models of Patient-Specific Blood Flow. arXiv 2021, arXiv:2111.04878. [Google Scholar] [CrossRef] [PubMed]
- Esmaily Moghadam, M.; Vignon-Clementel, I.E.; Figliola, R.; Marsden, A.L. A modular numerical method for implicit 0D/3D coupling in cardiovascular finite element simulations. J. Comput. Phys. 2013, 244, 63–79. [Google Scholar] [CrossRef]
- Taelman, L.; Degroote, J.; Verdonck, P.; Vierendeels, J.; Segers, P. Modeling Hemodynamics in Vascular Networks Using a Geometrical Multiscale Approach: Numerical Aspects. Ann. Biomed. Eng. 2013, 41, 1445–1458. [Google Scholar] [CrossRef]

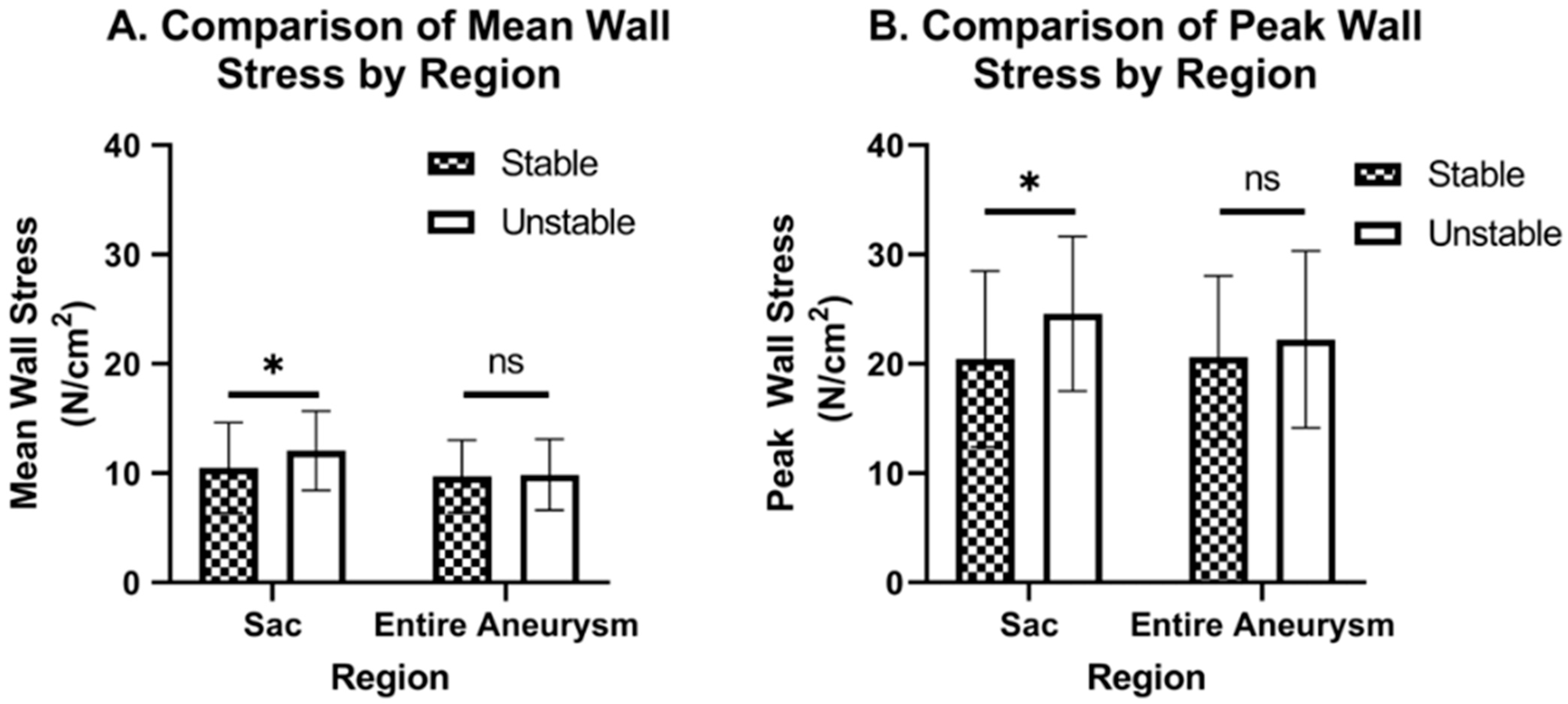
| Mean Wall Stress (N/cm2) | Peak Wall Stress (N/cm) | |
|---|---|---|
| Stable Sac (n = 222) | 10.5 ± 4.11 | 20.5 ± 8.04 |
| Stable Entire aneurysm (n = 222) | 9.71 ± 3.30 | 20.6 ± 7.45 |
| Unstable Sac (n = 23) | 12.0 ± 3.63 | 24.6 ± 7.06 |
| Unstable entire aneurysm (n = 23) | 9.87 ± 3.25 | 22.2 ± 8.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, T.K.; Gueldner, P.H.; Kickliter, T.M.; Liang, N.L.; Vorp, D.A. An Objective and Repeatable Sac Isolation Technique for Comparing Biomechanical Metrics in Abdominal Aortic Aneurysms. Bioengineering 2022, 9, 601. https://doi.org/10.3390/bioengineering9110601
Chung TK, Gueldner PH, Kickliter TM, Liang NL, Vorp DA. An Objective and Repeatable Sac Isolation Technique for Comparing Biomechanical Metrics in Abdominal Aortic Aneurysms. Bioengineering. 2022; 9(11):601. https://doi.org/10.3390/bioengineering9110601
Chicago/Turabian StyleChung, Timothy K., Pete H. Gueldner, Trevor M. Kickliter, Nathan L. Liang, and David A. Vorp. 2022. "An Objective and Repeatable Sac Isolation Technique for Comparing Biomechanical Metrics in Abdominal Aortic Aneurysms" Bioengineering 9, no. 11: 601. https://doi.org/10.3390/bioengineering9110601
APA StyleChung, T. K., Gueldner, P. H., Kickliter, T. M., Liang, N. L., & Vorp, D. A. (2022). An Objective and Repeatable Sac Isolation Technique for Comparing Biomechanical Metrics in Abdominal Aortic Aneurysms. Bioengineering, 9(11), 601. https://doi.org/10.3390/bioengineering9110601








