Numerical Models Can Assist Choice of an Aortic Phantom for In Vitro Testing
Abstract
:1. Introduction
2. Materials and Methods
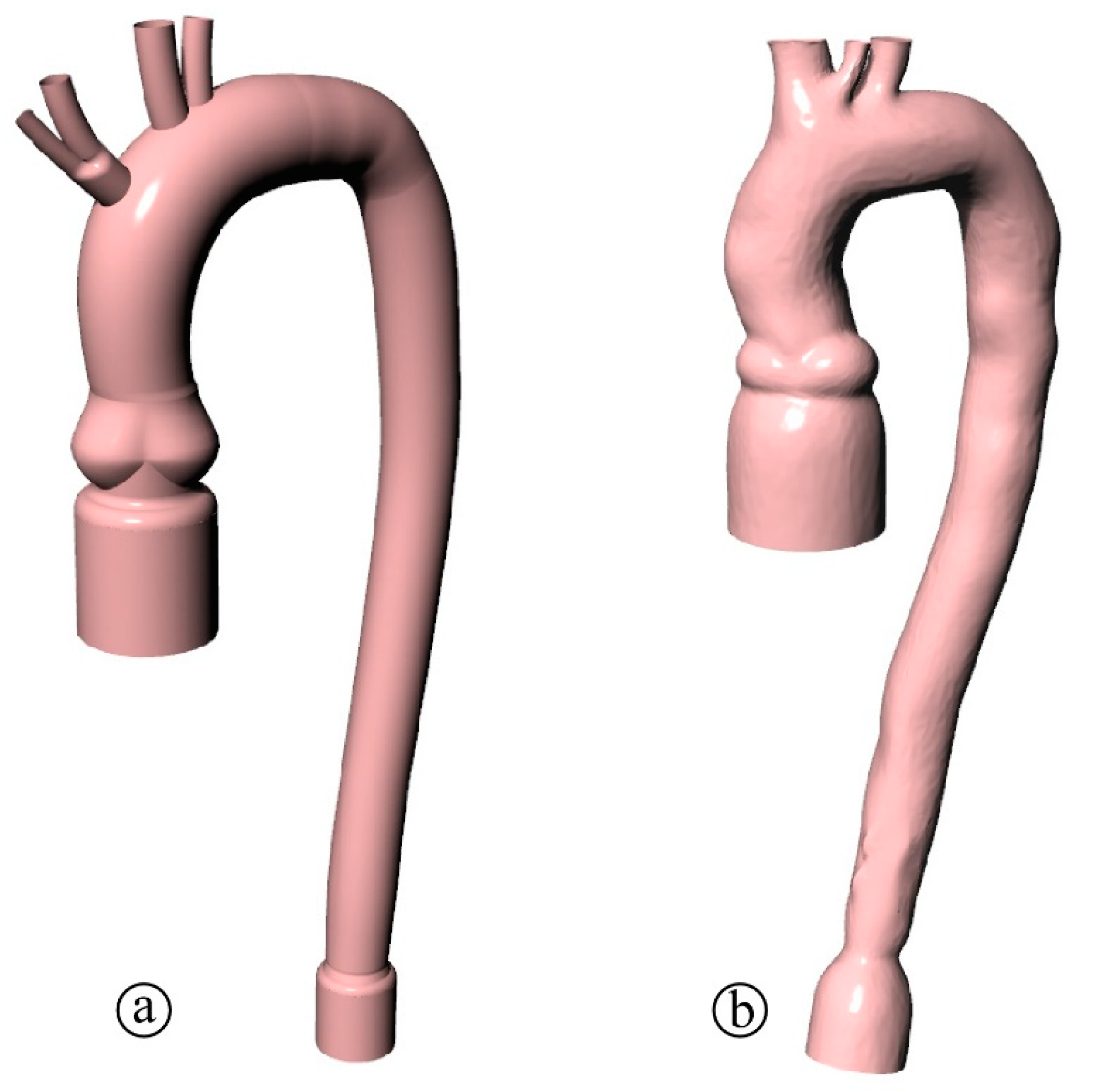
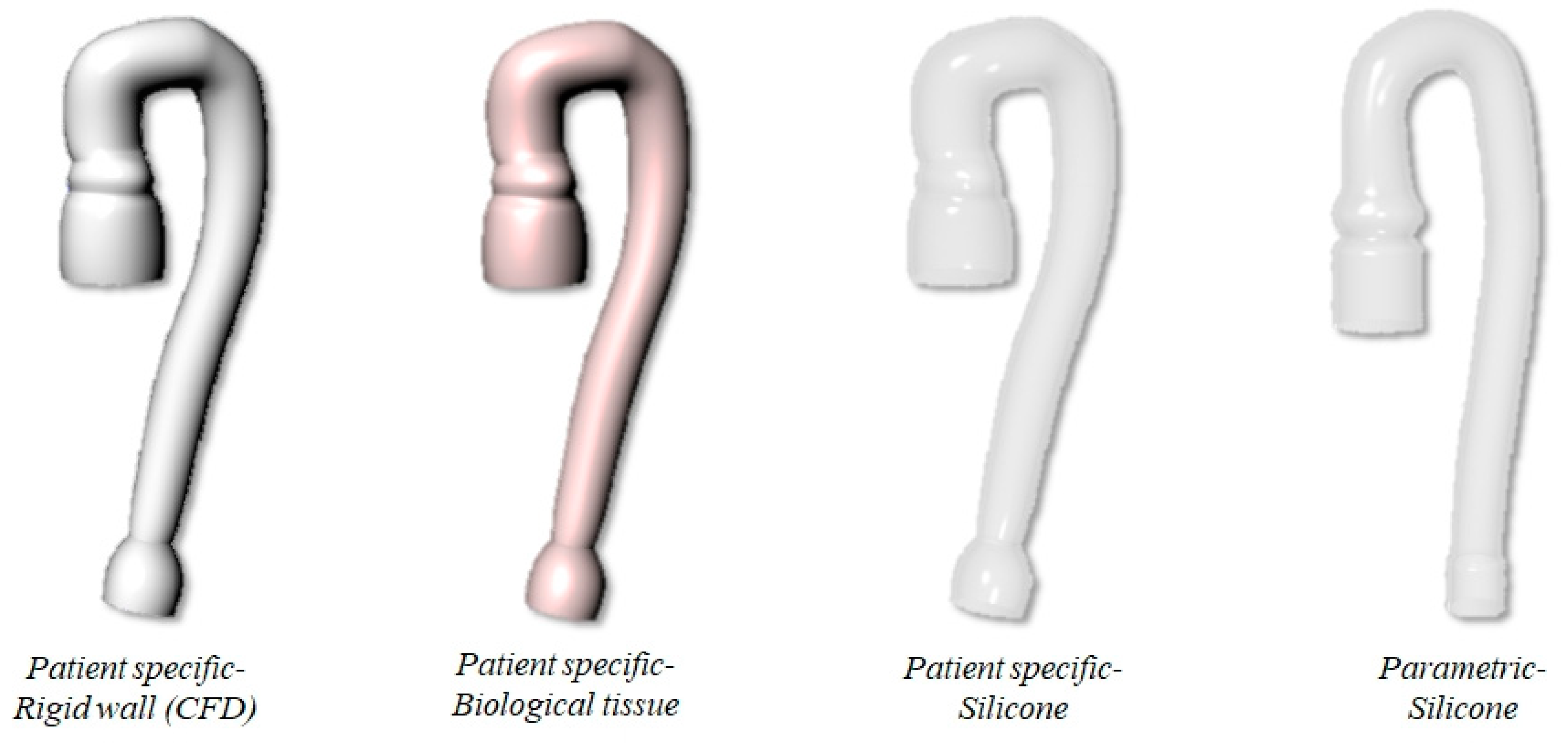
2.1. Description of the Numerical Models
- Dirichlet conditions in portions of the solid domain, i.e., null displacements of the nodes;
- Neumann conditions at the inlet of the fluid domain, i.e., flow condition at the aortic inlet;
- Dirichlet conditions at the outlet of the fluid domain, i.e., pressure condition at the phantom outlet.
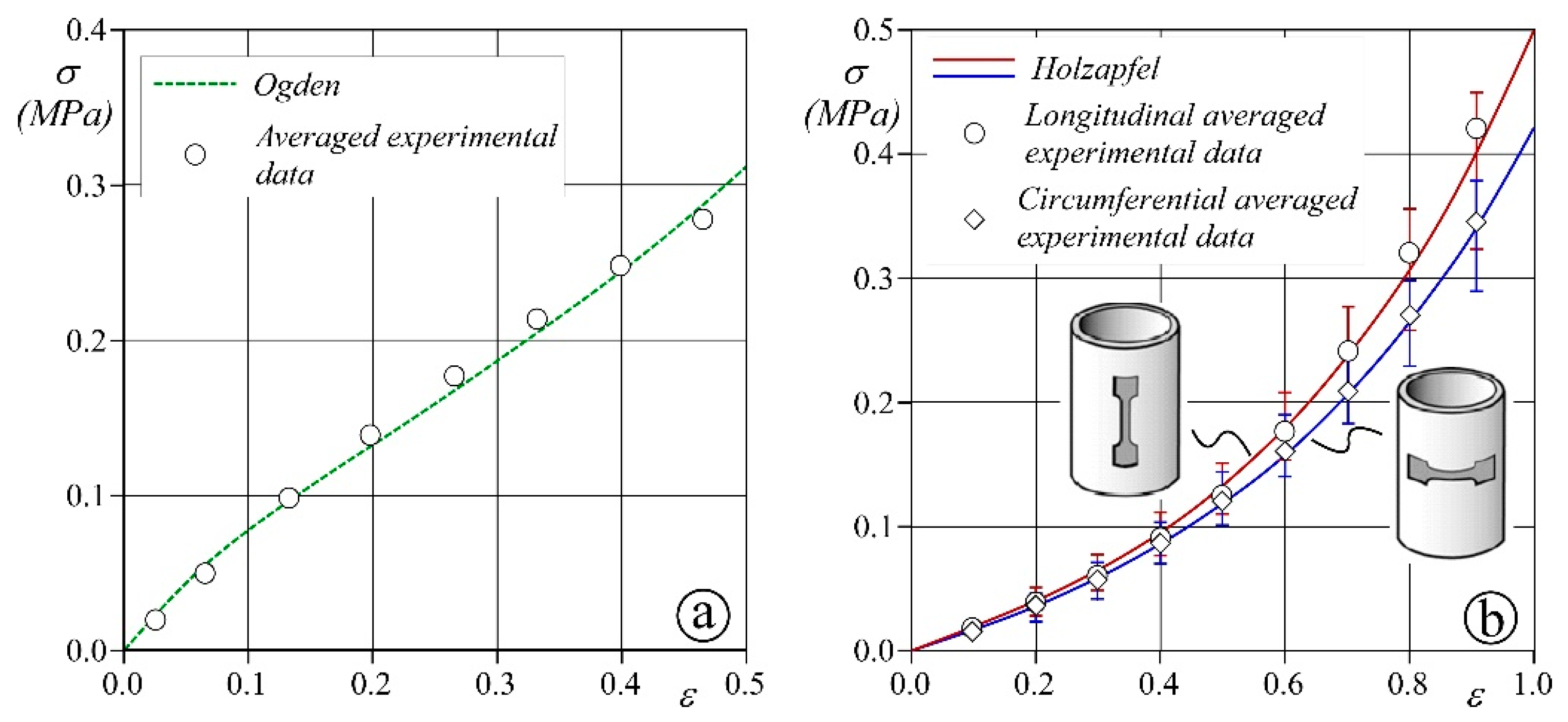
2.2. Materials Characterization
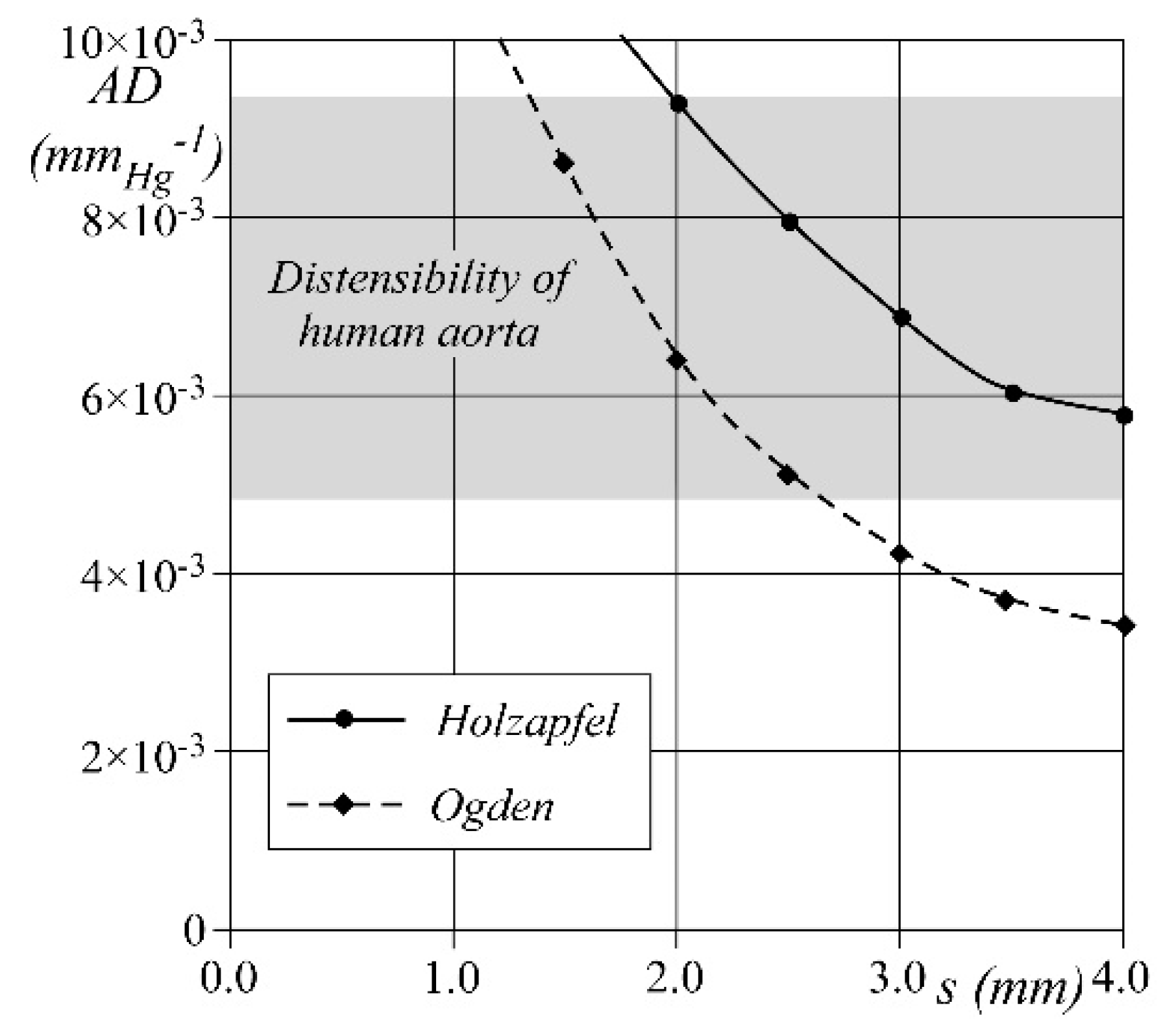
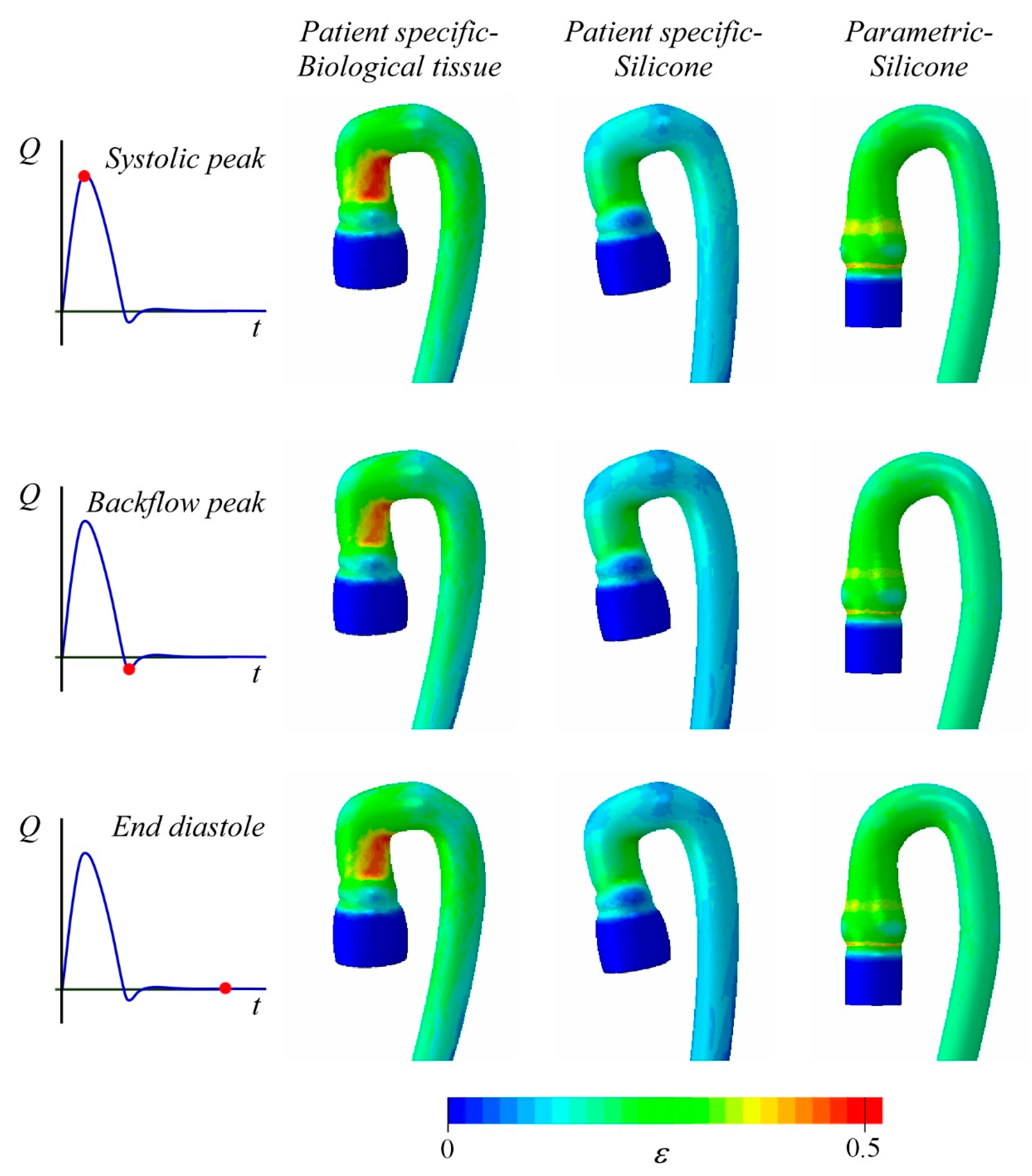
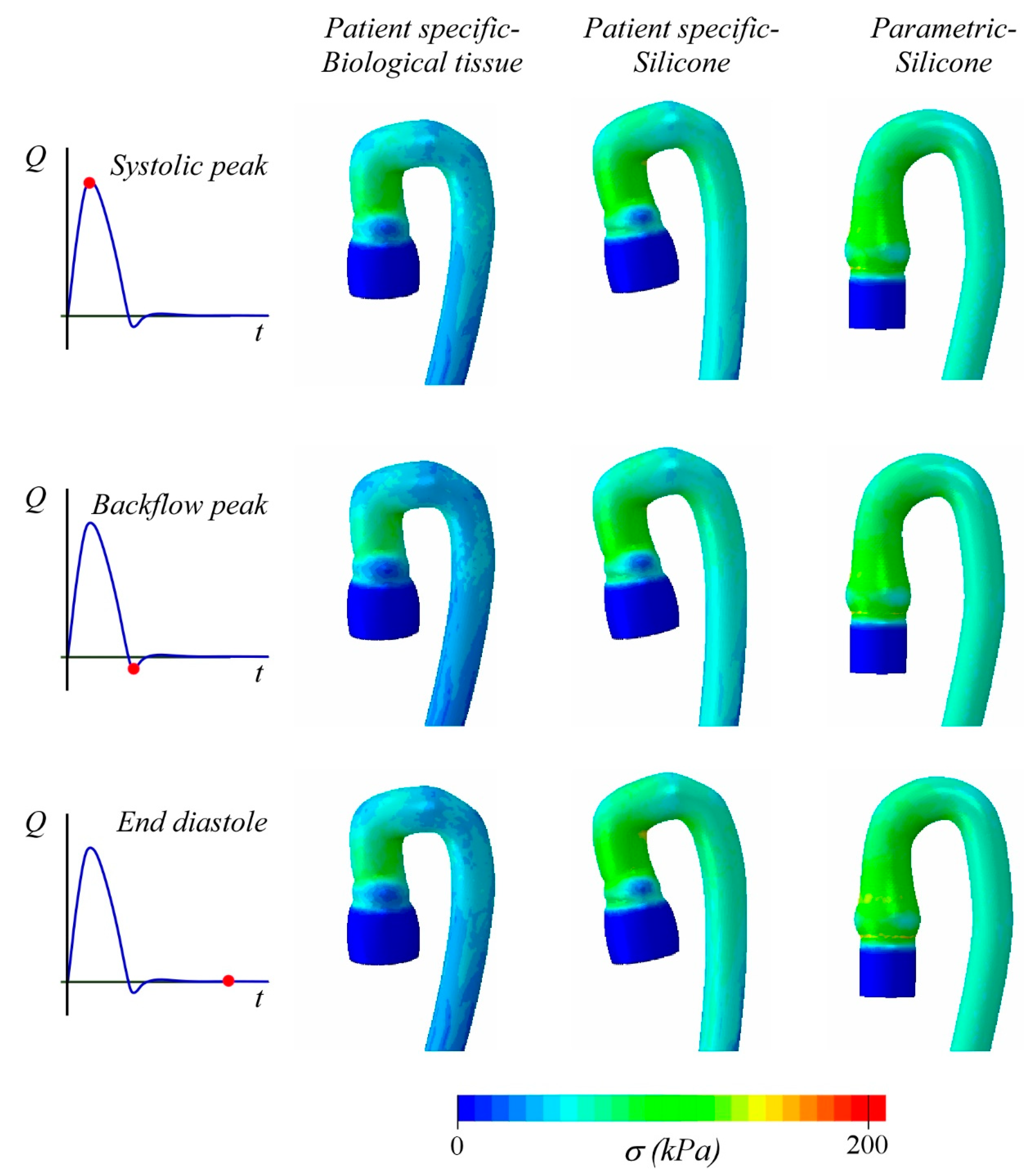
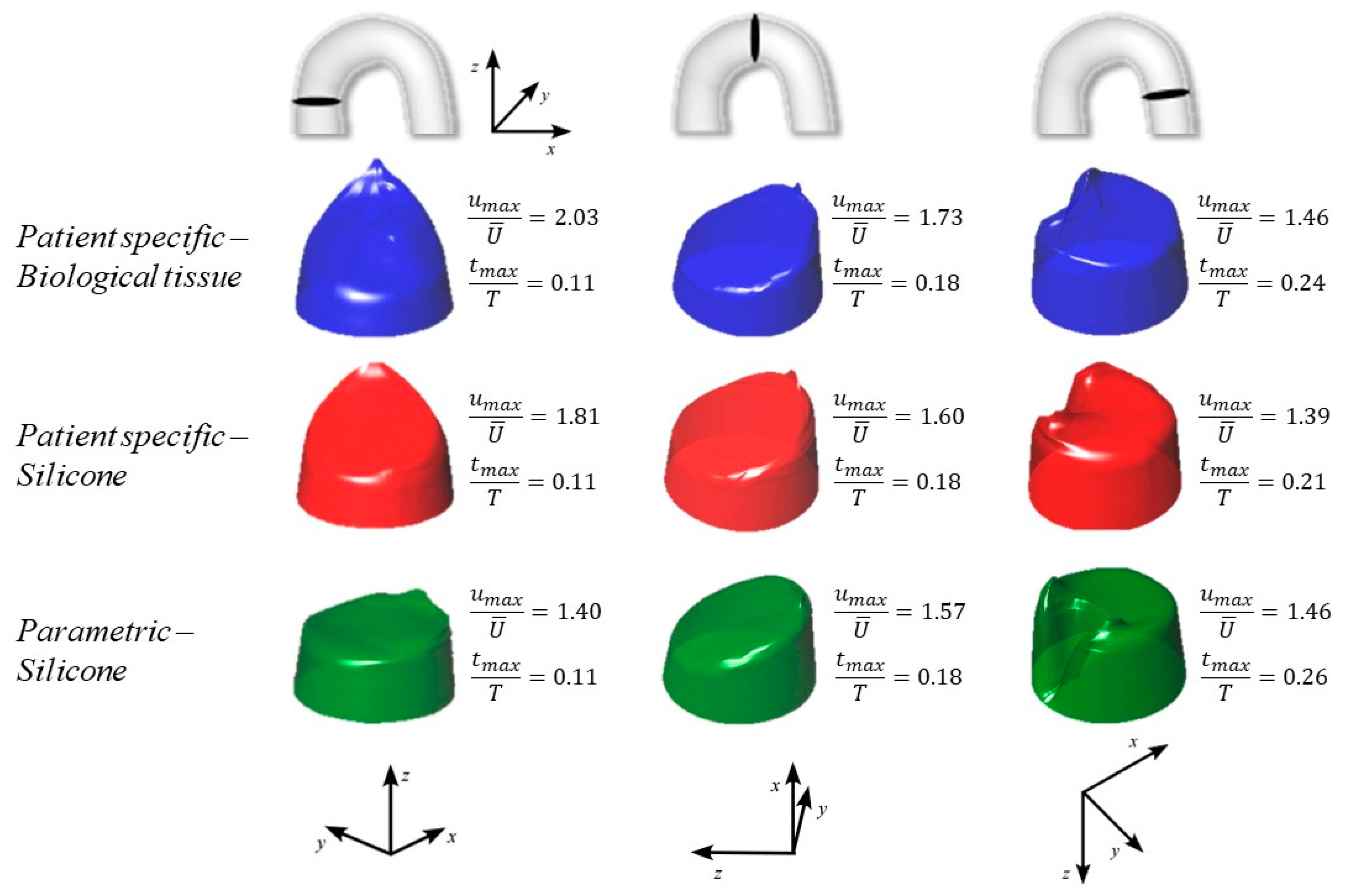
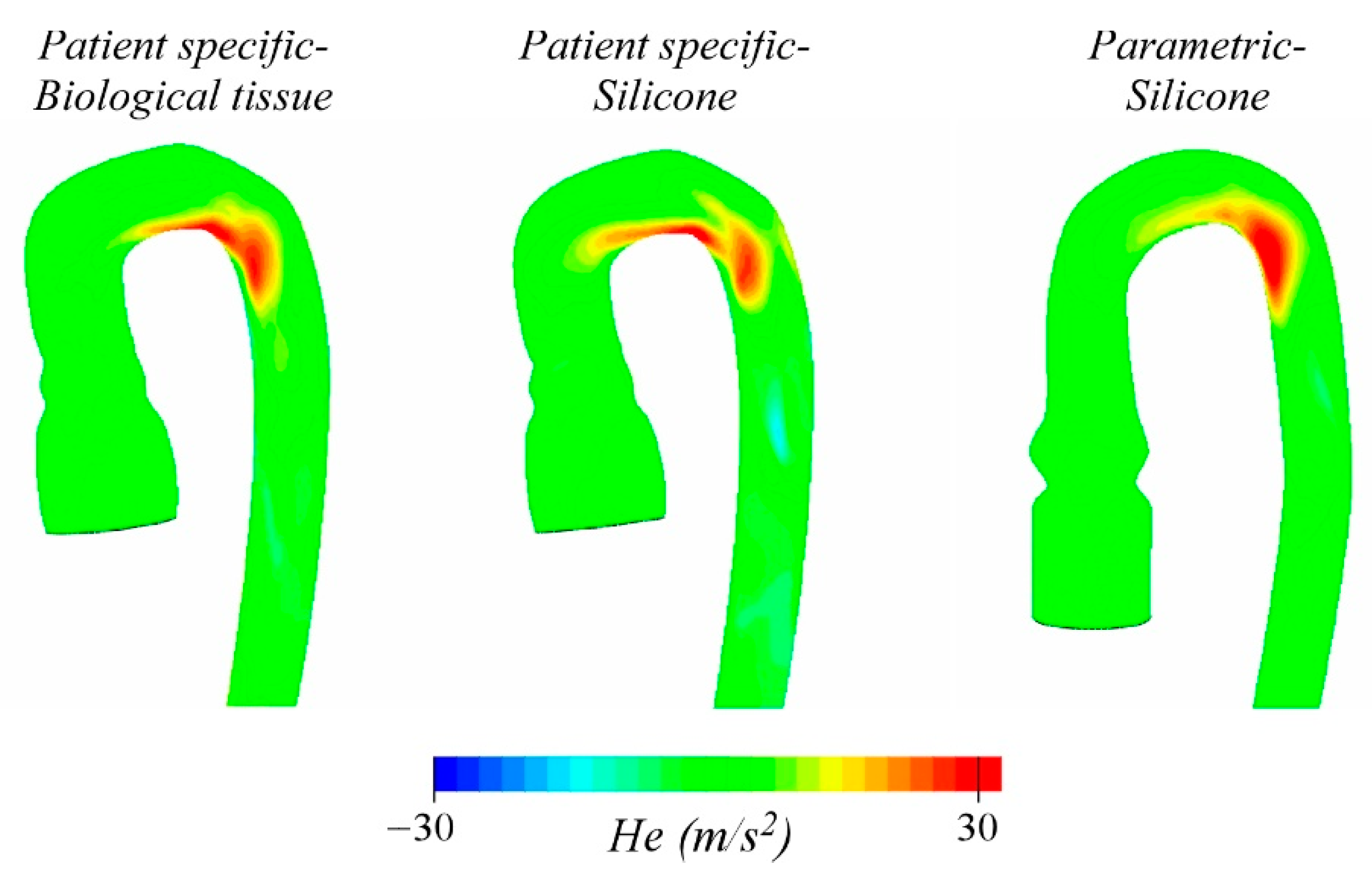
3. Results and Discussion
Study limitations and Future Developments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Colli, A.; Besola, L.; Bizzotto, E.; Peruzzo, P.; Pittarello, D.; Gerosa, G. Edge-to-edge mitral valve repair with transapical neochord implantation. J. Thorac. Cardiovasc. Surg. 2018, 156, 144–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, G.-R.; Pedrizzetti, G.; Tonti, G.; Li, P.; Wei, Z.; Kim, J.K.; Baweja, A.; Liu, S.; Chung, N.; Houle, H.; et al. Characterization and Quantification of Vortex Flow in the Human Left Ventricle by Contrast Echocardiography Using Vector Particle Image Velocimetry. JACC Cardiovasc. Imaging 2008, 1, 705–717. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burriesci, G.; Peruzzo, P.; Susin, F.M.; Tarantini, G.; Colli, A. In vitro hemodynamic testing of Amplatzer plugs for paravalvular leak occlusion after transcatheter aortic valve implantation. Int. J. Cardiol. 2016, 203, 1093–1099. [Google Scholar] [CrossRef] [PubMed]
- Peruzzo, P.; Susin, F.M.; Colli, A.; Burriesci, G. In vitro assessment of pacing as therapy for aortic regurgitation. Open Heart 2019, 6, e000976. [Google Scholar] [CrossRef] [Green Version]
- Bevan, R.L.T.; Sazonov, I.; Saksono, P.H.; Nithiarasu, P.; Van Loon, R.; Luckraz, H.; Ashraf, S. Patient-specific blood flow simulation through an aneurysmal thoracic aorta with a folded proximal neck. Int. J. Numer. Methods Biomed. Eng. 2010, 27, 1167–1184. [Google Scholar] [CrossRef]
- Polanczyk, A.; Klinger, M.; Nanobachvili, J.; Huk, I.; Neumayer, C. Artificial Circulatory Model for Analysis of Human and Artificial Vessels. Appl. Sci. 2018, 8, 1017. [Google Scholar] [CrossRef] [Green Version]
- Rahmani, B.; Tzamtzis, S.; Ghanbari, H.; Burriesci, G.; Seifalian, A. Manufacturing and hydrodynamic assessment of a novel aortic valve made of a new nanocomposite polymer. J. Biomech. 2012, 45, 1205–1211. [Google Scholar] [CrossRef]
- Annio, G.; Franzetti, G.; Bonfanti, M.; Gallarello, A.; Palombi, A.; De Momi, E.; Homer-Vanniasinkam, S.; Wurdemann, H.A.; Tsang, V.; Diáz-Zuccarini, V.; et al. Low-Cost Fabrication of Polyvinyl Alcohol-Based Personalized Vascular Phantoms for In Vitro Hemodynamic Studies: Three Applications. J. Eng. Sci. Med. Diagn. Ther. 2020, 3. [Google Scholar] [CrossRef]
- Biffi, B.; Bruse, J.L.; Zuluaga, M.A.; Ntsinjana, H.N.; Taylor, A.M.; Schievano, S. Investigating Cardiac Motion Patterns Using Synthetic High-Resolution 3D Cardiovascular Magnetic Resonance Images and Statistical Shape Analysis. Front. Pediatr. 2017, 5, 34. [Google Scholar] [CrossRef] [Green Version]
- Biglino, G.; Verschueren, P.; Zegels, R.; Taylor, A.M.; Schievano, S. Rapid prototyping compliant arterial phantoms for in-vitro studies and device testing. J. Cardiovasc. Magn. Reson. 2013, 15, 2. [Google Scholar] [CrossRef] [Green Version]
- Hütter, L.; Geoghegan, P.H.; Docherty, P.D.; Lazarjan, M.S.; Clucas, D.; Jermy, M. Fabrication of a compliant phantom of the human aortic arch for use in Particle Image Velocimetry (PIV) experimentation. Curr. Dir. Biomed. Eng. 2016, 2, 493–497. [Google Scholar] [CrossRef]
- Chandran, K.B. Flow dynamics in the human aorta: Techniques and applications. In Cardiovascular Techniques: Biomechanical Systems, Techniques and Applications; Leondes, C.T., Ed.; CRC Press: Boca Raton, FL, USA, 2001; Volume 5, pp. 1–25. [Google Scholar]
- Karimi, A.; Navidbakhsh, M.; Shojaei, A.; Faghihi, S. Measurement of the uniaxial mechanical properties of healthy and atherosclerotic human coronary arteries. Mater. Sci. Eng. C 2013, 33, 2550–2554. [Google Scholar] [CrossRef]
- Peruzzo, P.; Burriesci, G.; Susin, F.M.; Colli, A. In Vitro and Ex Vivo Hemodynamic Testing of an Innovative Occluder for Paravalvular Leak After Transcather Aortic Valve Implantation. J. Cardiovasc. Transl. Res. 2019, 12, 551–559. [Google Scholar] [CrossRef]
- Schampaert, S.S.; Van Nunen, L.X.; Pijls, N.H.J.; Rutten, M.C.M.; Van Tuijl, S.S.; van de Vosse, F.; van’t Veer, M. Intra-Aortic Balloon Pump Support in the Isolated Beating Porcine Heart in Nonischemic and Ischemic Pump Failure. Artif. Organs 2015, 39, 931–938. [Google Scholar] [CrossRef]
- Ogden, R.W.; Saccomandi, G.; Sgura, I. Fitting hyperelastic models to experimental data. Comput. Mech. 2004, 34, 484–502. [Google Scholar] [CrossRef] [Green Version]
- Holzapfel, G.A.; Sommer, G.; Gasser, C.T.; Regitnig, P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am. J. Physiol. Circ. Physiol. 2005, 289, H2048–H2058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Ogden, R. Constitutive modelling of arteries. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1551–1597. [Google Scholar] [CrossRef]
- Stefanadis, C.; Stratos, C.; Boudoulas, H.; Kourouklis, C.; Toutouzas, P. Distensibility of the ascending aorta: Comparison of invasive and non-invasive techniques in healthy men and in men with coronary artery disease. Eur. Hear. J. 1990, 11, 990–996. [Google Scholar] [CrossRef]
- Mendez, V.; Di Giuseppe, M.; Pasta, S. Comparison of hemodynamic and structural indices of ascending thoracic aortic aneurysm as predicted by 2-way FSI, CFD rigid wall simulation and patient-specific displacement-based FEA. Comput. Biol. Med. 2018, 100, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Shahcheraghi, N.; Dwyer, H.A.; Cheer, A.Y.; Barakat, A.I.; Rutaganira, T. Unsteady and Three-Dimensional Simulation of Blood Flow in the Human Aortic Arch. J. Biomech. Eng. 2002, 124, 378–387. [Google Scholar] [CrossRef]
- Liu, X.; Fan, Y.; Deng, X. Effect of Spiral Flow on the Transport of Oxygen in the Aorta: A Numerical Study. Ann. Biomed. Eng. 2009, 38, 917–926. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Fan, Y.; Deng, X.; Zhan, F. Effect of non-Newtonian and pulsatile blood flow on mass transport in the human aorta. J. Biomech. 2011, 44, 1123–1131. [Google Scholar] [CrossRef]
- Rinaudo, A.; Raffa, G.M.; Scardulla, F.; Pilato, M.; Scardulla, C.; Pasta, S. Biomechanical implications of excessive endograft protrusion into the aortic arch after thoracic endovascular repair. Comput. Biol. Med. 2015, 66, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Alimohammadi, M.; Agu, O.; Balabani, S.; Díaz-Zuccarini, V. Development of a patient-specific simulation tool to analyse aortic dissections: Assessment of mixed patient-specific flow and pressure boundary conditions. Med. Eng. Phys. 2014, 36, 275–284. [Google Scholar] [CrossRef] [PubMed]
- Romarowski, R.M.; Lefieux, A.; Morganti, S.; Veneziani, A.; Auricchio, F. Patient-specific CFD modelling in the thoracic aorta with PC-MRI--based boundary conditions: A least-square three-element Windkessel approach. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e3134. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Jansen, K.E.; Taylor, C.A. Incorporating Autoregulatory Mechanisms of the Cardiovascular System in Three-Dimensional Finite Element Models of Arterial Blood Flow. Ann. Biomed. Eng. 2010, 38, 2314–2330. [Google Scholar] [CrossRef]
- Comunale, G.; Peruzzo, P.; Castaldi, B.; Razzolini, R.; Di Salvo, G.; Padalino, M.A.; Susin, F.M. Understanding and recognition of the right ventricular function and dysfunction via a numerical study. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef]
- Jalali, A.; Jones, G.F.; Licht, D.J.; Nataraj, C. Application of Mathematical Modeling for Simulation and Analysis of Hypoplastic Left Heart Syndrome (HLHS) in Pre- and Postsurgery Conditions. BioMed Res. Int. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
- Maksuti, E.; Westerhof, B.E.; Ugander, M.; Donker, D.W.; Carlsson, M.; Broome, M. Cardiac remodeling in aortic and mitral valve disease: A simulation study with clinical validation. J. Appl. Physiol. 2019, 126, 1377–1389. [Google Scholar] [CrossRef]
- Polanczyk, A.; Podgorski, M.; Polanczyk, M.; Veshkina, N.; Zbicinski, I.; Stefanczyk, L.; Neumayer, C. A novel method for describing biomechanical properties of the aortic wall based on the three-dimensional fluid-structure interaction model. Interact. Cardiovasc. Thorac. Surg. 2018, 28, 306–315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Toninato, R.; Salmon, J.; Susin, F.M.; Ducci, A.; Burriesci, G. Physiological vortices in the sinuses of Valsalva: An in vitro approach for bio-prosthetic valves. J. Biomech. 2016, 49, 2635–2643. [Google Scholar] [CrossRef] [PubMed]
- Morris, P.D.; Narracott, A.; von Tengg-Kobligk, H.; Soto, D.A.S.; Hsiao, S.; Lungu, A.; Evans, P.; Bressloff, N.W.; Lawford, P.V.; Hose, D.R.; et al. Computational fluid dynamics modelling in cardiovascular medicine. Heart 2016, 102, 18–28. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Ogden | |||||
| μ1 | α1 | D1 (MPa−1) | |||
| 1.73 × 10−1 | 4.39 | 1.193 | |||
| Holzapfel | |||||
| C (MPa) | k1 (MPa) | k2 | k | D (MPa−1) | θ° |
| 2.89 × 10−2 | 1.20 × 10−1 | 0.4 | 0.25 | 0.7 | 27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Comunale, G.; Di Micco, L.; Boso, D.P.; Susin, F.M.; Peruzzo, P. Numerical Models Can Assist Choice of an Aortic Phantom for In Vitro Testing. Bioengineering 2021, 8, 101. https://doi.org/10.3390/bioengineering8080101
Comunale G, Di Micco L, Boso DP, Susin FM, Peruzzo P. Numerical Models Can Assist Choice of an Aortic Phantom for In Vitro Testing. Bioengineering. 2021; 8(8):101. https://doi.org/10.3390/bioengineering8080101
Chicago/Turabian StyleComunale, Giulia, Luigi Di Micco, Daniela Paola Boso, Francesca Maria Susin, and Paolo Peruzzo. 2021. "Numerical Models Can Assist Choice of an Aortic Phantom for In Vitro Testing" Bioengineering 8, no. 8: 101. https://doi.org/10.3390/bioengineering8080101
APA StyleComunale, G., Di Micco, L., Boso, D. P., Susin, F. M., & Peruzzo, P. (2021). Numerical Models Can Assist Choice of an Aortic Phantom for In Vitro Testing. Bioengineering, 8(8), 101. https://doi.org/10.3390/bioengineering8080101






