A Deep Classifier for Upper-Limbs Motor Anticipation Tasks in an Online BCI Setting
Abstract
1. Introduction
Contributions of This Work
- We introduce a new input representation of EEG data that allows to preserve the spatio-temporal dependencies between the different channels.
- We develop a novel convolutional deep learning model for the efficient processing of raw EEG data.
- We compare our model with previous results on the same dataset, showing that our approach leads to a significantly higher accuracy with the advantage of a sensibly reduced processing overhead.
2. Methods
2.1. Dataset
2.2. Data Epoching and Movement Onset Detection
2.3. Input Representation and Preprocessing
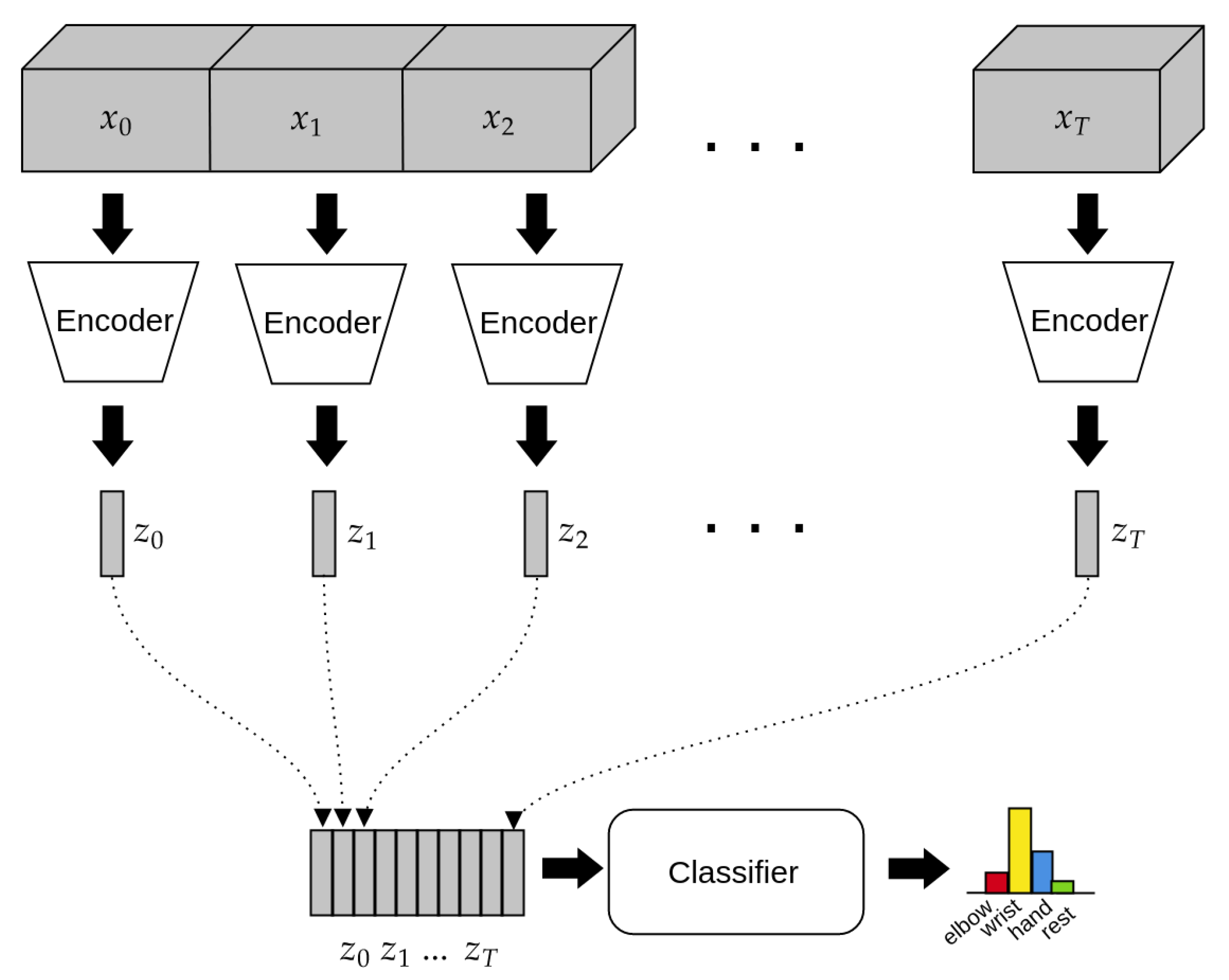
2.4. Architecture of the Model
2.4.1. Encoder
2.4.2. Classifier
2.5. Training Scheme
2.6. Comparison with Previous Work
3. Results
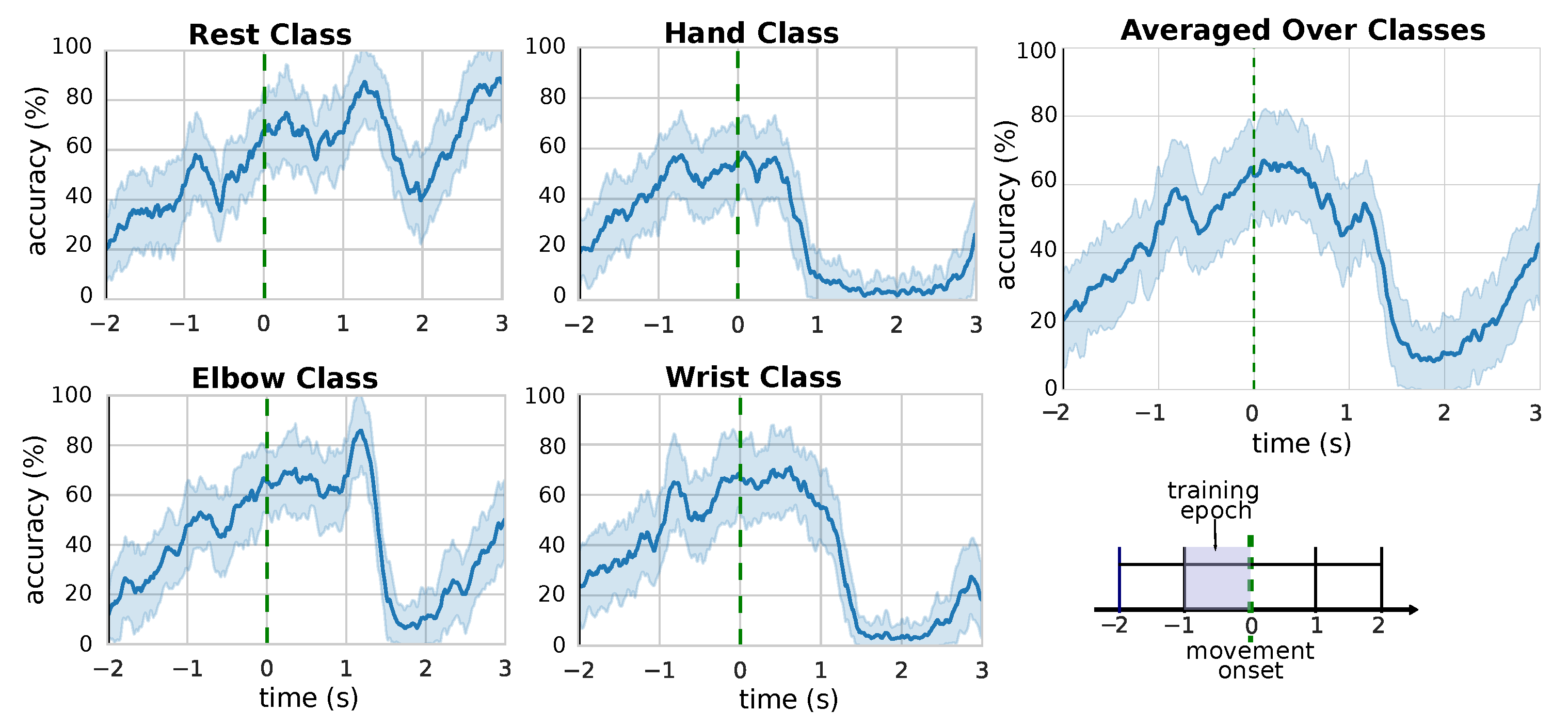
3.1. Classification Accuracy
3.2. Performance over Time
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Enhanced Movement Onset Detection Heuristic
References
- Mrachacz-Kersting, N.; Jiang, N.; Stevenson, A.J.T.; Niazi, I.K.; Kostic, V.; Pavlovic, A.; Radovanovic, S.; Djuric-Jovicic, M.; Agosta, F.; Dremstrup, K.; et al. Efficient neuroplasticity induction in chronic stroke patients by an associative brain–computer interface. J. Neurophysiol. 2016, 115, 1410–1421. [Google Scholar] [CrossRef] [PubMed]
- Lazarou, I.; Nikolopoulos, S.; Petrantonakis, P.C.; Kompatsiaris, I.; Tsolaki, M. EEG-based brain–computer interfaces for communication and rehabilitation of people with motor impairment: A novel approach of the 21st century. Front. Hum. Neurosci. 2018, 12, 14. [Google Scholar] [CrossRef] [PubMed]
- Cervera, M.A.; Soekadar, S.R.; Ushiba, J.; Millán, J.d.R.; Liu, M.; Birbaumer, N.; Garipelli, G. Brain–computer interfaces for post-stroke motor rehabilitation: A meta-analysis. Ann. Clin. Transl. Neurol. 2018, 5, 651–663. [Google Scholar] [CrossRef]
- Lebedev, M.A.; Nicolelis, M.A. Brain-machine interfaces: From basic science to neuroprostheses and neurorehabilitation. Physiol. Rev. 2017, 97, 767–837. [Google Scholar] [CrossRef] [PubMed]
- Robinson, N.; Vinod, A. Noninvasive brain–computer interface: Decoding arm movement kinematics and motor control. IEEE Syst. Man Cybern. Mag. 2016, 2, 4–16. [Google Scholar] [CrossRef]
- Barsotti, M.; Leonardis, D.; Vanello, N.; Bergamasco, M.; Frisoli, A. Effects of continuous kinaesthetic feedback based on tendon vibration on motor imagery BCI performance. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 26, 105–114. [Google Scholar] [CrossRef]
- Birbaumer, N.; Elbert, T.; Canavan, A.G.; Rockstroh, B. Slow potentials of the cerebral cortex and behavior. Physiol. Rev. 1990, 70, 1–41. [Google Scholar] [CrossRef]
- Arvaneh, M.; Guan, C.; Ang, K.K.; Quek, C. Optimizing the channel selection and classification accuracy in EEG-based BCI. IEEE Trans. Biomed. Eng. 2011, 58, 1865–1873. [Google Scholar] [CrossRef]
- Bhagat, N.A.; Venkatakrishnan, A.; Abibullaev, B.; Artz, E.J.; Yozbatiran, N.; Blank, A.A.; French, J.; Karmonik, C.; Grossman, R.G.; O’Malley, M.K.; et al. Design and optimization of an EEG-based brain machine interface (BMI) to an upper-limb exoskeleton for stroke survivors. Front. Neurosci. 2016, 10, 122. [Google Scholar] [CrossRef]
- Bhagat, N.A.; Yozbatiran, N.; Sullivan, J.L.; Paranjape, R.; Losey, C.; Hernandez, Z.; Keser, Z.; Grossman, R.; Francisco, G.E.; O’Malley, M.K.; et al. Neural activity modulations and motor recovery following brain-exoskeleton interface mediated stroke rehabilitation. NeuroImage Clin. 2020, 28, 102502. [Google Scholar] [CrossRef] [PubMed]
- Ang, K.K.; Chin, Z.Y.; Zhang, H.; Guan, C. Filter bank common spatial pattern (FBCSP) in brain–computer interface. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 2390–2397. [Google Scholar]
- Bhattacharyya, S.; Konar, A.; Tibarewala, D. Motor imagery and error related potential induced position control of a robotic arm. IEEE/CAA J. Autom. Sin. 2017, 4, 639–650. [Google Scholar] [CrossRef]
- Liao, X.; Yao, D.; Wu, D.; Li, C. Combining spatial filters for the classification of single-trial EEG in a finger movement task. IEEE Trans. Biomed. Eng. 2007, 54, 821–831. [Google Scholar] [CrossRef]
- Ofner, P.; Schwarz, A.; Pereira, J.; Müller-Putz, G.R. Upper limb movements can be decoded from the time-domain of low-frequency EEG. PLoS ONE 2017, 12, e0182578. [Google Scholar] [CrossRef]
- Karimi, F.; Kofman, J.; Mrachacz-Kersting, N.; Farina, D.; Jiang, N. Detection of movement related cortical potentials from EEG using constrained ICA for brain–computer interface applications. Front. Neurosci. 2017, 11, 356. [Google Scholar] [CrossRef]
- Gu, X.; Cao, Z.; Jolfaei, A.; Xu, P.; Wu, D.; Jung, T.P.; Lin, C.T. EEG-based Brain–Computer Interfaces (BCIs): A Survey of Recent Studies on Signal Sensing Technologies and Computational Intelligence Approaches and Their Applications. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021. [Google Scholar] [CrossRef]
- Craik, A.; He, Y.; Contreras-Vidal, J.L. Deep learning for electroencephalogram (EEG) classification tasks: A review. J. Neural Eng. 2019, 16, 031001. [Google Scholar] [CrossRef] [PubMed]
- Tortora, S.; Tonin, L.; Chisari, C.; Micera, S.; Menegatti, E.; Artoni, F. Hybrid Human-Machine Interface for Gait Decoding Through Bayesian Fusion of EEG and EMG Classifiers. Front. Neurorobot. 2020, 14, 89. [Google Scholar] [CrossRef]
- Tayeb, Z.; Fedjaev, J.; Ghaboosi, N.; Richter, C.; Everding, L.; Qu, X.; Wu, Y.; Cheng, G.; Conradt, J. Validating deep neural networks for online decoding of motor imagery movements from EEG signals. Sensors 2019, 19, 210. [Google Scholar] [CrossRef]
- Padfield, N.; Zabalza, J.; Zhao, H.; Masero, V.; Ren, J. EEG-based brain–computer interfaces using motor-imagery: Techniques and challenges. Sensors 2019, 19, 1423. [Google Scholar] [CrossRef]
- Vecchiato, G.; Del Vecchio, M.; Ascari, L.; Antopolskiy, S.; Deon, F.; Kubin, L.; Ambeck-Madsen, J.; Rizzolatti, G.; Avanzini, P. Electroencephalographic time-frequency patterns of braking and acceleration movement preparation in car driving simulation. Brain Res. 2019, 1716, 16–26. [Google Scholar] [CrossRef]
- Zeng, H.; Sun, Y.; Xu, G.; Wu, C.; Song, A.; Xu, B.; Li, H.; Hu, C. The Advantage of Low-Delta Electroencephalogram Phase Feature for Reconstructing the Center-Out Reaching Hand Movements. Front. Neurosci. 2019, 13, 480. [Google Scholar] [CrossRef]
- Mondini, V.; Kobler, R.J.; Sburlea, A.I.; Müller-Putz, G.R. Continuous low-frequency EEG decoding of arm movement for closed-loop, natural control of a robotic arm. J. Neural Eng. 2020, 17, 046031. [Google Scholar] [CrossRef] [PubMed]
- Mammone, N.; Ieracitano, C.; Morabito, F.C. A deep CNN approach to decode motor preparation of upper limbs from time–frequency maps of EEG signals at source level. Neural Netw. 2020, 124, 357–372. [Google Scholar] [CrossRef] [PubMed]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef] [PubMed]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain–computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lorena, A.C.; De Carvalho, A.C.; Gama, J.M. A review on the combination of binary classifiers in multiclass problems. Artif. Intell. Rev. 2008, 30, 19. [Google Scholar] [CrossRef]
- Valenti, A.; Barsotti, M.; Brondi, R.; Bacciu, D.; Ascari, L. ROS-Neuro Integration of Deep Convolutional Autoencoders for EEG Signal Compression in Real-time BCIs. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 2019–2024. [Google Scholar]
- Bacciu, D.; Errica, F.; Micheli, A.; Podda, M. A gentle introduction to deep learning for graphs. Neural Netw. 2020, 129, 203–221. [Google Scholar] [CrossRef]
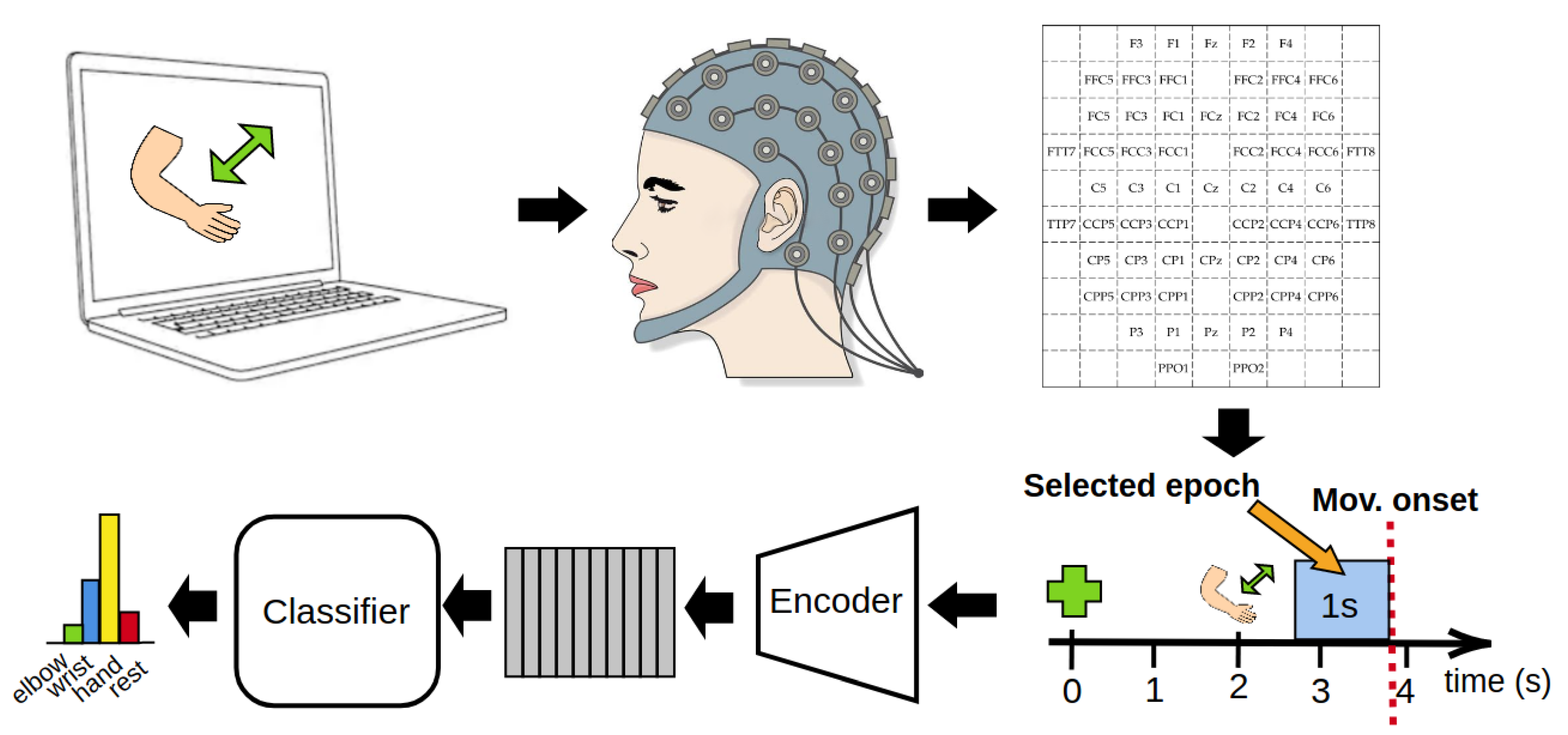

| F3 | F1 | Fz | F2 | F4 | ||||
| FFC5 | FFC3 | FFC1 | FFC2 | FFC4 | FFC6 | |||
| FC5 | FC3 | FC1 | FCz | FC2 | FC4 | FC6 | ||
| FTT7 | FCC5 | FCC3 | FCC1 | FCC2 | FCC4 | FCC6 | FTT8 | |
| C5 | C3 | C1 | Cz | C2 | C4 | C6 | ||
| TTP7 | CCP5 | CCP3 | CCP1 | CCP2 | CCP4 | CCP6 | TTP8 | |
| CP5 | CP3 | CP1 | CPz | CP2 | CP4 | CP6 | ||
| CPP5 | CPP3 | CPP1 | CPP2 | CPP4 | CPP6 | |||
| P3 | P1 | Pz | P2 | P4 | ||||
| PPO1 | PPO2 |
| Module | Layers |
|---|---|
| Encoder | Conv3d (1, 16, kernel_size = (5, 2, 2), stride = (1, 1, 1)) |
| ReLU() | |
| BatchNorm3d (16, eps = , momentum = 0.1, affine = True, track_running_stats = True) | |
| Conv3d (16, 32, kernel_size = (5, 1, 1), stride = (1, 1, 1)) | |
| ReLU() | |
| BatchNorm3d (32, eps = , momentum = 0.1, affine = True, track_running_stats = True) | |
| MaxPool3d (kerne_size = (3, 2, 2), stride = (3, 2, 2), padding = 0, dilation = 1, ceil_mode = False) | |
| Linear (in_features = 576, out_features = 128, bias = True) | |
| ReLU() | |
| BatchNorm1d (128, eps = , momentum = 0.1, affine = True, track_running_stats = True) | |
| Classifier | LSTM (input_size=128, hidden_size = 64, bidirectional = False, dropout = 0) |
| Linear (in_features = 64, out_features = 4, bias = True) | |
| Softmax (n_classes = 4) |
| Name | Description | Values |
|---|---|---|
| batch_size | Number of neurons of the encoder’s output. | 1024 |
| z_dim | Number of neurons of the encoder’s output. | [512, 256, 128] |
| lstm_hidden_size | Number of neurons of LSTM’s hidden state. | [32, 64, 128] |
| conv1_channels | Number of channels of first convolutional layer. | [8, 16, 32] |
| conv2_channels | Number of channels of second convolutional layer. | [32, 64, 128] |
| lstm_depth | Number of LSTM layers. | 1 |
| conv_depth | Number of convolutional layers. | 2 |
| ADAM initial learning rate. | [0.001, , ] | |
| ADAM parameter. | 0.9 | |
| ADAM parameter. | 0.999 | |
| lstm_dropout | Percentage of dropped units in the LSTM layers. | 0 |
| smoothing | Amount of label smoothing. | [0, 0.2, 0.4] |
| L2_penalty | Amount of L2 regularization during training (weight decay). | 0 |
| Subject | Our Work | Previous Work [24] |
|---|---|---|
| Subject 02 | 42.58 ± 1.56 | 39.09 |
| Subject 03 | 76.72 ± 0.51 | 57.86 |
| Subject 04 | 81.44 ± 0.35 | 68.69 |
| Subject 05 | 50.05 ± 1.74 | 38.62 |
| Subject 06 | 58.22 ± 2.04 | 36.94 |
| Subject 07 | 36.39 ± 1.50 | 28.02 |
| Subject 08 | 54.82 ± 1.66 | 41.12 |
| Subject 09 | 47.55 ± 0.89 | 45.72 |
| Subject 10 | 36.01 ± 1.34 | 58.17 |
| Subject 11 | 40.05 ± 0.29 | 37.62 |
| Subject 12 | 37.50 ± 0.26 | 35.48 |
| Subject 13 | 50.98 ± 1.31 | 47.37 |
| Subject 14 | 49.22 ± 0.17 | 49.85 |
| Subject 15 | 49.56 ± 0.45 | 39.80 |
| Average | 50.79 ± 13.82 | 44.59 ± 10.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valenti, A.; Barsotti, M.; Bacciu, D.; Ascari, L. A Deep Classifier for Upper-Limbs Motor Anticipation Tasks in an Online BCI Setting. Bioengineering 2021, 8, 21. https://doi.org/10.3390/bioengineering8020021
Valenti A, Barsotti M, Bacciu D, Ascari L. A Deep Classifier for Upper-Limbs Motor Anticipation Tasks in an Online BCI Setting. Bioengineering. 2021; 8(2):21. https://doi.org/10.3390/bioengineering8020021
Chicago/Turabian StyleValenti, Andrea, Michele Barsotti, Davide Bacciu, and Luca Ascari. 2021. "A Deep Classifier for Upper-Limbs Motor Anticipation Tasks in an Online BCI Setting" Bioengineering 8, no. 2: 21. https://doi.org/10.3390/bioengineering8020021
APA StyleValenti, A., Barsotti, M., Bacciu, D., & Ascari, L. (2021). A Deep Classifier for Upper-Limbs Motor Anticipation Tasks in an Online BCI Setting. Bioengineering, 8(2), 21. https://doi.org/10.3390/bioengineering8020021






