Techno-Economic Assessment of Bio-Syngas Production for Methanol Synthesis: A Focus on the Water–Gas Shift and Carbon Capture Sections
Abstract
1. Introduction
2. Materials and Methods
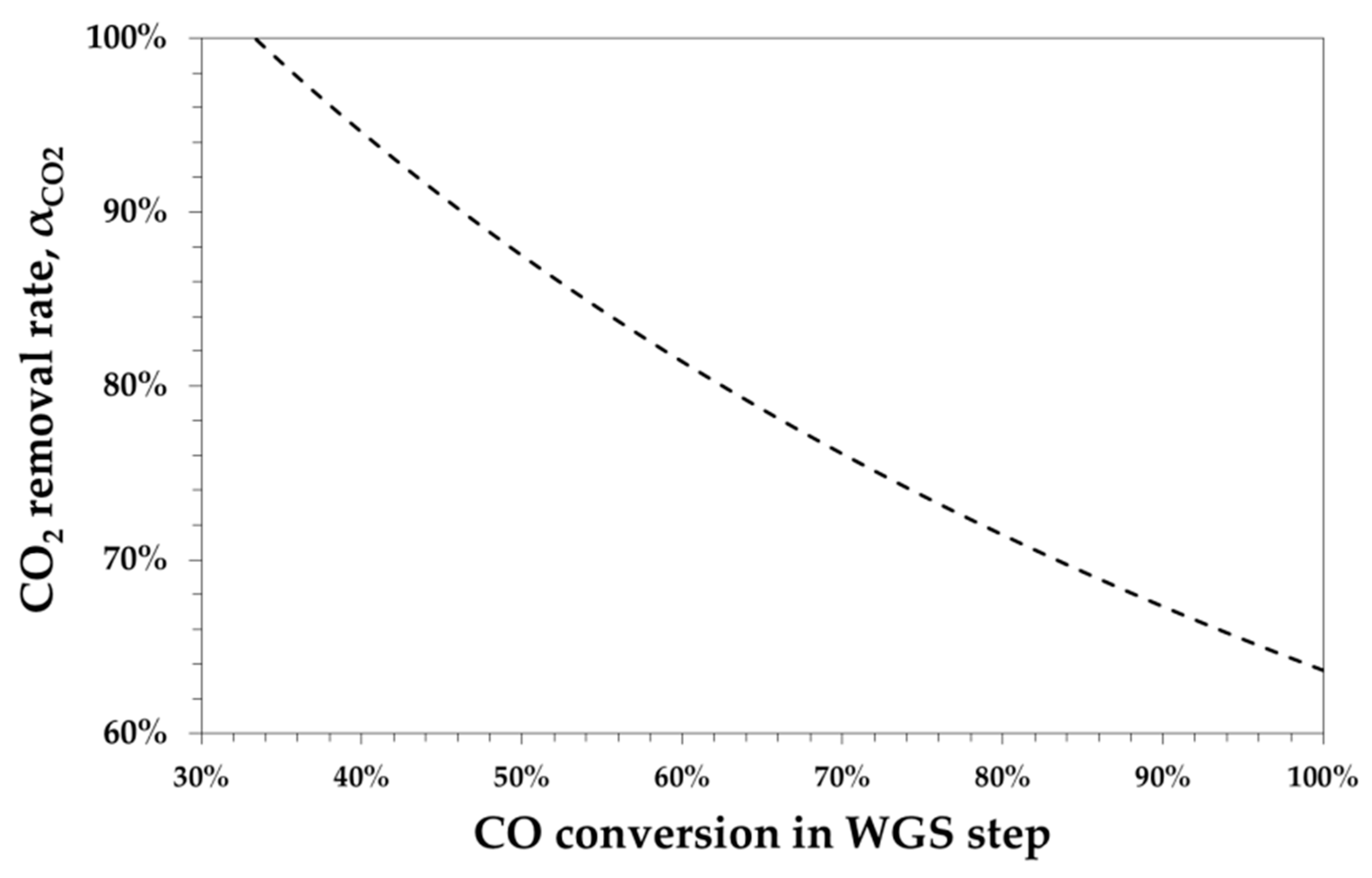
2.1. R-Ratio and WGS Conversion/Carbon Capture Relationship
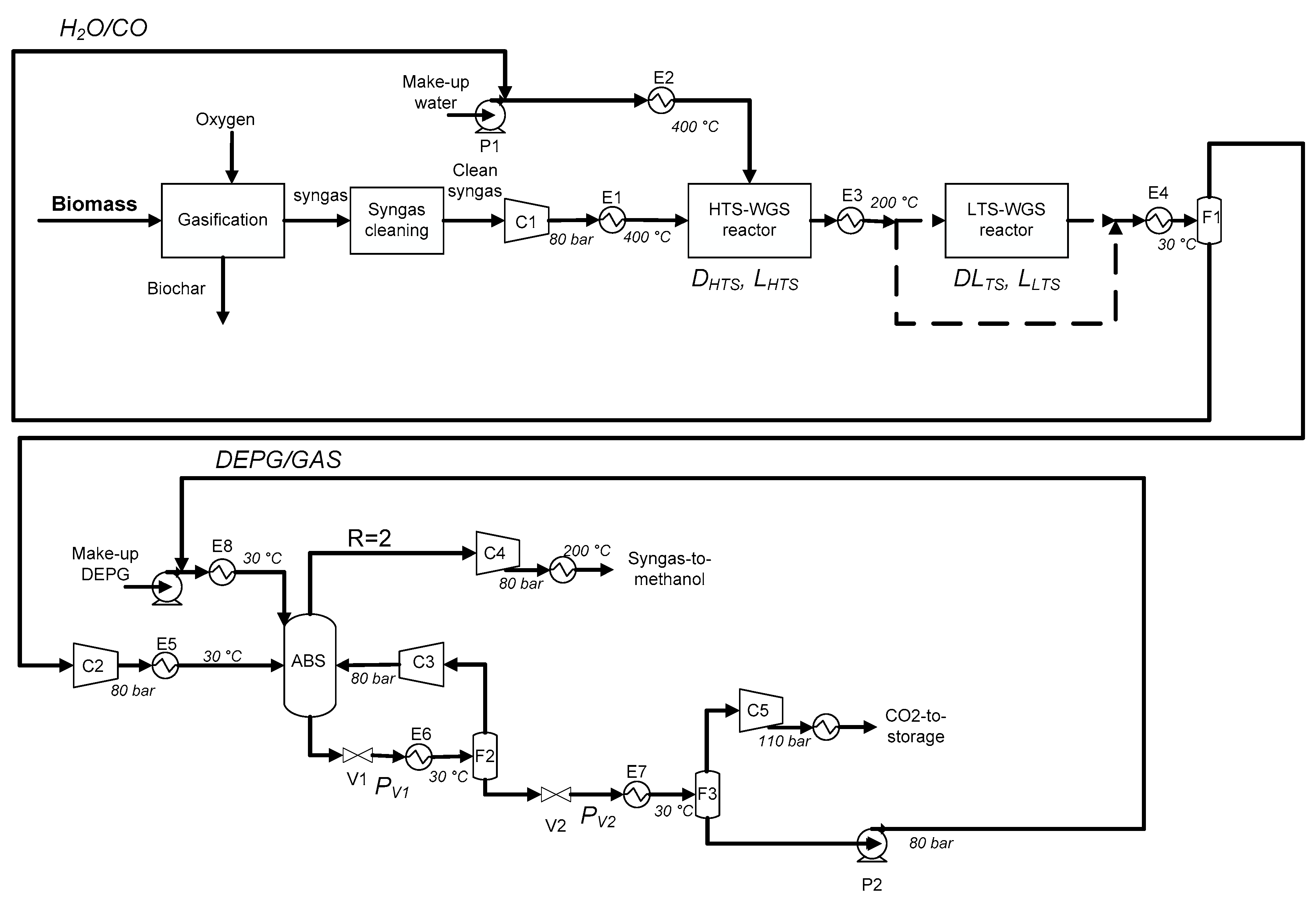
2.2. Flowsheet Description
- -
- C1 is the main compressor of the process, because the clean biomass-derived syngas is considered at 1 bar.
- -
- E2 is the main heat exchanger of the process, because it vaporizes water at high pressure (80 bar); at this pressure the vaporization temperature of water is about 295 °C, so a boiler (fueled with natural gas) is necessary for both vaporization and superheating. Hence, the H2O/CO ratio for the WGS sets the thermal power (and the natural gas demand) of E2.
- -
- C3 is the compressor of the gaseous stream recycled to the ABS column and the electricity required depends on the pressure drop at the throttling valve necessary to release volatile compounds (H2 and CO), leaving CO2 into the solvent.
- -
- C5 is considered to compress CO2 at 110 bar for storage [43].
- -
- P2 is an energy-intensive pump, as a large amount of DEPG solvent is requested to make the CO2 capture possible.
2.3. Process Simulation Description
2.4. Economic Assessment Description
3. Results
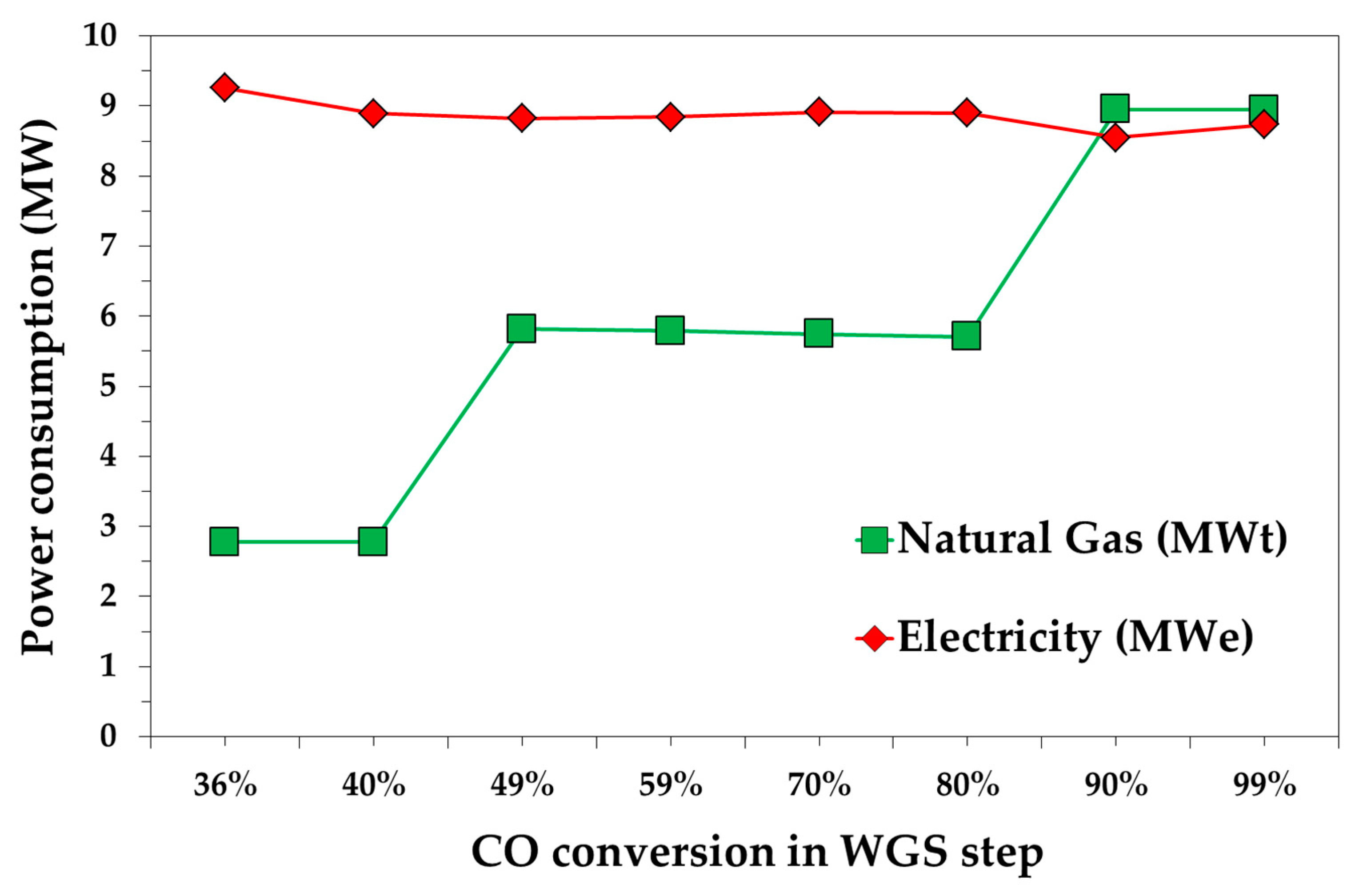
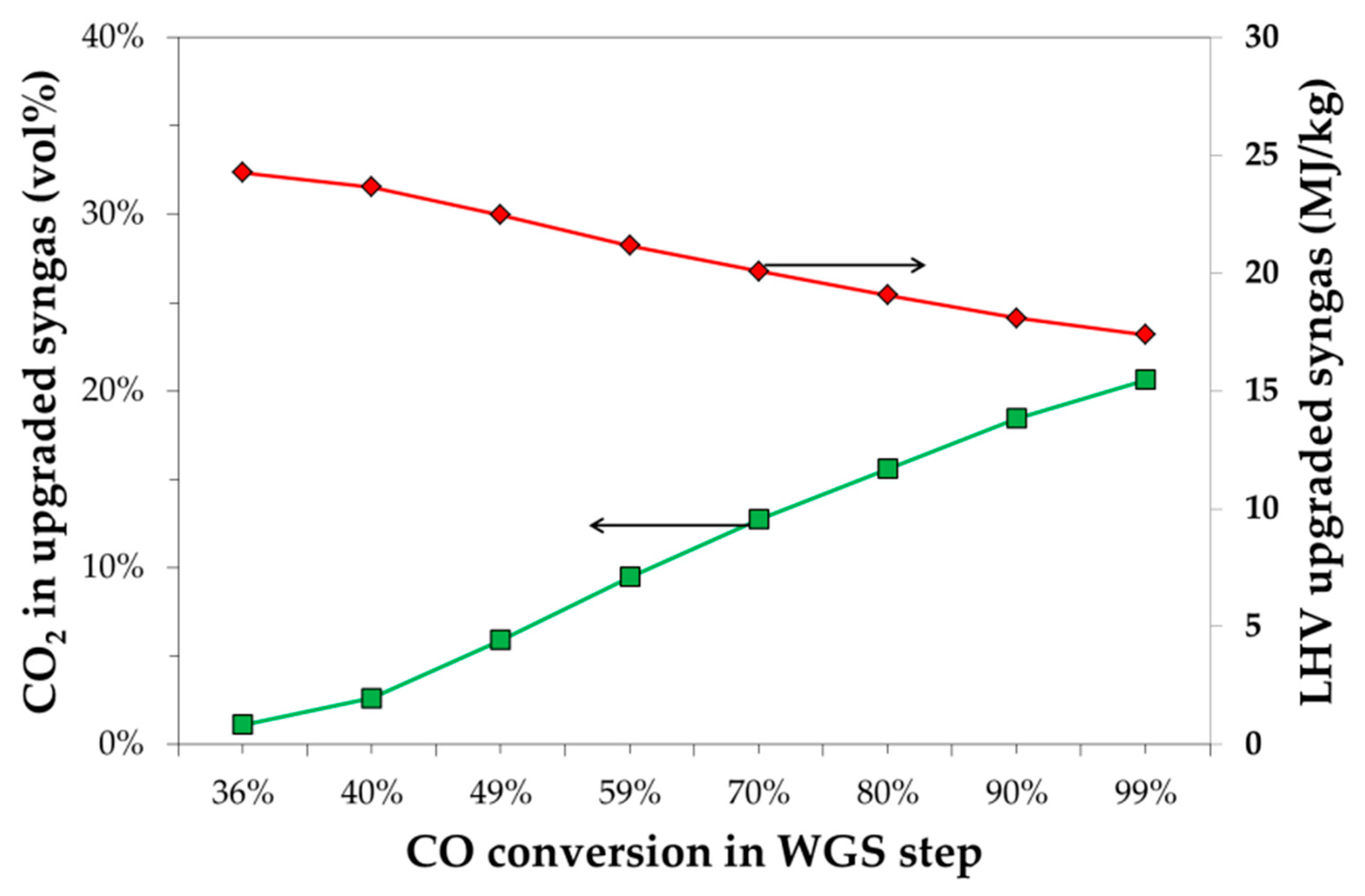
3.1. Process Results
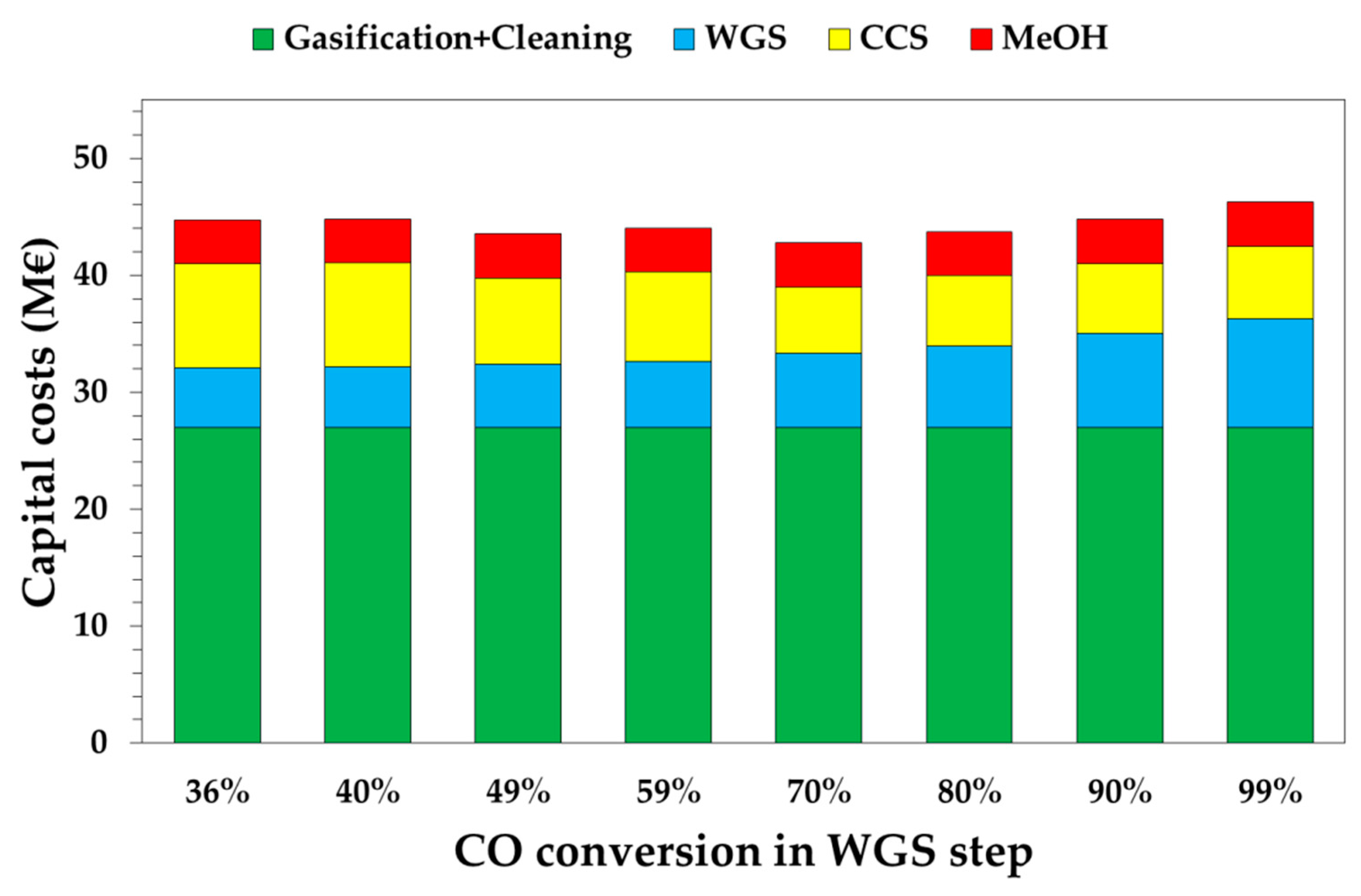
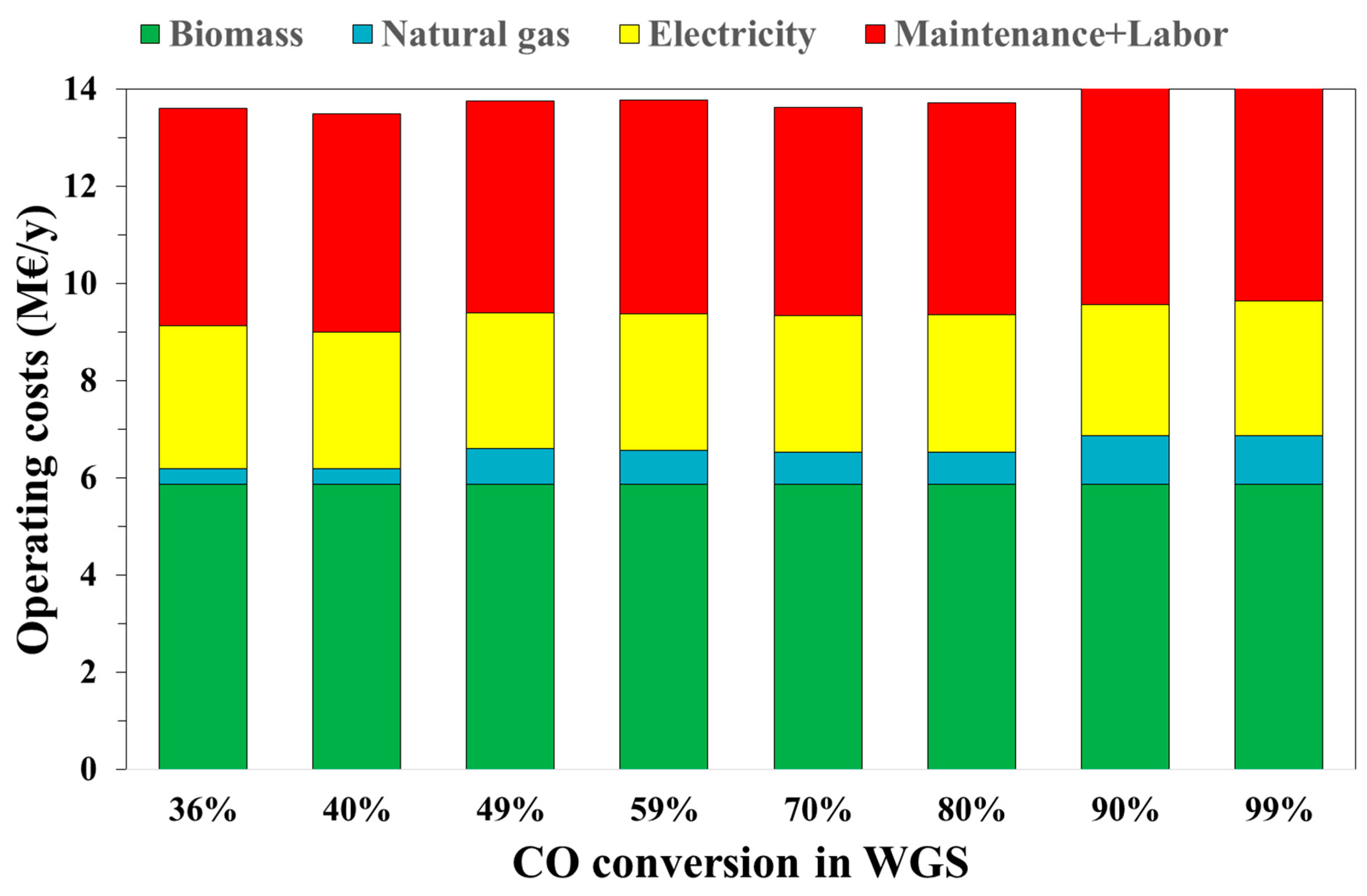
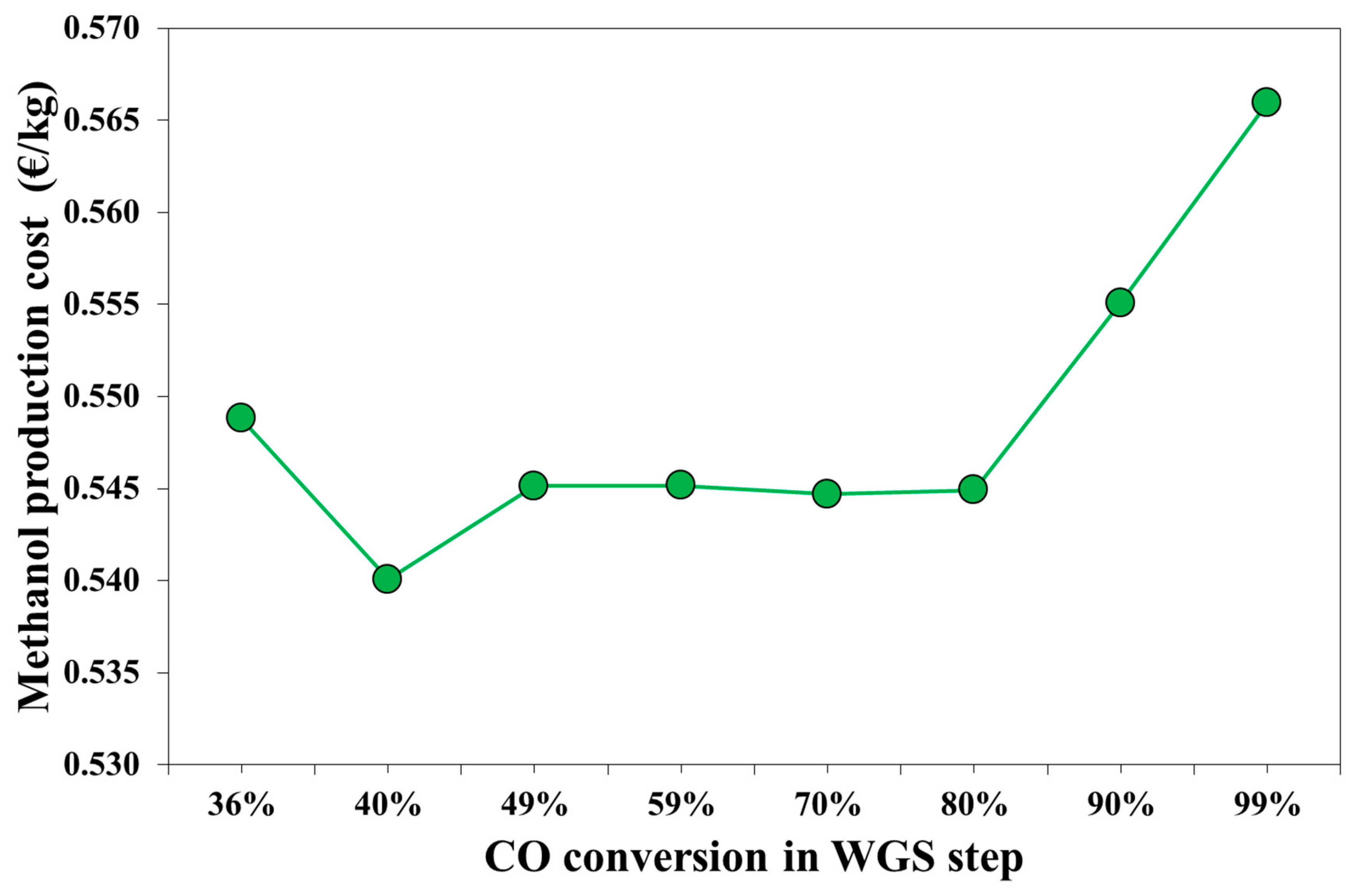
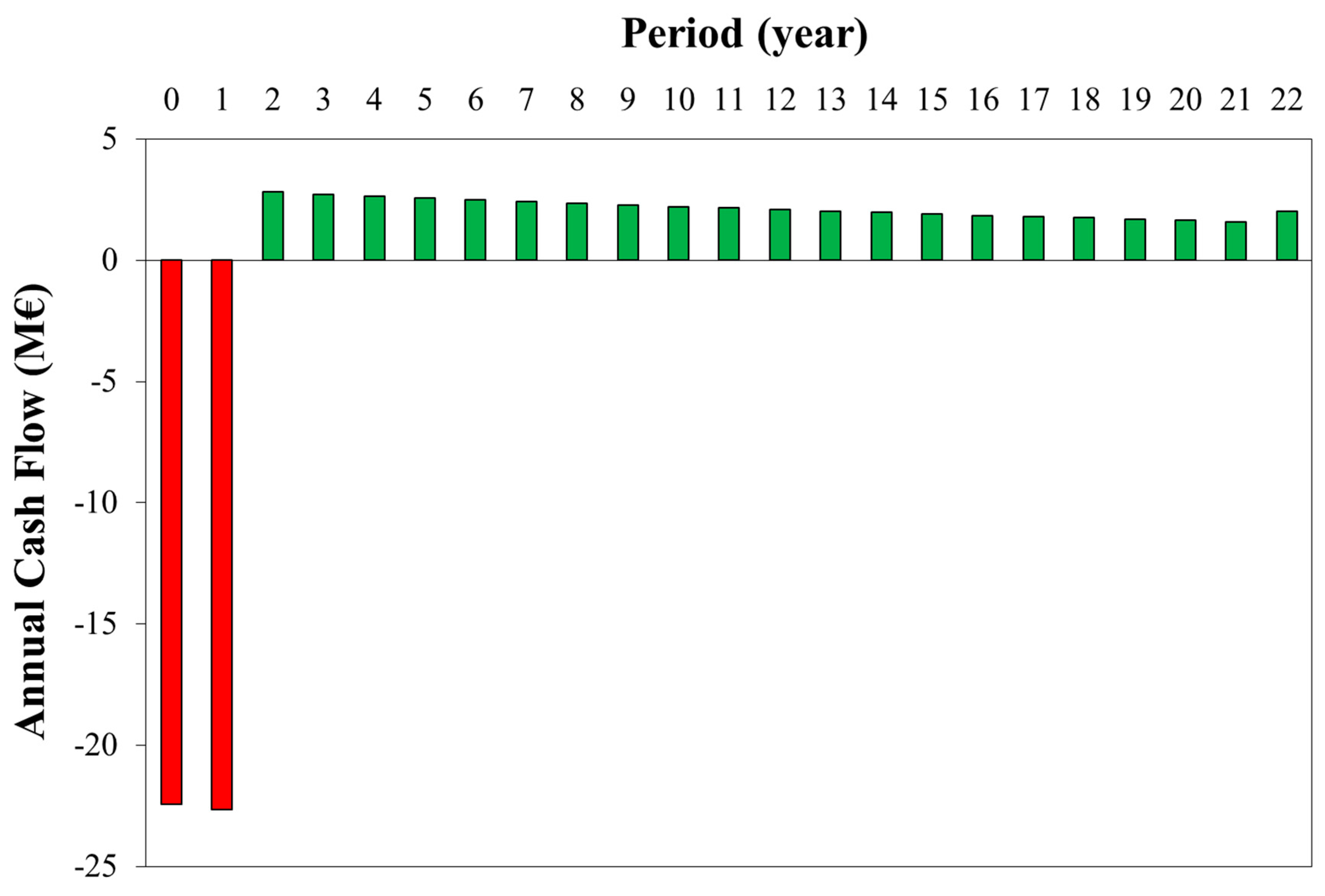
3.2. Economic Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hasler, P.; Nussbaumer, T. Gas cleaning for IC engine applications from fixed bed biomass gasification. Biomass Bioenergy 1999, 16, 385–395. [Google Scholar] [CrossRef]
- Wu, C.; Huang, H.; Zheng, S.; Yin, X. An economic analysis of biomass gasification and power generation in China. Bioresour. Technol. 2002, 83, 65–70. [Google Scholar] [CrossRef]
- Zhou, Z.; Yin, X.; Xu, J.; Ma, L. The development situation of biomass gasification power generation in China. Energy Policy 2012, 51, 52–57. [Google Scholar] [CrossRef]
- De Bari, I.; Barisano, D.; Cardinale, M.; Matera, D.; Nanna, F.; Viggiano, D. Air Gasification of Biomass in a Downdraft Fixed Bed: A Comparative Study of the Inorganic and Organic Products Distribution. Energy Fuels 2000, 14, 889–898. [Google Scholar] [CrossRef]
- Available online: www.inerco.com (accessed on 11 May 2020).
- Olah, G.A. Beyond oil and gas: The Methanol Economy. Angew. Chem. Int. Ed. 2005, 44, 2636–2639. [Google Scholar] [CrossRef] [PubMed]
- Goeppert, A.; Olah, G.A.; Prakash, G.K.S. Towards a sustainable carbon cycle: The methanol economy. In Green Chemistry; Royal Society of Chemistry: London, UK, 2018; pp. 919–962. [Google Scholar]
- Migliori, M.; Catizzone, E.; Aloise, A.; Bonura, G.; Gómez-Hortigüela, L.; Frusteri, L.; Cannilla, C.; Frusteri, F.; Giordano, G. New insights about coke deposition in methanol-to-DME reaction over MOR-, MFI-, and FER-type zeolites. J. Ind. Eng. Chem. 2018, 68, 196–208. [Google Scholar] [CrossRef]
- Keil, F.J. Methanol-to-hydrocarbons: Process technology. Microp. Mesop. Mater. 1999, 29, 49–66. [Google Scholar] [CrossRef]
- Catizzone, E.; Cirelli, Z.; Aloise, A.; Lanzafame, P.; Migliori, M.; Giordano, G. Methanol conversion over ZSM-12, ZSM-22 and EU-1 zeolites: From DME to hydrocarbons production. Catal. Today 2018, 304, 39–50. [Google Scholar] [CrossRef]
- Tian, P.; Wei, Y.; Ye, M.; Liu, Z. Methanol to Olefins (MTO): From Fundamentals to Commercialization. ACS Catal. 2015, 5, 1922–1938. [Google Scholar] [CrossRef]
- Galadima, A.; Muraza, O. From synthesis gas production to methanol synthesis and potential upgrade to gasoline range hydrocarbons: A review. J. Nat. Gas Sci. Eng. 2015, 25, 303–316. [Google Scholar] [CrossRef]
- Torres, W.; Pansare, S.S.; Goodwin, J.G. Hot Gas Removal of Tars, Ammonia, and Hydrogen Sulfide from Biomass Gasification Gas. Catal. Rev. 2007, 49, 407–456. [Google Scholar] [CrossRef]
- Guan, G.; Keawpanha, M.; Hao, X.; Abudula, A. Catalytic steam reforming of biomass tar: Prospects and challenges. Renew. Sustain. Energy Rev. 2016, 58, 450–461. [Google Scholar] [CrossRef]
- Giuliano, A.; Catizzone, E.; Freda, C.; Cornacchia, G. Valorization of OFMSW Digestate-Derived Syngas toward Methanol, Hydrogen, or Electricity: Process Simulation and Carbon Footprint Calculation. Processes 2020, 8, 526. [Google Scholar] [CrossRef]
- McCaffrey, Z.; Thy, P.; Long, M.; Oliveira, M.; Wang, L.; Torres, L.; Aktas, T.; Chiou, B.; Orts, W.; Jenkins, B.M. Air and Steam Gasification of Almond Biomass. Front. Energy Res. 2019, 7, 84. [Google Scholar] [CrossRef]
- Campoy, M.; Gòmez-Barea, A.; Villanueva, A.L.; Ollero, P. Air-Steam Gasification of Biomass in a Fluidized Bed under Simulated Autothermal and Adiabatic Conditions. Ind. Eng. Chem. Res. 2008, 47, 5957–5965. [Google Scholar] [CrossRef]
- Belaissaoui, B.; Le Moullec, Y.; Hagi, H.; Favre, E. Energy Efficiency of Oxygen Enriched Air Production Technologies: Cryogeny vs. Membranes. Energy Procedia 2014, 63, 497–503. [Google Scholar] [CrossRef]
- Smith, A.R.; Klosek, J. A review of air separation technologies and their integration with energy conversion processes. Fuel Process. Technol. 2011, 70, 115–134. [Google Scholar] [CrossRef]
- Meng, X.; de Jong, W.; Fu, N.; Verkooijen, A.H.M. Biomass gasification in a 100 kWth steam-oxygen blown circulating fluidized bed gasifier: Effects of operational conditions on product gas distribution and tar formation. Biomass Bioenergy 2011, 35, 2910–2924. [Google Scholar] [CrossRef]
- Barisano, D.; Canneto, G.; Nanna, F.; Braccio, G. Steam/oxygen biomass gasification at pilot scale in an internally circulating bubbling fluidized bed reactor. Fuel Process. Technol. 2016, 141, 74–81. [Google Scholar] [CrossRef]
- Pfeifer, C.; Koppatz, S.; Hofbauer, H. Steam gasification of various feedstocks at a dual fluidised bed gasifier: Impacts of operation conditions and bed materials. Biomass Conv. Bioref. 2011, 11, 39–53. [Google Scholar] [CrossRef]
- Catizzone, E.; Bonura, G.; Migliori, M.; Frusteri, F.; Giordano, G. CO2 recycling to dimethyl ether: State-of-the-art and perspectives. Molecules 2018, 23, 31. [Google Scholar] [CrossRef] [PubMed]
- Bonura, G.; Cannilla, C.; Frusteri, L.; Catizzone, E.; Todaro, S.; Migliori, M.; Giordano, G.; Frusteri, F. Interaction effects between CuO-ZnO-ZrO2 methanol phase and zeolite surface affecting stability of hybrid systems during one-step CO2 hydrogenation to DME. Catal. Today 2020, 345, 175–182. [Google Scholar] [CrossRef]
- Macrì, D.; Catizzone, E.; Molino, A.; Migliori, M. Supercritical waster gasification of biomass and agro-food residues: Energy assessment from modelling approach. Renew. Energy 2020, 150, 624–636. [Google Scholar] [CrossRef]
- Iaquaniello, G.; Centi, G.; Salladini, A.; Palo, E.; Spadacini, L. Waste-to-methanol: Process and economics assessment. Biores. Technol. 2017, 243, 611–619. [Google Scholar] [CrossRef] [PubMed]
- Perathoner, S.; Centi, G. CO2 recycling: A key strategy to introduce green energy in the chemical production chain. ChemSusChem 2014, 7, 1274–1282. [Google Scholar] [CrossRef]
- Feng, W.; Ji, P.; Chen, B.; Zheng, D. Analysis of methanol production from biomass gasification. Chem. Eng. Technol. 2011, 34, 307–317. [Google Scholar] [CrossRef]
- Puig-Gamero, M.; Argudo-Santamaria, J.; Valverde, J.L.; Sànchez, P.; Sanchez-Silva, L. Three integrated process simulation using aspen plus: Pine gasification, syngas cleaning and methanol synthesis. Energy Conv. Manag. 2018, 177, 416–427. [Google Scholar] [CrossRef]
- LeValley, T.L.; Richard, A.R.; Fan, M. The progress in water gas shift and steam reforming hydrogen production technologies—A review. Int. J. Hydrogen Energy 2014, 39, 16983–17000. [Google Scholar] [CrossRef]
- Ju, F.; Chen, H.; Ding, X.; Yang, H.; Wang, X.; Zhang, S.; Dai, Z. Process simulation of single-step dimethyl ether production via biomass gasification. Biotechnol. Adv. 2009, 27, 599–605. [Google Scholar] [CrossRef]
- Robinson, P.J.; Luyben, W.L. Integrated Gasification Combined Cycle Dynamic Model: H2S Absorption/Stripping, Water-Gas Shift Reactors, and CO2 Absorption/Stripping. Ind. Eng. Chem. Res. 2010, 49, 4766–4781. [Google Scholar] [CrossRef]
- Giuliano, A.; Poletto, M.; Barletta, D. Pure hydrogen co-production by membrane technology in an IGCC power plant with carbon capture. Int. J. Hydrogen Energy 2018, 43, 19279–19292. [Google Scholar] [CrossRef]
- Chiodini, A.; Bua, L.; Carnelli, L.; Zwart, R.; Vreugdenhil, B.; Vocciante, M. Enhancements in Biomass-to- Liquid processes: Gasification aiming at high hydrogen/carbon monoxide ratios for direct Fischer-Tropsch synthesis applications. Biomass Bioenergy 2017, 106, 104–114. [Google Scholar] [CrossRef]
- Giuliano, A.; Catizzone, E.; Barisano, D.; Nanna, F.; Villone, A.; De Bari, I. Towards Methanol Economy: A Techno-environmental Assessment for a Bio-methanol OFMSW/Biomass/Carbon Capture-based Integrated Plant. Int. J. Heat. Technol. 2019, 37, 665–674. [Google Scholar] [CrossRef]
- Dinca, C.; Slavu, N.; Cormoş, C.C.; Badea, A. CO2 capture from syngas generated by a biomass gasification power plant with chemical absorption process. Energy 2018, 149, 925–936. [Google Scholar] [CrossRef]
- Centi, G.; Perathoner, S. Towards solar fuels from water and CO2. ChemSusChem 2010, 3, 195–208. [Google Scholar] [CrossRef] [PubMed]
- Gazzani, M.; MacChi, E.; Manzolini, G. CO2 capture in integrated gasification combined cycle with SEWGS—Part A: Thermodynamic performances. Fuel 2013, 5, 206–219. [Google Scholar] [CrossRef]
- Yang, Q.; Li, X.; Yang, Q.; Huang, W.; Yu, P.; Zhang, D. Opportunities for CO2 Utilization in Coal to Green Fuel Process: Optimal Design and Performance Evaluation. ACS Sustain. Chem. Eng. 2020, 8, 1329–1342. [Google Scholar] [CrossRef]
- Khanipour, M.; Mirvakili, A.; Bakhtyari, A.; Farniaei, M.; Rahimpour, M.R. A membrane-assisted hydrogen and carbon oxides separation from flare gas and recovery to a commercial methanol reactor. Int. J. Hydrogen Energy 2020, 45, 7386–7400. [Google Scholar] [CrossRef]
- Hla, S.S.; Park, D.; Duffy, G.J.; Edwards, J.H.; Roberts, D.G.; Ilyushechkin, A. Kinetics of high-temperature water-gas shift reaction over two iron-based commercial catalysts using simulated coal-derived syngases. Chem. Eng. J. 2009, 146, 148–154. [Google Scholar] [CrossRef]
- Bozzano, G.; Manenti, F. Efficient methanol synthesis: Perspectives, technologies and optimization strategies. Prog. Energy Combust. Sci. 2016, 56, 71–105. [Google Scholar] [CrossRef]
- Choi, Y.; Stenger, H.G. Water gas shift reaction kinetics and reactor modeling for fuel cell grade hydrogen. J. Power Sources 2003, 124, 432–439. [Google Scholar] [CrossRef]
- Sofia, D.; Giuliano, A.; Poletto, M.; Barletta, D. Techno-economic analysis of power and hydrogen coproduction by an IGCC plant with CO2 capture based on membrane technology. Comp. Aided Chem. Eng. 2015, 37, 1373–1378. [Google Scholar]
- Sandler, S.I. Chemical, Biochemical, and Engineering Themodynamcs, 4th ed.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Menin, L.; Vakalis, S.; Benedetti, V.; Patuzzi, F.; Baratieri, M. Techno-economic assessment of an integrated biomass gasification, electrolysis, and syngas biomethanation process. Biomass Conv. Bioref. 2020, 1–15. [Google Scholar] [CrossRef]
- Giuliano, A.; Poletto, M.; Barletta, D. Process Design of a Multi-Product Lignocellulosic Biorefinery. Comput. Aided Chem. Eng. 2015, 37, 1313–1318. [Google Scholar]
- Dorris, C.C.; Lu, E.; Park, S.; Toro, F.H. High-Purity Oxygen Production Using Mixed Ionic-Electronic Conducting Sorbents. Penn Engineering. Available online: http://repository.upenn.edu/cbe_sdr/78 (accessed on 30 June 2020).
- Seider, W.D.; Lewin, D.R.; Seader, D.J.; Widagdo, S.; Gani, R.; Ng, K.M. Product and Process Design Principles: Synthesis, Analysis and Evaluation, 4th ed.; Wiley: New York, NY, USA, 2016. [Google Scholar]
- Giuliano, A.; Barletta, D.; De Bari, I.; Poletto, M. Techno-economic assessment of a lignocellulosic biorefinery co-producing ethanol and xylitol or furfural. Comput. Aided Chem. Eng. 2018, 43, 585–590. [Google Scholar]
- Giuliano, A.; Cerulli, R.; Poletto, M.; Raiconi, G.; Barletta, D. Process Pathways Optimization for a Lignocellulosic Biorefinery Producing Levulinic Acid, Succinic Acid, and Ethanol. Ind. Eng. Chem. Res. 2016, 55, 10699–10717. [Google Scholar] [CrossRef]
- Hamelinck, C.N.; Van Hooijdonk, G.; Faaij, A.P. Ethanol from lignocellulosic biomass: Techno-economic performance in short-, middle- and long-term. Biomass Bioenergy 2005, 28, 384–410. [Google Scholar] [CrossRef]
- Leonzio, G. Methanol Synthesis: Optimal Solution for a Better Efficiency of the Process. Processes 2018, 6, 20. [Google Scholar] [CrossRef]
- Hamelinck, C.N.; Faaij, A.P.C. Future prospects for production of methanol and hydrogen from biomass. J. Power Source 2002, 111, 1–22. [Google Scholar] [CrossRef]
- Pérez-Arteaga, L.E.; Gómez-Cápiro, O.; Karelovic, A.; Jiménez, R. A modelling apporach to the techno-economics of biomass-to-DNG/Methanol systems: Standalone vs integrated topologies. Chem. Eng. J. 2016, 286, 663–678. [Google Scholar] [CrossRef]
- Calabrò, P.S.; Fazzino, F.; Folino, A.; Paone, E.; Komilis, D. Semi-continuous anaerobic digestion of orange peel waste: Effect of activated carbon addition and alkaline pretreatment on the process. Sustainability 2019, 11, 3386. [Google Scholar] [CrossRef]
- Fasolini, A.; Cucciniello, R.; Paone, E.; Mauriello, F.; Tabanelli, T. A Short Overview on the Hydrogen Production Via Aqueous Phase Reforming (APR) of Cellulose, C6-C5 Sugars and Polyols. Catalysts 2019, 9, 917. [Google Scholar] [CrossRef]
- Paone, E.; Tabanelli, T.; Mauriello, F. The rise of lignin biorefinery. Curr. Opin. Green Sustain. Chem. 2020, 24, 1–6. [Google Scholar] [CrossRef]
- Cherubini, F. The Biorefinery concept: Using biomass instead of oil for producing energy and chemicals. Energy Conv. Manag. 2010, 51, 1412–1421. [Google Scholar] [CrossRef]
- Menon, V.; Rao, M. Trends in bioconversion of lignocellulose: Biofuels, platform chemicals and Biorefinery concept. Progress Energy Comb. Sci. 2012, 38, 522–550. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Pérez-Fortes, M.; Van herle, J.; Maréchal, F.; Desideri, U. Techno-economic optimization of biomass-to-methanol with solid-oxide electrolyze. Appl. Energy 2020, 258, 114071. [Google Scholar] [CrossRef]
- Kumabe, K.; Fujimoto, S.; Yanagida, T.; Ogata, M.; Fukuda, T.; Yabe, A.; Minowa, T. Environmental and economic analysis of methanol production process via biomass gasification. Fuel 2008, 87, 1422–1427. [Google Scholar] [CrossRef]
- Michailos, S.; Parker, D.; Webb, C. A multicriteria comparison of utilizing sugar cane bagasse for methanol to gasoline and butanol production. Biomass Bioenergy 2016, 95, 436–448. [Google Scholar] [CrossRef]
- Wang, S.-W.; Li, D.-X.; Ruan, W.-B.; Jin, C.-L.; Farahani, M.R. A techno-economic review of biomass gasification for production of chemicals. Energy Sources Econ. Plan. Policy 2018, 13, 351–356. [Google Scholar] [CrossRef]
- Available online: https://phyllis.nl/Browse/Standard/ECN-Phyllis (accessed on 30 June 2020).
- Saletnik, B.; Zaguła, G.; Bajcar, M.; Tarapatskyy, M.; Bobula, G.; Puchalski, C. Biochar as a Multifunctional Component of the Environment—A Review. Appl. Sci. 2019, 9, 1139. [Google Scholar] [CrossRef]
| CO | H2 | CO2 | CH4 | N2 |
|---|---|---|---|---|
| 30 | 30 | 25 | 10 | 5 |
| Section | Equipment | Equipment Kind | Utility or Steam Required/Produced |
|---|---|---|---|
| WGS | C1 | Compressor | Electricity |
| WGS | E1 | Heat exchanger | Natural gas |
| WGS | E2 | Heat exchanger | LPS produced |
| WGS | P1 | Pump | Electricity |
| WGS | HTS-WGS | Reactor | / |
| WGS | E3 | Heat exchanger | LPS produced |
| WGS | LTS-WGS | Reactor | / |
| WGS | E4 | Heat exchanger | Cooling water |
| WGS | F1 | Condenser | / |
| CCS | C2 | Compressor | Electricity |
| CCS | E5 | Heat exchanger | Cooling water |
| CCS | ABS | Absorption column | / |
| CCS | E8 | Heat exchanger | LPS required |
| CCS | V1 | Valve | / |
| CCS | E6 | Heat exchanger | LPS required |
| CCS | F2 | Flash | / |
| CCS | C3 | Compressor | Electricity |
| CCS | V2 | Valve | / |
| CCS | E7 | Heat exchanger | LPS required |
| CCS | F3 | Flash | / |
| CCS | C5 | Compressor | Electricity |
| CCS | P2 | Pump | Electricity |
| CCS | C4 | Compressor | Electricity |
| Section | Process Variable | Units | Range | Effect |
|---|---|---|---|---|
| WGS | H2O/CO | - | 1–3 | WGS Conversion |
| WGS | WGS-HTS length | m | 0–2 | WGS Conversion/ WGS-HTS Pressure drop |
| WGS | WGS-LTS length | m | 0–5 | WGS Conversion/ WGS-LTS Pressure drop |
| CCS | DEPG/GAS | - | 0.5–1 | CO2 absorption |
| CCS | V1 output pressure | bar | 10–70 | CO2 absorption/ Captured CO2 purity |
| CCS | V2 output pressure | bar | 0.7–2 | CO2 absorption/ Captured CO2 purity |
| Economic Parameter | Units | Calculation | Value | Reference |
|---|---|---|---|---|
| Biomass supply chain cost (CB) | €/t | 40 | [47] | |
| Oxygen purchase cost | €/t | 40 | [48] | |
| LPS | €/t | 7 | [49] | |
| MPS | €/t | 11 | [49] | |
| Natural gas | €/Nm3 | 0.136 | [49] | |
| DEPG cost | €/t | 5000 | [32] | |
| Column packing | €/m3 | 1000 | [32] | |
| Electricity | €/MWh | 40 | - | |
| Column stage height | M | 0.5 | [32] | |
| ABS stage | - | 12 | [32] | |
| Working hour per year | h/y | 7920 | [32] | |
| Fp | 0.5/7/50 bar | 1/1.5/1.9 | [49] | |
| Ft | 100/300/500 °C | 1/1.6/2.1 | [49] | |
| Construction years | Y | 2 | - | |
| Depreciation years (yD) | Y | 20 | [50] | |
| Maintenance and labor (OCM) | M€/y | % of total capital cost | 10 | [51] |
| Working capital (WC) | M€ | % of total capital cost | 2 | [32] |
| Taxes (t) | % | of the gross profit | 40 | [32] |
| Discount rate (r) | % | 3 | - |
| WGS Conversion (%) | Removed CO2 (%) | H2O/CO | DEPG/GAS | V1/V2 Pressure (bar) |
|---|---|---|---|---|
| 36 | 98 | 1 | 1 | 25/0.7 |
| 40 | 95 | 1 | 1 | 20/1.6 |
| 49 | 88 | 2 | 0.7 | 21/1.3 |
| 59 | 82 | 2 | 0.7 | 19/1.5 |
| 70 | 76 | 2 | 0.5 | 58/0.7 |
| 80 | 72 | 2 | 0.5 | 28/0.7 |
| 90 | 67 | 3 | 0.5 | 27/1.5 |
| 99 | 64 | 3 | 0.5 | 23/1.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giuliano, A.; Freda, C.; Catizzone, E. Techno-Economic Assessment of Bio-Syngas Production for Methanol Synthesis: A Focus on the Water–Gas Shift and Carbon Capture Sections. Bioengineering 2020, 7, 70. https://doi.org/10.3390/bioengineering7030070
Giuliano A, Freda C, Catizzone E. Techno-Economic Assessment of Bio-Syngas Production for Methanol Synthesis: A Focus on the Water–Gas Shift and Carbon Capture Sections. Bioengineering. 2020; 7(3):70. https://doi.org/10.3390/bioengineering7030070
Chicago/Turabian StyleGiuliano, Aristide, Cesare Freda, and Enrico Catizzone. 2020. "Techno-Economic Assessment of Bio-Syngas Production for Methanol Synthesis: A Focus on the Water–Gas Shift and Carbon Capture Sections" Bioengineering 7, no. 3: 70. https://doi.org/10.3390/bioengineering7030070
APA StyleGiuliano, A., Freda, C., & Catizzone, E. (2020). Techno-Economic Assessment of Bio-Syngas Production for Methanol Synthesis: A Focus on the Water–Gas Shift and Carbon Capture Sections. Bioengineering, 7(3), 70. https://doi.org/10.3390/bioengineering7030070