An Analysis of the Effects of Noisy Electrocardiogram Signal on Heartbeat Detection Performance
Abstract
1. Introduction
2. Materials and Methods
2.1. Ambulatory ECG Data for Beat Detection Evaluation
2.2. Beat Detection Algorithms
3. Results and Discussion
3.1. Evaluation Metrics
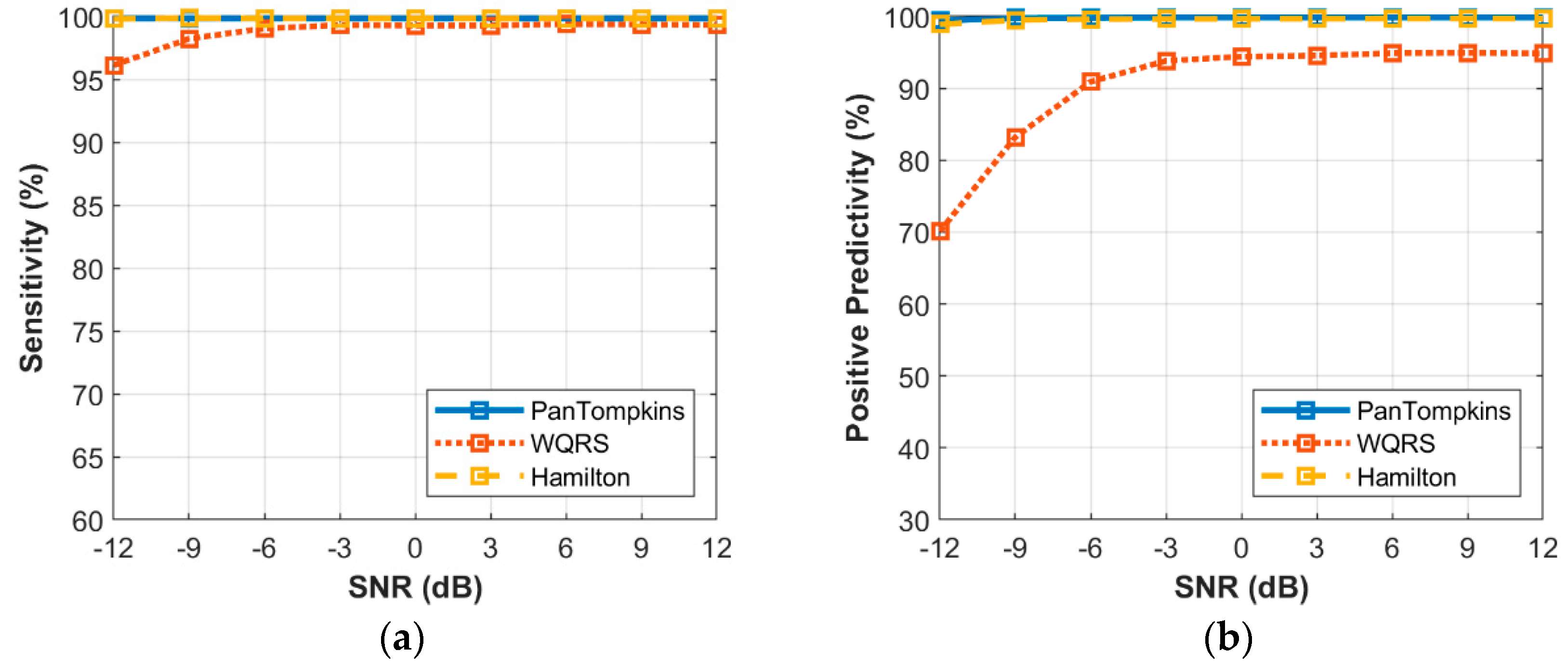
3.2. Effect of Beat Detector Performance on a Clean ECG
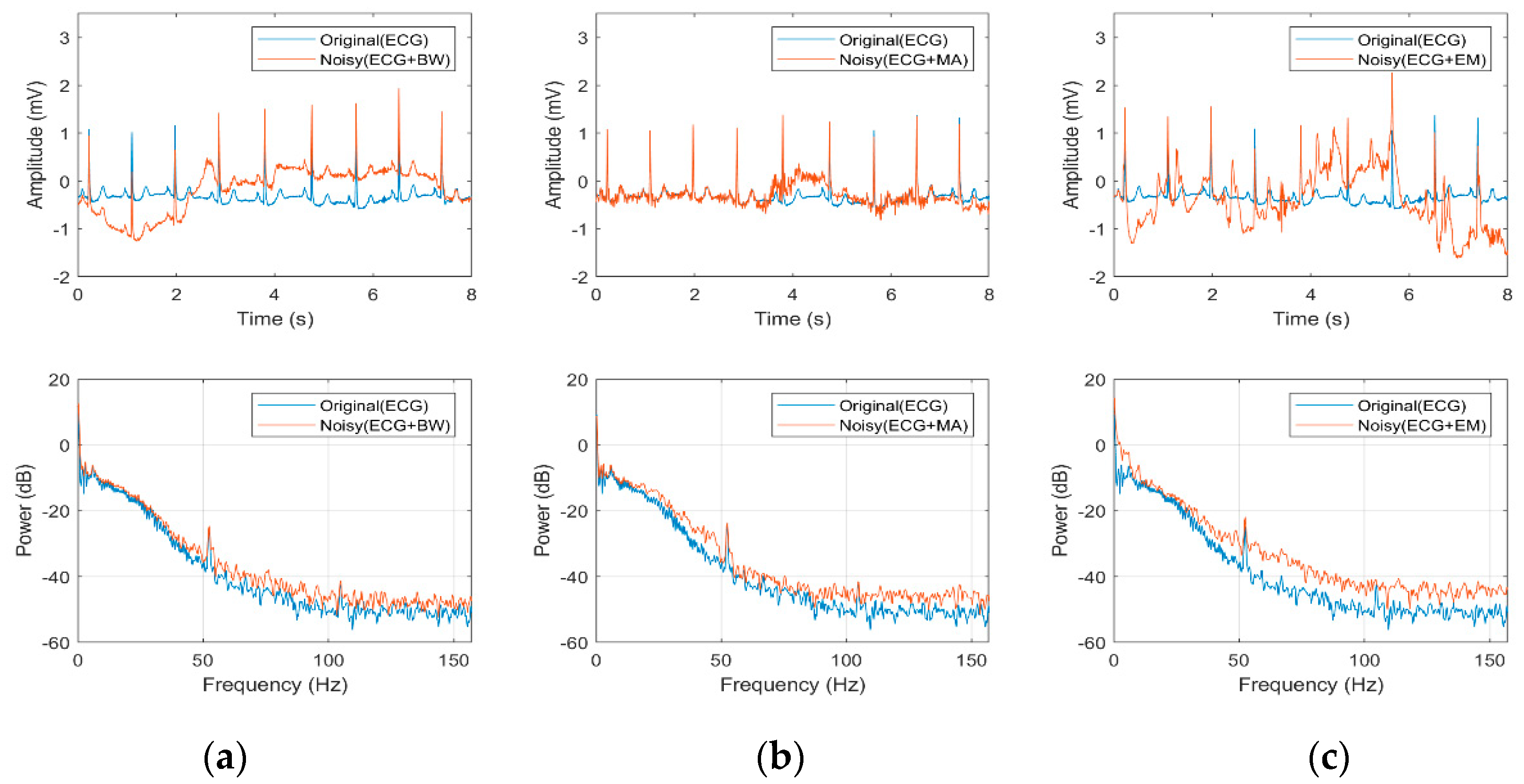
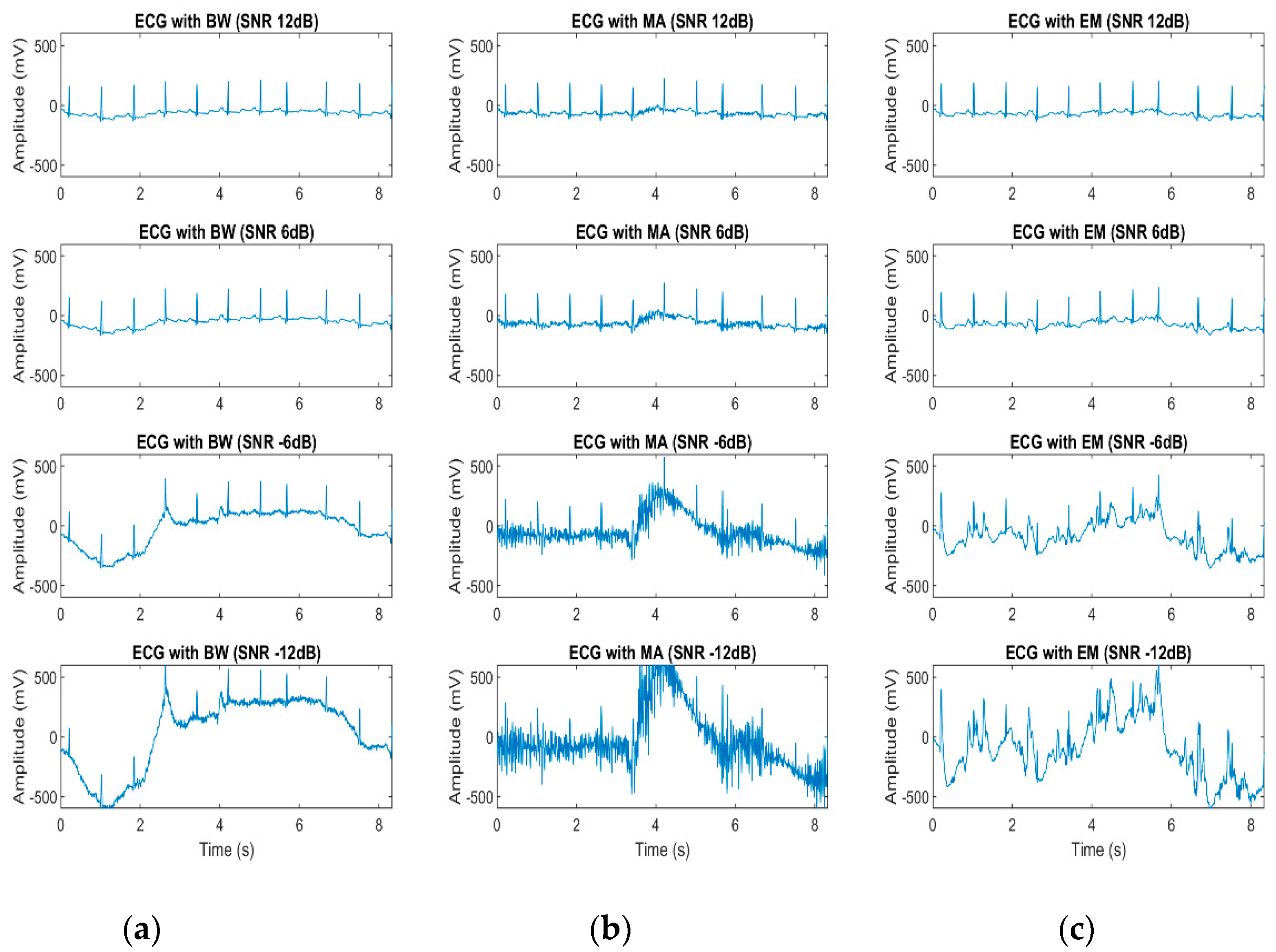
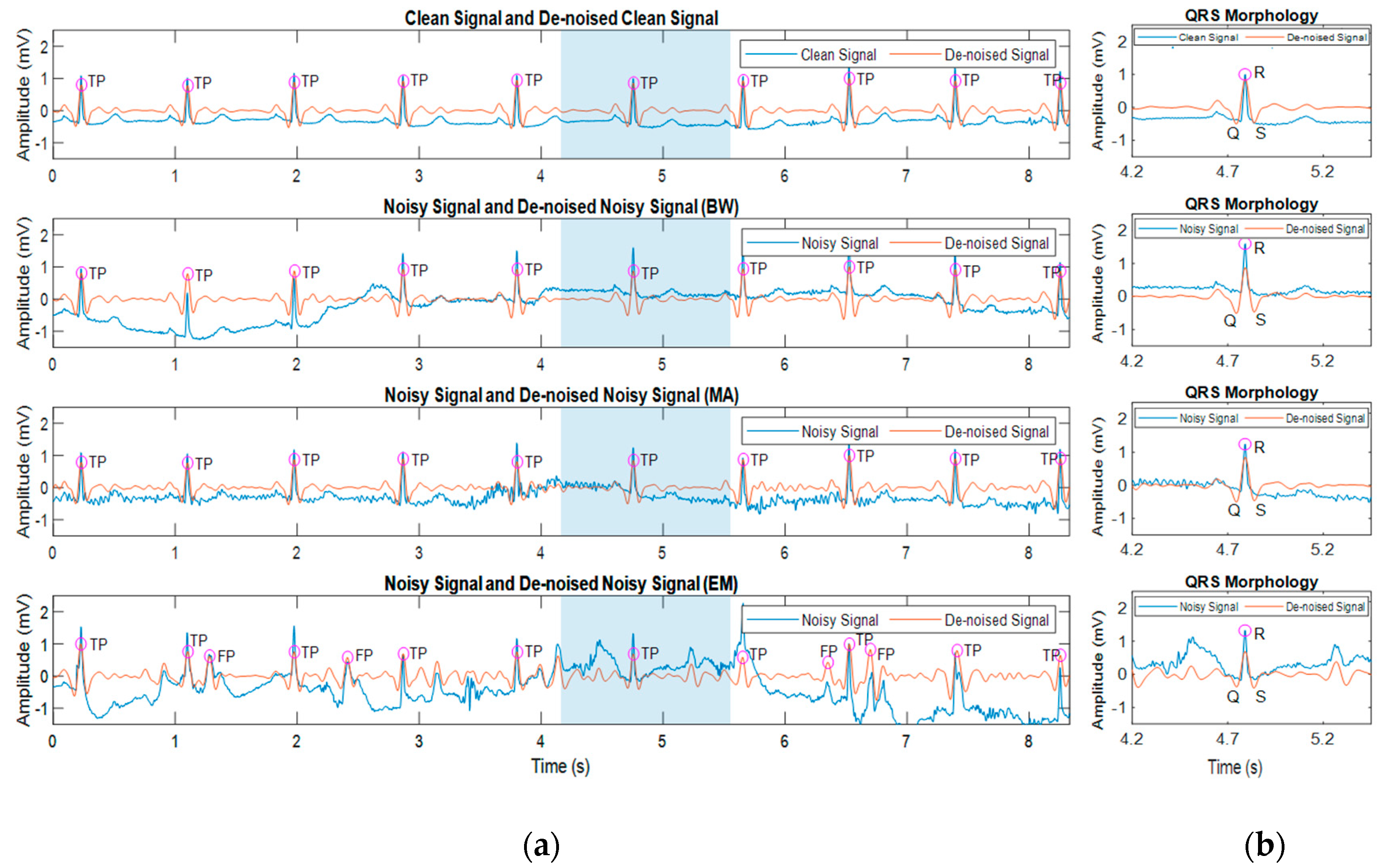
3.3. Effect of Noisy Signal on Heart Beat Morphology
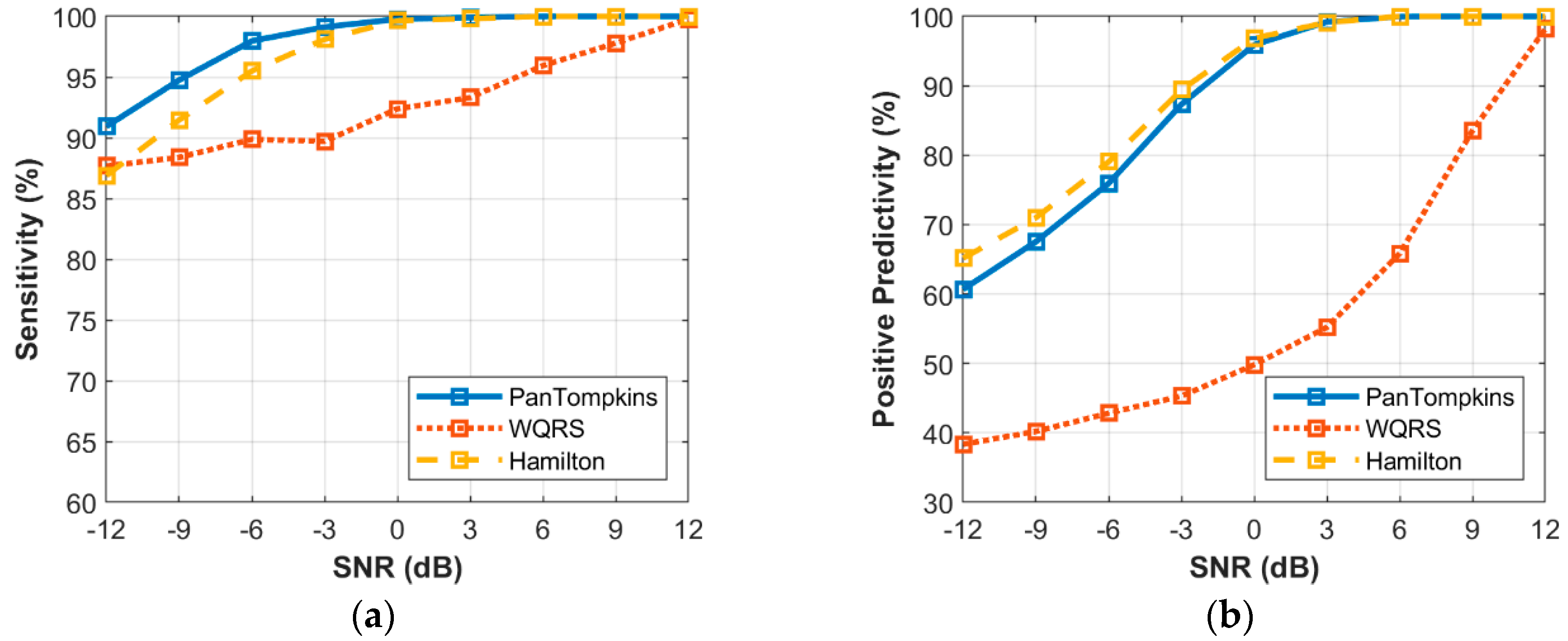
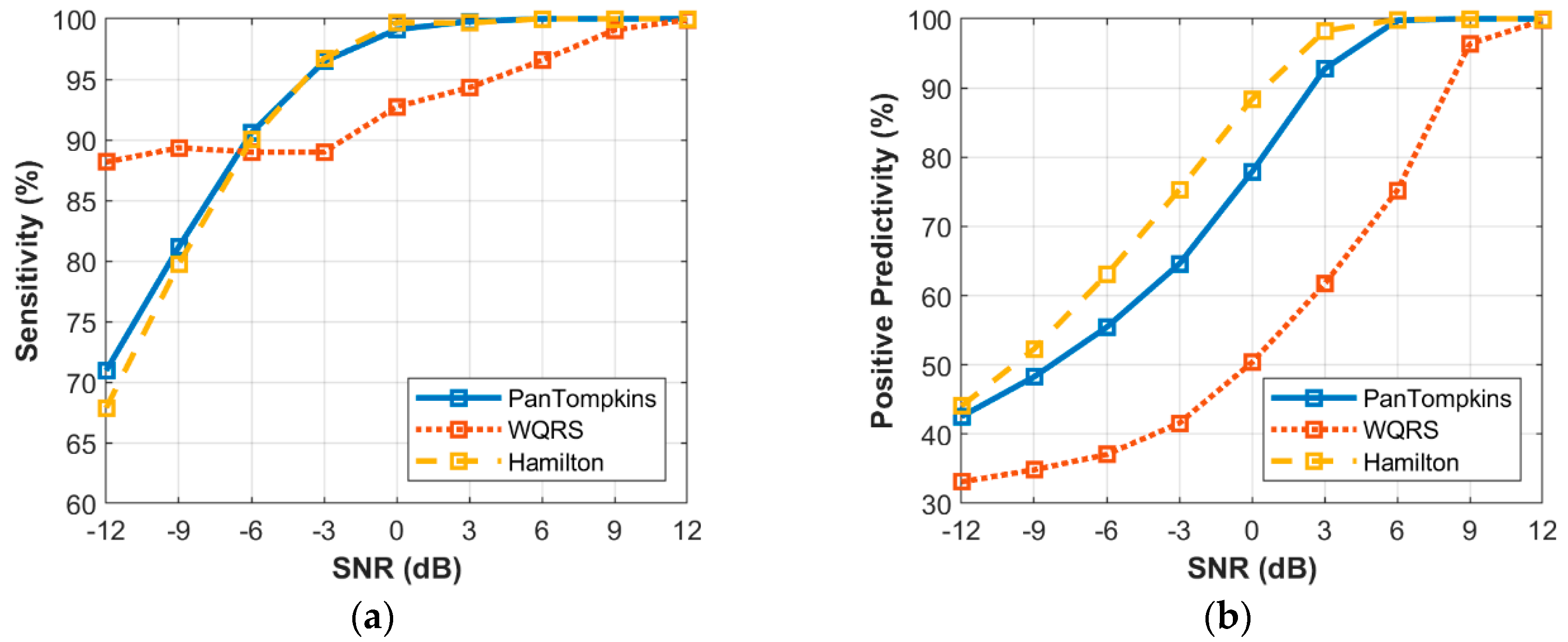
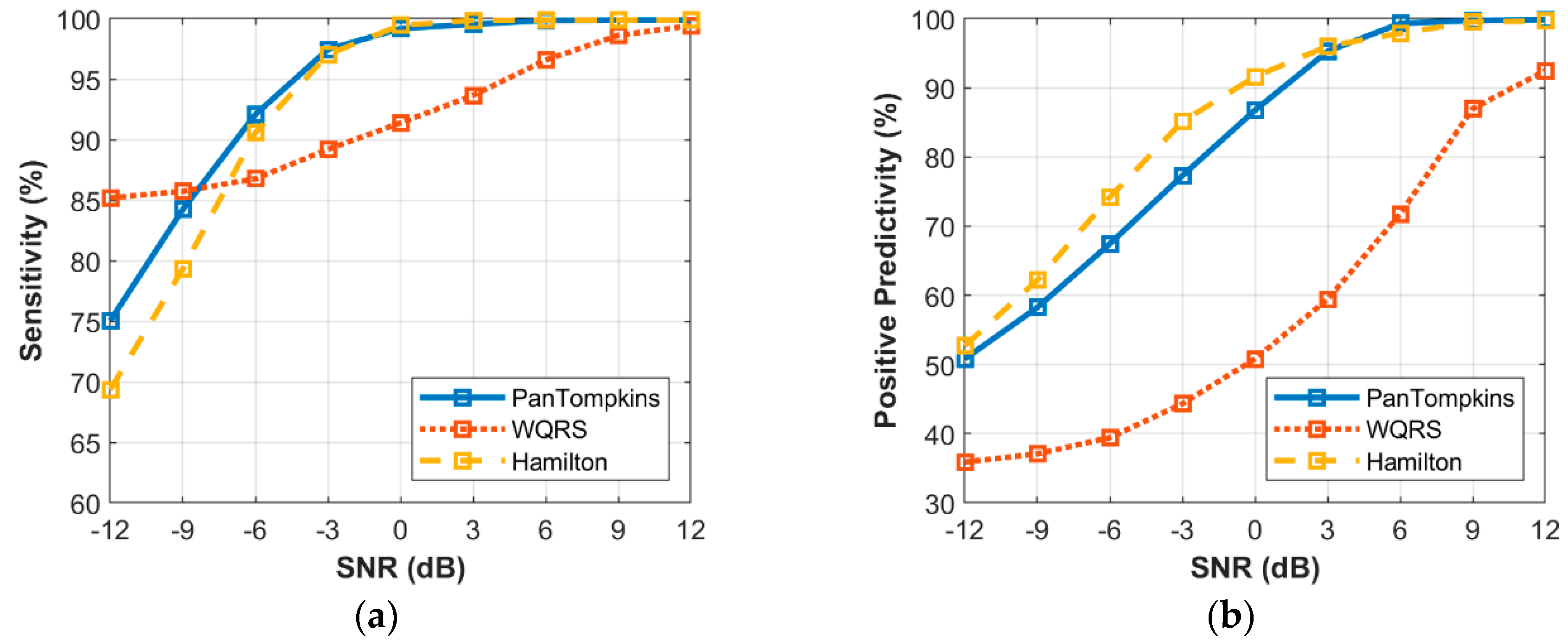
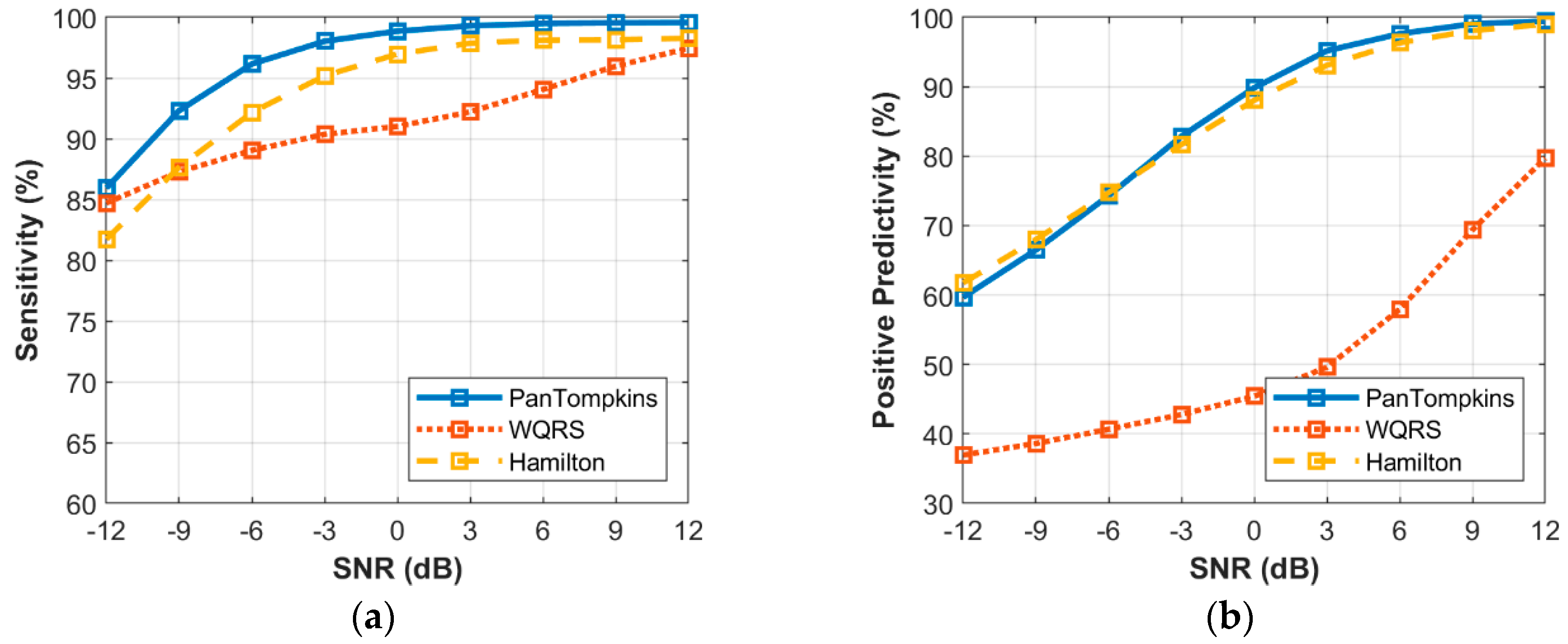
3.4. Effect of Beat Detector Performance on the Noisy Signal of Record 100
3.5. Effect of Beat Detector Performance on Noisy Abnormal Signal of Record 200
3.6. Effect of Beat Detector Performance on Noisy Signal of all Records from the MIT-BIH Database
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Majumder, S.; Mondal, T.; Deen, M.J. Wearable Sensors for Remote Health Monitoring. Sensors 2017, 17, 130. [Google Scholar] [CrossRef]
- Kowey, P.R.; Kocovic, D.Z. Ambulatory Electrocardiographic Recording. Circulation 2003, 108, e31–e33. [Google Scholar] [CrossRef]
- Nemati, E.; Deen, M.; Mondal, T. A wireless wearable ECG sensor for long-term applications. IEEE Commun. Mag. 2012, 50, 36–43. [Google Scholar] [CrossRef]
- Mastoi, Q.U.A.; Wah, T.Y.; Raj, R.G.; Iqbal, U. Automated Diagnosis of Coronary Artery Disease: A Review and Workflow. Cardiol. Res. Pract. 2018, 2018, 2016282. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Soliman, E.Z. A new Approach for Analysis of Heart Rate Variability and QT Variability in Long-term ECG Recording. Biomed. Eng. Online 2018, 17, 54. [Google Scholar] [CrossRef] [PubMed]
- Tanmay, P.; Subhasis, C.; Siddhartha, D. Body Movement Activity Recognition for Ambulatory Cardiac Monitoring. IEEE Trans. Biomed. Eng. 2007, 54, 874–882. [Google Scholar] [CrossRef]
- Rahul, K.; Tanmay, P.; Vishvjit, T.; Hitesh, S. Physical Activities Recognition from Ambulatory ECG Signals using Neuro-Fuzzy Classifiers and Support Vector Machines. Med. Eng. Technol. 2015, 39, 138–152. [Google Scholar] [CrossRef]
- Nguyen, L.T.N.; Eager, D.; Nguyen, H. The Relationship between Compression Garments and Electrocardiogram Signals during Exercise and Recovery Phase. Biomed. Eng. Online 2019, 18. [Google Scholar] [CrossRef]
- Eduardo, L.; William, S.; Guillermo, C.; David, M. ECG-based Heartbeat Classification for Arrhythmia Detection: A Survey. Comput. Meth. Prog. Biomed. 2015, 127. [Google Scholar] [CrossRef]
- Apandi, Z.F.M.; Ikeura, R.; Hayakawa, S. Arrhythmia Detection Using MIT-BIH Dataset: A Review. In Proceedings of the International Conference on Computational Approach in Smart Systems Design and Applications (ICASSDA), Kuching, Malaysia, 15–17 August 2018; pp. 1–5. [Google Scholar]
- Kohler, B.; Hennig, C.; Orglmeister, R. The principles of software QRS detection. IEEE Eng. Med. Biol. Mag. 2002, 21, 42–57. [Google Scholar] [CrossRef]
- Ghaleb, F.A.; Kamat, M.B.; Salleh, M.; Rohani, M.F.; Abd Razak, S. Two-stage Motion Artefact Reduction Algorithm for Electrocardiogram using Weighted Adaptive Noise Cancelling and Recursive Hampel Filter. PLoS ONE 2018, 13, e0207176. [Google Scholar] [CrossRef] [PubMed]
- Pawar, T.; Anantakrishnan, N.S.; Chaudhuri, S.; Duttagupta, S.P. Impact Analysis of Body Movement in Ambulatory ECG. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 5453–5456. [Google Scholar]
- Satija, U.; Ramkumar, B.; Manikandan, M. Real-Time Signal Quality-Aware ECG Telemetry System for IoT-Based Health Care Monitoring. IEEE Internet Things J. 2017, 4, 815–823. [Google Scholar] [CrossRef]
- Clifford, G.D.; Azuaje, F.; Mesharry, P. ECG statistics, noise artifacts and missing data. In Advanced Methods and Tools for ECG Data Analysis; Artech House Inc.: London, UK, 2006. [Google Scholar]
- Luo, Y.; Hargraves, R.; Belle, A.; Bai, O.; Qi, X.; Ward, K.; Pfaffenberger, M.; Najarian, K. A Hierarchical Method for Removal of Baseline Drift from Biomedical Signals: Application in ECG Analysis. Sci. World 2013, 2013, 896056. [Google Scholar] [CrossRef] [PubMed]
- Taji, B.; Chan, A.; Shirmohammadi, S. Effect of Pressure on Skin-Electrode Impedance in Wearable Biomedical Measurement Devices. IEEE Trans. Inst. Meas. 2018, 99, 1–13. [Google Scholar] [CrossRef]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef]
- Zong, W.; Moody, G.B.; Jiang, D. A robust open-source algorithm to detect onset and duration of QRS complexes. Comput. Cardiol. 2003, 30, 737–740. [Google Scholar]
- Hamilton, P. Open Source ECG Analysis. Comput. Cardiol. 2002, 1, 101–104. [Google Scholar]
- Cuiwei, L.; Chongxun, Z.; Changfeng, T. Detection of ECG Characteristic Points using Wavelet Transforms. IEEE Trans. Biomed. Eng. 1995, 42, 21–28. [Google Scholar] [CrossRef]
- Friesen, G.M.; Jannett, T.C.; Jadallah, M.A.; Yates, S.L.; Quint, S.R.; Nagle, H.T. A comparison of the noise sensitivity of nine QRS detection algorithms. IEEE Trans. Biomed. Eng. 1990, 37, 85–98. [Google Scholar] [CrossRef]
- Kalidas, V.; Tamil, L. Real-time QRS detector using Stationary Wavelet Transform for Automated ECG Analysis. In Proceedings of the IEEE 17th International Conference on Bioinformatics and Bioengineering (BIBE), Washington, DC, USA, 23–25 October 2017; pp. 457–461. [Google Scholar] [CrossRef]
- D’Aloia, M.; Longo, A.; Rizzi, M. Noisy ECG Signal Analysis for Automatic Peak Detection. Information 2019, 10, 35. [Google Scholar] [CrossRef]
- Dev Sharma, L.; Sunkaria, R.K. A robust QRS detection using novel pre-processing techniques and kurtosis based enhanced efficiency. Measurement 2016, 87, 194–204. [Google Scholar] [CrossRef]
- Vollmer, M. Robust Detection of Heart Beats using Dynamic Thresholds and Moving Windows. Comput. Cardiol. 2014, 41, 569–572. [Google Scholar]
- Kovács, P.; Böck, C.; Meier, J.; Huemer, M. ECG segmentation using adaptive Hermite functions. Procedings of the 51st Asilomar Conference on Signal, System, and Computer, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 1476–1480. [Google Scholar]
- Chieng, T.M.; Wen Hau, Y.; Omar, Z.B.; Wen Lim, C. An Efficient Instantaneous ECG Delineation Algorithm. In Proceedings of the 2019 Computing in Cardiology (CinC) Conference, Singapore, 8–11 September 2019; pp. 1–4. [Google Scholar]
- Moody, G.; Mark, R. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.B.; Muldrow, W.; Mark, R. A noise stress test for arrhythmia detectors. IEEE Comput. Cardiol. 1984, 11, 381–384. [Google Scholar]
- PhysioNet WFDB Applications, WQRS. Available online: http://www.physionet.org/physiotools/wag/wqrs-1.htm (accessed on 15 January 2020).
- Phukpattaranont, P. QRS detection algorithm based on the quadratic filter. Expert Syst. Appl. 2015, 42, 4867–4877. [Google Scholar] [CrossRef]
- Bouaziz, F.; Boutana, D.; Benidir, M. Multiresolution wavelet-based QRS complex detection algorithm suited to several abnormal morphologies. IET Signal Process. 2014, 8, 774–782. [Google Scholar] [CrossRef]
- MIT-BIH Arrhythmia Database Directory. Available online: https://www.physionet.org/physiobank/database/html/mitdbdir/records.htm (accessed on 4 January 2020).
- Portet, F.; Hernandez, A.I.; Carrault, G. Evaluation of real-time QRS detection algorithms in variable contexts. Med. Biol. Eng. Comput. 2005, 43, 379–385. [Google Scholar] [CrossRef]






| Record | Beats | Record | Beats | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total | N 1 | S 2 | V 3 | F 4 | Q 5 | Total | N 1 | S 2 | V 3 | F 4 | Q 5 | ||
| 100 | 2273 | 2239 | 33 | 1 | 0 | 0 | 201 | 1963 | 1635 | 128 | 198 | 2 | 0 |
| 101 | 1865 | 1860 | 3 | 0 | 0 | 2 | 202 | 2136 | 2061 | 55 | 19 | 1 | 0 |
| 102 | 2187 | 99 | 0 | 4 | 56 | 2028 | 203 | 2980 | 2529 | 2 | 444 | 1 | 4 |
| 103 | 2084 | 2082 | 2 | 0 | 0 | 0 | 205 | 2656 | 2571 | 3 | 71 | 11 | 0 |
| 104 | 2229 | 163 | 0 | 2 | 666 | 1398 | 207 | 1860 | 1543 | 107 | 210 | 0 | 0 |
| 105 | 2572 | 2526 | 0 | 41 | 0 | 5 | 208 | 2955 | 1586 | 2 | 992 | 373 | 2 |
| 106 | 2027 | 1507 | 0 | 520 | 0 | 0 | 209 | 3005 | 2621 | 383 | 1 | 0 | 0 |
| 107 | 2137 | 0 | 0 | 59 | 0 | 2078 | 210 | 2650 | 2423 | 22 | 195 | 10 | 0 |
| 108 | 1774 | 1740 | 4 | 17 | 2 | 0 | 212 | 2748 | 923 | 1825 | 0 | 0 | 0 |
| 109 | 2532 | 2492 | 0 | 38 | 2 | 0 | 213 | 3251 | 2641 | 28 | 220 | 362 | 0 |
| 111 | 2124 | 2123 | 0 | 1 | 0 | 0 | 214 | 2262 | 2003 | 0 | 256 | 1 | 2 |
| 112 | 2539 | 2537 | 2 | 0 | 0 | 0 | 215 | 3363 | 3195 | 3 | 164 | 1 | 0 |
| 113 | 1795 | 1789 | 6 | 0 | 0 | 0 | 217 | 2208 | 244 | 0 | 162 | 260 | 1542 |
| 114 | 1879 | 1820 | 12 | 43 | 4 | 0 | 219 | 2154 | 2082 | 7 | 64 | 1 | 0 |
| 115 | 1953 | 1953 | 0 | 0 | 0 | 0 | 220 | 2048 | 1954 | 94 | 0 | 0 | 0 |
| 116 | 2412 | 2302 | 1 | 109 | 0 | 0 | 221 | 2427 | 2031 | 0 | 396 | 0 | 0 |
| 117 | 1535 | 1534 | 1 | 0 | 0 | 0 | 222 | 2483 | 2274 | 209 | 0 | 0 | 0 |
| 118 | 2278 | 2166 | 96 | 16 | 0 | 0 | 223 | 2605 | 2045 | 73 | 473 | 14 | 0 |
| 119 | 1987 | 1543 | 0 | 444 | 0 | 0 | 228 | 2053 | 1688 | 3 | 362 | 0 | 0 |
| 121 | 1863 | 1861 | 1 | 1 | 0 | 0 | 230 | 2256 | 2255 | 1 | 0 | 0 | 0 |
| 122 | 2476 | 2476 | 0 | 0 | 0 | 0 | 231 | 1571 | 1568 | 1 | 2 | 0 | 0 |
| 123 | 1518 | 1515 | 0 | 3 | 0 | 0 | 232 | 1780 | 398 | 1382 | 0 | 0 | 0 |
| 124 | 1619 | 1536 | 31 | 47 | 5 | 0 | 233 | 3079 | 2230 | 7 | 831 | 11 | 0 |
| 200 | 2601 | 1743 | 30 | 826 | 2 | 0 | 234 | 2753 | 2700 | 50 | 3 | 0 | 0 |
| Record | Pan Tompkins [18] | WQRS [19] | Hamilton [20] | |||
|---|---|---|---|---|---|---|
| SE (%) | PP (%) | SE (%) | PP (%) | SE (%) | PP (%) | |
| 105 | 99.46 | 98.27 | 98.83 | 92.10 | 99.57 | 98.88 |
| 108 | 99.77 | 83.27 1 | 99.38 | 84.19 1 | 99.32 | 99.38 |
| 121 | 99.89 | 100 | 99.79 | 99.73 | 99.95 | 100 |
| 200 | 99.85 | 99.85 | 99.85 | 99.31 | 99.85 | 99.73 |
| 202 | 99.53 | 100 | 99.81 | 99.95 | 99.67 | 100 |
| 207 | 98.98 | 99.68 | 99.41 | 98.40 | 99.25 | 99.84 |
| 217 | 99.82 | 99.91 | 99.55 | 98.30 | 99.18 | 99.64 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohd Apandi, Z.F.; Ikeura, R.; Hayakawa, S.; Tsutsumi, S. An Analysis of the Effects of Noisy Electrocardiogram Signal on Heartbeat Detection Performance. Bioengineering 2020, 7, 53. https://doi.org/10.3390/bioengineering7020053
Mohd Apandi ZF, Ikeura R, Hayakawa S, Tsutsumi S. An Analysis of the Effects of Noisy Electrocardiogram Signal on Heartbeat Detection Performance. Bioengineering. 2020; 7(2):53. https://doi.org/10.3390/bioengineering7020053
Chicago/Turabian StyleMohd Apandi, Ziti Fariha, Ryojun Ikeura, Soichiro Hayakawa, and Shigeyoshi Tsutsumi. 2020. "An Analysis of the Effects of Noisy Electrocardiogram Signal on Heartbeat Detection Performance" Bioengineering 7, no. 2: 53. https://doi.org/10.3390/bioengineering7020053
APA StyleMohd Apandi, Z. F., Ikeura, R., Hayakawa, S., & Tsutsumi, S. (2020). An Analysis of the Effects of Noisy Electrocardiogram Signal on Heartbeat Detection Performance. Bioengineering, 7(2), 53. https://doi.org/10.3390/bioengineering7020053





