Computational Biomechanics: In-Silico Tools for the Investigation of Surgical Procedures and Devices
Abstract
1. Introduction
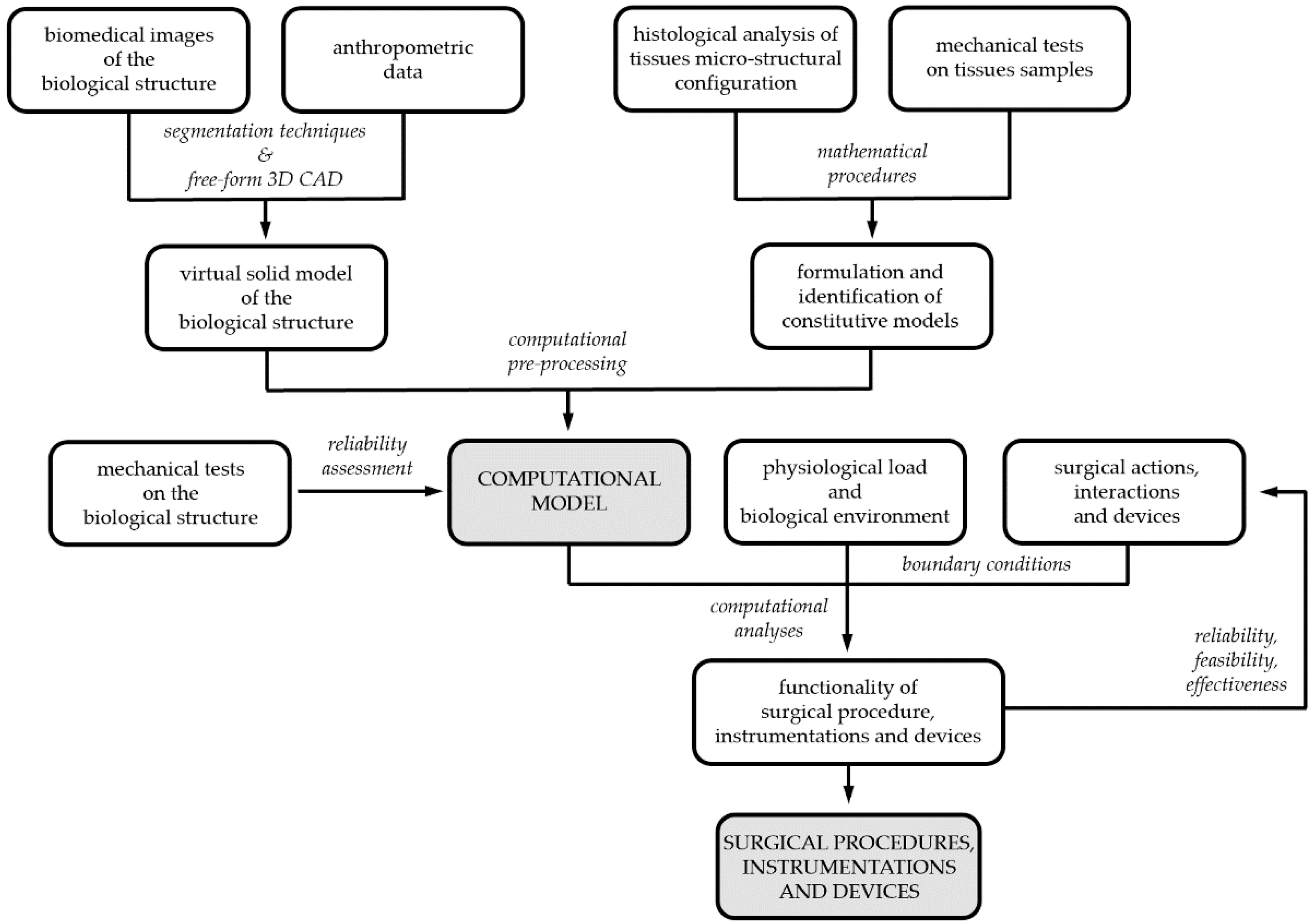
2. Overview on Computational Modeling of Biological Structures
3. Geometrical Characterization of Biological Structures
4. Constitutive Analysis of Biological Tissues’ Mechanics
4.1. Hard Tissues
4.2. Soft Tissues
4.3. Identification of Constitutive Parameters
5. Computational Analysis Techniques
6. In Silico Analysis of Surgical Procedures: Case Studies
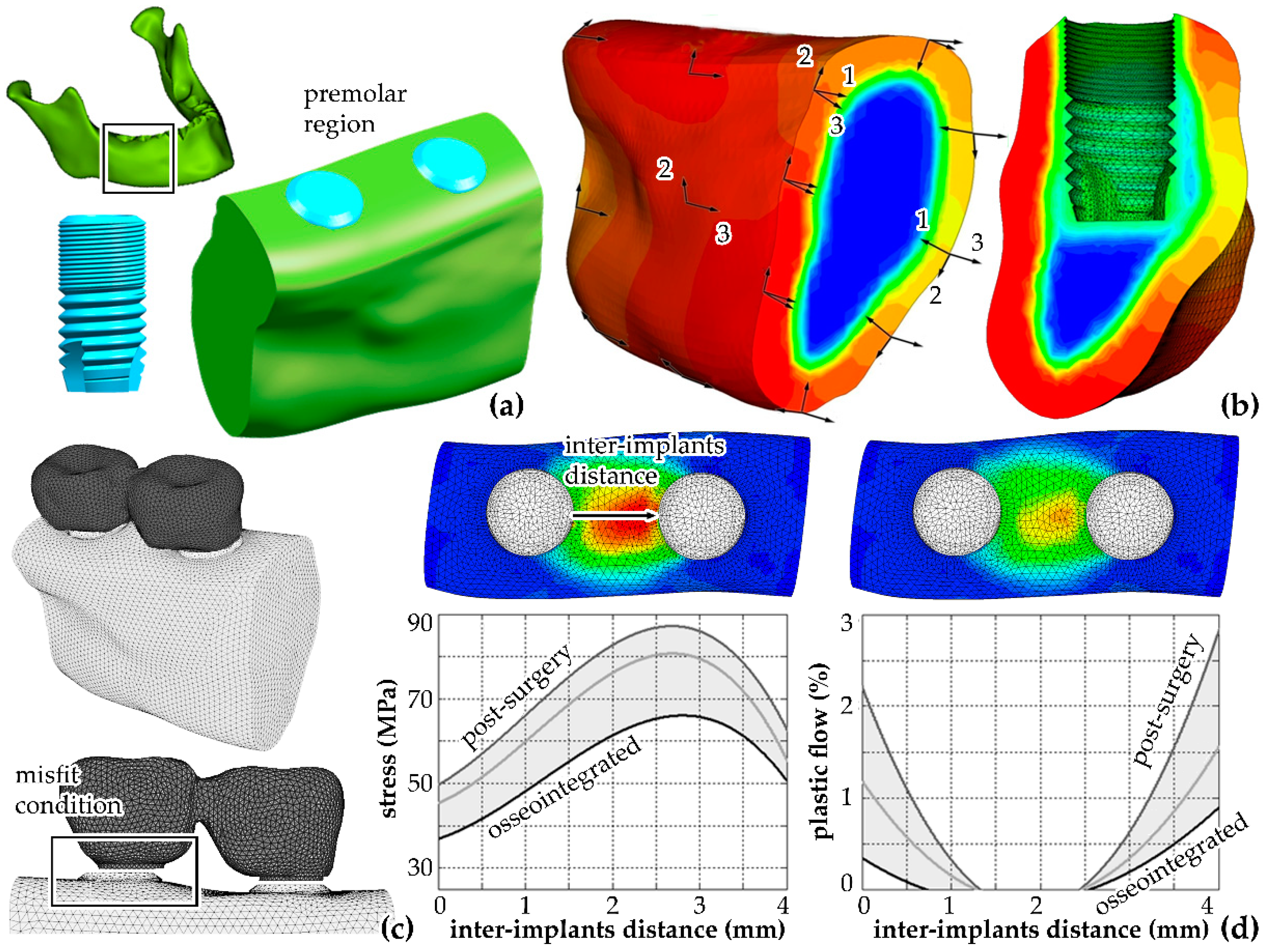
6.1. Biomechanical Tools for the Reliability Assessment of Multi-Implant Systems in Dental Implantology
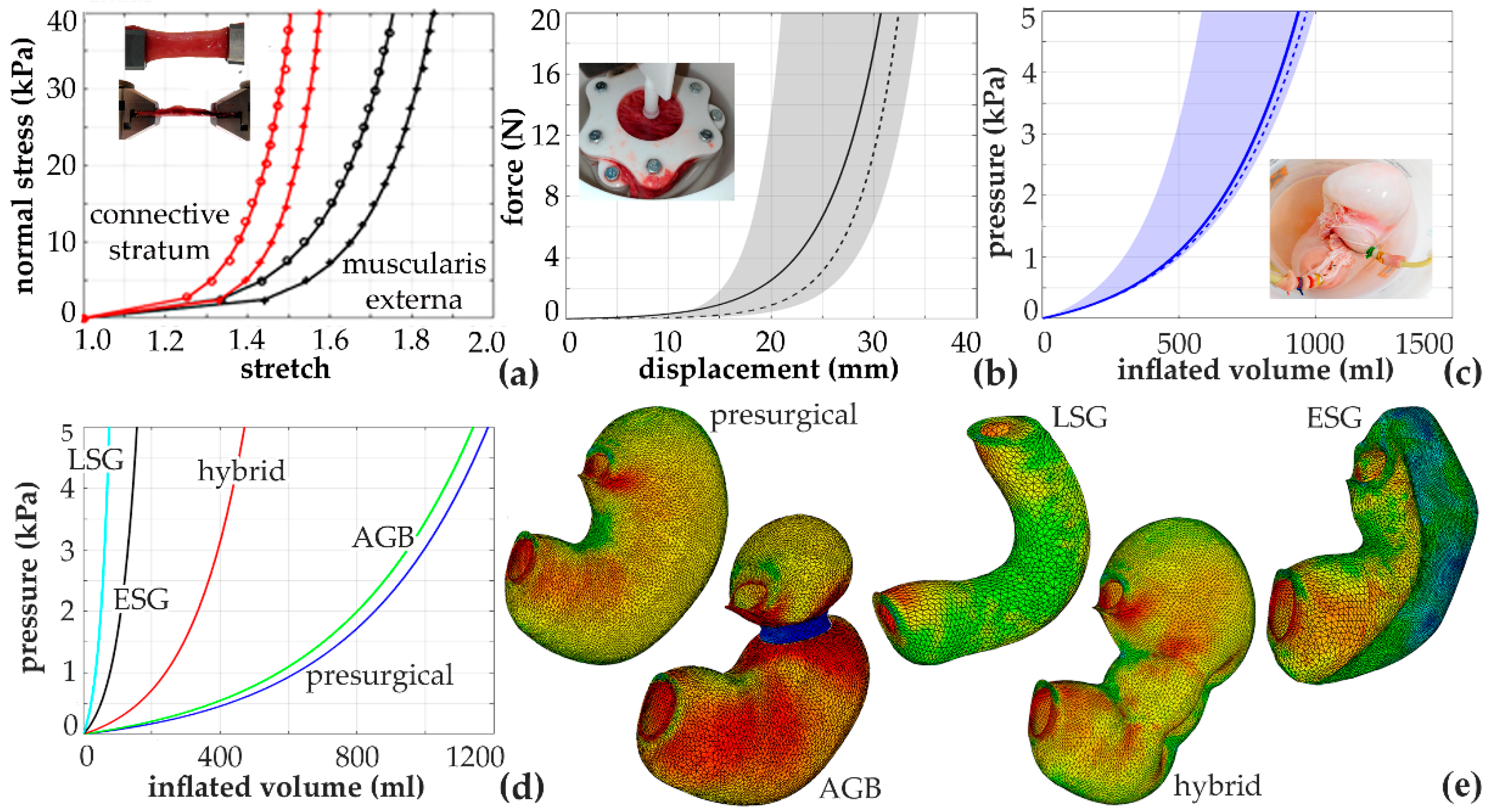
6.2. Biomechanical Models for the Computational Evaluation of Gastrointestinal Bariatric Procedures
7. Future Perspectives and Concluding Remark
Author Contributions
Funding
Conflicts of Interest
References
- Huiskes, R.; Chao, E.Y.S. A survey of finite element analysis in orthopedic biomechanics: The first decade. J. Biomech. 1983, 16, 385–409. [Google Scholar] [CrossRef]
- Payan, Y. Biomechanics Applied to Computer Assisted Surgery; Research Signpost: Kerala, India, 2005. [Google Scholar]
- Carniel, E.L.; Fontanella, C.G.; Polese, L.; Merigliano, S.; Natali, A.N. Computational tools for the analysis of mechanical functionality of gastrointestinal structures. Technol. Health Care 2013, 21, 271–283. [Google Scholar] [CrossRef] [PubMed]
- Carusi, A. In silico medicine: Social, technological and symbolic mediation. HUMANA. MENTE J. Studies 2016, 9, 67–86. [Google Scholar]
- Carniel, E.L.; Frigo, A.; Fontanella, C.G.; De Benedictis, G.M.; Rubini, A.; Barp, L.; Pluchino, G.; Sabbadini, B.; Polese, L. A biomechanical approach to the analysis of methods and procedures of bariatric surgery. J. Biomech. 2017, 56, 32–41. [Google Scholar] [CrossRef] [PubMed]
- Natali, A.N.; Fontanella, C.G.; Carniel, E.L. Biomechanical analysis of the interaction phenomena between artificial urinary sphincter and urethral duct. Int. J. Numer. Method Biomed. Eng. 2020, 36, e3308. [Google Scholar] [CrossRef] [PubMed]
- Viceconti, M.; Henney, A.; Morley-Fletcher, E. In silico clinical trials: How computer simulation will transform the biomedical industry. Int. J. Clin. Trials 2016, 3, 37–46. [Google Scholar] [CrossRef]
- Carniel, E.L.; Gramigna, V.; Fontanella, C.G.; Stefanini, C.; Natali, A.N. Constitutive formulations for the mechanical investigation of colonic tissues. J. Biomed. Mater. Res. A 2014, 102, 1243–1254. [Google Scholar] [CrossRef]
- Henninger, H.B.; Reese, S.P.; Anderson, A.E.; Weiss, J.A. Validation of computational models in biomechanics. Proc. Inst. Mech. Eng. H 2010, 224, 801–812. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; Wiley: Hoboken, NJ, USA, 2000; Chapter 6; pp. 205–304. [Google Scholar]
- Belytschko, T.; Liu, W.K.; Moran, B.; Elkhodary, K. Nonlinear Finite Elements for Continua and Structures, 2nd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: Mineola, NY, USA, 2000. [Google Scholar]
- Young, P.G.; Beresford-West, T.B.; Coward, S.R.; Notarberardino, B.; Walker, B.; Abdul-Aziz, A. non-linear viscoelastic laws for soft biological tissues. Philos. Trans. A Math. Phys. Eng. Sci. 2008, 366, 3155–3173. [Google Scholar] [CrossRef]
- Zhang, Y.J. Geometric Modeling and Mesh Generation from Scanned Images; Taylor & Francis Group: Abingdon, UK, 2016. [Google Scholar]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer: Berlin/Heidelberg, Germany, 1998; Chapter 10; pp. 336–366. [Google Scholar]
- Cowin, S.C. Bone Mechanics Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2001; Chapter 6; pp. 13–14. [Google Scholar]
- Fritsch, A.; Hellmich, C. ‘Universal’ microstructural patterns in cortical and trabecular, extracellular and extravascular bone materials: Micromechanics-based prediction of anisotropic elasticity. J. Theor. Biol. 2007, 244, 597–620. [Google Scholar] [CrossRef]
- Natali, A.N.; Carniel, E.L.; Pavan, P.G. Constitutive modelling of inelastic behaviour of cortical bone. Med. Eng. Phys. 2008, 30, 905–912. [Google Scholar] [CrossRef] [PubMed]
- Maurel, W.; Wu, Y.; Magnenat Thalmann, N.; Thalmann, D. Biomechanical Models for Soft Tissue Simulation; Springer: Berlin/Heidelberg, Germany, 1998; Chapter 4; pp. 101–120. [Google Scholar]
- Chagnon, G.; Rebouah, M.; Favier, D. Hyperelastic energy densities for soft biological tissues: A review. J. Elast. 2015, 120, 129–160. [Google Scholar] [CrossRef]
- Carniel, E.L.; Fontanella, C.G.; Stefanini, C.; Natali, A.N. A procedure for the computational investigation of stress-relaxation phenomena. Mech. Time-Depend Mat. 2013, 17, 25–38. [Google Scholar] [CrossRef]
- Pioletti, D.P.; Rakotomanana, L.R. Non-Linear Viscoelastic Laws for Soft Biological Tissues. Eur. J. Mech. A/Solids 2000, 19, 749–759. [Google Scholar] [CrossRef]
- Natali, A.N.; Fontanella, C.G.; Carniel, E.L. Constitutive formulation and numerical analysis of the heel pad region. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 401–409. [Google Scholar] [CrossRef]
- Marsden, J.E.; Hughes, T.J.R. Mathematical Foundations of Elasticity; Prentice Hall Inc: Upper saddle river, NJ, USA, 1983. [Google Scholar]
- Arora, J.S.; Elwakeil, O.A.; Chahande, A.I.; Hsieh, C.C. Global optimization methods for engineering applications: A review. Struct. Multidiscip. Optim. 1995, 9, 137–159. [Google Scholar] [CrossRef]
- Natali, A.N.; Gasparetto, A.; Carniel, E.L.; Pavan, P.G.; Fabbro, S. Interaction phenomena between oral implants and bone tissue in single and multiple implant frames under occlusal loads and misfit conditions: A numerical approach. J. Biomed. Mater. Res. B Appl. Biomater. 2007, 83, 332–339. [Google Scholar] [CrossRef]
- Toniolo, I.; Salmaso, C.; Bruno, G.; De Stefani, A.; Stefanini, C.; Gracco, A.L.T.; Carniel, E.L. Anisotropic computational modelling of bony structures from CT data: An almost automatic procedure. Comput. Methods Programs Biomed. 2020, 189, 105319. [Google Scholar] [CrossRef]
- World Health Organization. Obesity and Overweight. Available online: https://www.who.int/news-room/fact-sheets/detail/obesity-and-overweight (accessed on 12 May 2020).
- Reges, O.; Greenland, P.; Dicker, D. Association of bariatric surgery using laparoscopic banding, Roux-en-Y gastric bypass, or laparoscopic sleeve gastrectomy vs usual care obesity management with all-cause mortality. JAMA 2018, 319, 279–290. [Google Scholar] [CrossRef]
- Abbas, M.; Khaitan, L. Primary endoluminal bariatric procedures. Tech. Gastrointest. Endosc. 2018, 20, 194–200. [Google Scholar] [CrossRef]
- Mathus-Vliegen, E.M.H.; Dargent, J. Current Endoscopic/Laparoscopic Bariatric Procedures. In Bariatric Therapy; Springer: Cham, Switzerland, 2018; pp. 85–176. [Google Scholar]
- Fontanella, C.G.; Salmaso, C.; Toniolo, I.; De Cesare, N.; Rubini, A.; De Benedictis, G.M.; Carniel, E.L. Computational models for the mechanical investigation of stomach tissues and structure. Ann. Biomed. Eng. 2019, 47, 1237–1249. [Google Scholar] [CrossRef] [PubMed]
- Woods, S.C. Gastrointestinal Satiety Signals. I. An overview of gastrointestinal signals that influence food intake. Am. J. Physiol. Gastrointest. Liver Physiol. 2004, 286, 7–13. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carniel, E.L.; Toniolo, I.; Fontanella, C.G. Computational Biomechanics: In-Silico Tools for the Investigation of Surgical Procedures and Devices. Bioengineering 2020, 7, 48. https://doi.org/10.3390/bioengineering7020048
Carniel EL, Toniolo I, Fontanella CG. Computational Biomechanics: In-Silico Tools for the Investigation of Surgical Procedures and Devices. Bioengineering. 2020; 7(2):48. https://doi.org/10.3390/bioengineering7020048
Chicago/Turabian StyleCarniel, Emanuele Luigi, Ilaria Toniolo, and Chiara Giulia Fontanella. 2020. "Computational Biomechanics: In-Silico Tools for the Investigation of Surgical Procedures and Devices" Bioengineering 7, no. 2: 48. https://doi.org/10.3390/bioengineering7020048
APA StyleCarniel, E. L., Toniolo, I., & Fontanella, C. G. (2020). Computational Biomechanics: In-Silico Tools for the Investigation of Surgical Procedures and Devices. Bioengineering, 7(2), 48. https://doi.org/10.3390/bioengineering7020048






