Synergistic Model of Cardiac Function with a Heart Assist Device
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mechanical/Chemical Model
2.2. Electric Activity Model
2.3. Basic Circulation Model and Control Case
2.4. Extended Circulation Model and Control Case
3. Results and Discussions
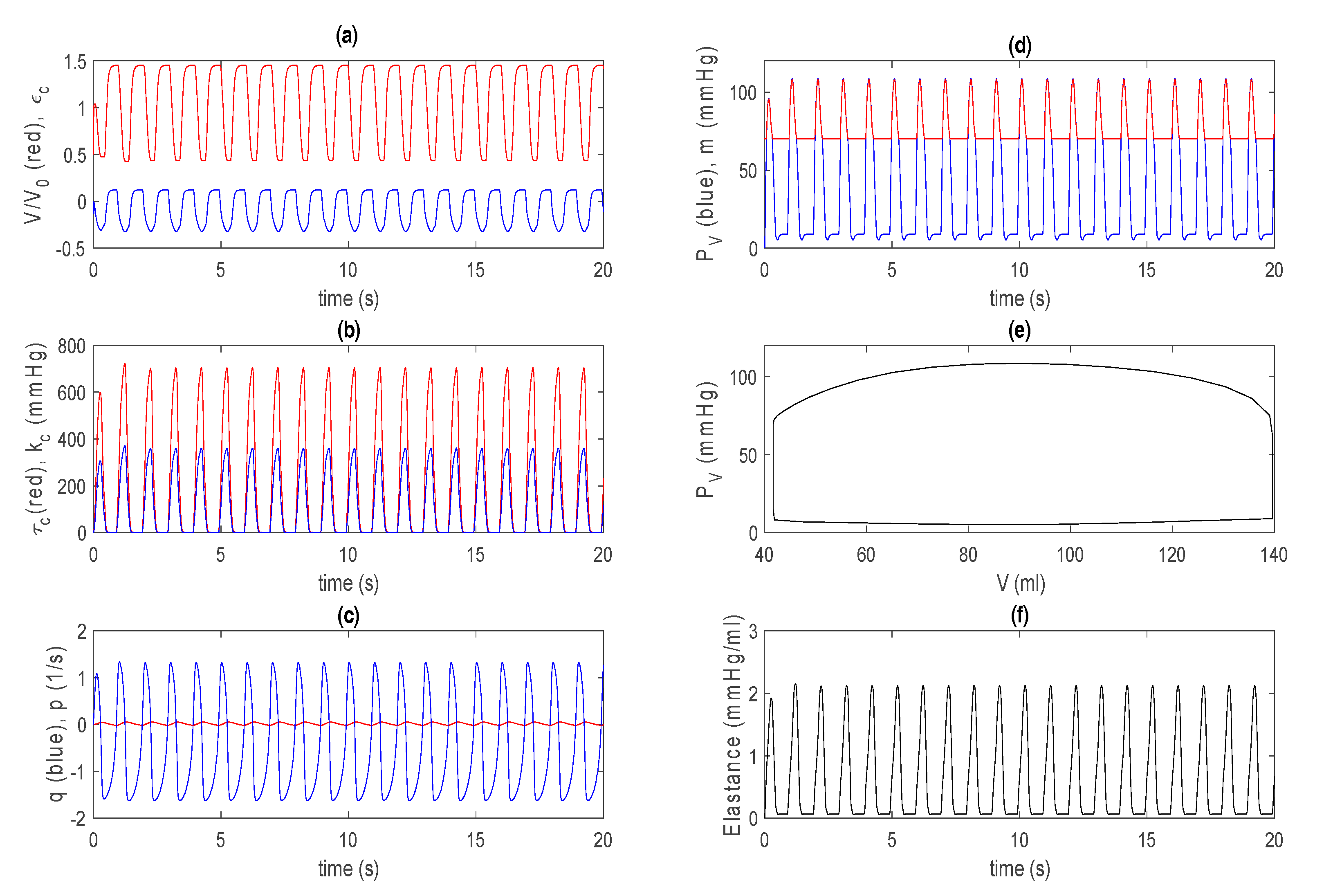
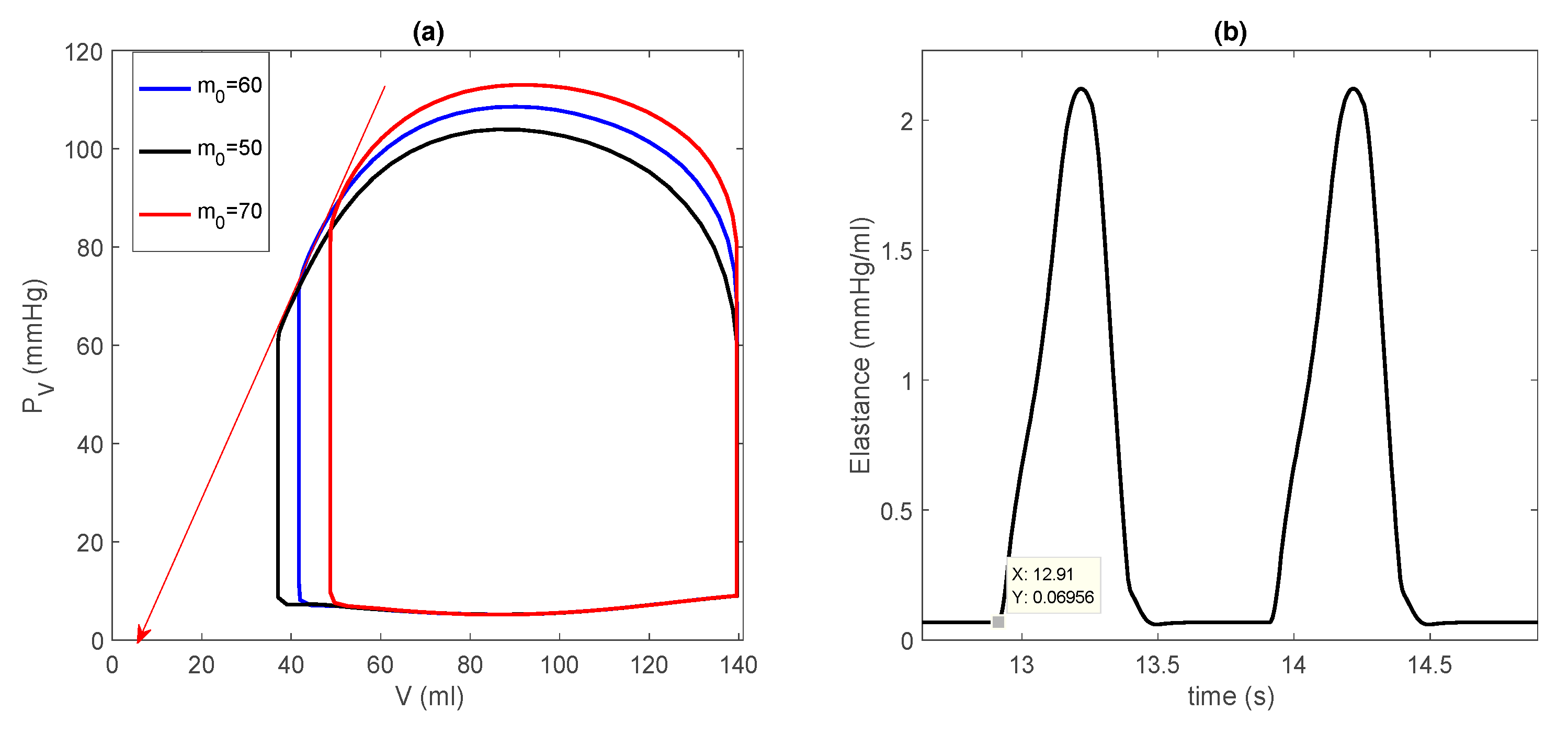
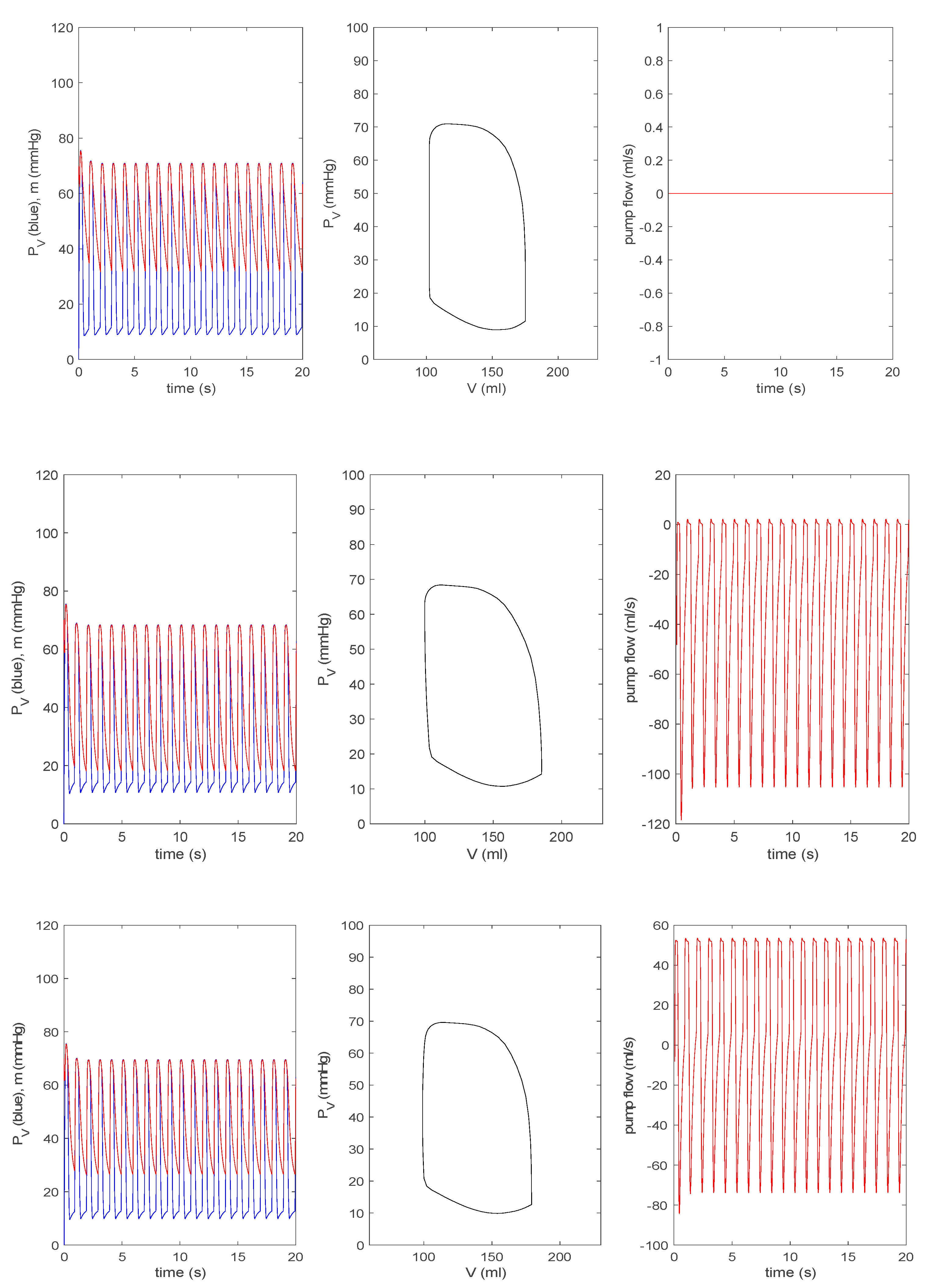
3.1. Control Case in Basic Model
3.2. Control Case in Extended Model
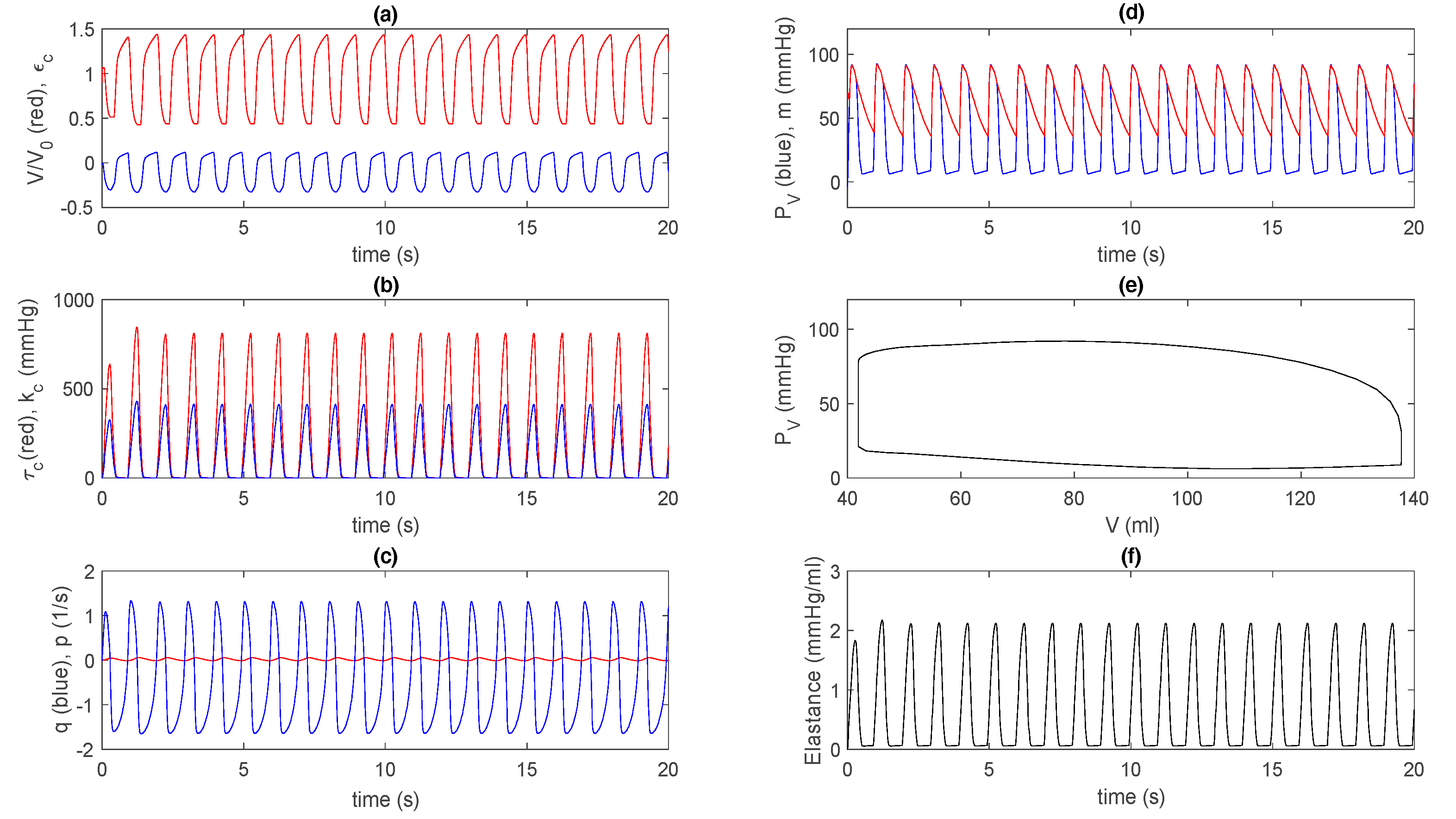
3.3. Dilated Cardiomyopathy
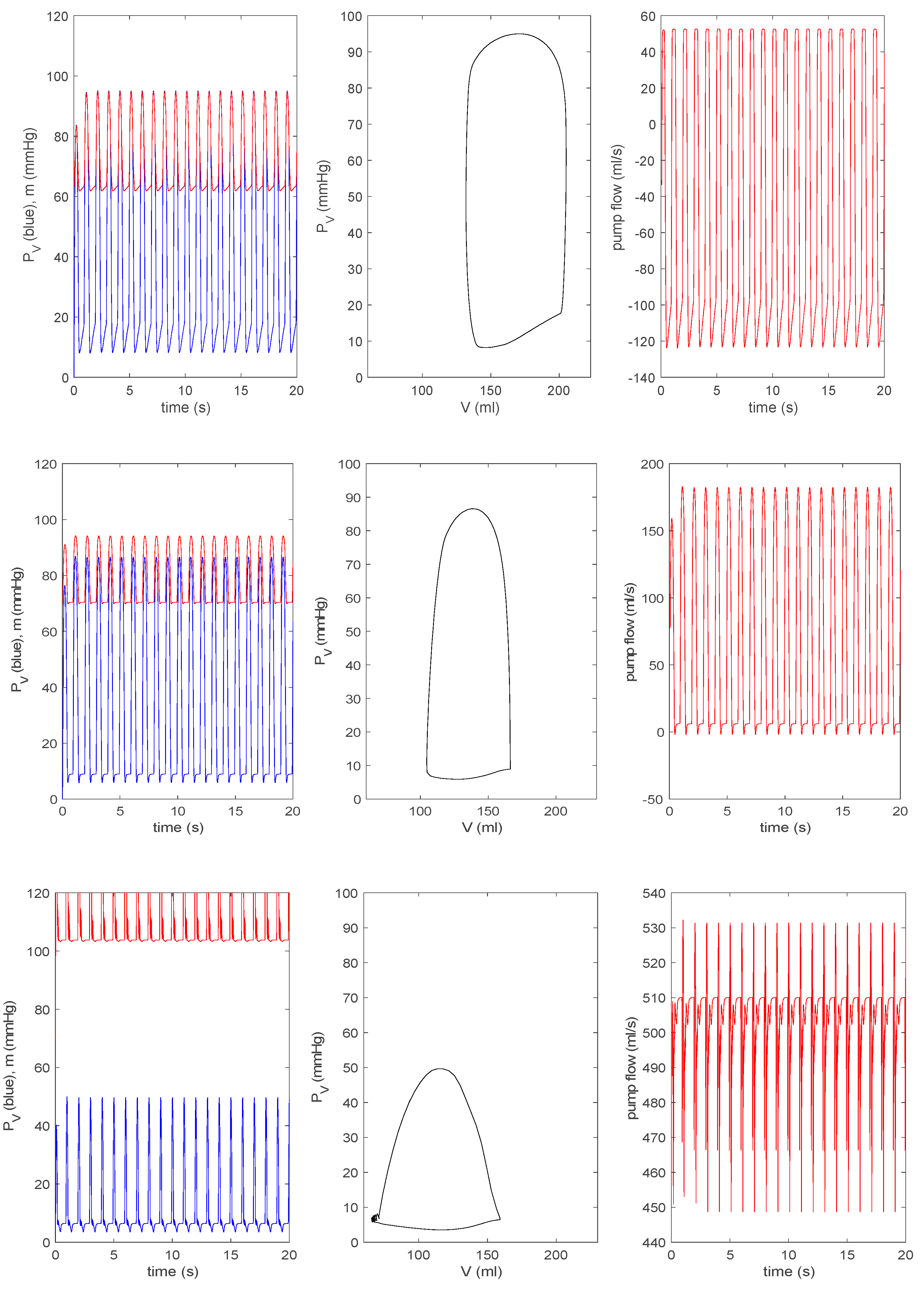
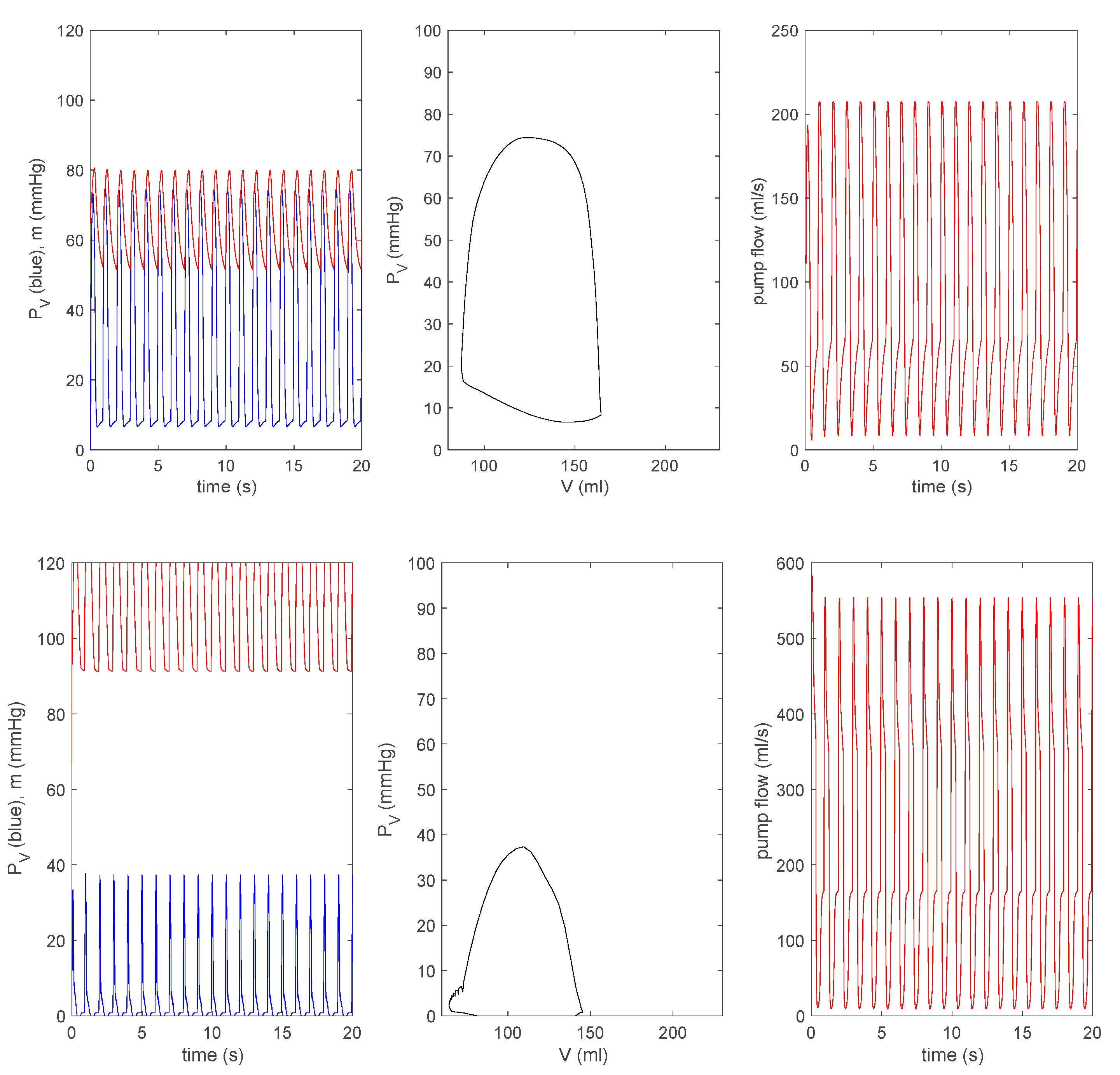
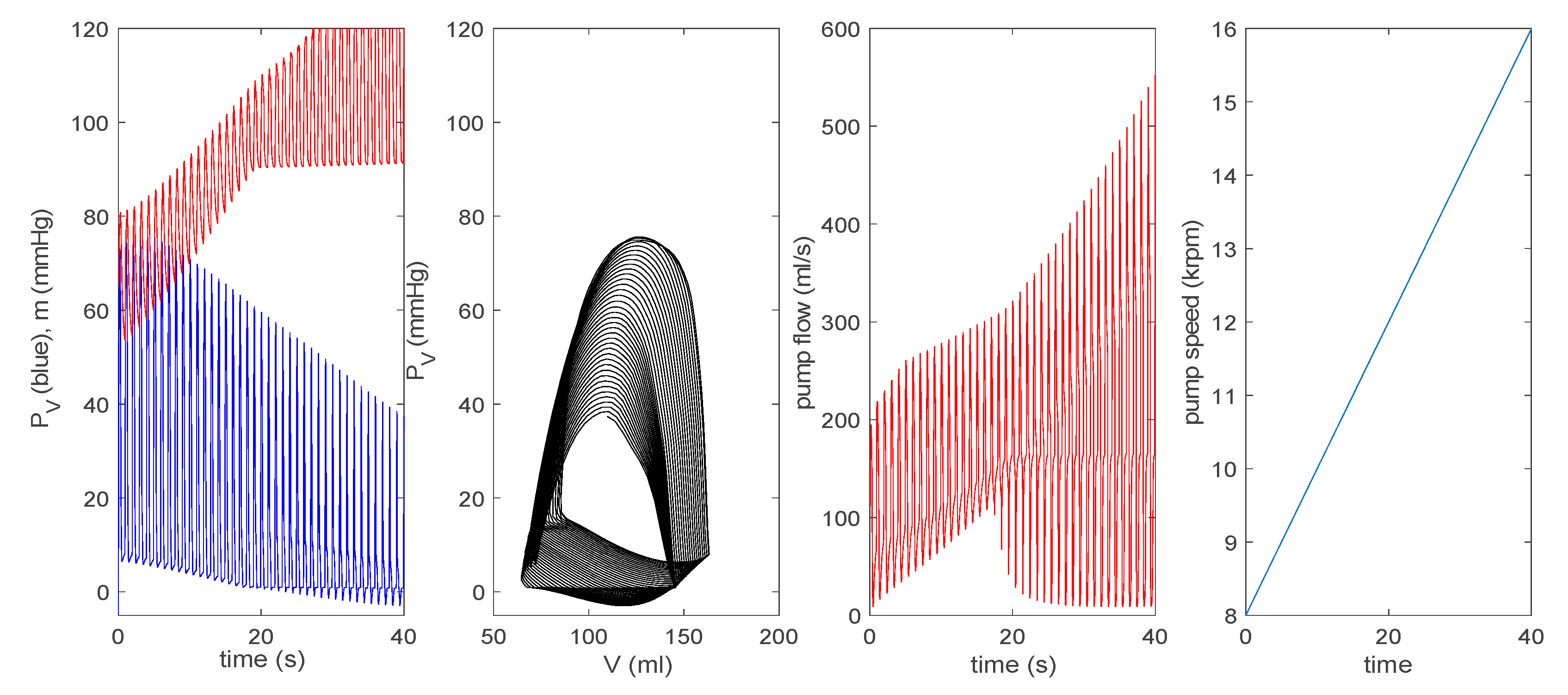
3.3.1. Effect of a Pump on Dilated Cardiomyopathy in Basic Model
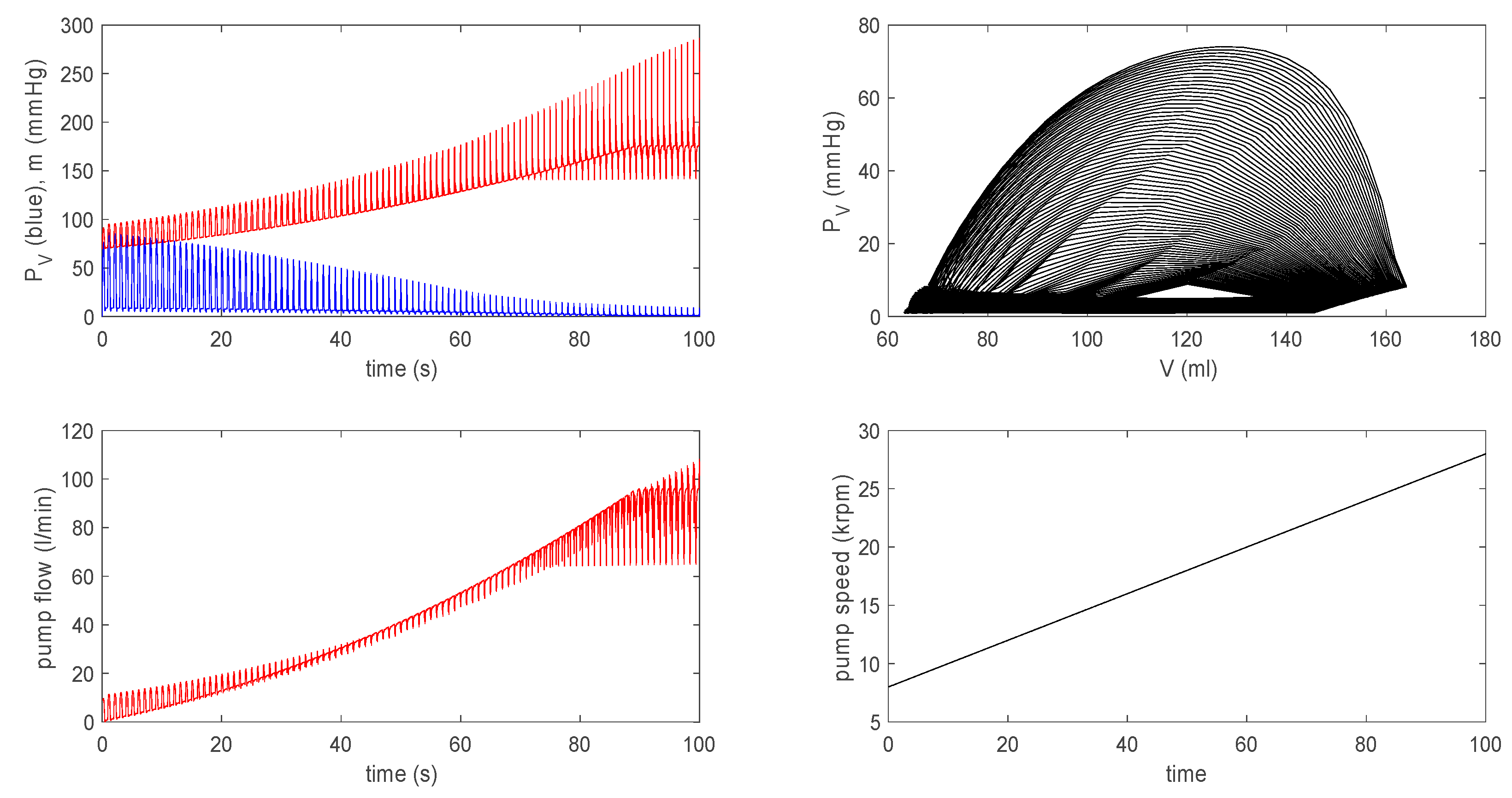
3.3.2. Effect of a Pump on Dilated Cardiomyopathy in Extended Model
3.4. Summary
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Haken, H. Information and Self-Organization: A Macroscopic Approach to Complex Systems; Springer Series in Synergetics; Springer: Berlin, Heidelberg, 2006. [Google Scholar]
- Wright, T.; Twaddle, J.; Humphries, C.; Hayes, S.; Kim, E. Variability and degradation of self-organization in self-sustained oscillators. Math. Biosci. 2016, 273, 57–69. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, F.H.; Russell, S.D. HeartMate® II continuous-flow left ventricular assist system. Expert Rev. Med. Devices 2011, 8, 811–821. [Google Scholar] [CrossRef] [PubMed]
- Tuzun, E.; Roberts, K.; Cohn, W.E.; Sargin, M.; Gemmato, C.J.; Radovancevic, B.; Frazier, O.H. In vivo evaluation of the HeartWare centrifugal ventricular assist device. Tex. Heart Inst. J. 2007, 34, 406–411. [Google Scholar]
- Capoccia, M. Development and Characterization of the Arterial Windkessel and Its Role during Left Ventricular Assist Device Assistance. Artif. Organs 2015, 39, 138–153. [Google Scholar] [CrossRef] [Green Version]
- Capoccia, M.; Marconi, S.; Singh, S.A.; Pisanelli, D.M.; De Lazzari, C. Simulation as a preoperative planning approach in advanced heart failure patients: A retrospective clinical analysis. Biomed. Eng. Online 2018, 17, 52. [Google Scholar] [CrossRef]
- Ferrari, G.; Di Molfetta, A.; Zieliñski, K.; Fresiello, L. Circulatory modelling as a clinical decision support and an educational tool. Biomed. Data J. 2015, 1, 45–50. [Google Scholar] [CrossRef] [Green Version]
- Griffith, B.P.; Kormos, R.L.; Borovetz, H.S.; Litwak, K.; Antaki, J.F.; Poirier, V.L.; Butler, K.C. HeartMate II left ventricular assist system: From concept to first clinical use. Ann. Thorac. Surg. 2001, 71, 116–120. [Google Scholar] [CrossRef]
- Giridharan, G.A.; Skliar, M.; Olsen, D.B.; Pantalos, G.M. Modeling and control of a brushless DC axial flow ventricular assist device. Am. Soc. Artif. Intern. Organs (ASAIO) J. 2001, 48, 272–289. [Google Scholar] [CrossRef]
- Moazami, N.; Fukamachi, K.; Kobayashi, M.; Smedira, N.G.; Hoercher, K.J.; Massiello, A.; Lee, S.J.; Horvath, D.J.; Starling, R.C. Axial and centrifugal continuous-flow rotary pumps: A translation from pump mechanics to clinical practice. J. Heart Lung Transplant. 2013, 32, 1–11. [Google Scholar] [CrossRef]
- Casas, B.; Lantz, J.; Viola, F.; Cedersund, G.; Bolger, A.F.; Carlhäll, C.J.; Karlsson, M.; Ebbers, T. Bridging the gap between measurements and modelling: A cardiovascular functional avatar. Sci. Rep. 2017, 7, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Suga, H.; Sagawa, K. Instantaneous pressure-volume relationships and their ratio in the excised, supported canine left ventricle. Circ. Res. 1974, 35, 117–126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Broomé, M.; Maksuti, E.; Bjällmark, A.; Frenckner, B.; Janerot-Sjöberg, B. Closed-loop real-time simulation model of hemodynamics and oxygen transport in the cardiovascular system. Biomed. Eng. Online 2013, 12, 69. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simaan, M.A. Rotary heart assist devices. In Springer Handbook of Automation; Nof, S.Y., Ed.; Springer: Berlin, German, 2009. [Google Scholar]
- Simaan, M.A.; Ferreira, A.; Chen, S.; Antaki, J.F.; Galati, D.G. A dynamical state space representation and performance analysis of feedback-controlled rotary left ventricular assist device. IEEE Trans. Control. Syst. Technol. 2019, 17, 15–28. [Google Scholar] [CrossRef]
- Shi, Y.; Korakianitis, T. Numerical Simulation of Cardiovascular Dynamics with Left Heart Failure and In-series Pulsatile Ventricular Assist Device. Artif. Organs 2006, 30, 929–948. [Google Scholar] [CrossRef] [PubMed]
- Claessens, T.E.; Georgakopoulos, D.; Afanasyeva, M.; Vermeersch, S.J.; Millar, H.D.; Stergiopulos, N.; Westerhof, N.; Verdonck, P.R.; Segers, P. Nonlinear isochrones in murine left ventricular pressure-volume loops: How well does the time-varying elastance concept hold? Am. J. Physiol. Heart Circ. Physiol. 2006, 290, 1474–1483. [Google Scholar] [CrossRef] [Green Version]
- Vandenberghe, S.; Segers, P.; Steendijk, P.; Meyns, B.; Dion, R.A.E.; Antaki, J.F.; Verdonck, P. Modelling Ventricular Function during Cardiac Assist: Does Time-Varying Elastance Work? Am. Soc. Artif. Intern. Organs (ASAIO) J. 2006, 52, 4–8. [Google Scholar] [CrossRef]
- McCormick, M.; Nordsletten, D.A.; Kay, D.; Smith, N.P. Simulating left ventricular fluid-solid mechanics through the cardiac cycle under LVAD support. J. Comput. Phys. 2013, 244, 80–96. [Google Scholar] [CrossRef]
- CircAdapt. Available online: http://www.circadapt.org/publications (accessed on 8 August 2019).
- Bestel, J.; Clément, F.; Sorine, M. A biomechanical model of muscle contraction. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Goos, G., Hartmanis, J., van Leeuwen, J., Eds.; Springer: Berlin, Germany, 2001; pp. 1159–1161. [Google Scholar]
- Sainte-Marie, J.; Chapelle, D.; Cimrman, R.; Sorine, M. Modeling and estimation of the cardiac electromechanical activity. Comput. Struct. 2006, 84, 1743–1759. [Google Scholar] [CrossRef] [Green Version]
- Bestel, J. Modèle diffréntiel de la contraction musculaire contrôlée: Application au système cardiovasculaire. Ph.D. Thesis, Université Paris 9, Paris, France, 2000. [Google Scholar]
- FitzHugh, R. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1962, 1, 445–466. [Google Scholar] [CrossRef] [Green Version]
- Knudsen, Z.; Holden, A.; Brindley, J. Qualitative modeling of mechano-electrical feedback in aventricular cell. Bull. Math. Biol. 1997, 6, 115–181. [Google Scholar]
- Tse, G.; Wong, S.T.; Tse, V.; Lee, Y.T.; Lin, H.Y.; Yeo, J.M. Cardiac dynamics: Alternans and arhythmogenesis. J. Arrhythm. 2016, 32, 411–417. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Franz, M.R. Mechano-electrical feedback in ventricular myocardium. Cardiovasc. Res. 1996, 32, 15–24. [Google Scholar] [CrossRef]
- Lab, M.J.; Allen, D.G.; Orchard, C.H. The effects of shortening on myoplasmic calcium concentration and action potential in mammalian ventricular muscle. Circ. Res. 1984, 55, 825–829. [Google Scholar] [CrossRef] [Green Version]
- Collet, A.; Bragard, J.; Dauby, P.C. Temperature, geometry, and bifurcations in the numerical modeling of the cardiac mechano-electric feedback. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 093924. [Google Scholar] [CrossRef]
- Burkhoff, D.; Sugiura, S.; Yue, D.T.; Sagawa, K. Contractility-dependent curvilinearity of endsystolic pressure-volume relations. Am. J. Physiol. Heart Circ. Physiol. 1987, 252, 1218–1227. [Google Scholar] [CrossRef] [Green Version]
- Scardulla, F.; Agnese, V.; Romano, G.; Di Gesaro, G.; Sciacca, S.; Bellavia, D.; Clemenza, F.; Pilato, M.; Pasta, S. Modeling right ventricle failure after continuous flow left ventricular assist device: A biventricular finite-element and lumped-parameter analysis. Cardiovasc. Eng. Technol. 2018, 9, 427–437. [Google Scholar] [CrossRef]





| Variable | Physiological Meaning (Unit) |
|---|---|
| Velocity of the contractile element (s−1) | |
| Strain of the contractile element | |
| Active tension of the contractile element (mmHg) | |
| Stiffness of the contractile element (mmHg) | |
| Passive stress (mmHg) | |
| Chemical activity (s−1) | |
| Slow electric variable | |
| Fast electric variable | |
| Left ventricular pressure (mmHg) | |
| Left ventricular volume (mL) | |
| Atrial pressure (mmHg) | |
| Arterial pressure (mmHg) | |
| Aortic pressure (mmHg) | |
| Arterial pressure parameter for the basic model (mmHg) | |
| Aortic (total) flow (mL/s) | |
| Pump flow (mL/s, mL/min) | |
| Pump parameter (1 for pump, 0 for no pump) |
| Parameter | Value | Physiological Meaning |
|---|---|---|
| mmHg s/mL | Aortic valve resistance | |
| mmHg s/mL | Mitral valve resistance | |
| mmHg s/mL | Systemic vascular resistance | |
| mmHg s/mL | Characteristic resistance | |
| Total pump resistance | ||
| ml/mmHg | Left atrial compliance | |
| ml/mmHg | Systemic compliance | |
| ml/mmHg | Aortic compliance | |
| mmHg·s2/mL | Inertance of blood in aorta | |
| mmHg·s2/mL | Total pump inertance | |
| kpa | Maximum sarcomere active tension | |
| kpa | Maximum sarcomere active elastance | |
| kpa | Model parameter for a passive tension | |
| kpa [40 kpa] | Model parameter for a passive tension | |
| s−1, 10 m−1 | Damping parameters in sarcomere | |
| s−1 | Sarcomere microscale oscillation frequency | |
| m·s−2 kpa−1, m·s−2 | Active and passive force parameters | |
| mL−2 | Length-tension parameter | |
| parameter | ||
| mL [144 mL] | Volume parameter | |
| kpa−1, 0 (s·mL)−1 | MEF parameters |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, E.-j.; Capoccia, M. Synergistic Model of Cardiac Function with a Heart Assist Device. Bioengineering 2020, 7, 1. https://doi.org/10.3390/bioengineering7010001
Kim E-j, Capoccia M. Synergistic Model of Cardiac Function with a Heart Assist Device. Bioengineering. 2020; 7(1):1. https://doi.org/10.3390/bioengineering7010001
Chicago/Turabian StyleKim, Eun-jin, and Massimo Capoccia. 2020. "Synergistic Model of Cardiac Function with a Heart Assist Device" Bioengineering 7, no. 1: 1. https://doi.org/10.3390/bioengineering7010001
APA StyleKim, E.-j., & Capoccia, M. (2020). Synergistic Model of Cardiac Function with a Heart Assist Device. Bioengineering, 7(1), 1. https://doi.org/10.3390/bioengineering7010001






