A Proof of Concept Study of Using Machine-Learning in Artificial Aortic Valve Design: From Leaflet Design to Stress Analysis
Abstract
1. Introduction
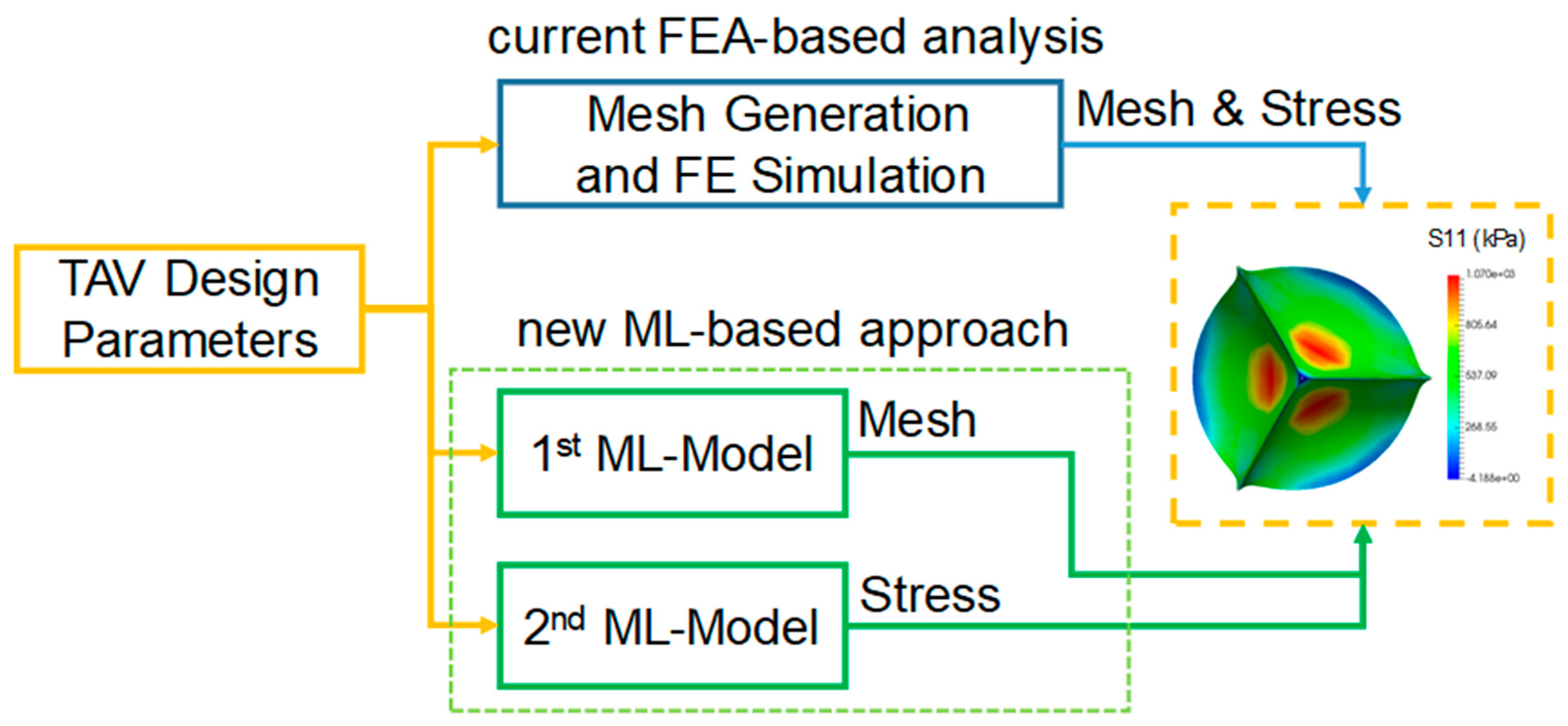
2. Materials and Methods
2.1. Data Preparation
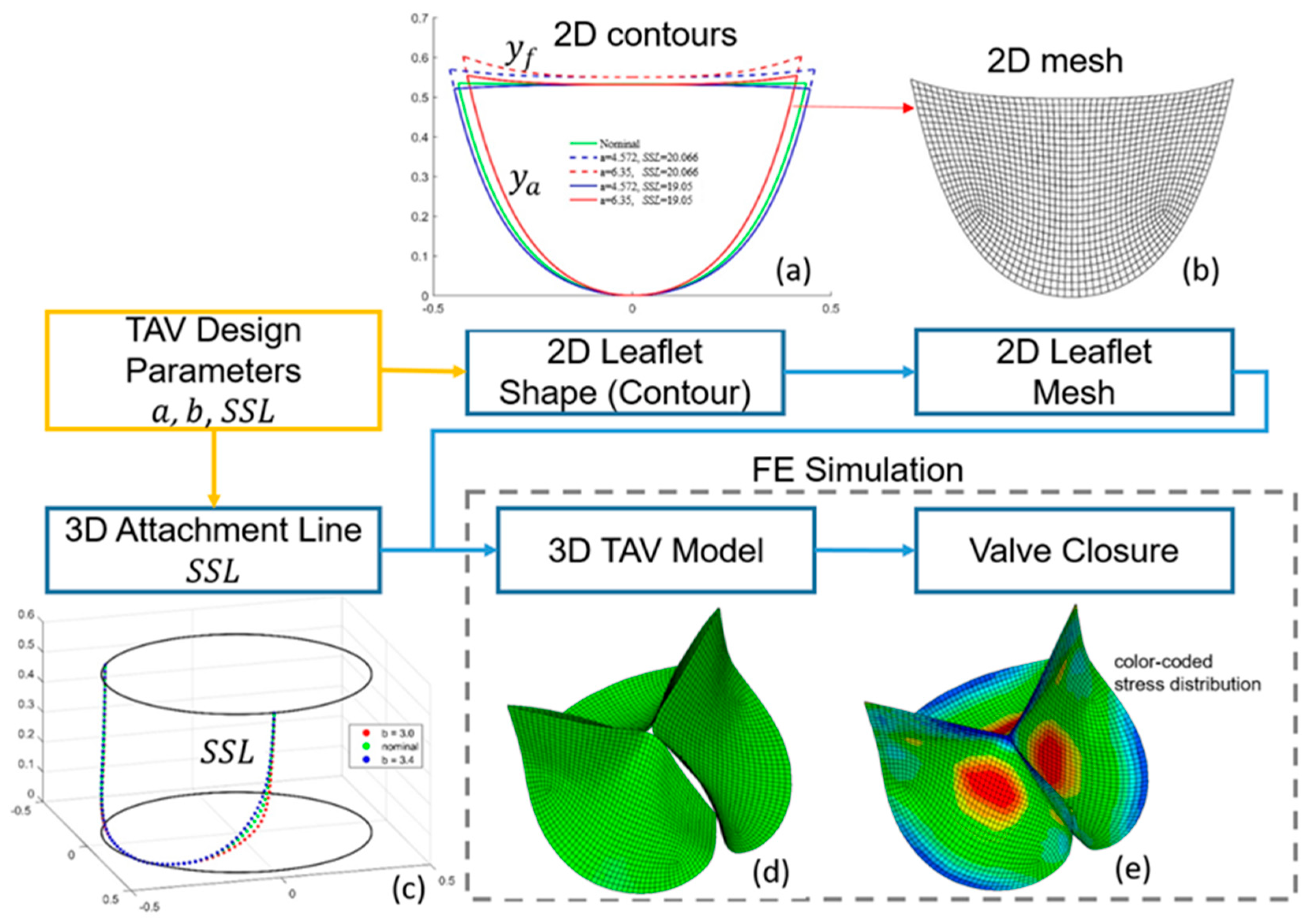
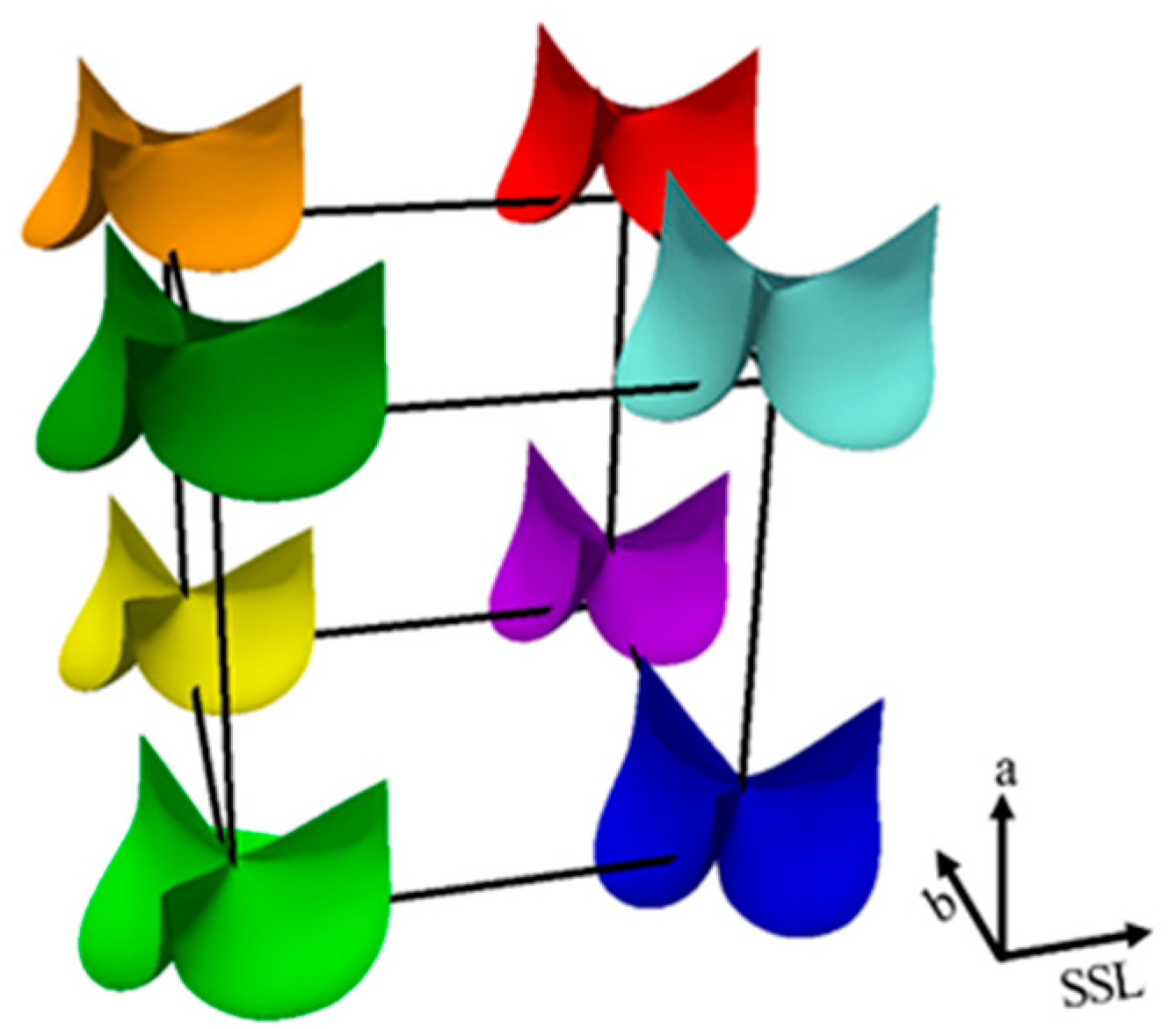
2.1.1. Obtain 2D Leaflet Geometries from Design Parameters
2.1.2. Obtain Deformed 3D Leaflet Geometries and Stress Distributions from FE Simulations
2.2. The ML-models
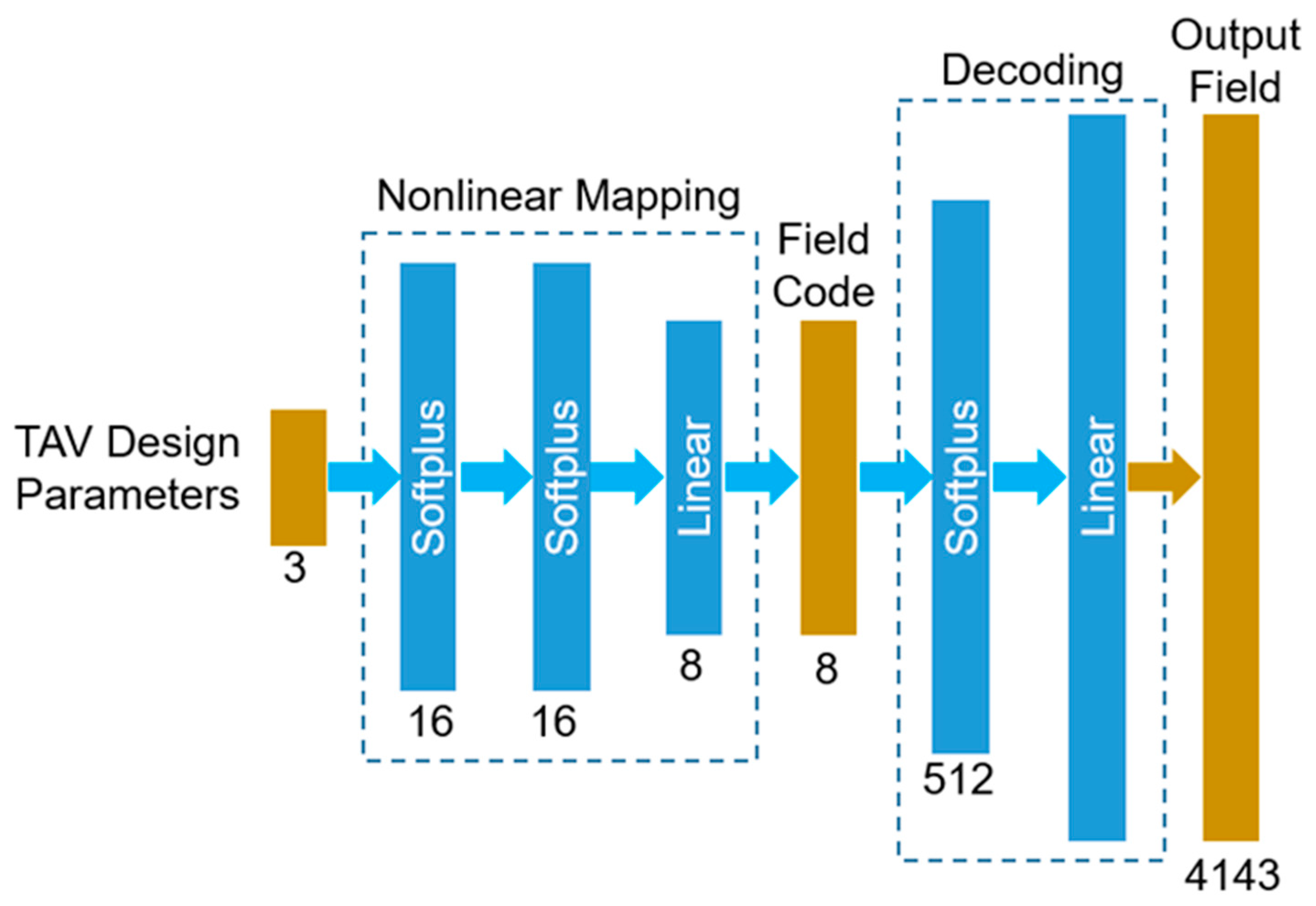
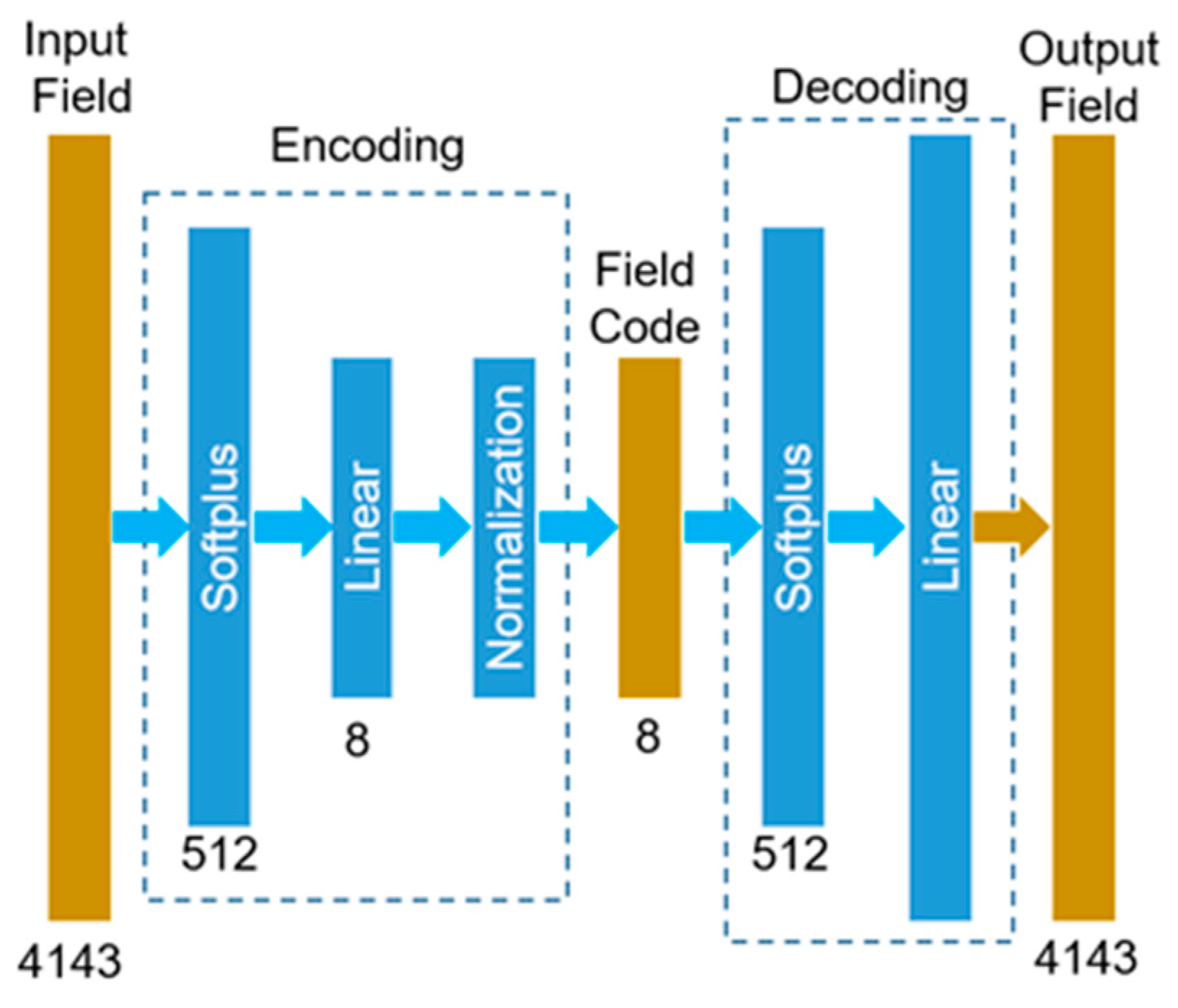
2.2.1. The Autoencoder-based ML-models
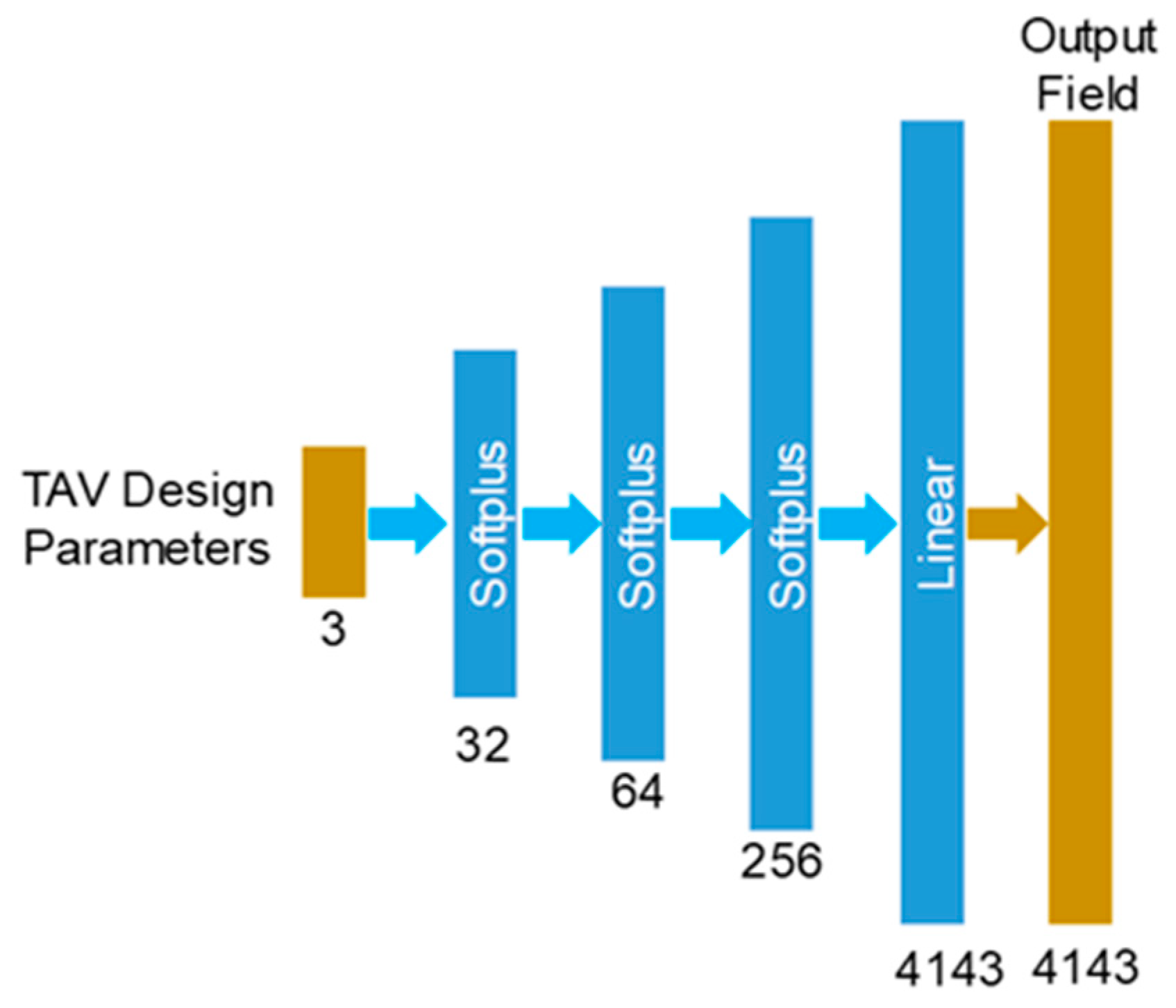
2.2.2. The Direct ML-models
2.2.3. Implementation of the ML-models
2.2.4. Evaluation of the ML-models
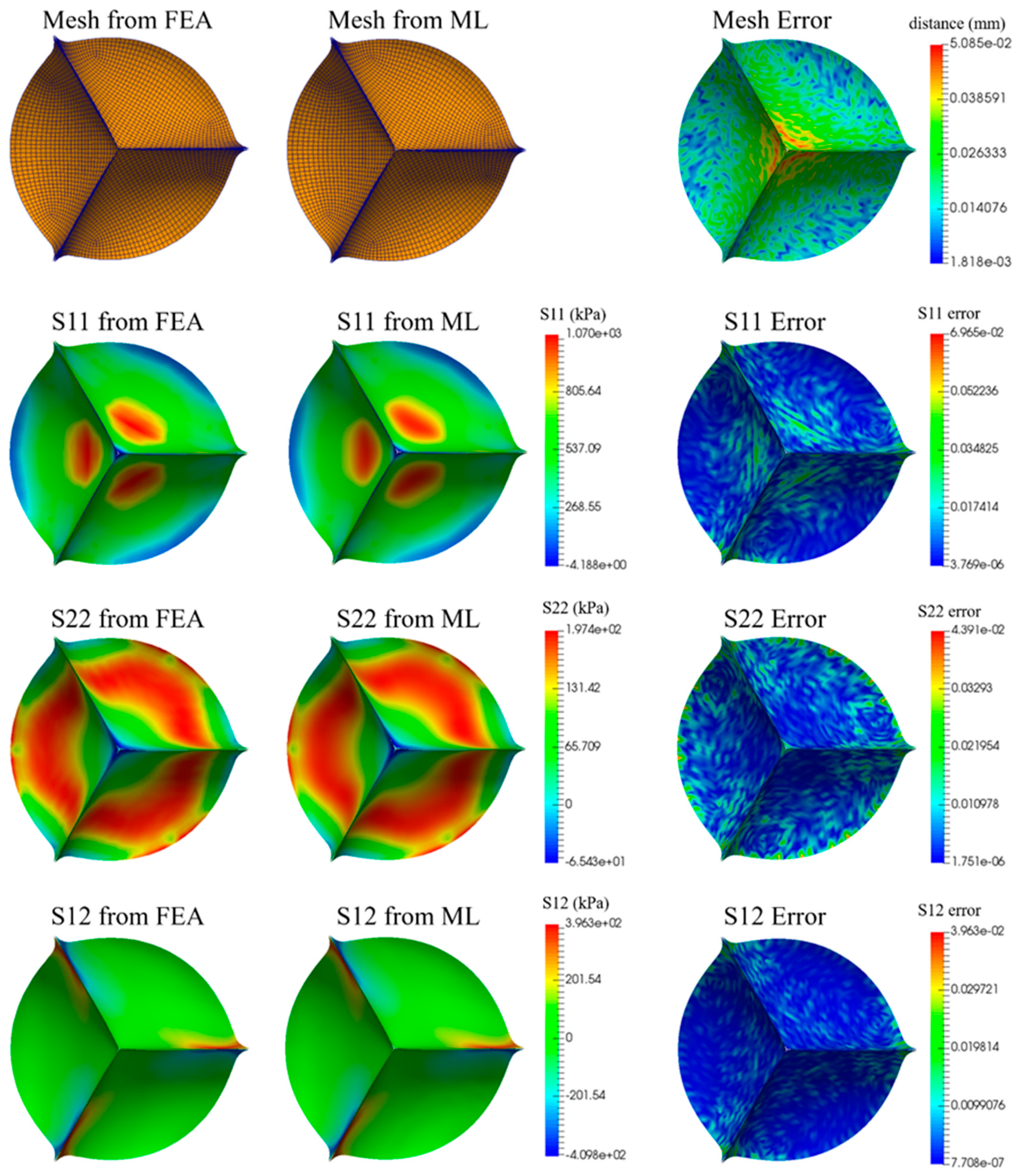
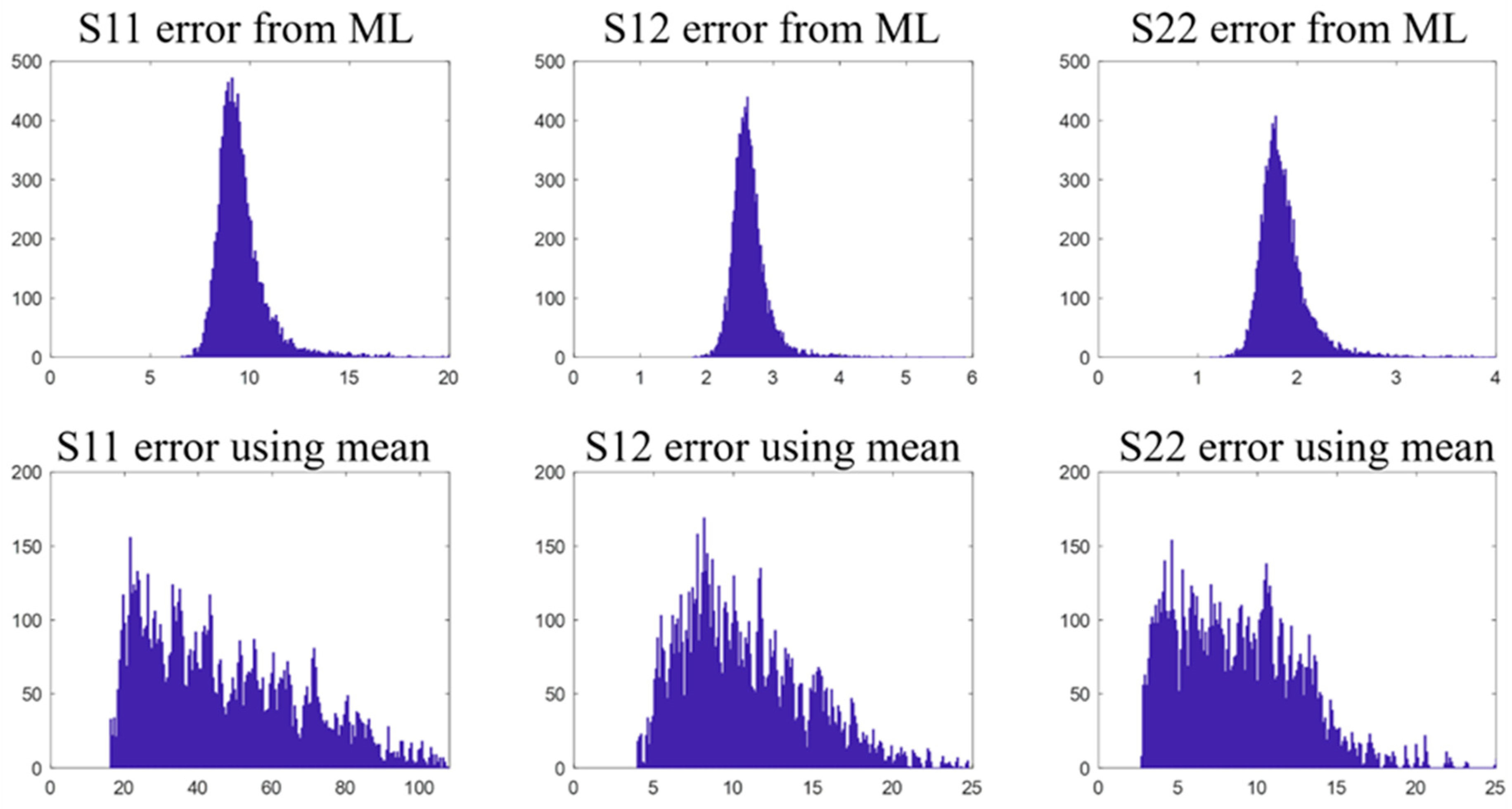
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cribier, A.; Eltchaninoff, H.; Bash, A.; Borenstein, N.; Tron, C.; Bauer, F.; Derumeaux, G.; Anselme, F.; Laborde, F.; Leon, M.B. Percutaneous transcatheter implantation of an aortic valve prosthesis for calcific aortic stenosis: First human case description. Circulation 2002, 106, 3006–3008. [Google Scholar] [CrossRef] [PubMed]
- Barbanti, M.; Webb, J.G.; Gilard, M.; Capodanno, D.; Tamburino, C. Transcatheter aortic valve implantation in 2017: State of the art. EuroIntervention 2017, 13, AA11–AA21. [Google Scholar] [CrossRef] [PubMed]
- Leon, M.B.; Smith, C.R.; Mack, M.; Miller, D.C.; Moses, J.W.; Svensson, L.G.; Tuzcu, E.M.; Webb, J.G.; Fontana, G.P.; Makkar, R.R.; et al. Transcatheter aortic-valve implantation for aortic stenosis in patients who cannot undergo surgery. N. Engl. J. Med. 2010, 363, 1597–1607. [Google Scholar] [CrossRef]
- USFDA. FDA Approves Expanded Indication for Two Transcatheter Heart Valves for Patients at Intermediate Risk for Death or Complications Associated with Open-Heart Surgery; FDA: White Oak, MD, USA, 2016. [Google Scholar]
- Bourantas, C.V.; Farooq, V.; Onuma, Y.; Piazza, N.; Van Mieghem, N.M.; Serruys, P.W. Transcatheter aortic valve implantation: New developments and upcoming clinical trials. EuroIntervention 2012, 8, 617–627. [Google Scholar] [CrossRef] [PubMed]
- De Backer, O.; Piazza, N.; Banai, S.; Lutter, G.; Maisano, F.; Herrmann, H.C.; Franzen, O.W.; Sondergaard, L. Percutaneous transcatheter mitral valve replacement: An overview of devices in preclinical and early clinical evaluation. Circ. Cardiovasc. Interv. 2014, 7, 400–409. [Google Scholar] [CrossRef] [PubMed]
- Mack, M.J.; Leon, M.B.; Thourani, V.H.; Makkar, R.; Kodali, S.K.; Russo, M.; Kapadia, S.R.; Malaisrie, S.C.; Cohen, D.J.; Pibarot, P.; et al. Transcatheter aortic-valve replacement with a balloon-expandable valve in low-risk patients. N. Engl. J. Med. 2019, 380, 1695–1705. [Google Scholar] [CrossRef]
- Popma, J.J.; Deeb, G.M.; Yakubov, S.J.; Mumtaz, M.; Gada, H.; O’Hair, D.; Bajwa, T.; Heiser, J.C.; Merhi, W.; Kleiman, N.S.; et al. Transcatheter aortic-valve replacement with a self-expanding valve in low-risk patients. N. Engl. J. Med. 2019, 380, 1706–1715. [Google Scholar] [CrossRef]
- Bourantas, C.V.; Modolo, R.; Baumbach, A.; Sondergaard, L.; Prendergast, B.D.; Ozkor, M.; Kennon, S.; Mathur, A.; Mullen, M.J.; Serruys, P.W. The evolution of device technology in transcatheter aortic valve implantation. EuroIntervention 2019, 14, e1826–e1833. [Google Scholar] [CrossRef]
- Caballero, A.; Sulejmani, F.; Martin, C.; Pham, T.; Sun, W. Evaluation of transcatheter heart valve biomaterials: Biomechanical characterization of bovine and porcine pericardium. J. Mech. Behav. Biomed. Mater. 2017, 75, 486–494. [Google Scholar] [CrossRef]
- Martin, C.; Sun, W. Fatigue damage of collagenous tissues: Experiment, modeling and simulation studies. J. Long Term Eff. Med. Implant. 2015, 25, 55–73. [Google Scholar] [CrossRef]
- Martin, C.; Sun, W. Comparison of transcatheter aortic valve and surgical bioprosthetic valve durability: A fatigue simulation study. J. Biomech. 2015, 48, 3026–3034. [Google Scholar] [CrossRef] [PubMed]
- ISO5840-3. Cardiovascular Implants—Cardiac Valve Prostheses—Part. 3: Heart Valve Substitutes Implanted by Transcatheter Techniques; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- Gunning, P.S.; Saikrishnan, N.; McNamara, L.M.; Yoganathan, A.P. An in vitro evaluation of the impact of eccentric deployment on transcatheter aortic valve hemodynamics. Ann. Biomed. Eng. 2014, 42, 1195–1206. [Google Scholar] [CrossRef] [PubMed]
- Gunning, P.S.; Saikrishnan, N.; Yoganathan, A.P.; McNamara, L.M. Total ellipse of the heart valve: The impact of eccentric stent distortion on the regional dynamic deformation of pericardial tissue leaflets of a transcatheter aortic valve replacement. J. R. Soc. Interface 2015, 12, 20150737. [Google Scholar] [CrossRef] [PubMed]
- Midha, P.A.; Raghav, V.; Condado, J.F.; Okafor, I.U.; Lerakis, S.; Thourani, V.H.; Babaliaros, V.; Yoganathan, A.P. Valve type, size, and deployment location affect hemodynamics in an in vitro valve-in-valve model. JACC Cardiovasc. Interv. 2016, 9, 1618–1628. [Google Scholar] [CrossRef]
- Midha, P.A.; Raghav, V.; Sharma, R.; Condado, J.F.; Okafor, I.U.; Rami, T.; Kumar, G.; Thourani, V.H.; Jilaihawi, H.; Babaliaros, V.; et al. The fluid mechanics of transcatheter heart valve leaflet thrombosis in the neosinus. Circulation 2017, 136, 1598–1609. [Google Scholar] [CrossRef]
- Eltchaninoff, H.; Nusimovici-Avadis, D.; Babaliaros, V.; Spenser, B.; Felsen, B.; Cribier, A. Five month study of percutaneous heart valves in the systemic circulation of sheep using a novel model of aortic insufficiency. EuroIntervention 2006, 1, 438–444. [Google Scholar]
- Sacks, M.S.; Merryman, W.D.; Schmidt, D.E. On the biomechanics of heart valve function. J. Biomech. 2009, 42, 1804–1824. [Google Scholar] [CrossRef]
- Sacks, M.S.; Yoganathan, A.P. Heart valve function: A biomechanical perspective. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 1369–1391. [Google Scholar] [CrossRef]
- Zakerzadeh, R.; Hsu, M.C.; Sacks, M.S. Computational methods for the aortic heart valve and its replacements. Expert Rev. Med. Devices 2017, 14, 849–866. [Google Scholar] [CrossRef]
- Grande-Allen, K.J.; Cochran, R.P.; Reinhall, P.G.; Kunzelman, K.S. Re-creation of sinuses is important for sparing the aortic valve: A finite element study. J. Thorac. Cardiovasc. Surg. 2000, 119, 753–763. [Google Scholar] [CrossRef]
- Grande-Allen, K.J.; Cochran, R.P.; Reinhall, P.G.; Kunzelman, K.S. Mechanisms of aortic valve incompetence: Finite-element modeling of Marfan syndrome. J. Thorac. Cardiovasc. Surg. 2001, 122, 946–954. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Grande-Allen, K.J.; Cochran, R.P.; Reinhall, P.G.; Kunzelman, K.S. Finite-element analysis of aortic valve-sparing: Influence of graft shape and stiffness. IEEE Trans. Biomed. Eng. 2001, 48, 647–659. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, A.; Pouch, A.M.; Lai, E.; Lesicko, J.; Yushkevich, P.A.; Gorman, J.H., III; Gorman, R.C.; Sacks, M.S. In-vivo heterogeneous functional and residual strains in human aortic valve leaflets. J. Biomech. 2016, 49, 2481–2490. [Google Scholar] [CrossRef] [PubMed]
- Stella, J.A.; Sacks, M.S. On the biaxial mechanical properties of the layers of the aortic valve leaflet. J. Biomech. Eng. 2007, 129, 757–766. [Google Scholar] [CrossRef] [PubMed]
- Stella, J.A.; Liao, J.; Sacks, M.S. Time-dependent biaxial mechanical behavior of the aortic heart valve leaflet. J. Biomech. 2007, 40, 3169–3177. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Sacks, M.S.; Sellaro, T.L.; Slaughter, W.S.; Scott, M.J. Biaxial mechanical response of bioprosthetic heart valve biomaterials to high in-plane shear. J. Biomech. Eng. 2003, 125, 372–380. [Google Scholar] [CrossRef]
- Sacks, M.S.; Sun, W. Multiaxial mechanical behavior of biological materials. Annu. Rev. Biomed. Eng. 2003, 5, 251–284. [Google Scholar] [CrossRef]
- Sun, W.; Li, K.; Sirois, E. Simulated elliptical bioprosthetic valve deformation: Implications for asymmetric transcatheter valve deployment. J. Biomech. 2010, 43, 3085–3090. [Google Scholar] [CrossRef]
- Li, K.; Sun, W. Simulated thin pericardial bioprosthetic valve leaflet deformation under static pressure-only loading conditions: Implications for percutaneous valves. Ann. Biomed. Eng. 2010, 38, 2690–2701. [Google Scholar] [CrossRef]
- Sun, W.; Abad, A.; Sacks, M.S. Simulated bioprosthetic heart valve deformation under quasi-static loading. J. Biomech. Eng. 2005, 127, 905–914. [Google Scholar] [CrossRef]
- Smuts, A.N.; Blaine, D.C.; Scheffer, C.; Weich, H.; Doubell, A.F.; Dellimore, K.H. Application of finite element analysis to the design of tissue leaflets for a percutaneous aortic valve. J. Mech. Behav. Biomed. Mater. 2010, 4, 85–98. [Google Scholar] [CrossRef] [PubMed]
- Auricchio, F.; Conti, M.; Morganti, S.; Reali, A. Simulation of transcatheter aortic valve implantation: A patient-specific finite element approach. Comput. Methods Biomech. Biomed. Engin. 2013. [Google Scholar] [CrossRef] [PubMed]
- Gunning, P.S.; Vaughan, T.J.; McNamara, L.M. Simulation of self expanding transcatheter aortic valve in a realistic aortic root: Implications of deployment geometry on leaflet deformation. Ann. Biomed. Eng. 2014. [Google Scholar] [CrossRef] [PubMed]
- Morganti, S.; Conti, M.; Aiello, M.; Valentini, A.; Mazzola, A.; Reali, A.; Auricchio, F. Simulation of transcatheter aortic valve implantation through patient-specific finite element analysis: Two clinical cases. J. Biomech. 2014, 47, 2547–2555. [Google Scholar] [CrossRef]
- Abbasi, M.; Azadani, A.N. Leaflet stress and strain distributions following incomplete transcatheter aortic valve expansion. J. Biomech. 2015, 48, 3672–3680. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G.E. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Martin, C.; Sun, W. A machine learning approach as a surrogate of finite element analysis-based inverse method to estimate the zero-pressure geometry of human thoracic aorta. Int. J. Numer. Method Biomed. Eng. 2018, 34, e3103. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Sun, W. A deep learning approach to estimate chemically-treated collagenous tissue nonlinear anisotropic stress-strain responses from microscopy images. Acta Biomater. 2017, 63, 227–235. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Martin, C.; Elefteriades, J.A.; Sun, W. A machine learning approach to investigate the relationship between shape features and numerically predicted risk of ascending aortic aneurysm. Biomech. Model. Mechanobiol. 2017, 16, 1519–1533. [Google Scholar] [CrossRef]
- Liang, L.; Kong, F.; Martin, C.; Pham, T.; Wang, Q.; Duncan, J.; Sun, W. Machine learning-based 3-D geometry reconstruction and modeling of aortic valve deformation using 3-D computed tomography images. Int. J. Numer. Method. Biomed. Eng. 2017, 33. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Liu, M.; Martin, C.; Sun, W. A deep learning approach to estimate stress distribution: A fast and accurate surrogate of finite-element analysis. J. R. Soc. Interface 2018, 15. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Martin, C.; Wang, Q.; Sun, W.; Duncan, J. Estimation of aortic valve leaflets from 3D CT images using local shape dictionaries and linear coding. In Proceedings of the SPIE Medical Imaging, San Diego, CA, USA, 27 February–3 March 2016. [Google Scholar]
- Liu, M.; Liang, L.; Sun, W. Estimation of in vivo constitutive parameters of the aortic wall using a machine learning approach. Comput. Methods Appl. Mech. Eng. 2019, 347, 201–217. [Google Scholar] [CrossRef] [PubMed]
- Travaglino, S.; Murdock, K.; Tran, A.; Martin, C.; Liang, L.; Wang, Y.; Sun, W. Computational optimization study of transcatheter aortic valve leaflet design using porcine and bovine leaflets. J. Biomech. Eng. 2019, 142. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Sun, W. Simulated transcatheter aortic valve deformation: A parametric study on the impact of leaflet geometry on valve peak stress. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e02814. [Google Scholar] [CrossRef] [PubMed]
- Murdock, K.; Martin, C.; Sun, W. Characterization of mechanical properties of pericardium tissue using planar biaxial tension and flexural deformation. J. Mech. Behav. Biomed. Mater. 2018, 77, 148–156. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef]
- Kim, H.; Lu, J.; Sacks, M.S.; Chandran, K.B. Dynamic Simulation Pericardial Bioprosthetic Heart Valve Function. J. Biomech. Eng. 2006, 128, 717–724. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Chollet, F. Keras. Available online: https://keras.io (accessed on 1 October 2018).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. An End-to-End Open Source Machine Learning Platform. Available online: https://www.tensorflow.org/ (accessed on 1 October 2018).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An end-user tool for large-data visualization. In Visualization Handbook; Hansen, C.D., Johnson, C.R., Eds.; Butterworth-Heinemann: Burlington, UK, 2005; pp. 717–731. [Google Scholar]
- Noor, A.K. AI and the future of the machine design. Mech. Eng. 2017, 139, 38–43. [Google Scholar] [CrossRef]
- Meziane, F.; Kobbacy, K.; Vadera, S.; Proudlove, N. Intelligent systems in manufacturing: Current developments and future prospects. Integr. Manuf. Sys. 2000, 11, 218–238. [Google Scholar] [CrossRef]
- Arel, I.; Rose, D.C.; Karnowski, T.P. Deep machine learning—A new frontier in artificial intelligence research. IEEE Comput. Intell. Mag. 2010, 5, 13–18. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Sonoda, S.; Murata, N. Neural network with unbounded activation functions is universal approximator. Appl. Comput. Harmon. Anal. 2017, 43, 233–268. [Google Scholar] [CrossRef]
- Shaham, U.; Cloninger, A.; Coifman, R.R. Provable approximation properties for deep neural networks. Appl. Comput. Harmon. Anal. 2016. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- Tompson, J.; Schlachter, K.; Sprechmann, P.; Perlin, K. Accelerating eulerian fluid simulation with convolutional networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3424–3433. [Google Scholar]
- Hennigh, O. Lat-Net: Compressing lattice boltzmann flow simulations using deep neural networks. arXiv 2017, arXiv:1705.09036. [Google Scholar]
- Guo, X.; Li, W.; Iorio, F. Convolutional neural networks for steady flow approximation. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 481–490. [Google Scholar]
- Miyanawala, T.P.; Jaiman, R.K. An efficient deep learning technique for the navier-stokes equations: Application to unsteady wake flow dynamics. arXiv 2017, arXiv:1710.09099. [Google Scholar]
- Itu, L.; Rapaka, S.; Passerini, T.; Georgescu, B.; Schwemmer, C.; Schoebinger, M.; Flohr, T.; Sharma, P.; Comaniciu, D. A machine-learning approach for computation of fractional flow reserve from coronary computed tomography. J. Appl. Phys. 2016, 121, 42–52. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems—Volume 1, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Regularized evolution for image classifier architecture search. arXiv 2018, arXiv:180201548. [Google Scholar] [CrossRef]
- Xie, S.; Kirillov, A.; Girshick, R.; He, K. Exploring randomly wired neural networks for image recognition. arXiv 2019, arXiv:1904.01569. [Google Scholar]
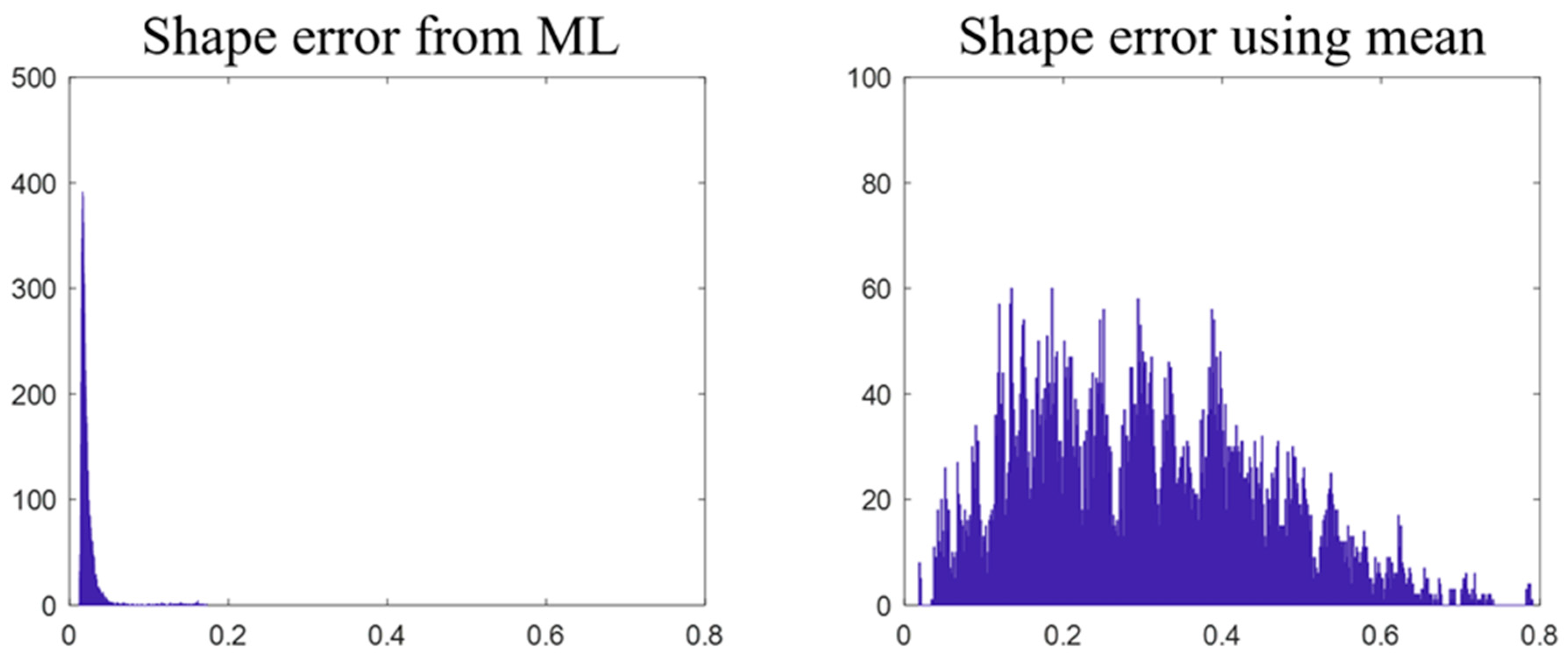
| ρ = 50 | ρ = 70 | ρ = 9 0 | |
|---|---|---|---|
| S11 MeanE (kPa) (1st ML-model-a) | 8.9218 ± 0.7605 | 8.8439 ± 0.7364 | 8.8005 ± 0.7412 |
| S11 MeanE (kPa) (1st ML-model-d) | 9.6913 ± 1.2928 | 9.6809 ± 1.2893 | 9.1142 ± 0.8929 |
| Stress Component | MeanE (kPa) | NMeanE (%) | MaxE (kPa) | NMaxE (%) |
|---|---|---|---|---|
| S11 (1st ML-model-a) | 8.8005 ± 0.7412 | 0.9771 ± 0.1115 | 15.7456 ± 10.7627 | 1.5913 ± 1.0787 |
| S22 (1st ML-model-a) | 1.7251 ± 0.2634 | 0.7068 ± 0.1026 | 4.1948 ± 3.7976 | 1.9873 ± 1.7882 |
| S12 (1st ML-model-a) | 2.5000 ± 0.1944 | 0.3638 ± 0.0350 | 4.3933 ± 3.4736 | 1.2560 ± 0.9766 |
| S11 (1st ML-model-d) | 9.1142 ± 0.8929 | 1.0117 ± 0.1229 | 16.3978 ± 11.2060 | 1.6570 ± 1.1235 |
| S22 (1st ML-model-d) | 1.7809 ± 0.2765 | 0.7295 ± 0.1071 | 4.1396 ± 3.7576 | 1.9622 ± 1.7716 |
| S12 (1st ML-model-d) | 2.5669 ± 0.2020 | 0.3734 ± 0.0358 | 5.3510 ± 4.6305 | 1.5411 ± 1.3590 |
| MeanE (mm) | NMeanE | MaxE (mm) | NMaxE | |
|---|---|---|---|---|
| Mean Value | 0.02164 | 0.2053% | 0.05451 | 0.5171% |
| Standard Deviation | 0.01235 | 0.1174% | 0.02203 | 0.2091% |
| MeanE | NMeanE | MaxE | NMaxE | |
|---|---|---|---|---|
| Mesh | 0.02046 (mm) | 0.1951% | 0.05085 (mm) | 0.4850% |
| Stress S11 | 9.0002 (kPa) | 0.8375% | 43.9637 (kPa) | 4.1070% |
| Stress S22 | 1.6559 (kPa) | 0.6300% | 2.8710 (kPa) | 1.4545% |
| Stress S12 | 2.6341 (kPa) | 0.3267% | 0.9901 (kPa) | 0.2416% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, L.; Sun, B. A Proof of Concept Study of Using Machine-Learning in Artificial Aortic Valve Design: From Leaflet Design to Stress Analysis. Bioengineering 2019, 6, 104. https://doi.org/10.3390/bioengineering6040104
Liang L, Sun B. A Proof of Concept Study of Using Machine-Learning in Artificial Aortic Valve Design: From Leaflet Design to Stress Analysis. Bioengineering. 2019; 6(4):104. https://doi.org/10.3390/bioengineering6040104
Chicago/Turabian StyleLiang, Liang, and Bill Sun. 2019. "A Proof of Concept Study of Using Machine-Learning in Artificial Aortic Valve Design: From Leaflet Design to Stress Analysis" Bioengineering 6, no. 4: 104. https://doi.org/10.3390/bioengineering6040104
APA StyleLiang, L., & Sun, B. (2019). A Proof of Concept Study of Using Machine-Learning in Artificial Aortic Valve Design: From Leaflet Design to Stress Analysis. Bioengineering, 6(4), 104. https://doi.org/10.3390/bioengineering6040104




