Effect of Residual and Transformation Choice on Computational Aspects of Biomechanical Parameter Estimation of Soft Tissues
Abstract
1. Introduction
2. Methods
2.1. Problem Setup
2.2. Constitutive Models
2.2.1. Gasser-Ogden-Holzapfel (GOH) Model
2.2.2. Humphrey Model
2.2.3. Lee–Sacks Model
2.2.4. May-Newman Model
2.3. Parameter Estimation Algorithm
| Algorithm 1: Parameter estimation using Gauss-Newton method with backtracking line search. |
| Data: Observed data and initial guess , , , Result: Parameters that fit the model to observed data by minimizing the functional (11) with the chosen residual (9) or (10) initialization ; ;  |
2.4. Parameter Transformations
3. Results
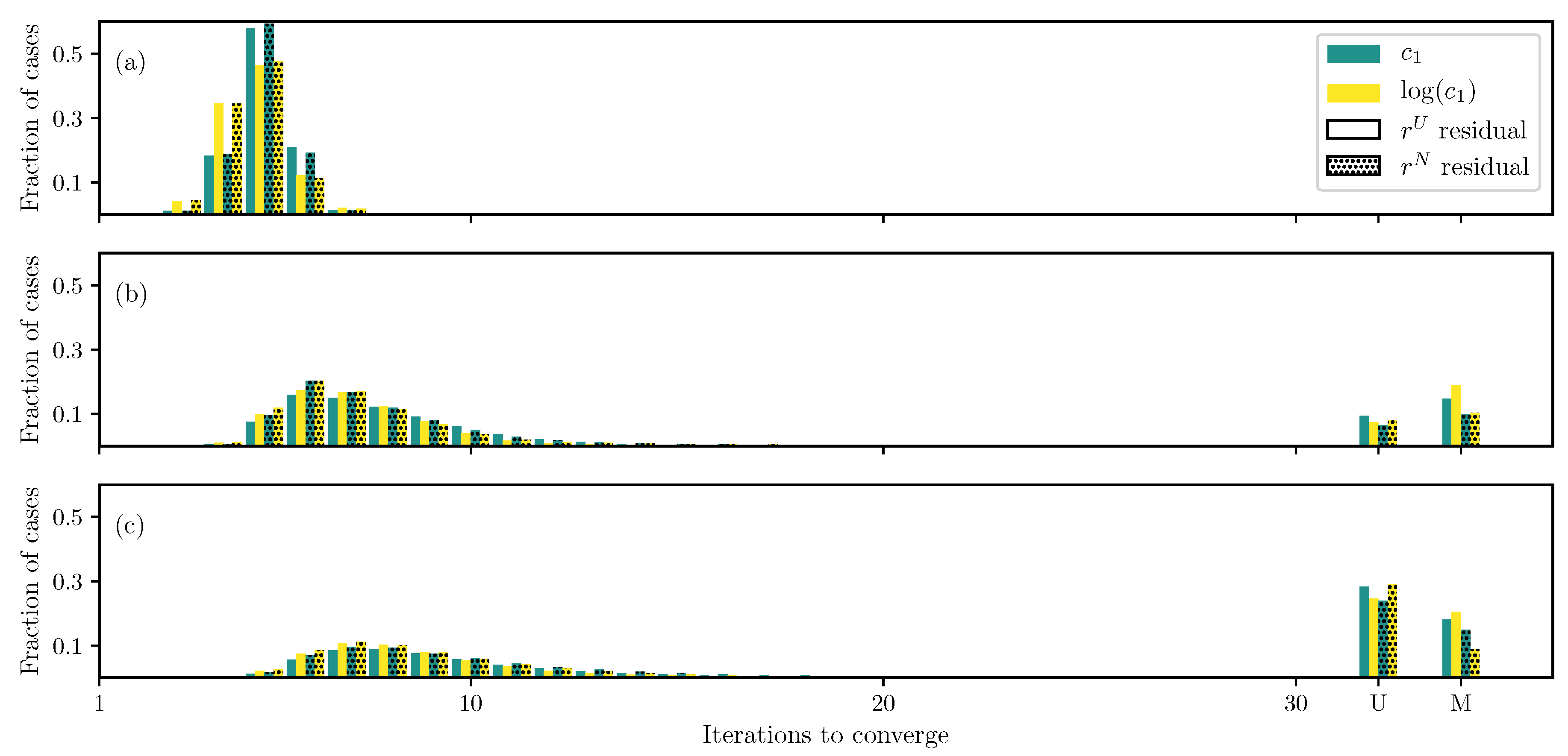
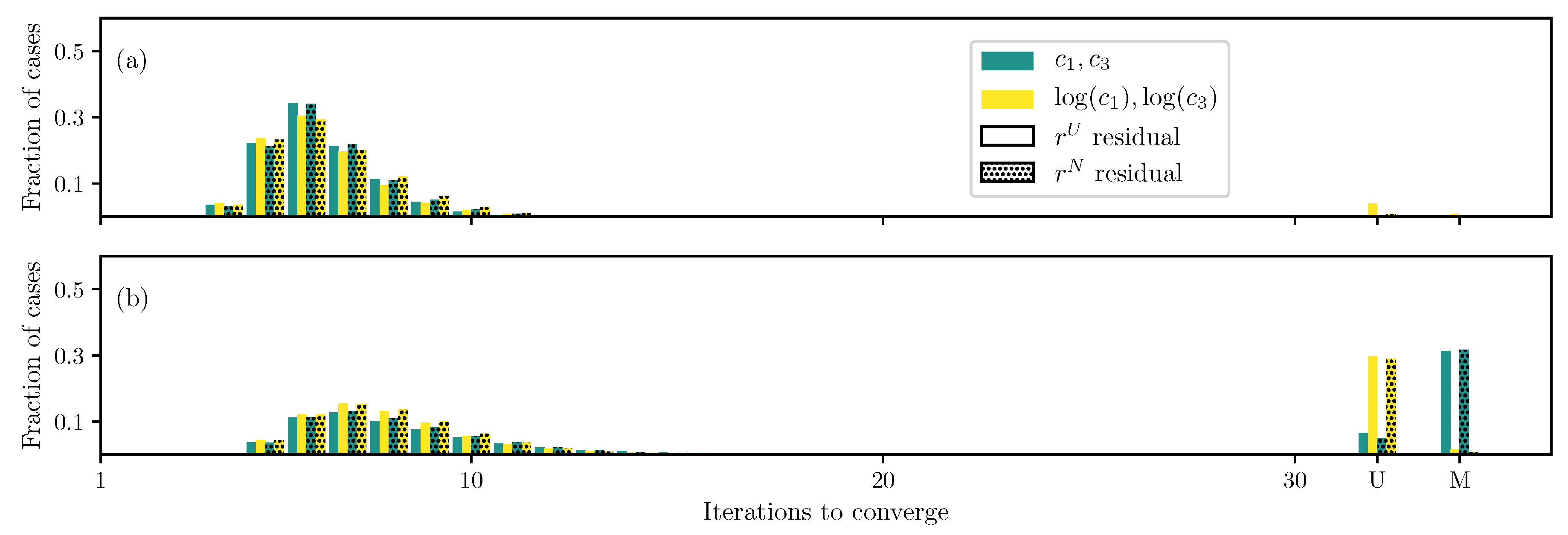
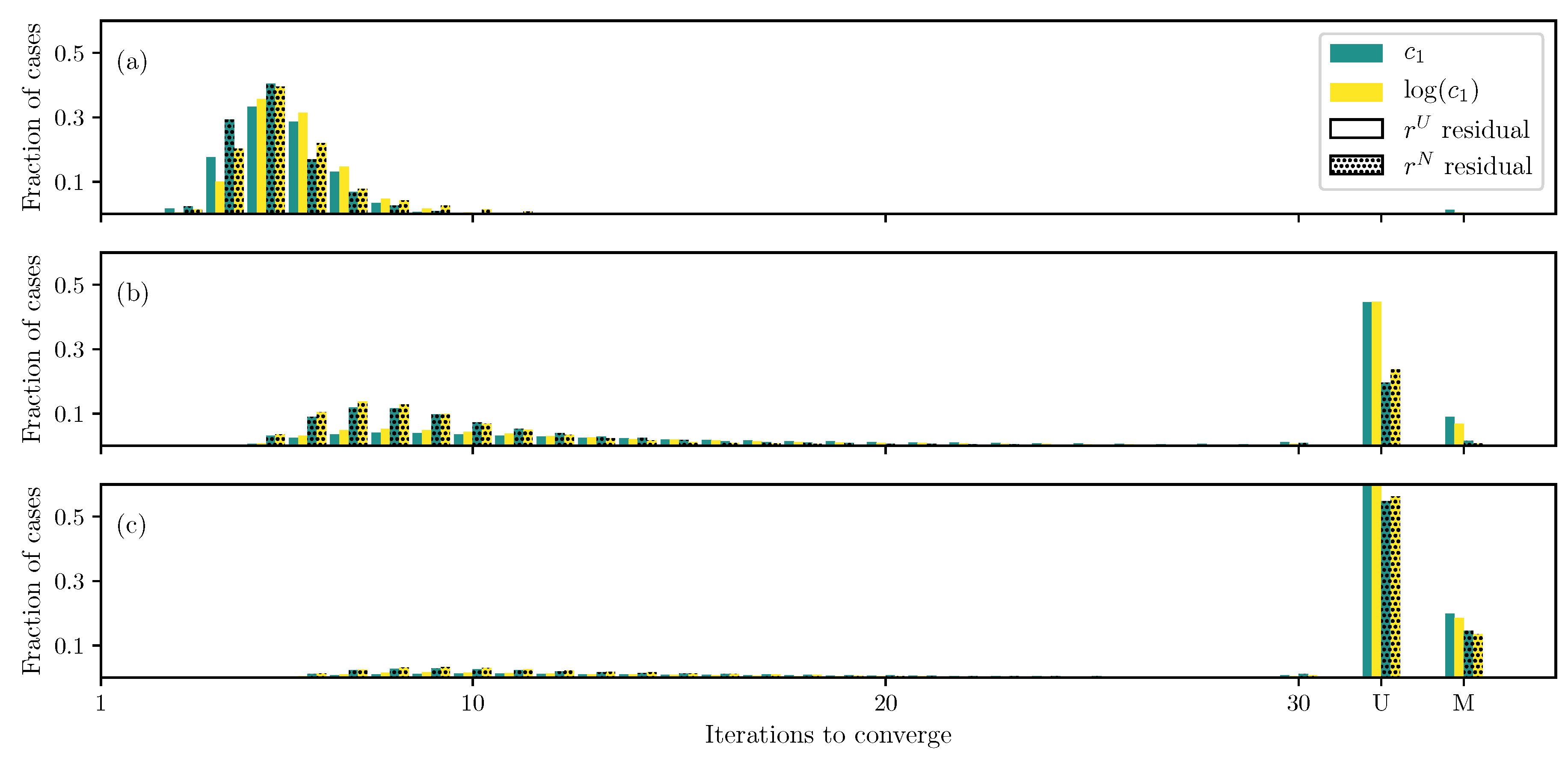
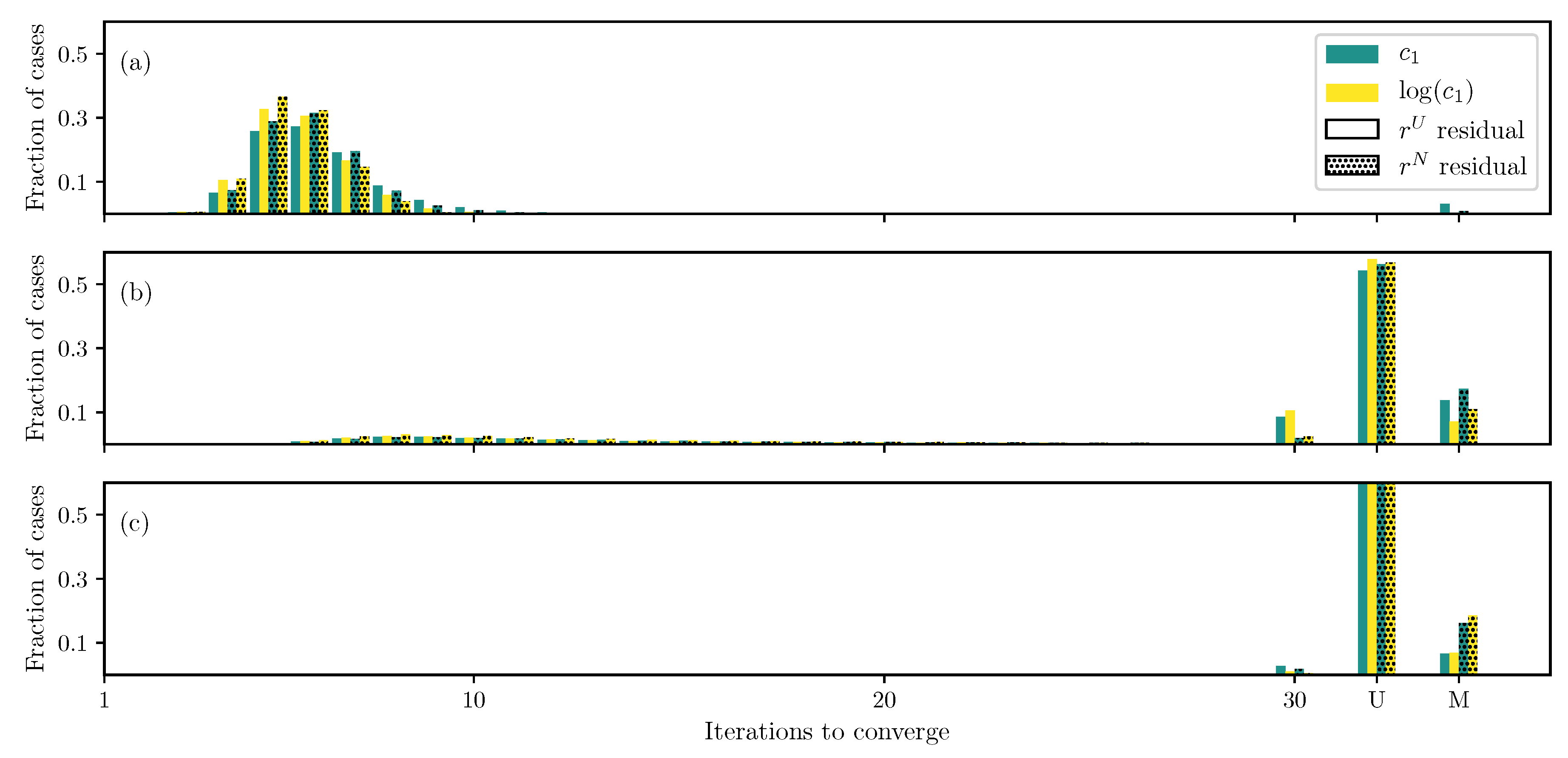
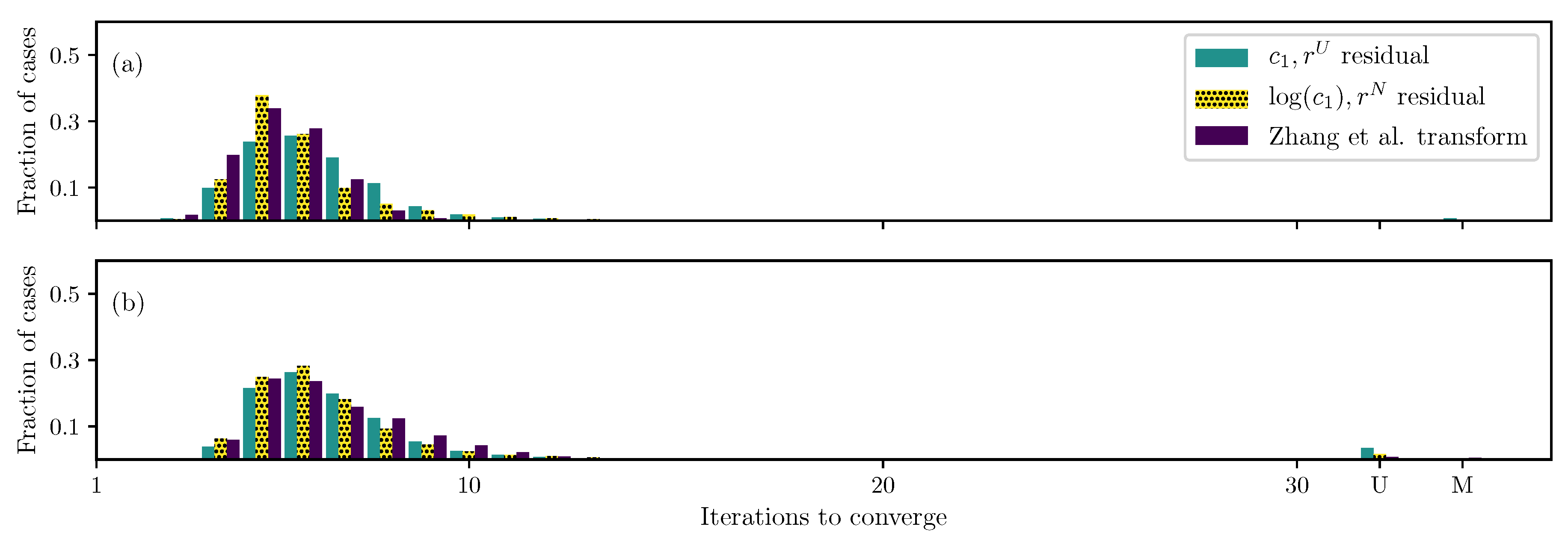
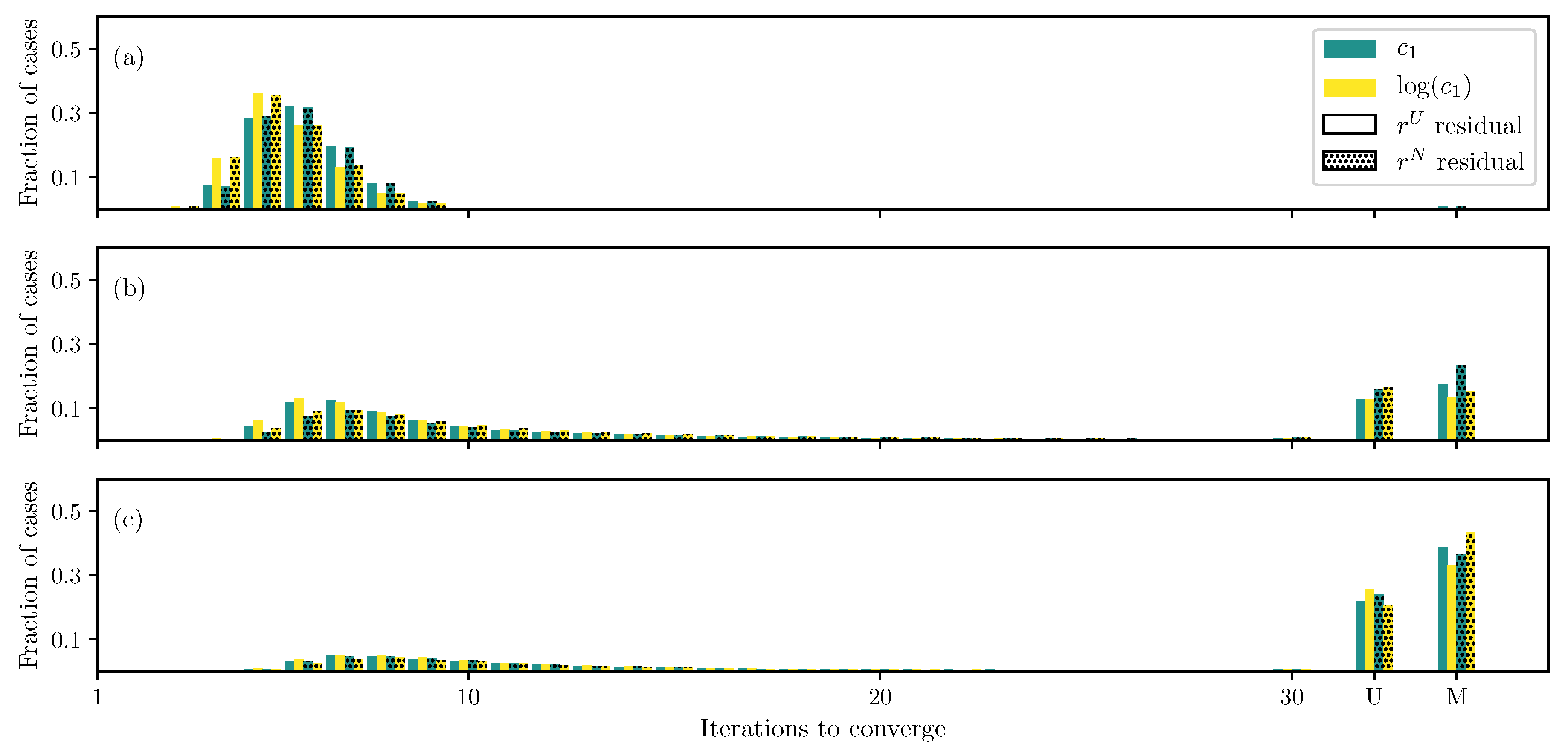
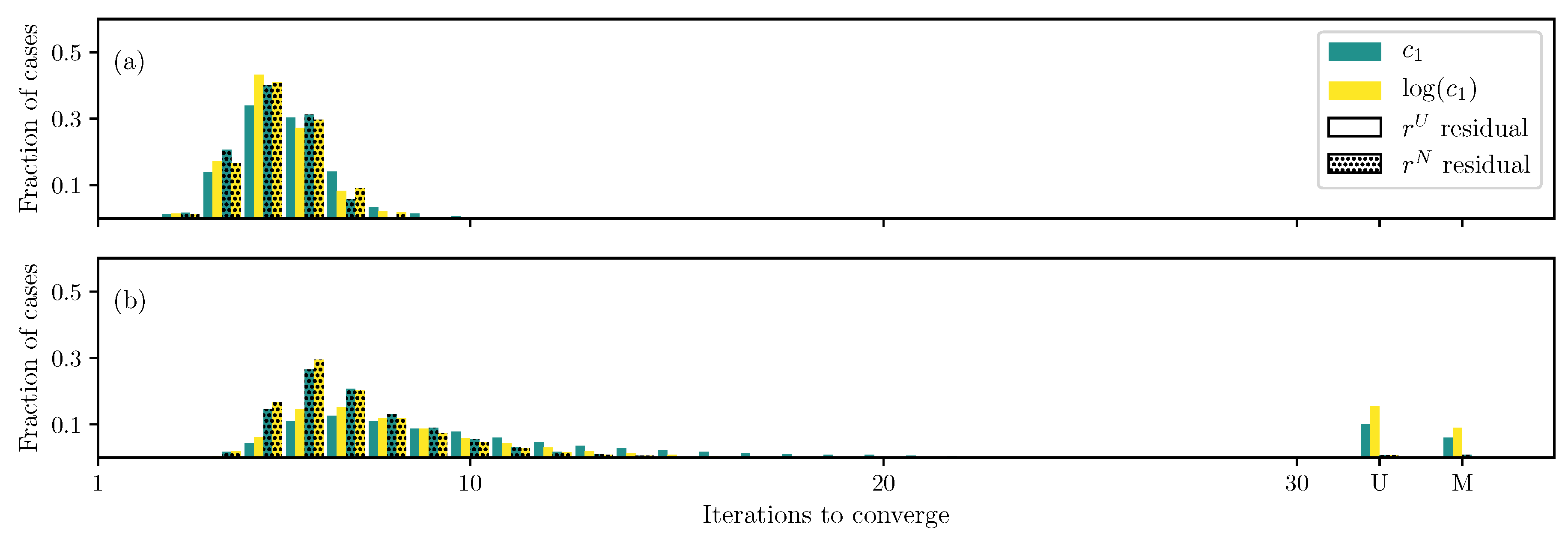
3.1. GOH Model
3.2. Humphrey Model
3.3. Lee–Sacks Model
3.4. May-Newman Model
4. Discussion
4.1. Nonlinear Preconditioning
4.2. Replacing with
4.3. Weighted Residual
4.4. Adding Fiber Angle as an Unknown
4.5. Displacement Controlled versus Force Controlled
4.6. Limitations and Future Work
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Fung, Y.C.; Skalak, R. Biomechanics: Mechanical Properties of Living Tissues; Springer: New York, NY, USA, 1981. [Google Scholar]
- Bersi, M.R.; Bellini, C.; Di Achille, P.; Humphrey, J.D.; Genovese, K.; Avril, S. Novel methodology for characterizing regional variations in the material properties of murine aortas. J. Biomech. Eng. 2016, 138, 071005. [Google Scholar] [CrossRef] [PubMed]
- Avazmohammadi, R.; Li, D.S.; Leahy, T.; Shih, E.; Soares, J.S.; Gorman, J.H.; Gorman, R.C.; Sacks, M.S. An integrated inverse model-experimental approach to determine soft tissue three-dimensional constitutive parameters: Application to post-infarcted myocardium. Biomech. Model. Mechanobiol. 2018, 17, 31–53. [Google Scholar] [CrossRef] [PubMed]
- Potter, S.; Graves, J.; Drach, B.; Leahy, T.; Hammel, C.; Feng, Y.; Baker, A.; Sacks, M.S. A novel small-specimen planar biaxial testing system with full in-plane deformation control. J. Biomech. Eng. 2018, 140, 051001. [Google Scholar] [CrossRef]
- Ross, C.; Laurence, D.; Wu, Y.; Lee, C.H. Biaxial mechanical characterizations of atrioventricular heart valves. JoVE (J. Vis. Exp.) 2019. [Google Scholar] [CrossRef]
- Maurel, W.; Thalmann, D.; Wu, Y.; Thalmann, N.M. Constitutive Modeling. In Biomechanical Models for Soft Tissue Simulation; Springer: Berlin/Heidelberg, Germany, 1998; pp. 79–120. [Google Scholar]
- Ramião, N.G.; Martins, P.S.; Rynkevic, R.; Fernandes, A.A.; Barroso, M.; Santos, D.C. Biomechanical properties of breast tissue, a state-of-the-art review. Biomech. Model. Mechanobiol. 2016, 15, 1307–1323. [Google Scholar] [CrossRef]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Lee, C.H.; Amini, R.; Gorman, R.C.; Gorman, J.H.; Sacks, M.S. An inverse modeling approach for stress estimation in mitral valve anterior leaflet valvuloplasty for in-vivo valvular biomaterial assessment. J. Biomech. 2014, 47, 2055–2063. [Google Scholar] [CrossRef]
- Aggarwal, A.; Sacks, M.S. An inverse modeling approach for semilunar heart valve leaflet mechanics: Exploitation of tissue structure. Biomech. Model. Mechanobiol. 2016, 15, 909–932. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2003; Volume 82. [Google Scholar]
- Aggarwal, A. An improved parameter estimation and comparison for soft tissue constitutive models containing an exponential function. Biomech. Model. Mechanobiol. 2017, 16, 1309–1327. [Google Scholar] [CrossRef]
- Moré, J.J.; Garbow, B.S.; Hillstrom, K.E. User Guide for MINPACK-1. Technical Report, CM-P00068642. 1980. Available online: http://cds.cern.ch/record/126569/files/?ln=en (accessed on 29 October 2019).
- Holzapfel, G.A. Nonlinear Solid Mechanics; Wiley: Chichester, UK, 2000; Volume 24. [Google Scholar]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef]
- Humphrey, J.; Yin, F. A new constitutive formulation for characterizing the mechanical behavior of soft tissues. Biophys. J. 1987, 52, 563–570. [Google Scholar] [CrossRef]
- May-Newman, K.; Yin, F.C.P. A Constitutive Law for Mitral Valve Tissue. J. Biomech. Eng. 1998, 120, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: Cham, Switzerland, 2006. [Google Scholar]
- Zhang, W.; Zakerzadeh, R.; Zhang, W.; Sacks, M.S. A material modeling approach for the effective response of planar soft tissues for efficient computational simulations. J. Mech. Behav. Biomed. Mater. 2019, 89, 168–198. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.C.; Keyes, D.E. Nonlinearly preconditioned inexact Newton algorithms. SIAM J. Sci. Comput. 2002, 24, 183–200. [Google Scholar] [CrossRef]
- Budde, M.; Annese, J. Quantification of anisotropy and fiber orientation in human brain histological sections. Front. Integr. Neurosci. 2013, 7, 3. [Google Scholar] [CrossRef]
- Sacks, M.S.; Smith, D.B.; Hiester, E.D. A small angle light scattering device for planar connective tissue microstructural analysis. Ann. Biomed. Eng. 1997, 25, 678–689. [Google Scholar] [CrossRef]
- Lei, F.; Szeri, A. Inverse analysis of constitutive models: Biological soft tissues. J. Biomech. 2007, 40, 936–940. [Google Scholar] [CrossRef]
- Martínez-Martínez, F.; Rupérez, M.; Martín-Guerrero, J.; Monserrat, C.; Lago, M.; Pareja, E.; Brugger, S.; López-Andújar, R. Estimation of the elastic parameters of human liver biomechanical models by means of medical images and evolutionary computation. Comput. Methods Programs Biomed. 2013, 111, 537–549. [Google Scholar] [CrossRef]
- Chabiniok, R.; Moireau, P.; Lesault, P.F.; Rahmouni, A.; Deux, J.F.; Chapelle, D. Estimation of tissue contractility from cardiac cine-MRI using a biomechanical heart model. Biomech. Model. Mechanobiol. 2012, 11, 609–630. [Google Scholar] [CrossRef]
- Aggarwal, A.; Ferrari, G.; Joyce, E.; Daniels, M.J.; Sainger, R.; Gorman, J.H., III; Gorman, R.; Sacks, M.S. Architectural trends in the human normal and bicuspid aortic valve leaflet and its relevance to valve disease. Ann. Biomed. Eng. 2014, 42, 986–998. [Google Scholar] [CrossRef]
- Nielsen, P.M.; Le Grice, I.J.; Smaill, B.H.; Hunter, P.J. Mathematical model of geometry and fibrous structure of the heart. Am. J. Physiol. Heart Circ. Physiol. 1991, 260, H1365–H1378. [Google Scholar] [CrossRef]
- Li, K.; Ogden, R.W.; Holzapfel, G.A. A discrete fibre dispersion method for excluding fibres under compression in the modelling of fibrous tissues. J. R. Soc. Interface 2018, 15, 20170766. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.c. Biomechanics: Mechanical Properties of Living Tissues; Springer Science & Business Media: Cham, Switzerland, 2013. [Google Scholar]
- Sun, W.; Sacks, M.S. Finite element implementation of a generalized Fung-elastic constitutive model for planar soft tissues. Biomech. Model. Mechanobiol. 2005, 4, 190–199. [Google Scholar] [CrossRef] [PubMed]




| Model | ||||||
|---|---|---|---|---|---|---|
| GOH Equation (2) | 0 to 100 kPa | 5 to 100 kPa | 20 to 100 | 0 to 0.3 | 0 to | − |
| Humphrey Equation (4) | − | 5 to 100 kPa | 1 to 100 | 5 to 100 kPa | 1 to 100 | 0 to |
| Lee–Sacks Equation (5) | 0 to 100 kPa | 5 to 100 kPa | 1 to 100 | 1 to 100 | 0 to 1 | 0 to |
| May-Newman Equation (6) | 0 to 100 kPa | 5 to 100 kPa | 1 to 100 | 1 to 1000 | 0 to | − |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aggarwal, A. Effect of Residual and Transformation Choice on Computational Aspects of Biomechanical Parameter Estimation of Soft Tissues. Bioengineering 2019, 6, 100. https://doi.org/10.3390/bioengineering6040100
Aggarwal A. Effect of Residual and Transformation Choice on Computational Aspects of Biomechanical Parameter Estimation of Soft Tissues. Bioengineering. 2019; 6(4):100. https://doi.org/10.3390/bioengineering6040100
Chicago/Turabian StyleAggarwal, Ankush. 2019. "Effect of Residual and Transformation Choice on Computational Aspects of Biomechanical Parameter Estimation of Soft Tissues" Bioengineering 6, no. 4: 100. https://doi.org/10.3390/bioengineering6040100
APA StyleAggarwal, A. (2019). Effect of Residual and Transformation Choice on Computational Aspects of Biomechanical Parameter Estimation of Soft Tissues. Bioengineering, 6(4), 100. https://doi.org/10.3390/bioengineering6040100





