Geometric Effect for Biological Reactors and Biological Fluids
Abstract
1. Introduction
- How are such experimental platforms utilized for research on biological systems?
- What have these technologies allowed us to understand?
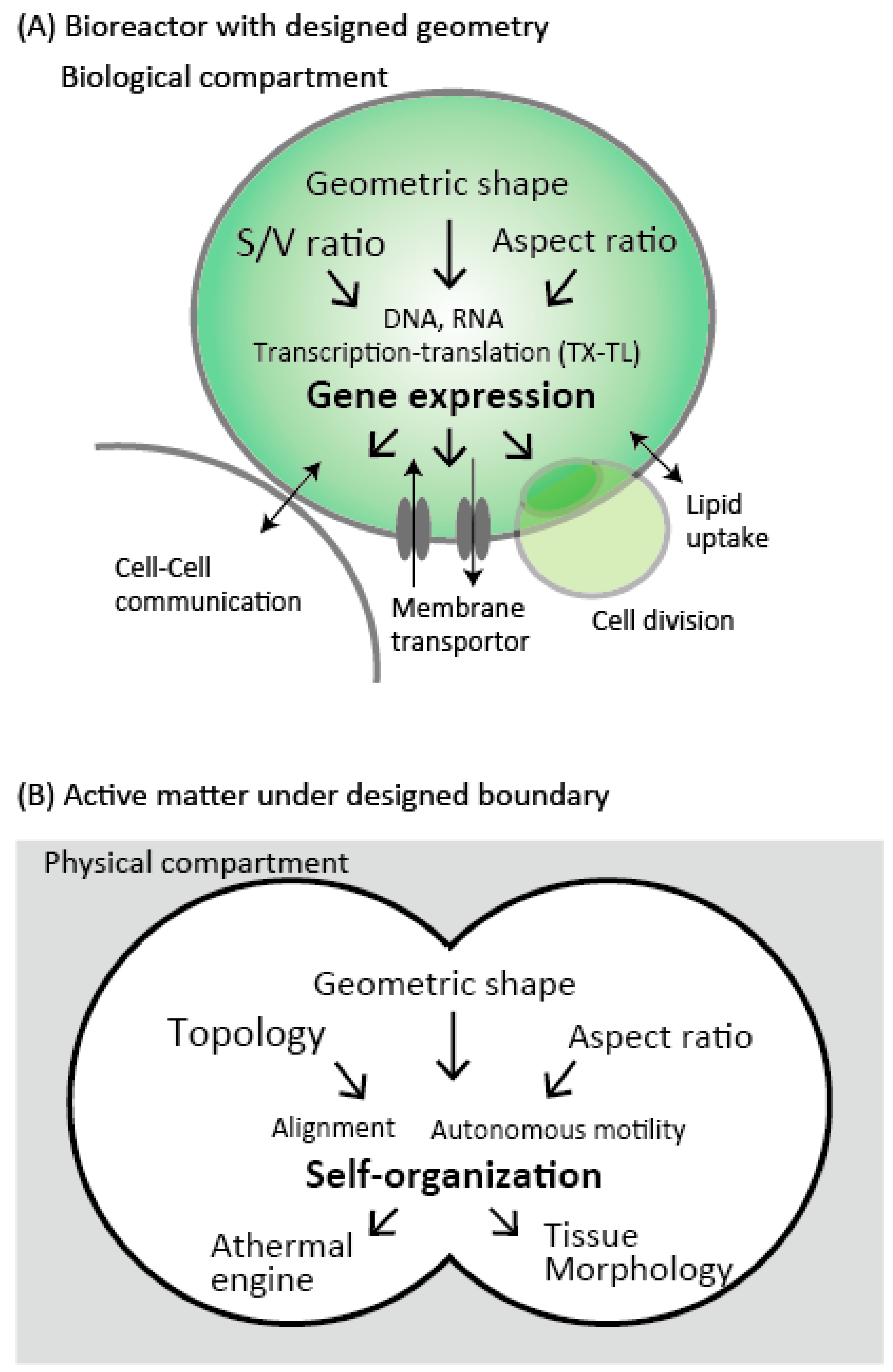
2. The Geometric Effect for Cell-Free Bioreactors
2.1. Cell-Free Expression as a Live-Cell Mimic
2.1.1. Compartmentalized Gene Expression
2.1.2. Gene Expression in Liposome
2.1.3. The Effect of the Spatial Confinement on Gene Expression
2.1.4. Kinetics and Noise in Cell-Free Gene Expression
2.2. On-Chip to Address Limits of Liposomes and Droplets
2.2.1. Biological Membranes on a Chip
2.2.2. Communication between Reactors
2.2.3. On-Chip Communication
3. Compartmentalized Active Dynamics
3.1. Collective Motion
3.1.1. Collective Motion of Active Biological Fluids
3.1.2. Geometric Principle of Active Bacterial Vortices
3.1.3. Topological Defects and Fluid Streaming
3.2. Application
3.2.1. Microfluidics to Harness the Power of Biological Fluids
3.2.2. Microfluidics for Self-Organization in Three-Dimensional Space
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schroeder, M. Fractals, Chaos and Power Laws: Minutes from an Infinite Paradise; W.H. Freeman and Company: New York, NY, USA, 1991. [Google Scholar]
- Kane, C.L.; Mele, E.J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin Hall phase. Nature 2008, 452, 970–974. [Google Scholar] [CrossRef] [PubMed]
- Zambelli, T.; Wintterlin, J.; Trost, J.; Ertl, G. Identification of the “active sites” of a surface-catalyzed reaction. Science 1996, 273, 1688–1690. [Google Scholar] [CrossRef]
- Jaramillo, T.F.; Jorgensen, K.P.; Bonde, J.; Nielsen, J.H.; Horch, S.; Chorkendorff, I. Identification of active edge sites for electrochemical H2 evolution from MoS2 nanocatalysis. Science 2007, 317, 100–102. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.R.; Forero-Vargas, M.; Withers, S.P.; Smith, R.S.; Traas, J.; Dewitte, W.; Murray, J.H.A. Cell-size dependent progression of the cell cycle creates homeostasis and flexibility of plant cell size. Nat. Commun. 2017, 8, 15060. [Google Scholar] [CrossRef]
- Murrell, M.; Oakes, P.W.; Lenz, M.; Gardel, M.L. Forcing cells into shape: The mechanics of actomyosin contractility. Nat. Rev. Mol. Cell Biol. 2015, 16, 486–498. [Google Scholar] [CrossRef]
- Hutchison, C.A., III; Chuang, Ra.; Noskov, V.N.; Assad-Garcia, N.; Deerinck, T.J.; Ellisman, M.H.; Gill, J.; Kannan, K.; Karas, B.J.; Ma, L. Design and synthesis of a minimal bacterial genome. Science 2016, 351, aad6253. [Google Scholar] [CrossRef]
- Zubay, G. In vitro synthesis of protein in microbial systems. Annu. Rev. Genet. 1973, 7, 267–287. [Google Scholar] [CrossRef]
- Chong, S. Overview of Cell-Free Protein Synthesis: Historic Landmarks, Commercial Systems, and Expanding Applications. Curr. Protoc. Mol. Biol. 2014, 108, 1–11. [Google Scholar]
- Shin, J.; Noireaux, V. An E. coli Cell-Free Expression Toolbox: Application to Synthetic Gene Circuits and Artificial Cells. ACS Synth. Biol. 2012, 1, 29–41. [Google Scholar] [CrossRef]
- Garamella, J.; Marchall, R.; Rustad, M.; Noireaux, V. The all E. coli TX-TL toolbox 2.0: A plat form for cell-free synthetic biology. ACS Synth. Biol. 2016, 5, 344–355. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Inoue, A.; Tomari, Y.; Suzuki, T.; Yokogawa, T.; Nishikawa, K.; Ueda, T. Cell-free translation reconstituted with purified components. Nat. Biotechnol. 2001, 19, 751–755. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, Y.; Kanamori, T.; Ueda, T. Protein synthesis by pure translation systems. Methods 2015, 36, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Karzbrun, E.; Shin, J.; Bar-Ziv, R.H.; Noireaux, V. Coarse-grained dynamics of protein synthesis in a cell-free system. Phys. Rev. Lett. 2011, 106, 048104. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, R.; Noireaux, V.; Maeda, Y.T. Anomalous scaling of gene expression in confined cell-free reactions. Sci. Rep. 2018, 8, 7346. [Google Scholar] [CrossRef] [PubMed]
- Chang, T.M.S. Semipermeable Microcapsules. Nature 1964, 146, 324–325. [Google Scholar] [CrossRef]
- Fygenson, D.K. Mechanics of Microtubule-Based Membrane Extension. Phys. Rev. Lett. 1997, 79, 4497–4500. [Google Scholar] [CrossRef]
- Noireaux, V.; Libchaber, A. A vesicle bioreactor as a step toward an artificial cell assembly. Proc. Natl. Acad. Sci. USA 2004, 101, 17669–17674. [Google Scholar] [CrossRef]
- Noireaux, V.; Bar-Ziv, R.; Godefroy, J.; Salman, H.; Libchaber, A. Toward an artificial cell based on gene expression in vesicles. Phys. Biol. 2005, 2, 1–8. [Google Scholar] [CrossRef]
- Karig, D.K.; Jung, S.-Y.; Srijanto, B.; Collier, C.P.; Simpson, M.L. Probing Cell-Free Gene Expression Noise in Femtoliter Volumes. ACS Synth Biol. 2013, 2, 497–505. [Google Scholar] [CrossRef] [PubMed]
- Basu, S.; Mehraja, R.; Thiberge, S.; Chen, M.-T.; Weiss, R. Spatiotemporal control of gene expression with pulse-generating networks. Proc. Natl. Acad. Sci. USA 2004, 101, 6355–6360. [Google Scholar] [CrossRef] [PubMed]
- Majumder, S.; Garamella, J.; Wang, Y.L.; DeNies, M.; Noireaux, V.; Liu, A.P. Cell-sized mechanosensitive and biosensing compartment programmed with DNA. Chem. Commun. 2017, 53, 7349. [Google Scholar] [CrossRef] [PubMed]
- Ho, K.Y.; Murray, V.L.; Liu, A.P. Engineering artificial cells by combining Hela-based cell-free expression and ultra-thin double emulsion template. Methods Cell Biol. 2015, 128, 303–318. [Google Scholar] [PubMed]
- White, C.L.; Gober, J.W. MreB: Pilot or passenger of cell wall synthesis? Trends Microbiol. 2012, 20, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Noireaux, V.; Maeda, Y.T.; Libchaber, A. Development of an artificial cell, from self-organization to computation and self-reproduction. Proc. Natl. Acad. Sci. USA 2011, 108, 3473–3480. [Google Scholar] [CrossRef] [PubMed]
- Maeda, Y.T.; Nakadai, T.; Shin, J.; Uryu, K.; Noireaux, V.; Libchaber, A. Assembly of MreB filaments on liposome membranes: A synthetic biology approach. ACS Synth. Biol. 2012, 1, 53–59. [Google Scholar] [CrossRef]
- Hooke, R. Micrographia, Some Physiological Descriptions of Minute Bodies Made by Magnifying Glasses with Observations and Inquiries Thereupon; J. Martyn and J. Allestry: London, UK, 1665. [Google Scholar]
- Marguerat, S.; Bähler, J. Coordinating genome expression with cell size. Trends Genet. 2012, 28, 560–565. [Google Scholar] [CrossRef] [PubMed]
- Okano, T.; Matsuura, T.; Suzuki, H.; Yomo, T. Cell-free Protein Synthesis in a Microchamber Revealed the Presence of an Optimum Compartment Volume for High-order Reactions. ACS Synth. Biol. 2014, 3, 347–352. [Google Scholar] [CrossRef] [PubMed]
- Bui, H.T.; Umakoshi, H.; Ngo, K.X.; Nishida, M.; Shimanouchi, T.; Kuboi, R. Liposome Membrane Itself Can Affect Gene Expression in the Escherichia coli Cell-Free Translation System. Langmuir 2008, 24, 10537–10542. [Google Scholar] [CrossRef]
- Kato, A.; Yanagisawa, M.; Sato, Y.T.; Fujiwara, K.; Yoshikawa, K. Cell-sized confinement in microspheres accelerates the reaction of gene expression. Sci. Rep. 2012, 2, 283. [Google Scholar] [CrossRef]
- Matsuura, T.; Hosoda, K.; Kazuta, Y.; Ishihashi, N.; Suzuki, H.; Yomo, T. Effects of compartment size on the kinetics of intracompartmental multimetric protein synthesis. ACS Synth. Biol. 2012, 1, 431–437. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Friedman, N.; Xie, S. Stochastic protein expression in individual cells at the single molecule level. Nature 2006, 440, 358–362. [Google Scholar] [CrossRef]
- Brenner, N.; Braun, E.; Yoney, A.; Susman, L.; Rotella, J.; Salman, H. Single-cell protein dynamics reproduce universal fluctuations in cell populations. Eur. Phys. J. E 2015, 38, 15102–15109. [Google Scholar] [CrossRef] [PubMed]
- Brenner, N.; Newman, C.M.; Osmanovic, D.; Rabi, Y.; Salman, H.; Stein, D.L. Universal protein distributions in a model of cell growth and division. Phys. Rev. E 2015, 92, 042713. [Google Scholar] [CrossRef] [PubMed]
- Bandiera, L.; Furini, S.; Giordano, E. Phenotipic Variability in Synthetic Biology Applications: Dealing with Noise in Microbial Gene Expression. Front. Microbiol. 2016, 7, 479. [Google Scholar] [CrossRef] [PubMed]
- Raser, J.M.; O’Shea, E.K. Control of Stochasticity in Eukaryotic Gene Expression. Science 2004, 304, 1811–1814. [Google Scholar] [CrossRef] [PubMed]
- Munsky, B.; Neuert, G.; van Oudenaarden, A. Using Gene Expression Noise to Understand Gene Regulation. Science 2012, 336, 183–187. [Google Scholar] [CrossRef]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef]
- Nishimura, K.; Tsuru, S.; Suzuki, H.; Yomo, T. Stochasticity in gene expression in a cell-sized compartment. ACS Synth. Biol. 2015, 4, 566–576. [Google Scholar] [CrossRef]
- Kapsner, K.; Simmel, F.C. Partitioning Variability of a Compartmentalized In Vitro Transcriptional Thresholding Circuit. ACS Synth. Biol. 2015, 4, 1136–1143. [Google Scholar] [CrossRef]
- Salman, H.; Brenner, N.; Tung, C.-K.; Elyahu, N.; Stolovicky, E.; Moore, L.; Libchaber, A.; Braun, E. Universal protein fluctuations in populations of microorganisms. Phys. Rev. Let. 2012, 108, 238105. [Google Scholar] [CrossRef] [PubMed]
- Soga, N.; Watanabe, R.; Noji, H. Attolitre-sized lipid bilayer chamber array for rapid detection of single transporters. Sci. Rep. 2015, 5, 11025. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.J.; Bong, K.W.; Reátegui, E.; Irimia, D.; Doyle, P.S. Porous Microwells for Geometry-Selective, Large-Scale Microparticle Arrays. Nat. Mat. 2017, 16, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Weibull, E.; Matsui, S.; Sakai, M.; Svahn, H.A.; Ohashi, T. Microfluidic Device for Generating a Stepwise Concentration Gradient on a Microwell Slide for Cell Analysis. Biomicrofluidics 2013, 7, 064115. [Google Scholar] [CrossRef] [PubMed]
- Yeh, S.I.; Hau, C.C.; Huang, C.J.; Chang, H.C.; Hsu, C.H.; Yang, J.T. Development of a Simple Static Microwell Array with Uniform Cell Seeding and a Chemical Concentration Gradient. Microfluid. Nanofluid. 2017, 21, 80. [Google Scholar] [CrossRef]
- Ren, K.; Zhou, J.; Wu, H. Materials for Microfluidic Chip Fabrication. Acc. Chem. Res. 2013, 46, 2396–2406. [Google Scholar] [CrossRef] [PubMed]
- Shirtcliffe, N.J.; Toon, R.; Roach, P. Surface Treatments for Microfluidic Biocompatibility. Methods Mol. Biol. 2013, 949, 241–268. [Google Scholar]
- Chadli, M.; Maniti, O.; Marquette, C.; Tillier, B.; Cortès, S.; Girard-Egrot, A. A new functional membrane protein microarray based on tethered phospholipid bilayers. Analyst 2018, 143, 2165–2173. [Google Scholar] [CrossRef]
- Le Pioufle, B.; Suzuki, H.; Tabata, K.V.; Noji, H.; Takeuchi, S. Lipid Bilayer Microarray for Parallel Recording of Transmembrane Ion Currents. Anal. Chem. 2008, 80, 328–332. [Google Scholar] [CrossRef]
- Ota, S.; Suzuki, H.; Takeuchi, S. Microfluidic Lipid Membrane Formation on Microchamber Arrays. Lab Chip 2011, 11, 2485–2487. [Google Scholar] [CrossRef]
- Schwarz-Schilling, M.; Aufinger, L.; Mückl, A.; Simmel, F.C. Chemical communication between bacteria and cell-free gene expression systems within linear chains of emulsion droplets. Integr. Biol. 2016, 8, 564–570. [Google Scholar] [CrossRef]
- Niederholtmeyer, H.; Chaggan, C.; Devaraj, N.K. Communication and quorum sensing in non-living mimics of eukaryotic cells. Nat. Commun. 2018, 9, 5027. [Google Scholar] [CrossRef] [PubMed]
- Karzbrun, E.; Tayar, A.M.; Noireaux, V.; Bar-Ziv, R.H. Programmable on-chip DNA compartments as artificial cells. Science 2014, 345, 6198. [Google Scholar] [CrossRef] [PubMed]
- Tayar, A.M.; Karzbrun, E.; Noireaux, V.; Bar-Ziv, R.H. Synchrony and pattern formation of coupled genetic oscillators on a chip of artificial cells. Proc. Natl. Acad. Sci. USA 2017, 114, 11609–11614. [Google Scholar] [CrossRef] [PubMed]
- Rothfield, L.; Taghbalout, A.; Shih, Y. Spatial control of bacterial division-site placement. Nat. Rev. Microbiol. 2005, 3, 959–968. [Google Scholar] [CrossRef]
- Loose, M.; Fischer-Friedrich, E.; Ries, J.; Kruse, K.; Schwille, P. Spatial Regulators for Bacterial Cell Division Self-Organize into Surface Waves in Vitro. Science 2008, 320, 789–792. [Google Scholar] [CrossRef]
- Loose, M.; Fischer-Friedrich, E.; Herold, C.; Kruse, K.; Schwille, P. Min protein patterns emerge from rapid rebinding and membrane interaction of MinE. Nat. Struct. Mol. Biol. 2010, 18, 577–583. [Google Scholar] [CrossRef]
- Vecchiarelli, A.G.; Li, M.; Mizuuchi, M.; Hwang, L.C.; Seol, Y.; Neuman, K.C.; Mizuuchi, K. Membrane-bound MinDE complex acts as a toggle switch that drives Min oscillation coupled to cytoplasmic depletion of MinD. Proc. Natl. Acad. Sci. USA 2016, 113, E1479–E1488. [Google Scholar] [CrossRef] [PubMed]
- Schweizer, J.; Loose, M.; Bonny, M.; Kruse, K.; Mönch, I.; Schwille, P. Geometry sensing by self-organized protein patterns. Proc. Natl. Acad. Sci. USA 2012, 109, 15283–15288. [Google Scholar] [CrossRef] [PubMed]
- Söderström, B.; Badrutdinov, A.; Chan, H.; Skoglund, U. Cell shape-independent FtsZ dynamics in synthetically remodeled bacterial cells. Nat. Commun. 2018, 9, 4323. [Google Scholar] [CrossRef]
- Wu, K.-T.; Hishamunda, J.B.; Chen, D.T.N.; DeCamp, S.J.; Chang, Y.-W.; Fernández-Nieves, A.; Fraden, S.; Dogic, Z. Transition from turbulent to coherent flows in confined three-dimensional active fluids. Science 2017, 355, eaal1979. [Google Scholar] [CrossRef] [PubMed]
- Marchetti, M.C.; Joanny, J.F.; Ramaswamy, S.; Liverpool, T.B.; Prost, J.; Rao, M.; Aditi Simha, R. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013, 85, 1143. [Google Scholar] [CrossRef]
- Bricard, A.; Caussin, J.-B.; Das, D.; Savoie, C.; Chikkadi, V.; Shitara, K.; Chepizhko, O.; Peruani, F.; Saintillan, D.; Bartolo, D. Emergent vortices in populations of colloidal rollers. Nat. Commun. 2015, 6, 7470. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.-L.; Libchaber, A. Particle Diffusion in a Quasi-Two-Dimensional Bacterial Bath. Phys. Rev. Lett. 2000, 84, 3017. [Google Scholar] [CrossRef] [PubMed]
- Dombrowski, C.; Cisneros, L.; Chatkaew, S.; Goldstein, R.E.; Kessler, J.O. Self-concentration and large-scale coherence in bacterial dynamics. Phys. Rev. Lett. 2004, 93, 098103. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, A.; Aranson, I.S.; Kessler, J.O.; Goldstein, R.E. Concentration dependence of the collective dynamics of swimming bacteria. Phys. Rev. Lett. 2007, 98, 158102. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, A.; Aranson, I.S. Physical Properties of Collective Motion in Suspensions of Bacteria. Phys. Rev. Lett. 2012, 109, 248109. [Google Scholar] [CrossRef]
- Wensink, H.H.; Dunkel, J.; Heidenreich, S.; Drescher, K.; Goldstein, R.E.; Lowen, H.; Yeomans, J.M. Meso-scale turbulence in living fluids. Proc. Natl. Acad. Sci. USA 2012, 109, 14308–14313. [Google Scholar] [CrossRef]
- Wioland, H.; Woodhouse, F.G.; Dunkel, J.; Kessler, J.O.; Goldstein, R.E. Confinement stabilizes a bacterial suspension into a spiral vortex. Phys. Rev. Lett. 2013, 110, 268102. [Google Scholar] [CrossRef]
- Wioland, H.; Woodhouse, F.G.; Dunkel, J.; Goldstein, R.E. Ferromagnetic and antiferromagnetic order in bacterial vortex lattices. Nat. Phys. 2016, 12, 341–345. [Google Scholar] [CrossRef]
- Beppu, K.; Izri, Z.; Gohya, J.; Eto, K.; Ichikawa, M.; Maeda, Y.T. Geometry-driven collective ordering of bacterial vortices. Soft Matter 2017, 13, 5038–5043. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirok, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys. Rev. Lett. 1995, 75, 1226. [Google Scholar] [CrossRef]
- Angelini, T.E.; Hannezo, E.; Trepat, X.; Marquez, M.; Fredberg, J.J.; Weitz, D.A. Glass-like dynamics of collective cell migration. Proc. Natl. Acad. Sci. USA 2011, 108, 4714–4719. [Google Scholar] [CrossRef]
- Saw, T.B.; Doostmohammadi, A.; Nier, V.; Kocgozlu, L.; Thampi, S.; Toyama, Y.; Marcq, P.; Lim, C.T.; Yeomans, J.M.; Ladoux, B. Topological defects in epithelia govern cell death and extrusion. Nature 2017, 544, 212–216. [Google Scholar] [CrossRef]
- Ravasio, A.; Cheddadi, I.; Chen, T.; Pereira, T.; Ong, H.T.; Bertocchi, C.; Brugues, A.; Jacinto, A.; Kabla, A.J.; Toyama, Y.; et al. Gap geometry dictates epithelial closure efficiency. Nature Commun. 2015, 6, 7683. [Google Scholar] [CrossRef]
- Vedula, S.R.K.; Peyret, G.; Cheddadi, I.; Chen, T.; Brugués, A.; Hirata, H.; Lopez-Menendez, H.; Toyama, Y.; de Almeida, L.N.; Trepat, X.; et al. Mechanics of epithelial closure over non-adherent environments. Nat. Commun. 2015, 6, 6111. [Google Scholar] [CrossRef]
- Duclos, G.; Erlenkämper, C.; Joanny, J.-F.; Silberzan, P. Topological defects in confined populations of spindle-shaped cells. Nat. Phys. 2017, 13, 58–62. [Google Scholar] [CrossRef]
- Deforet, M.; Hakim, V.; Yevick, H.G.; Duclos, G.; Silberzan, P. Emergence of collective modes and tri-dimensional structures from epithelial confinement. Nat. Commun. 2014, 5, 3747. [Google Scholar] [CrossRef]
- Xi, W.; Sonam, S.; Saw, T.B.; Ladoux, B.; Lim, C.T. Emergent patterns of collective cell migration under tubular confinement. Nat. Commun. 2017, 8, 1517. [Google Scholar] [CrossRef]
- Vedula, S.R.K.; Leong, M.C.; Lai, T.L.; Hersen, P.; Kabla, A.J.; Lim, C.T.; Ladoux, B. Emerging modes of collective cell migration induced by geometrical constraints. Proc. Natl. Acad. Sci. USA 2012, 109, 12974–12979. [Google Scholar] [CrossRef]
- Suzuki, K.; Miyazaki, M.; Takagi, J.; Itabashi, T.; Ishiwata, S.-I. Spatial confinement of active microtubule networks induces large-scale rotational cytoplasmic flow. Proc. Natl. Acad. Sci. USA 2017, 114, 2922–2927. [Google Scholar] [CrossRef]
- Norton, M.M.; Baskaran, A.; Opathalage, A.; Langeslay, B.; Fraden, S.; Baskaran, A.; Hagan, M.F. Insensitivity of active nematic liquid crystal dynamics to topological constraints. Phys. Rev. E 2018, 97, 012702. [Google Scholar] [CrossRef]
- Sokolov, A.; Apodaca, M.M.; Grzybowski, B.A.; Aranson, I.S. Swimming bacteria power microscopic gears. Proc. Natl. Acad. Sci. USA 2010, 107, 969–974. [Google Scholar] [CrossRef]
- Thampi, S.P.; Doostmohammadi, A.; Shendruk, T.N.; Golestanian, R.; Yeomans, J.M. Active micromachines: Microfluidics powered by mesoscale turbulence. Sci. Adv. 2016, 2, e1501854. [Google Scholar] [CrossRef]
- Keber, F.C.; Loiseau, E.; Sanchez, T.; DeCamp, S.J.; Giomi, L.; Bowick, M.J.; Marchetti, M.C.; Dogic, Z.; Bausch, A.R. Topology and dynamics of active nematic vesicles. Science 2014, 345, 1135–1139. [Google Scholar] [CrossRef]
- Ohzono, T.; Monobe, H. Microwrinkles: Shape-tunability and applications. J. Colloid Int. Sci. 2012, 368, 1–8. [Google Scholar] [CrossRef]
- Warmflash, A.; Sorre, B.; Etoc, F.; Siggia, E.D.; Brivanlou, A.H. A method to recapitulate early embryonic spatial patterning in human embryonic stem cells. Nat. Methods 2014, 11, 847–854. [Google Scholar] [CrossRef]
- Morgani, S.M.; Metzger, J.J.; Nichols, J.; Siggia, E.D.; Hadjantonakis, A.-K. Micropattern differentiation of mouse pluripotent stem cells recapitulates embryo regionalized cell fate patterning. eLife 2018, 7, e32839. [Google Scholar] [CrossRef]
- Kamei, K.; Koyama, Y.; Tokunaga, Y.; Mashimo, Y.; Yoshioka, M.; Fockenberg, C.; Mosbergen, R.; Korn, O.; Wells, C.; Chen, Y. Characterization of Phenotypic and Transcriptional Differences in Human Pluripotent Stem Cells under 2D and 3D Culture Conditions. Adv. Healthc. Mater. 2016, 5, 2951–2958. [Google Scholar] [CrossRef]
- Lopez-Leon, T.; Koning, V.K.; Devaiah, B.S.; Vitelli, V.; Fernandez-Nieves, A. Frustrated nematic order in spherical geometries. Nat. Phys. 2011, 7, 391–394. [Google Scholar] [CrossRef]


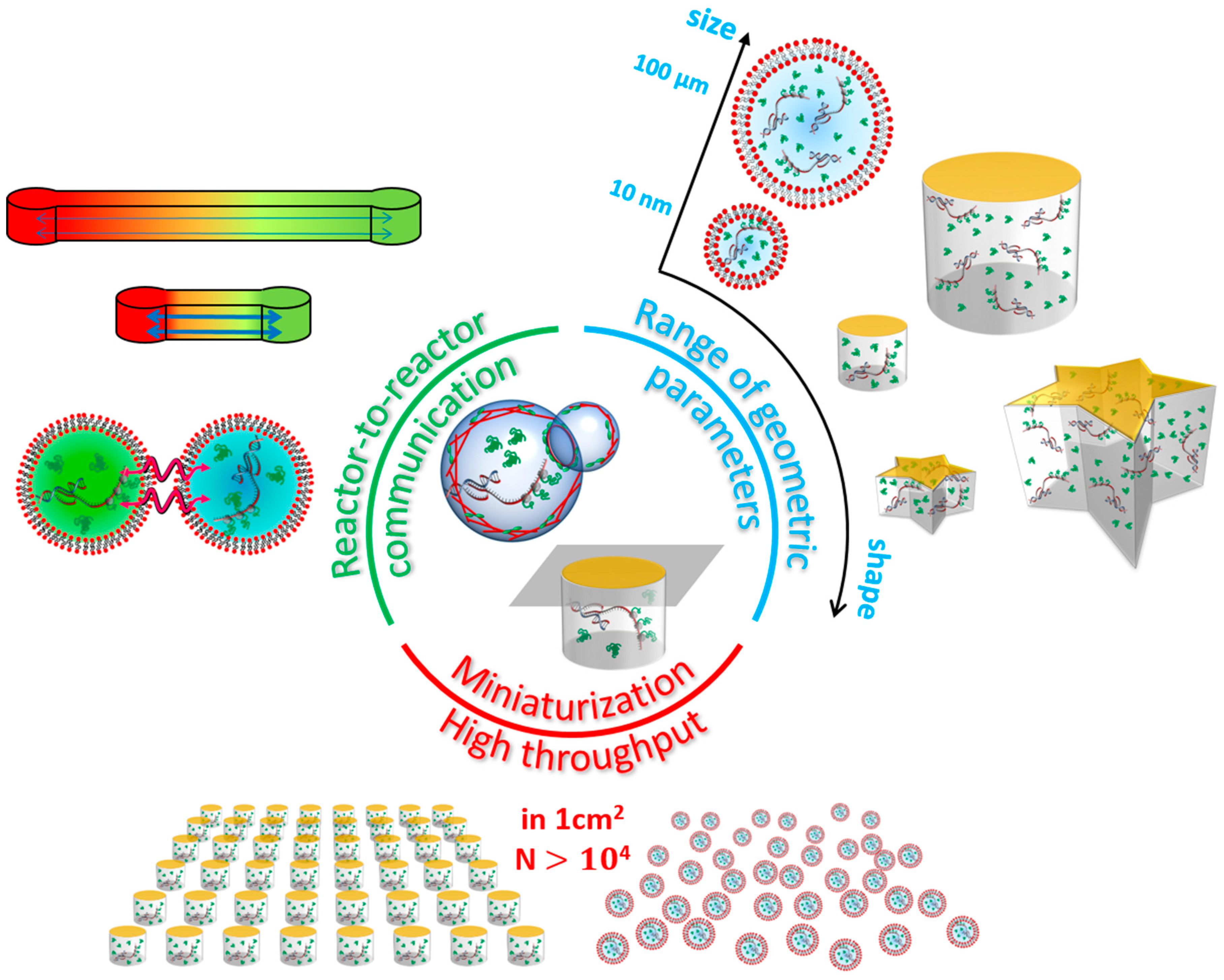
| Reactor | Typical Volume Range | Smallest Geometric Parameter | Number of Copies per Experiment | Stability | Fabrication | Notable Properties |
|---|---|---|---|---|---|---|
| Test tube | 10 µL to 1 mL | Radius: 1 mm | Up to 100 | ∞ | - | Easiest |
| Cheapest | ||||||
| Bulk only | ||||||
| Droplet | 10 aL to 1 µL | Radius: 100 nm | ≥ | From hours to days | Simple | Very easy |
| Requires two immiscible phases | ||||||
| No functional membrane | ||||||
| Well-controlled size | ||||||
| Only spherical | ||||||
| Very limited cell-to-cell communication | ||||||
| Liposome | 10 aL to 1 pL | Radius: 100 nm | ≥ | A few hours | Difficult | Close to biological systems |
| Functional membrane | ||||||
| Wide dispersity of size | ||||||
| Lacks stability | ||||||
| Only spherical | ||||||
| Limited cell-to-cell communication | ||||||
| Microwell | 10 aL to 1 µL | Height: 10 nm | ≥ | ∞ | Simple | Easy |
| Functional membrane | ||||||
| Wide range of shapes and aspect ratios | ||||||
| Well-controlled geometry | Boundaries not completely functionalizable | |||||
| Low stability of biological membrane | ||||||
| No cell-to-cell communication | ||||||
| Microchannel | 100 aL to 1 mL | Height: 10 nm | ≥ | ∞ | Simple | Easy |
| Wide range of shapes, aspect ratios and connectivities | ||||||
| Well-controlled geometry | ||||||
| Best for cell-to-cell communication | ||||||
| No functional membrane |
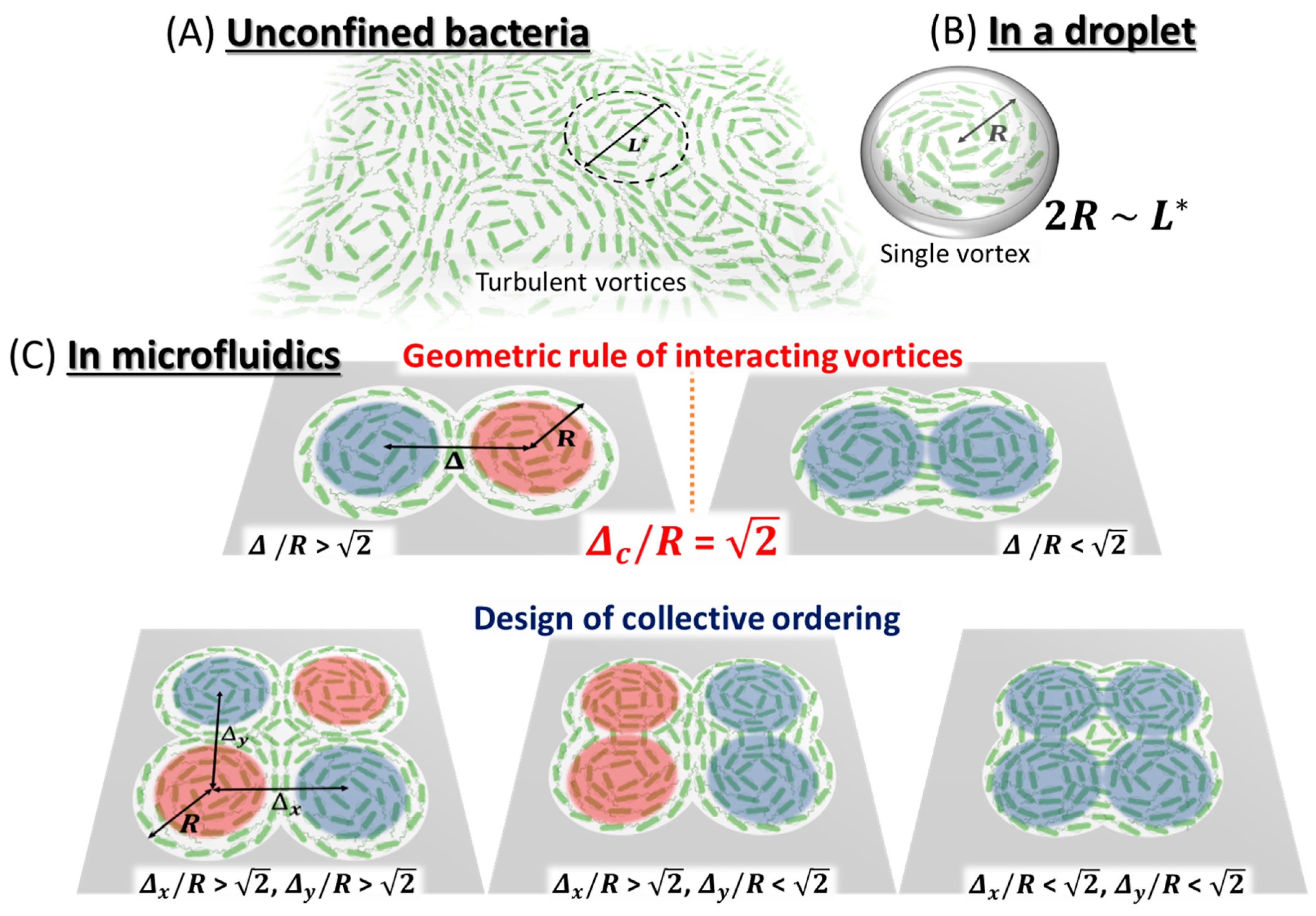
| Bacteria | Geometry | Height | Radius | Geometrical Control Parameter | Ordered Collective Motion | ||
|---|---|---|---|---|---|---|---|
| Wensink et al. (2012) [70] | Bacillus subtilis (strain 168) | Boundary-free | 5 µm | - | - | Meso-scale Turbulence (Typical Vortex Radius ~25 µm) | |
| Wioland et al. (2013) [71] | Bacillus subtilis (strain 168) | Cylinder | 25 µm | 35 µm | 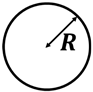 Radius R | Single Isolated Vortex | |
| Wioland et al. (2016) [72] | Bacillus subtilis (strain 168) | Array of Cylindrical Microwells | 18 µm | 25 µm |  Channel Width W | 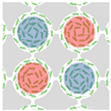 W < W* Anti-ferromagnetic Order |  W > W* Ferromagnetic Order |
| Beppu et al. (2017) [73] | Escherichia coli (strain RP4979) | Multiplet of Cylindrical Microwells | 20 µm | 28 µm | 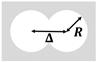 Radius R Distance Between Centers Δ | 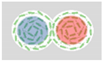 Δ/R > Anti-ferromagnetic Vortices |  Δ/R < Ferromagnetic Vortices |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beppu, K.; Izri, Z.; Maeda, Y.T.; Sakamoto, R. Geometric Effect for Biological Reactors and Biological Fluids. Bioengineering 2018, 5, 110. https://doi.org/10.3390/bioengineering5040110
Beppu K, Izri Z, Maeda YT, Sakamoto R. Geometric Effect for Biological Reactors and Biological Fluids. Bioengineering. 2018; 5(4):110. https://doi.org/10.3390/bioengineering5040110
Chicago/Turabian StyleBeppu, Kazusa, Ziane Izri, Yusuke T. Maeda, and Ryota Sakamoto. 2018. "Geometric Effect for Biological Reactors and Biological Fluids" Bioengineering 5, no. 4: 110. https://doi.org/10.3390/bioengineering5040110
APA StyleBeppu, K., Izri, Z., Maeda, Y. T., & Sakamoto, R. (2018). Geometric Effect for Biological Reactors and Biological Fluids. Bioengineering, 5(4), 110. https://doi.org/10.3390/bioengineering5040110




