Development and Characterization of a Parallelizable Perfusion Bioreactor for 3D Cell Culture
Abstract
:1. Introduction
2. Materials and Methods
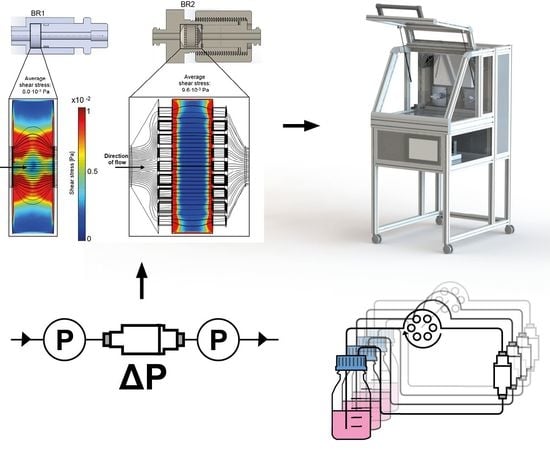
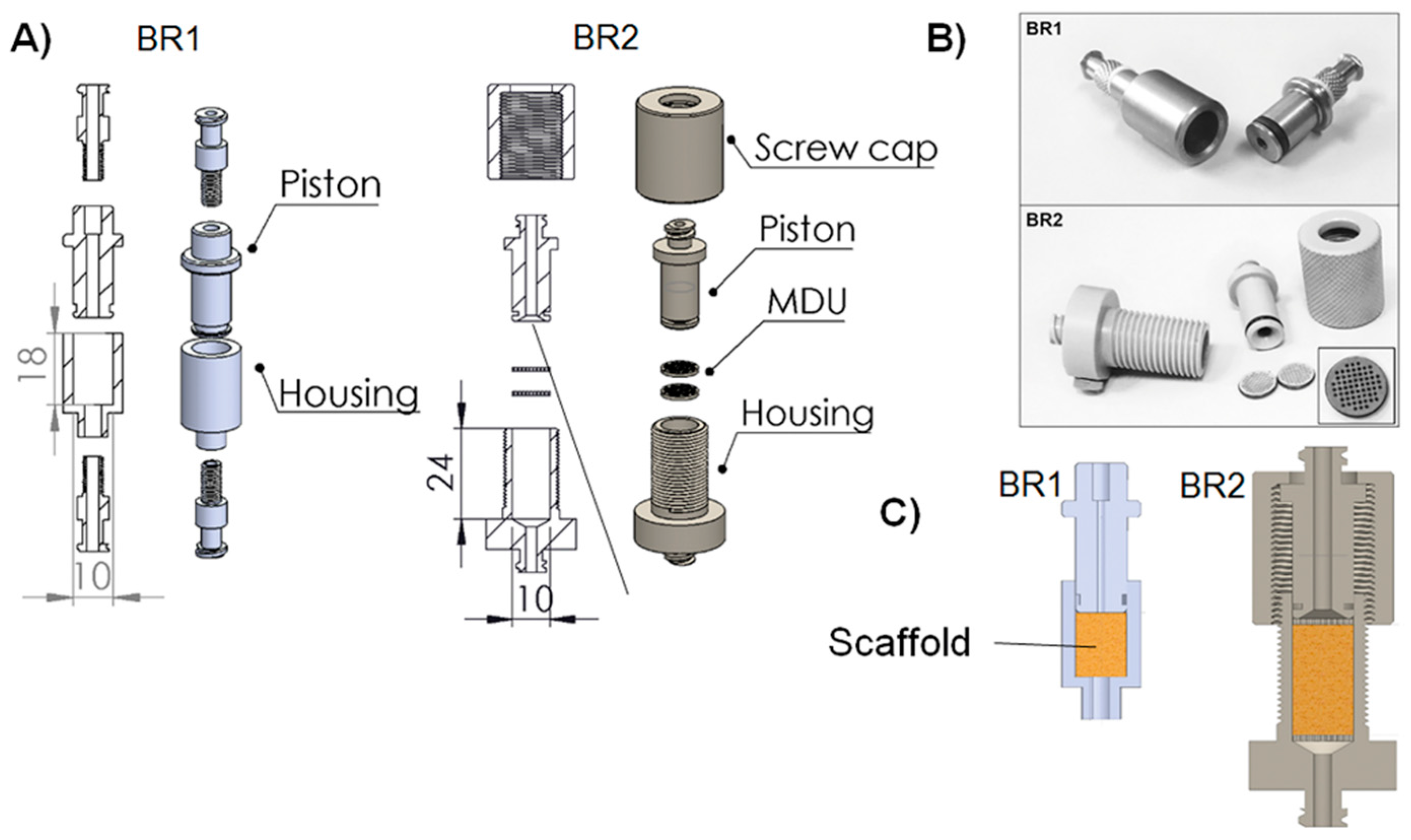
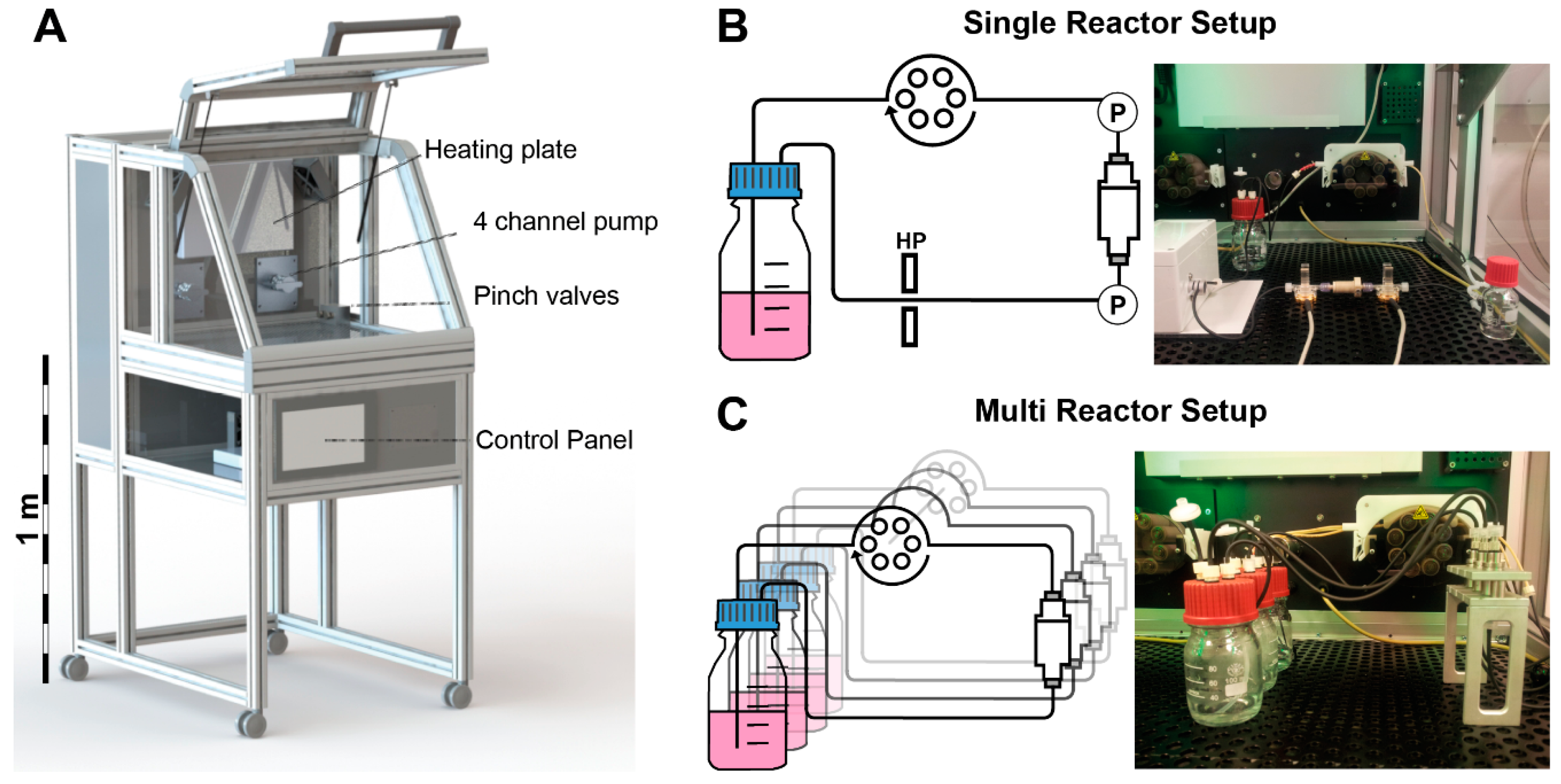
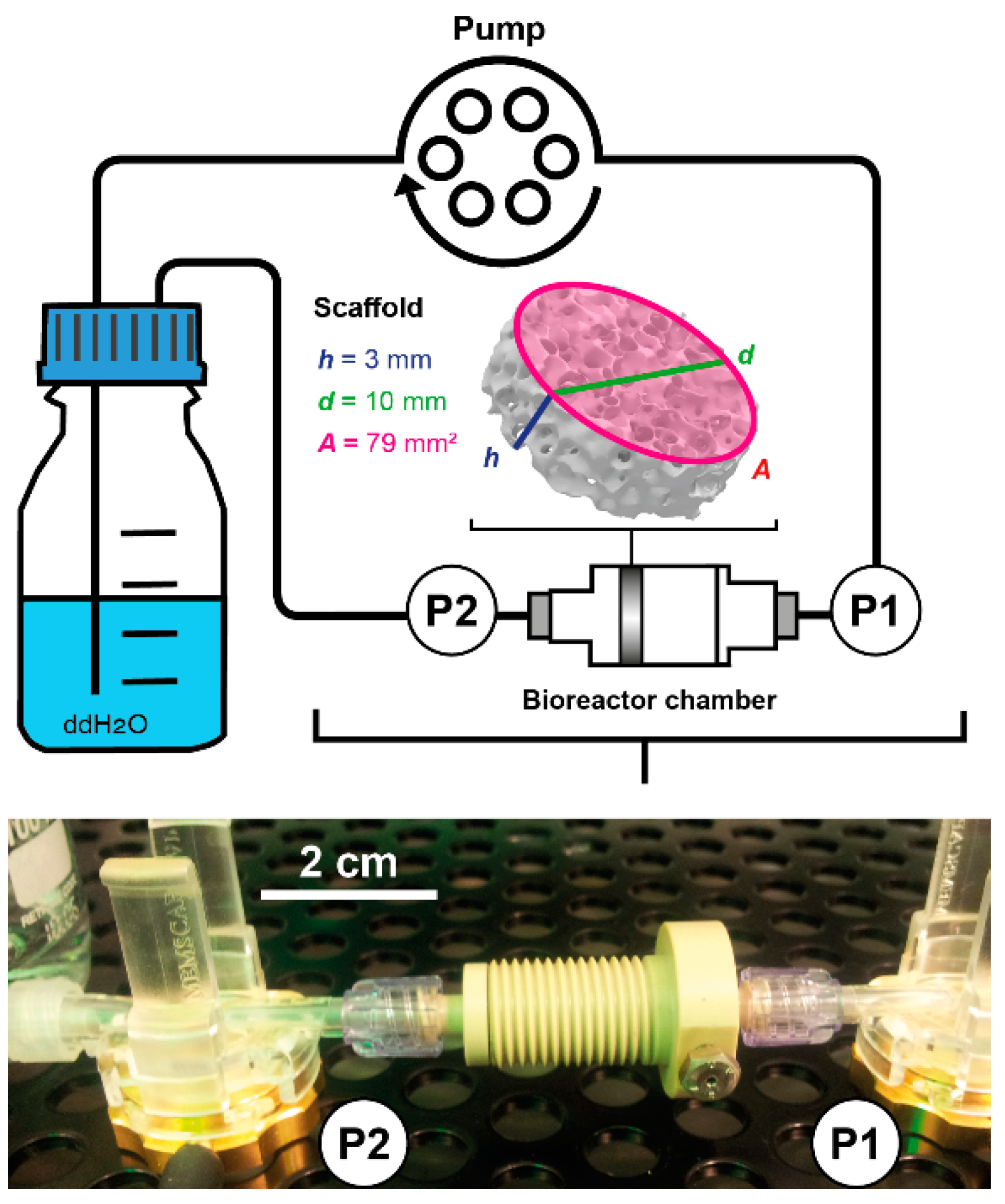
2.1. Bioreactor Design
2.2. Incubator System
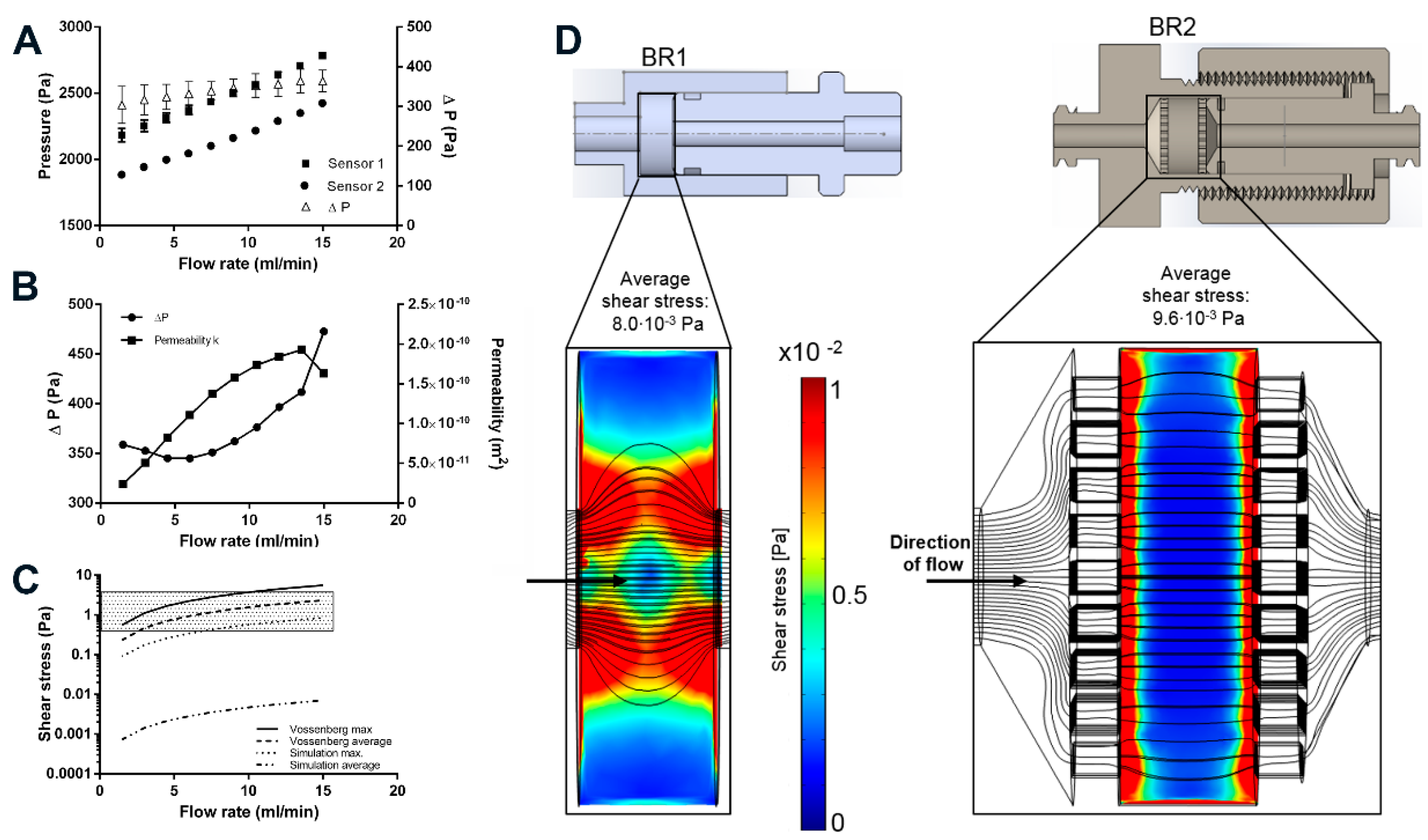
2.3. Pressure Sensor Characterization
2.4. Determination of Permeability
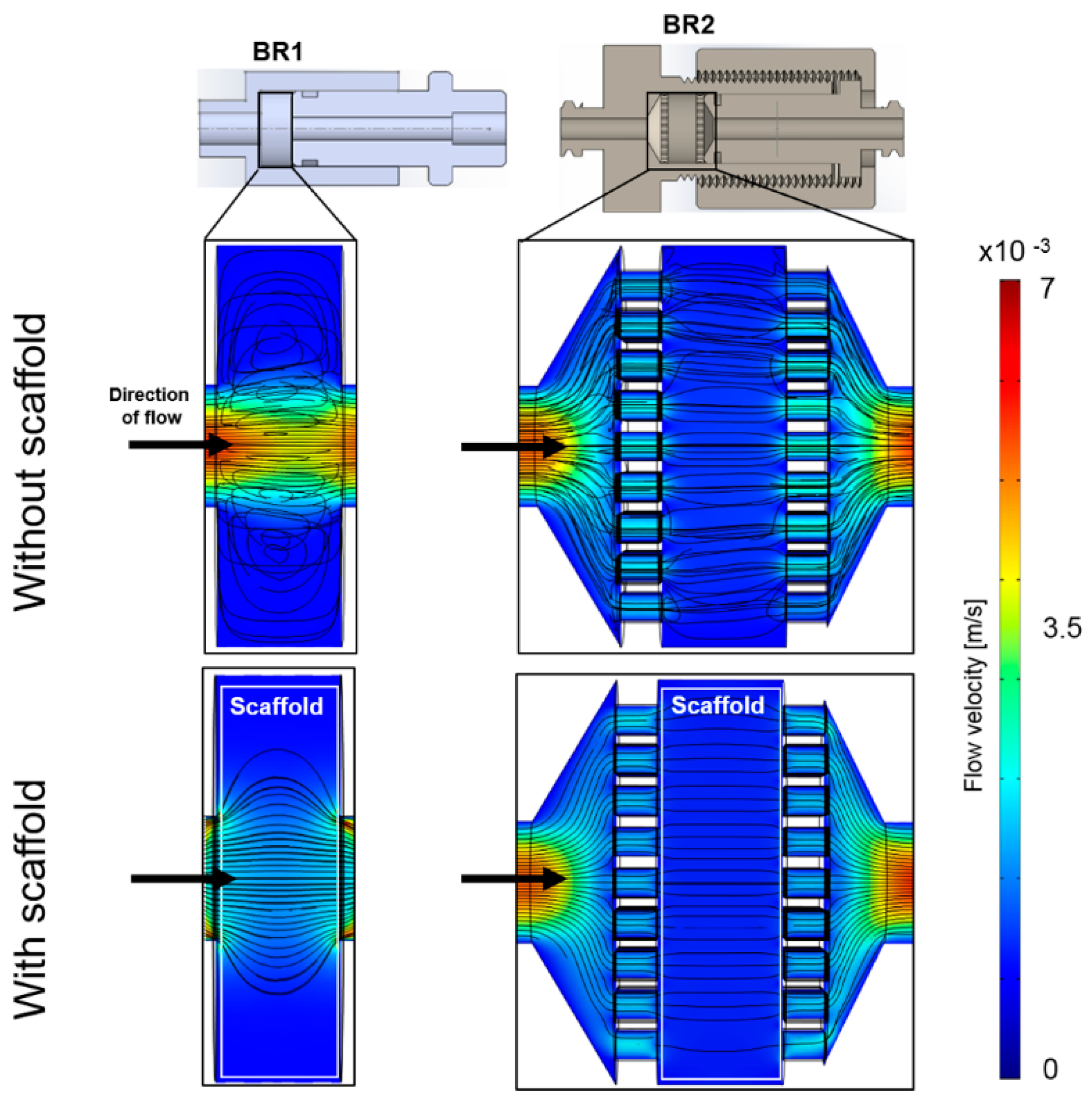
2.5. Computational Fluid Dynamics
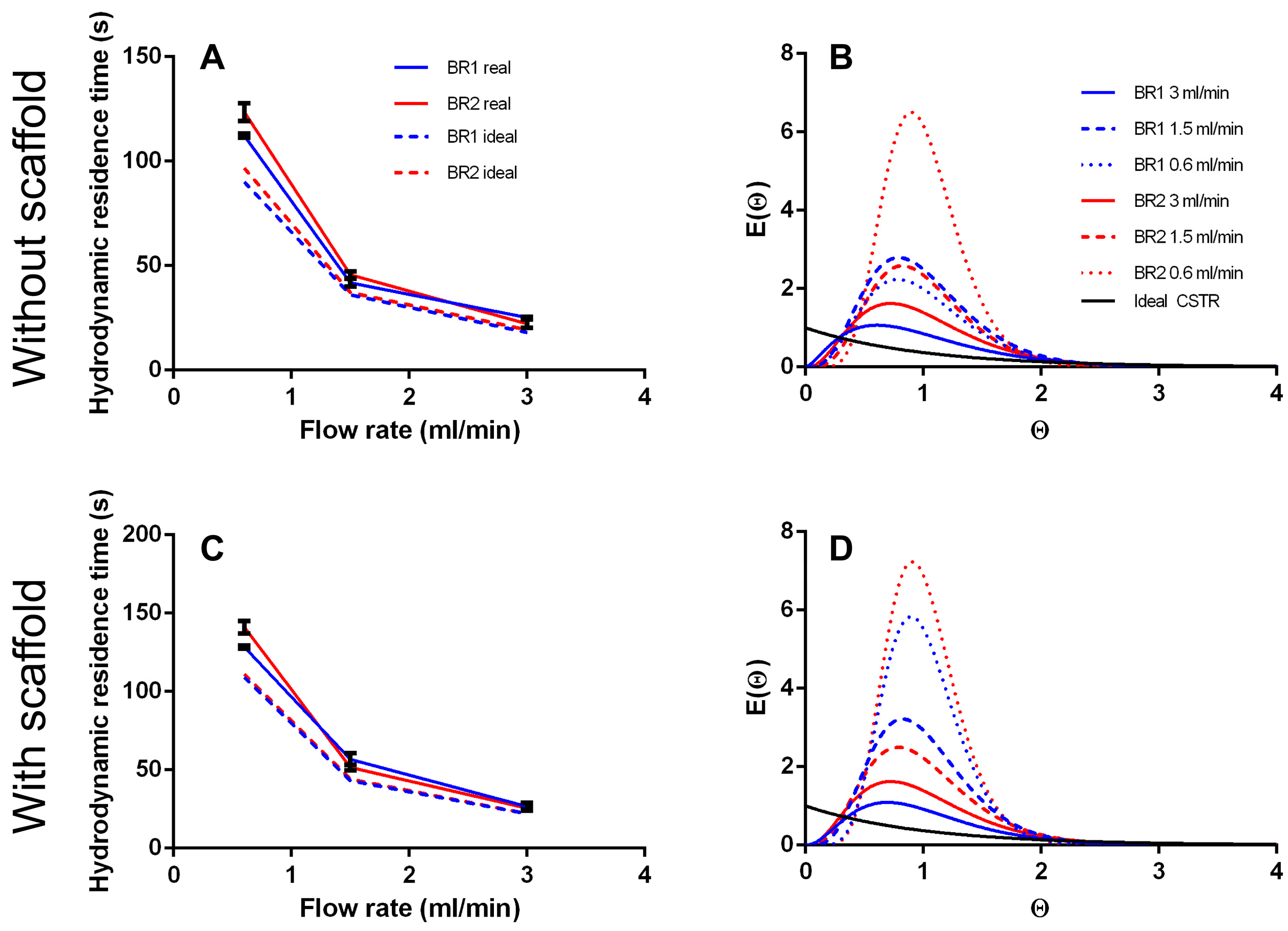
2.6. Residence Time Distribution
2.7. Fluid Shear Stress Estimation
2.8. Cell Culture
2.9. Bioreactor Cultivation
2.10. DNA Quantification
2.11. Alkaline Phosphatase Activity
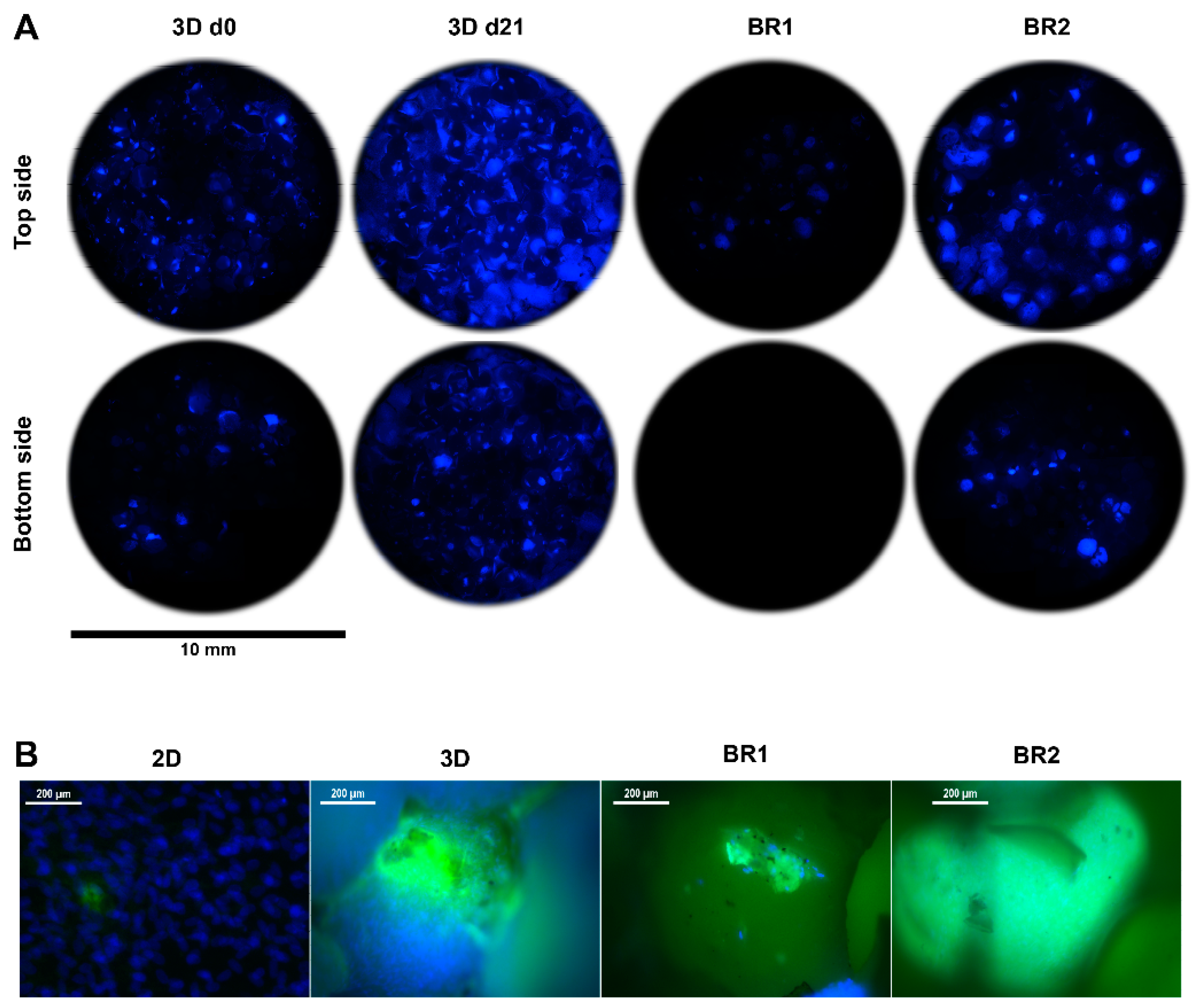
2.12. DAPI Staining
2.13. Matrix Mineralization
2.14. Statistical Analysis
3. Results
3.1. Flow Profile and Residence Time Distribution
3.2. Sensor Characterization and Determination of Permeability
3.3. Fluid Shear Stress Estimation
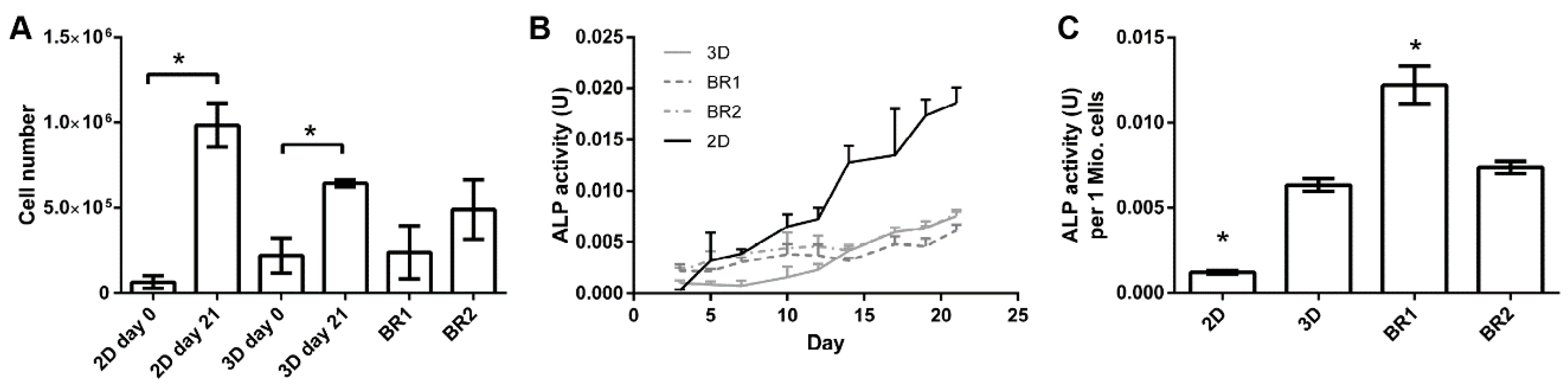
3.4. Bioreactor Cultivation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Volkmer, E.; Drosse, I.; Otto, S.; Stangelmayer, A.; Stengele, M.; Kallukalam, B.C.; Mutschler, W.; Schieker, M. Hypoxia in static and dynamic 3D culture systems for tissue engineering of bone. Tissue Eng. Part A 2008, 14, 1331–1340. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, A.S.; Juarez, T.M.; Helmke, C.D.; Gustin, M.C.; Mikos, A.G. Effect of convection on osteoblastic cell growth and function in biodegradable polymer foam scaffolds. Biomaterials 2001, 22, 1279–1288. [Google Scholar] [CrossRef]
- Stiehler, M.; Bünger, C.; Baatrup, A.; Lind, M.; Kassem, M.; Mygind, T. Effect of dynamic 3-D culture on proliferation, distribution, and osteogenic differentiation of human mesenchymal stem cells. J. Biomed. Mater. Res. Part A 2009, 89, 96–107. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Wu, H.; Wang, H.; Lin, F.; Sun, J. Regulation of adult human mesenchymal stem cells into osteogenic and chondrogenic lineages by different bioreactor systems. J. Biomed. Mater. Res. Part A 2009, 88, 935–946. [Google Scholar] [CrossRef]
- Gooch, K.J.; Kwon, J.H.; Blunk, T.; Langer, R.; Freed, L.E.; Vunjak-Novakovic, G. Effects of mixing intensity on tissue-engineered cartilage. Biotechnol. Bioeng. 2001, 72, 402–407. [Google Scholar] [CrossRef]
- Sikavitsas, V.I.; Bancroft, G.N.; Mikos, A.G. Formation of three-dimensional cell/polymer constructs for bone tissue engineering in a spinner flask and a rotating wall vessel bioreactor. J. Biomed. Mater. Res. 2002, 62, 136–148. [Google Scholar] [CrossRef] [PubMed]
- Begley, C.M.; Kleis, S.J. The fluid dynamic and shear environment in the NASA/JSC rotating-wall perfused-vessel bioreactor. Biotechnol. Bioeng. 2000, 70, 32–40. [Google Scholar] [CrossRef]
- Diederichs, S.; Röker, S.; Marten, D.; Peterbauer, A.; Scheper, T.; van Griensven, M.; Kasper, C. Dynamic cultivation of human mesenchymal stem cells in a rotating bed bioreactor system based on the Z® RP platform. Biotechnol. Prog. 2009, 25, 1762–1771. [Google Scholar] [CrossRef] [PubMed]
- Neumann, A.; Lavrentieva, A.; Heilkenbrinker, A.; Loenne, M.; Kasper, C. Characterization and Application of a Disposable Rotating Bed Bioreactor for Mesenchymal Stem Cell Expansion. Bioengineering 2014, 1, 231–245. [Google Scholar] [CrossRef]
- Bancroft, G.N.; Sikavitsas, V.I.; Mikos, A.G. Technical note: Design of a flow perfusion bioreactor system for bone tissue-engineering applications. Tissue Eng. 2003, 9, 549–554. [Google Scholar] [CrossRef] [PubMed]
- Sailon, A.M.; Allori, A.C.; Davidson, E.H.; Reformat, D.D.; Allen, R.J.; Warren, S.M. A novel flow-perfusion bioreactor supports 3D dynamic cell culture. Biomed. Res. Int. 2009, 2009, 873816. [Google Scholar] [CrossRef] [PubMed]
- Piola, M.; Soncini, M.; Cantini, M.; Sadr, N.; Ferrario, G.; Fiore, G.B. Design and Functional Testing of a Multichamber Perfusion Platform for Three-Dimensional Scaffolds. Sci. World J. 2013, 2013, 123974. [Google Scholar] [CrossRef] [PubMed]
- Hansmann, J.; Groeber, F.; Kahlig, A.; Kleinhans, C.; Walles, H. Bioreactors in tissue engineering—principles, applications and commercial constraints. Biotechnol. J. 2013, 8, 298–307. [Google Scholar] [CrossRef] [PubMed]
- Lee, P.J.; Hung, P.J.; Rao, V.M.; Lee, L.P. Nanoliter scale microbioreactor array for quantitative cell biology. Biotechnol. Bioeng. 2006, 94, 5–14. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Qu, H.; Hu, G.; Zhang, Q.; Song, K.; Guan, H.; Liu, T. A microfluidic-based multi-shear device for investigating the effects of low fluid-induced stresses on osteoblasts. PLoS ONE 2014, 9, e89966. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Chella, R.; Ma, T. Effects of shear stress on 3-D human mesenchymal stem cell construct development in a perfusion bioreactor system: Experiments and hydrodynamic modeling. Biotechnol. Bioeng. 2007, 96, 584–595. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.Y.; Park, S.H.; Shin, J.W.; Kang, Y.G.; Han, K.-H.; Shin, J.-W. Effects of intermittent hydrostatic pressure magnitude on the chondrogenesis of MSCs without biochemical agents under 3D co-culture. J. Mater. Sci. Mater. Med. 2012, 23, 2773–2781. [Google Scholar] [CrossRef] [PubMed]
- Fröhlich, M.; Grayson, W.L.; Marolt, D.; Gimble, J.M.; Kregar-Velikonja, N.; Vunjak-Novakovic, G. Bone grafts engineered from human adipose-derived stem cells in perfusion bioreactor culture. Tissue Eng. Part A 2009, 16, 179–189. [Google Scholar] [CrossRef] [PubMed]
- Grayson, W.L.; Bhumiratana, S.; Cannizzaro, C.; Chao, P.-H.G.; Lennon, D.P.; Caplan, A.I.; Vunjak-Novakovic, G. Effects of initial seeding density and fluid perfusion rate on formation of tissue-engineered bone. Tissue Eng. Part A 2008, 14, 1809–1820. [Google Scholar] [CrossRef] [PubMed]
- Wendt, D.; Marsano, A.; Jakob, M.; Heberer, M.; Martin, I. Oscillating perfusion of cell suspensions through three-dimensional scaffolds enhances cell seeding efficiency and uniformity. Biotechnol. Bioeng. 2003, 84, 205–214. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Ma, T. Perfusion bioreactor system for human mesenchymal stem cell tissue engineering: Dynamic cell seeding and construct development. Biotechnol. Bioeng. 2005, 91, 482–493. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Ogawa, R. Effect of hydrostatic pressure on bone regeneration using human mesenchymal stem cells. Tissue Eng. Part A 2012, 18, 2106–2113. [Google Scholar] [CrossRef] [PubMed]
- Egger, D.; Spitz, S.; Fischer, M.; Handschuh, S.; Glösmann, M.; Friemert, B.; Egerbacher, M.; Kasper, C. Application of a Parallelizable Perfusion Bioreactor for Physiologic 3D Cell Culture. Cells Tissues Organs 2017, 203, 316–326. [Google Scholar] [CrossRef] [PubMed]
- Gugerell, A.; Neumann, A.; Kober, J.; Tammaro, L.; Hoch, E.; Schnabelrauch, M.; Kamolz, L.; Kasper, C.; Keck, M. Adipose-derived stem cells cultivated on electrospun l-lactide/glycolide copolymer fleece and gelatin hydrogels under flow conditions–aiming physiological reality in hypodermis tissue engineering. Burns 2015, 41, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Sanz-Herrera, J.A.; Kasper, C.; van Griensven, M.; Garcia-Aznar, J.M.; Ochoa, I.; Doblare, M. Mechanical and flow characterization of Sponceram carriers: Evaluation by homogenization theory and experimental validation. J. Biomed. Mater. Res. B Appl. Biomater. 2008, 87, 42–48. [Google Scholar] [CrossRef] [PubMed]
- Fogler, H.S. Elements of Chemical Reaction Engineering; Prentice-Hall PTR: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Vossenberg, P.; Higuera, G.A.; van Straten, G.; van Blitterswijk, C.A.; van Boxtel, A.J.B. Darcian permeability constant as indicator for shear stresses in regular scaffold systems for tissue engineering. Biomech. Model. Mechanobiol. 2009, 8, 499–507. [Google Scholar] [CrossRef] [PubMed]
- Chor, M.V.; Li, W. A permeability measurement system for tissue engineering scaffolds. Meas. Sci. Technol. 2006, 18, 208. [Google Scholar] [CrossRef]
- Steward, A.J.; Kelly, D.J. Mechanical regulation of mesenchymal stem cell differentiation. J. Anat. 2015, 227, 717–731. [Google Scholar] [CrossRef] [PubMed]
- Martin, I.; Wendt, D.; Heberer, M. The role of bioreactors in tissue engineering. TRENDS Biotechnol. 2004, 22, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Jungreuthmayer, C.; Donahue, S.W.; Jaasma, M.J.; Al-Munajjed, A.A.; Zanghellini, J.; Kelly, D.J.; O’Brien, F.J. A comparative study of shear stresses in collagen-glycosaminoglycan and calcium phosphate scaffolds in bone tissue-engineering bioreactors. Tissue Eng. Part A 2008, 15, 1141–1149. [Google Scholar] [CrossRef] [PubMed]
- Fritton, S.P.; Weinbaum, S. Fluid and Solute Transport in Bone: Flow-Induced Mechanotransduction. Annu. Rev. Fluid Mech. 2009, 41, 347–374. [Google Scholar] [CrossRef] [PubMed]
- Bilgen, B.; Chang-Mateu, I.M.; Barabino, G.A. Characterization of mixing in a novel wavy-walled bioreactor for tissue engineering. Biotechnol. Bioeng. 2005, 92, 907–919. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Shih, Y.V.; Kuo, T.K.; Lee, O.K.; Wei, Y. Coordinated changes of mitochondrial biogenesis and antioxidant enzymes during osteogenic differentiation of human mesenchymal stem cells. Stem Cells 2008, 26, 960–968. [Google Scholar] [CrossRef] [PubMed]
- Pattappa, G.; Heywood, H.K.; De Bruijn, J.D.; Lee, D.A. The metabolism of human mesenchymal stem cells during proliferation and differentiation. J. Cell. Physiol. 2011, 226, 2562–2570. [Google Scholar] [CrossRef] [PubMed]
- Bjerre, L.; Bünger, C.E.; Kassem, M.; Mygind, T. Flow perfusion culture of human mesenchymal stem cells on silicate-substituted tricalcium phosphate scaffolds. Biomaterials 2008, 29, 2616–2627. [Google Scholar] [CrossRef] [PubMed]
- Janssen, F.W.; Oostra, J.; van Oorschot, A.; van Blitterswijk, C.A. A perfusion bioreactor system capable of producing clinically relevant volumes of tissue-engineered bone: In vivo bone formation showing proof of concept. Biomaterials 2006, 27, 315–323. [Google Scholar] [CrossRef] [PubMed]
- Grellier, M.; Bareille, R.; Bourget, C.; Amédée, J. Responsiveness of human bone marrow stromal cells to shear stress. J. Tissue Eng. Regen Med. 2009, 3, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.J.; Batra, N.N.; You, L.D.; Meier, S.C.; Coe, I.A.; Yellowley, C.E.; Jacobs, C.R. Oscillatory fluid flow affects human marrow stromal cell proliferation and differentiation. J. Orthop. Res. 2004, 22, 1283–1289. [Google Scholar] [CrossRef] [PubMed]
- Haeri, S.M.J.; Sadeghi, Y.; Salehi, M.; Farahani, R.M.; Mohsen, N. Osteogenic differentiation of human adipose-derived mesenchymal stem cells on gum tragacanth hydrogel. Biologicals 2016, 44, 123–128. [Google Scholar] [CrossRef] [PubMed]
- Jaasma, M.J.; O’Brien, F.J. Mechanical stimulation of osteoblasts using steady and dynamic fluid flow. Tissue Eng. Part A 2008, 14, 1213–1223. [Google Scholar] [CrossRef] [PubMed]
- Bancroft, G.N.; Sikavitsas, V.I.; Van Den Dolder, J.; Sheffield, T.L.; Ambrose, C.G.; Jansen, J.A.; Mikos, A.G. Fluid flow increases mineralized matrix deposition in 3D perfusion culture of marrow stromal osteoblasts in a dose-dependent manner. Proc. Natl. Acad. Sci.USA 2002, 99, 12600–12605. [Google Scholar] [CrossRef] [PubMed]
- Scaglione, S.; Wendt, D.; Miggino, S.; Papadimitropoulos, A.; Fato, M.; Quarto, R.; Martin, I. Effects of fluid flow and calcium phosphate coating on human bone marrow stromal cells cultured in a defined 2D model system. J. Biomed. Mater. Res. Part A 2008, 86, 411–419. [Google Scholar] [CrossRef] [PubMed]
- Gardel, L.S.; Correia-Gomes, C.; Serra, L.A.; Gomes, M.E.; Reis, R.L. A novel bidirectional continuous perfusion bioreactor for the culture of large-sized bone tissue-engineered constructs. J. Biomed. Mater. Res. Part B Appl. Biomater. 2013, 101, 1377–1386. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Córdova, R.; Mathew, D.A.; Balint, R.; Carrillo-Escalante, H.J.; Cervantes-Uc, J.M.; Hidalgo-Bastida, L.A.; Hernández-Sánchez, F. Indirect three-dimensional printing: A method for fabricating polyurethane-urea based cardiac scaffolds. J. Biomed. Mater. Res. Part A 2016, 104, 1912–1921. [Google Scholar] [CrossRef] [PubMed]
- Porter, B.D.; Lin, A.S.P.; Peister, A.; Hutmacher, D.; Guldberg, R.E. Noninvasive image analysis of 3D construct mineralization in a perfusion bioreactor. Biomaterials 2007, 28, 2525–2533. [Google Scholar] [CrossRef] [PubMed]
- Filipowska, J.; Reilly, G.C.; Osyczka, A.M. A single short session of media perfusion induces osteogenesis in hBMSCs cultured in porous scaffolds, dependent on cell differentiation stage. Biotechnol. Bioeng. 2016, 113, 1814–1824. [Google Scholar] [CrossRef] [PubMed]

| Bioreactor | Inlet Velocity [mm/s] | Average Velocity [mm/s] | Maximum Velocity [mm/s] | Maximum/Average Velocity |
|---|---|---|---|---|
| BR1 | 3.5 | 0.4 | 6.2 | 16.0 |
| 17.7 | 1.9 | 30.0 | 15.4 | |
| 35.4 | 3.9 | 56.5 | 14.5 | |
| BR2 | 3.5 | 0.3 | 1.7 | 5.3 |
| 17.7 | 1.6 | 8.6 | 5.3 | |
| 35.4 | 3.2 | 17.3 | 5.4 |
| Condition | Difference to T [%] | ||
|---|---|---|---|
| Flow rate (mL/min) | 0.6 | 1.5 | 3.0 |
| BR1 empty | 16 ± 0.1 | 12 ± 0.4 | 30 ± 0.3 |
| BR2 empty | 37 ± 1.1 | 27 ± 0.8 | 23 ± 1.7 |
| BR1 with scaffold | 18 ± 0.1 | 31 ± 1.7 | 23 ± 1.7 |
| BR2 with scaffold | 27 ± 0.6 | 16 ± 0.5 | 15 ± 0.7 |
| Flow Rate (mL/min) | Tanks in Series | Bodenstein Number | ||||
|---|---|---|---|---|---|---|
| 0.6 | 1.5 | 3.0 | 0.6 | 1.5 | 3.0 | |
| BR1 empty | 4.6 | 4.8 | 2.5 | 6.1 | 6.3 | 7.0 |
| BR2 empty | 9.7 | 4.8 | 2.5 | 7.4 | 6.7 | 5.9 |
| BR1 with scaffold | 9.7 | 5.7 | 3.3 | 8.0 | 7.3 | 7.7 |
| BR2 with scaffold | 10.7 | 4.7 | 3.4 | 9.1 | 7.2 | 7.6 |
| Bioreactor | Inlet Velocity [mm/s] | CFD Simulation | Vossenberg Model | ||
|---|---|---|---|---|---|
| Average Shear Stress [10−2 Pa] | Maximum Shear Stress [10−2 Pa] | Average Shear Stress [10−2 Pa] | Maximum Shear Stress [10−2 Pa] | ||
| BR1 | 3.5 | 0.1 | 8.8 | 23.4 | 56.0 |
| 17.7 | 0.4 | 43.4 | 117.2 | 280.0 | |
| 35.4 | 0.8 | 85.3 | 234.4 | 560.0 | |
| BR2 | 3.5 | 0.1 | 4.6 | - | - |
| 17.7 | 0.5 | 22.9 | - | - | |
| 35.4 | 1.0 | 45.4 | - | - | |
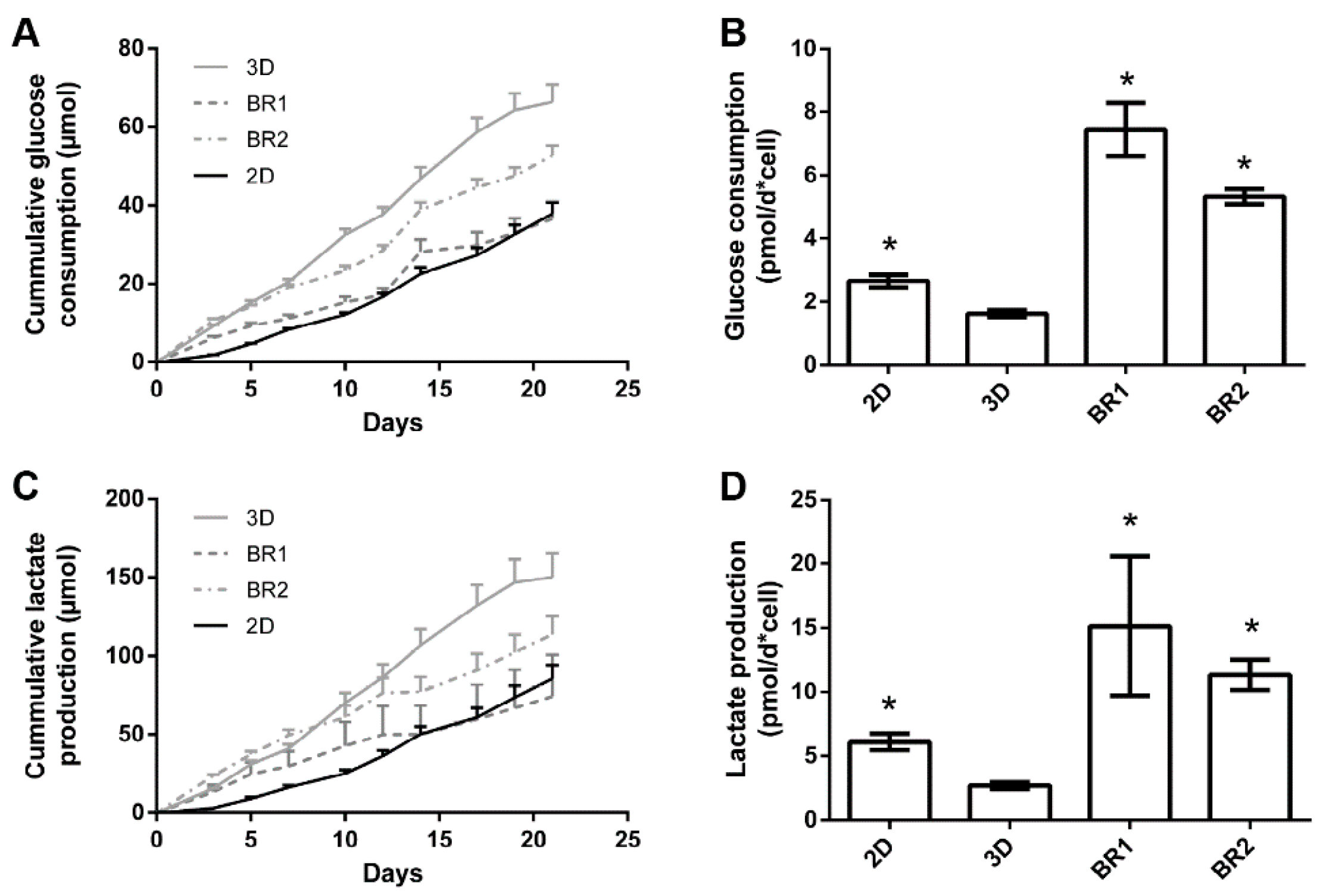
| Condition | Cumulative Glucose Consumption (µmol) | Cumulative Lactate Consumption (µmol) | Ratio |
|---|---|---|---|
| 2D | 37.9 ± 2.9 | 85.5 ± 8.7 | 2.26 |
| 3D | 66.3 ± 4.5 | 150.1 ± 15.0 | 2.26 |
| BR1 | 36.6 ± 4.1 | 74.2 ± 26.7 | 2.15 |
| BR2 | 52.8 ± 2.4 | 113.6 ± 11.7 | 2.02 |
| Aspect | BR1 | BR2 |
|---|---|---|
| Advantages | - Sufficient mixing - Increased matrix mineralization - Increased ALP activity/cell | - Sufficient mixing - Homogeneous flow profile and shear stress distribution throughout the scaffold - Increased proliferation - More homogeneous growth on the scaffold |
| Disadvantages | - Inhomogeneous flow profile and shear stress distribution | - Comparably low matrix mineralization |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egger, D.; Fischer, M.; Clementi, A.; Ribitsch, V.; Hansmann, J.; Kasper, C. Development and Characterization of a Parallelizable Perfusion Bioreactor for 3D Cell Culture. Bioengineering 2017, 4, 51. https://doi.org/10.3390/bioengineering4020051
Egger D, Fischer M, Clementi A, Ribitsch V, Hansmann J, Kasper C. Development and Characterization of a Parallelizable Perfusion Bioreactor for 3D Cell Culture. Bioengineering. 2017; 4(2):51. https://doi.org/10.3390/bioengineering4020051
Chicago/Turabian StyleEgger, Dominik, Monica Fischer, Andreas Clementi, Volker Ribitsch, Jan Hansmann, and Cornelia Kasper. 2017. "Development and Characterization of a Parallelizable Perfusion Bioreactor for 3D Cell Culture" Bioengineering 4, no. 2: 51. https://doi.org/10.3390/bioengineering4020051
APA StyleEgger, D., Fischer, M., Clementi, A., Ribitsch, V., Hansmann, J., & Kasper, C. (2017). Development and Characterization of a Parallelizable Perfusion Bioreactor for 3D Cell Culture. Bioengineering, 4(2), 51. https://doi.org/10.3390/bioengineering4020051