Hybrid Approach to State Estimation for Bioprocess Control
Abstract
:1. Introduction
2. Experimental Data
3. Process Modeling
3.1. State Propagation Model
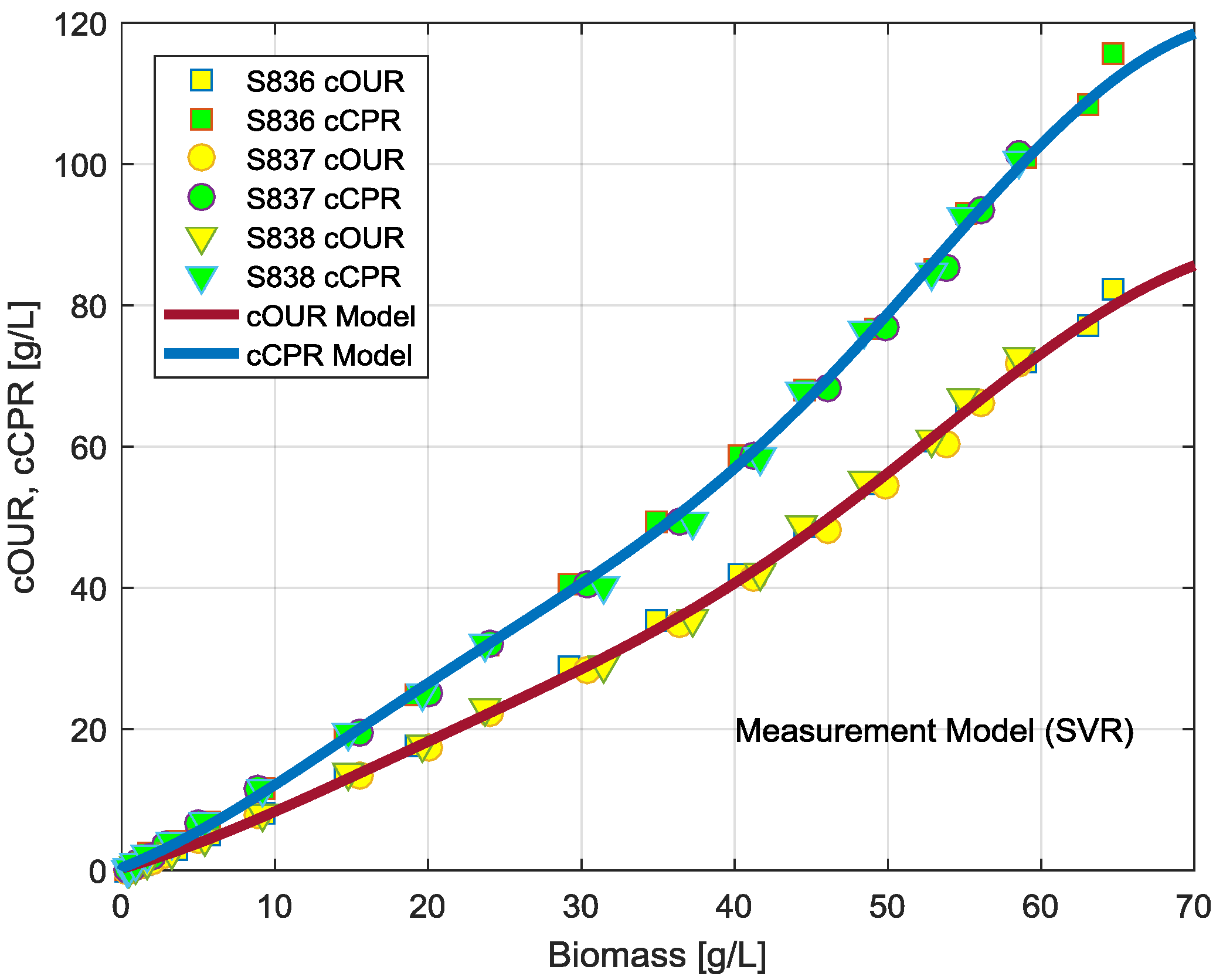
3.2. Observation Model
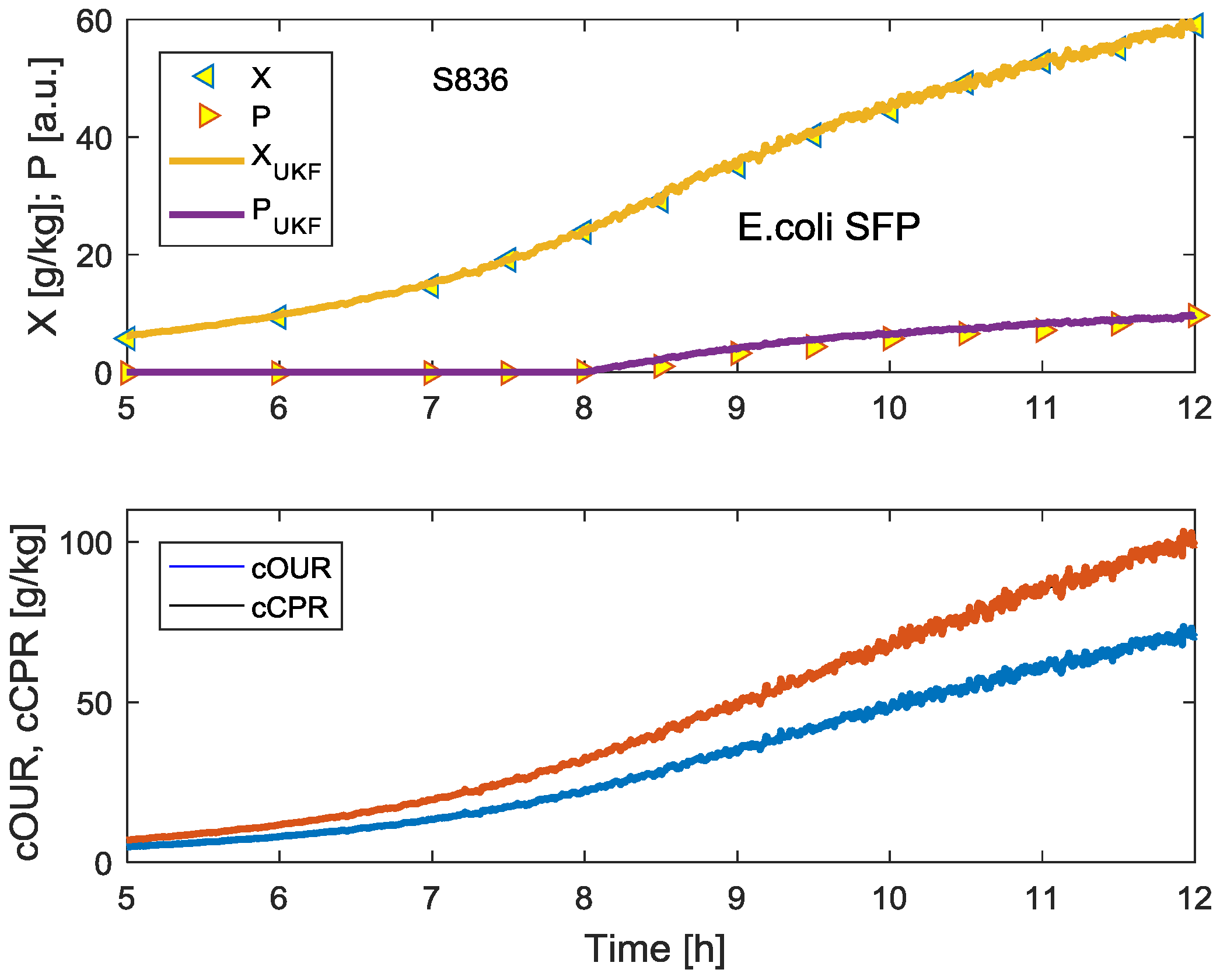
4. Employing the Unscented Kalman Filter
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Dochain, D. Bioprocess Control; John Wiley & Sons: London, UK, 2008. [Google Scholar]
- Mandenius, C.F. Recent developments in the monitoring, modeling and control of biological production systems. Bioprocess Biosyst. Eng. 2004, 26, 347–351. [Google Scholar] [CrossRef] [PubMed]
- Simutis, R.; Lübbert, A. Bioreactor control improves bioprocess performance. Biotechnol. J. 2015, 10, 1115–1130. [Google Scholar] [CrossRef] [PubMed]
- Gade, K. A non-singular horizontal position representation. J. Navig. 2010, 63, 395–417. [Google Scholar] [CrossRef]
- Huang, S.C.; Wang, N.Y.; Li, T.Y.; Lee, Y.C.; Chang, L.F.; Pan, T.H. Financial forecasting by modified Kalman Filters and kernel machines. J. Stat. Mang. Syst. 2013, 16, 163–176. [Google Scholar] [CrossRef]
- Simon, D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar] [CrossRef]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory; Academic Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity and Nonlinear Approaches; John Wiley and Sons: Chichester, UK, 2006. [Google Scholar]
- Stephanopoulos, G.; San, K.Y. Studies on on-line bioreactor identification: Theory. Biotechnol. Bioeng. 1984, 26, 1176–1188. [Google Scholar] [CrossRef] [PubMed]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Julier, S.J.; Ullmann, J.K. A New Extension of the Kalman Filter to Nonlinear Systems. Available online: https://people.eecs.berkeley.edu/~pabbeel/cs287-fa15/optreadings/JulierUhlmann-UKF.pdf (accessed on 6 March 2017).
- Wan, E.A.; van der Merwe, R. The Unscented Kalman Filter for Nonlinear Estimation. Available online: https://www.seas.harvard.edu/courses/cs281/papers/unscented.pdf ( accessed on 6 March 2017).
- Gustafsson, F.; Hendeby, F.; Some, G. Some Relations between Extended and Unscented Kalman Filters. IEEE Trans. Signal Process. 2012, 60, 545–555. [Google Scholar] [CrossRef]
- Schaepe, S.; Kuprijanov, A.; Simutis, R.; Lübbert, A. Avoiding overfeeding in high cell density fed-batch cultures of E. coli during the production of heterologous proteins. J. Biotechnol. 2014, 192, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Pedelacq, J.D.; Cabantous, S.; Tran, T.; Terwilliger, T.C.; Waldo, G.S. Engineering and characterization of a superfolder green fluorescent protein. Nat. Biotechnol. 2006, 24, 79–88. [Google Scholar] [CrossRef] [PubMed]
- Gnoth, S.; Jenzsch, M.; Simutis, R.; Lübbert, A. Control of cultivation processes for recombinant protein production: A review. Bioprocess Biosyst. Eng. 2007, 31, 21–39. [Google Scholar] [CrossRef] [PubMed]
- Luedeking, R.; Piret, E.L. A kinetic study of the lactic acid fermentation. Batch process at controlled pH. J. Biochem. Microbiol. Technol. Eng. 1959, 1, 393–412. [Google Scholar] [CrossRef]
- Jenzsch, M.; Simutis, R.; Eisbrenner, G.; Stuckrath, I.; Lübbert, A. Estimation of biomass concentrations in fermentation processes for recombinant protein production. Bioprocess Biosyst. Eng. 2006, 29, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Mathworks. Matlab, the Language of Technical Computing; The Mathworks: Natick, MA, USA, 2015. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM—A Library for Support Vector Machines. Available online: http://www.csie.ntu.edu.tw/~cjlin/libsvm (accessed on 6 March 2017).
- Tipping, M. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. 2001, 1, 211–214. [Google Scholar]
- Tipping, M. Bayesian inference: An introduction to principles and practice in machine learning. In Advanced Lectures on Machine Learning; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin, Germany, 2004; pp. 41–62. [Google Scholar]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simutis, R.; Lübbert, A. Hybrid Approach to State Estimation for Bioprocess Control. Bioengineering 2017, 4, 21. https://doi.org/10.3390/bioengineering4010021
Simutis R, Lübbert A. Hybrid Approach to State Estimation for Bioprocess Control. Bioengineering. 2017; 4(1):21. https://doi.org/10.3390/bioengineering4010021
Chicago/Turabian StyleSimutis, Rimvydas, and Andreas Lübbert. 2017. "Hybrid Approach to State Estimation for Bioprocess Control" Bioengineering 4, no. 1: 21. https://doi.org/10.3390/bioengineering4010021
APA StyleSimutis, R., & Lübbert, A. (2017). Hybrid Approach to State Estimation for Bioprocess Control. Bioengineering, 4(1), 21. https://doi.org/10.3390/bioengineering4010021




