Lagrangian Trajectories to Predict the Formation of Population Heterogeneity in Large-Scale Bioreactors
Abstract
:1. Introduction
2. Materials and Methods
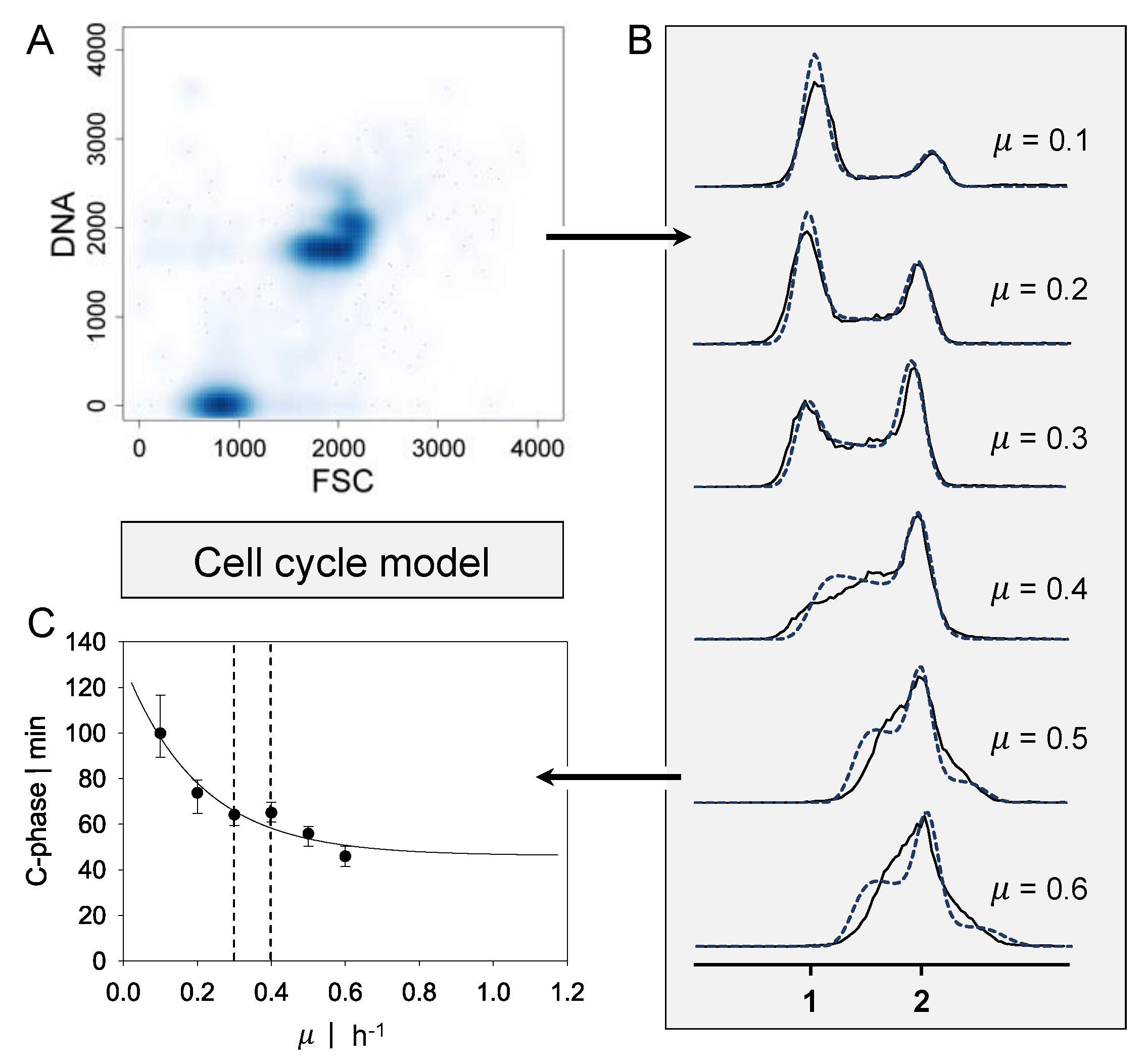
2.1. Cell Cycle Model
2.2. Numerical Simulation
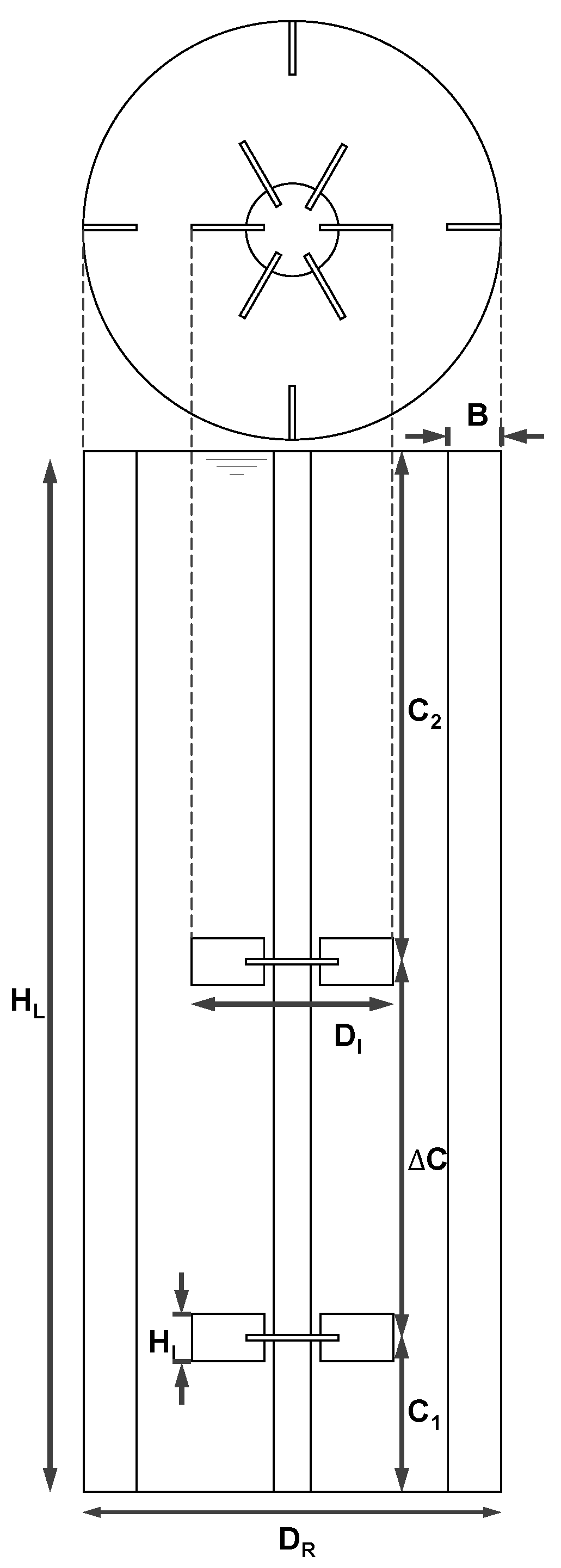
2.2.1. Geometry and Reactor Setup
2.2.2. Simulation Setup
2.3. Statistical Evaluation
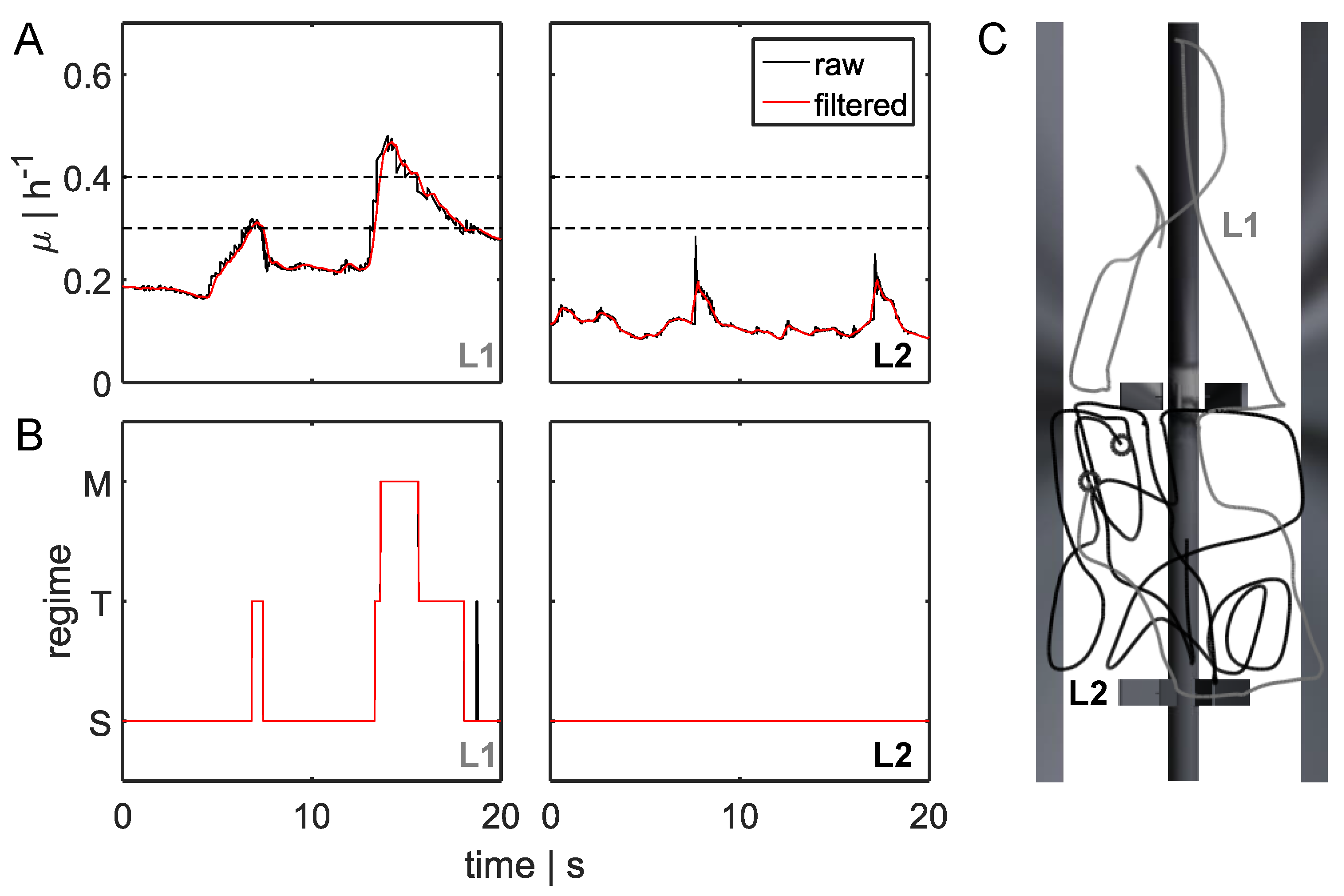
- STM: transition from standard forked to multiforked with a retention time in the transition area.
- STS: standard forked, retention in the transition area, and back to standard forked
- TST: starting from the transition area with retention in a single forked area and back to transition
- MTS: multiforked replication regime to single forked replication with a retention time in the transition area
- MTM: beginning in the multifork regime with retention in the transition area and back to the multifork regime
- TMT: circulation from transition back to transition area with retention time in the multifork replication regime
3. Results and Discussion
3.1. Gradient and Flow Field
3.2. Lagrangian Trajectory
3.3. Statistical Evaluation
3.3.1. Regime Transition Frequency
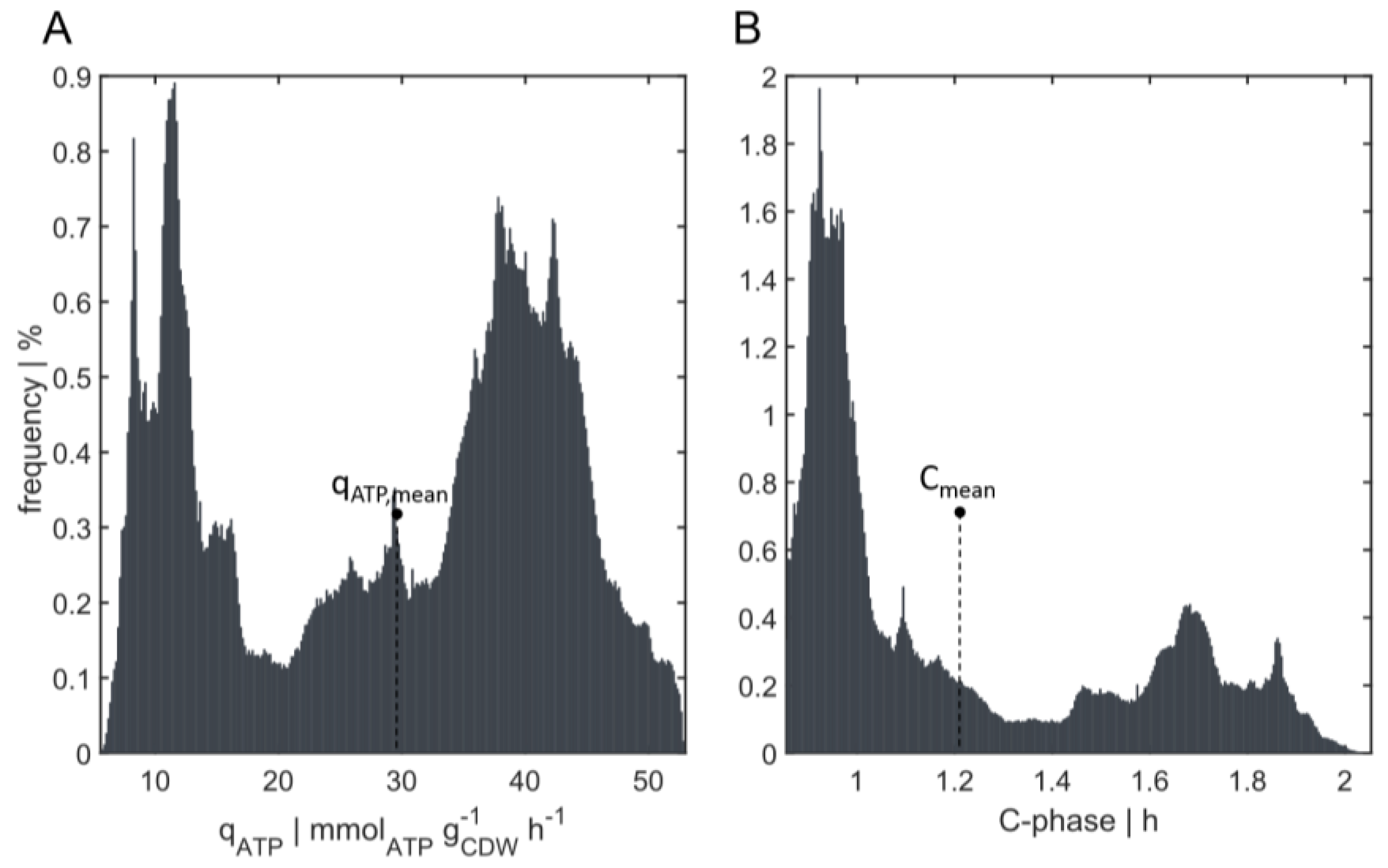
3.3.2. Energy and C-Phase Duration Distribution
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Description | Symbol | Relation |
|---|---|---|
| Reactor diameter | DR | 3.00 m |
| Impeller diameter | DI | 0.43 DR |
| Impeller height | HI | 0.21 DI |
| Bottom clearance | C1 | 0.30 DR |
| Impeller spacing | ΔC | 1.00 DR |
| Upper clearance | C2 | 1.27 DR |
| Baffle width | B | 0.10 DR |
| Liquid height | HL | C1 + ΔC + C2 |
Appendix B
References
- Müller, S.; Harms, H.; Bley, T. Origin and analysis of microbial population heterogeneity in bioprocesses. Curr. Opin. Biotechnol. 2010, 21, 100–113. [Google Scholar] [CrossRef] [PubMed]
- Bylund, F.; Collet, E.; Enfors, S.; Larsson, G. Substrate gradient formation in the large-scale bioreactor lowers cell yield and increases by-product formation. Bioprocess Eng. 1998, 18, 171–180. [Google Scholar] [CrossRef]
- Enfors, S.; Jahic, M.; Rozkov, A.; Xu, B.; Hecker, M.; Ju, B. Physiological responses to mixing in large scale bioreactors. J. Biotechnol. 2001, 85, 175–185. [Google Scholar] [CrossRef]
- Takors, R. Scale-up of microbial processes: Impacts, tools and open questions. J. Biotechnol. 2012, 160, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Makinoshima, H.; Nishimura, A.; Ishihama, A. Fractionation of Escherichia coli cell populations at different stages during growth transition to stationary phase. Mol. Microbiol. 2002, 43, 269–279. [Google Scholar] [CrossRef] [PubMed]
- Lieder, S.; Jahn, M.; Koepff, J.; Müller, S.; Takors, R. Environmental stress speeds up DNA replication in Pseudomonas putida in chemostat cultivations. Biotechnol. J. 2016, 11, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Cooper, S.; Helmstetter, C.E. Chromosome replication and the division cycle of Escherichia coli. J. Mol. Biol. 1968, 31, 519–540. [Google Scholar] [CrossRef]
- Girault, M.; Kim, H.; Arakawa, H.; Matsuura, K.; Odaka, M.; Hattori, A.; Terazono, H.; Yasuda, K. An on-chip imaging droplet-sorting system: A real-time shape recognition method to screen target cells in droplets with single cell resolution. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.H.; Chen, Y.C.; Brien, R.; Yoon, E. Scaling and automation of a high-throughput single-cell-derived tumor sphere assay chip. Lab Chip 2016, 16, 3708–3717. [Google Scholar] [CrossRef] [PubMed]
- Helmstetter, C.E. Timing of Synthetic Activities in the Cell Cycle. In Escherichia coli and Salmonella. Cellular and Molecular Biology; Neidhardt, F.C., Ed.; American Society for Microbiology (ASM) Press: Washington, DC, USA, 1996; pp. 1627–1639. [Google Scholar]
- Müller, S. Modes of cytometric bacterial DNA pattern: A tool for pursuing growth. Cell Prolif. 2007, 40, 621–639. [Google Scholar] [CrossRef] [PubMed]
- Skarstad, K.; Steen, H.B.; Boye, E. Escherichia coli DNA distributions measured by flow cytometry and compared with theoretical computer simulations. J. Bacteriol. 1985, 163, 661–668. [Google Scholar] [PubMed]
- Larsson, G.; Törnkvist, M.; Ståhl Wernersson, E.; Trägårdh, C.; Noorman, H.; Enfors, S.O. Substrate gradients in bioreactors: Origin and consequences. Bioprocess Eng. 1996, 14, 281–289. [Google Scholar] [CrossRef]
- Noorman, H.; Morud, K.; Hjertager, B.H.; Traegaardh, C.; Larsson, G.; Enfors, S.O. CFD modeling and verification of flow and conversion in a 1 m3 bioreactor. BHR Gr. Conf. Ser. Publ. 1993, 5, 241–258. [Google Scholar]
- Schmalzriedt, S.; Jenne, M.; Mauch, K.; Reuss, M. Integration of physiology and fluid dynamics. Adv. Biochem. Eng. 2003, 80, 19–68. [Google Scholar]
- Morchain, J.; Gabelle, J.-C.; Cockx, A. A coupled population balance model and CFD approach for the simulation of mixing issues in lab-scale and industrial cioreactors. Am. Inst. Chem. Eng. 2014, 60, 27–40. [Google Scholar] [CrossRef]
- Bezzo, F.; Macchietto, S.; Pantelides, C.C. General hybrid multizonal/CFD approach for bioreactor modeling. AIChE J. 2003, 49, 2133–2148. [Google Scholar] [CrossRef]
- Mantzaris, N.V.; Liou, J.; Daoutidis, P.; Srienc, F. Numerical solution of a mass structured cell population balance model in an environment of changing substrate concentration. J. Biotechnol. 1999, 71, 157–174. [Google Scholar]
- Henson, M.A. Dynamic modeling of microbial cell populations. Curr. Opin. Biotechnol. 2003, 14, 460–467. [Google Scholar] [CrossRef]
- Lapin, A.; Müller, D.; Reuss, M. Dynamic behavior of microbial populations in stirred bioreactors simulated with Euler-Lagrange methods: Traveling along the lifelines of single cells. Ind. Eng. Chem. Res. 2004, 43, 4647–4656. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.; Deshmukh, A.T.; Xia, J.; Reuss, M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Euler-Lagrange computational fluid dynamics for (bio)reactor scale-down: An analysis of organism life-lines. Eng. Life Sci. 2016, 16, 652–663. [Google Scholar] [CrossRef] [PubMed]
- Lieder, S. Deciphering Population Dynamics as a Key for Process Optimization; University of Stuttgart: Stuttgart, Germany, 2014. [Google Scholar]
- Keasling, J.D.; Kuo, H.; Vahanian, G. A Monte Carlo simulation of the Escherichia coli cell cycle. J. Theor. Biol. 1995, 176, 411–30. [Google Scholar] [CrossRef] [PubMed]
- Van Duuren, J.B.J.H.; Puchałka, J.; Mars, A.E.; Bücker, R.; Eggink, G.; Wittmann, C.; Dos Santos, V.A.P.M. Reconciling in vivo and in silico key biological parameters of Pseudomonas putida KT2440 during growth on glucose under carbon-limited condition. BMC Biotechnol. 2013, 13, 93. [Google Scholar] [CrossRef] [PubMed]
- Pirt, S.J. The maintenance energy of bacteria in growing cultures. Proc. R. Soc. Lond. Ser. B. Biol. Sci. 1965, 163, 224–231. [Google Scholar] [CrossRef]
- Löffler, M.; Simen, J.D.; Jäger, G.; Schäferhoff, K.; Freund, A.; Takors, R. Engineering E. coli for large-scale production—Strategies considering ATP expenses and transcriptional responses. Metab. Eng. 2016, 38, 73–85. [Google Scholar] [CrossRef] [PubMed]
- Lieder, S.; Jahn, M.; Seifert, J.; von Bergen, M.; Müller, S.; Takors, R. Subpopulation-proteomics reveal growth rate, but not cell cycling, as a major impact on protein composition in Pseudomonas putida KT2440. AMB Express 2014, 4, 71. [Google Scholar] [CrossRef] [PubMed]

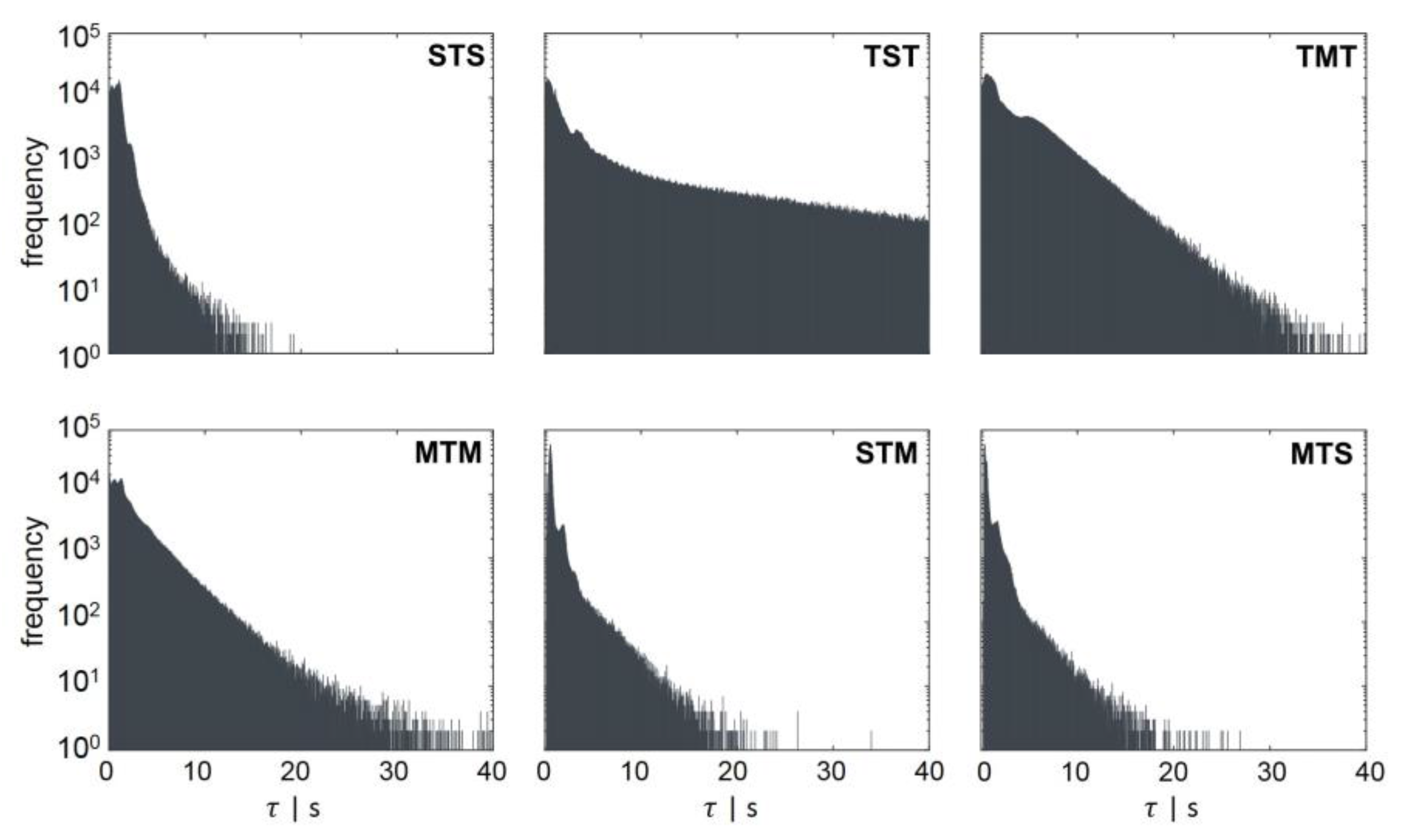
| Regime Transition | [s] | [s] |
|---|---|---|
| STS | 0.99 | 3.7 |
| TST | 8.54 | 73.5 |
| TMT | 3.53 | 16.25 |
| MTM | 2.45 | 13 |
| STM | 0.95 | 6.6 |
| MTS | 0.88 | 5.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuschel, M.; Siebler, F.; Takors, R. Lagrangian Trajectories to Predict the Formation of Population Heterogeneity in Large-Scale Bioreactors. Bioengineering 2017, 4, 27. https://doi.org/10.3390/bioengineering4020027
Kuschel M, Siebler F, Takors R. Lagrangian Trajectories to Predict the Formation of Population Heterogeneity in Large-Scale Bioreactors. Bioengineering. 2017; 4(2):27. https://doi.org/10.3390/bioengineering4020027
Chicago/Turabian StyleKuschel, Maike, Flora Siebler, and Ralf Takors. 2017. "Lagrangian Trajectories to Predict the Formation of Population Heterogeneity in Large-Scale Bioreactors" Bioengineering 4, no. 2: 27. https://doi.org/10.3390/bioengineering4020027
APA StyleKuschel, M., Siebler, F., & Takors, R. (2017). Lagrangian Trajectories to Predict the Formation of Population Heterogeneity in Large-Scale Bioreactors. Bioengineering, 4(2), 27. https://doi.org/10.3390/bioengineering4020027