Development of a Computationally Efficient CFD Method for Blood Flow Analysis Following Flow Diverter Stent Deployment and Its Application to Treatment Planning
Abstract
1. Introduction
2. Materials and Methods
2.1. Case Selection
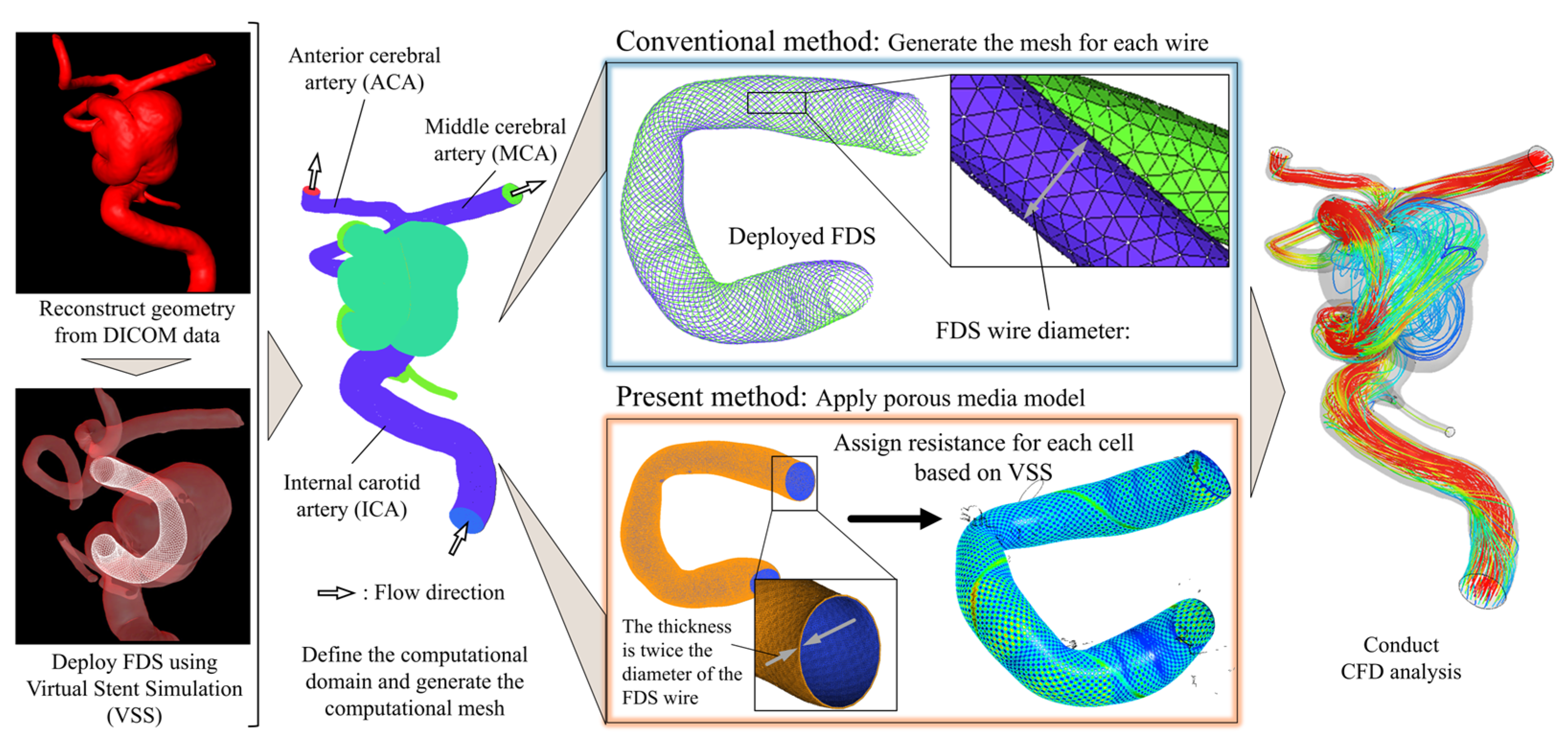
2.2. Outline of the Analysis and Development
2.3. Development of LDPM for FDSs
2.4. Analysis Conditions
3. Results
3.1. Clinical Overview of the Selected Cases
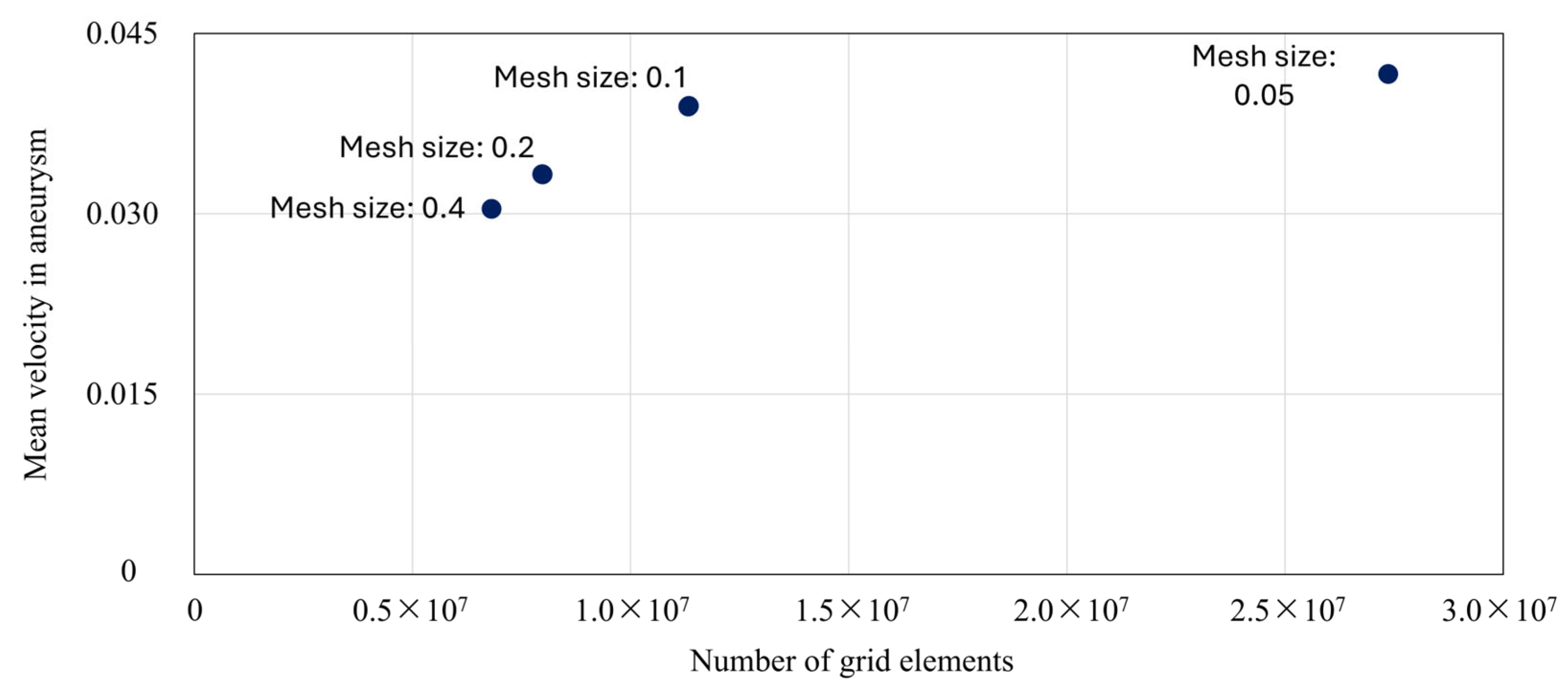
3.2. Grid Independence in CFD Analysis
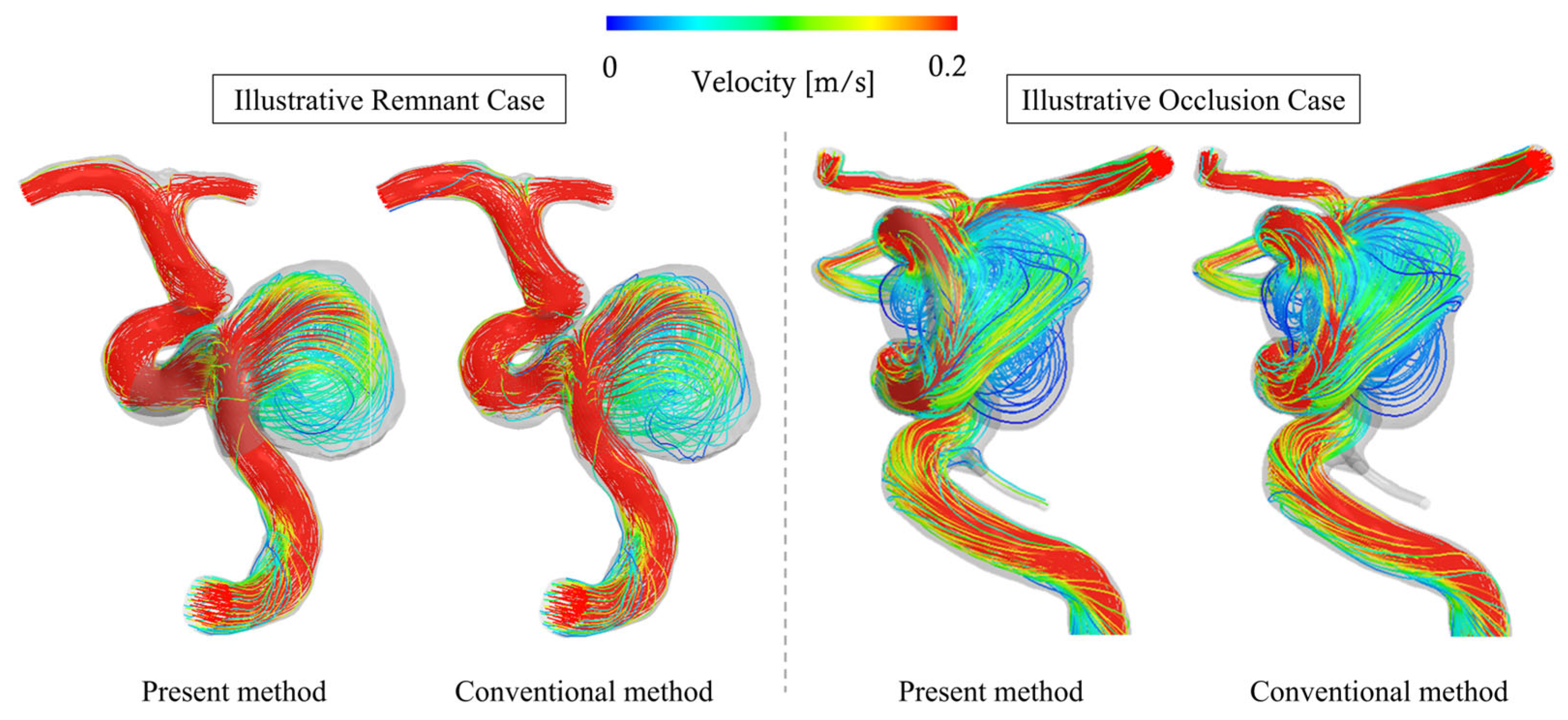
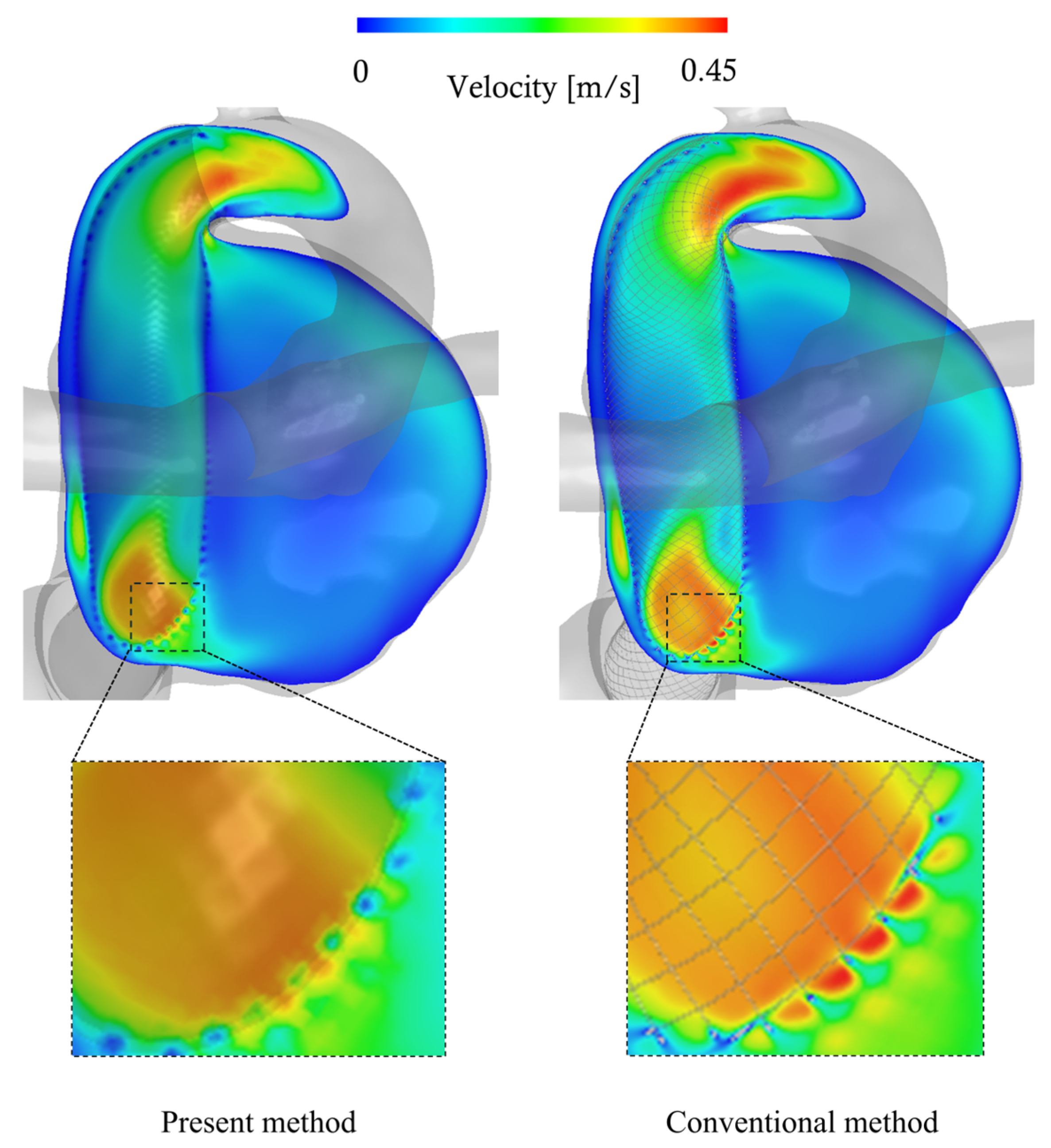
3.3. Comparison with Conventional Method
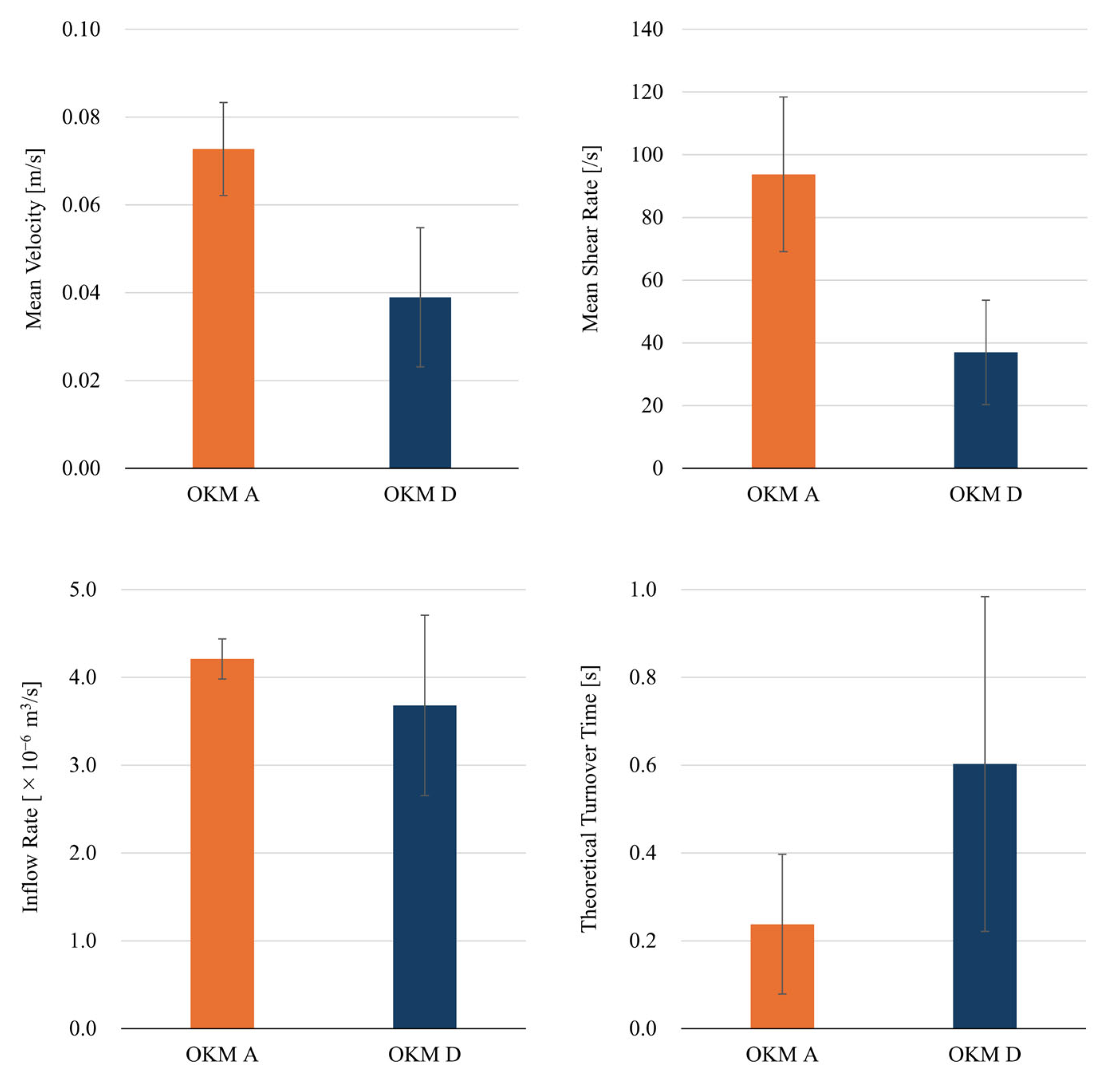
3.4. Comparison Between Total-Filling (OKM Grade A) and Occlusion (OKM Grade D) Cases
3.5. Evaluation of the Impact of FDS Size and Deployment Position
3.6. Effects of Coil-Assisted Treatment on the Illustrative Total-Filling Case
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DSA | Digital Subtraction Angiography |
| FDS | Flow Diverter Stent |
| iPM | inhomogeneous porous medium |
| LDPM | Local Density Porous Model |
| OKM | O’Kelly–Marotta |
| PED | Pipeline Embolization Device |
| SAH | subarachnoid hemorrhage |
| VER | Volume Embolization Ratio |
References
- Vlak, M.H.; Algra, A.; Brandenburg, R.; Rinkel, G.J. Prevalence of unruptured intracranial aneurysms, with emphasis on sex, age, comorbidity, country, and time period: A systematic review and meta-analysis. Lancet Neurol. 2011, 10, 626–636. [Google Scholar] [CrossRef] [PubMed]
- Connolly, E.S., Jr.; Rabinstein, A.A.; Carhuapoma, J.R.; Derdeyn, C.P.; Dion, J.; Higashida, R.T.; Hoh, B.L.; Kirkness, C.J.; Naidech, A.M.; Ogilvy, C.S.; et al. Guidelines for the management of aneurysmal subarachnoid hemorrhage: A guideline for healthcare professionals from the American Heart Association/American Stroke Association. Stroke 2012, 43, 1711–1737. [Google Scholar] [CrossRef]
- Schievink, W.I.; Wijdicks, E.F.; Parisi, J.E.; Piepgras, D.G.; Whisnant, J.P. Sudden death from aneurysmal subarachnoid hemorrhage. Neurology 1995, 45, 871–874. [Google Scholar] [CrossRef] [PubMed]
- Al-Khindi, T.; Macdonald, R.L.; Schweizer, T.A. Cognitive and functional outcome after aneurysmal subarachnoid hemorrhage. Stroke 2010, 41, e519–e536. [Google Scholar] [CrossRef]
- Ma, Y.; Krepuska, M.; Madjidyar, J.; Schubert, T.; Thurner, P.; Kulcsar, Z. Ongoing geometric remodeling of the parent artery after flow-diverter stent reconstruction in cerebral aneurysms: The device design matters. World Neurosurg. 2024, 182, e597–e601. [Google Scholar] [CrossRef] [PubMed]
- Vivanco-Suarez, J.; Mendez-Ruiz, A.; Farooqui, M.; Bekelis, K.; Singer, J.A.; Javed, K.; Altschul, D.J.; Fifi, J.T.; Matsoukas, S.; Cooper, J.; et al. Safety and efficacy of the Surpass Streamline for intracranial aneurysms (SESSIA): A multi-center US experience pooled analysis. Interv. Neuroradiol. 2023, 29, 589–598. [Google Scholar] [CrossRef]
- Paliwal, N.; Yu, H.; Xu, J.; Xiang, J.; Siddiqui, A.; Yang, X.; Li, H.; Meng, H. Virtual stenting workflow with vessel-specific initialization and adaptive expansion for neurovascular stents and flow diverters. Comput. Methods Biomech. Biomed. Engin. 2016, 19, 1423–1431. [Google Scholar] [CrossRef]
- Pierot, L.; Wakhloo, A.K. Endovascular treatment of intracranial aneurysms: Current status. Stroke 2013, 44, 2046–2054. [Google Scholar] [CrossRef]
- Starke, R.M.; Turk, A.; Ding, D.; Crowley, R.W.; Liu, K.C.; Chalouhi, N.; Hasan, D.M.; Dumont, A.S.; Jabbour, P.; Durst, C.R.; et al. Technology developments in endovascular treatment of intracranial aneurysms. J. Neurointerv. Surg. 2016, 8, 135–144. [Google Scholar] [CrossRef]
- Nelson, P.K.; Lylyk, P.; Szikora, I.; Wetzel, S.G.; Wanke, I.; Fiorella, D. The Pipeline Embolization Device for the Intracranial Treatment of Aneurysms trial. AJNR Am. J. Neuroradiol. 2011, 32, 34–40. [Google Scholar] [CrossRef]
- Kadirvel, R.; Ding, Y.H.; Dai, D.; Rezek, I.; Lewis, D.A.; Kallmes, D.F. Cellular mechanisms of aneurysm occlusion after treatment with a flow diverter. Radiology 2014, 270, 394–399. [Google Scholar] [CrossRef] [PubMed]
- Fischer, S.; Vajda, Z.; Aguilar Perez, M.; Schmid, E.; Hopf, N.; Bäzner, H.; Henkes, H. Pipeline embolization device (PED) for neurovascular reconstruction: Initial experience in the treatment of 101 intracranial aneurysms and dissections. Neuroradiology 2012, 54, 369–382. [Google Scholar] [CrossRef]
- Brinjikji, W.; Murad, M.H.; Lanzino, G.; Cloft, H.J.; Kallmes, D.F. Endovascular treatment of intracranial aneurysms with flow diverters: A meta-analysis. Stroke 2013, 44, 442–447. [Google Scholar] [CrossRef]
- Becske, T.; Kallmes, D.F.; Saatci, I.; McDougall, C.G.; Szikora, I.; Lanzino, G.; Moran, C.J.; Woo, H.H.; Lopes, D.K.; Berez, A.L.; et al. Pipeline for uncoilable or failed aneurysms: Results from a multicenter clinical trial. Radiology 2013, 267, 858–868. [Google Scholar] [CrossRef] [PubMed]
- Touzé, R.; Gravellier, B.; Rolla-Bigliani, C.; Touitou, V.; Shotar, E.; Lenck, S.; Boch, A.L.; Degos, V.; Sourour, N.A.; Clarençon, F.; et al. Occlusion rate and visual complications with flow-diverter stent placed across the ophthalmic artery’s origin for carotid-ophthalmic aneurysms: A meta-analysis. Neurosurgery 2020, 86, 455–463. [Google Scholar] [CrossRef]
- Hanel, R.A.; Cortez, G.M.; Lopes, D.K.; Nelson, P.K.; Siddiqui, A.H.; Jabbour, P.; Mendes Pereira, V.; István, I.S.; Zaidat, O.O.; Bettegowda, C.; et al. Prospective study on embolization of intracranial aneurysms with the Pipeline device (PREMIER study): 3-year results with the application of a flow diverter specific occlusion classification. J. Neurointerv. Surg. 2023, 15, 248–254. [Google Scholar] [CrossRef]
- O’Kelly, C.J.; Krings, T.; Fiorella, D.; Marotta, T.R. A novel grading scale for the angiographic assessment of intracranial aneurysms treated using flow diverting stents. Interv. Neuroradiol. 2010, 16, 133–137. [Google Scholar] [CrossRef]
- Fujimura, S.; Brehm, A.; Takao, H.; Uchiyama, Y.; Karagiozov, K.; Fukudome, K.; Yamamoto, M.; Murayama, Y.; Psychogios, M.N. Hemodynamic characteristics and clinical outcome for intracranial aneurysms treated with the Derivo Embolization Device, a novel second-generation flow diverter. World Neurosurg. 2022, 159, e252–e259. [Google Scholar] [CrossRef]
- Zhang, M.; Tupin, S.; Anzai, H.; Kohata, Y.; Shojima, M.; Suzuki, K.; Okamoto, Y.; Tanaka, K.; Yagi, T.; Fujimura, S.; et al. Implementation of computer simulation to assess flow diversion treatment outcomes: Systematic review and meta-analysis. J. Neurointerv. Surg. 2021, 13, 164–170. [Google Scholar] [CrossRef]
- Chong, W.; Zhang, Y.; Qian, Y.; Lai, L.; Parker, G.; Mitchell, K. Computational hemodynamics analysis of intracranial aneurysms treated with flow diverters: Correlation with clinical outcomes. AJNR Am. J. Neuroradiol. 2014, 35, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Mut, F.; Raschi, M.; Scrivano, E.; Bleise, C.; Chudyk, J.; Ceratto, R.; Lylyk, P.; Cebral, J.R. Association between hemodynamic conditions and occlusion times after flow diversion in cerebral aneurysms. J. Neurointerv. Surg. 2015, 7, 286–290. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Y.; Zhao, X.; Verrelli, D.I.; Chong, W.; Ohta, M.; Qian, Y. Haemodynamic effects of stent diameter and compaction ratio on flow-diversion treatment of intracranial aneurysms: A numerical study of a successful and an unsuccessful case. J. Biomech. 2017, 58, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Paliwal, N.; Jaiswal, P.; Tutino, V.M.; Shallwani, H.; Davies, J.M.; Siddiqui, A.H.; Rai, R.; Meng, H. Outcome prediction of intracranial aneurysm treatment by flow diverters using machine learning. Neurosurg. Focus. 2018, 45, E7. [Google Scholar] [CrossRef] [PubMed]
- Beppu, M.; Tsuji, M.; Ishida, F.; Shirakawa, M.; Suzuki, H.; Yoshimura, S. Computational fluid dynamics using a porous media setting predicts outcome after flow-diverter treatment. AJNR Am. J. Neuroradiol. 2020, 41, 2107–2113. [Google Scholar] [CrossRef]
- Uchiyama, Y.; Fujimura, S.; Takao, H.; Suzuki, T.; Hayakawa, M.; Ishibashi, T.; Karagiozov, K.; Fukudome, K.; Murayama, Y.; Yamamoto, M.; et al. Hemodynamic investigation of the effectiveness of a two overlapping flow diverter configuration for cerebral aneurysm treatment. Bioengineering 2021, 8, 143. [Google Scholar] [CrossRef]
- Reymond, P.; Bernava, G.; Brina, O.; Hofmeister, J.; Rosi, A.; Lövblad, K.O.; Machi, P. A novel method for brain aneurysms computed fluid dynamics analysis after flow diverter stent implantation based on micro-computed tomography reconstruction. J. Biomech. 2025, 186, 112634. [Google Scholar] [CrossRef]
- Augsburger, L.; Reymond, P.; Rufenacht, D.A.; Stergiopulos, N. Intracranial stents being modeled as a porous medium: Flow simulation in stented cerebral aneurysms. Ann. Biomed. Eng. 2011, 39, 850–863. [Google Scholar] [CrossRef]
- Yadollahi-Farsani, H.; Scougal, E.; Herrmann, M.; Wei, W.; Frakes, D.; Chong, B. Numerical study of hemodynamics in brain aneurysms treated with flow diverter stents using porous medium theory. Comput. Methods Biomech. Biomed. Engin. 2019, 22, 961–971. [Google Scholar] [CrossRef] [PubMed]
- Abdehkakha, A.; Hammond, A.L.; Patel, T.R.; Siddiqui, A.H.; Dargush, G.F.; Meng, H. Cerebral aneurysm flow diverter modeled as a thin inhomogeneous porous medium in hemodynamic simulations. Comput. Biol. Med. 2021, 139, 104988. [Google Scholar] [CrossRef]
- Fujimura, S.; Kan, I.; Takao, H.; Uchiyama, Y.; Ishibashi, T.; Otani, K.; Fukudome, K.; Murayama, Y.; Yamamoto, M. Development of a virtual stent deployment application to estimate patient-specific braided stent sizes. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2021, 2021, 4184–4187. [Google Scholar] [CrossRef]
- Takao, H.; Murayama, Y.; Otsuka, S.; Qian, Y.; Mohamed, A.; Masuda, S.; Yamamoto, M.; Abe, T. Hemodynamic differences between unruptured and ruptured intracranial aneurysms during observation. Stroke 2012, 43, 1436–1439. [Google Scholar] [CrossRef]
- Umeda, Y.; Ishida, F.; Tsuji, M.; Furukawa, K.; Shiba, M.; Yasuda, R.; Toma, N.; Sakaida, H.; Suzuki, H. Computational fluid dynamics (CFD) using porous media modeling predicts recurrence after coiling of cerebral aneurysms. PLoS ONE 2017, 12, e0190222. [Google Scholar] [CrossRef]
- Fujimura, S.; Takao, H.; Suzuki, T.; Uchiyama, Y.; Tanaka, K.; Otani, K.; Ishibashi, T.; Fukudome, K.; Mamori, H.; Yamamoto, M.; et al. Blood flow analysis in coil embolized aneurysms: Difference between porous media and real coil geometry model. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2018, 2018, 1331–1334. [Google Scholar] [CrossRef]
- Idelchik, I.E. Handbook of Hydraulic Resistance; Hemisphere Publishing Corp.: Washington, DC, USA, 1986. [Google Scholar]
- Uchiyama, Y.; Fujimura, S.; Takao, H.; Suzuki, T.; Ishibashi, T.; Otani, K.; Karagiozov, K.; Fukudome, K.; Yamamoto, H.; Yamamoto, M.; et al. Role of patient-specific blood properties in computational fluid dynamics simulation of flow diverter deployed cerebral aneurysms. Technol. Health Care 2022, 30, 839–850. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, H.; Kawamura, K.; Omura, K.; Tokudome, S. Development of a compact-sized falling needle rheometer for measurement of flow properties of fresh human blood. Int. J. Thermophys. 2010, 31, 2361–2379. [Google Scholar] [CrossRef]
- Yamamoto, H.; Yabuta, T.; Negi, Y.; Horikawa, D.; Kawamura, K.; Tamura, E.; Tanaka, K.; Ishida, F. Measurement of human blood viscosity using Falling Needle Rheometer and the correlation to the Modified Herschel-Bulkley model equation. Heliyon 2020, 6, e04792. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Karmonik, C.; Yu, Y.; Lv, N.; Shi, Z.; Liu, J.M.; Huang, Q. Modeling flow diverters using a porous medium approach: A fast alternative to virtual flow diverter deployment. World Neurosurg. 2022, 164, e501–e508. [Google Scholar] [CrossRef]
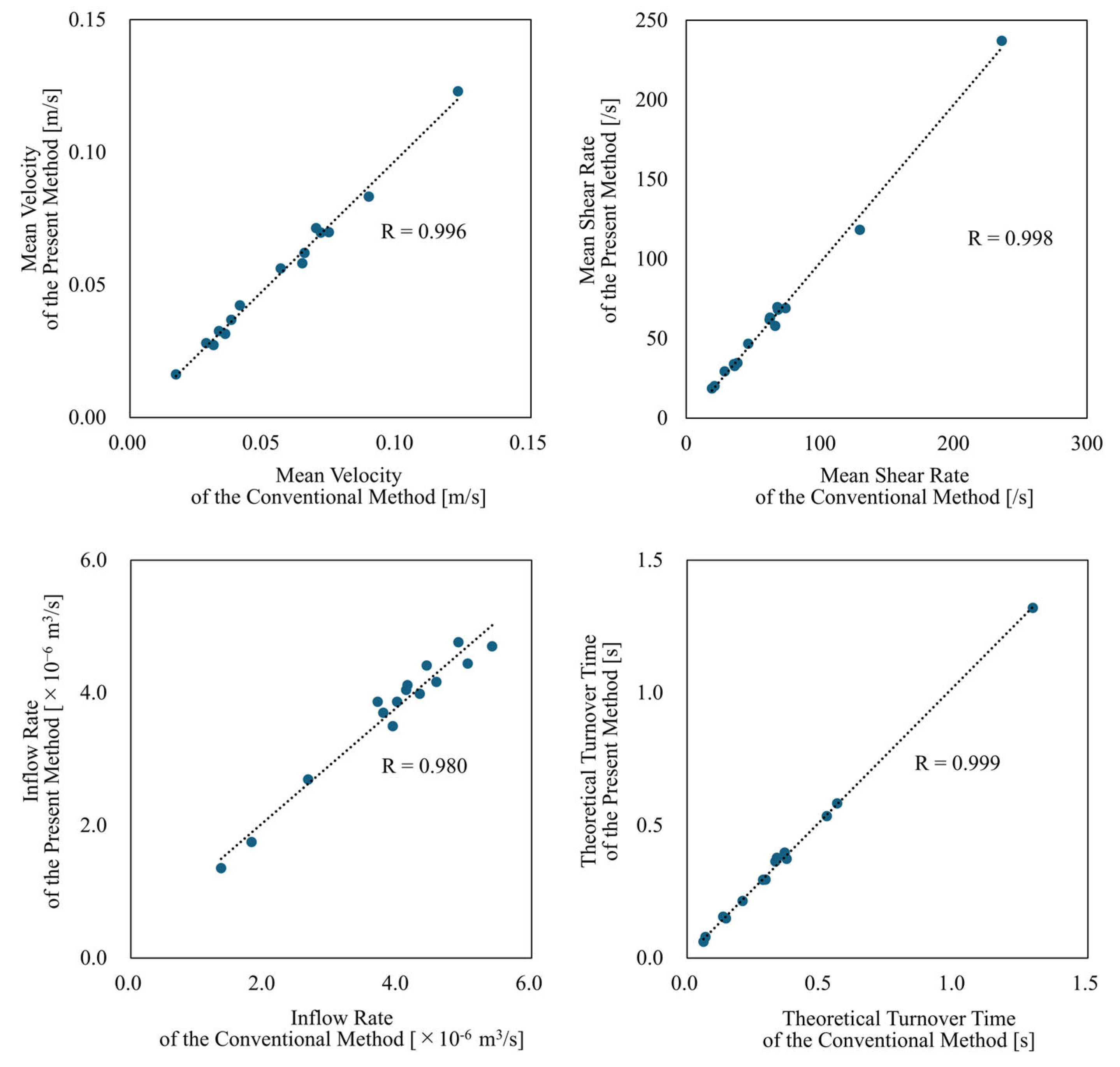
| Conventional Method | Present Method | Relative Error or Reduction [%] | ||
|---|---|---|---|---|
| Mean Velocity | [m/s] | 0.056 ± 0.027 | 0.054 ± 0.027 | −4.03 ± 4.56 |
| Mean Shear Rate | [/s] | 66.3 ± 52.7 | 64.1 ± 52.5 | −3.77 ± 4.78 |
| Inflow Rate | [×10−6 m3/s] | 3.88 ± 1.10 | 3.69 ± 0.973 | −4.13 ± 5.17 |
| Theoretical Turnover Time | [s] | 0.352 ± 0.288 | 0.366 ± 0.293 | −5.04 ± 5.19 |
| Number of Grid Elements | [×10−6] | 213.2 ± 65.9 | 7.44 ± 2.24 | −96.4 ± 1.07 |
| Data Size | [GB] | 11.1 ± 3.32 | 0.526 ± 0.162 | −95.1 ± 1.55 |
| Original with Pipeline 4.5 × 20 | Position A with Pipeline 5.0 × 20 (Change Rate) | Position B with Pipeline 5.0 × 20 (Change Rate) | Pipeline 4.5 × 20 with one Coil (Change Rate) | Pipeline 4.5 × 20 with two Coils (Change Rate) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean Velocity | [m/s] | 0.070 | 0.072 | (3.0 [%]) | 0.073 | (4.8 [%]) | 0.038 | (−45.4 [%]) | 0.026 | (−63.1 [%]) |
| Mean Shear Rate | [/s] | 77.6 | 79.9 | (3.0 [%]) | 81.9 | (5.5 [%]) | 41.9 | (−46.0 [%]) | 28.7 | (−63.0 [%]) |
| Inflow Rate | [×10−6 m3/s] | 3.29 | 3.35 | (1.7 [%]) | 3.49 | (6.0 [%]) | 3.28 | (−0.3 [%]) | 3.31 | (0.7 [%]) |
| Theoretical Turnover Time | [s] | 0.520 | 0.511 | (−1.7 [%]) | 0.490 | (−5.7 [%]) | 0.521 | (0.26 [%]) | 0.516 | (−0.7 [%]) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujimura, S.; Kanebayashi, H.; Karagiozov, K.; Sano, T.; Hataoka, S.; Fuga, M.; Kan, I.; Takao, H.; Ishibashi, T.; Yamamoto, M.; et al. Development of a Computationally Efficient CFD Method for Blood Flow Analysis Following Flow Diverter Stent Deployment and Its Application to Treatment Planning. Bioengineering 2025, 12, 881. https://doi.org/10.3390/bioengineering12080881
Fujimura S, Kanebayashi H, Karagiozov K, Sano T, Hataoka S, Fuga M, Kan I, Takao H, Ishibashi T, Yamamoto M, et al. Development of a Computationally Efficient CFD Method for Blood Flow Analysis Following Flow Diverter Stent Deployment and Its Application to Treatment Planning. Bioengineering. 2025; 12(8):881. https://doi.org/10.3390/bioengineering12080881
Chicago/Turabian StyleFujimura, Soichiro, Haruki Kanebayashi, Kostadin Karagiozov, Tohru Sano, Shunsuke Hataoka, Michiyasu Fuga, Issei Kan, Hiroyuki Takao, Toshihiro Ishibashi, Makoto Yamamoto, and et al. 2025. "Development of a Computationally Efficient CFD Method for Blood Flow Analysis Following Flow Diverter Stent Deployment and Its Application to Treatment Planning" Bioengineering 12, no. 8: 881. https://doi.org/10.3390/bioengineering12080881
APA StyleFujimura, S., Kanebayashi, H., Karagiozov, K., Sano, T., Hataoka, S., Fuga, M., Kan, I., Takao, H., Ishibashi, T., Yamamoto, M., & Murayama, Y. (2025). Development of a Computationally Efficient CFD Method for Blood Flow Analysis Following Flow Diverter Stent Deployment and Its Application to Treatment Planning. Bioengineering, 12(8), 881. https://doi.org/10.3390/bioengineering12080881







