Construction of a Structurally Unbiased Brain Template with High Image Quality from MRI Scans of Saudi Adult Females
Abstract
1. Introduction
2. Related Work
| Year | Study | Dataset | Unbiasedness | Image Quality | Efficiency | ||
|---|---|---|---|---|---|---|---|
| Sharpness | Contrast | Robustness | |||||
| 2003 | Rueckert et al. [31] | 25 T1 MRI scans | SDMs + non-rigid registration | – | – | – | – |
| 2004 | Jongen et al. [32] | 96 CT scans | – | – | – | – | Two-step iterative average construction |
| 2004 | Joshi et al. [33] | T1 MRI scans of 50 subjects | Iterative minimization of deformation and intensity dissimilarity | – | – | – | – |
| 2006 | Christensen et al. [34] | 22 T1 MRI scans | Inverse consistent image registration | Averaging reference transformations | – | – | – |
| 2008 | Noblet et al. [35] | 15 T1 MRI scans | – | – | – | – | Symmetric pairwise non-rigid registration with invertible fields |
| 2010 | Avants et al. [36] | T1 MRI scans of 16 subjects | SyGN method | – | – | – | – |
| 2010 | Coupé et al. [37] | 20 T1 MRI scans | MDT algorithm | Patch-based median estimation | – | ||
| 2011 | Fonov et al. [38] | 542 T1, T2, and PD MRI scans | MDT algorithm | ANIMAL registration algorithm | – | – | – |
| 2014 | Zhang et al. [43] | T1 MRI scans of 42 subjects | – | VTE method | – | – | |
| 2017 | Yang et al. [44] | Synthetic + diffusion MRI | – | Patch-based mean-shift algorithm | – | ||
| 2018 | Schuh et al. [46] | 275 T2 MRI scans | group-wise method | Topology-preserving alignment, Laplacian sharpening | – | – | Linear scaling |
| 2018 | Parvathaneni et al. [47] | T1 MRI scans of 41 subjects | Feature-space covariance weighting | – | – | – | – |
| 2019 | Dalca et al. [48] | MNIST + QuickDraw + 7829 T1 MRI scans | Leveraging shared information | Reducing spatial deformations | – | – | Function to generate templates on demand |
| 2020 | Ridwan et al. [51] | 222 T1 MRI scans | Unbiased iterative technique | High-quality scans and accurate spatial matching | – | – | – |
| 2020 | Wang et al. [53] | 4 synthetic images + 20 synthetic 3D volumes + 20 T1 MRI | SMC approach | Iterative minimization of intensity/gradient dissimilarity | – | – | |
| 2023 | Gu et al. [54] | 646 T1 MRI scans | – | DL-mapping sharpening | – | – | Fast DL-registration |
| 2023 | Arthofer et al. [25] | 240 multimodal MRI scans | Unbiased iterative with mid-space affine | Voxel-wise medians | – | – | |
- New Population-Specific Template: We introduce a structural template derived from T1-weighted MRI scans of healthy Saudi female subjects aged 25 to 30. This template addresses a significant gap in the representation of the Saudi population in neuroimaging.
- High-Quality Intensity Estimation: We apply a patch-based intensity estimation approach, combining patch-based median estimation and the mean-shift algorithm, specifically tailored for T1-weighted MRI scans. This technique produces sharper templates with enhanced tissue contrast and robustness to outliers, outperforming traditional voxel-wise averaging.
- Computational Efficiency Enhancements: We enhance processing speed through the parallelization of independent tasks, which further improves the efficiency of the SMC framework. Additionally, we optimize matrix operations by using vectorization and filter out zero-intensity voxels during the patch-based intensity estimation process.
3. Materials and Methods
3.1. Dataset
3.2. Preprocessing
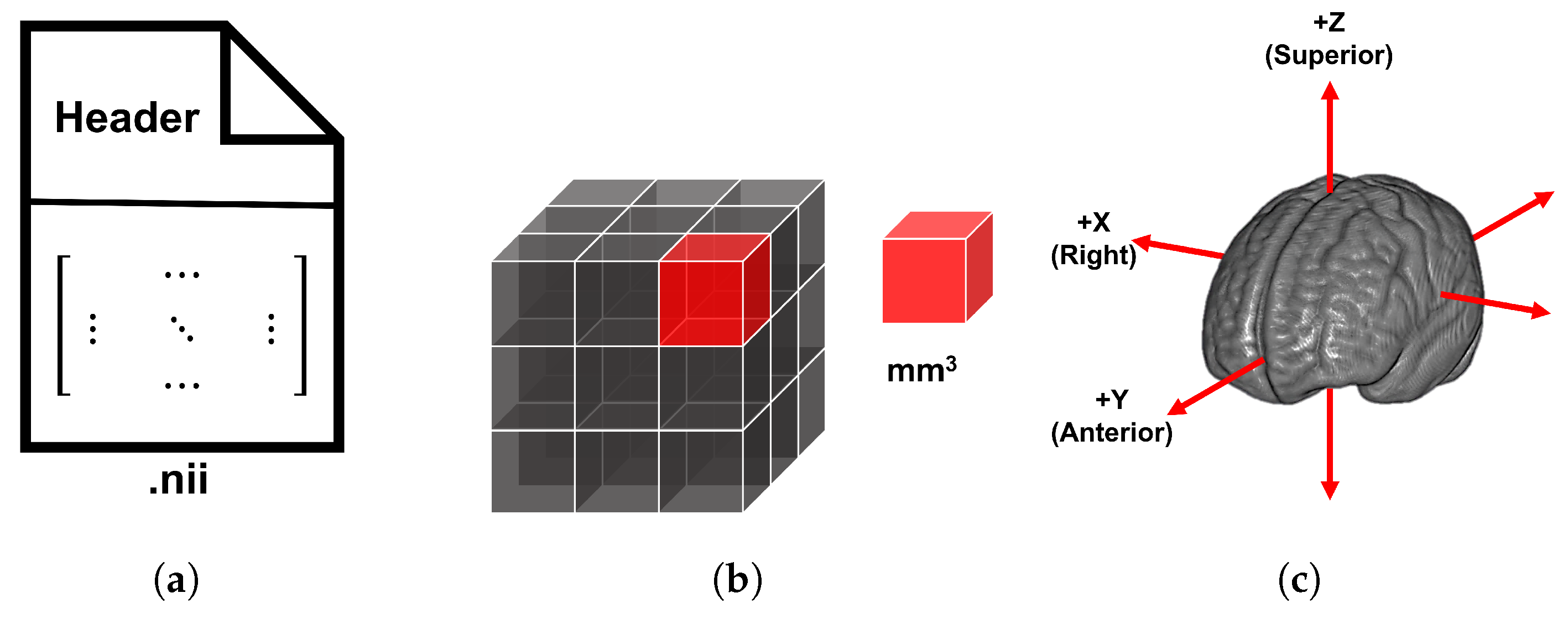
- Variability in raw data, which includes differences in matrix size, voxel size, spatial orientation, and intensity ranges.
- Scanner artifacts, such as bias fields and noise, which can affect image quality.
- Removal of irrelevant anatomical structures, such as non-brain regions, to create a brain-specific template.
| Algorithm 1 Preprocessing Algorithm. |
|
3.2.1. Spatial Normalization
3.2.2. Bias Field Correction
3.2.3. Denoising
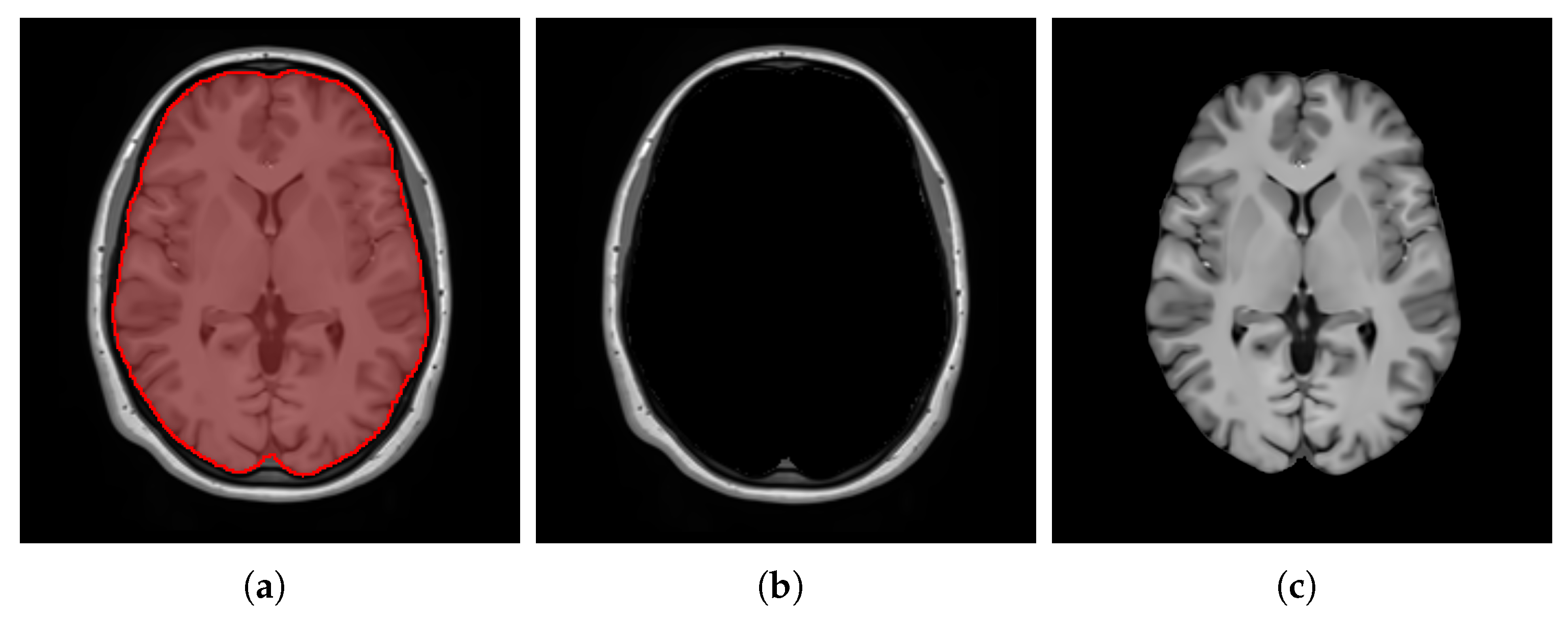
3.2.4. Brain Extraction
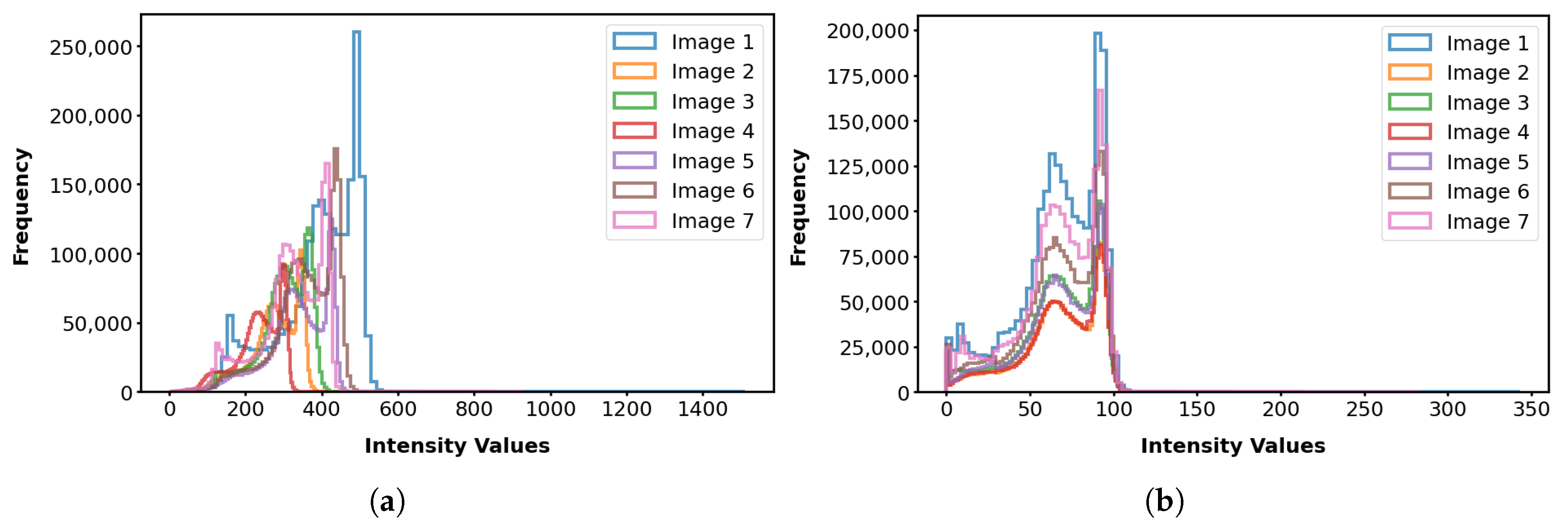
3.2.5. Intensity Normalization
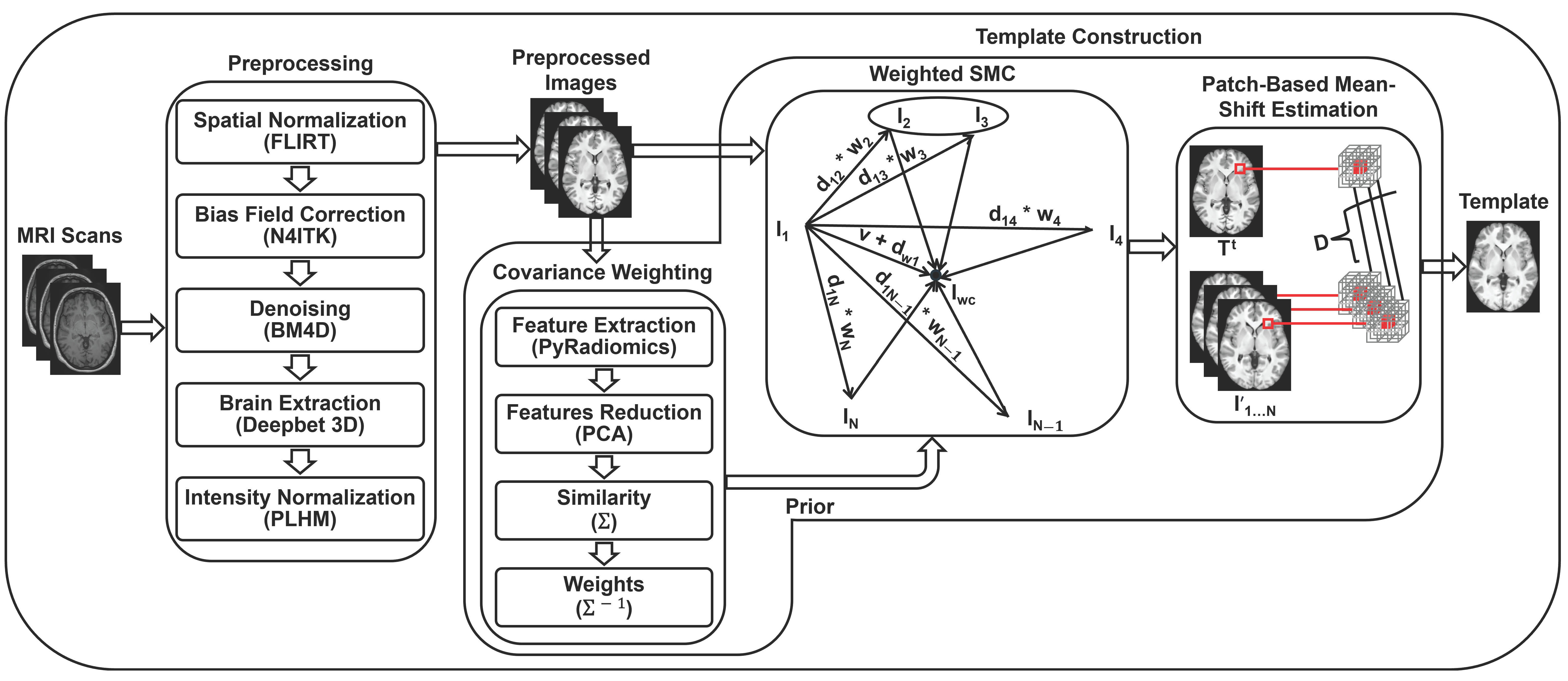
3.3. Template Construction
| Algorithm 2 Template Construction Algorithm. |
|
3.3.1. Covariance Weighting
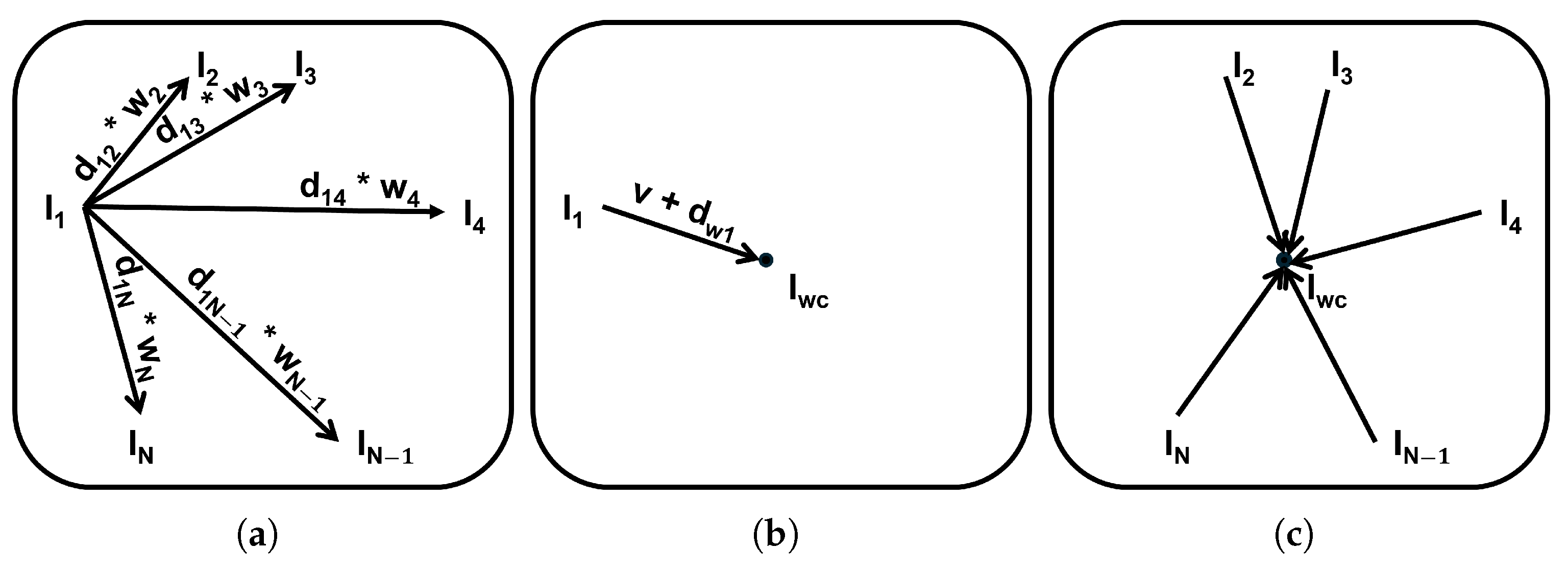
3.3.2. Weighted SMC
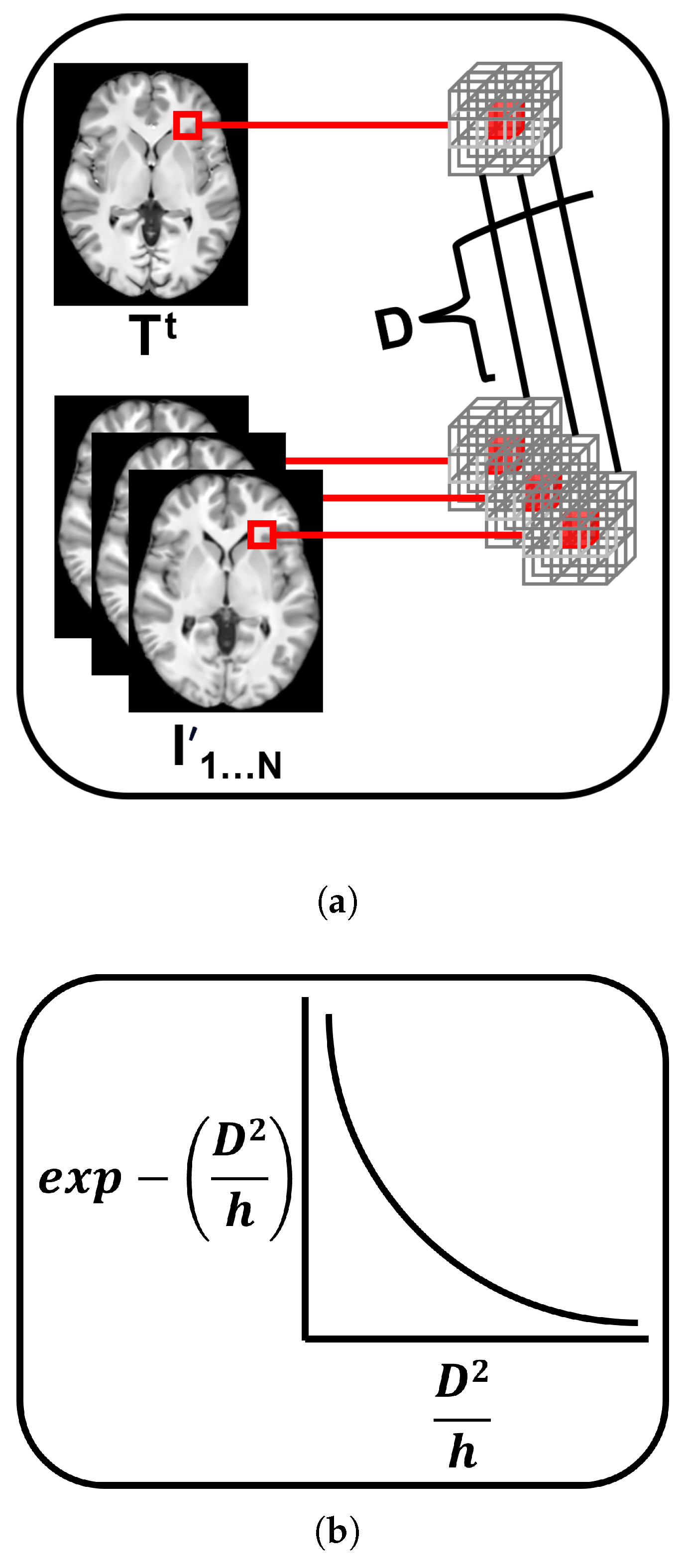
3.3.3. Patch-Based Mean-Shift Estimation
3.4. Evaluation Methods
- Evaluating the structural unbiasedness of the templates computed in Section 3.3.2.
- Assessing the intensity quality of the templates computed in Section 3.3.3, in terms of sharpness, contrast, and robustness to outliers.
- Investigating the necessity of constructing a brain template specifically for Saudi adult females by evaluating its effectiveness as a target registration space in comparison with other population-specific templates.
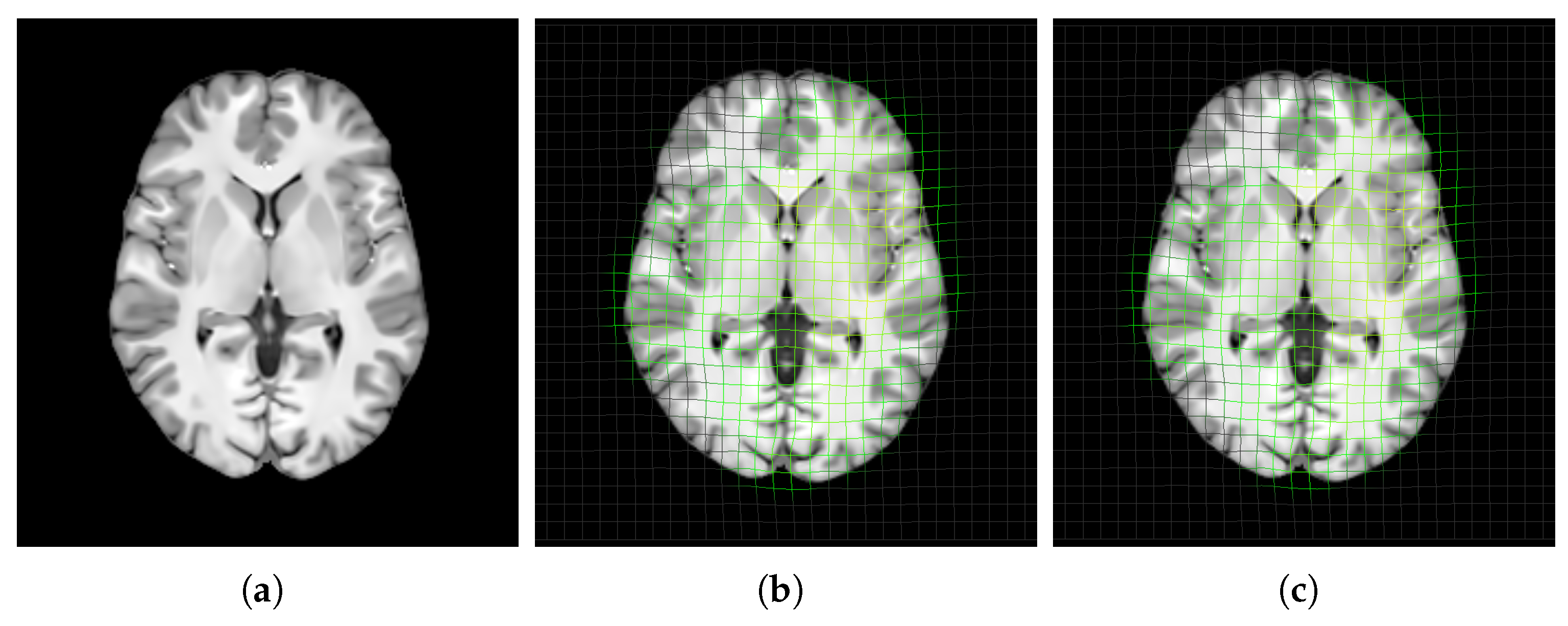
3.4.1. Unbiasedness of Template Structure
3.4.2. Quality of Template Intensity
- SharpnessTo evaluate the sharpness and edge definition of the templates, we computed the magnitude of the gradient for each voxel. Sharp edges and well-defined details correspond to regions with rapid changes in intensity, which are reflected in high gradient magnitudes. To assess the overall sharpness, we averaged the gradient magnitudes across all voxels in the template. This metric—as used in Wang et al. [53]—which we refer to as Average Gradient Magnitude (), quantifies the overall sharpness of the template:where is the intensity value of the template at voxel index v, ∇ is the gradient operator, and M is the total number of voxels in the template.
- ContrastTo evaluate the contrast between white matter (WM) and gray matter (GM) of the templates, we used the Normalized Michelson Contrast [92]. This metric provides a standardized measure of contrast by comparing the maximum intensity of WM to the minimum intensity of GM. To identify WM and GM voxels, we utilized the BrainSuite tool (version 23a) [93] to segment the templates into different tissue types. This allowed us to isolate voxels corresponding to pure WM and GM, excluding those with other tissue types. It is worth noting that we utilized the BrainSuite tool [93] on a local machine, not within the Google Colaboratory environment [57]. This metric, Normalized Michelson Contrast (), quantifies the contrast between WM and GM; higher values indicate greater contrast:where is the maximum intensity value within the WM voxels, and is the minimum intensity value within the GM voxels.
- Robustness to OutliersTo assess the robustness to outliers of the templates, we used the Kullback-Leibler Divergence [94]. This metric, denoted as , measures the similarity between the intensity distributions of the templates and the population. We introduced an outlier image by adding noise to one of the images to make its intensity distribution significantly different. For each template, we computed the between its intensity distribution and the intensity distribution of each image in the population. Lower values indicate greater similarity between the two distributions, with a value of 0 indicating identical distributions:where represents the probability of intensity value x in the template’s distribution, and represents the probability of intensity value x in the population image distribution.
3.4.3. Usability of Saudi Brain Template
4. Results
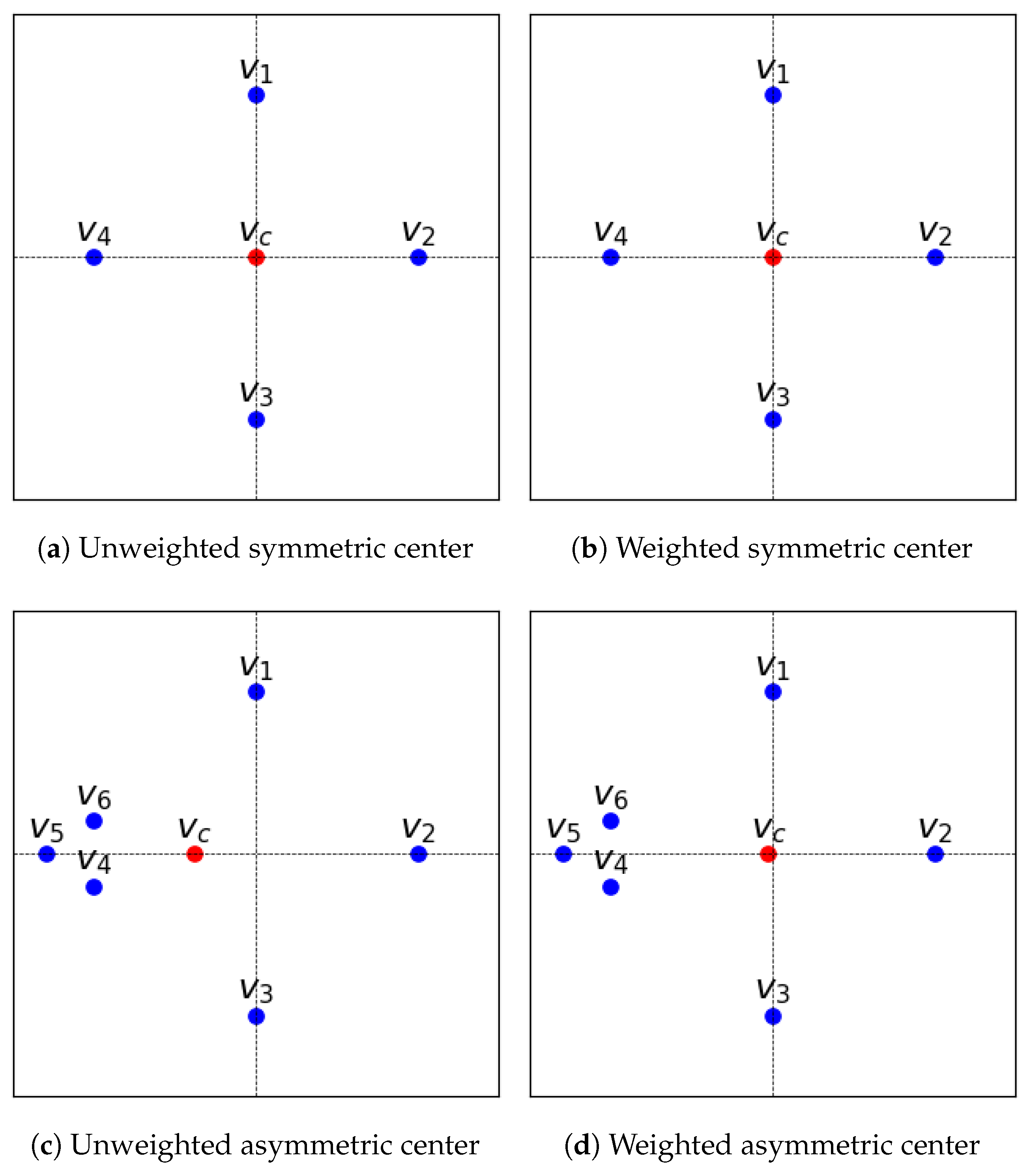
- The unbiasedness of the template structure computed with versus without incorporating weights.
- The quality of template intensity using patch-based estimation versus voxel-based averaging.
- The necessity of using a brain template specifically tailored to healthy Saudi adult females as the standard space for registering subjects from the same population.
4.1. Unbiasedness of Template Structure
4.2. Quality of Template Intensity
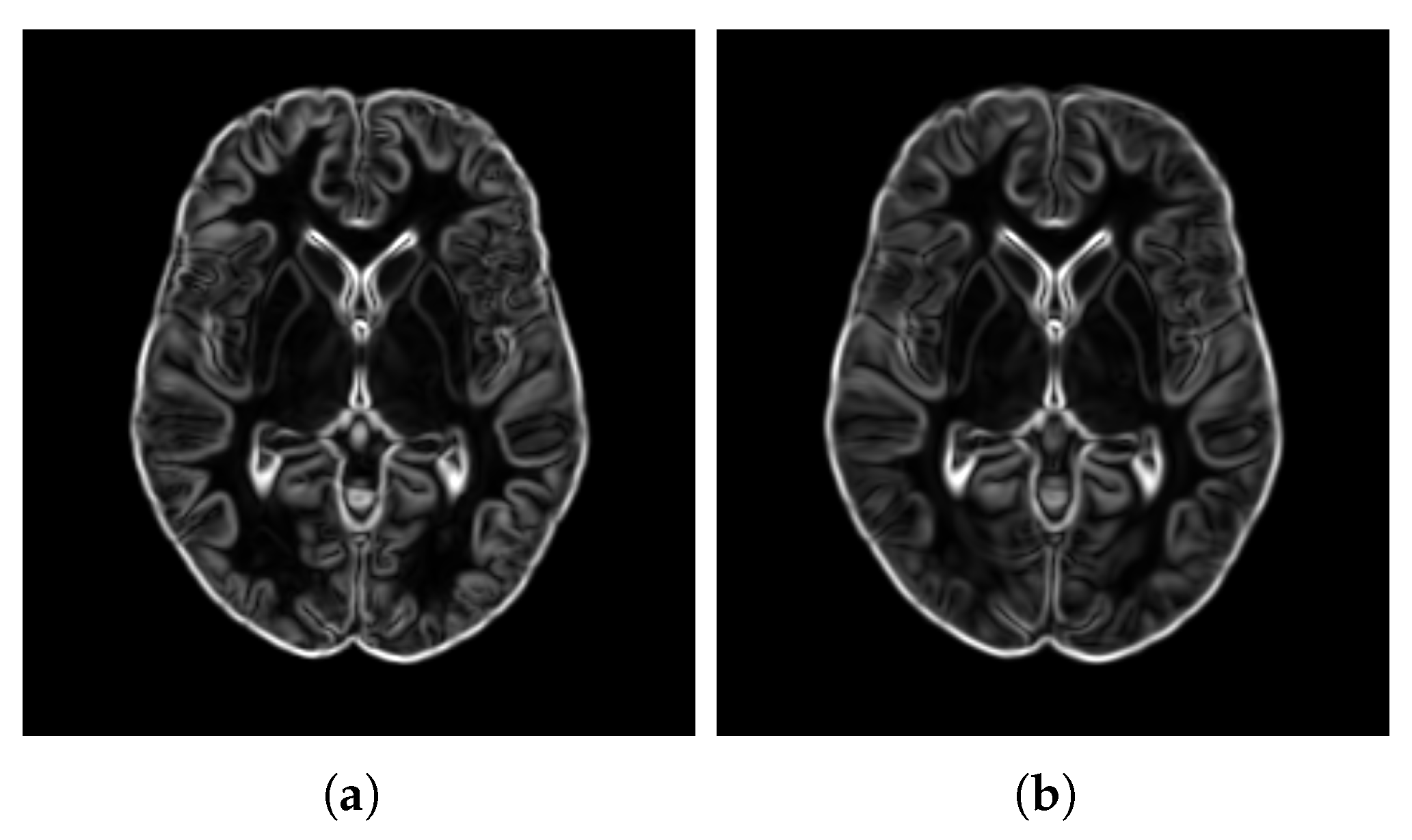
- SharpnessFigure 14 visualizes the gradient magnitude for and , with their corresponding values summarized in Table 4. The value for (60.958) was higher than that of (55.175). The higher value for indicates that the patch-based approach resulted in a template with sharper edges compared with the voxel-based averaging method. This finding suggests that patch-based estimation of template intensity can lead to sharper templates compared with traditional voxel-based averaging.
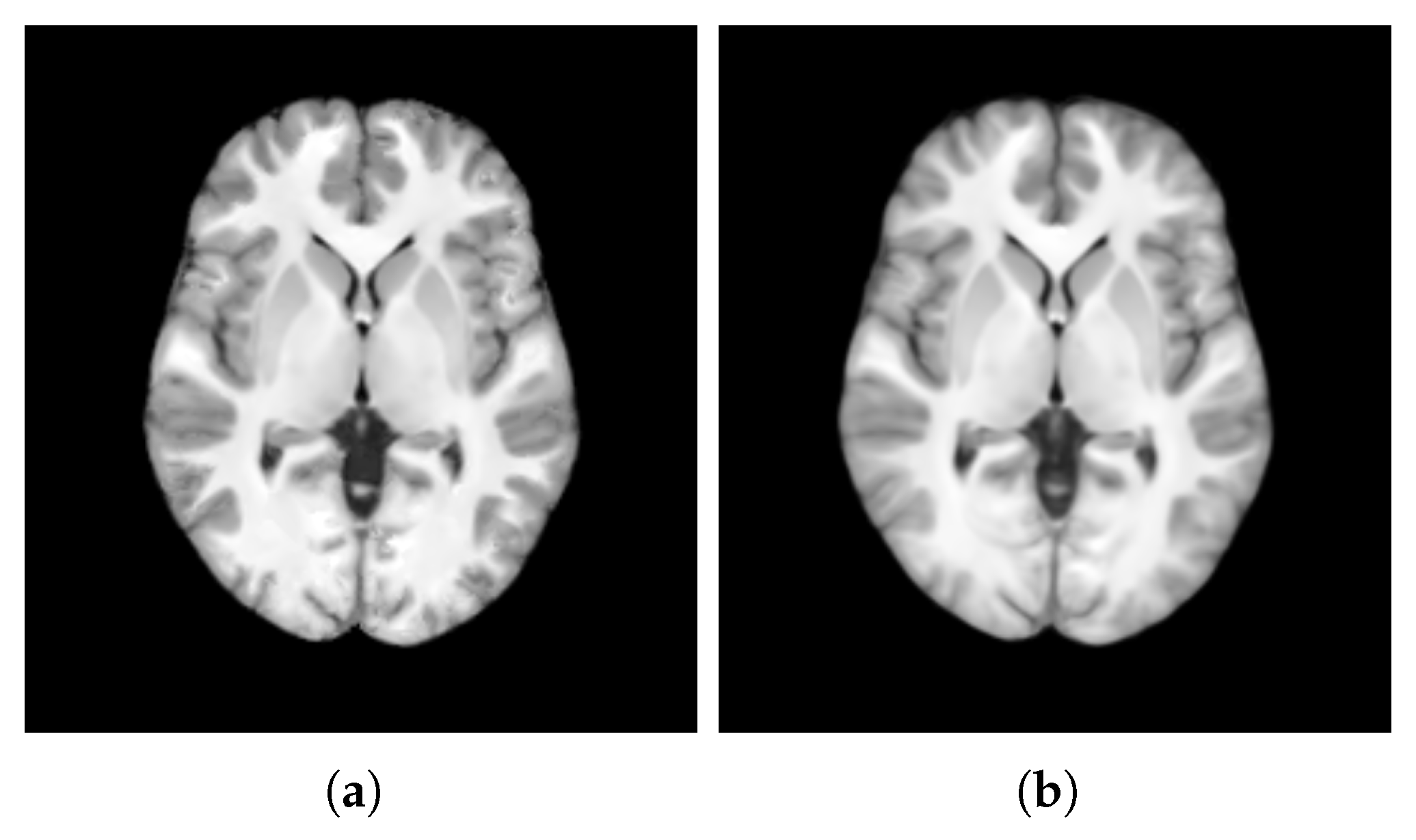
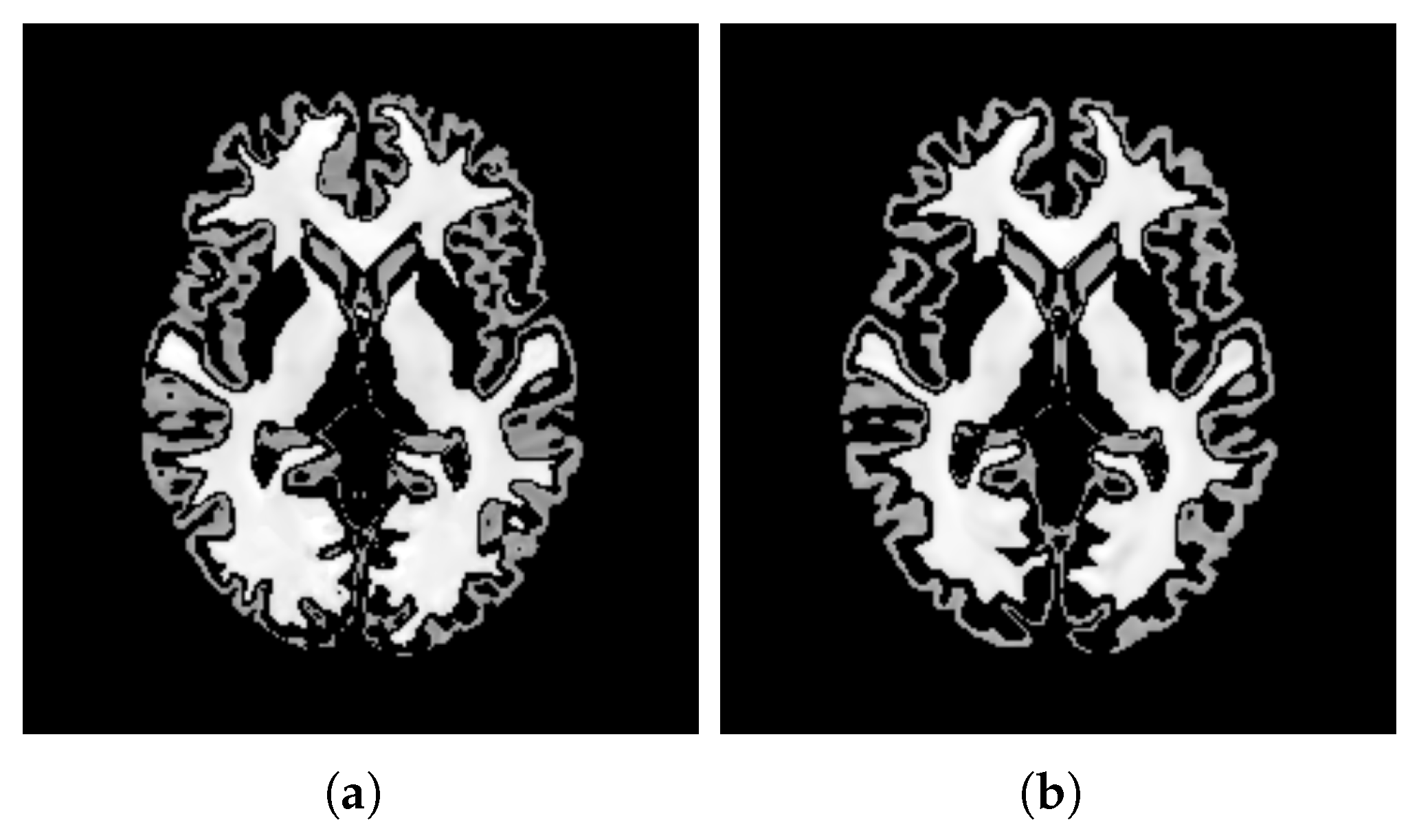
- ContrastTable 4 presents the values calculated for the pure WM and GM regions of the templates generated using the patch-based () and voxel-based () methods. Figure 15 visualizes these pure tissue regions in both templates. As shown in the table, the value for (0.418) is higher than that of (0.393), indicating higher contrast in the former. This suggests that the patch-based approach yields a template with enhanced contrast between these tissues compared with the voxel-based averaging method.
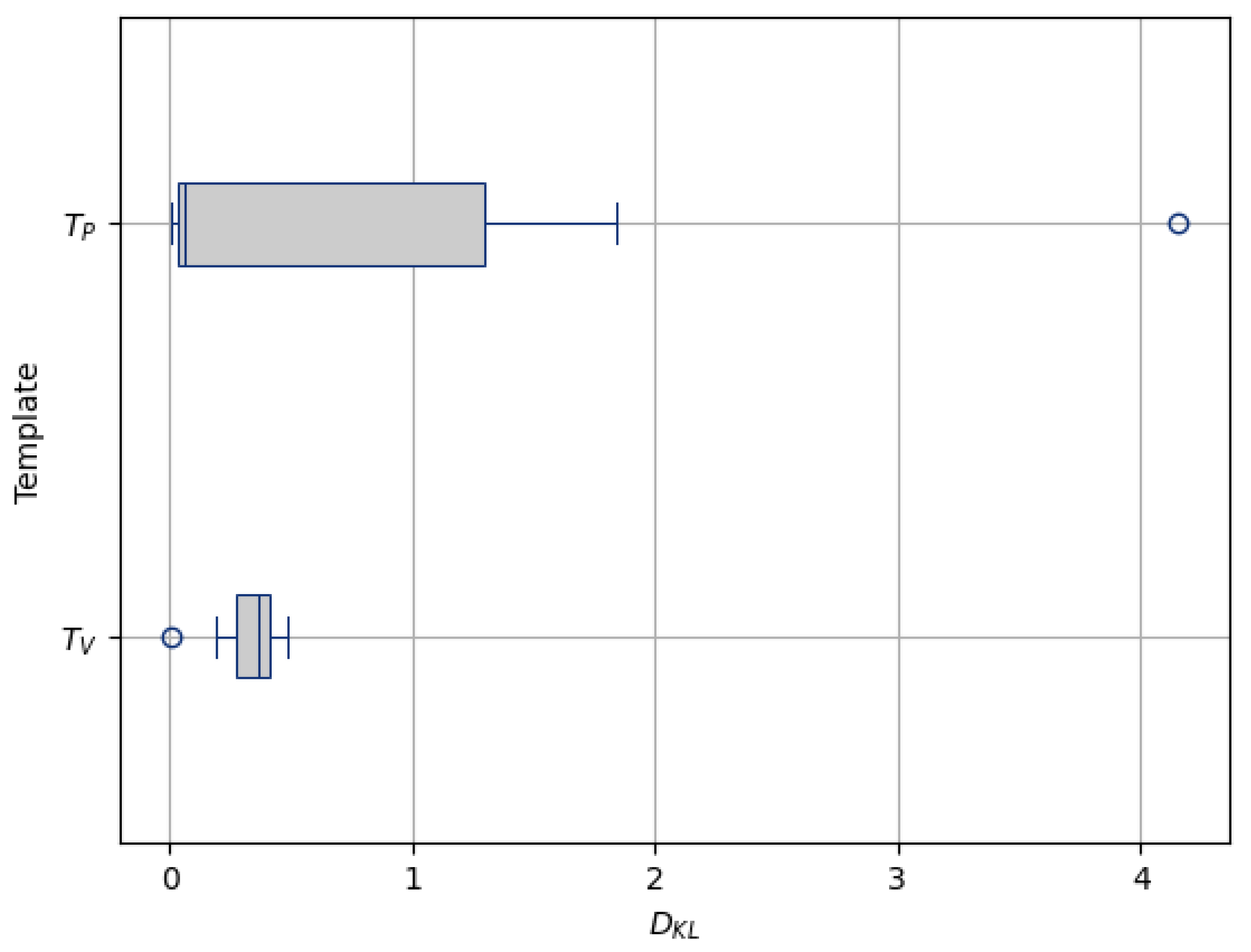
- Robustness to OutliersFigure 16 shows the distribution of the values calculated for each template ( and ) and the population images, with their median values summarized in Table 4. The median value for (0.057) is less than that of (0.368). Also, the value for the introduced outlier image is 4.159 with , while it is 0.001 with , indicating that the former intensity is more similar to the population and is less influenced by outliers. This finding suggests that patch-based estimation of template intensity results in a template that more accurately reflects the most common intensity values in the population and is less sensitive to outliers compared with traditional voxel-based averaging.
4.3. Usability of Saudi Brain Template
5. Discussion
- The current template was constructed using only one subset of the Saudi population (Section 3.1), and templates for other subsets were not developed.
- The sample size for this subset is relatively small, which limits the generalizability of the resulting brain template despite the dataset’s homogeneity and restricts the potential for meaningful statistical comparisons.
- Linear characteristics of the subset (e.g., brain length, width, and height) were not addressed; these were normalized through affine spatial normalization (Section 3.2.1), while the focus remained on nonlinear anatomical details solely (Section 3.3.2).
- The similarity weighting step assigned a single weight per brain image (Section 3.3.1), applied uniformly across all voxels.
- In the template intensity estimation step (Section 3.3.3), all patches were included in each iteration without selective filtering.
- Constructing multiple brain templates for a broader range of Saudi population subsets, using sufficiently large sample sizes and accounting for variations in gender, age groups, and pathological conditions.
- Incorporating multiple imaging modalities (e.g., T2-weighted MRI, CT, fMRI, PET, DTI) to enhance both anatomical and functional relevance of the templates.
- Developing a comprehensive Saudi brain atlas that includes tissue probability maps and region labeling alongside various types of brain and head templates, providing a richer resource for neuroimaging studies.
- Integrating the developed atlas into widely used neuroimaging tools such as FreeSurfer [95], FSL [61,62,63], and SPM [96] to facilitate adoption in research and clinical workflows in Saudi Arabia. This integration could support automated segmentation, early abnormality detection, and treatment or surgical planning, particularly as advanced neuroimaging protocols become more common in clinical practice [97].
- Replacing affine spatial normalization with rigid registration and directly incorporating linear anatomical characteristics into the template construction process to yield more representative templates.
- Using localized similarity weights (rather than a single global weight per image) to improve structural unbiasedness.
- Implementing early discarding of mismatched patches, as proposed by Coupé et al. [91], to reduce computational costs and improve robustness.
- Exploring the effects of different patch sizes on the quality of the constructed template.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| S | Raw scans |
| I | Preprocessed images set |
| N | Number of images |
| Random image from the set I | |
| Aligned I | |
| Weighted center image | |
| Unweighted center image | |
| T | Template |
| t | Iteration counter |
| Template at iteration t | |
| Difference between and | |
| Template from patch-based estimation | |
| Template from voxel-based averaging | |
| F | Features |
| Principal components | |
| Covariance matrix | |
| Inverse of | |
| W | Image similarity weights |
| Normalized image similarity weights | |
| Displacement from to each | |
| Weighted displacement for to reach | |
| Displacement from to center image | |
| Set of template patches | |
| Set of patches | |
| D | Euclidean distances |
| h | Gaussian bandwidths |
| w | nonzero voxel weights |
| nonzero voxel normalized weights | |
| V | Set of nonzero voxel indices |
| K | Number of nonzero voxel indices |
| v | Voxel index |
| * | Element-wise multiplication |
| Weighted Displacement | |
| Average Gradient Magnitude | |
| Normalized Michelson Contrast | |
| Kullback-Leibler Divergence | |
| Maximum intensity in WM | |
| Minimum intensity in GM | |
| The L2-norm | |
| The absolute value | |
| x | Intensity or voxel value |
| M | Number of template voxels |
| Probability of x in template distribution | |
| Probability of x in distribution | |
| Jacobian matrix at v | |
| Determinant of | |
| ∇ | Gradient operator |
| X | Total computational time |
| C | Processing cores |
References
- Bear, M.; Connors, B.; Paradiso, M.A. Neuroscience: Exploring the Brain, Enhanced Edition: Exploring the Brain; Jones & Bartlett Learning: Burlington, MA, USA, 2020. [Google Scholar]
- Squire, L.R.; Bloom, F.E.; Spitzer, N.C.; Gage, F.H.; Albright, T.D. Encyclopedia of Neuroscience; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Ajtai, B.; Masdeu, J.C.; Lindzen, E. Structural Imaging using Magnetic Resonance Imaging and Computed Tomography. In Bradley’s Neurology in Clinical Practice; Daroff, R.B., Jankovic, J., Mazziotta, J.C., Pomeroy, S.L., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 411–458.e7. [Google Scholar]
- Meyer, P.T.; Rijntjes, M.; Hellwig, S.; Klöppel, S.; Weiller, C. Functional Neuroimaging: Functional Magnetic Resonance Imaging, Positron Emission Tomography, and Single-Photon Emission Computed Tomography. In Bradley’s Neurology in Clinical Practice; Daroff, R.B., Jankovic, J., Mazziotta, J.C., Pomeroy, S.L., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 486–503.e5. [Google Scholar]
- Toga, A.; Mazziotta, J. Brain Mapping: The Methods; Academic Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Evans, A.C.; Janke, A.L.; Collins, D.L.; Baillet, S. Brain templates and atlases. Neuroimage 2012, 62, 911–922. [Google Scholar] [CrossRef]
- Mandal, P.K.; Mahajan, R.; Dinov, I.D. Structural Brain Atlases: Design, Rationale, and Applications in Normal and Pathological Cohorts. J. Alzheimer’s Dis. 2012, 31, S169–S188. [Google Scholar] [CrossRef]
- Ciric, R.; Thompson, W.H.; Lorenz, R.; Goncalves, M.; MacNicol, E.E.; Markiewicz, C.J.; Halchenko, Y.O.; Ghosh, S.S.; Gorgolewski, K.J.; Poldrack, R.A.; et al. TemplateFlow: FAIR-sharing of multi-scale, multi-species brain models. Nat. Methods 2022, 19, 1568–1571. [Google Scholar] [CrossRef] [PubMed]
- Team, C.P.P. Chinese Brain PET Template. 2025. Available online: https://www.nitrc.org/projects/cnpet/ (accessed on 4 May 2025).
- Team, F. Oxford-MM Templates. 2025. Available online: https://pages.fmrib.ox.ac.uk/fsl/oxford-mm-templates/ (accessed on 4 May 2025).
- Talairach, J. Co-Planar Stereotaxic Atlas of the Human Brain-3-Dimensional Proportional System: An Approach to Cerebral Imaging; Thieme Medical Publishers: Stuttgart, New York, 1988. [Google Scholar]
- Evans, A.C.; Collins, D.L.; Mills, S.; Brown, E.D.; Kelly, R.L.; Peters, T.M. 3D statistical neuroanatomical models from 305 MRI volumes. In Proceedings of the 1993 IEEE Conference Record Nuclear Science Symposium and Medical Imaging Conference, San Francisco, CA, USA, 31 October–6 November 1993; IEEE: Piscataway, NJ, USA, 1993; pp. 1813–1817. [Google Scholar]
- Mazziotta, J.; Toga, A.; Evans, A.; Fox, P.; Lancaster, J.; Zilles, K.; Woods, R.; Paus, T.; Simpson, G.; Pike, B.; et al. A probabilistic atlas and reference system for the human brain: International Consortium for Brain Mapping (ICBM). Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2001, 356, 1293–1322. [Google Scholar] [CrossRef] [PubMed]
- Mazziotta, J.; Toga, A.; Evans, A.; Fox, P.; Lancaster, J.; Zilles, K.; Woods, R.; Paus, T.; Simpson, G.; Pike, B.; et al. A Four-Dimensional Probabilistic Atlas of the Human Brain. J. Am. Med. Inform. Assoc. 2001, 8, 401–430. [Google Scholar] [CrossRef]
- Tang, Y.; Hojatkashani, C.; Dinov, I.D.; Sun, B.; Fan, L.; Lin, X.; Qi, H.; Hua, X.; Liu, S.; Toga, A.W. The construction of a Chinese MRI brain atlas: A morphometric comparison study between Chinese and Caucasian cohorts. Neuroimage 2010, 51, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Bhalerao, G.V.; Parlikar, R.; Agrawal, R.; Shivakumar, V.; Kalmady, S.V.; Rao, N.P.; Agarwal, S.M.; Narayanaswamy, J.C.; Reddy, Y.J.; Venkatasubramanian, G. Construction of population-specific Indian MRI brain template: Morphometric comparison with Chinese and Caucasian templates. Asian J. Psychiatry 2018, 35, 93–100. [Google Scholar] [CrossRef]
- Pai, P.P.; Mandal, P.K.; Punjabi, K.; Shukla, D.; Goel, A.; Joon, S.; Roy, S.; Sandal, K.; Mishra, R.; Lahoti, R. BRAHMA: Population specific T1, T2, and FLAIR weighted brain templates and their impact in structural and functional imaging studies. Magn. Reson. Imaging 2020, 70, 5–21. [Google Scholar] [CrossRef]
- Yang, G.; Zhou, S.; Bozek, J.; Dong, H.M.; Han, M.; Zuo, X.N.; Liu, H.; Gao, J.H. Sample sizes and population differences in brain template construction. NeuroImage 2020, 206, 116318. [Google Scholar] [CrossRef]
- Wang, H.; Tian, Y.; Liu, Y.; Chen, Z.; Zhai, H.; Zhuang, M.; Zhang, N.; Jiang, Y.; Gao, Y.; Feng, H.; et al. Population-specific brain [18F]-FDG PET templates of Chinese subjects for statistical parametric mapping. Sci. Data 2021, 8, 305. [Google Scholar] [CrossRef]
- Sivaswamy, J.; Thottupattu, A.J.; Mehta, R.; Sheelakumari, R.; Kesavadas, C. Construction of Indian human brain atlas. Neurol. India 2019, 67, 229–234. [Google Scholar] [CrossRef]
- Liang, P.; Shi, L.; Chen, N.; Luo, Y.; Wang, X.; Liu, K.; Mok, V.C.; Chu, W.C.; Wang, D.; Li, K. Construction of brain atlases based on a multi-center MRI dataset of 2020 Chinese adults. Sci. Rep. 2015, 5, 18216. [Google Scholar] [CrossRef]
- Xie, W.; Richards, J.E.; Lei, D.; Zhu, H.; Lee, K.; Gong, Q. The construction of MRI brain/head templates for Chinese children from 7 to 16 years of age. Dev. Cogn. Neurosci. 2015, 15, 94–105. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Yoo, B.I.; Han, J.W.; Lee, J.J.; Lee, E.Y.; Kim, J.H.; Kim, K.W. Construction and validation of brain MRI templates from a Korean normal elderly population. Psychiatry Investig. 2016, 13, 135–145. [Google Scholar] [CrossRef] [PubMed]
- Holla, B.; Taylor, P.A.; Glen, D.R.; Lee, J.A.; Vaidya, N.; Mehta, U.M.; Venkatasubramanian, G.; Pal, P.K.; Saini, J.; Rao, N.P.; et al. A series of five population-specific Indian brain templates and atlases spanning ages 6–60 years. Hum. Brain Mapp. 2020, 41, 5164–5175. [Google Scholar] [CrossRef] [PubMed]
- Arthofer, C.; Smith, S.M.; Douaud, G.; Bartsch, A.; Alfaro-Almagro, F.; Andersson, J.; Lange, F.J. Internally-consistent and fully-unbiased multimodal MRI brain template construction from UK Biobank: Oxford-MM. Imaging Neurosci. 2024, 2, 1–27. [Google Scholar] [CrossRef]
- Geng, X.; Chan, P.H.; Lam, H.S.; Chu, W.C.; Wong, P.C. Brain templates for Chinese babies from newborn to three months of age. NeuroImage 2024, 289, 120536. [Google Scholar] [CrossRef]
- Feng, L.; Li, H.; Oishi, K.; Mishra, V.; Song, L.; Peng, Q.; Ouyang, M.; Wang, J.; Slinger, M.; Jeon, T.; et al. Age-specific gray and white matter DTI atlas for human brain at 33, 36 and 39 postmenstrual weeks. Neuroimage 2019, 185, 685–698. [Google Scholar] [CrossRef]
- Jae, S.L.; Dong, S.L.; Kim, J.; Yu, K.K.; Kang, E.; Kang, H.; Keon, W.K.; Jong, M.L.; Kim, J.J.; Park, H.J.; et al. Development of Korean standard brain templates. J. Korean Med. Sci. 2005, 20, 483–488. [Google Scholar] [CrossRef]
- Xing, W.; Nan, C.; ZhenTao, Z.; Rong, X.; Luo, J.; Zhuo, Y.; DingGang, S.; KunCheng, L. Probabilistic MRI Brain Anatomical Atlases Based on 1000 Chinese Subjects. PLoS ONE 2013, 8, e50939. [Google Scholar] [CrossRef]
- Zhao, T.; Liao, X.; Fonov, V.S.; Wang, Q.; Men, W.; Wang, Y.; Qin, S.; Tan, S.; Gao, J.H.; Evans, A.; et al. Unbiased age-specific structural brain atlases for Chinese pediatric population. NeuroImage 2019, 189, 55–70. [Google Scholar] [CrossRef]
- Rueckert, D.; Frangi, A.; Schnabel, J. Automatic construction of 3-D statistical deformation models of the brain using nonrigid registration. IEEE Trans. Med. Imaging 2003, 22, 1014–1025. [Google Scholar] [CrossRef]
- Jongen, C.; Pluim, J.P.; Nederkoorn, P.J.; Viergever, M.A.; Niessen, W.J. Construction and evaluation of an average CT brain image for inter-subject registration. Comput. Biol. Med. 2004, 34, 647–662. [Google Scholar] [CrossRef]
- Joshi, S.; Davis, B.; Jomier, M.; Gerig, G. Unbiased diffeomorphic atlas construction for computational anatomy. NeuroImage 2004, 23, S151–S160. [Google Scholar] [CrossRef] [PubMed]
- Christensen, G.E.; Johnson, H.J.; Vannier, M.W. Synthesizing average 3D anatomical shapes. NeuroImage 2006, 32, 146–158. [Google Scholar] [CrossRef] [PubMed]
- Noblet, V.; Heinrich, C.; Heitz, F.; Armspach, J.P. Symmetric Nonrigid Image Registration: Application to Average Brain Templates Construction. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2008, New York, NY, USA, 6–10 September 2008; Metaxas, D., Axel, L., Fichtinger, G., Székely, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 897–904. [Google Scholar][Green Version]
- Avants, B.B.; Yushkevich, P.; Pluta, J.; Minkoff, D.; Korczykowski, M.; Detre, J.; Gee, J.C. The optimal template effect in hippocampus studies of diseased populations. NeuroImage 2010, 49, 2457–2466. [Google Scholar] [CrossRef] [PubMed]
- Coupé, P.; Fonov, V.; Manjón, J.V.; Collins, L.D. Template Construction using a Patch-based Robust Estimator. In Proceedings of the Organization for Human Brain Mapping 2010 Annual Meeting, Barcelona, Spain, 6–10 June 2010. [Google Scholar][Green Version]
- Fonov, V.; Evans, A.C.; Botteron, K.; Almli, C.R.; McKinstry, R.C.; Collins, D.L. Unbiased average age-appropriate atlases for pediatric studies. NeuroImage 2011, 54, 313–327. [Google Scholar] [CrossRef]
- Guimond, A.; Meunier, J.; Thirion, J.P. Automatic computation of average brain models. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI’98, Cambridge, MA, USA, 11–13 October 1998; Wells, W.M., Colchester, A., Delp, S., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 631–640. [Google Scholar][Green Version]
- Guimond, A.; Roche, A.; Ayache, N.; Meunier, J. Three-dimensional multimodal brain warping using the Demons algorithm and adaptive intensity corrections. IEEE Trans. Med. Imaging 2001, 20, 58–69. [Google Scholar] [CrossRef]
- Miller, M.; Banerjee, A.; Christensen, G.; Joshi, S.; Khaneja, N.; Grenander, U.; Matejic, L. Statistical methods in computational anatomy. Stat. Methods Med. Res. 1997, 6, 267–299. [Google Scholar] [CrossRef]
- Collins, D.L.; Neelin, P.; Peters, T.M.; Evans, A.C. Automatic 3D intersubject registration of MR volumetric data in standardized Talairach space. J. Comput. Assist. Tomogr. 1994, 18, 192–205. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Hsu, J.; Oishi, K.; Faria, A.V.; Albert, M.; Miller, M.I.; Mori, S. Evaluation of group-specific, whole-brain atlas generation using Volume-based Template Estimation (VTE): Application to normal and Alzheimer’s populations. NeuroImage 2014, 84, 406–419. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Chen, G.; Shen, D.; Yap, P.T. Robust fusion of diffusion MRI data for template construction. Sci. Rep. 2017, 7, 12950. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Schuh, A.; Makropoulos, A.; Robinson, E.C.; Cordero-Grande, L.; Hughes, E.; Hutter, J.; Price, A.N.; Murgasova, M.; Teixeira, R.P.A.G.; Tusor, N.; et al. Unbiased construction of a temporally consistent morphological atlas of neonatal brain development. bioRxiv 2018. [Google Scholar] [CrossRef]
- Parvathaneni, P.; Lyu, I.; Huo, Y.; Blaber, J.; Hainline, A.E.; Kang, H.; Woodward, N.D.; Landman, B.A. Constructing statistically unbiased cortical surface templates using feature-space covariance. In Proceedings of the Medical Imaging 2018: Image Processing, Houston, TX, USA, 10–15 February 2018; Angelini, E.D., Landman, B.A., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2018; Volume 10574, p. 1057406. [Google Scholar] [CrossRef]
- Dalca, A.; Rakic, M.; Guttag, J.; Sabuncu, M. Learning Conditional Deformable Templates with Convolutional Networks. In Proceedings of the Advances in Neural Information Processing Systems 32, Vancouver, BC, Canada, 8–14 December 2019; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Lecun, Y. THE MNIST DATABASE of Handwritten Digits. 1998. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 26 April 2025).
- Jongejan, J.; Rowley, H.; Kawashima, T.; Kim, J.; Fox-Gieg, N. The quick, draw!-ai experiment. Mt. View, CA, Accessed Feb 2016, 17, 4. [Google Scholar]
- Ridwan, A.R.; Niaz, M.R.; Wu, Y.; Qi, X.; Zhang, S.; Kontzialis, M.; Javierre-Petit, C.; Tazwar, M.; Initiative, A.D.N.; Bennett, D.A.; et al. Development and evaluation of a high performance T1-weighted brain template for use in studies on older adults. Hum. Brain Mapp. 2021, 42, 1758–1776. [Google Scholar] [CrossRef]
- Guimond, A.; Meunier, J.; Thirion, J.P. Average Brain Models: A Convergence Study. Comput. Vis. Image Underst. 2000, 77, 192–210. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, F.; Liu, Y. Reference-free brain template construction with population symmetric registration. Med. Biol. Eng. Comput. 2020, 58, 2083–2093. [Google Scholar] [CrossRef]
- Gu, D.; Shi, F.; Hua, R.; Wei, Y.; Li, Y.; Zhu, J.; Zhang, W.; Zhang, H.; Yang, Q.; Huang, P.; et al. An artificial-intelligence-based age-specific template construction framework for brain structural analysis using magnetic resonance images. Hum. Brain Mapp. 2023, 44, 861–875. [Google Scholar] [CrossRef]
- Gu, D.; Cao, X.; Ma, S.; Chen, L.; Liu, G.; Shen, D.; Xue, Z. Pair-Wise and Group-Wise Deformation Consistency in Deep Registration Network. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2020, Lima, Peru, 4–8 October 2020; Martel, A.L., Abolmaesumi, P., Stoyanov, D., Mateus, D., Zuluaga, M.A., Zhou, S.K., Racoceanu, D., Joskowicz, L., Eds.; Springer: Cham, Switzerland, 2020; pp. 171–180. [Google Scholar]
- Miolane, N.; Holmes, S.; Pennec, X. Topologically Constrained Template Estimation via Morse–Smale Complexes Controls Its Statistical Consistency. SIAM J. Appl. Algebra Geom. 2018, 2, 348–375. [Google Scholar] [CrossRef]
- Google Colab—colab.research.google.com. Available online: https://colab.research.google.com/ (accessed on 20 February 2025).
- Lancaster, J.L.; Fox, P.T. Talairach space as a tool for intersubject standardization in the brain. In Handbook of Medical Imaging; Academic Press: Cambridge, MA, USA, 2000; pp. 555–567. [Google Scholar]
- Fonov, V.S.; Evans, A.C.; McKinstry, R.C.; Almli, C.R.; Collins, D. Unbiased nonlinear average age-appropriate brain templates from birth to adulthood. NeuroImage 2009, 47, S102. [Google Scholar] [CrossRef]
- Hawkes, D.; Barratt, D.; Carter, T.; McClelland, J.; Crum, B. Nonrigid Registration. In Image-Guided Interventions; Springer: Boston, MA, USA, 2008; pp. 193–218. [Google Scholar] [CrossRef]
- Jenkinson, M.; Smith, S. A global optimisation method for robust affine registration of brain images. Med. Image Anal. 2001, 5, 143–156. [Google Scholar] [CrossRef] [PubMed]
- Jenkinson, M.; Bannister, P.; Brady, M.; Smith, S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 2002, 17, 825–841. [Google Scholar] [CrossRef]
- Greve, D.N.; Fischl, B. Accurate and robust brain image alignment using boundary-based registration. Neuroimage 2009, 48, 63–72. [Google Scholar] [CrossRef] [PubMed]
- McRobbie, D.W.; Moore, E.A.; Graves, M.J.; Prince, M.R. Improving Your Image: How to Avoid Artefacts. In MRI from Picture to Proton; Cambridge University Press: Cambridge, UK, 2017; pp. 81–101. [Google Scholar]
- Juntu, J.; Sijbers, J.; Van Dyck, D.; Gielen, J. Bias field correction for MRI images. In Proceedings of the Computer Recognition Systems: Proceedings of the 4th International Conference on Computer Recognition Systems CORES’05, Rydzyna Castle, Poland, 22–25 May 2005; Kurzyński, M., Puchała, E., Woźniak, M., żołnierek, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 543–551. [Google Scholar]
- Tustison, N.J.; Avants, B.B.; Cook, P.A.; Zheng, Y.; Egan, A.; Yushkevich, P.A.; Gee, J.C. N4ITK: Improved N3 Bias Correction. IEEE Trans. Med. Imaging 2010, 29, 1310–1320. [Google Scholar] [CrossRef]
- Tustison, N.; Gee, J. N4ITK: Nick’s N3 ITK implementation for MRI bias field correction. Insight J. 2009, 29, 1310–1320. [Google Scholar] [CrossRef]
- Constantinides, C. Signal, Noise, Resolution, and Image Contrast. In Magnetic Resonance Imaging: The Basics; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2016; Chapter 9; pp. 103–114. [Google Scholar]
- Chaudhari, A. Denoising for Magnetic Resonance Imaging; Stanford University: Stanford, CA, USA, 2016. [Google Scholar]
- Moreno López, M.; Frederick, J.M.; Ventura, J. Evaluation of MRI denoising methods using unsupervised learning. Front. Artif. Intell. 2021, 4, 642731. [Google Scholar] [CrossRef]
- Mäkinen, Y.; Azzari, L.; Foi, A. Collaborative filtering of correlated noise: Exact transform-domain variance for improved shrinkage and patch matching. IEEE Trans. Image Process. 2020, 29, 8339–8354. [Google Scholar] [CrossRef]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. Nonlocal Transform-Domain Filter for Volumetric Data Denoising and Reconstruction. IEEE Trans. Image Process. 2013, 22, 119–133. [Google Scholar] [CrossRef]
- Mäkinen, Y.; Marchesini, S.; Foi, A. Ring artifact and Poisson noise attenuation via volumetric multiscale nonlocal collaborative filtering of spatially correlated noise. J. Synchrotron Radiat. 2022, 29, 829–842. [Google Scholar] [CrossRef]
- Leung, K.K.; Barnes, J.; Modat, M.; Ridgway, G.R.; Bartlett, J.W.; Fox, N.C.; Ourselin, S. Brain MAPS: An automated, accurate and robust brain extraction technique using a template library. NeuroImage 2011, 55, 1091–1108. [Google Scholar] [CrossRef] [PubMed]
- Fennema-Notestine, C.; Ozyurt, I.B.; Clark, C.P.; Morris, S.; Bischoff-Grethe, A.; Bondi, M.W.; Jernigan, T.L.; Fischl, B.; Segonne, F.; Shattuck, D.W.; et al. Quantitative evaluation of automated skull-stripping methods applied to contemporary and legacy images: Effects of diagnosis, bias correction, and slice location. Hum. Brain Mapp. 2006, 27, 99–113. [Google Scholar] [CrossRef] [PubMed]
- Kalavathi, P.; Prasath, V.S. Methods on skull stripping of MRI head scan images—A review. J. Digit. Imaging 2016, 29, 365–379. [Google Scholar] [CrossRef]
- Chaurasia, A.; Culurciello, E. LinkNet: Exploiting encoder representations for efficient semantic segmentation. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Fisch, L.; Zumdick, S.; Barkhau, C.; Emden, D.; Ernsting, J.; Leenings, R.; Sarink, K.; Winter, N.R.; Risse, B.; Dannlowski, U.; et al. deepbet: Fast brain extraction of T1-weighted MRI using Convolutional Neural Networks. Comput. Biol. Med. 2024, 179, 108845. [Google Scholar] [CrossRef]
- Weinreb, J.; Redman, H. Sources Of Contrast And Pulse Sequences. In Magnetic Resonance Imaging of the Body: Advanced Exercises in Diagnostic Radiology Series; Saunders: Philadelphia, PA, USA, 1987; pp. 12–16. [Google Scholar]
- Carré, A.; Klausner, G.; Edjlali, M.; Lerousseau, M.; Briend-Diop, J.; Sun, R.; Ammari, S.; Reuzé, S.; Alvarez Andres, E.; Estienne, T.; et al. Standardization of brain MR images across machines and protocols: Bridging the gap for MRI-based radiomics. Sci. Rep. 2020, 10, 12340. [Google Scholar] [CrossRef]
- Reinhold, J.C.; Dewey, B.E.; Carass, A.; Prince, J.L. Evaluating the impact of intensity normalization on MR image synthesis. In Proceedings of the Medical Imaging 2019: Image Processing, San Diego, CA, USA, 16–21 February 2019; Angelini, E.D., Landman, B.A., Eds.; SPIE: Bellingham, WA, USA, 2019. [Google Scholar] [CrossRef]
- Nyúl, L.G.; Udupa, J.K.; Zhang, X. New variants of a method of MRI scale standardization. IEEE Trans. Med. Imaging 2000, 19, 143–150. [Google Scholar] [CrossRef]
- Van Griethuysen, J.J.; Fedorov, A.; Parmar, C.; Hosny, A.; Aucoin, N.; Narayan, V.; Beets-Tan, R.G.; Fillion-Robin, J.C.; Pieper, S.; Aerts, H.J. Computational radiomics system to decode the radiographic phenotype. Cancer Res. 2017, 77, e104–e107. [Google Scholar] [CrossRef]
- Olivieri, A.C. Principal Component Analysis. In Introduction to Multivariate Calibration: A Practical Approach; Springer International Publishing: Cham, Switzerland, 2018; pp. 57–71. [Google Scholar] [CrossRef]
- Ben-Israel, A.; Greville, T.N.E. Generalized Inverses: Theory and Applications, 2nd ed.; CMS Books in Mathematics; Originally published by Wiley-Interscience, 1974; Springer: New York, NY, USA, 2003; pp. 1–5. [Google Scholar] [CrossRef]
- Advanced Normalization Tools. Available online: https://stnava.github.io/ANTs/ (accessed on 20 February 2025).
- Avants, B.B.; Epstein, C.L.; Grossman, M.; Gee, J.C. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 2008, 12, 26–41. [Google Scholar] [CrossRef] [PubMed]
- Avants, B.B.; Tustison, N.; Johnson, H. Advanced Normalization Tools (ANTS) Release 2.X. 2014. Available online: https://gaetanbelhomme.files.wordpress.com/2016/08/ants2.pdf (accessed on 20 February 2025).
- Marquart, G.D.; Tabor, K.M.; Horstick, E.J.; Brown, M.; Geoca, A.K.; Polys, N.F.; Nogare, D.D.; Burgess, H.A. High-precision registration between zebrafish brain atlases using symmetric diffeomorphic normalization. GigaScience 2017, 6, gix056. [Google Scholar] [CrossRef]
- Coupé, P.; Yger, P.; Prima, S.; Hellier, P.; Kervrann, C.; Barillot, C. An optimized blockwise nonlocal means denoising filter for 3-D magnetic resonance images. IEEE Trans. Med. Imaging 2008, 27, 425–441. [Google Scholar] [CrossRef]
- Michelson, A.A. Studies in Optics; University of Chicago Press: Chicago, IL, USA, 1927. [Google Scholar]
- Shattuck, D.W.; Sandor-Leahy, S.R.; Schaper, K.A.; Rottenberg, D.A.; Leahy, R.M. Magnetic Resonance Image Tissue Classification Using a Partial Volume Model. NeuroImage 2001, 13, 856–876. [Google Scholar] [CrossRef] [PubMed]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Fischl, B. FreeSurfer. NeuroImage 2012, 62, 774–781. [Google Scholar] [CrossRef] [PubMed]
- Laboratory, F.I. Statistical Parametric Mapping. Available online: https://www.fil.ion.ucl.ac.uk/spm/ (accessed on 20 June 2025).
- Alfano, V.; Granato, G.; Mascolo, A.; Tortora, S.; Basso, L.; Farriciello, A.; Coppola, P.; Manfredonia, M.; Toro, F.; Tarallo, A.; et al. Advanced neuroimaging techniques in the clinical routine: A comprehensive MRI case study. J. Adv. Health Care 2024, 6, 1–7. [Google Scholar] [CrossRef]


| Image | Weight |
|---|---|
| 1 | 0.143001 |
| 2 | 0.143001 |
| 3 | 0.138172 |
| 4 | 0.145285 |
| 5 | 0.135802 |
| 6 | 0.147039 |
| 7 | 0.147702 |
| Template | Sum | Average |
|---|---|---|
| 33,566,831.060 | 3.935 | |
| 33,735,950.577 | 3.955 |
| Template | † | ||
|---|---|---|---|
| 60.958 | 0.418 | 0.057 | |
| 55.175 | 0.393 | 0.368 |
| Template | |
|---|---|
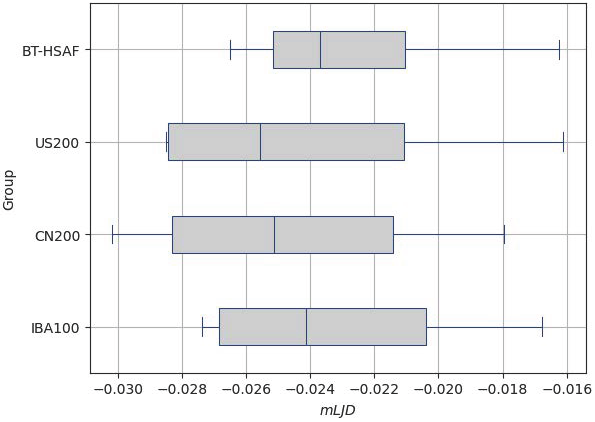
| BT-HSAF | −0.02368 |
| US200 | −0.02557 |
| CN200 | −0.02513 |
| IBA100 | −0.02413 |
| Evaluation Aspect | Current Study | Previous Work |
|---|---|---|
| Unbiasedness |
|
|
| Image Quality |
| |
| Usability |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Althobaiti, N.; Moria, K.; Elrefaei, L.; Alghamdi, J.; Tayeb, H. Construction of a Structurally Unbiased Brain Template with High Image Quality from MRI Scans of Saudi Adult Females. Bioengineering 2025, 12, 722. https://doi.org/10.3390/bioengineering12070722
Althobaiti N, Moria K, Elrefaei L, Alghamdi J, Tayeb H. Construction of a Structurally Unbiased Brain Template with High Image Quality from MRI Scans of Saudi Adult Females. Bioengineering. 2025; 12(7):722. https://doi.org/10.3390/bioengineering12070722
Chicago/Turabian StyleAlthobaiti, Noura, Kawthar Moria, Lamiaa Elrefaei, Jamaan Alghamdi, and Haythum Tayeb. 2025. "Construction of a Structurally Unbiased Brain Template with High Image Quality from MRI Scans of Saudi Adult Females" Bioengineering 12, no. 7: 722. https://doi.org/10.3390/bioengineering12070722
APA StyleAlthobaiti, N., Moria, K., Elrefaei, L., Alghamdi, J., & Tayeb, H. (2025). Construction of a Structurally Unbiased Brain Template with High Image Quality from MRI Scans of Saudi Adult Females. Bioengineering, 12(7), 722. https://doi.org/10.3390/bioengineering12070722







