Half Squat Mechanical Analysis Based on PBT Framework
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Subjects
2.3. Instrumental
2.4. Procedure
2.4.1. Protocol
2.4.2. Signal Processing
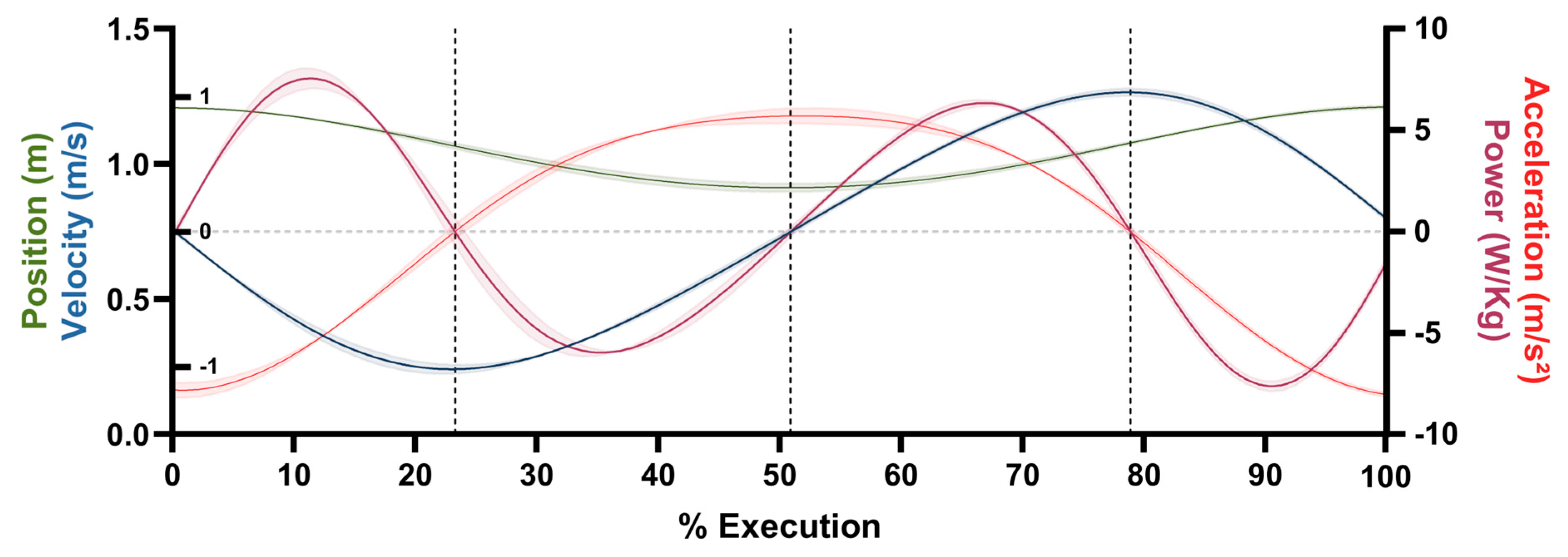
2.4.3. Determination of the Phases
- The first phase, lowering acceleration, is characterized by negative velocity and acceleration, where the resulting force acts in the same direction as the downward motion, generating positive mechanical power.
- The second phase, lowering deceleration, is defined by a negative velocity and a positive acceleration, at which point the resulting force opposes the downward movement, progressively reducing the velocity and producing negative mechanical power.
- The third phase, lifting acceleration, is distinguished by positive velocity and acceleration, where the resulting force cooperates with the upward movement, generating positive mechanical power and reflecting concentric mechanical work to overcome resistance.
- The fourth phase, lifting deceleration, presents a positive velocity and a negative acceleration, where the resulting force opposes the upward motion, progressively decreasing the velocity and the negative mechanical power as the cycle is completed.
2.5. Statistical Analysis
3. Results
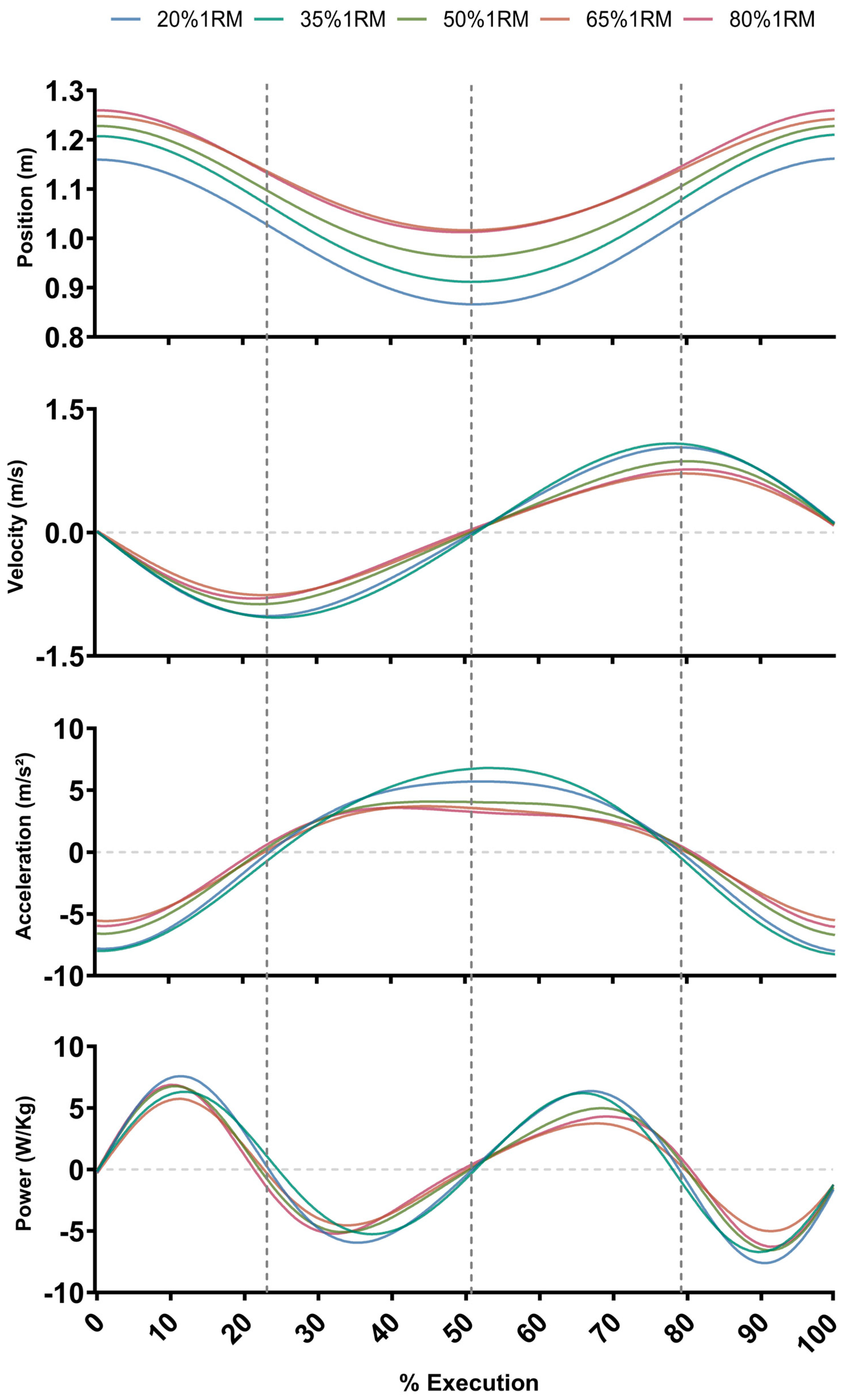
3.1. Phases of the Movement
3.2. Time Parameters
3.3. Kinematics
3.4. Dynamics
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Quiceno, C.; Mantilla, J.I.A.; Samudio, M.A.; Arévalo, J.C. Caracterización de Fuerza de Cadena Muscular Anterior y Posterior En Futbolistas Colombianos, Categorías U17 y U20. VIREF Rev. Educ. Física 2020, 9, 38–47. [Google Scholar]
- Aliaga Reynaldo, J.R.; Núñez Aliaga, F. Distribución del volumen de trabajo de la fuerza muscular en atletas del área de velocidad del atletismo (Original). Olimp. Publ. Científica Fac. Cult. Física Univ. Granma 2016, 13, 192–201. [Google Scholar]
- Rosa-Guillamón, A.; García-Cantó, E. Relación entre fuerza muscular y otros parámetros de la condición física en escolares de primaria. SPORT TK-Rev. Euroam. Cienc. Deporte 2017, 6, 107–116. [Google Scholar] [CrossRef]
- Fernandez Ortega, J.A.; Hoyos Cuartas, L.A. Efectos de La Velocidad de Entrenamiento En Fuerza Sobre Diversas Manifestaciones de La Fuerza En Mujeres Adultas Mayores (Effect of the Velocity Resistance Training on Various Manifestations of Resistance in Older Women). Retos 2020, 38, 325–332. [Google Scholar] [CrossRef]
- Registre, F.; Lopes, L.M.P.; Souza, P.M.; Becker, L.K.; de Alcantara Borba, D.; Ferreira Júnior, J.B.; de Oliveira, E.C.; Coelho, D.B. Effects of Different Strength Training Protocols on Sarcopenia Influencing Parameters in Older Adults: A Systematic Review. ABCS Health Sci. 2022, 47, e022308. [Google Scholar] [CrossRef]
- Suárez Manzano, S.; Rusillo Magdaleno, A.; Solas Martínez, J.L.; Brandão Loureiro, V. Asociación de La Fuerza Muscular Con Atención, Comportamiento Hiperactivo-Desatento, Cálculo Matemáti-Co y Razonamiento Lingüístico En Escolares Diagnosticados TDAH (Association of Muscle Strength with Attention, Hyperactive-Attentive Behavior, Mathematical Calculation and Linguistic Reasoning in Schoolchildren Diagnosed with ADHD). Retos 2023, 47, 753–760. [Google Scholar] [CrossRef]
- Hori, N.; Newton, R.U.; Nosaka, K.; Stone, M.H. Weightlifting Exercises Enhance Athletic Performance That Requires High-Load Speed Strength. Strength Cond. J. 2005, 27, 50. [Google Scholar] [CrossRef]
- Comfort, P.; Haff, G.G.; Suchomel, T.J.; Soriano, M.A.; Pierce, K.C.; Hornsby, W.G.; Haff, E.E.; Sommerfield, L.M.; Chavda, S.; Morris, S.J.; et al. National Strength and Conditioning Association Position Statement on Weightlifting for Sports Performance. J. Strength Cond. Res. 2023, 37, 1163–1190. [Google Scholar] [CrossRef]
- Schoenfeld, B.J.; Grgic, J.; Ogborn, D.; Krieger, J.W. Strength and Hypertrophy Adaptations Between Low- vs. High-Load Resistance Training: A Systematic Review and Meta-Analysis. J. Strength Cond. Res. 2017, 31, 3508–3523. [Google Scholar] [CrossRef]
- Lacio, M.; Vieira, J.G.; Trybulski, R.; Campos, Y.; Santana, D.; Filho, J.E.; Novaes, J.; Vianna, J.; Wilk, M. Effects of Resistance Training Performed with Different Loads in Untrained and Trained Male Adult Individuals on Maximal Strength and Muscle Hypertrophy: A Systematic Review. Int. J. Environ. Res. Public. Health 2021, 18, 11237. [Google Scholar] [CrossRef]
- Storey, A.; Smith, H.K. Unique Aspects of Competitive Weightlifting: Performance, Training and Physiology. Sports Med. Auckl. NZ 2012, 42, 769–790. [Google Scholar] [CrossRef] [PubMed]
- Gacesa, J.Z.P.; Klasnja, A.V.; Grujic, N.G. Changes in Strength, Endurance, and Fatigue During a Resistance-Training Program for the Triceps Brachii Muscle. J. Athl. Train. 2013, 48, 804–809. [Google Scholar] [CrossRef] [PubMed]
- Redwood, J.Q.; Almeida, M.D. The Combined Effects of Endurance and Strength Training on Exercise Tolerance and Quality of Life in Patients with COPD. Stud. Sports Sci. Phys. Educ. 2024, 2, 43–51. [Google Scholar] [CrossRef]
- McKelvie, R.S.; McCartney, N. Weightlifting Training in Cardiac Patients. Considerations. Sports Med. Auckl. NZ 1990, 10, 355–364. [Google Scholar] [CrossRef]
- Simpson, K.; Killian, K.; McCartney, N.; Stubbing, D.G.; Jones, N.L. Randomised Controlled Trial of Weightlifting Exercise in Patients with Chronic Airflow Limitation. Thorax 1992, 47, 70–75. [Google Scholar] [CrossRef]
- Nguyen, C.; Lefèvre-Colau, M.-M.; Poiraudeau, S.; Rannou, F. Rehabilitation (Exercise and Strength Training) and Osteoarthritis: A Critical Narrative Review. Ann. Phys. Rehabil. Med. 2016, 59, 190–195. [Google Scholar] [CrossRef] [PubMed]
- Noguchi, K.S.; Moncion, K.; Wiley, E.; Morgan, A.; Huynh, E.; Balbim, G.M.; Elliott, B.; Harris-Blake, C.; Krysa, B.; Koetsier, B.; et al. Prescribing Strength Training for Stroke Recovery: A Systematic Review and Meta-Analysis of Randomised Controlled Trials. Br. J. Sports Med. 2025, 59, 185–197. [Google Scholar] [CrossRef]
- Nabutovsky, I.; Sabah, R.; Moreno, M.; Epstein, Y.; Klempfner, R.; Scheinowitz, M. Evaluating the Effects of an Enhanced Strength Training Program in Remote Cardiological Rehabilitation: A Shift from Aerobic Dominance-A Pilot Randomized Controlled Trial. J. Clin. Med. 2024, 13, 1445. [Google Scholar] [CrossRef]
- Bird, S.P.; Tarpenning, K.M.; Marino, F.E. Designing Resistance Training Programmes to Enhance Muscular Fitness. Sports Med. 2005, 35, 841–851. [Google Scholar] [CrossRef]
- Nigro, F.; Bartolomei, S. A Comparison Between the Squat and the Deadlift for Lower Body Strength and Power Training. J. Hum. Kinet. 2020, 73, 145–152. [Google Scholar] [CrossRef]
- Bauer, P.; Uebellacker, F.; Mitter, B.; Aigner, A.J.; Hasenoehrl, T.; Ristl, R.; Tschan, H.; Seitz, L.B. Combining Higher-Load and Lower-Load Resistance Training Exercises: A Systematic Review and Meta-Analysis of Findings from Complex Training Studies. J. Sci. Med. Sport. 2019, 22, 838–851. [Google Scholar] [CrossRef] [PubMed]
- Enes, A.; Oneda, G.; Leonel, D.F.; Lemos, L.; Alves, F.; Ferreira, L.H.B.; Escalante, G.; Schoenfeld, B.J.; Souza-Junior, T.P. The Effects of Squat Variations on Strength and Quadriceps Hypertrophy Adaptations in Recreationally Trained Females. Eur. J. Sport. Sci. 2024, 24, 6–15. [Google Scholar] [CrossRef]
- Hartmann, H.; Wirth, K.; Klusemann, M. Analysis of the Load on the Knee Joint and Vertebral Column with Changes in Squatting Depth and Weight Load. Sports Med. 2013, 43, 993–1008. [Google Scholar] [CrossRef]
- Li, X.; Adrien, N.; Baker, J.S.; Mei, Q.; Gu, Y. Novice Female Exercisers Exhibited Different Biomechanical Loading Profiles during Full-Squat and Half-Squat Practice. Biology 2021, 10, 1184. [Google Scholar] [CrossRef]
- Schoenfeld, B.J. Squatting Kinematics and Kinetics and Their Application to Exercise Performance. J. Strength Cond. Res. 2010, 24, 3497–3506. [Google Scholar] [CrossRef]
- Marshall, J.; Bishop, C.; Turner, A.; Haff, G.G. Optimal Training Sequences to Develop Lower Body Force, Velocity, Power, and Jump Height: A Systematic Review with Meta-Analysis. Sports Med. 2021, 51, 1245–1271. [Google Scholar] [CrossRef]
- Korak, J.A.; Paquette, M.R.; Fuller, D.K.; Caputo, J.L.; Coons, J.M. Muscle Activation Patterns of Lower-Body Musculature Among 3 Traditional Lower-Body Exercises in Trained Women. J. Strength Cond. Res. 2018, 32, 2770–2775. [Google Scholar] [CrossRef] [PubMed]
- Jaeggi, J.S.; Achermann, B.; Lorenzetti, S.R. Female Lower Body Muscle Forces: A Musculoskeletal Modeling Comparison of Back Squats, Split Squats and Good Mornings. J. Funct. Morphol. Kinesiol. 2024, 9, 68. [Google Scholar] [CrossRef]
- Wong, D.P.; Tan, E.C.H.; Chaouachi, A.; Carling, C.; Castagna, C.; Bloomfield, J.; Behm, D.G. Using Squat Testing to Predict Training Loads for Lower-Body Exercises in Elite Karate Athletes. J. Strength Cond. Res. 2010, 24, 3075–3080. [Google Scholar] [CrossRef]
- Perez-Castilla, A.; Garcia-Ramos, A.; Padial, P.; Morales-Artacho, A.; Feriche, B. Load-Velocity Relationship in Variations of the Half-Squat Exercise: Influence of Execution Technique. J. Strength Cond. Res. 2020, 34, 1024–1031. [Google Scholar] [CrossRef]
- Weakley, J.; Mann, B.; Banyard, H.; McLaren, S.; Scott, T.; Garcia-Ramos, A. Velocity-Based Training: From Theory to Application. Strength Cond. J. 2021, 43, 31–49. [Google Scholar] [CrossRef]
- Velocity-Based Training: Prescribing and Assessing the Effects of Resistance Training; Routledge: New York, NY, USA, 2025; ISBN 978-1-003-16359-6.
- Gullett, J.C.; Tillman, M.D.; Gutierrez, G.M.; Chow, J.W. A Biomechanical Comparison of Back and Front Squats in Healthy Trained Individuals. J. Strength Cond. Res. 2009, 23, 284. [Google Scholar] [CrossRef] [PubMed]
- Swinton, P.A.; Lloyd, R.; Keogh, J.W.L.; Agouris, I.; Stewart, A.D. A Biomechanical Comparison of the Traditional Squat, Powerlifting Squat, and Box Squat. J. Strength Cond. Res. 2012, 26, 1805. [Google Scholar] [CrossRef]
- Kingston, D.C.; Tennant, L.M.; Chong, H.C.; Acker, S.M. Lower Limb Muscular Activation During Transitions to Symmetric High Knee Flexion Postures in Young Females. IISE Trans. Occup. Ergon. Hum. Factors 2017, 5, 82–91. [Google Scholar] [CrossRef]
- Coratella, G.; Tornatore, G.; Caccavale, F.; Longo, S.; Esposito, F.; Cè, E. The Activation of Gluteal, Thigh, and Lower Back Muscles in Different Squat Variations Performed by Competitive Bodybuilders: Implications for Resistance Training. Int. J. Environ. Res. Public. Health 2021, 18, 772. [Google Scholar] [CrossRef]
- Gantois, P.; de Souza Fonseca, F.; Nakamura, F.; de Sousa Fortes, L.; Fernandez-Fernandez, J.; Ricarte Batista, G. Analysis of Velocity- and Power-Load Relationships of the Free-Weight Back-Squat and Hexagonal Bar Deadlift Exercises. Biol. Sport. 2023, 40, 201–208. [Google Scholar] [CrossRef]
- Banyard, H.G.; Tufano, J.J.; Delgado, J.; Thompson, S.W.; Nosaka, K. Comparison of the Effects of Velocity-Based Training Methods and Traditional 1RM-Percent-Based Training Prescription on Acute Kinetic and Kinematic Variables. Int. J. Sports Physiol. Perform. 2019, 14, 246–255. [Google Scholar] [CrossRef]
- Alcazar, J.; Cornejo-Daza, P.J.; Sánchez-Valdepeñas, J.; Alegre, L.M.; Pareja-Blanco, F. Dose-Response Relationship Between Velocity Loss During Resistance Training and Changes in the Squat Force-Velocity Relationship. Int. J. Sports Physiol. Perform. 2021, 16, 1736–1745. [Google Scholar] [CrossRef]
- Pareja-Blanco, F.; Rodríguez-Rosell, D.; Sánchez-Medina, L.; Sanchis-Moysi, J.; Dorado, C.; Mora-Custodio, R.; Yáñez-García, J.M.; Morales-Alamo, D.; Pérez-Suárez, I.; Calbet, J.A.L.; et al. Effects of Velocity Loss during Resistance Training on Athletic Performance, Strength Gains and Muscle Adaptations. Scand. J. Med. Sci. Sports 2017, 27, 724–735. [Google Scholar] [CrossRef]
- Spudić, D.; Smajla, D.; Šarabon, N. Validity and Reliability of Force–Velocity Outcome Parameters in Flywheel Squats. J. Biomech. 2020, 107, 109824. [Google Scholar] [CrossRef]
- Zatsiorsky, V.M. Metrología Deportiva: Libro de Texto; Planeta: Madrid, Spain, 1989; ISBN 978-5-85250-257-5. [Google Scholar]
- Komi, P.V. (Ed.) Strength and Power in Sport; Osney Mead: Oxford, UK; Malden, MA, USA, 2002; ISBN 978-0-632-05911-9. [Google Scholar]
- Knudson, D.V. Correcting the Use of the Term “Power” in the Strength and Conditioning Literature. J. Strength Cond. Res. 2009, 23, 1902. [Google Scholar] [CrossRef] [PubMed]
- Enoka, R.M. Neuromechanics of Human Movement; Human Kinetics: Champaign, IL, USA, 2024; ISBN 978-1-7182-1373-9. [Google Scholar]
- Zatsiorsky, V.M. Kinetics of Human Motion; Human Kinetics: Champaign, IL, USA, 2002; ISBN 978-0-7360-3778-5. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-0-470-39818-0. [Google Scholar]
- Bernshteĭn, N.A. The Co-Ordination and Regulation of Movements; Pergamon Press: Oxford, UK, 1967. [Google Scholar]
- Zatsiorsky, V. Biomechanics in Sport. Performance Enhancement and Injury Prevention; John Wiley & Sons: Hoboken, NJ, USA, 2000; Volume 33, ISBN 978-0-632-05392-6. [Google Scholar]
- Behm, D.G.; Sale, D.G. Velocity Specificity of Resistance Training. Sports Med. 1993, 15, 374–388. [Google Scholar] [CrossRef]
- Morales, J.; Sobonya, S. Use of Submaximal Repetition Tests for Predicting 1-RM Strength in Class Athletes. J. Strength Cond. Res. 1996, 10, 186. [Google Scholar]
- Enoki, S.; Shiba, J.; Hakozaki, T.; Suzuki, Y.; Kuzuhara, K. Correlations between One-Repetition Maximum Weights of Different Back Squat Depths. Isokinet. Exerc. Sci. 2023, 31, 97–102. [Google Scholar] [CrossRef]
- Vicon Motion Systems Ltd. Vicon Motion Capture System 2024. Available online: https://www.vicon.com (accessed on 28 May 2025).
- Vicon Motion Systems Ltd. Vicon Nexus 2024. Available online: https://www.vicon.com/software/nexus (accessed on 28 May 2025).
- Vicon Motion Systems Ltd. Plug-in Gait Reference Guide Vicon Help 2023. Available online: https://help.vicon.com/space/Nexus216/11611993/PDF+downloads+for+Vicon+Nexus (accessed on 28 May 2025).
- Matos, F.; Ferreira, B.; Guedes, J.; Saavedra, F.; Reis, V.M.; Vilaça-Alves, J. Effect of Rest Interval Between Sets in the Muscle Function During a Sequence of Strength Training Exercises for the Upper Body. J. Strength Cond. Res. 2021, 35, 1628. [Google Scholar] [CrossRef] [PubMed]
- de Jesus Santana, W.; Bocalini, D.S.; João, G.A.; Caperuto, E.C.; de Araujo, I.P.; Figueira Junior, A. Recovery between Sets in Strength Training: Systematic Review and Meta-Analysis. Rev. Bras. Med. Esporte 2023, 30, e2021_0037. [Google Scholar] [CrossRef]
- Harris, J. Establishing an Optimal Recovery Time between Repeated Maximal Stength Sets on the Squat and Bench Press. 2008. Available online: https://www.semanticscholar.org/paper/Establishing-an-optimal-recovery-time-between-sets-Harris/5a6bd288edf99464dd917a13d3b2bffe5bc566a8#cited-papers (accessed on 28 May 2025).
- Yu, B.; Gabriel, D.; Noble, L.; An, K.-N. Estimate of the Optimum Cutoff Frequency for the Butterworth Low-Pass Digital Filter. J. Appl. Biomech. 1999, 15, 318–329. [Google Scholar] [CrossRef]
- Roithner, R.; Schwameder, H.; Müller, E. Determination of Optimal Filter Parameters for Filtering Kinematic Walking Data Using Butterworth Low-Pass Filter. In Proceedings of the 18 International Symposium on Biomechanics in Sports, Hong Kong, China, 25–30 June 2000. [Google Scholar]
- Escamilla, R.F. Knee Biomechanics of the Dynamic Squat Exercise. Med. Sci. Sports Exerc. 2001, 33, 127. [Google Scholar] [CrossRef]
- Carzoli, J.P.; Sousa, C.A.; Belcher, D.J.; Helms, E.R.; Khamoui, A.V.; Whitehurst, M.; Zourdos, M.C. The Effects of Eccentric Phase Duration on Concentric Outcomes in the Back Squat and Bench Press in Well-Trained Males. J. Sports Sci. 2019, 37, 2676–2684. [Google Scholar] [CrossRef]
- Armstrong, R.; Baltzopoulos, V.; Langan-Evans, C.; Clark, D.; Jarvis, J.; Stewart, C.; O’Brien, T. An Investigation of Movement Dynamics and Muscle Activity during Traditional and Accentuated-Eccentric Squatting. PLoS ONE 2022, 17, e0276096. [Google Scholar] [CrossRef]
- Orantes-Gonzalez, E.; Heredia-Jimenez, J.; Lindley, S.B.; Richards, J.D.; Chapman, G.J. An Exploration of the Motor Unit Behaviour during the Concentric and Eccentric Phases of a Squat Task Performed at Different Speeds. Sports Biomech. 2023, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, R.; Baltzopoulos, V.; Langan-Evans, C.; Clark, D.; Jarvis, J.; Stewart, C.; O’Brien, T.D. Determining Concentric and Eccentric Force–Velocity Profiles during Squatting. Eur. J. Appl. Physiol. 2022, 122, 769–779. [Google Scholar] [CrossRef] [PubMed]
- Wagle, J.P.; Taber, C.B.; Carroll, K.M.; Cunanan, A.J.; Sams, M.L.; Wetmore, A.; Bingham, G.E.; DeWeese, B.H.; Sato, K.; Stuart, C.A.; et al. Repetition-to-Repetition Differences Using Cluster and Accentuated Eccentric Loading in the Back Squat. Sports 2018, 6, 59. [Google Scholar] [CrossRef] [PubMed]
- Rodal, M.; Franco-García, J.M.; Carlos-Vivas, J.; García-Muro San José, F.; Pérez Gosálvez, A.; Charneco Salguero, G.; Gianikellis, K.; Pérez-Gómez, J. Spatio-Temporal and Mechanical Analysis of Bench Press Phases: Barbell Kinematics and Dynamics Across Different Load Intensities. Appl. Sci. 2024, 14, 11783. [Google Scholar] [CrossRef]
- Sanchez-Medina, L.; Perez, C.E.; Gonzalez-Badillo, J.J. Importance of the Propulsive Phase in Strength Assessment. Int. J. Sports Med. 2010, 31, 123–129. [Google Scholar] [CrossRef]
- Loturco, I.; Suchomel, T.; Bishop, C.; Kobal, R.; Pereira, L.; McGuigan, M. Determining the Optimum Bar Velocity in the Barbell Hip Thrust Exercise. Int. J. Sports Physiol. Perform. 2020, 15, 585–589. [Google Scholar] [CrossRef]
- Gianikellis, K.; Bote García, A.; Pulido Gil, J.M.; Pérez, A. Análisis biomecánico del salto vertical con contramovimiento en personas con parálisis cerebral. Eur. J. Hum. Mov. 2004, 12, 187–194. [Google Scholar]
- Masci, I.; Vannozzi, G.; Gizzi, L.; Bellotti, P.; Felici, F. Neuromechanical Evidence of Improved Neuromuscular Control around Knee Joint in Volleyball Players. Eur. J. Appl. Physiol. 2010, 108, 443–450. [Google Scholar] [CrossRef]
- Eliassen, W.; Saeterbakken, A.; Tillaar, R. van den Comparison of Bilateral and Unilateral Squat Exercises on Barbell Kinematics and Muscle Activation. Int. J. Sports Phys. Ther. 2018, 13, 871–881. [Google Scholar] [CrossRef]
- Goodin, J. Comparison of External Kinetic and Kinematic Variables between High Barbell Back Squats and Low Barbell Back Squats across a Range of Loads. Ph.D. Thesis, East Tennessee State University, Johnson City, TN, USA, 2015. [Google Scholar]
- Larsen, S.; Kristiansen, E.; Falch, H.N.; Haugen, M.E.; Fimland, M.; van den Tillaar, R. Effects of Barbell Load on Kinematics, Kinetics, and Myoelectric Activity in Back Squats. Sports Biomech. 2022, 1–15. [Google Scholar] [CrossRef]
- Giustino, V.; Vicari, D.S.S.; Figlioli, F.; Gervasi, M.; Fernández Peña, E.; Schifaudo, N.; Tedesco, M.; Drid, P.; Paoli, A.; Battaglia, G.; et al. Kinematic Analysis of the Back Squat at Different Load Intensities in Powerlifters and Weightlifters. Front. Sports Act. Living 2024, 6, 1454309. [Google Scholar] [CrossRef] [PubMed]
- Sinclair, J.; Taylor, P.J.; Jones, B.; Butters, B.; Bentley, I.; Edmundson, C.J. A Multi-Experiment Investigation of the Effects Stance Width on the Biomechanics of the Barbell Squat. Sports Basel Switz. 2022, 10, 136. [Google Scholar] [CrossRef] [PubMed]
- Zink, A.J.; Perry, A.C.; Robertson, B.L.; Roach, K.E.; Signorile, J.F. Peak Power, Ground Reaction Forces, and Velocity during the Squat Exercise Performed at Different Loads. J. Strength Cond. Res. 2006, 20, 658. [Google Scholar] [PubMed]
- Hochmuth, G. Biomechanics of Athletic Movement; Sportverlag: Zürich, Switzerland, 1984. [Google Scholar]
- Hill, A. The Heat of Shortening and the Dynamic Constants of Muscle. Proc. R. Soc. Lond. Ser. B Biol. Sci. 1938, 126, 136–195. [Google Scholar] [CrossRef]
- González-Badillo, J.J.; Sánchez-Medina, L. Movement Velocity as a Measure of Loading Intensity in Resistance Training. Int. J. Sports Med. 2010, 31, 347–352. [Google Scholar] [CrossRef]
- Torrejón, A.; Balsalobre-Fernández, C.; Haff, G.G.; García-Ramos, A. The Load-Velocity Profile Differs More between Men and Women than between Individuals with Different Strength Levels. Sports Biomech. 2019, 18, 245–255. [Google Scholar] [CrossRef]
- Sánchez-Medina, L.; González-Badillo, J.J.; Pérez, C.E.; Pallarés, J.G. Velocity- and Power-Load Relationships of the Bench Pull vs. Bench Press Exercises. Int. J. Sports Med. 2014, 35, 209–216. [Google Scholar] [CrossRef]
- Stergiou, N. Innovative Analyses of Human Movement; Human Kinetics: Champaign, IL, USA, 2004; ISBN 978-0-7360-4467-7. [Google Scholar]
- Schoner, G. Recent Developments and Problems in Human Movement Science and Their Conceptual Implications. Ecol. Psychol. 1995, 7, 291–314. [Google Scholar] [CrossRef]
- Scholz, J.P.; Schöner, G. The Uncontrolled Manifold Concept: Identifying Control Variables for a Functional Task. Exp. Brain Res. 1999, 126, 289–306. [Google Scholar] [CrossRef]
- Latash, M.L. The Bliss (Not the Problem) of Motor Abundance (Not Redundancy). Exp. Brain Res. 2012, 217, 1–5. [Google Scholar] [CrossRef]
- Latash, M.L.; Scholz, J.P.; Schöner, G. Motor Control Strategies Revealed in the Structure of Motor Variability. Exerc. Sport. Sci. Rev. 2002, 30, 26–31. [Google Scholar] [CrossRef] [PubMed]
- Gianikellis, K.; Skiadopoulos, A.; Caro, B. Ergonomics and “Usability” Applied on The Training of Muscular Force Qualities. ISBS Proc. Arch. 2017, 35, 181. [Google Scholar]
| Avg. Duration | Position (m) | Velocity (m/s) | Acceleration (m/s2) | Mechanical Power (W/Kg) | Mechanical Work (J/Kg) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Phase | Sets | (s) | (%) | Range | SD | Avg. | SD | Max | SD | Avg. | SD | Max | SD | Avg. | SD | Max | SD | Avg. | SD | Max | SD |
| P1 | S1 | 0.42 | 28.9% | 0.17 | −0.48 | −0.90 | −3.03 | −5.04 | 2.43 | 4.79 | 0.63 | 0.69 | |||||||||
| S2 | 0.33 | 24.4% | 0.16 | −0.50 | −0.89 | −3.05 | −5.20 | 2.80 | 5.54 | 0.71 | 0.79 | ||||||||||
| S3 | 0.34 | 24.3% | 0.16 | −0.46 | −0.80 | −2.52 | −4.45 | 2.36 | 4.65 | 0.67 | 0.74 | ||||||||||
| S4 | 0.31 | 22.5% | 0.14 | −0.46 | −0.78 | −2.58 | −4.47 | 2.67 | 5.21 | 0.75 | 0.80 | ||||||||||
| S5 | 0.31 | 21.4% | 0.15 | −0.46 | −0.77 | −2.48 | −4.39 | 2.76 | 5.47 | 0.78 | 0.84 | ||||||||||
| P2 | S1 | 0.34 | 25.0% | 0.19 | −0.55 | −0.90 | 3.11 | 5.40 | 4,5 | −2.35 | −4.10 | −0.59 | −0.65 | ||||||||
| S2 | 0.38 | 28.2% | 0.20 | −0.52 | −0.89 | 2.74 | 4.63 | 4,5 | −2.34 | −4.20 | −0.68 | −0.76 | |||||||||
| S3 | 0.39 | 27.5% | 0.18 | −0.45 | −0.80 | 2.32 | 3.59 | 4,5 | −2.02 | −3.61 | −0.65 | −0.71 | |||||||||
| S4 | 0.40 | 28.6% | 0.18 | −0.44 | −0.78 | 2.15 | 3.10 | 1,2,3,5 | −2.10 | −3.58 | −0.73 | −0.78 | |||||||||
| S5 | 0.41 | 28.5% | 0.18 | −0.42 | −0.77 | 1.97 | 2.81 | 1,2,3,4 | −2.05 | −3.82 | −0.77 | −0.83 | |||||||||
| P3 | S1 | 0.28 | 22.0% | 0.18 | 0.61 | 4,5 | 1.04 | 4 | 4.00 | 4,5 | 5.78 | 4,5 | 3.22 | 5.48 | 0.81 | 0.86 | |||||
| S2 | 0.30 | 23.9% | 0.19 | 0.59 | 4,5 | 1.02 | 4,5 | 3.44 | 3,4,5 | 4.98 | 4,5 | 3.31 | 5.76 | 0.93 | 0.99 | ||||||
| S3 | 0.34 | 25.0% | 0.18 | 0.51 | 5 | 0.86 | 2.51 | 2,5 | 3.56 | 4,5 | 2.43 | 4.10 | 0.78 | 0.82 | |||||||
| S4 | 0.38 | 28.0% | 0.19 | 0.48 | 1,2 | 0.81 | 1,2 | 2.12 | 1,2 | 3.09 | 1,2,3,5 | 2.23 | 3.69 | 0.82 | 0.84 | ||||||
| S5 | 0.45 | 31.2% | 0.21 | 0.43 | 1,2,3 | 0.77 | 2 | 1.75 | 1,2,3 | 2.50 | 1,2,3,4 | 1.91 | 3.63 | 0.81 | 0.84 | ||||||
| P4 | S1 | 0.34 | 24.1% | 0.16 | 2,3,4,5 | 0.58 | 1.04 | 4 | −3.88 | −6.12 | −3.10 | −5.83 | −0.76 | −0.80 | |||||||
| S2 | 0.33 | 23.5% | 0.15 | 1,4,5 | 0.56 | 1.02 | 4,5 | −3.91 | −6.18 | −3.68 | −7.11 | −0.88 | −0.95 | ||||||||
| S3 | 0.34 | 23.3% | 0.14 | 1,4, 5 | 0.47 | 0.86 | −3.04 | −5.04 | −2.88 | −5.58 | −0.75 | −0.79 | |||||||||
| S4 | 0.29 | 20.9% | 0.13 | 1, 2, 3 | 0.47 | 0.81 | 1,2 | −3.15 | −5.08 | −3.21 | −5.90 | −0.79 | −0.82 | ||||||||
| S5 | 0.27 | 18.8% | 0.12 | 1, 2, 3 | 0.46 | 0.77 | 2 | −3.05 | −5.08 | −3.22 | −6.03 | −0.79 | −0.82 | ||||||||
| Raise | S1 | 0.63 | 46.1% | 0.34 | 0.59 | 1.04 | 4 | 0.06 | 2,3,4,5 | 5.78 | 4,5 | 0.10 | 5.48 | 0.05 | 4, 5 | 0.05 | 4, 5 | ||||
| (P3 + P4) | S2 | 0.63 | 47.3% | 0.34 | 0.57 | 1.02 | 4,5 | 0.00 | 1 | 4.98 | 4,5 | 0.08 | 5.76 | 0.04 | 4, 5 | 0.05 | 4, 5 | ||||
| S3 | 0.68 | 48.3% | 0.33 | 0.49 | 0.86 | −0.03 | 1 | 3.56 | 4,5 | 0.04 | 4.10 | 0.03 | 0.03 | ||||||||
| S4 | 0.67 | 48.9% | 0.32 | 0.47 | 0.81 | 1,2 | −0.04 | 1 | 3.09 | 1,2,3,5 | 0.04 | 3.69 | 0.02 | 1, 2 | 0.02 | 1, 2, 5 | |||||
| S5 | 0.72 | 50.0% | 0.33 | 0.44 | 0.78 | 2 | −0.03 | 1 | 2.50 | 1,2,3,4 | 0.03 | 3.63 | 0.02 | 1, 2 | 0.02 | 1, 2, 4 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodal, M.; Arrayales-Millán, E.M.; Gonzalez-Macías, M.E.; Pérez-Gómez, J.; Gianikellis, K. Half Squat Mechanical Analysis Based on PBT Framework. Bioengineering 2025, 12, 603. https://doi.org/10.3390/bioengineering12060603
Rodal M, Arrayales-Millán EM, Gonzalez-Macías ME, Pérez-Gómez J, Gianikellis K. Half Squat Mechanical Analysis Based on PBT Framework. Bioengineering. 2025; 12(6):603. https://doi.org/10.3390/bioengineering12060603
Chicago/Turabian StyleRodal, Miguel, Emilio Manuel Arrayales-Millán, Mirvana Elizabeth Gonzalez-Macías, Jorge Pérez-Gómez, and Kostas Gianikellis. 2025. "Half Squat Mechanical Analysis Based on PBT Framework" Bioengineering 12, no. 6: 603. https://doi.org/10.3390/bioengineering12060603
APA StyleRodal, M., Arrayales-Millán, E. M., Gonzalez-Macías, M. E., Pérez-Gómez, J., & Gianikellis, K. (2025). Half Squat Mechanical Analysis Based on PBT Framework. Bioengineering, 12(6), 603. https://doi.org/10.3390/bioengineering12060603







