Exploring Bio-Impedance Sensing for Intelligent Wearable Devices
Abstract
1. Introduction
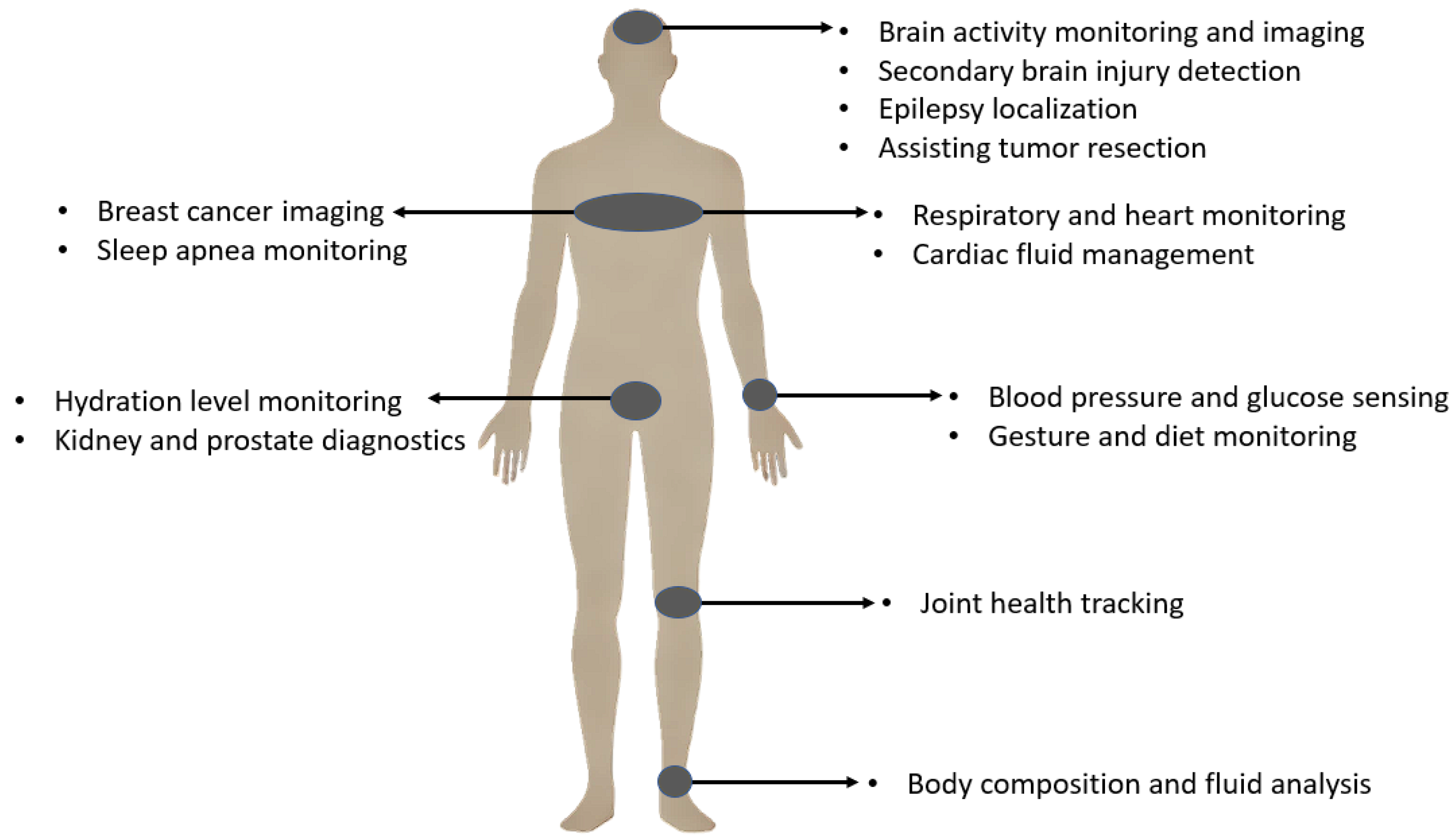
General Bio-Impedance Applications
| Main Applications | Subcategories |
|---|---|
| Clinical Diagnostics and Therapeutic Monitoring |
|
| Advanced Bio-Impedance Techniques and Research Applications |
|
2. Bio-Impedance Application in Neuroscience and Brain Diseases
2.1. Transcranial Impedance Changes (Epilepsy, Tumor, Ischemia, Blood Flow, Stroke)
2.2. Secondary Brain Injury (Ischemic (High-Impedance), Hemorrhagic (Low-Impedance), and Post-Surgical Monitoring)
3. Bio-Impedance Biological Meaning and Properties
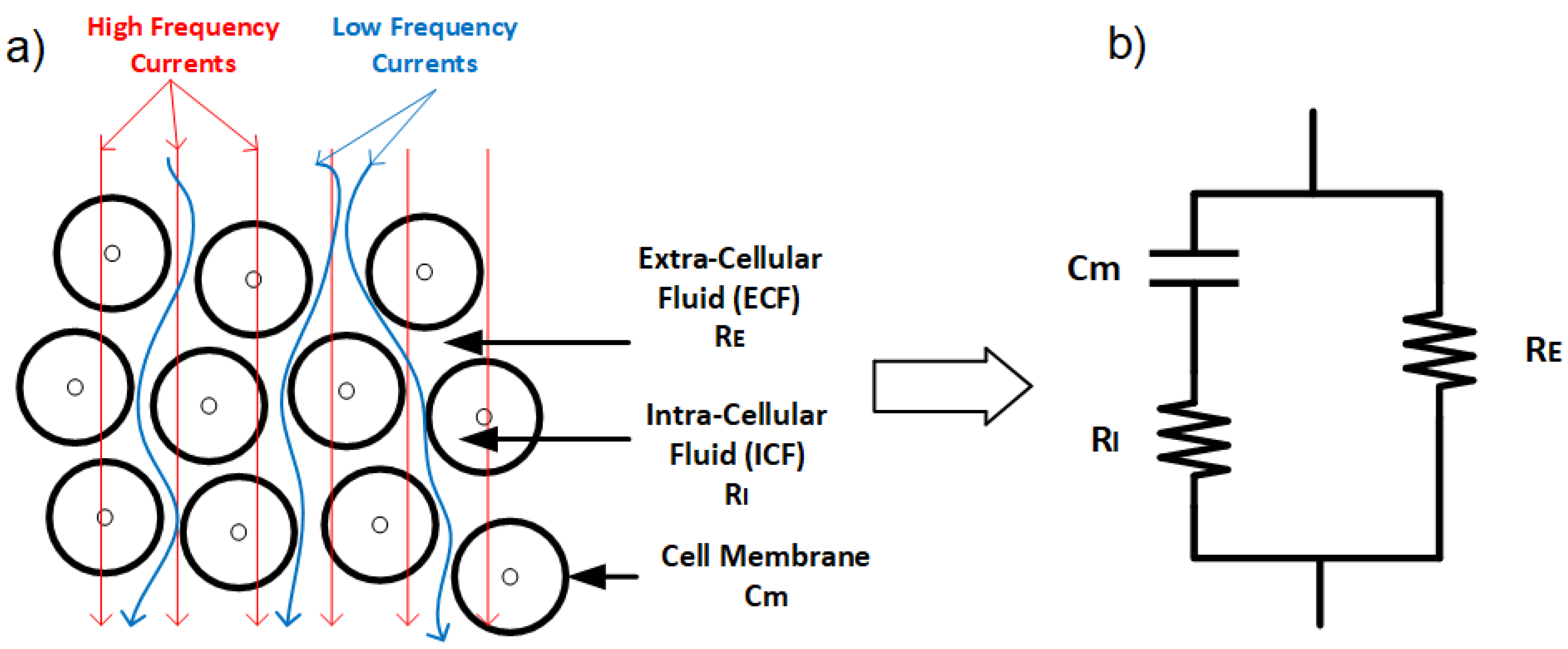
3.1. Passive Properties of Biological Tissues
3.2. Electrical Properties of Biological Tissues
- -dispersion (10 Hz to a few kHz): Generally associated with the diffusion processes of ionic species, related to tissue interfaces, such as membranes [77].
- -dispersion (1 kHz to several MHz): Attributable to the polarization of cellular membranes and large biological molecules, like proteins.
- -dispersion (≥10 GHz): associated with the polarization of small molecules, like water molecules.
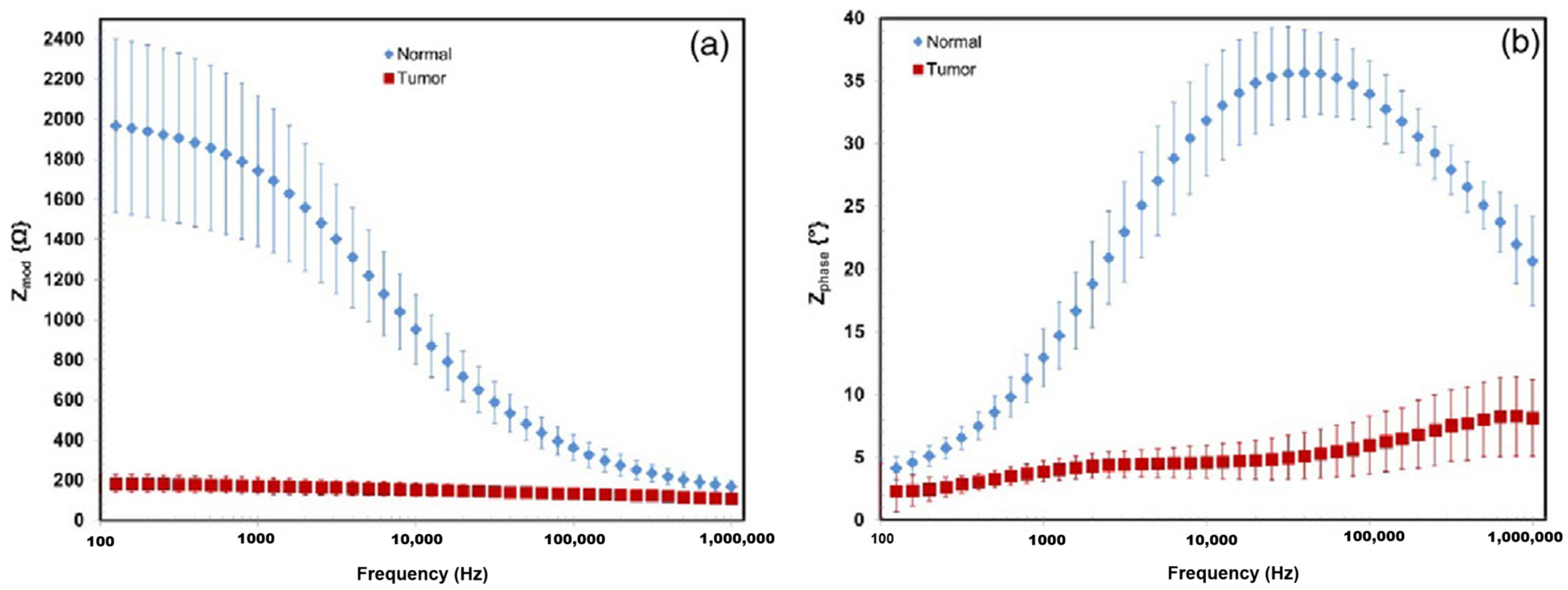
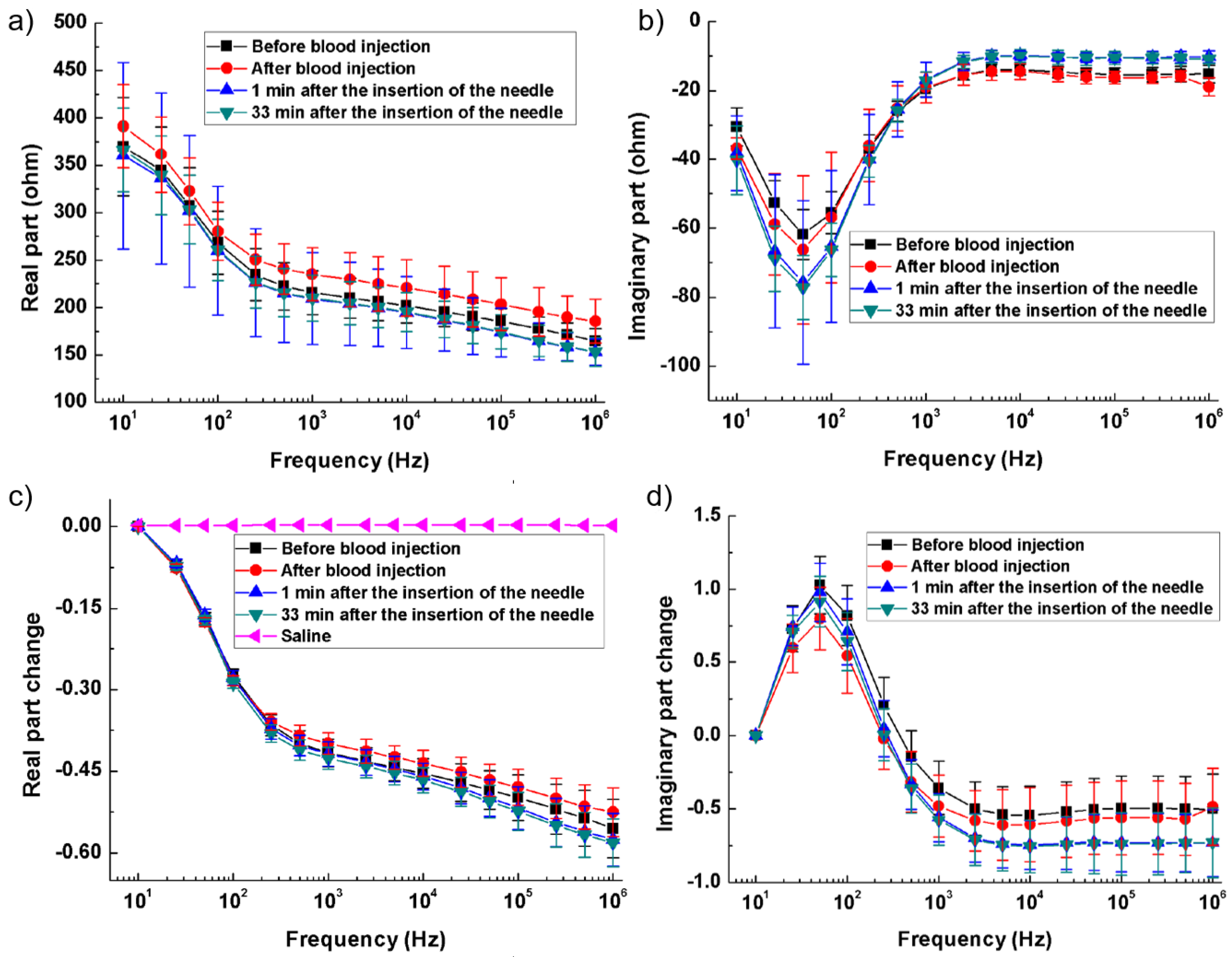
3.3. Brain Tissue Bio-Impedance
4. Electrodes and Tissue Electrical Models
4.1. Bio-Impedance Electrical Models and Plots
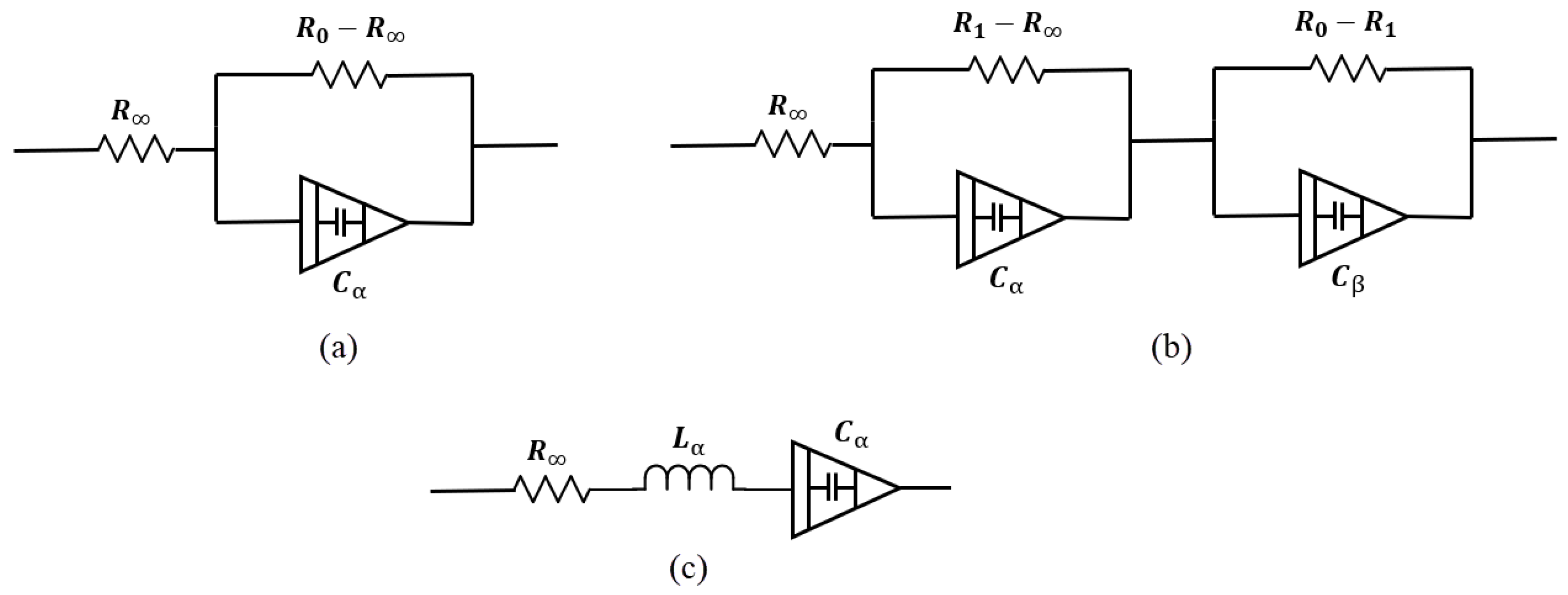
4.2. Electrical Models
- : Resistance at high frequency,
- : Resistance at low frequency,
- : Capacitance term associated with fractional-order behavior,
- : Fractional exponent ().
- : Resistance at high frequency,
- : Resistances associated with the intermediate and low-frequency dispersions,
- : Capacitance terms for the two relaxation processes,
- : Fractional exponents for the two dispersions ().
4.3. Data Visualization
4.4. Electrode Types
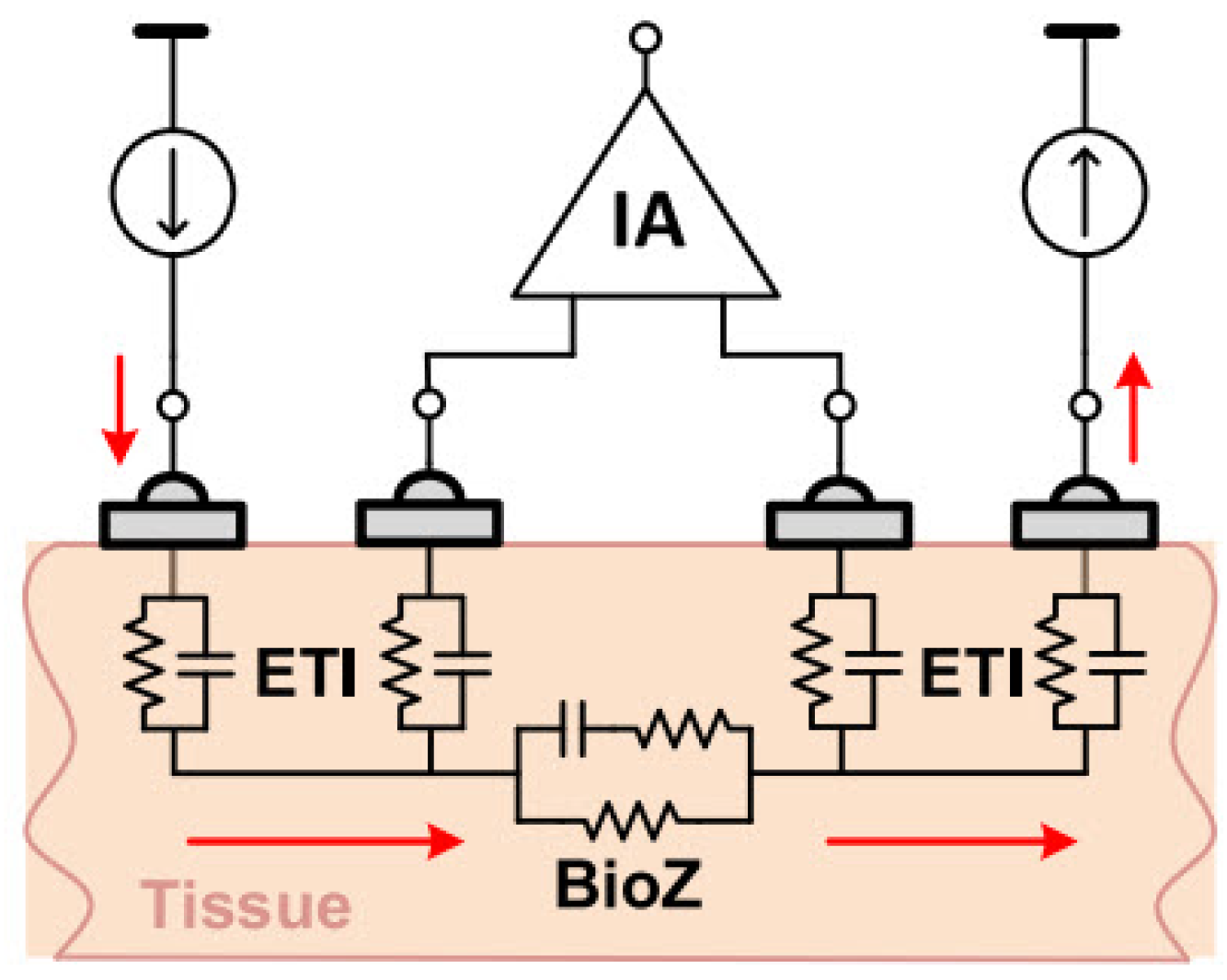
4.5. Electrode Configuration
4.6. Artifact Noises
5. Bio-Impedance Measurement Techniques
5.1. Single-Frequency
5.2. Multi-Frequency
5.3. Electric Impedance Tomography (EIT)
5.4. Bio-Impedance Spectroscopy (BIS/BIA)
6. Bio-Impedance Hardware Implementations and Mathematical Equations
6.1. Magnitude/Phase Measurement

6.2. IQ Demodulator
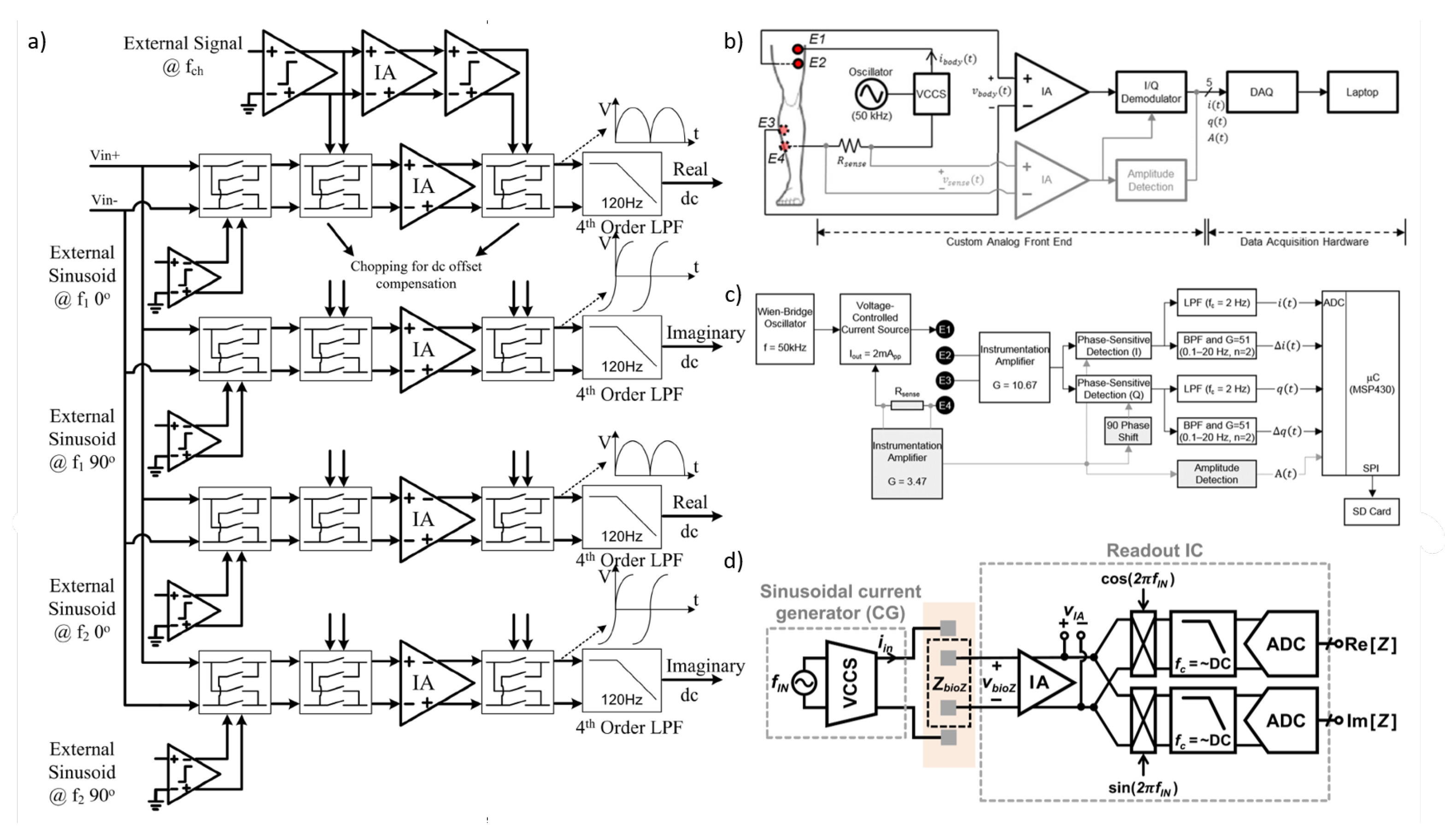
6.3. Direct Digitization

7. Discussion and Perspective
7.1. Power Consumption
7.2. Electrode Design
7.3. Digital Implementation
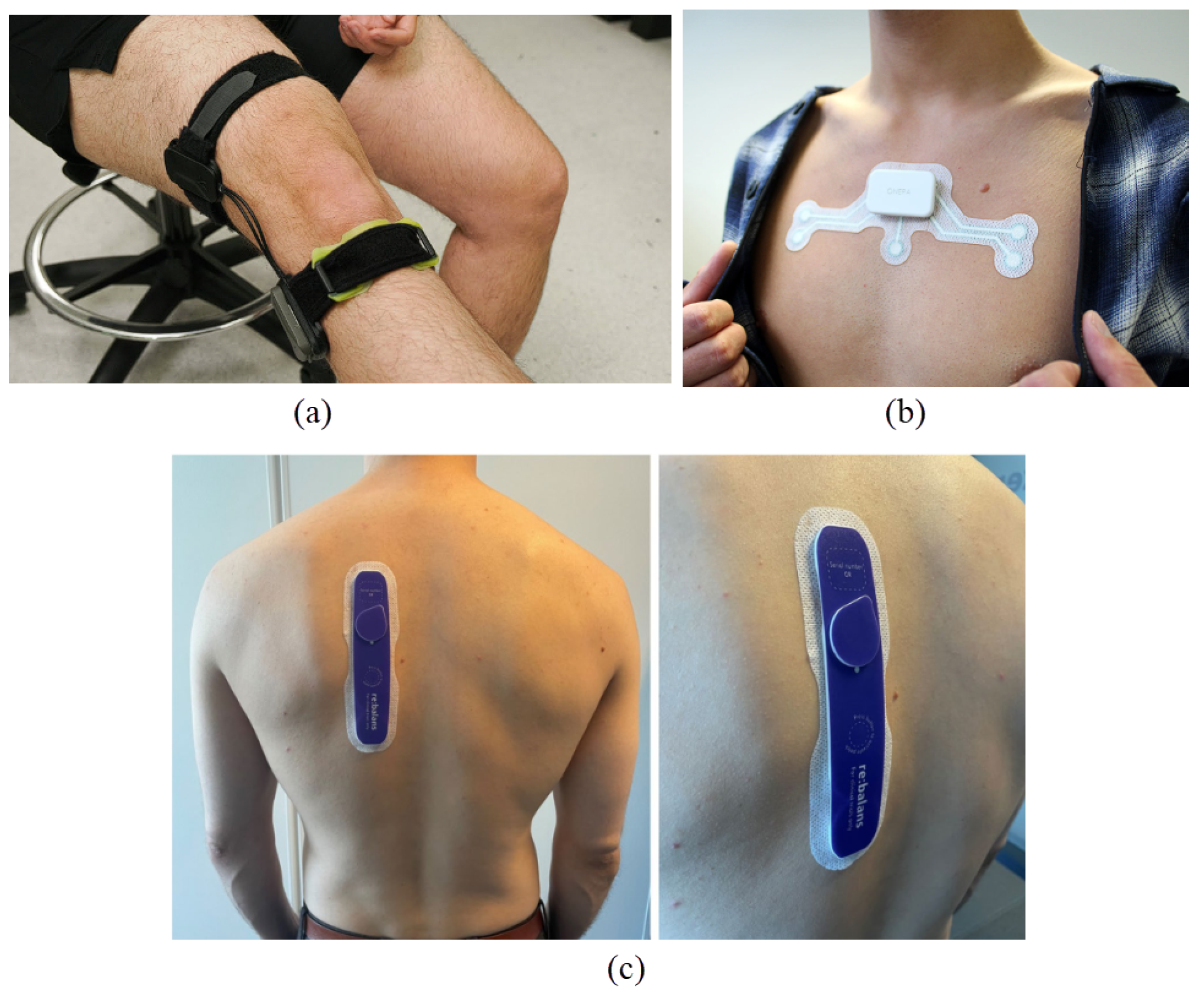
7.4. Toward Intelligent Wearable Bio-Impedance Measurement Devices
7.5. Neuromorphic Computing and Bio-Impedance: A Synergistic Approach for Intelligent Wearable Devices
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EIT | Electrical Impedance Tomography |
| EIS | Electrical Impedance Spectroscopy |
| MFEIT | Multi-frequency EIT |
| ECS | Extracellular space |
| REG | rheoencephalography |
| CBF | Cerebral blood flow |
| CSF | Cerebrospinal fluid |
| TBI | Traumatic brain injury |
| SBI | Secondary brain injury |
| TCB | Transcranial bio-impedance |
| ICP | Intracranial pressure |
| BIM | Bio-impedance monitoring |
| ECG | Electrocardiogram |
| EEG | Electroencephalogram |
| ECF | Extracellular fluid |
| ICF | Intracellular fluid |
| BIS | Bio-Impedance Spectroscopy |
| BIA | Bio-Impedance Analysis |
| SF-BIA | Single frequency BIA |
| ICW | Intracellular water |
| ECW | Extracellular water |
| TBW | Total body water |
| BMI | Body mass index |
| CPE | Constant phase elements |
| ETI | Electrode tissue impedance |
| MRI | Magnetic resonance imaging |
| fMRI | Functional MRI |
| ICV | Intracranial volume |
| IQ | In-phase and quadrature |
| IA | Instrumentation amplifier |
| ADC | Analog-to-digital converter |
| OTA | Operational Transconductance Amplifier |
| SNR | Signal-to-noise ratio |
| FFT | Fast fourier transform |
| MRPDD | Magnitude-ratio and phase-difference detection |
| GPD | Gain-phase detector |
| SD | Synchronous detection |
| DLF | Digital loop filter |
| CG | Current generator |
| CM | Common-mode |
| TC | Transconductance |
| AE | Active electrodes |
| ANN | Artificial Neural Network |
| ML | Machine learning |
| DL | Deep learning |
| GAN | Generative Adversarial Network |
| SNN | Spiking neural network |
| SEEG | Stereoelectroencephalography |
| PSG | Polysomnography |
| EBS | Electrical brain stimulation |
| REM | Rapid eye movement |
| NREM | Non-REM |
| CT | Computed tomography |
References
- Van Helleputte, N.; Konijnenburg, M.; Pettine, J.; Jee, D.W.; Kim, H.; Morgado, A.; Van Wegberg, R.; Torfs, T.; Mohan, R.; Breeschoten, A.; et al. A 345 μW multi-sensor biomedical SoC with bio-impedance, 3-channel ECG, motion artifact reduction, and integrated DSP. IEEE J. Solid-State Circuits 2014, 50, 230–244. [Google Scholar] [CrossRef]
- Xu, J.; Konijnenburg, M.; Ha, H.; Van Wegberg, R.; Song, S.; Blanco-Almazán, D.; Van Hoof, C.; Van Helleputte, N. A 36 μW 1.1 mm2 reconfigurable analog front-end for cardiovascular and respiratory signals recording. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 774–783. [Google Scholar] [CrossRef]
- Hedayatipour, A.; Aslanzadeh, S.; Hesari, S.H.; Haque, M.A.; McFarlane, N. A wearable CMOS impedance to frequency sensing system for non-invasive impedance measurements. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 1108–1121. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Kim, J.H.; Gweon, S.; Kim, M.; Yoo, H.J. A 0.5-V sub-10-μW 15.28-mΩ/Hz bio-impedance sensor IC with sub-1° phase error. IEEE J. Solid-State Circuits 2020, 55, 2161–2173. [Google Scholar] [CrossRef]
- Zhang, T.T.; Son, H.; Zhao, J.; Heng, C.H.; Gao, Y. A 26.6–119.3-μW 101.9-dB SNR Direct Digitization Bio-Impedance Readout IC. IEEE J. Solid-State Circuits 2023, 58, 2619–2631. [Google Scholar] [CrossRef]
- Konijnenburg, M.; Stanzione, S.; Yan, L.; Jee, D.W.; Pettine, J.; van Wegberg, R.; Kim, H.; Van Liempd, C.; Fish, R.; Schuessler, J.; et al. A Multi(bio)sensor Acquisition System with Integrated Processor, Power Management, 8 × 8 LED Drivers, and Simultaneously Synchronized ECG, BIO-Z, GSR, and Two PPG Readouts. IEEE J. Solid-State Circuits 2016, 51, 2584–2595. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, D.; Habibollahi, M.; Almarri, N.; Demosthenous, A. Time stamp–a novel time-to-digital demodulation method for bioimpedance implant applications. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 997–1007. [Google Scholar] [CrossRef]
- Zeng, L.; Heng, C.H. An 8-channel 1.76-mW 4.84-mm 2 electrical impedance tomography SoC with direct IF frequency division multiplexing. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3401–3405. [Google Scholar]
- Pan, Q.; Qu, T.; Tang, B.; Shan, F.; Hong, Z.; Xu, J. A 0.5-mΩ/hz dry-electrode bioimpedance interface with current mismatch cancellation and input impedance of 100 mΩat 50 kHz. IEEE J. Solid-State Circuits 2022, 58, 1735–1745. [Google Scholar] [CrossRef]
- Ko, H.; Lee, T.; Kim, J.H.; Park, J.A.; Kim, J.P. Ultralow-power bioimpedance IC with intermediate frequency shifting chopper. IEEE Trans. Circuits Syst. II Express Briefs 2015, 63, 259–263. [Google Scholar] [CrossRef]
- Rodriguez, S.; Ollmar, S.; Waqar, M.; Rusu, A. A batteryless sensor ASIC for implantable bio-impedance applications. IEEE Trans. Biomed. Circuits Syst. 2015, 10, 533–544. [Google Scholar] [CrossRef]
- Danesh, M.; Sanyal, A. 0.13 pW/Hz ring VCO-based continuous-time read-out ADC for bio-impedance measurement. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2823–2827. [Google Scholar]
- Kweon, S.J.; Rafi, A.K.; Cheon, S.I.; Je, M.; Ha, S. On-chip sinusoidal signal generators for electrical impedance spectroscopy: Methodological review. IEEE Trans. Biomed. Circuits Syst. 2022, 16, 337–360. [Google Scholar] [CrossRef] [PubMed]
- Takhti, M.; Odame, K. A power adaptive, 1.22-pW/Hz, 10-MHz read-out front-end for bio-impedance measurement. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 725–734. [Google Scholar] [CrossRef]
- ElAnsary, M.; Soltani, N.; Kassiri, H.; Machado, R.; Dufour, S.; Carlen, P.L.; Thompson, M.; Genov, R. 50 nW opamp-less ΔΣ-modulated bioimpedance spectrum analyzer for electrochemical brain interfacing. IEEE J. Solid-State Circuits 2020, 55, 1971–1983. [Google Scholar] [CrossRef]
- Cheon, S.I.; Choi, H.; Kang, H.; Suh, J.H.; Park, S.; Kweon, S.J.; Je, M.; Ha, S. Impedance-readout integrated circuits for electrical impedance spectroscopy: Methodological review. IEEE Trans. Biomed. Circuits Syst. 2023, 18, 215–232. [Google Scholar] [CrossRef]
- Georgia Institute of Technology. Arthroba: Smart Wearable for Joint Health. 2025. Available online: https://research.gatech.edu/feature/arthroba (accessed on 30 April 2025).
- Pretz, K. Prototype Wearable Monitors Sleep Apnea. 2020. Available online: https://spectrum.ieee.org/prototype-wearable-monitor-sleep-apnea-news (accessed on 30 April 2025).
- Bremnes, F.; Øien, C.M.; Kvaerness, J.; Jaatun, E.A.; Aas, S.N.; Saether, T.; Lund, H.; Romundstad, S. Measuring fluid balance in end-stage renal disease with a wearable bioimpedance sensor. BMC Nephrol. 2025, 26, 14. [Google Scholar] [CrossRef]
- Xu, J.; Hong, Z. Low power bio-impedance sensor interfaces: Review and electronics design methodology. IEEE Rev. Biomed. Eng. 2020, 15, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Groenendaal, W.; Lee, S.; Van Hoof, C. Wearable bioimpedance monitoring: Viewpoint for application in chronic conditions. JMIR Biomed. Eng. 2021, 6, e22911. [Google Scholar] [CrossRef]
- Ibrahim, B.; Jafari, R. Cuffless blood pressure monitoring from a wristband with calibration-free algorithms for sensing location based on bio-impedance sensor array and autoencoder. Sci. Rep. 2022, 12, 319. [Google Scholar] [CrossRef]
- Jaffrin, M.Y.; Morel, H. Body fluid volumes measurements by impedance: A review of bioimpedance spectroscopy (BIS) and bioimpedance analysis (BIA) methods. Med. Eng. Phys. 2008, 30, 1257–1269. [Google Scholar] [CrossRef] [PubMed]
- Rossi, S.; Pessione, M.; Radicioni, V.; Baglione, G.; Vatteroni, M.; Dario, P.; Della Torre, L. A low power bioimpedance module for wearable systems. Sens. Actuators A Phys. 2015, 232, 359–367. [Google Scholar] [CrossRef]
- Allegri, D.; Donida, A.; Malcovati, P.; Barrettino, D. CMOS-based multifrequency impedance analyzer for biomedical applications. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 1301–1312. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Kim, S.; Yoo, H.J. Design of sub-10-μW sub-0.1% THD sinusoidal current generator IC for bio-impedance sensing. IEEE J. Solid-State Circuits 2021, 57, 586–595. [Google Scholar] [CrossRef]
- Bertemes-Filho, P.; Morcelles, K.F. Wearable bioimpedance measuring devices. In Medicine-Based Informatics and Engineering; Springer: Berlin/Heidelberg, Germany, 2022; pp. 81–101. [Google Scholar]
- Van Steenkiste, T.; Groenendaal, W.; Dreesen, P.; Lee, S.; Klerkx, S.; de Francisco, R.; Deschrijver, D.; Dhaene, T. Portable detection of apnea and hypopnea events using bio-impedance of the chest and deep learning. IEEE J. Biomed. Health Inform. 2020, 24, 2589–2598. [Google Scholar] [CrossRef]
- Holder, D.S. Electrical impedance tomography (EIT) of brain function. Brain Topogr. 1992, 5, 87–93. [Google Scholar] [CrossRef]
- Everitt, A.; Root, B.; Calnan, D.; Manwaring, P.; Bauer, D.; Halter, R. A bioimpedance-based monitor for real-time detection and identification of secondary brain injury. Sci. Rep. 2021, 11, 15454. [Google Scholar] [CrossRef]
- Abboud, T.; Mielke, D.; Rohde, V. Mini review: Impedance measurement in neuroscience and its prospective application in the field of surgical neurooncology. Front. Neurol. 2022, 12, 825012. [Google Scholar] [CrossRef]
- Langlois, P.J.; Neshatvar, N.; Demosthenous, A. A sinusoidal current driver with an extended frequency range and multifrequency operation for bioimpedance applications. IEEE Trans. Biomed. Circuits Syst. 2014, 9, 401–411. [Google Scholar] [CrossRef]
- Ollmar, S.; Fernandez Schrunder, A.; Birgersson, U.; Kristoffersson, T.; Rusu, A.; Thorsson, E.; Hedenqvist, P.; Manell, E.; Rydén, A.; Jensen-Waern, M.; et al. A battery-less implantable glucose sensor based on electrical impedance spectroscopy. Sci. Rep. 2023, 13, 18122. [Google Scholar] [CrossRef]
- Jung, M.H.; Namkoong, K.; Lee, Y.; Koh, Y.J.; Eom, K.; Jang, H.; Jung, W.; Bae, J.; Park, J. Wrist-wearable bioelectrical impedance analyzer with miniature electrodes for daily obesity management. Sci. Rep. 2021, 11, 1238. [Google Scholar] [CrossRef] [PubMed]
- Ben Atitallah, B.; Kallel, A.Y.; Bouchaala, D.; Derbel, N.; Kanoun, O. Comparative study of measurement methods for embedded bioimpedance spectroscopy systems. Sensors 2022, 22, 5801. [Google Scholar] [CrossRef]
- Kassanos, P. Bioimpedance sensors: A tutorial. IEEE Sens. J. 2021, 21, 22190–22219. [Google Scholar] [CrossRef]
- Teague, C.N.; Heller, J.A.; Nevius, B.N.; Carek, A.M.; Mabrouk, S.; Garcia-Vicente, F.; Inan, O.T.; Etemadi, M. A wearable, multimodal sensing system to monitor knee joint health. IEEE Sens. J. 2020, 20, 10323–10334. [Google Scholar] [CrossRef]
- Dheman, K.; Mayer, P.; Eggimann, M.; Schuerle, S.; Magno, M. ImpediSense: A long lasting wireless wearable bio-impedance sensor node. Sustain. Comput. Inform. Syst. 2021, 30, 100556. [Google Scholar]
- Kassanos, P.; Constantinou, L.; Triantis, I.F.; Demosthenous, A. An integrated analog readout for multi-frequency bioimpedance measurements. IEEE Sens. J. 2014, 14, 2792–2800. [Google Scholar] [CrossRef]
- Amini, M.; Hisdal, J.; Kalvøy, H. Applications of bioimpedance measurement techniques in tissue engineering. J. Electr. Bioimpedance 2018, 9, 142–158. [Google Scholar] [CrossRef]
- Corchia, L.; Monti, G.; Raheli, F.; Candelieri, G.; Tarricone, L. Dry textile electrodes for wearable bio-impedance analyzers. IEEE Sens. J. 2020, 20, 6139–6147. [Google Scholar] [CrossRef]
- Mohsen, M.; Said, L.A.; Madian, A.H.; Radwan, A.G.; Elwakil, A.S. Fractional-order bio-impedance modeling for interdisciplinary applications: A review. IEEE Access 2021, 9, 33158–33168. [Google Scholar] [CrossRef]
- Mirhoseini, M.; Gatabi, Z.R.; Das, S.; Joveini, S.; Gatabi, I.R. Applications of Electrical Impedance Tomography in Neurology. Basic Clin. Neurosci. 2022, 13, 595. [Google Scholar] [CrossRef]
- Goren, N.; Avery, J.; Dowrick, T.; Mackle, E.; Witkowska-Wrobel, A.; Werring, D.; Holder, D. Multi-frequency electrical impedance tomography and neuroimaging data in stroke patients. Sci. Data 2018, 5, 180112. [Google Scholar] [CrossRef] [PubMed]
- Ke, X.Y.; Hou, W.; Huang, Q.; Hou, X.; Bao, X.Y.; Kong, W.X.; Li, C.X.; Qiu, Y.Q.; Hu, S.Y.; Dong, L.H. Advances in electrical impedance tomography-based brain imaging. Mil. Med. Res. 2022, 9, 10. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.P.V.S.R.; Bera, S.; Das, D.; Rathore, N.K. Bioelectrical impedance analysis for assessment of fluid status and congestion in heart failure: Clinical utility and future directions. Front. Cardiovasc. Med. 2024, 11, 11041432. [Google Scholar]
- Zhao, Y.; Wang, J.; Yang, H.; Li, Q.; Chen, L.; Liu, M.; Zhang, T.; Wu, K.; Xu, Z.; Ma, R.; et al. Wearable Doppler ultrasound for continuous cardiovascular monitoring: Recent advances and clinical prospects. Biosensors 2023, 13, 72. [Google Scholar]
- Liu, J.; Zhang, X.; Guo, Y.; Li, H.; Wang, M.; Chen, L.; Zhao, Q.; Huang, R.; Xu, T.; Wu, D.; et al. Recent advances in functional near-infrared spectroscopy for brain monitoring. Front. Neurosci. 2024, 17, 11119551. [Google Scholar]
- Li, H.; Chen, M.; Wang, Y.; Liu, Q.; Zhang, T.; Zhao, X.; Xu, L.; Wu, J.; Huang, K.; Gu, Z.; et al. Diffuse speckle pulsatile flowmetry for non-invasive vascular assessment: A novel tool for PAD diagnosis. Biomed. Opt. Express 2024, 15, 204–217. [Google Scholar]
- Hannan, S.; Aristovich, K.; Faulkner, M.; Avery, J.; Walker, M.C.; Holder, D.S. Imaging slow brain activity during neocortical and hippocampal epileptiform events with electrical impedance tomography. Physiol. Meas. 2021, 42, 014001. [Google Scholar] [CrossRef]
- Mivalt, F.; Kremen, V.; Sladky, V.; Cui, J.; Gregg, N.M.; Balzekas, I.; Marks, V.; St Louis, E.K.; Croarkin, P.; Lundstrom, B.N.; et al. Impedance rhythms in human limbic system. J. Neurosci. 2023, 43, 6653–6666. [Google Scholar] [CrossRef]
- Meghdadi, A.H.; Popovic, D.; Rupp, G.; Smith, S.; Berka, C.; Verma, A. Transcranial impedance changes during sleep: A rheoencephalography study. IEEE J. Transl. Eng. Health Med. 2019, 7, 2700107. [Google Scholar] [CrossRef]
- Wu, Y.; Hanzaee, F.F.; Jiang, D.; Bayford, R.H.; Demosthenous, A. Electrical impedance tomography for biomedical applications: Circuits and systems review. IEEE Open J. Circuits Syst. 2021, 2, 380–397. [Google Scholar] [CrossRef]
- Nalepa, D.; Czrkowska, M.; Zaluska, W.; Jakubowska, K.; Chrusciel, P. Electrical bioimpedance in patients after ischemic stroke, a civilization disease. Ann. Agric. Environ. Med. 2019, 26. [Google Scholar] [CrossRef] [PubMed]
- Cohen, R.; Abboud, S.; Arad, M. Monitoring brain damage using bioimpedance technique in a 3D numerical model of the head. Med. Eng. Phys. 2015, 37, 453–459. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.; Wang, Y.; Li, W.; Zhu, M.; Wang, W.; Xu, C.; Li, K.; Liu, B.; Shi, X. A preliminary study on the application of electrical impedance tomography based on cerebral perfusion monitoring to intracranial pressure changes. Front. Neurosci. 2024, 18, 1390977. [Google Scholar] [CrossRef]
- Agnelli, J.P.; Cöl, A.; Lassas, M.; Murthy, R.; Santacesaria, M.; Siltanen, S. Classification of stroke using neural networks in electrical impedance tomography. Inverse Probl. 2020, 36, 115008. [Google Scholar] [CrossRef]
- Paldanius, A.; Dekdouk, B.; Toivanen, J.; Kolehmainen, V.; Hyttinen, J. Sensitivity analysis highlights the importance of accurate head models for electrical impedance tomography monitoring of intracerebral hemorrhagic stroke. IEEE Trans. Biomed. Eng. 2021, 69, 1491–1501. [Google Scholar] [CrossRef]
- Hawthorne, C.; Shaw, M.; Piper, I.; Moss, L.; Kinsella, J. Transcranial bioimpedance measurement as a non-invasive estimate of intracranial pressure. In Intracranial Pressure & Neuromonitoring XVI; Springer: Berlin/Heidelberg, Germany, 2018; pp. 89–92. [Google Scholar]
- Arjun, B.; Alekya, B.; Hari, R.; Vikas, V.; Hardik, J.P. Electromechanical characterization of human brain tissues: A potential biomarker for tumor delineation. IEEE Trans. Biomed. Eng. 2022, 69, 3484–3493. [Google Scholar]
- Pethig, R.; Kell, D.B. The passive electrical properties of biological systems: Their significance in physiology, biophysics and biotechnology. Phys. Med. Biol. 1987, 32, 933. [Google Scholar] [CrossRef]
- Miklavčič, D.; Pavšelj, N.; Hart, F.X. Electric Properties of Tissues. Wiley Encycl. Biomed. Eng. 2006, 6, 3578–3589. [Google Scholar] [CrossRef]
- Schwan, H.P. Electrical properties of tissues and cell suspensions: Mechanisms and models. In Proceedings of the 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Baltimore, MD, USA, 3–6 November 1994; Volume 1, pp. 70–71. [Google Scholar] [CrossRef]
- Kyle, U.G.; Bosaeus, I.; Lorenzo, A.D.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.C.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part I: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef]
- Grimnes, S.; Ørjan, G.M. Bioimpedance and Bioelectricity Basics, 3rd ed.; Academic Press: London, UK, 2014. [Google Scholar] [CrossRef]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Transport into the Cell from the Plasma Membrane: Endocytosis. In Molecular Biology of the Cell, 4th ed.; Garland Science: New York, NY, USA, 2002; pp. 759–804. [Google Scholar]
- Asami, K. Characterization of heterogeneous systems by dielectric spectroscopy. Prog. Polym. Sci. 2002, 27, 1617–1659. [Google Scholar] [CrossRef]
- Heileman, K.; Daoud, J.; Tabrizian, M. Dielectric spectroscopy as a viable biosensing tool for cell and tissue characterization and analysis. Biosens. Bioelectron. 2013, 49, 348–359. [Google Scholar] [CrossRef] [PubMed]
- Pitts, R.F. Physiology of the Kidney and Body Fluids: An Introductory Text; Year Book Medical Publishers: Chicago, IL, USA, 1968. [Google Scholar]
- Riu, P.J. Comments on “Bioelectrical parameters of the whole human body obtained through bioelectrical impedance analysis”. Bioelectromagnetics 2004, 25, 69–71. [Google Scholar] [CrossRef]
- Gabriel, C.; Gabriel, S.; Corthout, E. The dielectric properties of biological tissues: I. Literature survey. Phys. Med. Biol. 1996, 41, 2231–2249. [Google Scholar] [CrossRef]
- Ørjan, G.M.; Grimnes, S.; Schwan, H.P. Interface Phenomena and Dielectric Properties of Biological Tissue. In Encyclopedia of Surface and Colloid Science; Marcel Dekker: New York, NY, USA, 2002; pp. 2643–2652. [Google Scholar]
- Dean, D.A.; Ramanathan, T.; Machado, D.; Sundararajan, R. Electrical Impedance Spectroscopy Study of Biological Tissues. J. Electrost. 2008, 66, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Kwon, H.; McEwan, A.L.; Oh, T.I.; Farooq, A.; Woo, E.J.; Seo, J.K. A local region of interest imaging method for electrical impedance tomography with internal electrodes. Comput. Math. Methods Med. 2013, 2013, 964918. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.K.; Bera, T.K.; Kwon, H.; Sadleir, R.J. Effective Admittivity of Biological Tissues as a Coefficient of Elliptic PDE. Comput. Math. Methods Med. 2013, 2013, 353849. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef]
- Schwan, H.P. Electrical properties of tissues and cell suspensions. Adv. Biol. Med. Phys. 1957, 5, 147–209. [Google Scholar] [CrossRef]
- El Khaled, D.; Castellano, N.N.; Gazquez, J.A.; Perea-Moreno, A.J. Dielectric Spectroscopy in Biomaterials: Agrophysics. Materials 2016, 9, 310. [Google Scholar] [CrossRef]
- Zajíček, R.; Oppl, L.; Vrba, J. Broadband Measurement of Complex Permittivity Using Reflection Method and Coaxial Probes. Radioengineering 2008, 17, 14–19. [Google Scholar]
- Vorlíček, J.; Oppl, L.; Vrba, J. Measurement of Complex Permittivity of Biological Tissues. In Proceedings of the Progress in Electromagnetics Research Symposium Proceedings, Cambridge, MA, USA, 5–8 July 2010; pp. 14–19. [Google Scholar]
- Markx, G.H. The use of electric fields in tissue engineering: A review. Organogenesis 2008, 4, 11–17. [Google Scholar] [CrossRef]
- Pliquett, U.; Prausnitz, M.R. Electrical Impedance Spectroscopy for Rapid and Noninvasive Analysis of Skin Electroporation. In Electrically Mediated Delivery of Molecules to Cells: Electrochemotherapy, Electrogenetherapy, and Transdermal Delivery by Electroporation; Jaroszeski, M.J., Heller, R., Gilbert, R., Eds.; Humana Press: Totowa, NJ, USA, 2000; pp. 377–406. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef]
- Smith, S.R.; Foster, K.R.; Wolf, G.L. Dielectric properties of VX-2 carcinoma versus normal liver tissue. IEEE Trans. Biomed. Eng. 1986, BME-33, 522–524. [Google Scholar] [CrossRef] [PubMed]
- Prakash, S.; Karnes, M.P.; Sequin, E.K.; West, J.D.; Hitchcock, C.L.; Nichols, S.D.; Bloomston, M.; Abdel-Misih, S.R.; Schmidt, C.R.; Martin, E.W., Jr.; et al. Ex vivo electrical impedance measurements on excised hepatic tissue from human patients with metastatic colorectal cancer. Physiol. Meas. 2015, 36, 315–328. [Google Scholar] [CrossRef]
- Efron, R. The alteration of electrical impedance of the brain during induced seizures (cat). In Proceedings of the Transactions of the Fifth Research Conference on Chemotherapy in Psychiatry, Cincinnati, OH, USA, 6–8 June 1961; pp. 11–11A. [Google Scholar]
- Van Harreveld, A.; Schade, J.P. Changes in the electrical conductivity of cerebral cortex during seizure activity. Exp. Neurol. 1962, 5, 383–400. [Google Scholar] [CrossRef]
- Elazar, Z.; Kado, R.T.; Adey, W.R. Impedance changes during epileptic seizures. Epilepsia 1966, 7, 291–307. [Google Scholar] [CrossRef] [PubMed]
- Fu, F.; Li, B.; Dai, M.; Hu, S.J.; Li, X.; Xu, C.H.; Wang, B.; Yang, B.; Tang, M.X.; Dong, X.Z.; et al. Use of electrical impedance tomography to monitor regional cerebral edema during clinical dehydration treatment. PLoS ONE 2014, 9, e113202. [Google Scholar] [CrossRef] [PubMed]
- Mestre, H.; Du, T.; Sweeney, A.M.; Liu, G.; Samson, A.J.; Peng, W.; Mortensen, K.N.; Stæger, F.F.; Bork, P.A.R.; Bashford, L.; et al. Cerebrospinal fluid influx drives acute ischemic tissue swelling. Science 2020, 367, eaax7171. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, Z.; Zhang, Z.; Wang, Z.; Li, Z.; Chen, Z. Development of a Portable Electrical Impedance Tomography System for Biomedical Applications. IEEE Sens. J. 2018, 18, 8117–8124. [Google Scholar] [CrossRef]
- Kalogeris, T.; Baines, C.P.; Krenz, M.; Korthuis, R.J. Cell biology of ischemia/reperfusion injury. Int. Rev. Cell Mol. Biol. 2012, 298, 229–317. [Google Scholar] [CrossRef]
- Dowrick, T.; Blochet, C.; Holder, D. In vivo bioimpedance changes during haemorrhagic and ischaemic stroke in rats: Towards 3D stroke imaging using electrical impedance tomography. Physiol. Meas. 2016, 37, 765–784. [Google Scholar] [CrossRef]
- Yang, L.; Liu, W.; Chen, R.; Zhang, G.; Li, W.; Fu, F.; Dong, X. In Vivo Bioimpedance Spectroscopy Characterization of Healthy, Hemorrhagic and Ischemic Rabbit Brain within 10 Hz–1 MHz. Sensors 2017, 17, 791. [Google Scholar] [CrossRef]
- Seoane, F.; Atefi, S.R.; Tomner, J.; Kostulas, K.; Lindecrantz, K. Electrical Bioimpedance Spectroscopy on Acute Unilateral Stroke Patients: Initial Observations regarding Differences between Sides. BioMed Res. Int. 2015, 2015, 613247. [Google Scholar] [CrossRef] [PubMed]
- Showkat, I.; Khanday, F.A.; Beigh, M.R. A review of bio-impedance devices. Med. Biol. Eng. Comput. 2023, 61, 927–950. [Google Scholar] [CrossRef]
- Fricke, H. A mathematical treatment of the electrical conductivity of colloids and cell suspensions. J. Gen. Physiol. 1924, 6, 375. [Google Scholar] [CrossRef] [PubMed]
- Fricke, H.; Morse, S. The electric resistance and capacity of blood for frequencies between 800 and 41/2 million cycles. J. Gen. Physiol. 1925, 9, 153. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Stupin, D.D.; Kuzina, E.A.; Abelit, A.A.; Emelyanov, A.K.; Nikolaev, D.M.; Ryazantsev, M.N.; Koniakhin, S.V.; Dubina, M.V. Bioimpedance spectroscopy: Basics and applications. ACS Biomater. Sci. Eng. 2021, 7, 1962–1986. [Google Scholar] [CrossRef]
- Ionescu, C.M.; De Keyser, R. Time domain validation of a fractional order model for human respiratory system. In Proceedings of the MELECON 2008—The 14th IEEE Mediterranean Electrotechnical Conference, Ajaccio, France, 5–7 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 89–95. [Google Scholar]
- Kumar, G.; Kasiviswanathan, U.; Mukherjee, S.; Mahto, S.K.; Sharma, N.; Patnaik, R. Changes in electrolyte concentrations alter the impedance during ischemia-reperfusion injury in rat brain. Physiol. Meas. 2019, 40, 105004. [Google Scholar] [CrossRef]
- Zhang, Y.; Verschooten, E.; Ourak, M.; Van Assche, K.; Borghesan, G.; Wu, D.; Niu, K.; Joris, P.X.; Vander Poorten, E. Physiological motion compensation for neuroscience research based on electrical bio-impedance sensing. IEEE Sens. J. 2023, 23, 25377–25389. [Google Scholar] [CrossRef]
- Sel, K.; Osman, D.; Jafari, R. Non-invasive cardiac and respiratory activity assessment from various human body locations using bioimpedance. IEEE Open J. Eng. Med. Biol. 2021, 2, 210–217. [Google Scholar] [CrossRef] [PubMed]
- Hanzaee, F.F.; Neshatvar, N.; Rahal, M.; Jiang, D.; Bayford, R.; Demosthenous, A. A low-power recursive I/Q signal generator and current driver for bioimpedance applications. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4108–4112. [Google Scholar]
- Robertz, L.; Rieppo, L.; Korkala, S.; Jaako, T.; Saarakkala, S. Inter-and Intra-Day Precision of a Low-Cost and Wearable Bioelectrical Impedance Analysis Device. In Nordic Conference on Digital Health and Wireless Solutions; Springer: Cham, Switzerland, 2024; pp. 441–450. [Google Scholar]
- Yúfera, A.; Rueda, A. Design of a CMOS closed-loop system with applications to bio-impedance measurements. Microelectron. J. 2010, 41, 231–239. [Google Scholar] [CrossRef]
- Kassanos, P.; Triantis, I.F.; Demosthenous, A. A CMOS magnitude/phase measurement chip for impedance spectroscopy. IEEE Sens. J. 2013, 13, 2229–2236. [Google Scholar] [CrossRef]
- Añorga, L.; Rebollo, A.; Herrán, J.; Arana, S.; Bandrés, E.; García-Foncillas, J. Development of a DNA microelectrochemical biosensor for CEACAM5 detection. IEEE Sens. J. 2010, 10, 1368–1374. [Google Scholar] [CrossRef]
- Jang, L.S.; Wang, M.H. Microfluidic device for cell capture and impedance measurement. Biomed. Microdevices 2007, 9, 737–743. [Google Scholar] [CrossRef]
- Holmes, D.; Morgan, H. Single cell impedance cytometry for identification and counting of CD4 T-cells in human blood using impedance labels. Anal. Chem. 2010, 82, 1455–1461. [Google Scholar] [CrossRef]
- Woods, V.M.; Triantis, I.F.; Toumazou, C. Offset prediction for charge-balanced stimulus waveforms. J. Neural Eng. 2011, 8, 046032. [Google Scholar] [CrossRef]
- Ackmann, J.J. Complex bioelectric impedance measurement system for the frequency range from 5 Hz to 1 MHz. Ann. Biomed. Eng. 1993, 21, 135–146. [Google Scholar] [CrossRef]
- Pallàs-Areny, R.; Webster, J.G. Bioelectric impedance measurements using synchronous sampling. IEEE Trans. Biomed. Eng. 1993, 40, 824–829. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J.; Yu, G.; Niu, F.; He, P. Design and preliminary evaluation of a portable device for the measurement of bioimpedance spectroscopy. Physiol. Meas. 2006, 27, 1293–1310. [Google Scholar] [CrossRef]
- Zamani, M.; Rezaeiyan, Y.; Shoaei, O.; Serdijn, W.A. A 1.55 μW bio-impedance measurement system for implantable cardiac pacemakers in 0.18 μm CMOS. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 211–221. [Google Scholar] [CrossRef] [PubMed]
- Kweon, S.J.; Shin, S.; Park, J.H.; Suh, J.H.; Yoo, H.J. A CMOS low-power polar demodulator for electrical bioimpedance spectroscopy using adaptive self-sampling schemes. In Proceedings of the IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, 17–19 October 2016; pp. 284–287. [Google Scholar] [CrossRef]
- IEC 60601-1; Medical Electrical Equipment—Part 1: General Requirements for Basic Safety and Essential Performance, Consolidated Version: 2005 + A1:2012 + A2:2020. IEC: Geneva, Switzerland, 2020.
- Cheon, S.I.; Kweon, S.J.; Kim, Y.; Koo, J.; Ha, S.; Je, M. A polar-demodulation-based impedance-measurement IC using frequency-shift technique with low power consumption and wide frequency range. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 1210–1220. [Google Scholar] [CrossRef]
- Koukourlis, C.S.; Trigonidis, V.K.; Sahalos, J.N. Differential synchronous demodulation for small-signal amplitude estimation. IEEE Trans. Instrum. Meas. 1993, 42, 926–931. [Google Scholar] [CrossRef]
- Min, M.; Parve, T.; Ronk, A.; Annus, P.; Paavle, T. Synchronous sampling and demodulation in an instrument for multifrequency bioimpedance measurement. IEEE Trans. Instrum. Meas. 2007, 56, 1365–1372. [Google Scholar] [CrossRef]
- Rahal, M.; Demosthenous, A. A synchronous chopping demodulator and implementation for high-frequency inductive position sensors. IEEE Trans. Instrum. Meas. 2009, 58, 3693–3701. [Google Scholar] [CrossRef]
- Triantis, I.F.; Demosthenous, A.; Rahal, M.; Hong, H.; Bayford, R. A multi-frequency bioimpedance measurement ASIC for electrical impedance tomography. In Proceedings of the European Solid-State Circuits Conference (ESSCIRC), Helsinki, Finland, 12–16 September 2011; pp. 331–334. [Google Scholar] [CrossRef]
- Pallàs-Areny, R.; Webster, J.G. Analog Signal Processing; Wiley: New York, NY, USA, 1999; pp. 259–269. [Google Scholar]
- Sanchez, B.; Vandersteen, G.; Bragos, R.; Schoukens, J. Basics of broadband impedance spectroscopy measurements using periodic excitations. Meas. Sci. Technol. 2012, 23, 105501. [Google Scholar] [CrossRef]
- Casanella, R.; Casas, O.; Pallàs-Areny, R. Differential synchronous demodulator for modulating sensors and impedance measurements. Meas. Sci. Technol. 2005, 16, 1637–1643. [Google Scholar] [CrossRef]
- Worapishet, A.; Demosthenous, A.; Liu, X. A CMOS instrumentation amplifier with 90-dB CMRR at 2-MHz using capacitive neutralization: Analysis, design considerations, and implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 699–710. [Google Scholar] [CrossRef]
- Hersek, S.; Töreyin, H.; Teague, C.N.; Millard-Stafford, M.L.; Jeong, H.K.; Sawka, M.N.; Inan, O.T. Wearable Vector Electrical Bioimpedance System to Assess Knee Joint Health. IEEE Trans. Biomed. Eng. 2017, 64, 2353–2360. [Google Scholar] [CrossRef]
- Hersek, S.; Töreyin, H.; Inan, O.T. A Robust System for Longitudinal Knee Joint Edema and Blood Flow Assessment Based on Vector Bioimpedance Measurements. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 545–555. [Google Scholar] [CrossRef]
- Takhti, M.; Odame, K. Structured design methodology to achieve a high SNR electrical impedance tomography. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 364–375. [Google Scholar] [CrossRef]
- Subhan, S.; Ha, S. A Harmonic Error Cancellation Method for Accurate Clock-Based Electrochemical Impedance Spectroscopy. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 710–724. [Google Scholar] [CrossRef]
- Darabi, H.; Chiu, J. A noise cancellation technique in active RF-CMOS mixers. IEEE J. Solid-State Circuits 2005, 40, 2628–2632. [Google Scholar] [CrossRef]
- Qu, G.; Wang, H.; Zhao, Y.; O’Donnell, J.; Lyden, C.; Liu, Y.; Ding, J.; Dempsey, D.; Chen, L.; Bourke, D.; et al. A 0.28 mΩ-sensitivity 105 dB-dynamic-range electrochemical impedance spectroscopy SoC for electrochemical gas detection. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 11–15 February 2018; pp. 286–288. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, D.; Bardill, A.; Bayford, R.; Demosthenous, A. A 122 fps, 1 MHz bandwidth multifrequency wearable EIT belt featuring novel active electrode architecture for neonatal thorax vital sign monitoring. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 927–937. [Google Scholar] [CrossRef] [PubMed]
- Rahal, M.; Dai, J.; Wu, Y.; Bardill, A.; Bayford, R.; Demosthenous, A. High frame rate electrical impedance tomography system for monitoring of regional lung ventilation. In Proceedings of the 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Scotland, UK, 11–15 July 2022; pp. 2487–2490. [Google Scholar] [CrossRef]
- Suh, J.H.; Choi, H.; Jung, Y.; Oh, S.; Cho, H.; Koo, N.; Kim, S.J.; Bae, C.; Ha, S.; Je, M. A 16-Channel Impedance-Readout IC with Synchronous Sampling and Baseline Cancelation for Fast Neural Electrical Impedance Tomography. IEEE Solid-State Circuits Lett. 2023, 6, 109–112. [Google Scholar] [CrossRef]
- Aristovich, K.Y.; Donegá, M.; Blochet, C.; Avery, J.; Hannan, S.; Chew, D.J.; Holder, D.S. Imaging fast neural traffic at fascicular level with electrical impedance tomography: Proof of principle in rat sciatic nerve. J. Neural Eng. 2018, 15, 056025. [Google Scholar] [CrossRef]
- Pandey, A.; Alamouti, S.F.; Doong, J.; Kaveh, R.; Yalcin, C.; Ghanbari, M.M.; Muller, R. A 6.8 μW AFE for Ear EEG Recording with Simultaneous Impedance Measurement for Motion Artifact Cancellation. In Proceedings of the IEEE International Custom Integrated Circuits Conference (CICC), Newport Beach, CA, USA, 24–27 April 2022; pp. 1–2. [Google Scholar]
- Ying, D.; Tseng, C.Y.; Chen, P.W.; Lo, Y.H.; Hall, D.A. A 30.3 fA/Hz biosensing current front-end with 139 dB cross-scale dynamic range. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 1368–1379. [Google Scholar] [CrossRef]
- Son, H.; Cho, H.; Koo, J.; Ji, Y.; Kim, B.; Park, H.J.; Sim, J.Y. A low-power wide dynamic-range current readout circuit for ion-sensitive FET sensors. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 523–533. [Google Scholar] [CrossRef]
- Djekic, D.; Fantner, G.E.; Lips, K.; Ortmanns, M.; Anders, J. A 0.1% THD, 1-MΩ to 1-GΩ Tunable, Temperature-Compensated Transimpedance Amplifier Using a Multi-Element Pseudo-Resistor. IEEE J. Solid-State Circuits 2018, 53, 1913–1923. [Google Scholar] [CrossRef]
- Songkakul, T.; Wu, S.; Ahmmed, P.; Reynolds, W.D.; Zhu, Y.; Bozkurt, A. Wearable Bioimpedance Hydration Monitoring System using Conformable AgNW Electrodes. In Proceedings of the 2021 IEEE Sensors, Sydney, Australia, 31 October–3 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–4. [Google Scholar]
- Buscaglia, L.A.; Oliveira, O.N.; Carmo, J.P. Roadmap for electrical impedance spectroscopy for sensing: A tutorial. IEEE Sens. J. 2021, 21, 22246–22257. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, B.; Rey, V.F.; Bian, S.; Lukowicz, P. iEat: Automatic wearable dietary monitoring with bio-impedance sensing. Sci. Rep. 2024, 14, 17873. [Google Scholar] [CrossRef] [PubMed]
- Hou, J.; Nesaragi, N.; Tronstad, C. Electrical bioimpedance in the era of artificial intelligence. J. Electr. Bioimpedance 2024, 15, 1. [Google Scholar] [CrossRef] [PubMed]
- Covi, E.; Donati, E.; Liang, X.; Kappel, D.; Heidari, H.; Payvand, M.; Wang, W. Adaptive extreme edge computing for wearable devices. Front. Neurosci. 2021, 15, 611300. [Google Scholar] [CrossRef]




| Electrolyte | Na+ | K+ | Ca2+ | Mg+ | Cl− | Protein | Org Acid | ||
|---|---|---|---|---|---|---|---|---|---|
| Plasma | 142 | 4 | 5 | 3 | 103 | 27 | 2 | 16 | 5 |
| Interstitial | 151 | 4.3 | 5.4 | 3.2 | 109.7 | 28.7 | 2.1 | 17 | 5.3 |
| ICW muscle | 10 | 160 | 35 | 2 | 8 | 140 | 55 |
| Phenomenon | Epileptic Seizures | Acute Stroke | Tumor | Hemorrhagic | Ischemic |
|---|---|---|---|---|---|
| Time Variation | Slow | Slow | Slow | Slow | Slow |
| Impedance Variation | Increase [29] | Decrease/Increase [95] | Decrease [84] | Decrease [71,93] | Increase [71,93] |
| 10–12% [88] | - | 6–7.5 × conductivity [84] | 10–60% [30,94] | 20–200% [30,89] | |
| Brain Region | Focal 1 | Focal/Global 2 | Focal | Focal/Global 2 | Focal/Global |
| Category | Sub-Type | Pros | Cons |
|---|---|---|---|
| Wearable Electrodes | General Features |
|
|
| Wet Electrodes |
|
| |
| Dry Electrodes |
|
|
| Technique | Mechanism of Operation | Cost | Wearable | Operability | Side Effects | Precision | Relationship with Bio-Impedance | Diagnosable Diseases |
|---|---|---|---|---|---|---|---|---|
| EIT | Electrical impedance | L | Yes | Maneuverable | No | L | EIT and EEG can be used simultaneously to monitor brain activity and improve the localization of brain events, such as seizures. | Epilepsy, stroke, brain tumors, brain edema |
| fcPAT | Optical excitation and acoustic detection | L | Yes | Maneuverable | No | H | fcPAT is a complementary technique to EEG, providing information about hemodynamic changes associated with brain activity. | Functional brain imaging, brain disorders |
| EEG | Electrical signals in the brain | M | Yes | Maneuverable | No | M | EEG measures electrical activity in the brain, while bio-impedance measures the opposition to the flow of an alternating electrical current through brain tissues. | Epilepsy, sleep disorders, brain death, coma, encephalopathies, brain tumors, stroke |
| CT | X-ray absorption by tissues | H | No | Stationary | Minimal | H | CT provides structural information about the brain, which can be used to interpret bio-impedance changes. | Brain tumors, stroke, head injuries |
| MRI | Nuclear magnetic resonance | H | No | Stationary | Minimal | H | MRI provides high-resolution structural information about the brain, which can be used to interpret bio-impedance changes. | Brain tumors, stroke, multiple sclerosis |
| PET | Radioactive tracer distribution | H | No | Stationary | Moderate | H | PET provides functional information about the brain, which can be used to interpret bio-impedance changes. | Brain tumors, Alzheimer’s disease, Parkinson’s disease |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arabsalmani, N.; Ghouchani, A.; Jafarabadi Ashtiani, S.; Zamani, M. Exploring Bio-Impedance Sensing for Intelligent Wearable Devices. Bioengineering 2025, 12, 521. https://doi.org/10.3390/bioengineering12050521
Arabsalmani N, Ghouchani A, Jafarabadi Ashtiani S, Zamani M. Exploring Bio-Impedance Sensing for Intelligent Wearable Devices. Bioengineering. 2025; 12(5):521. https://doi.org/10.3390/bioengineering12050521
Chicago/Turabian StyleArabsalmani, Nafise, Arman Ghouchani, Shahin Jafarabadi Ashtiani, and Milad Zamani. 2025. "Exploring Bio-Impedance Sensing for Intelligent Wearable Devices" Bioengineering 12, no. 5: 521. https://doi.org/10.3390/bioengineering12050521
APA StyleArabsalmani, N., Ghouchani, A., Jafarabadi Ashtiani, S., & Zamani, M. (2025). Exploring Bio-Impedance Sensing for Intelligent Wearable Devices. Bioengineering, 12(5), 521. https://doi.org/10.3390/bioengineering12050521








