A Multitask Deep Learning Model for Predicting Myocardial Infarction Complications
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description
- At hospital admission (all columns except 93–95, 100–105);
- At 24 h after admission (all columns except 94, 95, 101, 102, 104, 105);
- At 48 h after admission (all columns except 95, 102, 105);
- At 72 h after admission (all columns 2–112).
2.2. Multitask Neural Network Model Architecture
2.3. Forward Pass and Activation Functions
2.4. Backpropagation, Class Imbalance and Loss Functions
2.5. Parameter Updates with Adam Optimizer
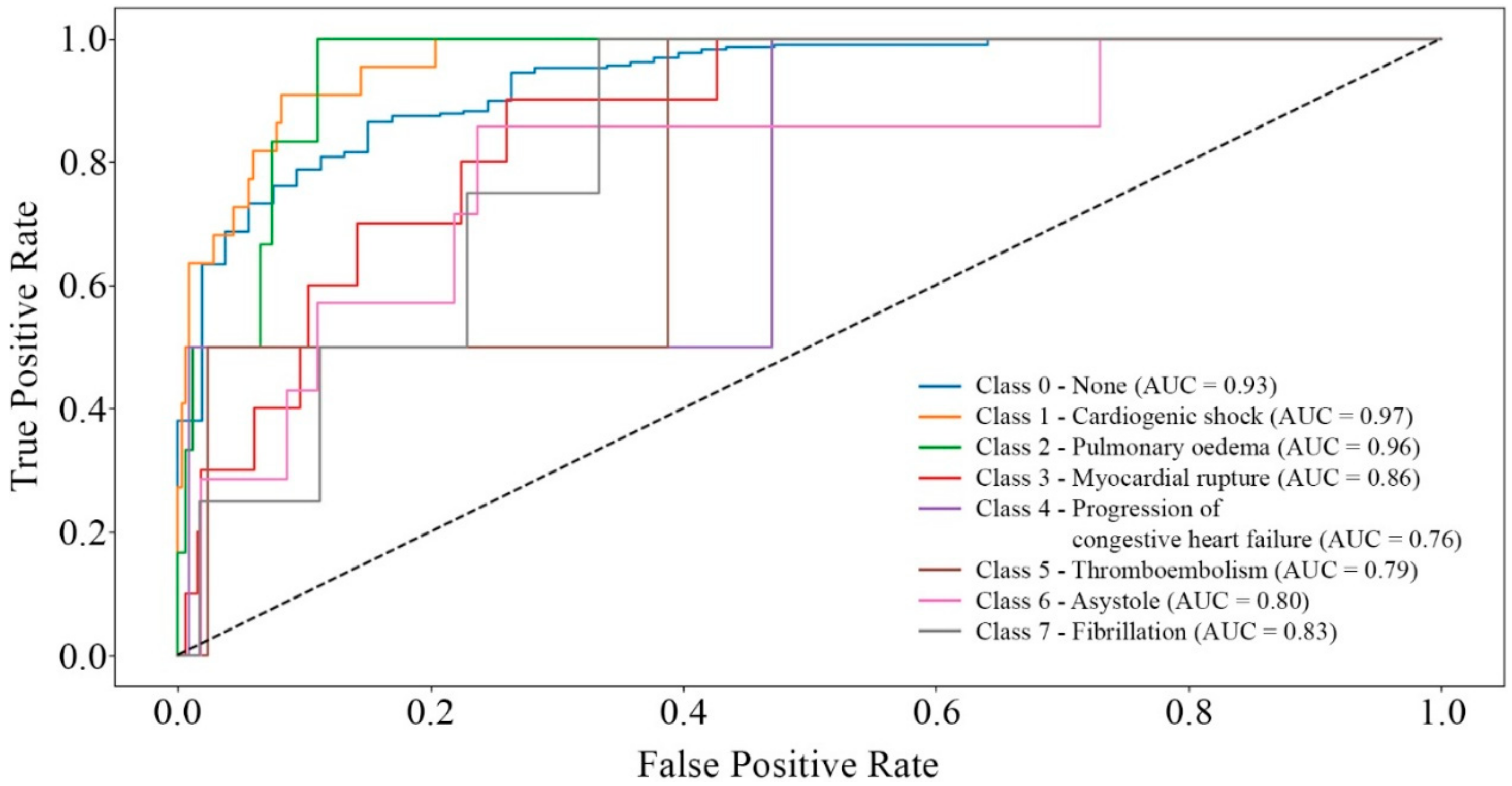
3. Results
4. Discussion
4.1. Comparison with Other ML Models
4.2. Clinical Interpretation and Feature Importance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Statistics 2024: Monitoring health for the SDGs, Sustainable Development Goals; World Health Organization: Geneva, Switzerland, 2024; pp. 12–14.
- Bokenberger, K.; Rahman, S.; Wang, M.; Vaez, M.; Dorner, T.E.; Helgesson, M.; Ivert, T.; Mittendorfer-Rutz, E. Work disability patterns before and after incident acute myocardial infarction and subsequent risk of common mental disorders: A Swedish cohort study. Sci. Rep. 2019, 9, 16086. [Google Scholar] [CrossRef] [PubMed]
- Bauer, D.; Toušek, P. Risk Stratification of Patients with Acute Coronary Syndrome. J. Clin. Med. 2021, 10, 4574. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.K.; Mustafiz, C.; Mutahar, D.; Zaka, A.; Parvez, R.; Mridha, N.; Stretton, B.; Kovoor, J.G.; Bacchi, S.; Ramponi, F.; et al. Machine Learning vs Traditional Approaches to Predict All-Cause Mortality for Acute Coronary Syndrome: A Systematic Review and Meta-analysis. Can. J. Cardiol. 2025. [Google Scholar] [CrossRef] [PubMed]
- Schlesinger, D.E.; Stultz, C.M. Deep Learning for Cardiovascular Risk Stratification. Curr. Treat. Options Cardiovasc. Med. 2020, 22, 15. [Google Scholar] [CrossRef]
- Salas-Nuñez, L.F.; Barrera-Ocampo, A.; Caicedo, P.A.; Cortes, N.; Osorio, E.H.; Villegas-Torres, M.F.; González Barrios, A.F. Machine Learning to Predict Enzyme–Substrate Interactions in Elucidation of Synthesis Pathways: A Review. Metabolites 2024, 14, 154. [Google Scholar] [CrossRef]
- Huang, J.; Huth, C.; Covic, M.; Troll, M.; Adam, J.; Zukunft, S.; Prehn, C.; Wang, L.; Nano, J.; Scheerer, M.F.; et al. Machine Learning Approaches Reveal Metabolic Signatures of Incident Chronic Kidney Disease in Individuals with Prediabetes and Type 2 Diabetes. Diabetes 2020, 69, 2756–2765. [Google Scholar] [CrossRef]
- Muntasir Nishat, M.; Faisal, F.; Jahan Ratul, I.; Al-Monsur, A.; Ar-Rafi, A.M.; Nasrullah, S.M.; Reza, M.T.; Khan, M.R.H. A comprehensive investigation of the performances of different machine learning classifiers with SMOTE-ENN oversampling technique and hyperparameter optimization for imbalanced heart failure dataset. Sci. Program. 2022, 2022, 3649406. [Google Scholar] [CrossRef]
- Fedai, H.; Sariisik, G.; Toprak, K.; Taşcanov, M.B.; Efe, M.M.; Arğa, Y.; Doğanoğulları, S.; Gez, S.; Demirbağ, R. A Machine Learning Model for the Prediction of No-Reflow Phenomenon in Acute Myocardial Infarction Using the CALLY Index. Diagnostics 2024, 14, 2813. [Google Scholar] [CrossRef]
- Ibrahim, L.; Mesinovic, M.; Yang, K.W.; Eid, M.A. Explainable prediction of acute myocardial infarction using machine learning and Shapley Values. IEEE Access 2020, 8, 210410–210417. [Google Scholar] [CrossRef]
- Choi, A.; Kim, M.J.; Sung, J.M.; Kim, S.; Lee, J.; Hyun, H.; Kim, H.C.; Kim, J.H.; Chang, H.-J., on behalf of the Connected Network for EMS Comprehensive Technical Support Using Artificial Intelligence Investigators. Development of Prediction Models for Acute Myocardial Infarction at Prehospital Stage with Machine Learning Based on a Nationwide Database. J. Cardiovasc. Dev. Dis. 2022, 9, 430. [Google Scholar] [CrossRef]
- Hasbullah, S.; Mohd Zahid, M.S.; Mandala, S. Detection of Myocardial Infarction Using Hybrid Models of Convolutional Neural Network and Recurrent Neural Network. BioMedInformatics 2023, 3, 478–492. [Google Scholar] [CrossRef]
- Zheng, H.; Sherazi, S.W.A.; Lee, J.Y. A cost-sensitive deep neural network-based prediction model for the mortality in acute myocardial infarction patients with hypertension on imbalanced data. Front. Cardiovasc. Med. 2024, 11, 1276608. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-J.; Lee, S.-H.; Choi, H.-I.; Lee, J.-Y.; Jeong, Y.-W.; Kang, D.-R.; Sung, K.-C. Deep learning improves prediction of cardiovascular disease-related mortality and admission in patients with hypertension: Analysis of the Korean national health information database. J. Clin. Med. 2022, 11, 6677. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.H.; Liu, Z.Y.; Chu, P.H.; Chen, J.S.; Wu, H.H.; Wen, M.S.; Kuo, C.F.; Chang, T.Y. A multitask deep learning model utilizing electrocardiograms for major cardiovascular adverse events prediction. NPJ Digit. Med. 2025, 8, 1. [Google Scholar] [CrossRef]
- Kim, M.; Kang, D.; Kim, M.S.; Choe, J.C.; Lee, S.-H.; Ahn, J.H.; Oh, J.-H.; Choi, J.H.; Lee, H.C.; Cha, K.S.; et al. Acute myocardial infarction prognosis prediction with reliable and interpretable artificial intelligence system. J. Am. Med. Inform. Assoc. 2024, 31, 1540–1550. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, C.; Qiang, Y.; Zhao, Z.; Song, K.; Luo, S. Multitask Interactive Attention Learning Model Based on Hand Images for Assisting Chinese Medicine in Predicting Myocardial Infarction. Comput. Math. Methods Med. 2021, 2021, 6046184. [Google Scholar] [CrossRef]
- Zheng, H.; Sherazi, S.W.A.; Lee, J.Y. A stacking ensemble prediction model for the occurrences of major adverse cardiovascular events in patients with acute coronary syndrome on imbalanced data. IEEE Access 2021, 9, 113692–113704. [Google Scholar] [CrossRef]
- Kwon, J.M. An algorithm based on deep learning for predicting in-hospital cardiac arrest. J. Am. Heart Assoc. 2018, 7, e008678. [Google Scholar] [CrossRef]
- Motwani, M.; Dey, D.; Berman, D.S.; Germano, G.; Achenbach, S.; Al-Mallah, M.H.; Andreini, D.; Budoff, M.J.; Cademartiri, F.; Callister, T.Q.; et al. Machine learning for prediction of all-cause mortality in patients with suspected coronary artery disease: A 5-year multicentre prospective registry analysis. Eur. Heart J. 2017, 38, 500–507. [Google Scholar] [CrossRef]
- Li, W.; Zuo, M.; Zhao, H.; Xu, Q.; Chen, D. Prediction of coronary heart disease based on combined reinforcement multitask progressive time-series networks. Methods 2022, 198, 96–106. [Google Scholar] [CrossRef]
- Yavru, İ.B.; Yılmaz Gündüz, S. Predicting Myocardial Infarction Complications and Outcomes with Deep Learning. Eskişehir Tech. Univ. J. Sci. Technol. A-Appl. Sci. Eng. 2022, 23, 184–194. [Google Scholar] [CrossRef]
- Boudali, I.; Chebaane, S.; Zitouni, Y. A predictive approach for myocardial infarction risk assessment using machine learning and big clinical data. Healthc. Anal. 2024, 5, 100319. [Google Scholar] [CrossRef]
- McNamara, R.L.; Kennedy, K.F.; Cohen, D.J.; Diercks, D.B.; Moscucci, M.; Ramee, S.; Wang, T.Y.; Connolly, T.; Spertus, J.A. Predicting in-hospital mortality in patients with acute myocardial infarction. J. Am. Coll. Cardiol. 2018, 68, 626–635. [Google Scholar] [CrossRef] [PubMed]
- Abbas, S.; Ojo, S.; Krichen, M.; Alamro, M.A.; Mihoub, A.; Vilcekova, L. A Novel Deep Learning Approach for Myocardial Infarction Detection and Multi-Label Classification. IEEE Access 2024, 12, 76003–76021. [Google Scholar] [CrossRef]
- Kwon, J.; Jeon, K.-H.; Kim, H.M.; Kim, M.J.; Lim, S.; Kim, K.-H.; Song, P.S.; Park, J.; Choi, R.K.; Oh, B.-H. Deep-learning-based risk stratification for mortality of patients with acute myocardial infarction. PLoS ONE 2019, 14, e0224502. [Google Scholar] [CrossRef]
- Kim, Y.J.; Saqlian, M.; Lee, J.Y. Deep learning–based prediction model of occurrences of major adverse cardiac events during 1-year follow-up after hospital discharge in patients with AMI using knowledge mining. Pers. Ubiquit Comput. 2022, 26, 259–267. [Google Scholar] [CrossRef]
- Lu, J.; Bennamoun, M.; Stewart, J.; Eshraghian, J.; Liu, Y.; Chow, B.; Sanfilippo, F.M.; Dwivedi, G. Multitask Deep Learning for Accurate Risk Stratification and Prediction of Next Steps for Coronary CT Angiography Patients. arXiv 2023, arXiv:2309.00330. [Google Scholar]
- Ghafari, R.; Azar, A.S.; Ghafari, A.; Aghdam, F.M.; Valizadeh, M.; Khalili, N.; Hatamkhani, S. Prediction of the Fatal Acute Complications of Myocardial Infarction via Machine Learning Algorithms. J. Tehran Heart Cent. 2023, 18, 278–287. [Google Scholar] [CrossRef]
- Shickel, B.; Loftus, T.J.; Ruppert, M.; Upchurch, G.R.; Ozrazgat-Baslanti, T.; Rashidi, P.; Bihorac, A. Dynamic predictions of postoperative complications from explainable, uncertainty-aware, and multi-task deep neural networks. Sci. Rep. 2023, 13, 1224. [Google Scholar] [CrossRef]
- Mandair, D.; Tiwari, P.; Simon, S.; Colborn, K.L.; Rosenberg, M.A. Prediction of incident myocardial infarction using machine learning applied to harmonized electronic health record data. BMC Med. Inform. Decis. Mak. 2020, 20, 252. [Google Scholar] [CrossRef]
- de Carvalho, L.S.F.; Alexim, G.; Nogueira, A.C.C.; Fernandez, M.D.; Rezende, T.B.; Avila, S.; Reis, R.T.B.; Soares, A.A.M.; Sposito, A.C. The framing of time-dependent machine learning models improves risk estimation among young individuals with acute coronary syndromes. Sci. Rep. 2023, 13, 1021. [Google Scholar] [CrossRef] [PubMed]
- Boonstra, M.J.; Weissenbacher, D.; Moore, J.H.; Gonzalez-Hernandez, G.; Asselbergs, F.W. Artificial intelligence: Revolutionizing cardiology with large language models. Eur. Heart J. 2024, 45, 332–345. [Google Scholar] [CrossRef] [PubMed]
- Golovenkin, S.E.; Gorban, A.; Mirkes, E.; Shulman, V.A.; Rossiev, D.A.; Shesternya, P.A.; Nikulina, S.Y.; Orlova, Y.V.; Dorrer, M.G. Myocardial Infarction Complications Database: Dataset; University of Leicester: Leicester, UK, 2020. [Google Scholar] [CrossRef]
- Golovenkin, S.E.; Gorban, A.N.; Mirkes, E.M.; Shulman, V.A.; Rossiev, D.A.; Shesternya, P.A.; Nikulina, S.Y.; Orlova, Y.V.; Dorrer, M.G. Complications of Myocardial Infarction: A Database for Testing Recognition and Prediction Systems. 2020. Available online: https://figshare.le.ac.uk/ndownloader/files/22803572 (accessed on 18 February 2024).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2017. [Google Scholar] [CrossRef]
- Newaz, A.; Mohosheu, S.; Noman, A. Predicting complications of myocardial infarction within several hours of hospitalization using data mining techniques. Inform. Med. Unlocked 2023, 42, 101361. [Google Scholar] [CrossRef]
- Farah, C.; Adla, Y.A.; Awad, M. Can machine learning predict mortality in myocardial infarction patients within several hours of hospitalization? A comparative analysis. In Proceedings of the IEEE 21st Mediterranean Electrotechnical Conference, Palermo, Italy, 14–16 June 2022; pp. 1135–1140. [Google Scholar] [CrossRef]
- Reddy, L.; Thangam, S. Predicting relapse of the myocardial infarction in hospitalized patients. In Proceedings of the 3rd International Conference for Emerging Technology, Belgaum, India, 27–29 May 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Joshi, A.; Gunwant, H.; Sharma, M.; Chaudhary, V. Early prognosis of acute myocardial infarction using machine learning techniques. In Lecture Notes on Data Engineering and Communications Technologies; Springer: Singapore, 2022; Volume 91, pp. 815–829. [Google Scholar] [CrossRef]
- Tukhtaev, A.; Turimov, D.; Kim, J.; Kim, W. Feature Selection and Machine Learning Approaches for Detecting Sarcopenia Through Predictive Modeling. Mathematics 2025, 13, 98. [Google Scholar] [CrossRef]
- Turimov, D.; Kim, W. Enhancing Sarcopenia Prediction Through an Ensemble Learning Approach: Addressing Class Imbalance for Improved Clinical Diagnosis. Mathematics 2025, 13, 26. [Google Scholar] [CrossRef]
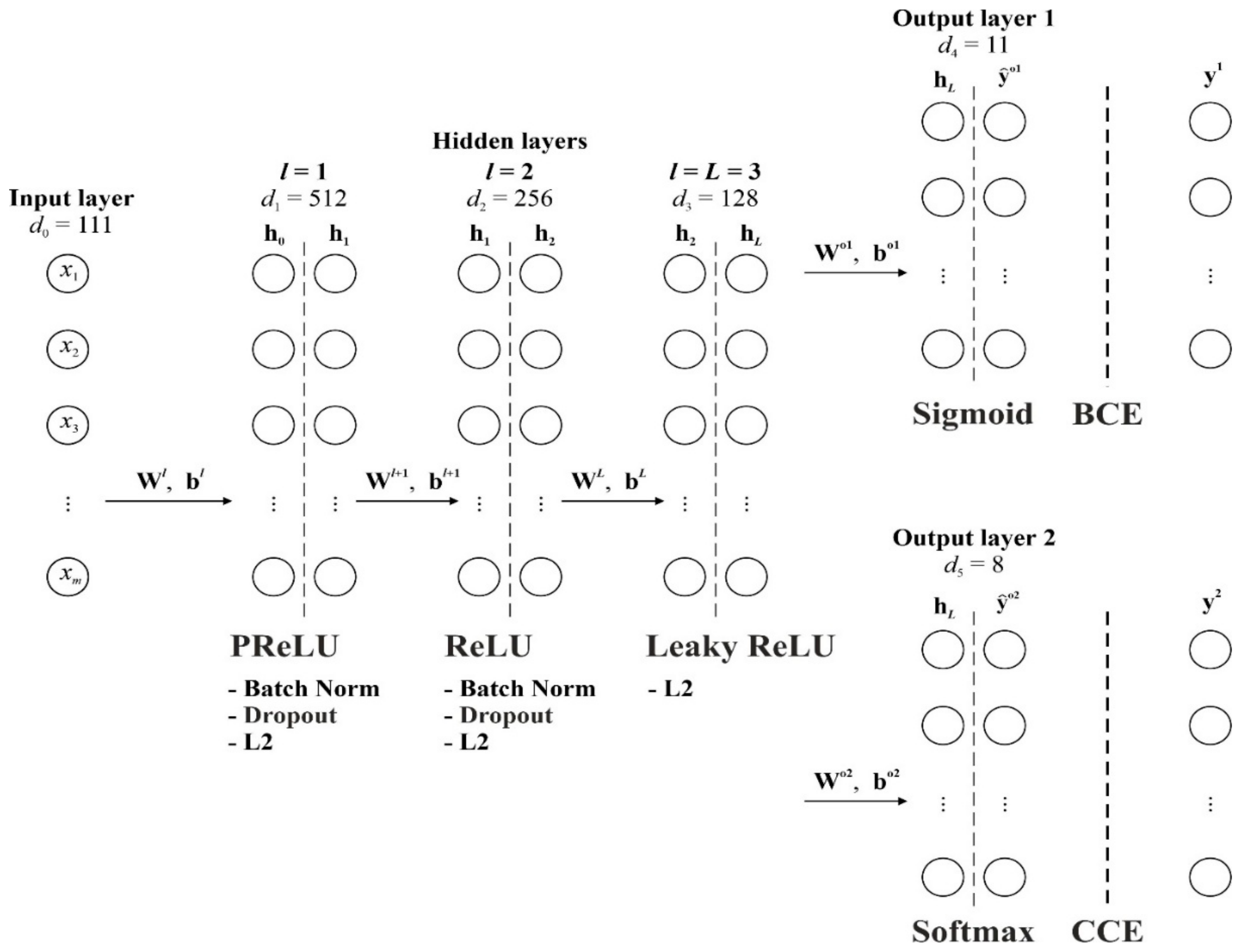
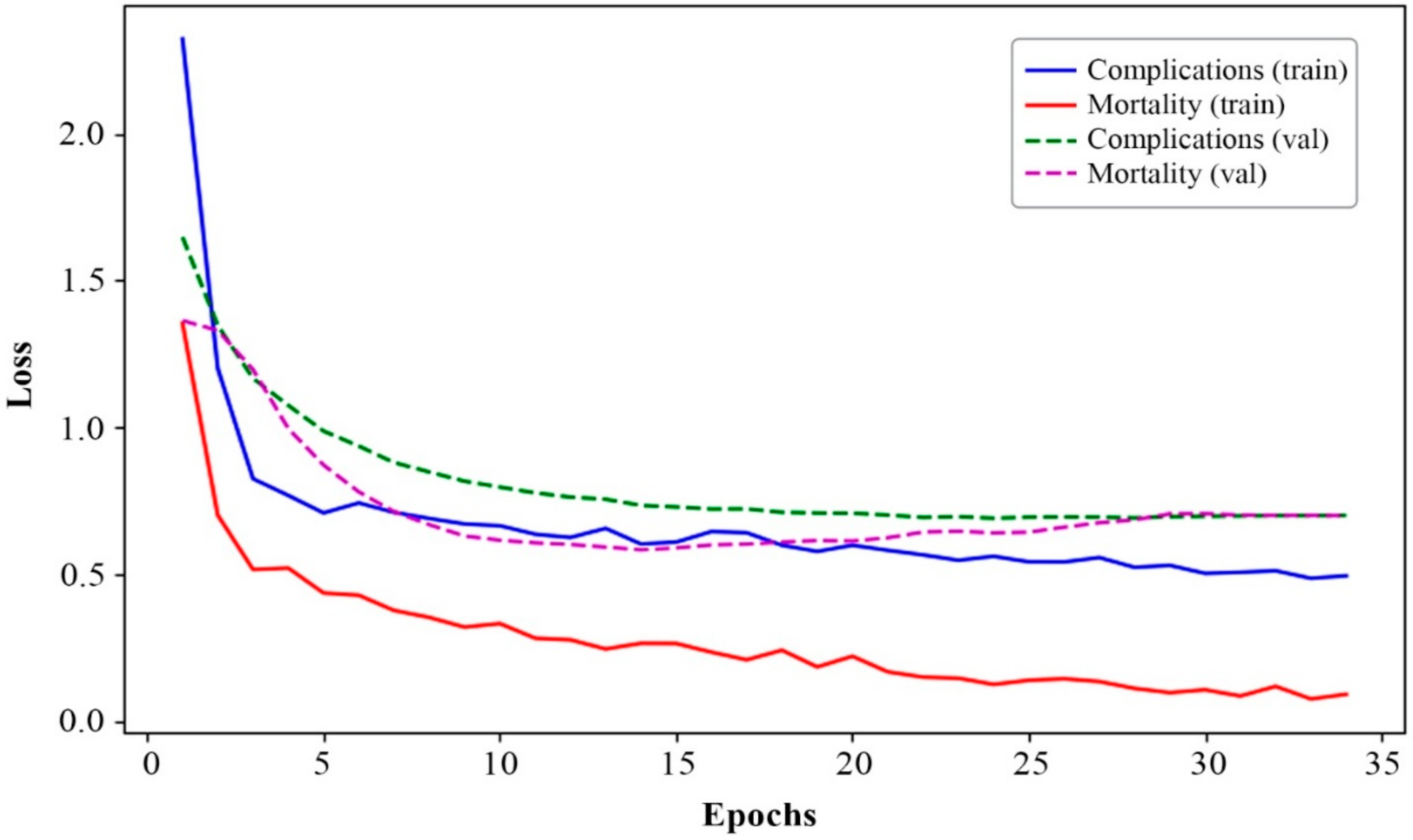
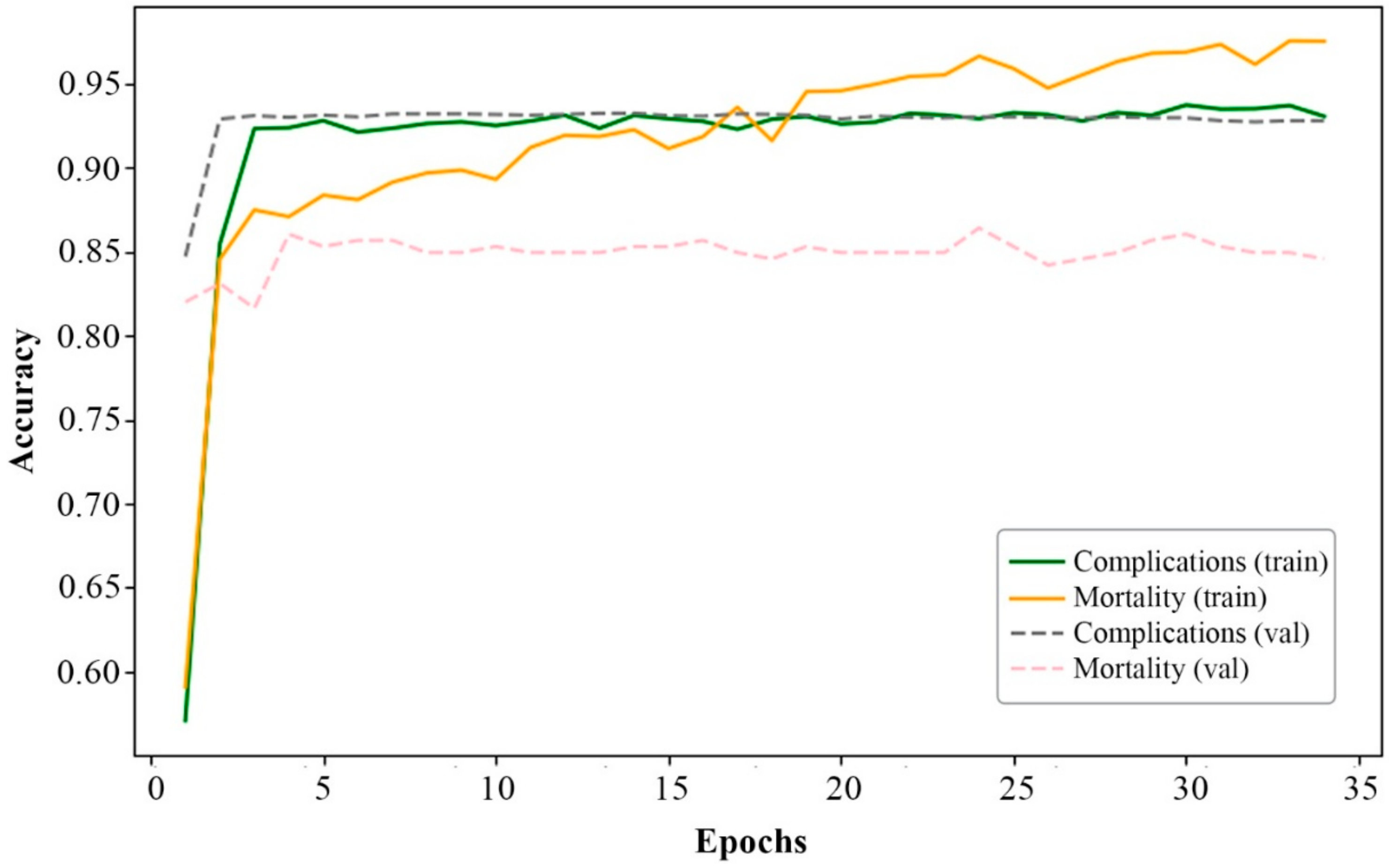
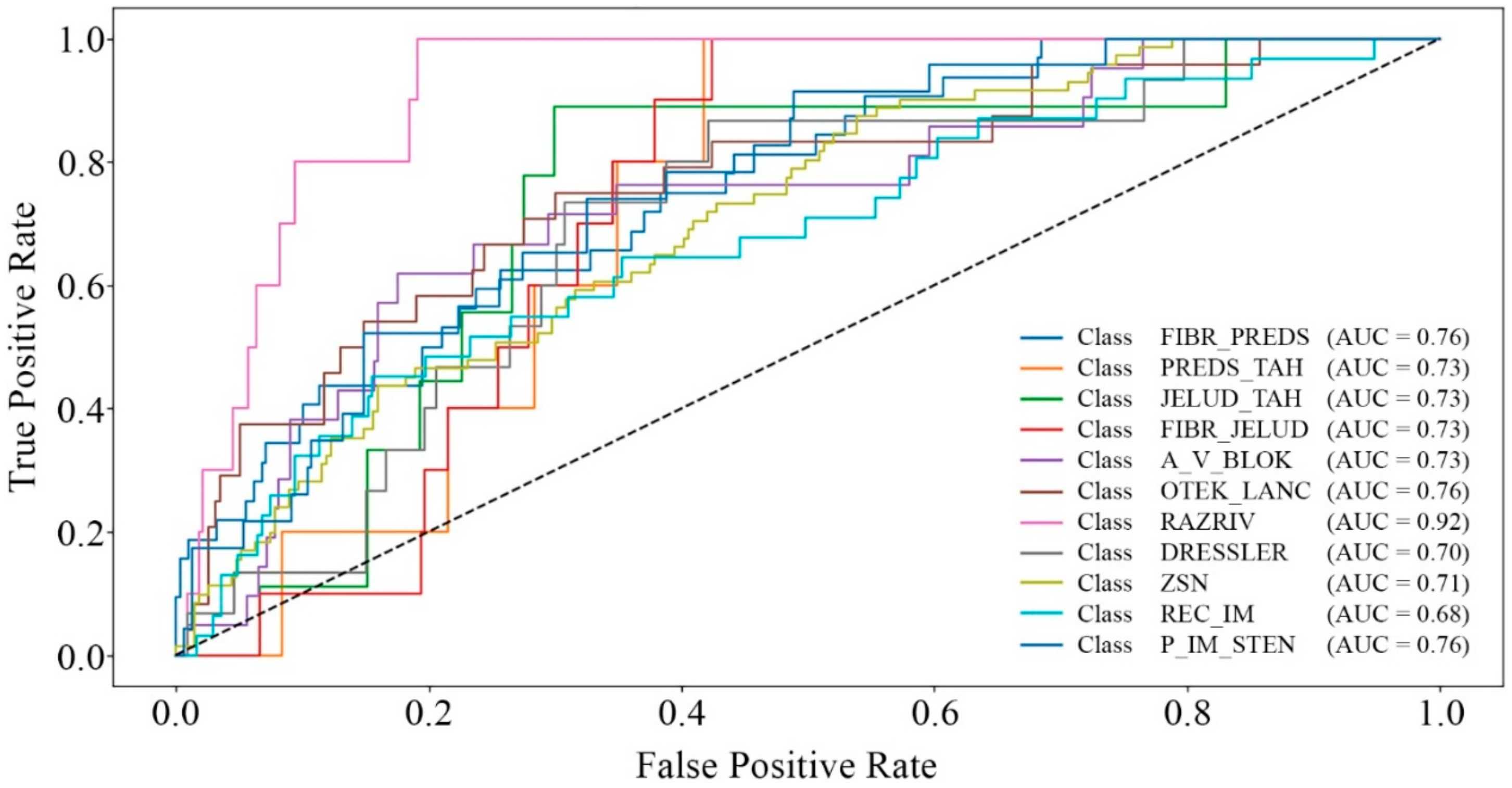
| Parameter | Value/Description |
|---|---|
| Input features | = 111 clinical and demographic variables |
| Hidden layers | 3 |
| Layer 1 | , PReLU, L2 regularization (), BatchNormalization, Dropout (rate = 0.4) |
| Layer 2 | , ReLU, L2 regularization (), BatchNormalization, Dropout (rate = 0.4) |
| Layer 3 | , LeakyReLU (), L2 regularization () |
| Output layers | 2 |
| Complications | , binary classification, Sigmoid activation |
| Mortality causes | , multiclass classification, Softmax activation |
| Optimizer | Adam (learning rate = 0.0005) |
| Batch size | 64 |
| Epochs | = 50 (with early stopping, patience = 10) |
| Loss function (complications) | Binary cross-entropy |
| Loss function (mortality) | Sparse categorical cross-entropy |
| Loss weights | Complications: 3.0; Mortality: 1.0 |
| Class imbalance handling | Random oversampling of minority classes up to 50% of the majority class (for complications) |
| Feature scaling | StandardScaler (zero mean, unit variance) |
| Validation strategy | Train/test split: 80/20; 20% of training set used for validation during training |
| Regularization | L2 regularization (); Dropout (rate = 0.4 on first two hidden layers) |
| Callbacks | EarlyStopping (patience = 10, restore best weights), ReduceLROnPlateau (factor = 0.1, patience = 5) |
| Evaluation metrics | Binary accuracy, AUC (for complications); Categorical accuracy (for mortality causes) |
| Metrics | Training Set | Validation Set | Weighted and Averaged Values over Epochs | |
|---|---|---|---|---|
| Loss | Complications | 0.5080 | 0.7002 | 0.6626 |
| Mortality | 0.0874 | 0.7033 | 0.4289 | |
| Overall loss | 1.1593 | 1.8873 | 1.7132 | |
| Accuracy | Complications | 0.9347 | 0.9278 | 0.7799 |
| Mortality | 0.9732 | 0.8529 | 0.8617 | |
| AUC | Complications | 0.9087 | 0.7847 | 0.9286 |
| KNN | SVM | LR | NB | RF | XGBoost | AdaBoost |
|---|---|---|---|---|---|---|
| 85.9724 | 86.2317 | 86.4902 | 20.75 | 91.1433 | 91.3370 | 90.1098 |
| SMOTE | ADASYN | RUS | Tomek-Link | ENN | Weighted XGBoost | This Model |
|---|---|---|---|---|---|---|
| 91.1431 | 91.4009 | 81.9014 | 90.8850 | 90.4317 | 91.5311 | 91.9843 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makhmudov, F.; Ravshanov, N.; Akhmedov, D.; Pekos, O.; Turimov, D.; Cho, Y.-I. A Multitask Deep Learning Model for Predicting Myocardial Infarction Complications. Bioengineering 2025, 12, 520. https://doi.org/10.3390/bioengineering12050520
Makhmudov F, Ravshanov N, Akhmedov D, Pekos O, Turimov D, Cho Y-I. A Multitask Deep Learning Model for Predicting Myocardial Infarction Complications. Bioengineering. 2025; 12(5):520. https://doi.org/10.3390/bioengineering12050520
Chicago/Turabian StyleMakhmudov, Fazliddin, Normakhmad Ravshanov, Dilshot Akhmedov, Oleg Pekos, Dilmurod Turimov, and Young-Im Cho. 2025. "A Multitask Deep Learning Model for Predicting Myocardial Infarction Complications" Bioengineering 12, no. 5: 520. https://doi.org/10.3390/bioengineering12050520
APA StyleMakhmudov, F., Ravshanov, N., Akhmedov, D., Pekos, O., Turimov, D., & Cho, Y.-I. (2025). A Multitask Deep Learning Model for Predicting Myocardial Infarction Complications. Bioengineering, 12(5), 520. https://doi.org/10.3390/bioengineering12050520






