Reduction of Spike-like Noise in Clinical Practice for Thoracic Electrical Impedance Tomography Using Robust Principal Component Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Formulation Using RPCA
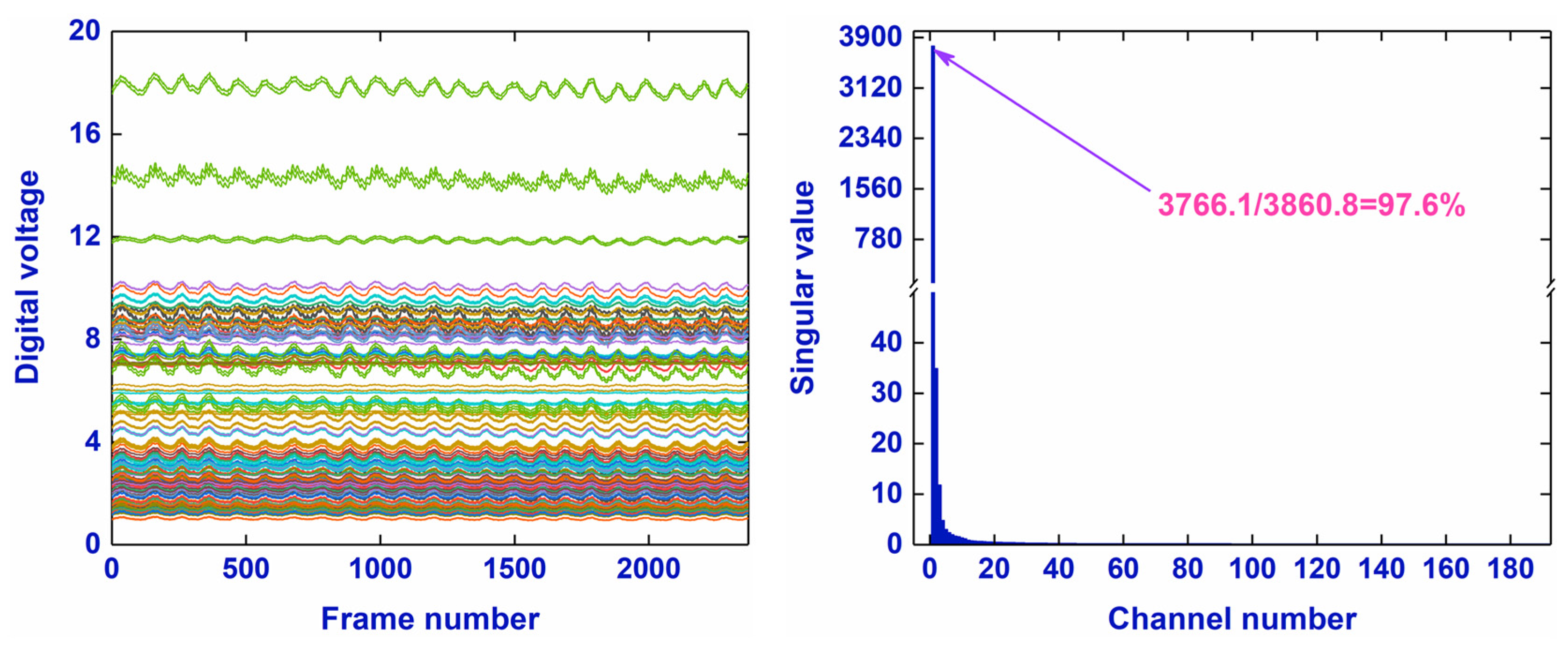
2.1.1. The Low-Rank Property of an EIT Data Matrix
2.1.2. Principle of RPCA
| Algorithm 1 Robust Principal Component Analysis |
| 1: Initialization: , , , , |
| 2: while do |
| 3: Solve |
| 4: Solve |
| 5: |
| 6: end while |
| 7: Output: |
2.2. Numerical Simulations
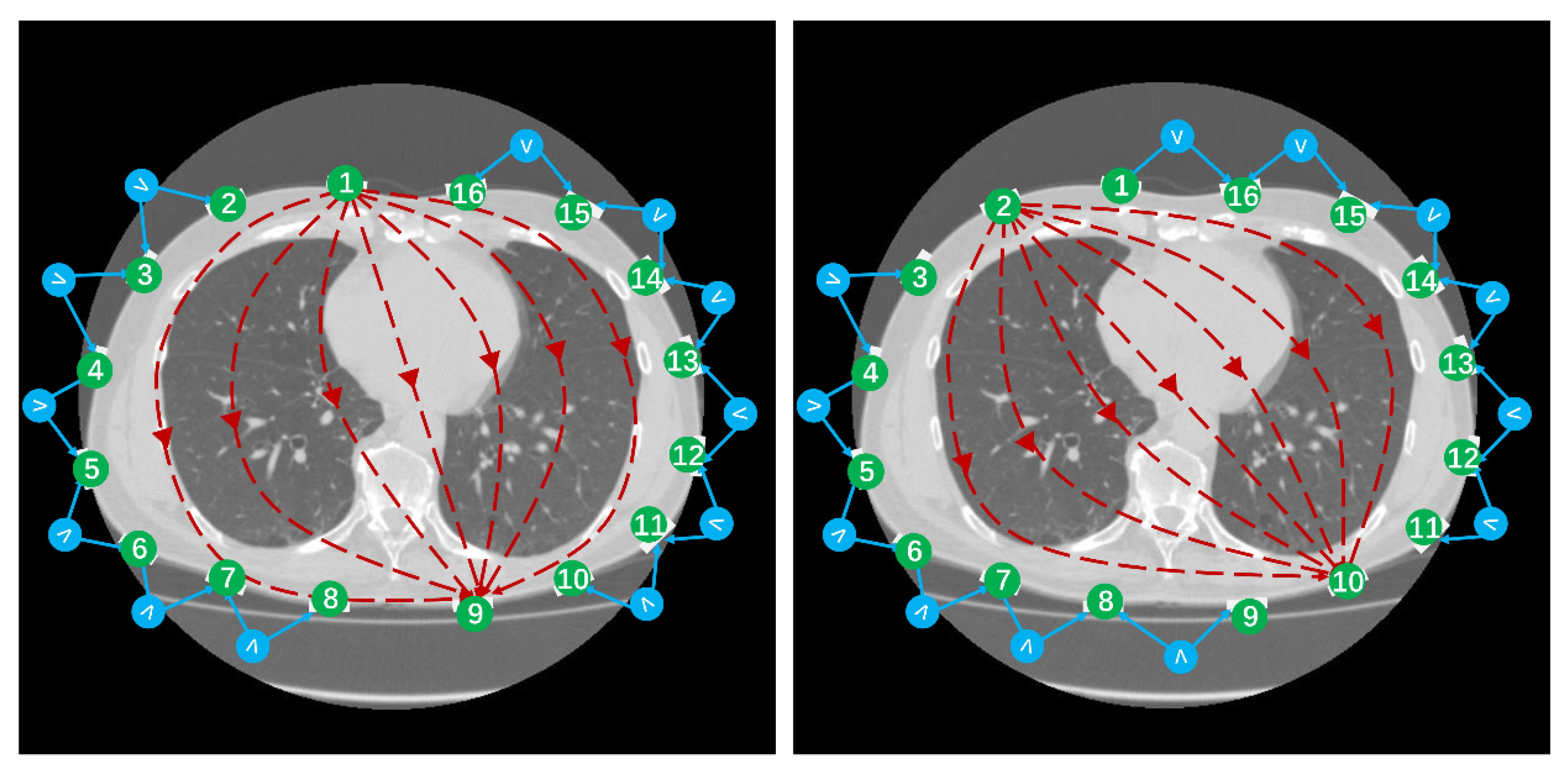
2.2.1. Generation of Respiratory EIT Boundary Voltages
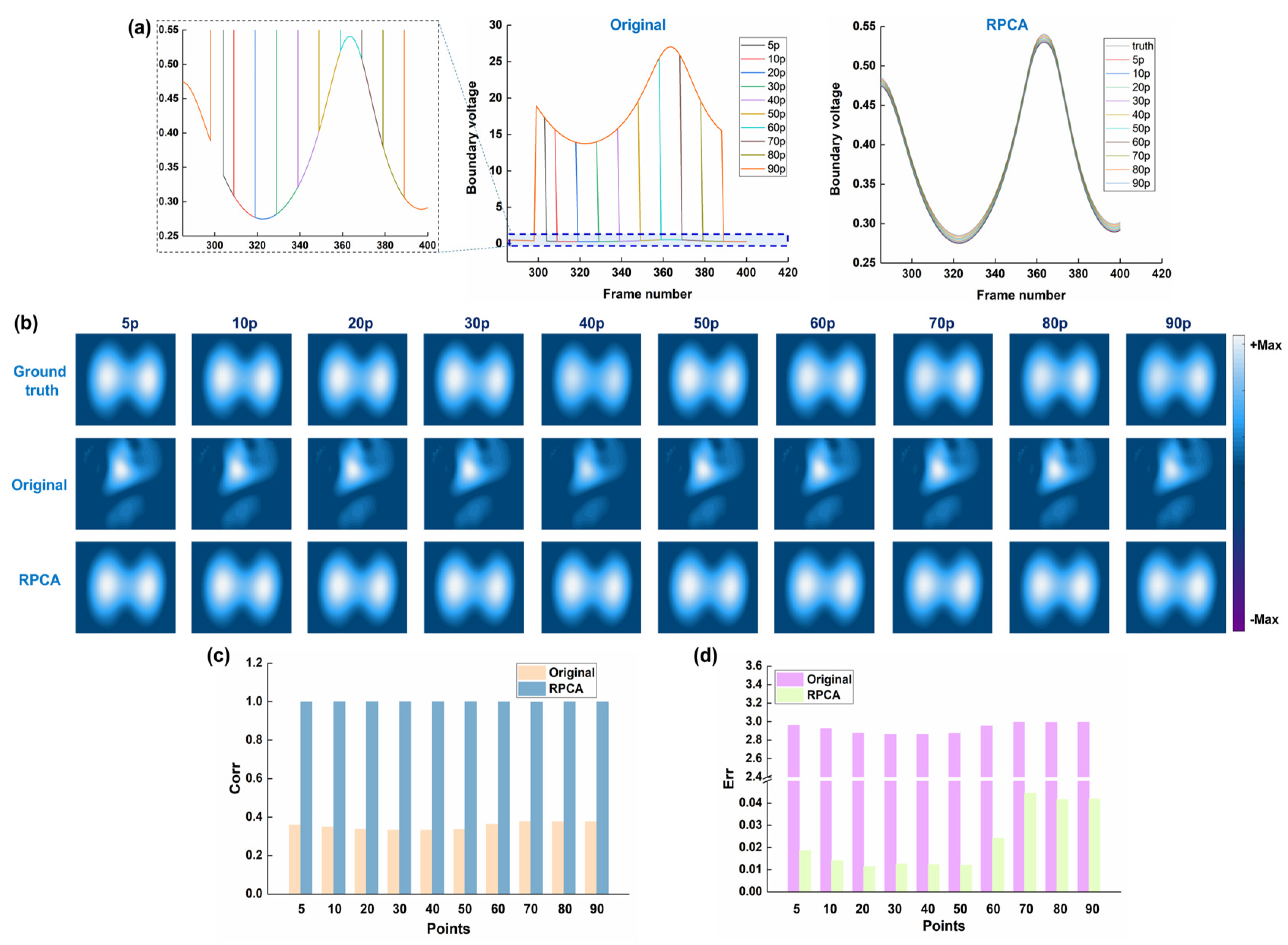
2.2.2. Spike-like Noise Synthesis and Imaging
2.3. Human Experiments
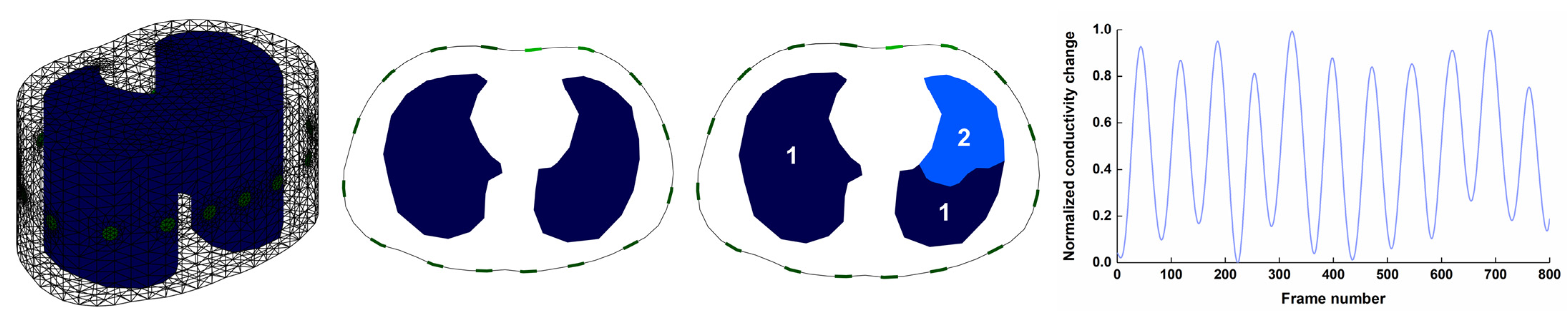
2.4. Image Analysis
3. Results
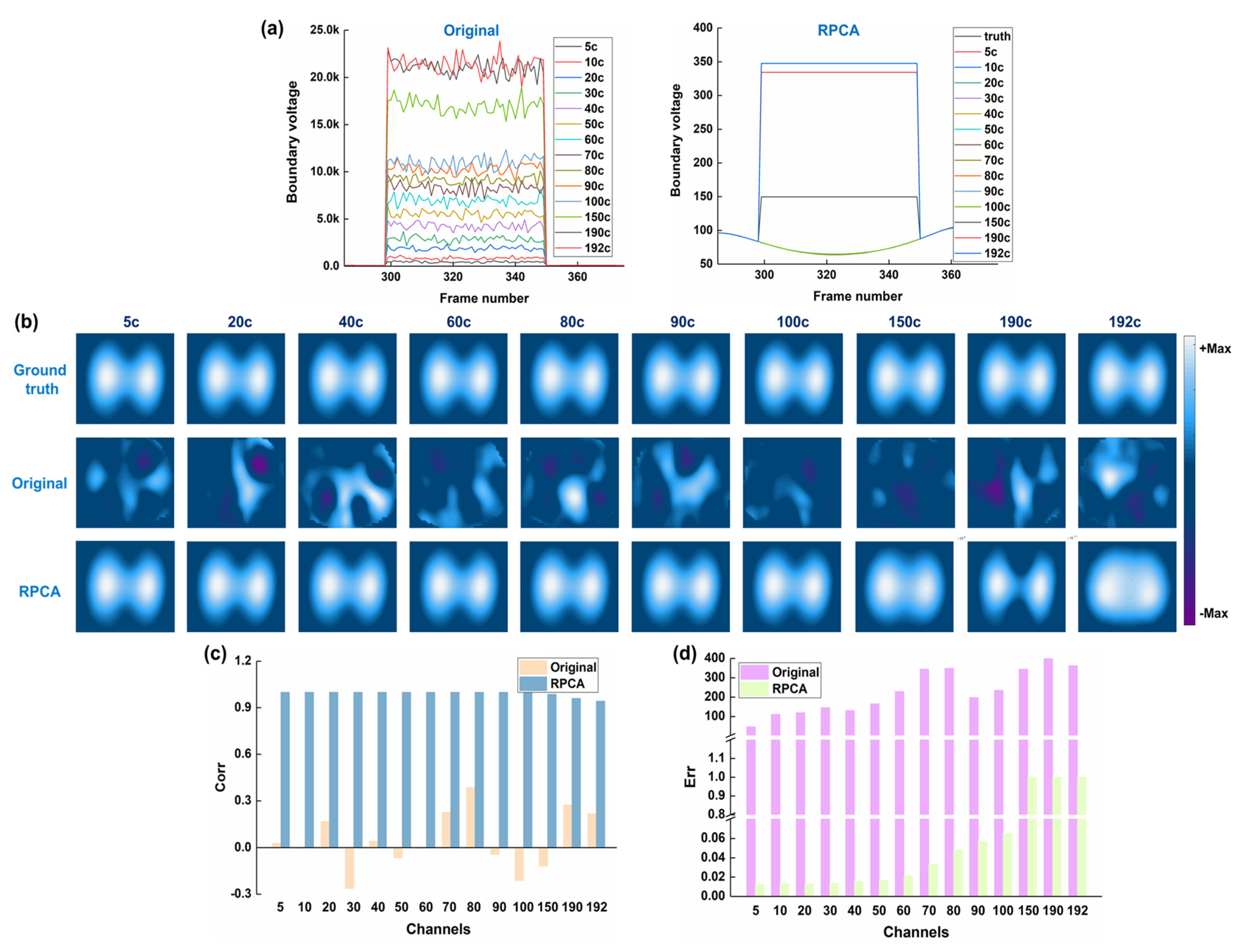
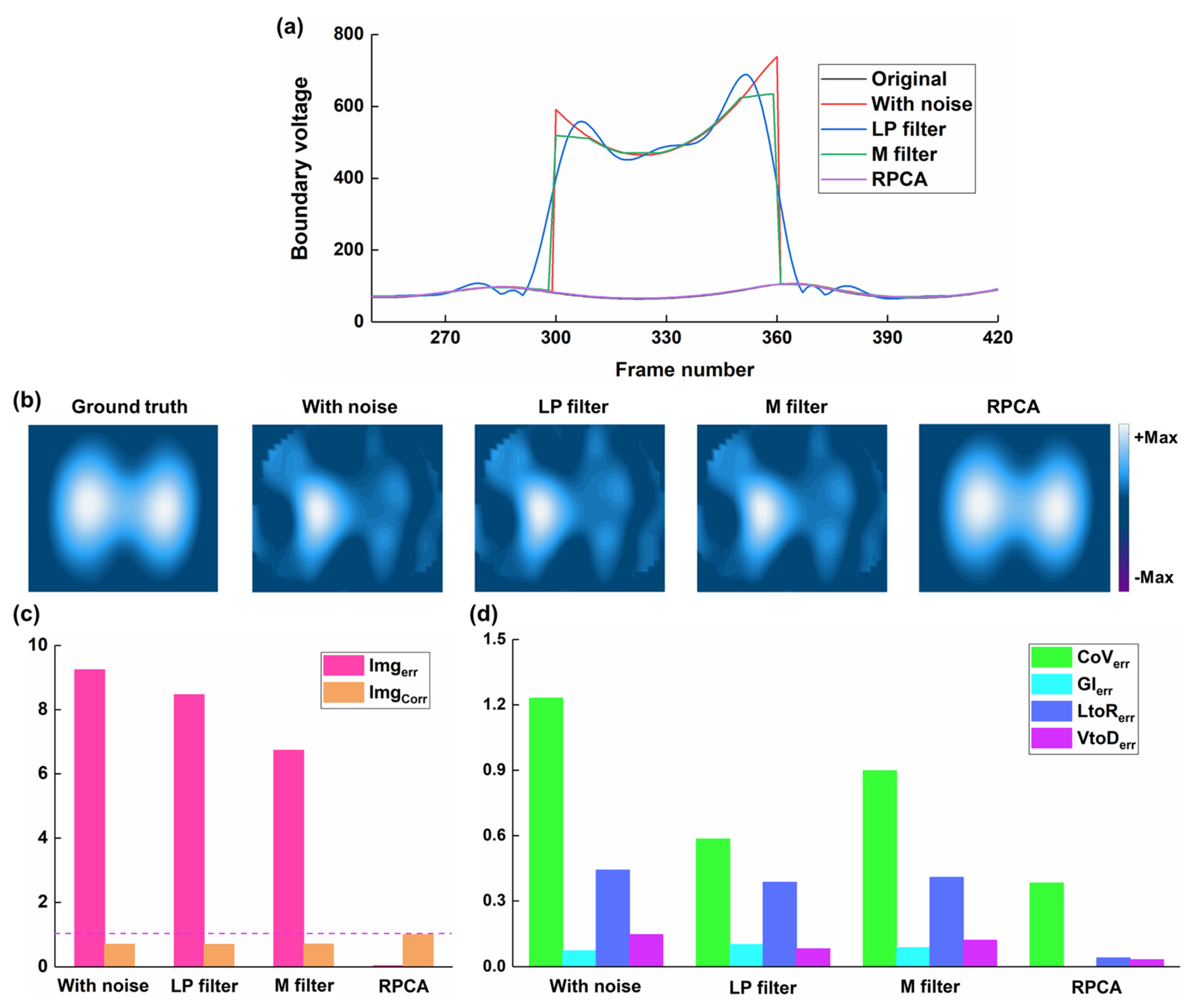
3.1. Results of Numerical Simulations
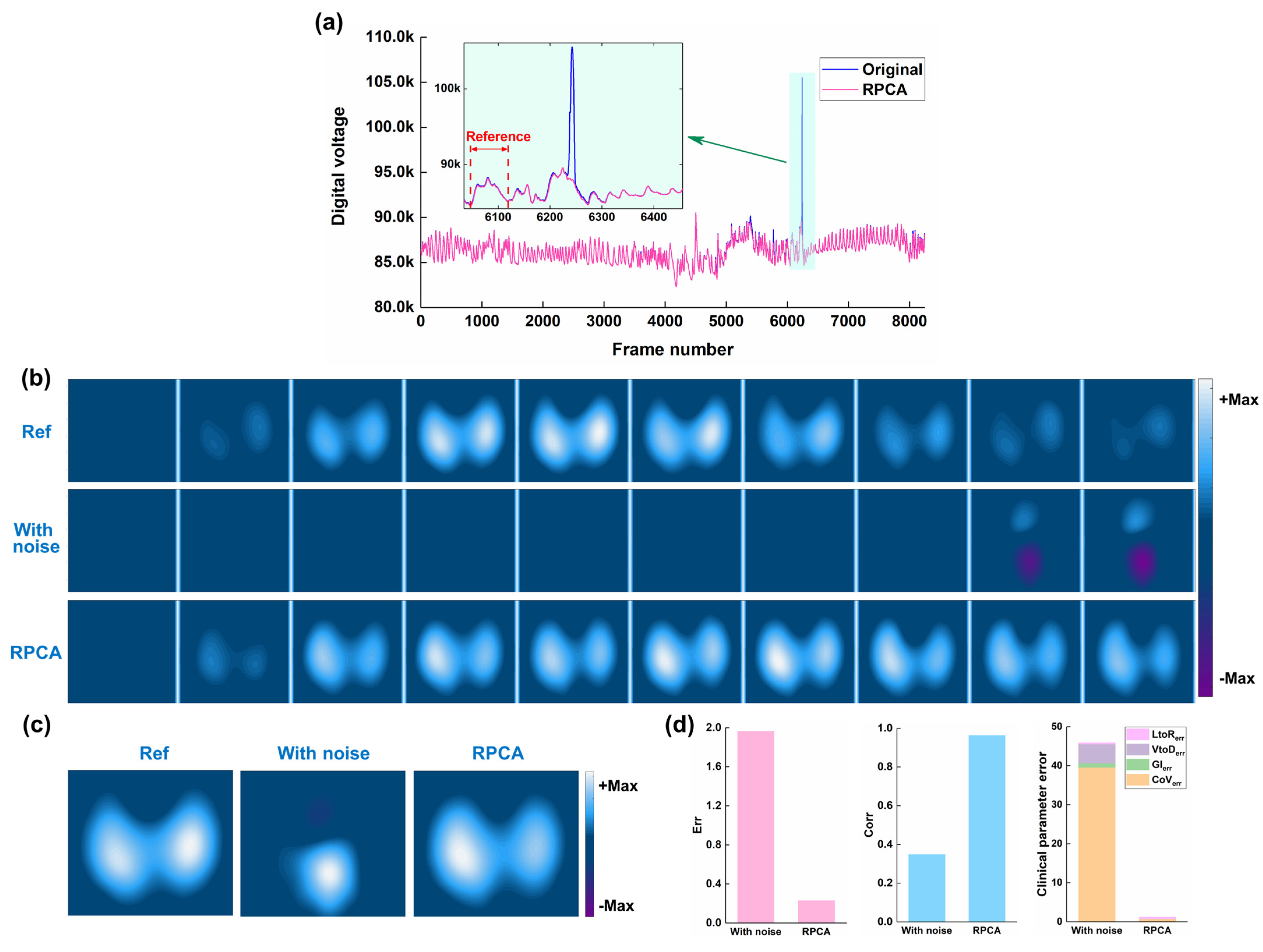
3.2. Results of Human Experiments
4. Discussion
5. Conclusions
- -
- RPCA can effectively decompose a thoracic EIT data matrix, containing spike-like noise, into a low-rank component representing the underlying respiratory signal and a sparse component representing the noise
- -
- Applying RPCA to remove spike-like noise from EIT data can improve the quality of reconstructed EIT images and the accuracy of derived clinical indices, in both simulated and clinical settings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Z.; Fu, F.; Frerichs, I. Thoracic electrical impedance tomography in Chinese hospitals: A review of clinical research and daily applications. Physiol. Meas. 2020, 41, 04TR01. [Google Scholar] [CrossRef] [PubMed]
- Frerichs, I.; Amato, M.B.; van Kaam, A.H.; Tingay, D.G.; Zhao, Z.; Grychtol, B.; Bodenstein, M.; Gagnon, H.; Bohm, S.H.; Teschner, E.; et al. Chest electrical impedance tomography examination, data analysis, terminology, clinical use and recommendations: Consensus statement of the TRanslational EIT developmeNt stuDy group. Thorax 2017, 72, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Lan, L.; Ni, Y.; Zhou, Y.; Fu, L.; Wu, W.; Li, P.; Yu, H.; Liang, G.; Luo, F. PEEP-Induced Lung Recruitment Maneuver Combined with Prone Position for ARDS: A Single-Center, Prospective, Randomized Clinical Trial. J. Clin. Med. 2024, 13, 853. [Google Scholar] [CrossRef]
- Jonkman, A.H.; Alcala, G.C.; Pavlovsky, B.; Roca, O.; Spadaro, S.; Scaramuzzo, G.; Chen, L.; Dianti, J.; Sousa, M.L.A.; Sklar, M.C.; et al. Lung Recruitment Assessed by Electrical Impedance Tomography (RECRUIT): A Multicenter Study of COVID-19 Acute Respiratory Distress Syndrome. Am. J. Respir. Crit. Care Med. 2023, 208, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Pequignot, B.; Combes, A.; Lescroart, M.; Levy, B.; Koszutski, M. Contribution of electrical impedance tomography to personalize positive end-expiratory pressure under ECCO2R. Crit. Care 2024, 28, 124. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Y.; Gao, X.; Peng, C.; Li, R.; Wang, A.; Zhang, J.; Yuan, S.; Yang, L.; Zou, X.; et al. Effects of different VV ECMO blood flow rates on lung perfusion assessment by hypertonic saline bolus-based electrical impedance tomography. Crit. Care 2024, 28, 274. [Google Scholar] [CrossRef]
- Hou, H.J.; Ning, F.L.; Li, W.X.; Zhai, Q.B.; Wei, J.; Wang, C.Q. Coherent Noise Denoising in Beamforming Based on Non-Convex Robust Principal Component Analysis. J. Theor. Comput. Acous 2024, 32, 2340004. [Google Scholar] [CrossRef]
- Liu, Y.F.; Du, B.; Chen, Y.Y.; Zhang, L.F.; Gong, M.M.; Tao, D.C. Convex-Concave Tensor Robust Principal Component Analysis. Int. J. Comput. Vis. 2024, 132, 1721–1747. [Google Scholar] [CrossRef]
- Aydeniz, E.; van Bussel, B.C.T.; de Jongh, S.; Schellens, J.; Heines, S.J.H.; van Kuijk, S.M.J.; Tas, J.; van Rosmalen, F.; van der Horst, I.C.C.; Bergmans, D.; et al. Serial electrical impedance tomography course in different treatment groups; The MaastrICCht cohort. J. Crit. Care 2024, 80, 154506. [Google Scholar] [CrossRef]
- Florio, G.; Zanella, A.; Slobod, D.; Guzzardella, A.; Protti, I.; Carlesso, E.; Canakoglu, A.; Fumagalli, J.; Scaravilli, V.; Colombo, S.M.; et al. Impact of Positive End-Expiratory Pressure and FiO2 on Lung Mechanics and Intrapulmonary Shunt in Mechanically Ventilated Patients with ARDS Due to COVID-19 Pneumonia. J. Intensive Care Med. 2024, 39, 420–428. [Google Scholar] [CrossRef]
- Oner, O.; Ergan, B.; Kizil, A.S.; Gurkok, M.C.; Dugral, E.; Gokmen, N. Investigation of high flow nasal cannule efficiency with electric impedance tomography based parameters in COVID-19 adults patients: A retrospective study. PeerJ 2023, 11, e15555. [Google Scholar] [CrossRef] [PubMed]
- Gremme, Y.; Derlien, S.; Katzer, K.; Reuken, P.A.; Stallmach, A.; Lewejohann, J.C.; Lemhofer, C. Visualizing exertional dyspnea in a post-COVID patient using electrical impedance tomography. Infection 2023, 51, 1841–1845. [Google Scholar] [CrossRef] [PubMed]
- Frerichs, I.; Strodthoff, C.; Vogt, B. Regional pulmonary function testing by electrical impedance tomography in pediatric asthma. Pediatr. Pulmonol. 2023, 58, 3320–3322. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Gao, Z.J.; Cao, X.S.; Sun, S.Y.; Wang, C.C.; Wang, H.; Dai, J.; Liu, Y.; Qin, Y.L.; Dai, M.; et al. Electrical impedance tomography as a bedside assessment tool for COPD treatment during hospitalization. Front. Physiol. 2024, 15, 1352391. [Google Scholar] [CrossRef]
- Yang, L.; Gao, Z.J.; Cao, X.S.; Wang, C.C.; Wang, H.; Dai, J.; Liu, Y.; Qin, Y.L.; Dai, M.; Zhang, B.H.; et al. Visualizing pursed lips breathing of patients with chronic obstructive pulmonary disease through evaluation of global and regional ventilation using electrical impedance tomography. Physiol. Meas. 2024, 45, 045005. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, K.; Gao, Z.; Fu, F.; Wang, H.; Wang, C.; Dai, J.; Liu, Y.; Qin, Y.; Dai, M.; et al. The Influence of Breathing Exercises on Regional Ventilation in Healthy and Patients with Chronic Obstructive Pulmonary Disease. COPD 2023, 20, 248–255. [Google Scholar] [CrossRef]
- Zhao, Z.; Fischer, R.; Frerichs, I.; Muller-Lisse, U.; Moller, K. Regional ventilation in cystic fibrosis measured by electrical impedance tomography. J. Cyst. Fibros. 2012, 11, 412–418. [Google Scholar] [CrossRef][Green Version]
- Lehmann, S.; Leonhardt, S.; Ngo, C.; Bergmann, L.; Ayed, I.; Schrading, S.; Tenbrock, K. Global and regional lung function in cystic fibrosis measured by electrical impedance tomography. Pediatr. Pulmonol. 2016, 51, 1191–1199. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Zhang, H.F.; Liu, Z.Y.; Zhu, J.; Gu, J.; Wang, X.B.; Zhu, Z.Y.; Tang, Y.J.; Wang, J. Glow and hot pixels removal using improved robust principal component analysis. J. Electron. Imaging 2023, 32, 043012. [Google Scholar] [CrossRef]
- Frerichs, I.; Pulletz, S.; Elke, G.; Gawelczyk, B.; Frerichs, A.; Weiler, N. Patient examinations using electrical impedance tomography--sources of interference in the intensive care unit. Physiol. Meas. 2011, 32, L1–L10. [Google Scholar] [CrossRef]
- Mamatjan, Y.; Grychtol, B.; Gaggero, P.; Justiz, J.; Koch, V.M.; Adler, A. Evaluation and real-time monitoring of data quality in electrical impedance tomography. IEEE Trans. Med. Imaging 2013, 32, 1997–2005. [Google Scholar] [CrossRef]
- Asfaw, Y.; Adler, A. Automatic detection of detached and erroneous electrodes in electrical impedance tomography. Physiol. Meas. 2005, 26, S175–S183. [Google Scholar] [CrossRef] [PubMed]
- Adler, A. Accounting for erroneous electrode data in electrical impedance tomography. Physiol. Meas. 2004, 25, 227–238. [Google Scholar] [CrossRef] [PubMed]
- Hartinger, A.E.; Guardo, R.; Adler, A.; Gagnon, H. Real-time management of faulty electrodes in electrical impedance tomography. IEEE Trans. Biomed. Eng. 2009, 56, 369–377. [Google Scholar] [CrossRef]
- Zhang, G.; Dai, M.; Yang, L.; Li, W.C.; Li, H.T.; Xu, C.H.; Shi, X.T.; Dong, X.Z.; Fu, F. Fast detection and data compensation for electrodes disconnection in long-term monitoring of dynamic brain electrical impedance tomography. Biomed. Eng. Online 2017, 16, 7. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.Y.; Lou, Y.J.; Wang, M.; Yang, K.; Gao, Z.; Fu, F. Densely Connected Convolutional Neural Network-Based Invalid Data Compensation for Brain Electrical Impedance Tomography. IEEE Trans. Comput. Imaging 2024, 10, 143–153. [Google Scholar] [CrossRef]
- Shi, Y.Y.; Yang, K.; Wang, M.; Lou, Y.J.; Tian, Z.W.; Yang, B.; Fu, F. Compensation of Contact Impedance Variation for Cerebral Electrical Impedance Tomography. IEEE Sens. J. 2022, 22, 24541–24549. [Google Scholar] [CrossRef]
- Shi, Y.Y.; Yang, K.; Wang, M.; Su, H.; Yang, B.; Fu, F. Inadequate Data Augmentation With Convolutional Neural Network in Brain Electrical Impedance Tomography. IEEE Sens. J. 2024, 24, 21490–21499. [Google Scholar] [CrossRef]
- Ye, J.A.; Tian, X.; Liu, X.C.; Zhang, W.R.; Zhang, T.; Zhang, L.L.; Wang, P.; Xue, H.J.; Xu, C.H.; Fu, F. Removal of Vibration Interference Artifacts in Electrical Impedance Tomography Monitoring Using Residual Learning Strategy. IEEE Trans. Instrum. Meas. 2024, 73, 4508510. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Li, S.L.; Duan, J.G.; Qin, J.Y.; Zhou, Y. Moving Object Detection Method Based on the Fusion of Online Moving Window Robust Principal Component Analysis and Frame Difference Method. Neural Process Lett. 2024, 56, 55. [Google Scholar] [CrossRef]
- Yu, J.Q.; Guo, Y.J.; Zhang, W.J. Anomaly Detection for Charging Voltage Profiles in Battery Cells in an Energy Storage Station Based on Robust Principal Component Analysis. Appl. Sci. 2024, 14, 7552. [Google Scholar] [CrossRef]
- Paul, D.; Chakraborty, S.; Das, S. Robust Principal Component Analysis: A Median of Means Approach. IEEE Trans. Neural Netw. Learn. 2024, 35, 16788–16800. [Google Scholar] [CrossRef] [PubMed]
- Wright, J.; Peng, Y.; Ma, Y.; Ganesh, A.; Rao, S. Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Matrices by Convex Optimization. In Proceedings of the 23rd International Conference on Neural Information Processing Systems, Curran Associates Inc., Vancouver, BC, Canada, 7–10 December 2009; pp. 2080–2088. [Google Scholar]
- Adler, A.; Lionheart, W.R. Uses and abuses of EIDORS: An extensible software base for EIT. Physiol. Meas. 2006, 27, S25–S42. [Google Scholar] [CrossRef] [PubMed]


| Author(s) | Pros | Cons |
|---|---|---|
| Mamatjan et al. [21] | Proposed a quantitative metric for assessing EIT data quality in real-time. | Did not offer methods for correcting or improving low-quality data. |
| Asfaw and Adler [22] | Proposed an automated method to detect erroneous electrodes by comparing measured data to estimates. | Sensitivity of the algorithm decreases significantly when the number of interfered electrodes is greater than three. |
| Adler [23] | Modeled erroneous EIT data as having infinite noise in the regularized inverse to improve EIT imaging. | The same as above |
| Hartinger et al. [24] | Presented an approach for real-time management of faulty electrodes based on voltage–current reciprocity, allowing image reconstruction without prior knowledge of faulty electrodes and automatic detection. | The same as above |
| Zhang et al. [25] | Presented an algorithm based on curve fitting to detect and filter out faulty electrode data. | Performance deteriorates when the actual number of faulty electrodes exceeds the assumed number. |
| Shi yanyan et al. [26,27,28,29] | Showed promise in phantom experiments for EIT data denoising for deep learning. | Clinical effectiveness remains to be further validated, as well as the challenge in obtaining large quantities of diverse clinical noise data for model training. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, M.; Li, X.; Zhao, Z.; Yang, L. Reduction of Spike-like Noise in Clinical Practice for Thoracic Electrical Impedance Tomography Using Robust Principal Component Analysis. Bioengineering 2025, 12, 402. https://doi.org/10.3390/bioengineering12040402
Dai M, Li X, Zhao Z, Yang L. Reduction of Spike-like Noise in Clinical Practice for Thoracic Electrical Impedance Tomography Using Robust Principal Component Analysis. Bioengineering. 2025; 12(4):402. https://doi.org/10.3390/bioengineering12040402
Chicago/Turabian StyleDai, Meng, Xiaopeng Li, Zhanqi Zhao, and Lin Yang. 2025. "Reduction of Spike-like Noise in Clinical Practice for Thoracic Electrical Impedance Tomography Using Robust Principal Component Analysis" Bioengineering 12, no. 4: 402. https://doi.org/10.3390/bioengineering12040402
APA StyleDai, M., Li, X., Zhao, Z., & Yang, L. (2025). Reduction of Spike-like Noise in Clinical Practice for Thoracic Electrical Impedance Tomography Using Robust Principal Component Analysis. Bioengineering, 12(4), 402. https://doi.org/10.3390/bioengineering12040402








