Prediction of the Atomization Process in Respimat® Soft MistTM Inhalers Using a Volume of Fluid-to-Discrete Phase Model
Abstract
:1. Introduction
2. Materials and Methods
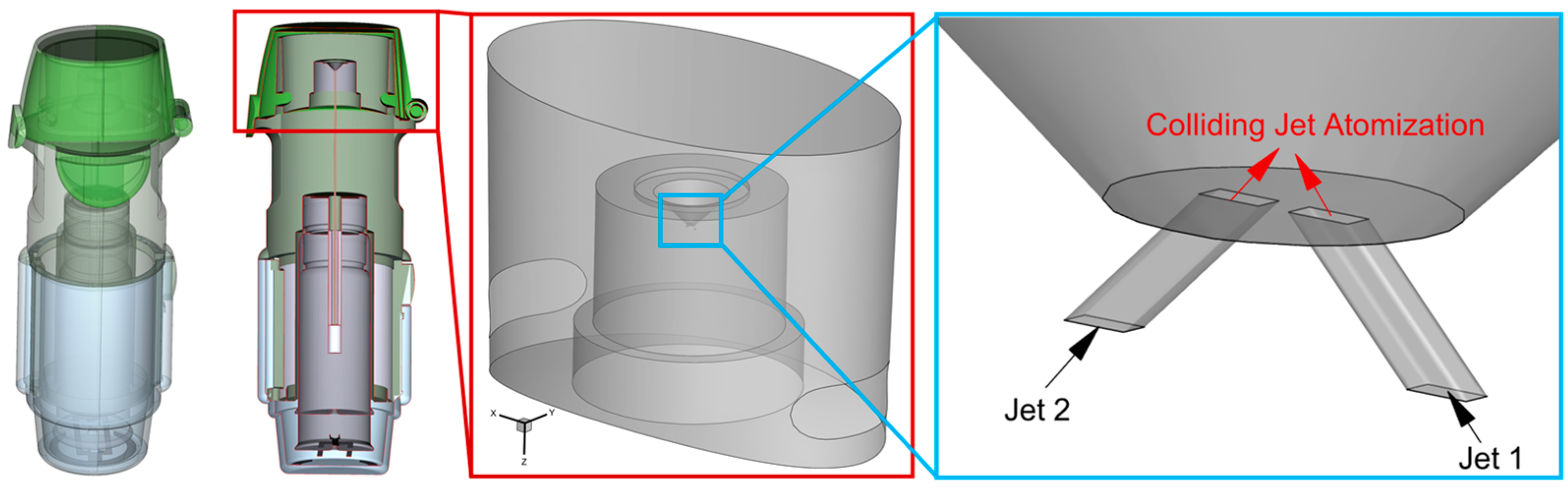
2.1. Geometry and Mesh
2.2. Governing Equations
2.2.1. VOF Model
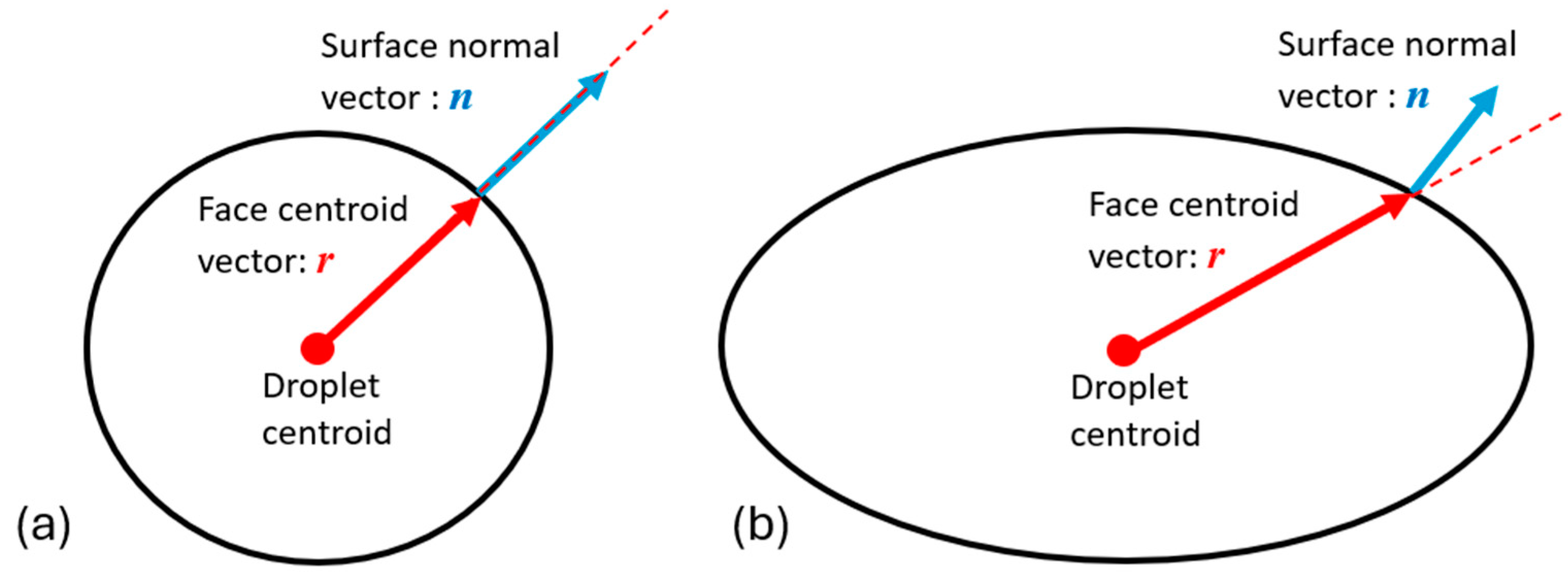
2.2.2. VOF-to-DPM Transition
2.2.3. DPM
2.3. Numerical Setup
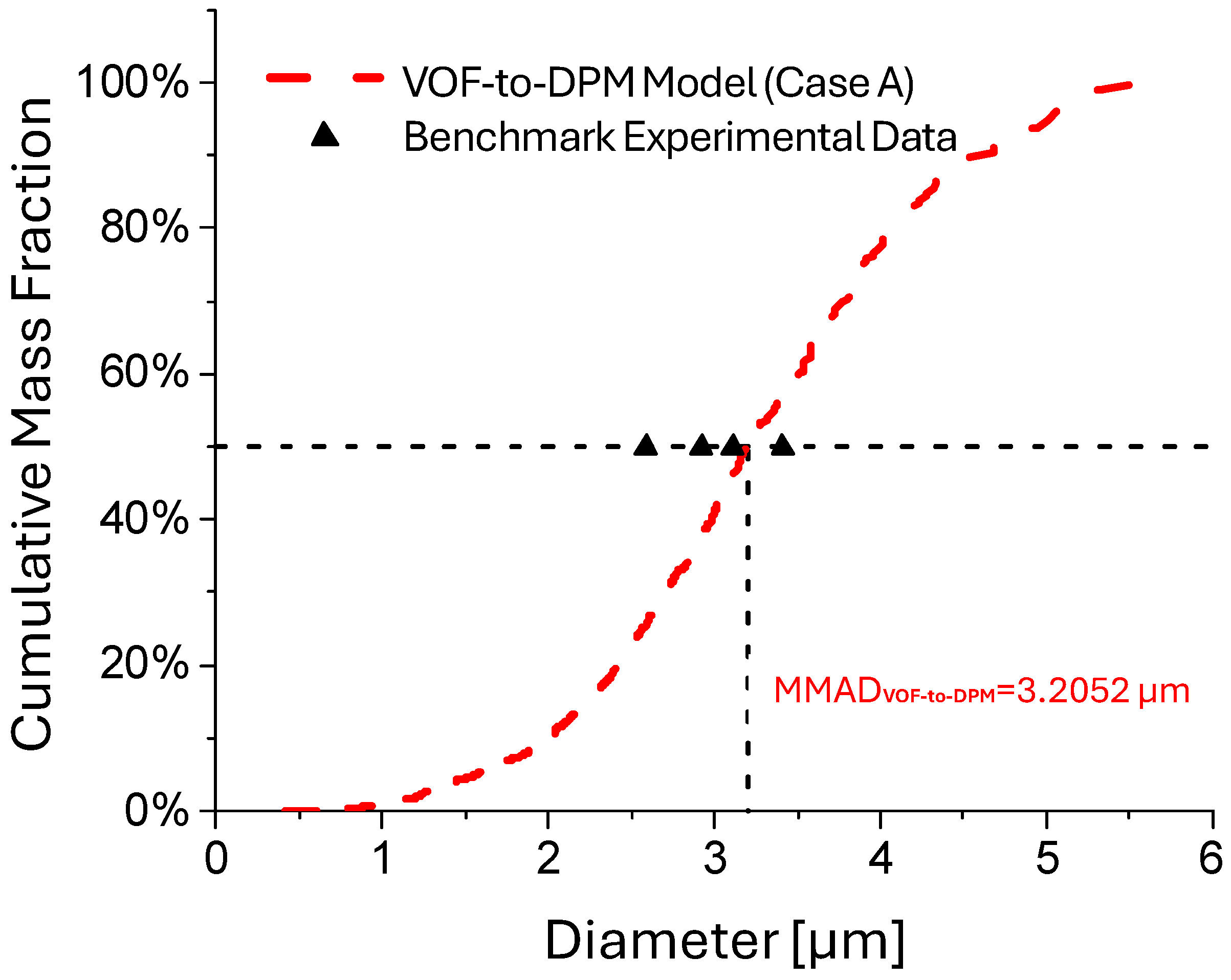
2.4. Model Calibration and Validation
3. Results and Discussion
3.1. Influence of Jet Inlet Velocity on Atomization
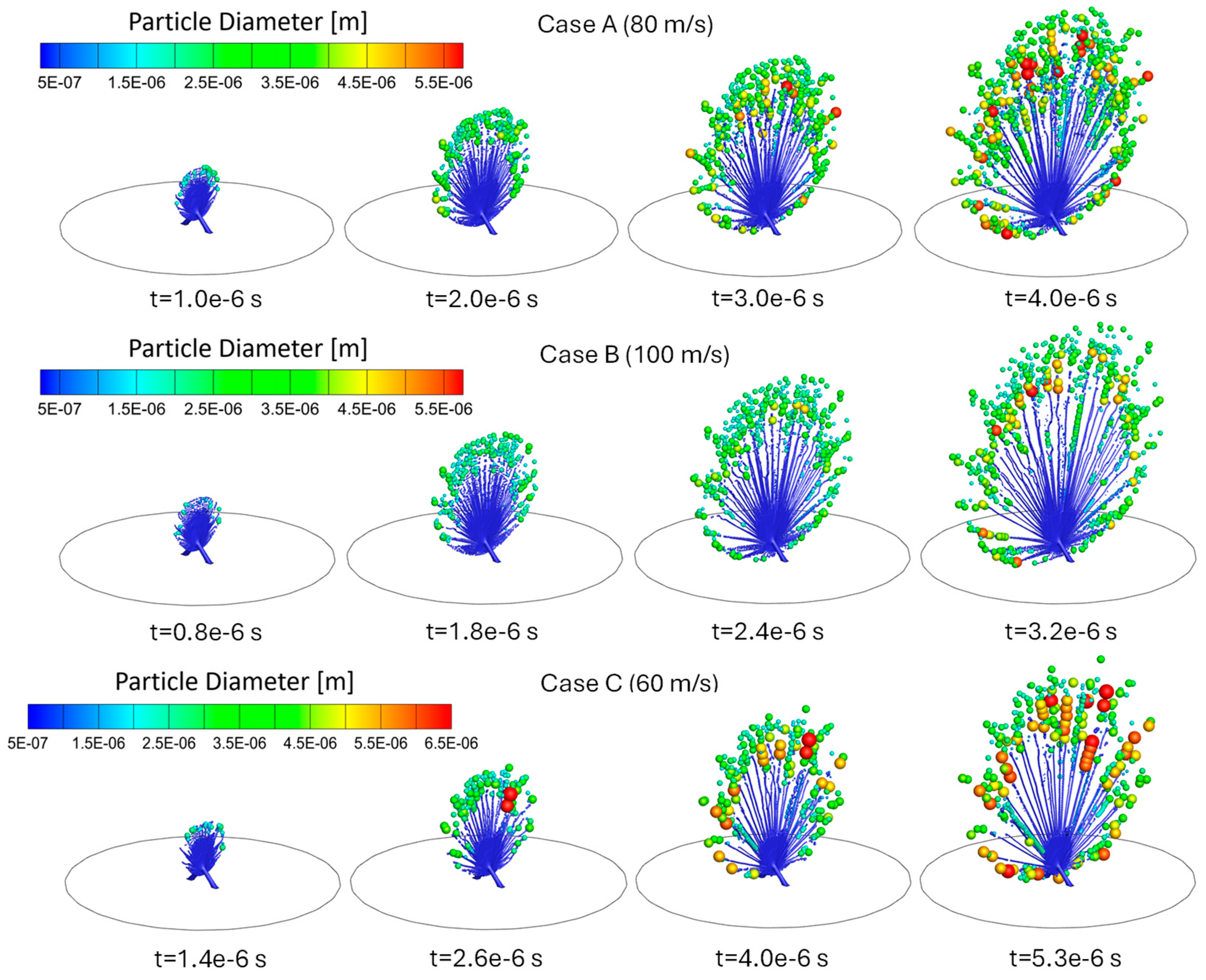
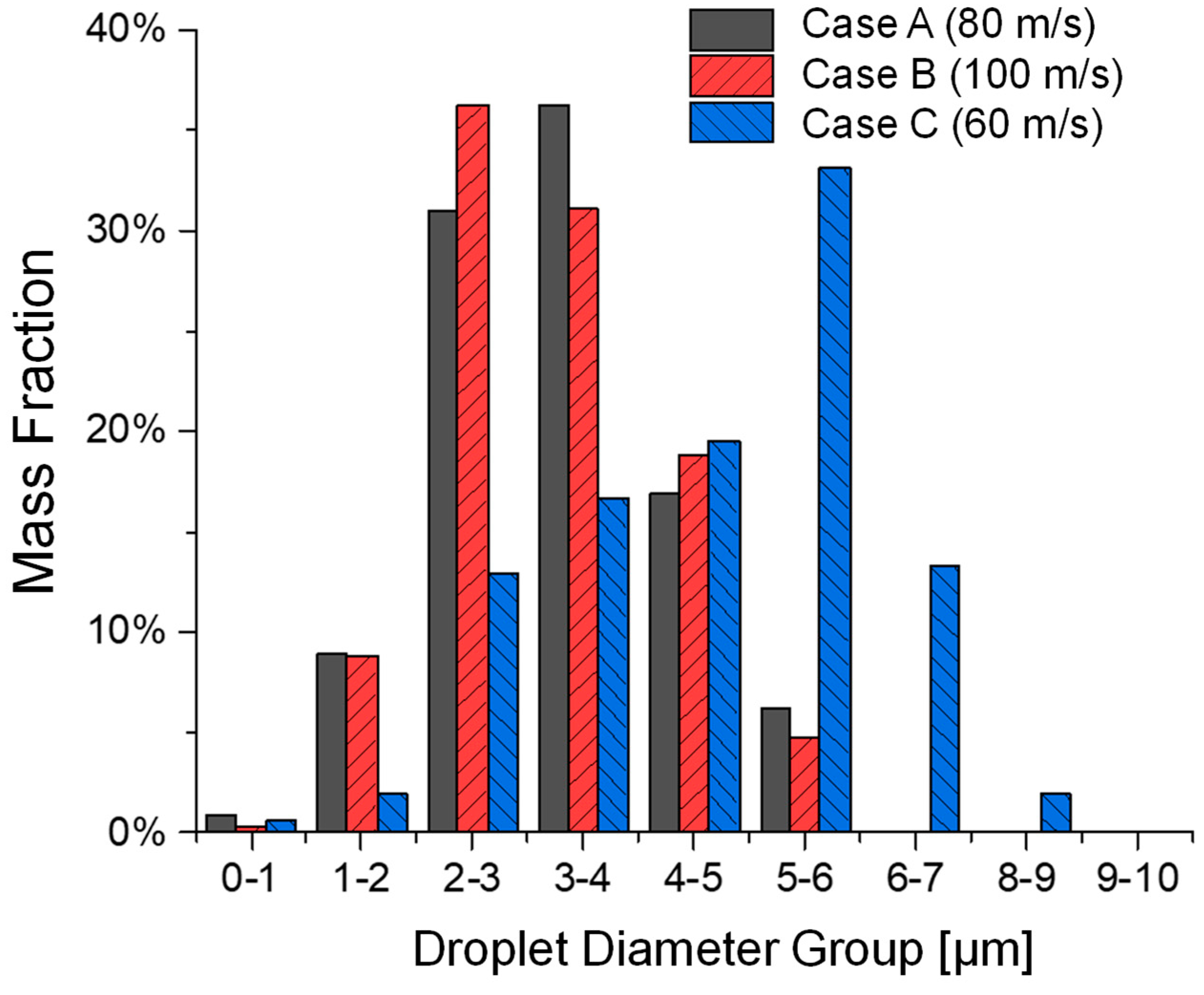
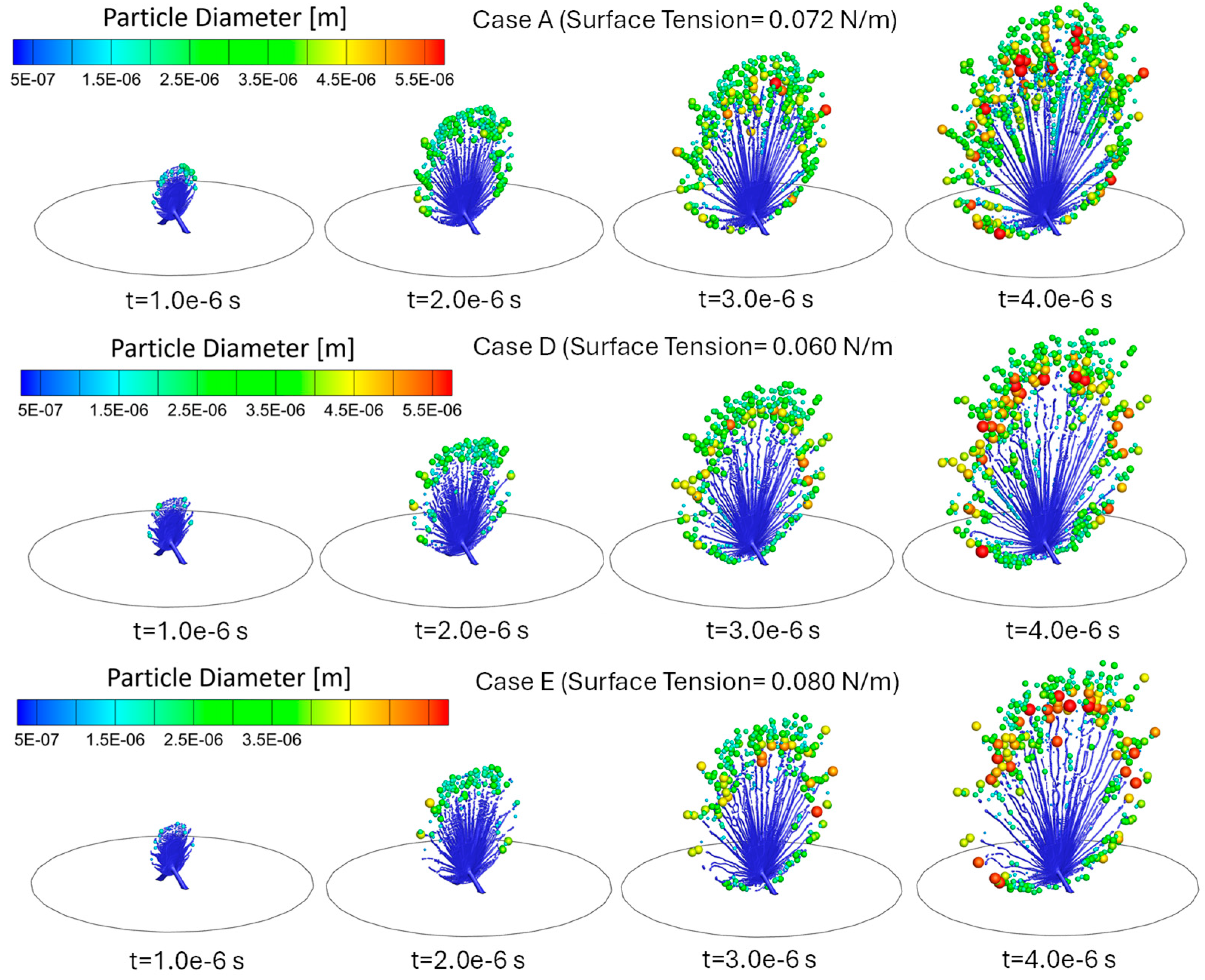
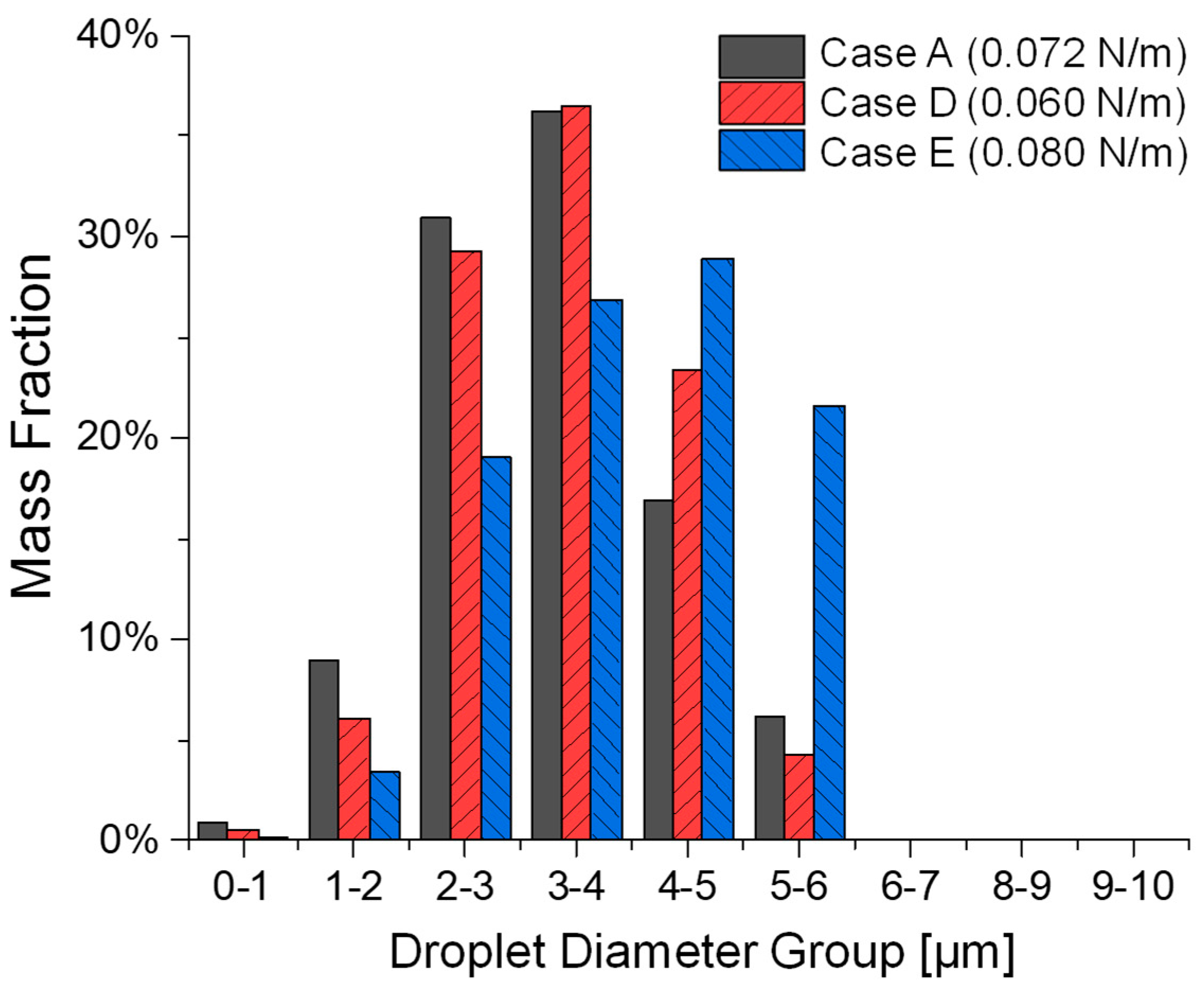
3.2. Influence of Liquid Surface Tension on Atomization
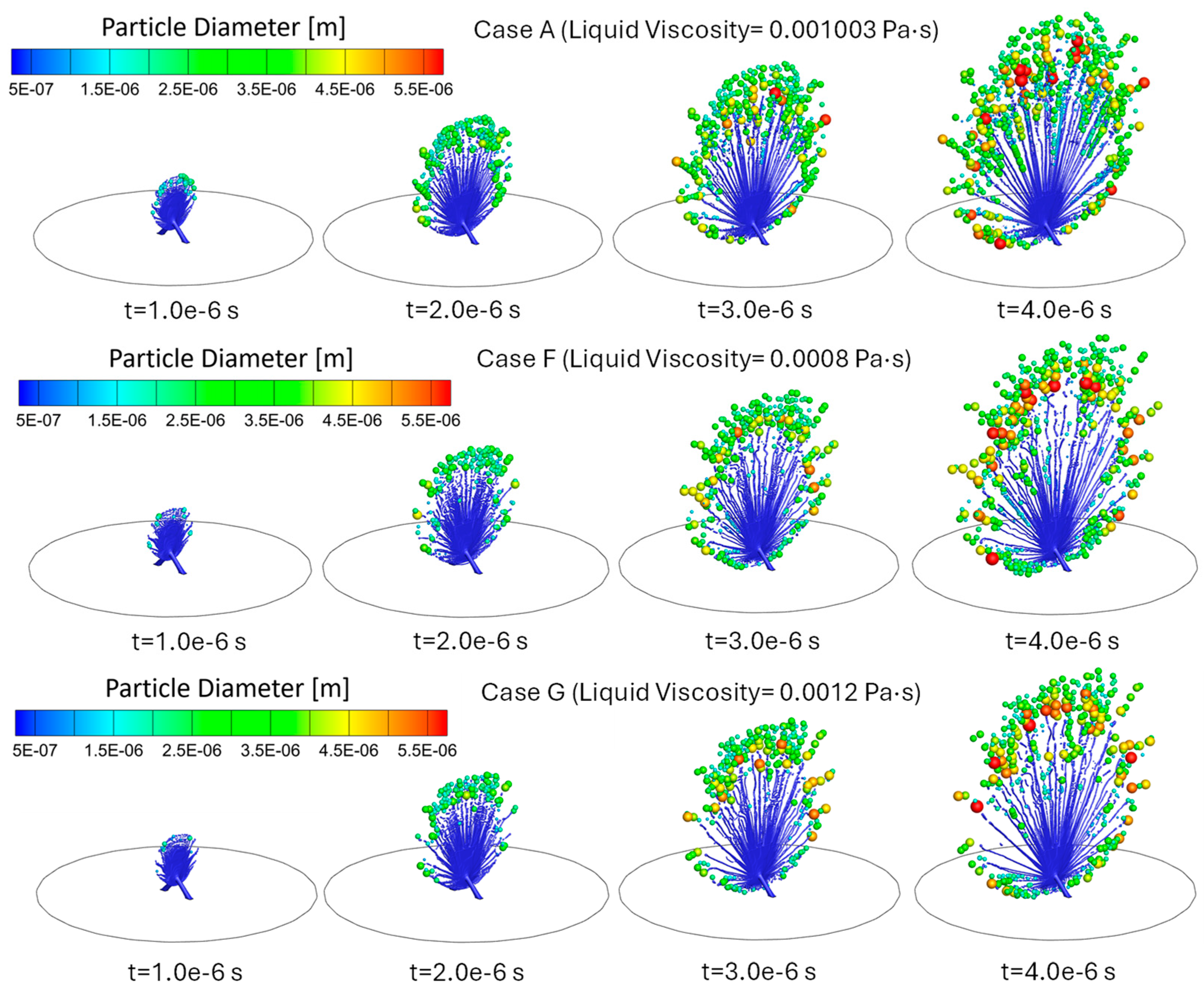
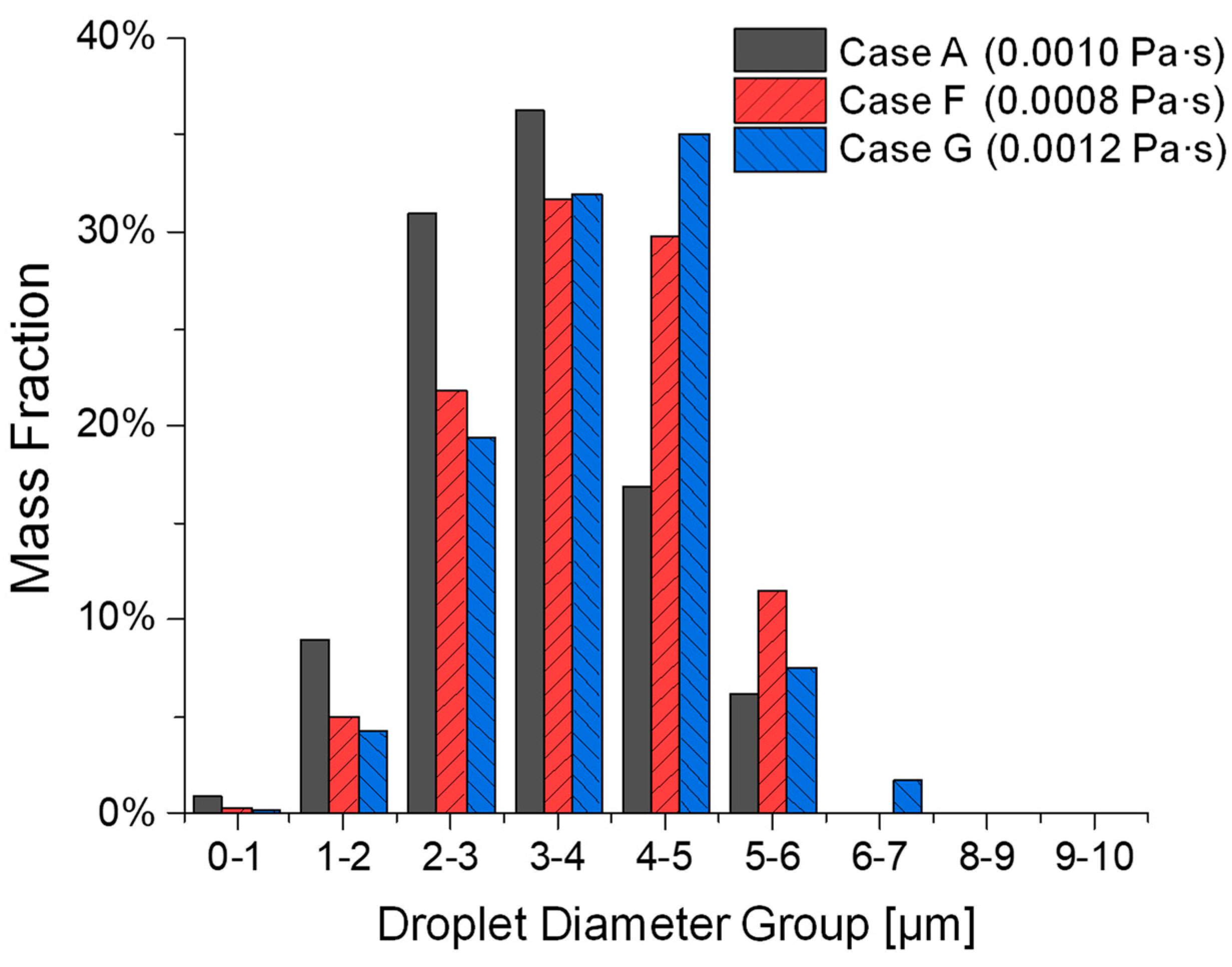
3.3. Influence of Liquid Viscosity on Atomization
4. Conclusions
- Increased colliding jet inlet velocities (i.e., Case C → A → B) improve atomization efficiency by enhancing ligament fragmentation, producing finer droplets with narrower size distributions. However, higher velocities (i.e., Case C → A → B) reduce the total atomized droplet mass, potentially reducing the emitted dose.
- Surface tension exhibits the non-monotonic effect on atomization. Lower surface tension (i.e., Case D vs. Case A and Case E) promotes droplet breakup but may also increase post-breakup coalescence, leading to larger median sizes. Conversely, higher surface tension (i.e., Case E vs. Case A and Case D) resists breakup, resulting in fewer, larger, and more stable droplets.
- Lower viscosity (i.e., Case F vs. Case A and Case G) aids atomization by reducing resistance to ligament breakup but can lead to coalescence, increasing droplet size. Higher viscosity (i.e., Case G vs. Case A and Case F) inhibits atomization, producing fewer, larger droplets with a lower total atomized mass.
5. Limitations of This Study and Future Work
- The non-monotonic trends observed in surface tension and the effects of viscosity require further exploration to fully understand the underlying mechanisms, including secondary breakup and droplet coalescence.
- This study focuses on the initial atomization process without considering downstream droplet transport, evaporation, or deposition in realistic airway geometries.
- To address the limitations mentioned above, future work should attempt the following:
- Extending the study with more surface tension and liquid viscosity properties can generate more insights into the underlying mechanisms leading to non-monotonic trends.
- Investigating the effects of nozzle geometry, impingement angles, and additional operational parameters on atomization dynamics, as well as exploring the role of drug formulation properties, such as surfactants and active ingredient concentrations, on atomization and delivery efficiency.
- Incorporating user-defined functions (UDFs) for the further customization of the VOF-to-DPM to capture droplet interactions, secondary breakup, and coalescence during transport.
- Couple atomization simulations with downstream airflow and deposition models to evaluate the performance of SMIs in realistic respiratory systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACI | Andersen Cascade Impactor |
| AMR | Adaptive mesh refinement |
| CFL | Courant–Friedrichs–Lewy |
| CFD | Computational fluid dynamics |
| DPM | Discrete Phase Model |
| MMAD | Mass Median Aerodynamic Diameter |
| NGI | Next Generation Impactor |
| Oh | Ohnesorge number |
| PDA | Phase Doppler Anemometry |
| PISO | Pressure-Implicit with Splitting of Operators |
| PLIC | Piecewise linear interface reconstruction |
| Re | Reynolds number |
| RR | Rosin–Rammler |
| SMI | Soft Mist inhaler |
| SST | Shear Stress Transport |
| UDF | User-Defined Function |
| VOF | Volume of Fluid |
| We | Weber number |
References
- Cazzola, M.; Blasi, F. There is still no established and accepted definition of COPD. Respir. Med. 2023, 214, 107262. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Kuhn, M.; Prettner, K.; Yu, F.; Yang, T.; Bärnighausen, T.; Bloom, D.E.; Wang, C. The global economic burden of chronic obstructive pulmonary disease for 204 countries and territories in 2020–50: A health-augmented macroeconomic modelling study. Lancet Glob. Health 2023, 11, e1183–e1193. [Google Scholar] [CrossRef]
- Walenga, R.L.; Longest, P.W. Current inhalers deliver very small doses to the lower tracheobronchial airways: Assessment of healthy and constricted lungs. J. Pharm. Sci. 2016, 105, 147–159. [Google Scholar] [CrossRef]
- Dalby, R.N.; Eicher, J.; Zierenberg, B. Development of Respimat® Soft Mist™ Inhaler and its clinical utility in respiratory disorders. Med. Devices Evid. Res. 2011, 4, 145–155. [Google Scholar]
- Myrdal, P.B.; Sheth, P.; Stein, S.W. Advances in metered dose inhaler technology: Formulation development. AAPS PharmSciTech 2014, 15, 434–455. [Google Scholar] [CrossRef]
- Gandertaon, D. Targeted delivery of inhaled drugs: Current challenges and future goals. J. Aerosol Med. 1999, 12, S-3–S-8. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Xiao, J.; Ren, H.; Li, C.; Zheng, Q.; Tong, Z. Three-dimensional simulation of impinging jet atomization of soft mist inhalers using the hybrid VOF-DPM model. Powder Technol. 2022, 407, 117622. [Google Scholar] [CrossRef]
- Li, L.; Jiang, B.; Wei, G.; Li, X.; Zhu, Z. Multiscale multiphase flow simulations using interface capturing and Lagrangian particle tracking. Phys. Fluids 2022, 34, 121801. [Google Scholar] [CrossRef]
- Chen, M.; Li, L.; Lin, Z.; Zhang, J.; Li, F. Investigation of Splashing Characteristics During Spray Impingement Using VOF–DPM Approach. Water 2025, 17, 394. [Google Scholar] [CrossRef]
- Shi, P.; Zhu, G.; Cheng, J.; Li, J.; Hou, X. Simulation on atomization process of gas–liquid pintle injector in LRE under periodic conditions based on the VOF to DPM method. Aerosp. Sci. Technol. 2023, 136, 108222. [Google Scholar] [CrossRef]
- Ou, H.; Su, L.; Shi, Y.; Ruan, S. Investigation on high-viscosity chemical waste liquid atomizer based on VOF-DPM. Energies 2023, 16, 3109. [Google Scholar] [CrossRef]
- Ge, Y.; Tong, Z.; Li, R.; Huang, F.; Yu, J. Numerical and experimental investigation on key parameters of the Respimat® spray inhaler. Processes 2020, 9, 44. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Martinez, J.; Chesneau, X.; Zeghmati, B. A new curvature technique calculation for surface tension contribution in PLIC-VOF method. Comput. Mech. 2006, 37, 182–193. [Google Scholar] [CrossRef]
- Allen, M.D.; Raabe, O.G. Slip correction measurements of spherical solid aerosol particles in an improved Millikan apparatus. Aerosol Sci. Technol. 1985, 4, 269–286. [Google Scholar] [CrossRef]
- Morsi, S.; Alexander, A. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Li, A.; Ahmadi, G. Dispersion and deposition of spherical particles from point sources in a turbulent channel flow. Aerosol Sci. Technol. 1992, 16, 209–226. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics; McGraw Hill: New York, NY, USA, 2011. [Google Scholar]
- Alatrash, A.; Mehri, R.; Ogrodnik, N.; Matida, E.; Fiorenza, F. Experimental study of Spiriva Respimat soft mist inhaler spray characterization: Size distributions and velocity. J. Aerosol Med. Pulm. Drug Deliv. 2019, 32, 293–302. [Google Scholar] [CrossRef]
- Rosin, P. The laws governing the fineness of powdered coal. J. Inst. Fuel 1933, 7, 29–36. [Google Scholar]
- Kirar, P.K.; Kumar, N.; Sahu, K.C. Dynamics of jet breakup and the resultant drop size distribution-effect of nozzle size and impingement velocity. Phys. Fluids 2024, 36, 102108. [Google Scholar] [CrossRef]
- Derby, B. Inkjet printing of functional and structural materials: Fluid property requirements, feature stability, and resolution. Annu. Rev. Mater. Res. 2010, 40, 395–414. [Google Scholar] [CrossRef]
- Shinjo, J.; Umemura, A. Simulation of liquid jet primary breakup: Dynamics of ligament and droplet formation. Int. J. Multiph. Flow 2010, 36, 513–532. [Google Scholar] [CrossRef]
- Lin, S.P.; Reitz, R.D. Drop and spray formation from a liquid jet. Annu. Rev. Fluid Mech. 1998, 30, 85–105. [Google Scholar] [CrossRef]

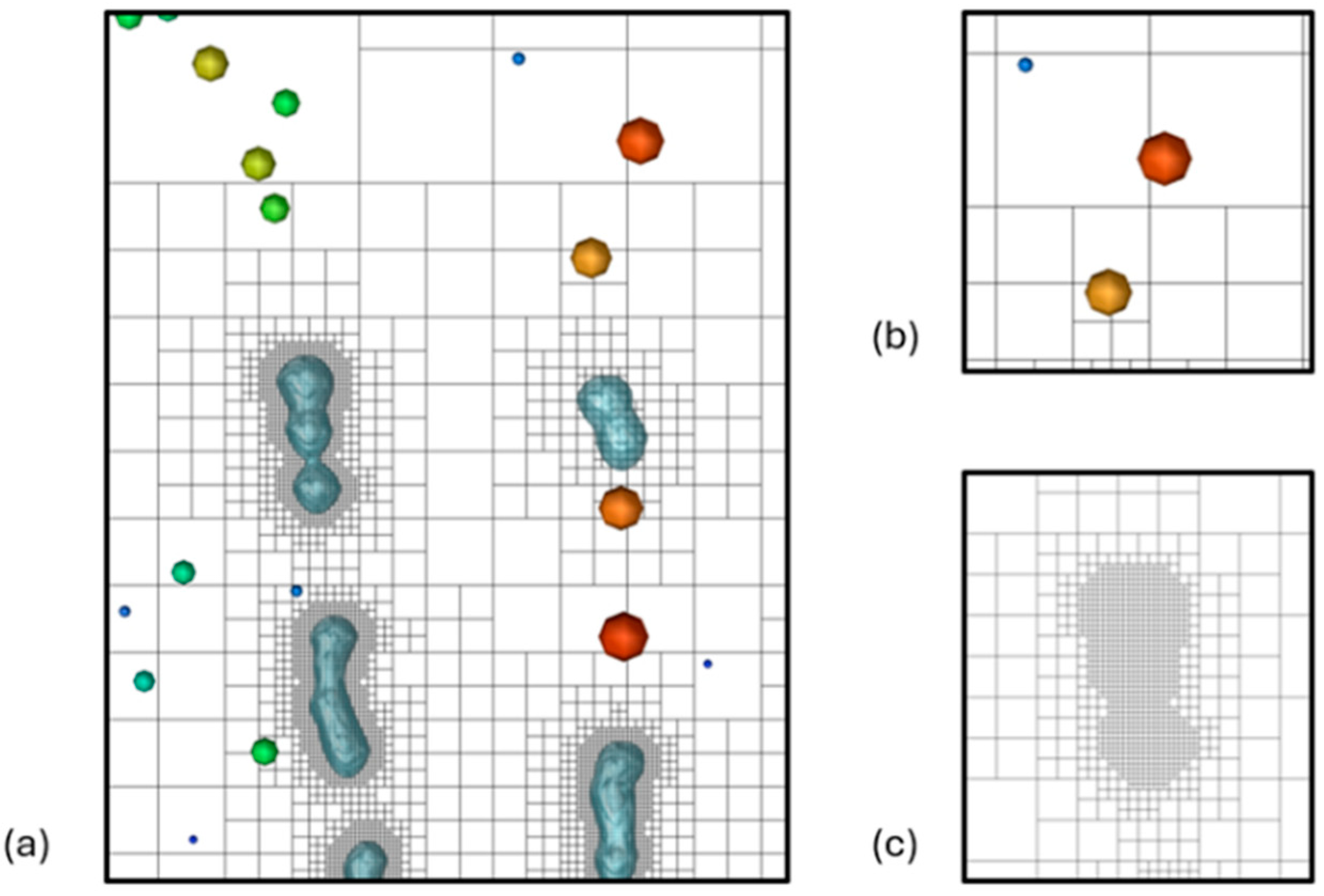
| Case | Average Jet Inlet Velocity () [m/s] | Surface Tension () [N/m] | Liquid Viscosity () [Pa·s] |
|---|---|---|---|
| A | 80 | 0.072 | 0.001003 |
| B | 100 | 0.072 | 0.001003 |
| C | 60 | 0.072 | 0.001003 |
| D | 80 | 0.06 | 0.001003 |
| E | 80 | 0.08 | 0.001003 |
| F | 80 | 0.072 | 0.0008 |
| G | 80 | 0.072 | 0.0012 |
| Case |
Liquid Weber Number () | Liquid Reynolds Number () | Ohnesorge Number () | |
|---|---|---|---|---|
| A | 711 | 638.1 | 0.0418 | |
| B | 1111 | 797.6 | 0.0418 | |
| C | 400 | 478.6 | 0.0418 | |
| D | 853 | 638.1 | 0.0458 | |
| E | 640 | 638.1 | 0.0396 | |
| F | 711 | 800.0 | 0.0333 | |
| G | 711 | 533.3 | 0.0500 | |
| Case | Arithmetic Mean Diameter () [m] | Total DPM Mass Atomized [kg] | MMAD [m] | |
| A | 1.89 × 10−6 | 8.37 × 10−12 | 3.21 × 10−6 | |
| B | 2.10 × 10−6 | 6.54 × 10−12 | 3.13 × 10−6 | |
| C | 2.18 × 10−6 | 9.36 × 10−12 | 4.87 × 10−6 | |
| D | 2.16 × 10−6 | 6.78 × 10−12 | 3.38 × 10−6 | |
| E | 2.52 × 10−6 | 6.21 × 10−12 | 4.01 × 10−6 | |
| F | 2.33 × 10−6 | 7.67 × 10−12 | 3.64 × 10−6 | |
| G | 2.51 × 10−6 | 6.59 × 10−12 | 3.76 × 10−6 | |
| Case | RR Diameter () [m] | Spread Parameter () | ||
| A | 3.54 × 10−6 | 3.68 | ||
| B | 3.47 × 10−6 | 3.62 | ||
| C | 5.34 × 10−6 | 4.0 | ||
| D | 3.72 × 10−6 | 3.92 | ||
| E | 4.37 × 10−6 | 3.89 | ||
| F | 4.11 × 10−6 | 3.78 | ||
| G | 4.11 × 10−6 | 4.19 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sperry, T.; Feng, Y. Prediction of the Atomization Process in Respimat® Soft MistTM Inhalers Using a Volume of Fluid-to-Discrete Phase Model. Bioengineering 2025, 12, 264. https://doi.org/10.3390/bioengineering12030264
Sperry T, Feng Y. Prediction of the Atomization Process in Respimat® Soft MistTM Inhalers Using a Volume of Fluid-to-Discrete Phase Model. Bioengineering. 2025; 12(3):264. https://doi.org/10.3390/bioengineering12030264
Chicago/Turabian StyleSperry, Ted, and Yu Feng. 2025. "Prediction of the Atomization Process in Respimat® Soft MistTM Inhalers Using a Volume of Fluid-to-Discrete Phase Model" Bioengineering 12, no. 3: 264. https://doi.org/10.3390/bioengineering12030264
APA StyleSperry, T., & Feng, Y. (2025). Prediction of the Atomization Process in Respimat® Soft MistTM Inhalers Using a Volume of Fluid-to-Discrete Phase Model. Bioengineering, 12(3), 264. https://doi.org/10.3390/bioengineering12030264







