Modelling of Escherichia coli Batch and Fed-Batch Processes in Semi-Defined Yeast Extract Media
Abstract
1. Introduction
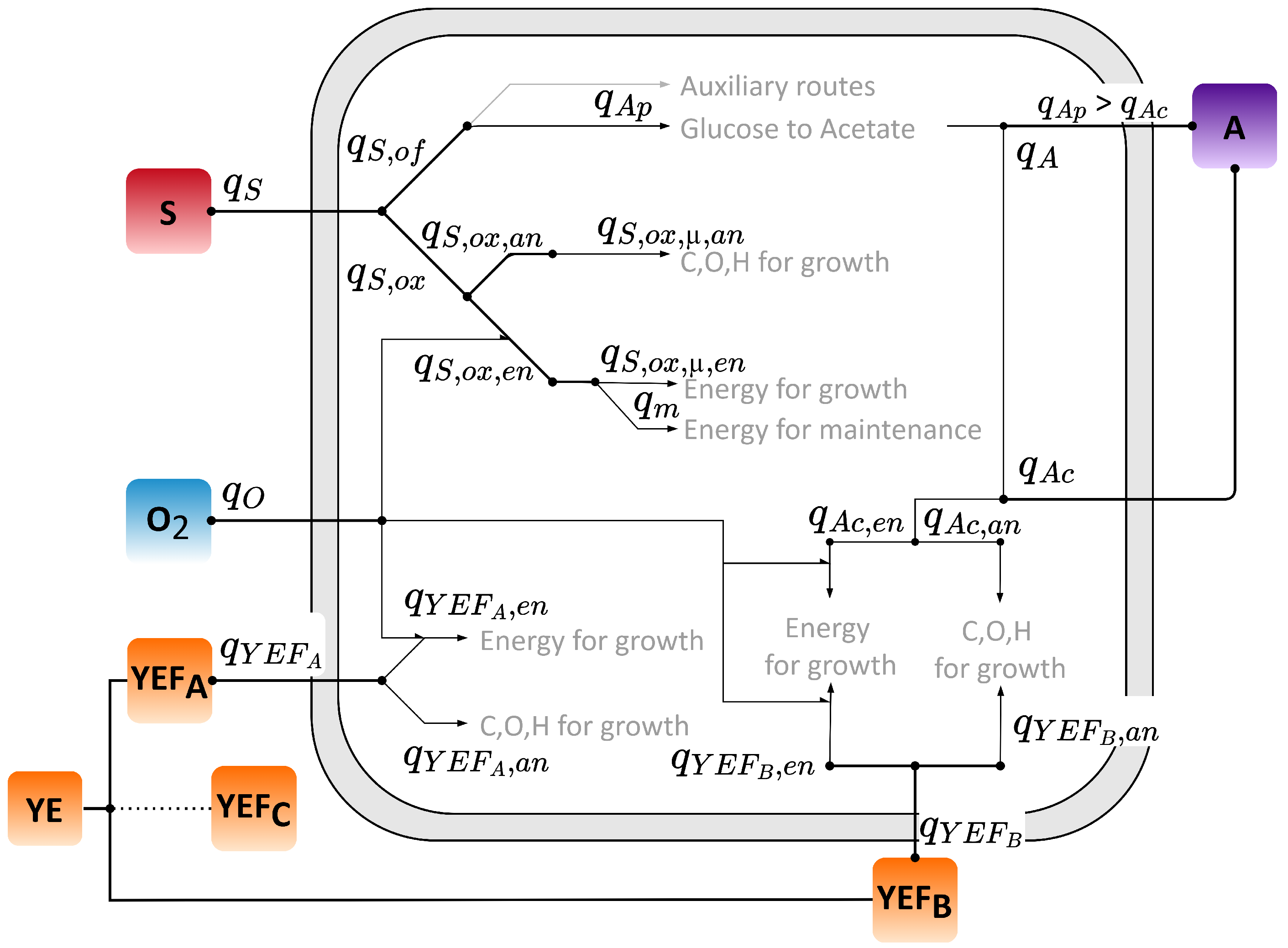
2. Macro-Kinetic Model Formulation
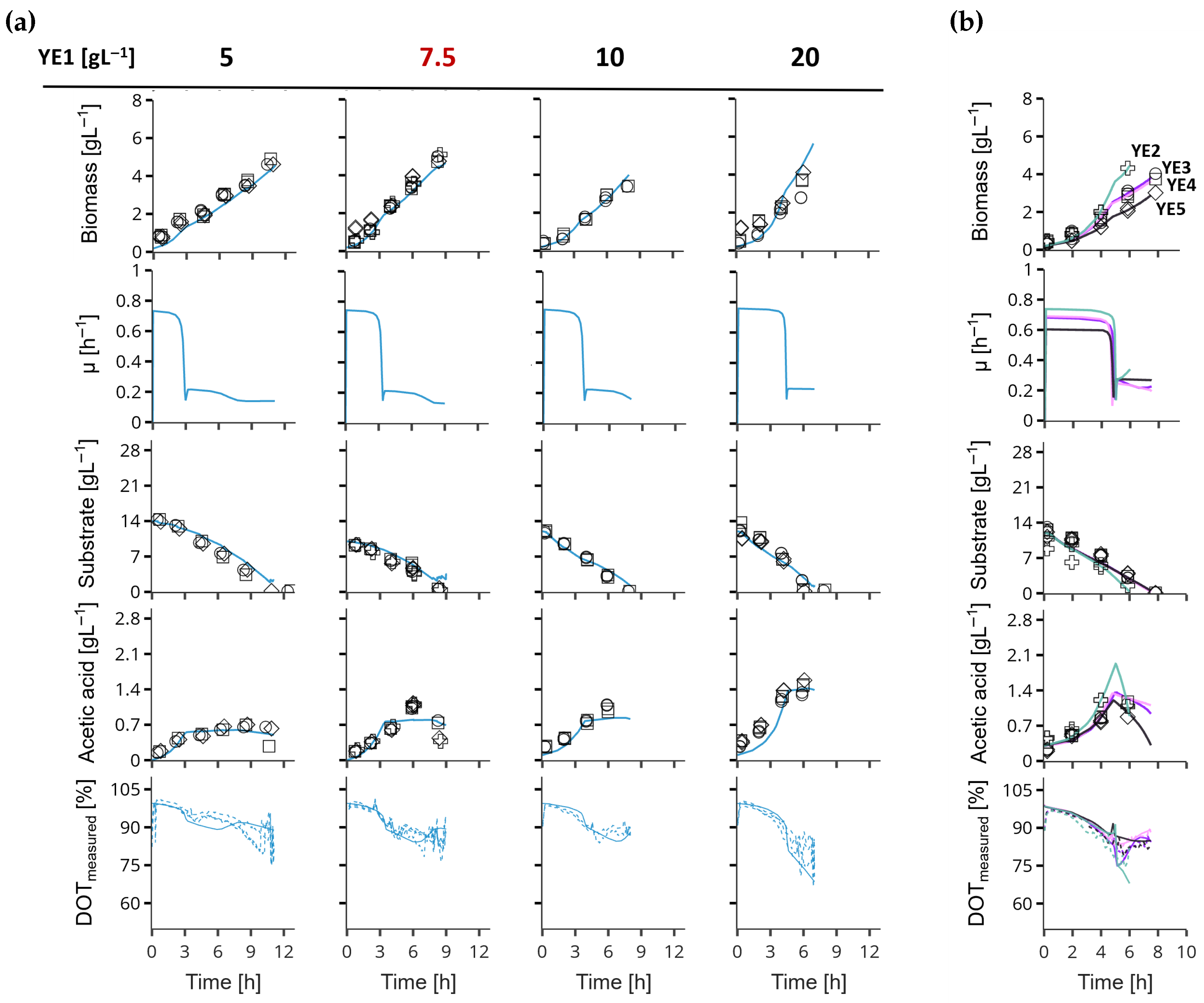
3. Results
Extended Model Validation
4. Discussion
5. Conclusions
6. Materials and Methods
6.1. Strain, Media and Cultivation Conditions
6.2. Analytics
6.3. Parameter Estimation
6.4. Parameter Uncertainty Quantification
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Nomenclature
| Abbreviation | Name | Unit | Bound [min, max] |
|---|---|---|---|
| A | Acetate | g L−1 | – |
| C | Carbon content | – | – |
| Dissolved oxygen tension in equilibrium with the gas phase | % air sat. L g−1 | – | |
| S | Substrate | g L−1 | – |
| Yeast Extract | g L−1 | – | |
| Yeast Extract Fraction i, where i denotes a specific yeast extract fraction | g L−1 | – | |
| X | Biomass | g L−1 | – |
| Affinity constant, acetate consumption | g L−1 | ||
| Inhibition constant, inhibition of oxidative substrate uptake by YE fraction B | g L−1 | ||
| Inhibition constant, inhibition of oxidative substrate uptake by YE fraction B | g L−1 | ||
| Inhibition constant, intracellular oxidative substrate uptake by YE fraction A | g L−1 | ||
| Volumetric mass transfer coefficient | h−1 | – | |
| Affinity constant, substrate consumption | g L−1 | ||
| Affinity constant, consumption of YE fraction A | g L−1 | ||
| Affinity constant, consumption of YE fraction B | g L−1 | ||
| Affinity constant, uptake of substrate for oxidative metabolism | g L−1 | ||
| Available specific maintenance coefficient | g g−1 h−1 | – | |
| Maximum specific substrate uptake rate | g g−1 h−1 | ||
| Maximum specific uptake rate for YE fraction A | g g−1 h−1 | ||
| Maximum specific uptake rate for YE fraction B | g g−1 h−1 | ||
| Specific acetate consumption rate | g g−1 h−1 | ||
| Yield of acetate per gram of substrate | g g−1 | – | |
| Oxygen used per gram of acetate metabolized | g g−1 | – | |
| Yield of biomass per gram of substrate (glucose) | g g−1 | ||
| Yield of biomass per gram of YE fraction A | g g−1 | ||
| Yield of biomass per gram of YE fraction B | g g−1 | ||
| Yield of biomass per gram of acetate | g g−1 | ||
| Oxygen used per gram of substrate metabolized | g g−1 | – | |
| Oxygen used per gram of YE metabolized | g g−1 | – | |
| Dissolved oxygen probe response time | h | – |
Appendix A.2. Constants
| Constant | Unit | Value | Comment |
|---|---|---|---|
| CA | g g−1 | 0.033 | stoichiometric constant |
| CP | g g−1 | 0.044 | stoichiometric constant |
| CS | g g−1 | 0.033 | stoichiometric constant |
| CX | g g−1 | 0.041 | stoichiometric constant |
| CYE | g g−1 | 0.036 | stoichiometric constant |
| DOT* | % air sat. | 100 | dissolved oxygen concentration at saturation |
| H | % air sat. | 14,000 | Henry law related constant |
| Si | g L−1 | 600 | feed stock concentration |
References
- Crueger, W.; Crueger, A.; Brock, T.D.; Brock, T.D. Biotechnology: A Textbook of Industrial Microbiology; Sinauer: Sunderland, MA, USA, 1990. [Google Scholar]
- Jacob, F.F.; Michel, M.; Zarnkow, M.; Hutzler, M.; Methner, F.J. The complexity of yeast extracts and its consequences on the utility in brewing: A review. BrewingScience 2019, 72, 50–62. [Google Scholar]
- Tao, Z.; Yuan, H.; Liu, M.; Liu, Q.; Zhang, S.; Liu, H.; Jiang, Y.; Huang, D.; Wang, T. Yeast Extract: Characteristics, Production, Applications and Future Perspectives. J. Microbiol. Biotechnol. 2023, 33, 151–166. [Google Scholar] [CrossRef]
- Selvarasu, S.; Ow, D.S.W.; Lee, S.Y.; Lee, M.M.; Oh, S.K.W.; Karimi, I.A.; Lee, D.Y. Characterizing Escherichia coli DH5α growth and metabolism in a complex medium using genome-scale flux analysis. Biotechnol. Bioeng. 2009, 102, 923–934. [Google Scholar] [CrossRef]
- Suárez, D.; Liria, C.; Kilikian, B. Effect of yeast extract on Escherichia coli growth and acetic acid production. World J. Microbiol. Biotechnol. 1998, 14, 331–335. [Google Scholar] [CrossRef]
- Tachibana, S.; Watanabe, K.; Konishi, M. Estimating effects of yeast extract compositions on Escherichia coli growth by a metabolomics approach. J. Biosci. Bioeng. 2019, 128, 468–474. [Google Scholar] [CrossRef] [PubMed]
- Amrane, A.; Prigent, Y. Influence of yeast extract concentrationon batch cultures of Lactobacillus helveticus: Growth and production coupling. World J. Microbiol. Biotechnol. 1998, 14, 529–534. [Google Scholar] [CrossRef]
- Zhang, J.; Reddy, J.; Buckland, B.; Greasham, R. Toward consistent and productive complex media for industrial fermentations: Studies on yeast extract for a recombinant yeast fermentation process. Biotechnol. Bioeng. 2003, 82, 640–652. [Google Scholar] [CrossRef]
- Tachibana, S.; Chiou, T.Y.; Konishi, M. Machine learning modeling of the effects of media formulated with various yeast extracts on heterologous protein production in Escherichia coli. MicrobiologyOpen 2021, 10, e1214. [Google Scholar] [CrossRef]
- Narayana, S.K.; Mallick, S.; Siegumfeldt, H.; van den Berg, F. Bacterial Flow Cytometry and Imaging as Potential Process Monitoring Tools for Industrial Biotechnology. Fermentation 2020, 6, 10. [Google Scholar] [CrossRef]
- Oliveira, A.L. Biotechnology, Big Data and Artificial Intelligence. Biotechnol. J. 2019, 14, 1800613. [Google Scholar] [CrossRef]
- Vázquez, J.A.; Murado, M.A. Mathematical tools for objective comparison of microbial cultures: Application to evaluation of 15 peptones for lactic acid bacteria productions. Biochem. Eng. J. 2008, 39, 276–287. [Google Scholar] [CrossRef]
- Bapat, P.M.; Bhartiya, S.; Venkatesh, K.; Wangikar, P.P. Structured kinetic model to represent the utilization of multiple substrates in complex media during rifamycin B fermentation. Biotechnol. Bioeng. 2006, 93, 779–790. [Google Scholar] [CrossRef]
- Anane, E.; López C, D.C.; Neubauer, P.; Cruz Bournazou, M.N. Modelling overflow metabolism in Escherichia coli by acetate cycling. Biochem. Eng. J. 2017, 125, 23–30. [Google Scholar] [CrossRef]
- Kager, J.; Horst, N.; Bartlechner, J.; Herwig, C.; Jakubek, S. Generic model based control of different specific rates in recombinant E. coli Fed-batch processes. IFAC-PapersOnLine 2022, 55, 756–761. [Google Scholar] [CrossRef]
- Neubauer, P.; Lin, H.Y.; Mathiszik, B. Metabolic load of recombinant protein production: Inhibition of cellular capacities for glucose uptake and respiration after induction of a heterologous gene in Escherichia coli. Biotechnol. Bioeng. 2003, 83, 53–64. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Jahic, M.; Enfors, S.O. Modeling of Overflow Metabolism in Batch and Fed-Batch Cultures of Escherichia coli. Biotechnol. Prog. 1999, 15, 81–90. [Google Scholar] [CrossRef] [PubMed]
- Pham, H.T.B.; Larsson, G.; Enfors, S.O. Growth and energy metabolism in aerobic fed-batch cultures of Saccharomyces cerevisiae: Simulation and model verification. Biotechnol. Bioeng. 1998, 60, 474–482. [Google Scholar] [CrossRef]
- Eslami, T.; Jungbauer, A. Control strategy for biopharmaceutical production by model predictive control. Biotechnol. Prog. 2024, 40, e3426. [Google Scholar] [CrossRef]
- Cruz Bournazou, M.; Barz, T.; Nickel, D.; Lopez Cárdenas, D.; Glauche, F.; Knepper, A.; Neubauer, P. Online optimal experimental re-design in robotic parallel fed-batch cultivation facilities: Online Optimal Experimental Re-Design in Robotic. Biotechnol. Bioeng. 2017, 114, 610–619. [Google Scholar] [CrossRef]
- Sundström, H.; Enfors, S.O. Software sensors for fermentation processes. Bioprocess Biosyst. Eng. 2008, 31, 145–152. [Google Scholar] [CrossRef]
- Franceschini, G.; Macchietto, S. Model-based design of experiments for parameter precision: State of the art. Chem. Eng. Sci. 2008, 63, 4846–4872. [Google Scholar] [CrossRef]
- Gschaedler, A.; Boudrant, J. Amino acid utilization during batch and continuous cultures of Escherichia coli on a semi-synthetic medium. J. Biotechnol. 1994, 37, 235–251. [Google Scholar] [CrossRef]
- Maser, A.; Peebo, K.; Vilu, R.; Nahku, R. Amino acids are key substrates to Escherichia coli BW25113 for achieving high specific growth rate. Res. Microbiol. 2020, 171, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Han, L. Physiology of Escherichia coli in Batch and Fed-Batch Cultures with Special Emphasis on Amino Acid and Glucose Metabolism. Ph.D. Thesis, KTH Biotechnology, Stockholm, Sweden, 2002. [Google Scholar]
- Duan, Z.; Wilms, T.; Neubauer, P.; Kravaris, C.; Cruz Bournazou, M.N. Model reduction of aerobic bioprocess models for efficient simulation. Chem. Eng. Sci. 2020, 217, 115512. [Google Scholar] [CrossRef]
- López Cárdenas, D.; Barz, T.; Peñuela, M.; Villegas, A.; Ochoa, S.; Wozny, G. Model-based identifiable parameter determination applied to a simultaneous saccharification and fermentation process model for bio-ethanol production. Biotechnol. Prog. 2013, 29, 1064–1082. [Google Scholar] [CrossRef]
- Smaluch, K.; Wollenhaupt, B.; Steinhoff, H.; Kohlheyer, D.; Grünberger, A.; Dusny, C. Assessing the growth kinetics and stoichiometry of Escherichia coli at the single-cell level. Eng. Life Sci. 2022, 23, e2100157. [Google Scholar] [CrossRef]
- Lange, C.; Seidel, S.; Altmann, M.; Stors, D.; Kemmer, A.; Cai, L.; Born, S.; Neubauer, P.; Bournazou, M.N.C. Automatic Raman Measurements in a High-Throughput Bioprocess Development Lab. arXiv 2025, arXiv:2504.11234. [Google Scholar] [CrossRef]
- Li, B.; Sirimuthu, N.M.S.; Ray, B.H.; Ryder, A.G. Using surface-enhanced Raman scattering (SERS) and fluorescence spectroscopy for screening yeast extracts, a complex component of cell culture media. J. Raman Spectrosc. 2012, 43, 1074–1082. [Google Scholar] [CrossRef]
- Kasprow, R.P.; Lange, A.J.; Kirwan, D.J. Correlation of Fermentation Yield with Yeast Extract Composition as Characterized by Near-Infrared Spectroscopy. Biotechnol. Prog. 1998, 14, 318–325. [Google Scholar] [CrossRef]
- Potvin, J.; Fonchy, E.; Conway, J.; Champagne, C.P. An automatic turbidimetric method to screen yeast extracts as fermentation nutrient ingredients. J. Microbiol. Methods 1997, 29, 153–160. [Google Scholar] [CrossRef]
- Riesenberg, D.; Menzel, K.; Schulz, V.; Schumann, K.; Veith, G.; Zuber, G.; Knorre, W.A. High cell density fermentation of recombinant Escherichia coli expressing human interferon alpha 1. Appl. Microbiol. Biotechnol. 1990, 34, 77–82. [Google Scholar] [CrossRef]
- Haby, B.; Hans, S.; Anane, E.; Sawatzki, A.; Krausch, N.; Neubauer, P.; Cruz Bournazou, M.N. Integrated Robotic Mini Bioreactor Platform for Automated, Parallel Microbial Cultivation With Online Data Handling and Process Control. SLAS Technol. Transl. Life Sci. Innov. 2019, 24, 569–582. [Google Scholar] [CrossRef]
- Kemmer, A.; Cai, L.; Cruz Bournazou, M.N.; Neubauer, P. High-Throughput Expression of Inclusion Bodies on an Automated Platform. In Inclusion Bodies: Methods and Protocols; Kopp, J., Spadiut, O., Eds.; Springer US: New York, NY, USA, 2023; pp. 31–47. [Google Scholar] [CrossRef]
- Weuster-Botz, D.; Puskeiler, R.; Kusterer, A.; Kaufmann, K.; John, G.T.; Arnold, M. Methods and milliliter scale devices for high-throughput bioprocess design. Bioprocess Biosyst. Eng. 2005, 28, 109–119. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.C.; Ryu, D.D.Y.; Park, C.S.; Kim, J.Y.; Ogrydziak, D.M. Recombinant bioprocess optimization for heterologous protein production using two-stage, cyclic fed-batch culture. Appl. Microbiol. Biotechnol. 1998, 49, 531–537. [Google Scholar] [CrossRef] [PubMed]
- Spadiut, O.; Rittmann, S.; Dietzsch, C.; Herwig, C. Dynamic process conditions in bioprocess development. Eng. Life Sci. 2013, 13, 88–101. [Google Scholar] [CrossRef]
- Andersson, J.; Åkesson, J.; Diehl, M. CasADi: A Symbolic Package for Automatic Differentiation and Optimal Control. In Recent Advances in Algorithmic Differentiation; Forth, S., Hovland, P., Phipps, E., Utke, J., Walther, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 87, pp. 297–307. [Google Scholar]
- Newville, M.; Stensitzki, T.; Allen, D.B.; Rawlik, M.; Ingargiola, A.; Nelson, A. LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python. Astrophysics Source Code Library. 2016. Available online: https://ascl.net/1606.014 (accessed on 17 September 2025).
- Cohen, A.; Migliorati, G. Optimal weighted least-squares methods. SMAI J. Comput. Math. 2017, 3, 181–203. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]

| Batch | Batch and Fed Batch | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Basic | One-YEF | Two-YEF | Three-YEF | Basic | One-YEF | Two-YEF | Three-YEF | |
| RMSE | 3.64 | 2.44 | 2.40 | 2.40 | 1.95 | 1.10 | 0.68 | 0.75 | |
| (3) | 1.02 ± 0.14 | 0.46 ± 0.01 | 0.55 ± 0.19 | 0.56 ± 0.23 | 1.62 ± 0.26 | 0.55 ± 0.05 | 0.62 ± 0.05 | 0.71 ± 0.27 | |
| — | 1.99 | 1.71 | 1.48 | — | 1.80 | 1.63 | 1.60 | ||
| — | — | 0.23 | 0.46 | — | — | 0.10 | 0.31 | ||
| (1) | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | |
| (4) | 0.70 ± 0.48 | 0.89 ± 0.47 | 0.37 ± 0.31 | 0.84 ± 0.45 | 0.42 ± 0.47 | 0.89 ± 0.40 | 0.55 ± 0.43 | 0.64 ± 0.45 | |
| (3) | 0.83 ± 0.09 | 0.33 ± 0.04 | 0.42 ± 0.07 | 0.42 ± 0.06 | 0.42 ± 0.03 | 0.43 ± 0.02 | 0.43 ± 0.02 | 0.43 ± 0.04 | |
| (3) | — | 0.41 ± 0.01 | 0.52 ± 0.03 | 0.50 ± 0.05 | — | 0.46 ± 0.01 | 0.56 ± 0.04 | 0.53 ± 0.11 | |
| (4) | — | — | 0.14 ± 0.05 | 0.31 ± 0.14 | — | — | 0.12 ± 0.05 | 0.21 ± 0.14 | |
| (1) | 0.27 | 0.28 | 0.30 | 0.42 | 0.37 | 0.50 | 0.42 | 0.42 | |
| (1) | 1.07 | 1.07 | 1.07 | 1.07 | 1.07 | 1.07 | 1.07 | 1.07 | |
| (1) | 1.07 | 1.07 | 1.07 | 1.07 | 1.07 | 1.07 | 1.07 | 1.07 | |
| Parameter | (1) | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 | 0.67 |
| (2) | — | 1.16 | 1.16 | 1.16 | — | 1.16 | 1.16 | 1.16 | |
| (1,3) | 0.05 ± 0.03 | 0.05 | 0.05 | 0.05 | 0.05 ± 0.03 | 0.05 | 0.05 | 0.05 | |
| — | 0.07 | 0.77 | 0.05 | — | 2.99 | 0.23 | 0.05 | ||
| — | — | 1.28 | 0.10 | — | — | 1.70 | 0.10 | ||
| 42.16 | 16.20 | 65.21 | 17.69 | 30.20 | 80.76 | 38.11 | 34.49 | ||
| 0.81 | 1.00 | 0.25 | 0.86 | 0.66 | 0.66 | 0.86 | 0.86 | ||
| — | — | 25.88 | 49.18 | — | — | 49.27 | 49.34 | ||
| 0.28 | 0.05 | 2.33 | 0.08 | 2.64 | 0.05 | 0.05 | 0.008 | ||
| — | 1.13 | 0.49 | 0.02 | — | 1.56 | 0.24 | 0.01 | ||
| (4) | — | 1 | 0.61 ± 0.11 | 0.43 ± 0.16 | — | 1 | 0.27 ± 0.10 | 0.21 ± 0.14 | |
| (4) | — | 1 | 1 | 0.71 ± 0.22 | — | 1 | 1 | 0.54 ± 0.27 | |
| Experiments | Scale [L] | OD600,init | Sinit [g L−1] | YEinit [g L−1] | YE Brand | Feed Regime | Feed Strategy | Si [g L−1] |
|---|---|---|---|---|---|---|---|---|
| Model evaluation | 3 | 0.0002 | 15 | 10 | Procelys® 1 | continuous | stepwise | 600 |
| YE1 | 0.01 | 0.3 | 9 | 0, 5, 7.5, 10 | Procelys® | bolus | exponential | 400 |
| YE2 | 0.01 | 0.5 | 12 | 10 | VWR 2 | — | — | — |
| YE3 | 0.01 | 0.5 | 12 | 10 | Difco 3 | — | — | — |
| YE4 | 0.01 | 0.5 | 12 | 10 | Bacto 3 | — | — | — |
| YE5 | 0.01 | 0.5 | 12 | 10 | Roth 4 | — | — | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schröder-Kleeberg, F.; Zoellkau, M.; Glaser, M.; Bosch, C.; Brunner, M.; Cruz Bournazou, M.N.; Neubauer, P. Modelling of Escherichia coli Batch and Fed-Batch Processes in Semi-Defined Yeast Extract Media. Bioengineering 2025, 12, 1081. https://doi.org/10.3390/bioengineering12101081
Schröder-Kleeberg F, Zoellkau M, Glaser M, Bosch C, Brunner M, Cruz Bournazou MN, Neubauer P. Modelling of Escherichia coli Batch and Fed-Batch Processes in Semi-Defined Yeast Extract Media. Bioengineering. 2025; 12(10):1081. https://doi.org/10.3390/bioengineering12101081
Chicago/Turabian StyleSchröder-Kleeberg, Fabian, Markus Zoellkau, Markus Glaser, Christian Bosch, Markus Brunner, Mariano Nicolas Cruz Bournazou, and Peter Neubauer. 2025. "Modelling of Escherichia coli Batch and Fed-Batch Processes in Semi-Defined Yeast Extract Media" Bioengineering 12, no. 10: 1081. https://doi.org/10.3390/bioengineering12101081
APA StyleSchröder-Kleeberg, F., Zoellkau, M., Glaser, M., Bosch, C., Brunner, M., Cruz Bournazou, M. N., & Neubauer, P. (2025). Modelling of Escherichia coli Batch and Fed-Batch Processes in Semi-Defined Yeast Extract Media. Bioengineering, 12(10), 1081. https://doi.org/10.3390/bioengineering12101081









