In Silico and In Vitro Comparison of Seven Closed and Semi-Closed Leaflet Designs for Transcatheter Heart Valve Replacements
Abstract
1. Introduction
2. Materials & Methods
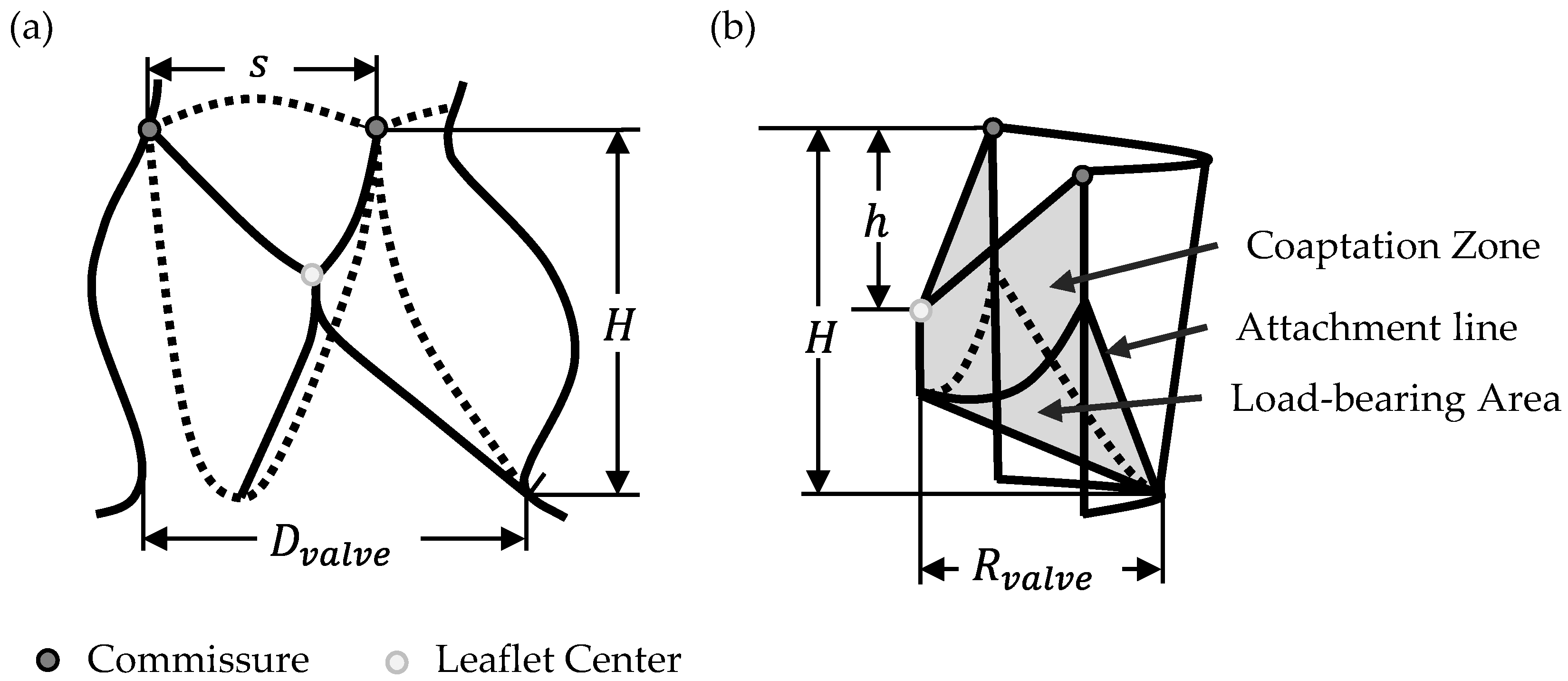
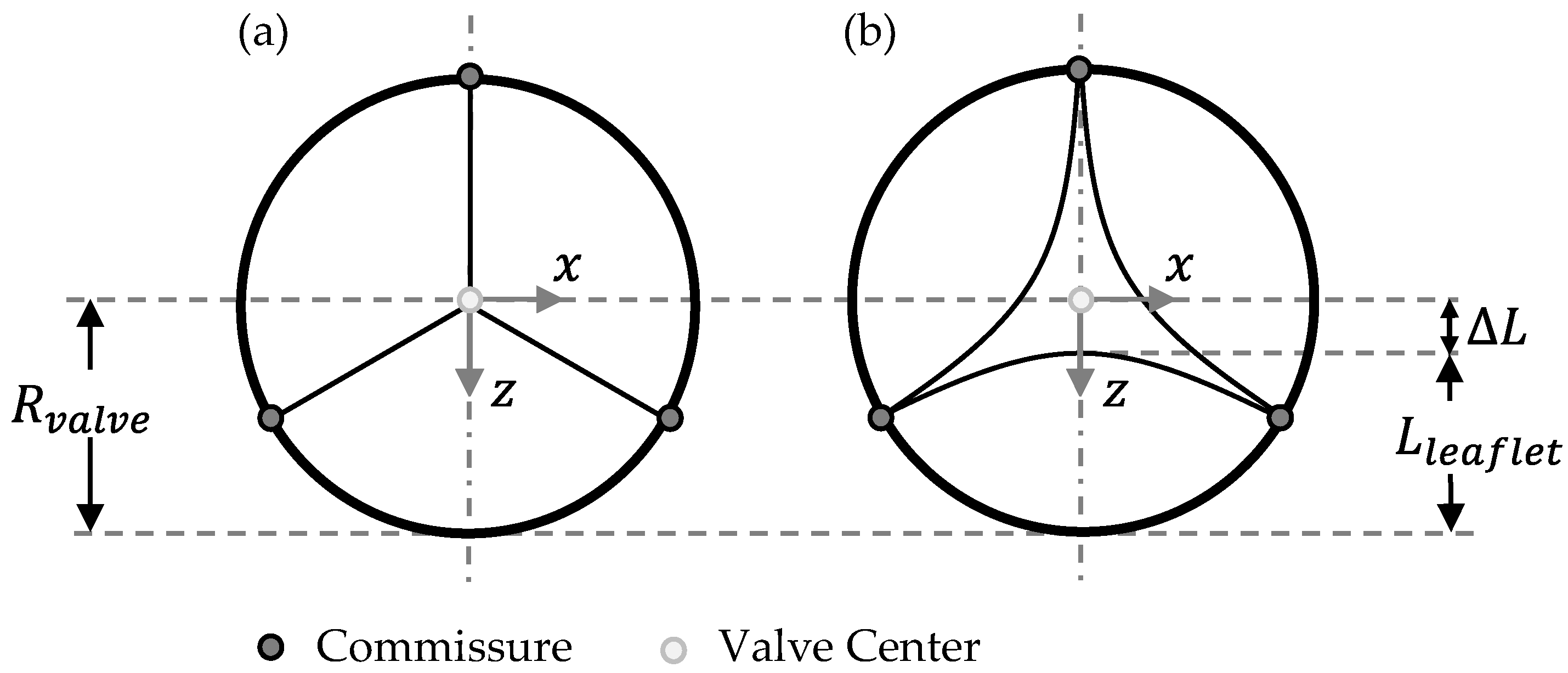
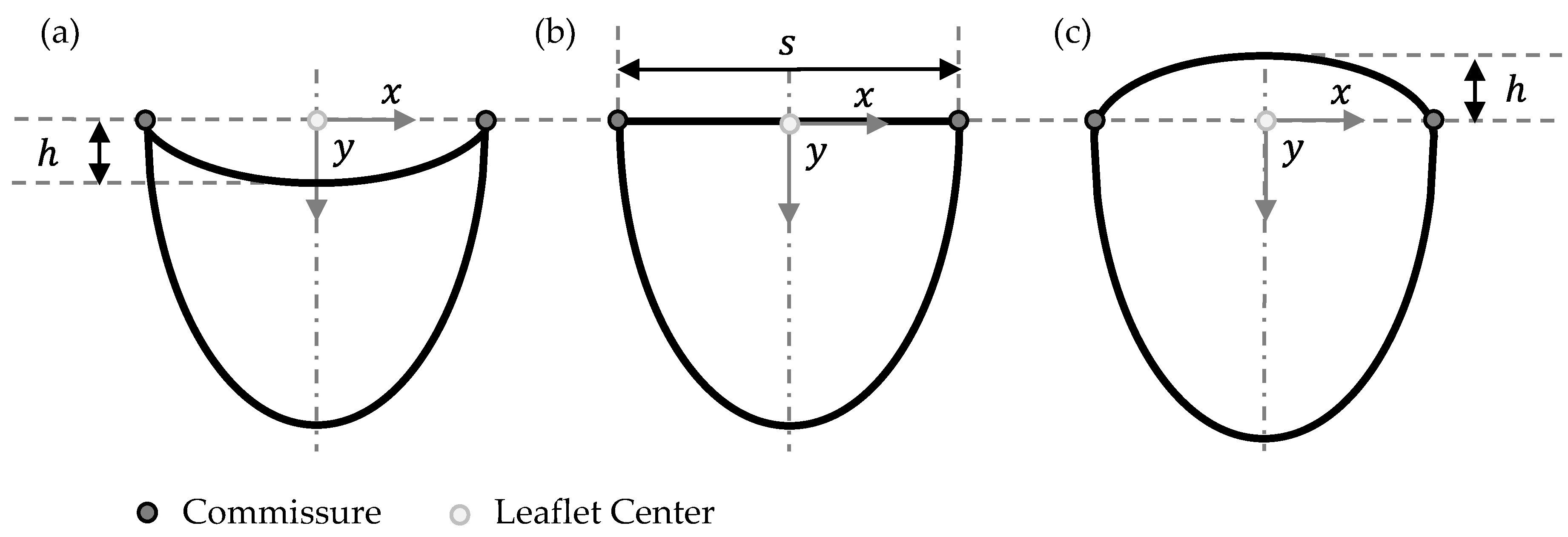
2.1. Parametrical Valve Geometry
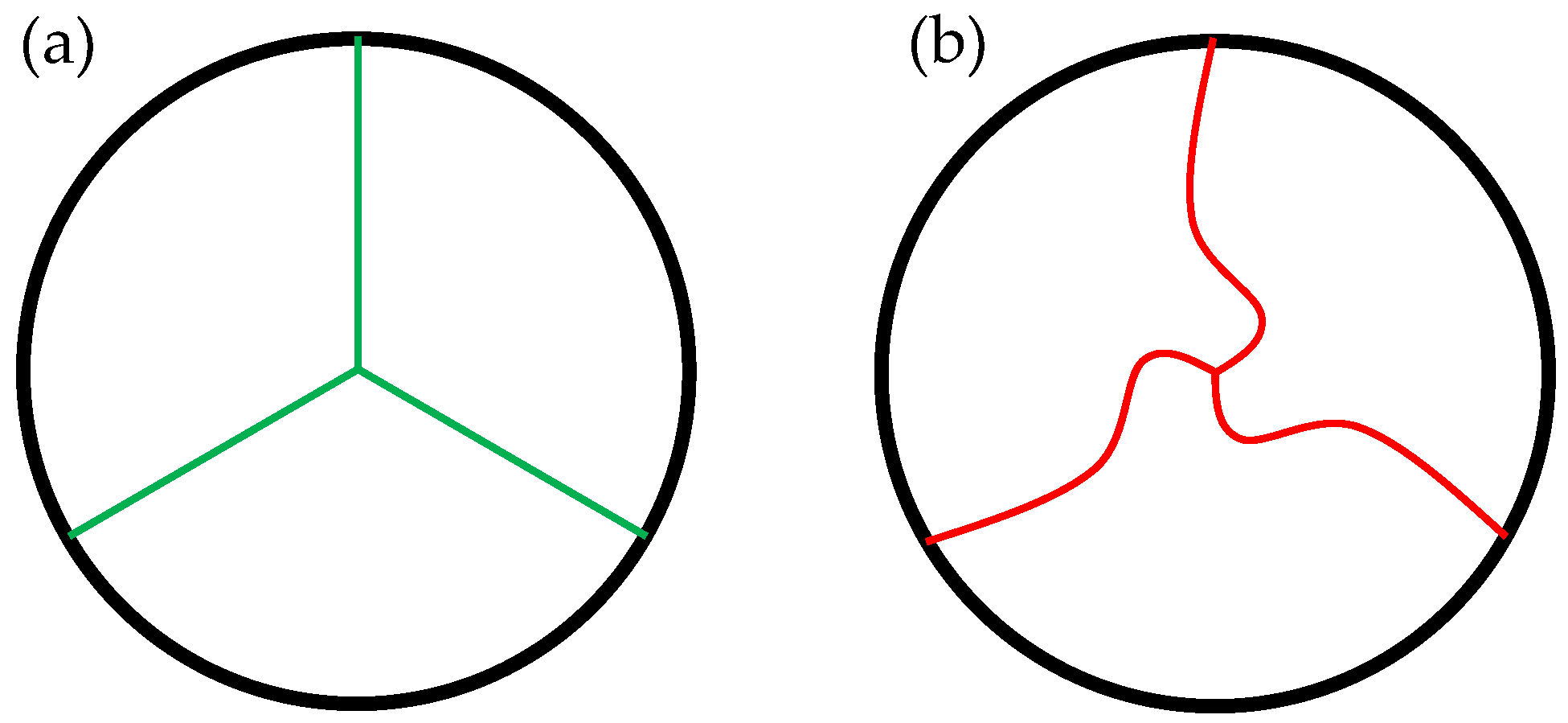
2.1.1. Opening Degree
2.1.2. Free-Edge Shape
2.1.3. Geometry Variations
2.2. TVR Fabrication
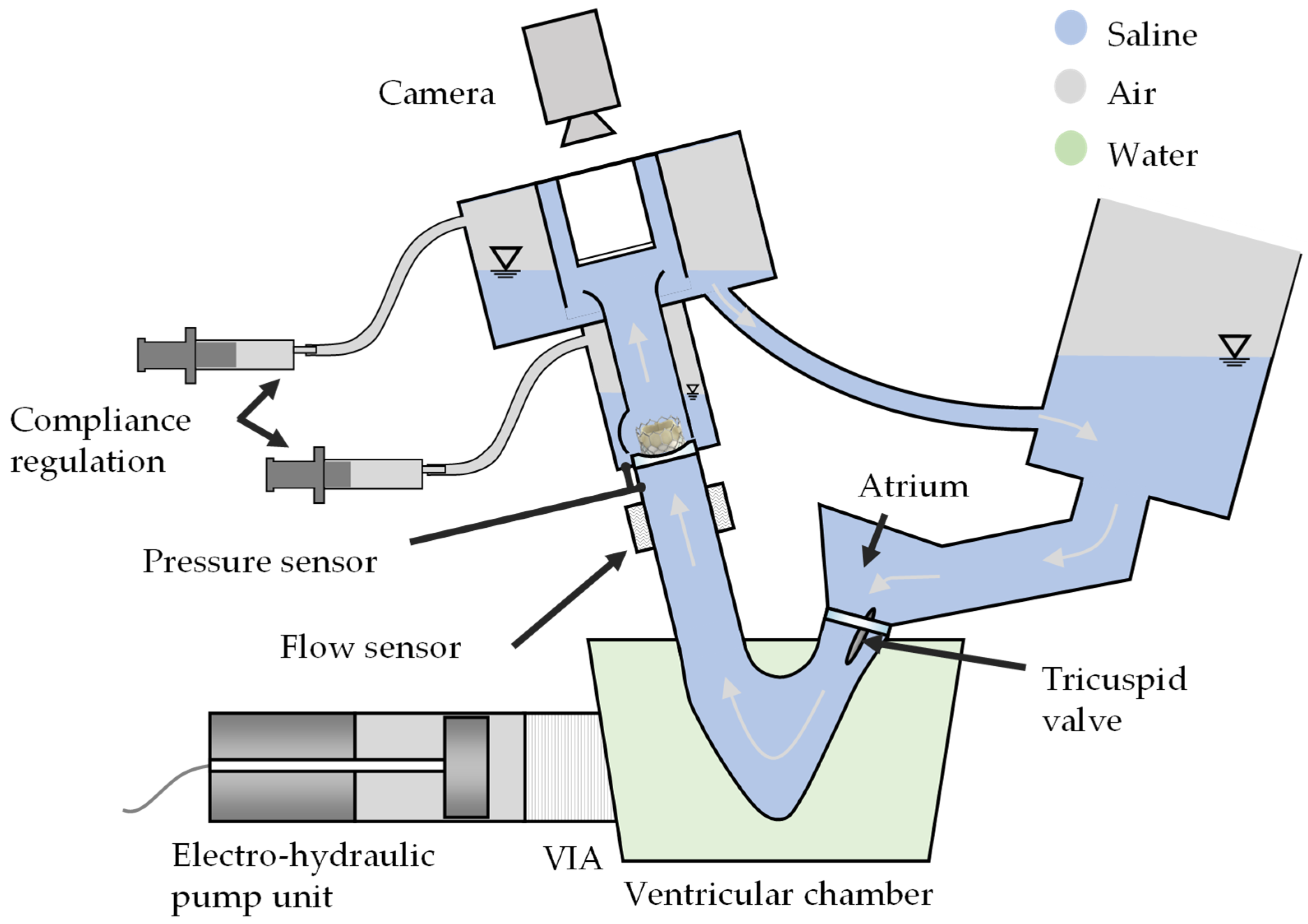
2.3. TVR Testing
2.3.1. Test Conditions
2.3.2. Test Parameters
- Simulated cardiac output
- Cycle rate
- Systolic duration
- Forward flow volume
- Mean and RMS flow rates
- Mean pressure difference
- Effective orifice area
- Regurgitant volume, closing volume and leakage volume
- Mean arterial pressure over the whole cycle
- Appropriate qualitative photographic documentation
2.3.3. In Silico Analysis
3. Results
3.1. Hydrodynamic Testing
In Silico Testing
4. Discussion
5. Limitations
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EOA | Effective Orifice Area |
| ISO | International Organization for Standardization |
| OD | Opening Degree |
| PI | Pinwheeling Index |
| RF | Regurgitation Fraction |
| SVR | Surgical valve replacement |
| TPG | Transvalvular Pressure Gradient |
| TVR | Transcatheter valve replacement |
References
- Davidson, L.J.; Davidson, C.J. Transcatheter Treatment of Valvular Heart Disease. JAMA 2021, 325, 2480–2494. [Google Scholar] [CrossRef]
- Cribier, A.; Eltchaninoff, H. Transcatheter Aortic Valve Implantation: Two Decades of a Revolutionary and Ongoing Odyssey. Circulation 2024, 150, 821–822. [Google Scholar] [CrossRef]
- Makkar, R.R.; Chikwe, J.; Chakravarty, T.; Chen, Q.; O’gAra, P.T.; Gillinov, M.; Mack, M.J.; Vekstein, A.; Patel, D.; Stebbins, A.L.; et al. Transcatheter Mitral Valve Repair for Degenerative Mitral Regurgitation. JAMA 2023, 329, 1778–1788. [Google Scholar] [CrossRef]
- Venus Medtech (Hangzhou) Inc. VenusP-Valve System Instruction for Use; Venus Medtech (Hangzhou) Inc.: Hangzhou, China, 2022. [Google Scholar]
- Medtronic CoreValve LL. CoreValveTM System Transcatheter Aortic Valve Delivery Catheter System Compression Loading System; Medtronic CoreValve LL: Santa Ana, CA, USA, 2014. [Google Scholar]
- Edwards Lifesciences LLC. Edwards SAPIEN 3 Transcatheter Heart Valve Instructions for Use; Edwards Lifesciences LLC: Irvine, CA, USA, 2021. [Google Scholar]
- Alkashkari, W.; AlRahimi, J.; Albugami, S.; Cao, Q.-L.; Hijazi, Z.M. Transcatheter Pulmonary Valve Replacement: The Venus P valve-Current Status. J. Struct. Heart Dis. 2018, 4, 1–8. [Google Scholar] [CrossRef]
- ISO 5840-1:2021; Cardiovascular Implants—Cardiac Valve Prostheses—Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/77033.html (accessed on 15 August 2025).
- Kouhi, E.; Morsi, Y.S. A parametric study on mathematical formulation and geometrical construction of a stentless aortic heart valve. J. Artif. Organs 2013, 16, 425–442. [Google Scholar] [CrossRef] [PubMed]
- Travaglino, S.; Murdock, K.; Tran, A.; Martin, C.; Liang, L.; Wang, Y.; Sun, W. Computational Optimization Study of Transcatheter Aortic Valve Leaflet Design Using Porcine and Bovine Leaflets. J. Biomech. Eng. 2020, 142, 011007. [Google Scholar] [CrossRef]
- Breitenstein-Attach, A.; Steitz, M.; Sun, X.; Hao, Y.; Kiekenap, J.; Emeis, J.; Tuladhar, S.R.; Berger, F.; Schmitt, B. In Vitro Comparison of a Closed and Semi-closed Leaflet Design for Adult and Pediatric Transcatheter Heart Valves. Ann. Biomed. Eng. 2024, 52, 2051–2064. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Morganti, S.; Zakerzadeh, R.; Kamensky, D.; Auricchio, F.; Reali, A.; Hughes, T.J.R.; Sacks, M.S.; Hsu, M. A framework for designing patient-specific bioprosthetic heart valves using immersogeometric fluid-structure interaction analysis. Int. J. Numer. Method Biomed. Eng. 2018, 34, e2938. [Google Scholar] [CrossRef]
- Sadat, N.; Bruhn, D.; Scharfschwerdt, M.; Schaller, T.; Aboud, A.; Saisho, H.; Eitel, I.; Ensminger, S.; Fujita, B. Impact of different valve-in-valve positions on the hydrodynamic performance of the newest-generation self-expanding transcatheter heart valve. Eur. J. Cardio-Thorac. Surg. 2022, 62, ezac158. [Google Scholar] [CrossRef]
- Sadat, N.; Lojenburg, J.H.; Scharfschwerdt, M.; Fujta, B.; Ensminger, S. Impact of different in vitro models on functional performance of the self-expanding transcatheter heart valve. Eur. J. Cardio-Thorac. Surg. 2023, 64, ezad333. [Google Scholar] [CrossRef]
- Ensminger, S.; Thiele, H.; Falk, V.; Rudolph, V. Der Deutsche Herzbericht—Update 2024—Eine Zusammenfassung der wichtigsten Erkenntnisse. Die Kardiol. 2024, 18, 476–484. [Google Scholar] [CrossRef]
- Fan, R.; Bayoumi, A.S.; Chen, P.; Hobson, C.M.; Wagner, W.R.; Mayer, J.E.; Sacks, M.S. Optimal elastomeric scaffold leaflet shape for pulmonary heart valve leaflet replacement. J. Biomech. 2013, 46, 662–669. [Google Scholar] [CrossRef]
- Christie, G.W.; Barratt-Boyes, B.G. Mechanical properties of porcine pulmonary valve leaflets: How do they differ from aortic leaflets? Ann. Thorac. Surg. 1995, 60, S195–S199. [Google Scholar] [CrossRef]
- Gaede, L.; Di Bartolomeo, R.; van der Kley, F.; Elsässer, A.; Iung, B.; Möllmann, H. Aortic valve stenosis: What do people know? A heart valve disease awareness survey of over 8800 people aged 60 or over. EuroIntervention 2016, 12, 883–889. [Google Scholar] [CrossRef] [PubMed]
- Thubrikar, M. The Aortic Valve; Routledge: Abingdon, UK, 2018; 232p. [Google Scholar] [CrossRef]
- Labrosse, M.R.; Beller, C.J.; Robicsek, F.; Thubrikar, M.J. Geometric modeling of functional trileaflet aortic valves: Development and clinical applications. J. Biomech. 2006, 39, 2665–2672. [Google Scholar] [CrossRef] [PubMed]
- Swanson, W.M.; Clark, R.E. Dimensions and Geometric Relationships of the Human Aortic Value as a Function of Pressure. Circ. Res. 1974, 35, 871–882. [Google Scholar] [CrossRef]
- Steitz, M.; Zouhair, S.; Khan, M.B.; Breitenstein-Attach, A.; Fritsch, K.; Tuladhar, S.R.; Wulsten, D.; Wolkers, W.-F.; Sun, X.; Hao, Y.; et al. A Glutaraldehyde-Free Crosslinking Method for the Treatment of Collagen-Based Biomaterials for Clinical Application. Bioengineering 2023, 10, 1247. [Google Scholar] [CrossRef]
- Deutsche Herzstiftung e.V. Deutscher Herzbericht 2021; Deutsche Herzstiftung e.V: Frankfurt am Main, Germany, 2022; Volume 33, p. 180. Available online: https://epaper.herzstiftung.de/#0 (accessed on 15 August 2025).
- Wu, C.; Saikrishnan, N.; Chalekian, A.J.; Fraser, R.; Ieropoli, O.; Retta, S.M.; Joseph, R.; Lee, S.; Marquez, S.; Mester, D.; et al. In-Vitro Pulsatile Flow Testing of Prosthetic Heart Valves: A Round-Robin Study by the ISO Cardiac Valves Working Group. Cardiovasc. Eng. Technol. 2019, 10, 397–422. [Google Scholar] [CrossRef]
- Lee, J.H.; Rygg, A.D.; Kolahdouz, E.M.; Rossi, S.; Retta, S.M.; Duraiswamy, N.; Scotten, L.N.; Craven, B.A.; Griffith, B.E. Fluid–Structure Interaction Models of Bioprosthetic Heart Valve Dynamics in an Experimental Pulse Duplicator. Ann. Biomed. Eng. 2020, 48, 1475–1490. [Google Scholar] [CrossRef]
- Hentschel, G.; Doll-Nikutta, K.; Mueller, M.; Berg, P.; Glasmacher, B. Development and characterization of a Dextran/CaCl2—based blood-mimicking fluid: A comparative study of rheological and mechanical properties in artificial erythrocyte suspensions. Soft Matter 2025, 21, 3101–3116. [Google Scholar] [CrossRef] [PubMed]
- Retta, S.M.; Kepner, J.; Marquez, S.; A Herman, B.; Shu, M.C.S.; Grossman, L.W. In-Vitro Pulsatile Flow Measurement in Prosthetic Heart Valves: An Inter-Laboratory Comparison. J. Heart Valve Dis. 2017, 26, 72–80. Available online: https://europepmc.org/article/med/28544834 (accessed on 15 August 2025).
- Sadek, S.H.; Rubio, M.; Lima, R.; Vega, E.J. Blood Particulate Analogue Fluids: A Review. Materials 2021, 14, 2451. [Google Scholar] [CrossRef]
- Moravia, A.; Simoëns, S.; El Hajem, M.; Bou-Saïd, B.; Kulisa, P.; Della-Schiava, N.; Lermusiaux, P. In vitro flow study in a compliant abdominal aorta phantom with a non-Newtonian blood-mimicking fluid. J. Biomech. 2022, 130, 110899. [Google Scholar] [CrossRef]
- ISO 5840-3:2021; Cardiovascular Implants—Cardiac Valve Prostheses—Part 3: Heart Valve Substitutes Implanted by Transcatheter Techniques. International Organization for Standardization: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/67606.html (accessed on 15 August 2025).
- Hui, S.; Mahmood, F.; Matyal, R. Aortic Valve Area—Technical Communication: Continuity and Gorlin Equations Revisited. J. Cardiothorac. Vasc. Anesth. 2018, 32, 2599–2606. [Google Scholar] [CrossRef]
- Midha, P.A.; Raghav, V.; Condado, J.F.; Okafor, I.U.; Lerakis, S.; Thourani, V.H.; Babaliaros, V.; Yoganathan, A.P. Valve Type, Size, and Deployment Location Affect Hemodynamics in an In Vitro Valve-in-Valve Model. JACC Cardiovasc. Interv. 2016, 9, 1618–1628. [Google Scholar] [CrossRef] [PubMed]
- Luraghi, G.; Wu, W.; De Gaetano, F.; Matas, J.F.R.; Moggridge, G.D.; Serrani, M.; Stasiak, J.; Costantino, M.L.; Migliavacca, F. Evaluation of an aortic valve prosthesis: Fluid-structure interaction or structural simulation? J. Biomech. 2017, 58, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Sadipour, M.; Azadani, A.N. The Measurement of Bovine Pericardium Density and Its Implications on Leaflet Stress Distribution in Bioprosthetic Heart Valves. Cardiovasc. Eng. Technol. 2023, 14, 853–861. [Google Scholar] [CrossRef]
- Labrosse, M.R.; Jafar, R.; Ngu, J.; Boodhwani, M. Planar biaxial testing of heart valve cusp replacement biomaterials: Experiments, theory and material constants. Acta Biomater. 2016, 45, 303–320. [Google Scholar] [CrossRef]
- Dvir, D. Aortic Valve-in-Valve Hemodynamics. Card. Interv. Today 2018, 12, 7–9. [Google Scholar]
- Ma, X.; Gao, B.; Tao, L.; Ding, J.; Li, S.; Qiao, A.; Chang, Y. Hemodynamic study of the effect of the geometric height of leaflets on the performance of the aortic valve under aortic valve reconstruction. J. Thorac. Dis. 2022, 14, 1515–1525. [Google Scholar] [CrossRef] [PubMed]
- Bui, H.T.; Ishrat, A.; James, S.P.; Dasi, L.P. Design consideration of a novel polymeric transcatheter heart valve through computational modeling. J. Mech. Behav. Biomed. Mater. 2022, 135, 105434. [Google Scholar] [CrossRef] [PubMed]
- Hatoum, H.; Lilly, S.; Maureira, P.; Crestanello, J.; Dasi, L.P. The hemodynamics of transcatheter aortic valves in transcatheter aortic valves. J. Thorac. Cardiovasc. Surg. 2021, 161, 565–576.e2. [Google Scholar] [CrossRef]
- Hasan, A.; Ragaert, K.; Swieszkowski, W.; Selimović, Š.; Paul, A.; Camci-Unal, G.; Mofrad, M.R.; Khademhosseini, A. Biomechanical properties of native and tissue engineered heart valve constructs. J. Biomech. 2014, 47, 1949–1963. [Google Scholar] [CrossRef]
- Gomel, M.A.; Lee, R.; Grande-Allen, K.J. Comparing the Role of Mechanical Forces in Vascular and Valvular Calcification Progression. Front. Cardiovasc. Med. 2019, 5, 197. [Google Scholar] [CrossRef]
- Balachandran, K.; Sucosky, P.; Jo, H.; Yoganathan, A.P. Elevated Cyclic Stretch Induces Aortic Valve Calcification in a Bone Morphogenic Protein-Dependent Manner. Am. J. Pathol. 2010, 177, 49–57. [Google Scholar] [CrossRef]
- Flameng, W.; Herregods, M.-C.; Vercalsteren, M.; Herijgers, P.; Bogaerts, K.; Meuris, B. Prosthesis-Patient Mismatch Predicts Structural Valve Degeneration in Bioprosthetic Heart Valves. Circulation 2010, 121, 2123–2129. [Google Scholar] [CrossRef]
- Flameng, W.; Rega, F.; Vercalsteren, M.; Herijgers, P.; Meuris, B. Antimineralization treatment and patient-prosthesis mismatch are major determinants of the onset and incidence of structural valve degeneration in bioprosthetic heart valves. J. Thorac. Cardiovasc. Surg. 2014, 147, 1219–1224. [Google Scholar] [CrossRef] [PubMed]
- Johnston, D.R.; Soltesz, E.G.; Vakil, N.; Rajeswaran, J.; Roselli, E.E.; Sabik, J.F.; Smedira, N.G.; Svensson, L.G.; Lytle, B.W.; Blackstone, E.H. Long-Term Durability of Bioprosthetic Aortic Valves: Implications From 12,569 Implants. Ann. Thorac. Surg. 2015, 99, 1239–1247. [Google Scholar] [CrossRef] [PubMed]
- Otto, C.M.; Nishimura, R.A.; Bonow, R.O.; Carabello, B.A.; Erwin, J.P., III; Gentile, F.; Jneid, H.; Krieger, E.V.; Mack, M.; McLeod, P.T.; et al. 2020 ACC/AHA Guideline for the Management of Patients with Valvular Heart Disease. J. Am. Coll. Cardiol. 2021, 77, e25–e197. [Google Scholar] [CrossRef]
- Svensson, L.G.; Adams, D.H.; Bonow, R.O.; Kouchoukos, N.T.; Miller, D.C.; O’GAra, P.T.; Shahian, D.M.; Schaff, H.V.; Akins, C.W.; Bavaria, J.E.; et al. Aortic Valve and Ascending Aorta Guidelines for Management and Quality Measures. Ann. Thorac. Surg. 2013, 95, S1–S66. [Google Scholar] [CrossRef]
- Qiu, D.; Azadani, A.N. Can the pinwheeling index serve as a surrogate for accelerated leaflet degeneration in transcatheter heart valves? J. Biomech. 2025, 186, 112731. [Google Scholar] [CrossRef]
- Fukui, M.; Cavalcante, J.L.; Bapat, V.N. Deformation in transcatheter heart valves: Clinical implications and considerations. J. Cardiol. 2024, 83, 351–358. [Google Scholar] [CrossRef]
- Stanová, V.; Zenses, A.; Thollon, L.; Kadem, L.; Barragan, P.; Rieu, R.; Pibarot, P. Effects of hemodynamic conditions and valve sizing on leaflet bending stress in self-expanding transcatheter aortic valve: An in vitro study. Artif. Organs 2020, 44, E277–E287. [Google Scholar] [CrossRef] [PubMed]
- Gunning, P.S.; Saikrishnan, N.; Yoganathan, A.P.; McNamara, L.M. Total ellipse of the heart valve: The impact of eccentric stent distortion on the regional dynamic deformation of pericardial tissue leaflets of a transcatheter aortic valve replacement. J. R. Soc. Interface 2015, 12, 20150737. [Google Scholar] [CrossRef]
- Bailey, J.; Curzen, N.; Bressloff, N.W. The impact of imperfect frame deployment and rotational orientation on stress within the prosthetic leaflets during transcatheter aortic valve implantation. J. Biomech. 2017, 53, 22–28. [Google Scholar] [CrossRef]
- Abbasi, M.; Azadani, A.N. Leaflet stress and strain distributions following incomplete transcatheter aortic valve expansion. J. Biomech. 2015, 48, 3663–3671. [Google Scholar] [CrossRef]
- Sun, W.; Li, K.; Sirois, E. Simulated elliptical bioprosthetic valve deformation: Implications for asymmetric transcatheter valve deployment. J. Biomech. 2010, 43, 3085–3090. [Google Scholar] [CrossRef] [PubMed]
- Visser, V.L.; Motta, S.E.; Hoerstrup, S.P.; Baaijens, F.P.T.; Loerakker, S.; Emmert, M.Y. Smooth leaflets with curved belly and attachment edge profiles promote adaptive remodeling in tissue-engineered heart valves: An in silico study. Biomech. Model. Mechanobiol. 2025, 24, 811–828. [Google Scholar] [CrossRef]
- Pibarot, P. Prosthesis-patient mismatch: Definition, clinical impact, and prevention. Heart 2006, 92, 1022–1029. [Google Scholar] [CrossRef]
- Laha, S.; Fourtakas, G.; Das, P.K.; Keshmiri, A. Smoothed particle hydrodynamics based FSI simulation of the native and mechanical heart valves in a patient-specific aortic model. Sci. Rep. 2024, 14, 6762. [Google Scholar] [CrossRef]
- Hirschhorn, M.; Tchantchaleishvili, V.; Stevens, R.; Rossano, J.; Throckmorton, A. Fluid–structure interaction modeling in cardiovascular medicine—A systematic review 2017–2019. Med. Eng. Phys. 2020, 78, 1–13. [Google Scholar] [CrossRef] [PubMed]
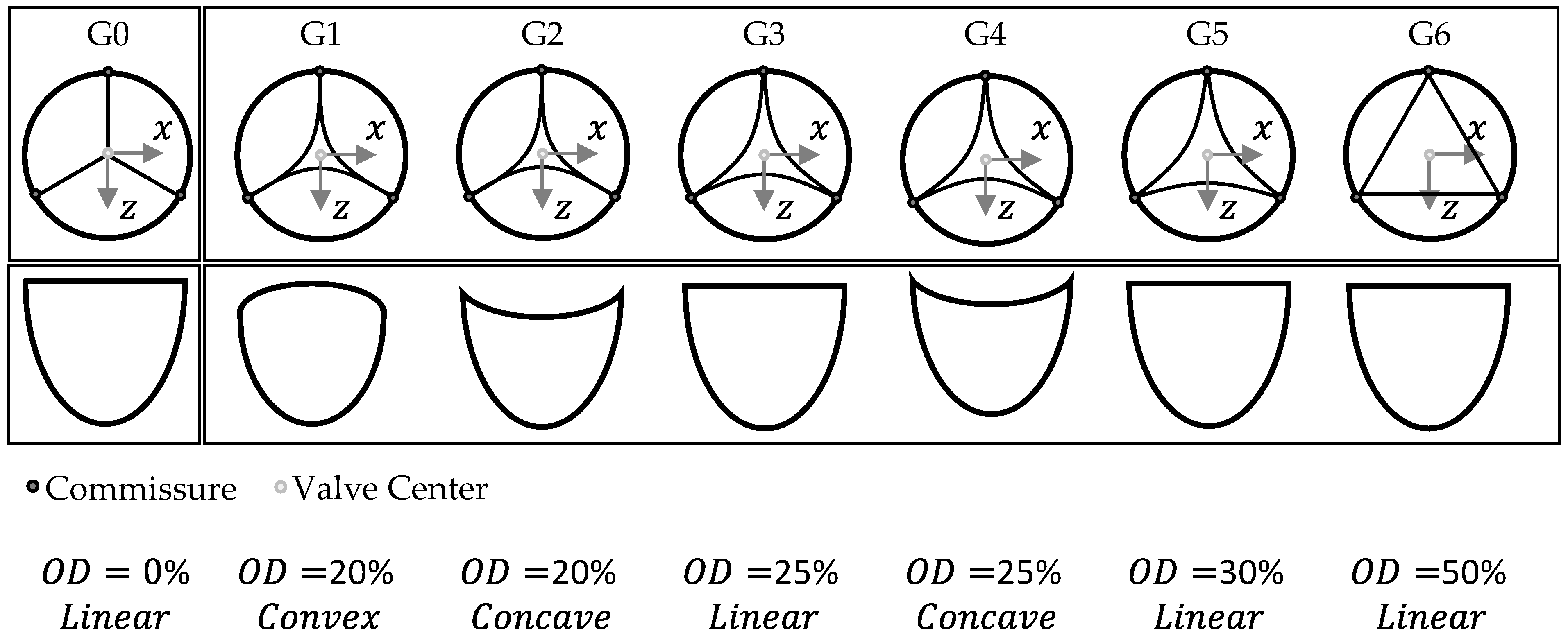




| Geometry Variation | OD [%] | Free Edge Shape [-] |
|---|---|---|
| G0 | 0 | Linear |
| G1 | 20 | Convex |
| G2 | 20 | Concave |
| G3 | 25 | Linear |
| G4 | 25 | Concave |
| G5 | 30 | Linear |
| G6 | 50 | Linear |
| Hydrodynamic Parameter | |||
|---|---|---|---|
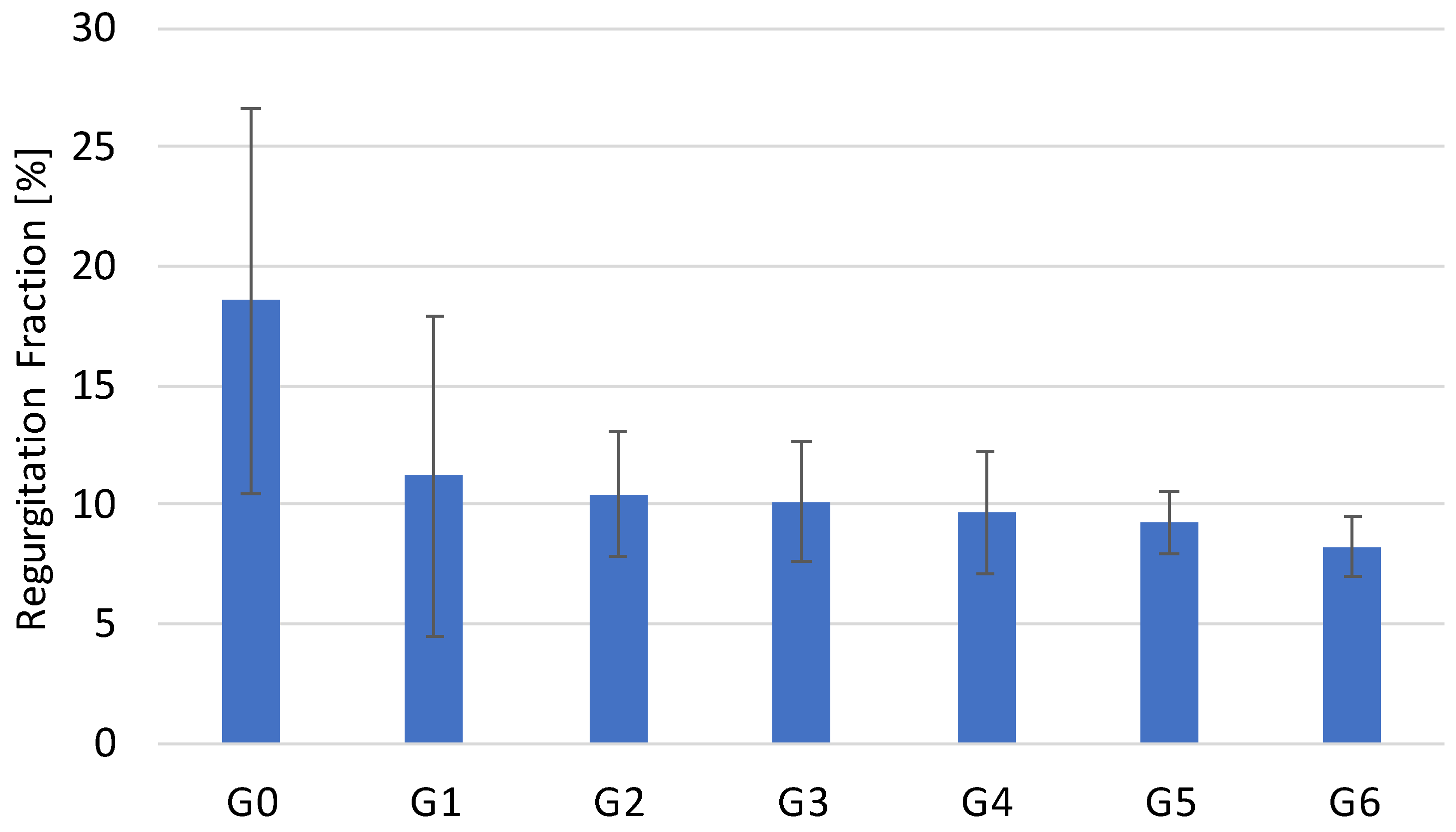
| Geometry Variation | RF [%] | TPG [mmHg] | EOA [cm2] |
| G0 | 18.54 ± 8.05 | 1.49 ± 0.64 | 3.79 ± 0.26 |
| G1 | 11.19 ± 6.75 | 1.89 ± 0.19 | 3.67 ± 0.33 |
| G2 | 10.41 ± 2.62 | 1.64 ± 0.76 | 3.56 ± 0.44 |
| G3 | 10.10 ± 2.51 | 1.25 ± 0.29 | 3.58 ± 0.55 |
| G4 | 9.66 ± 2.55 | 1.98 ± 0.23 | 3.64 ± 0.23 |
| G5 | 9.22 ± 1.28 | 2.00 ± 0.24 | 3.61 ± 0.17 |
| G6 | 8.22 ± 1.27 | 3.06 ± 1.00 | 3.26 ± 0.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Breitenstein-Attach, A.; Steitz, M.; Modolell, J.; Tuladhar, S.R.; Warnack, B.; Kramer, P.; Edelmann, F.; Berger, F.; Schmitt, B. In Silico and In Vitro Comparison of Seven Closed and Semi-Closed Leaflet Designs for Transcatheter Heart Valve Replacements. Bioengineering 2025, 12, 1044. https://doi.org/10.3390/bioengineering12101044
Breitenstein-Attach A, Steitz M, Modolell J, Tuladhar SR, Warnack B, Kramer P, Edelmann F, Berger F, Schmitt B. In Silico and In Vitro Comparison of Seven Closed and Semi-Closed Leaflet Designs for Transcatheter Heart Valve Replacements. Bioengineering. 2025; 12(10):1044. https://doi.org/10.3390/bioengineering12101044
Chicago/Turabian StyleBreitenstein-Attach, Alexander, Marvin Steitz, Jordi Modolell, Sugat Ratna Tuladhar, Boris Warnack, Peter Kramer, Frank Edelmann, Felix Berger, and Boris Schmitt. 2025. "In Silico and In Vitro Comparison of Seven Closed and Semi-Closed Leaflet Designs for Transcatheter Heart Valve Replacements" Bioengineering 12, no. 10: 1044. https://doi.org/10.3390/bioengineering12101044
APA StyleBreitenstein-Attach, A., Steitz, M., Modolell, J., Tuladhar, S. R., Warnack, B., Kramer, P., Edelmann, F., Berger, F., & Schmitt, B. (2025). In Silico and In Vitro Comparison of Seven Closed and Semi-Closed Leaflet Designs for Transcatheter Heart Valve Replacements. Bioengineering, 12(10), 1044. https://doi.org/10.3390/bioengineering12101044









