Hemodynamic Alteration in Aortic Valve Stenosis: CFD Insights from Leaflet-Resolved Models
Abstract
1. Introduction
2. Methods
2.1. Physical Model and Boundary Conditions
2.2. Governing Equations
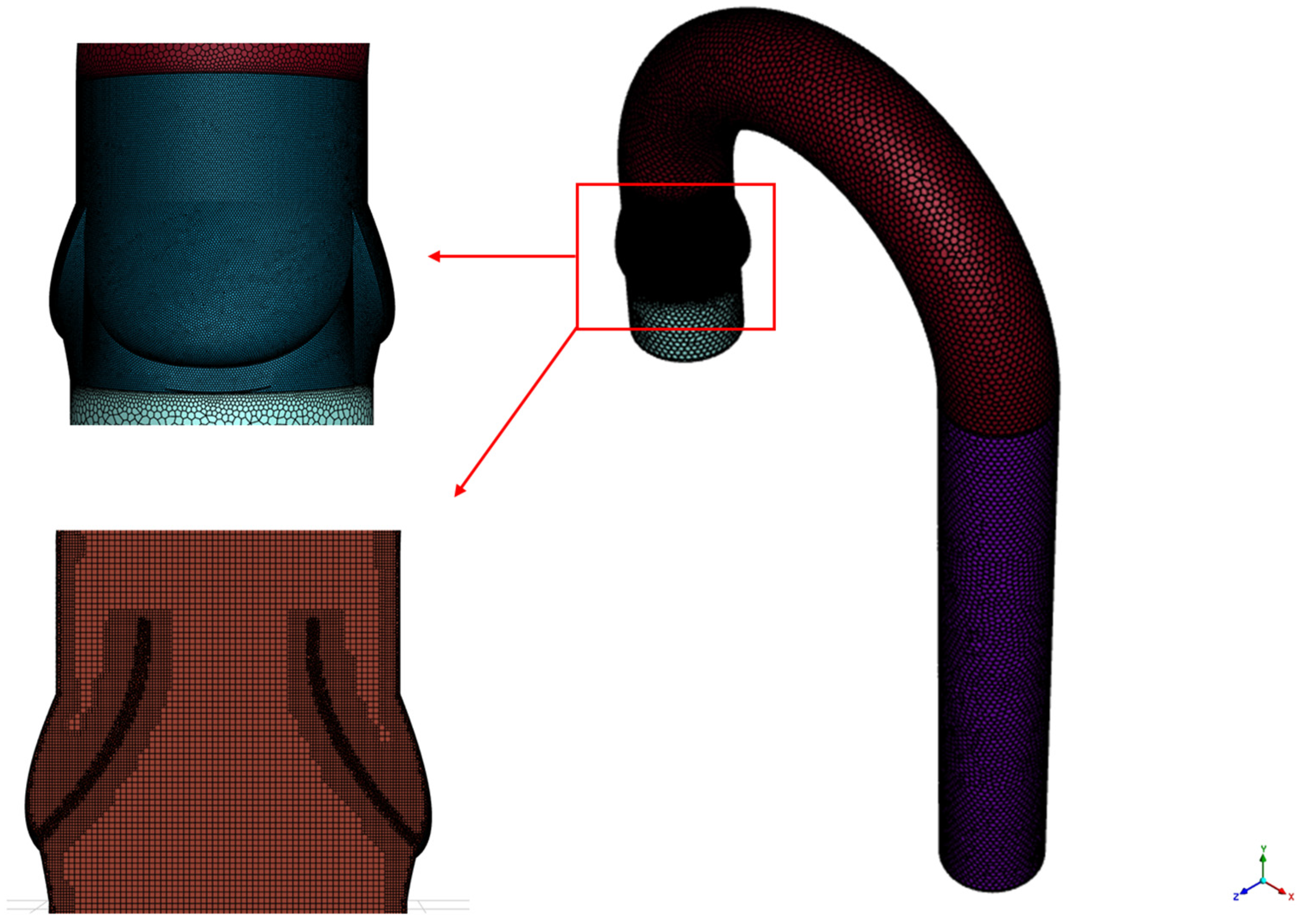
2.3. Mesh Sensitivity Analysis and Numerical Methods
3. Results
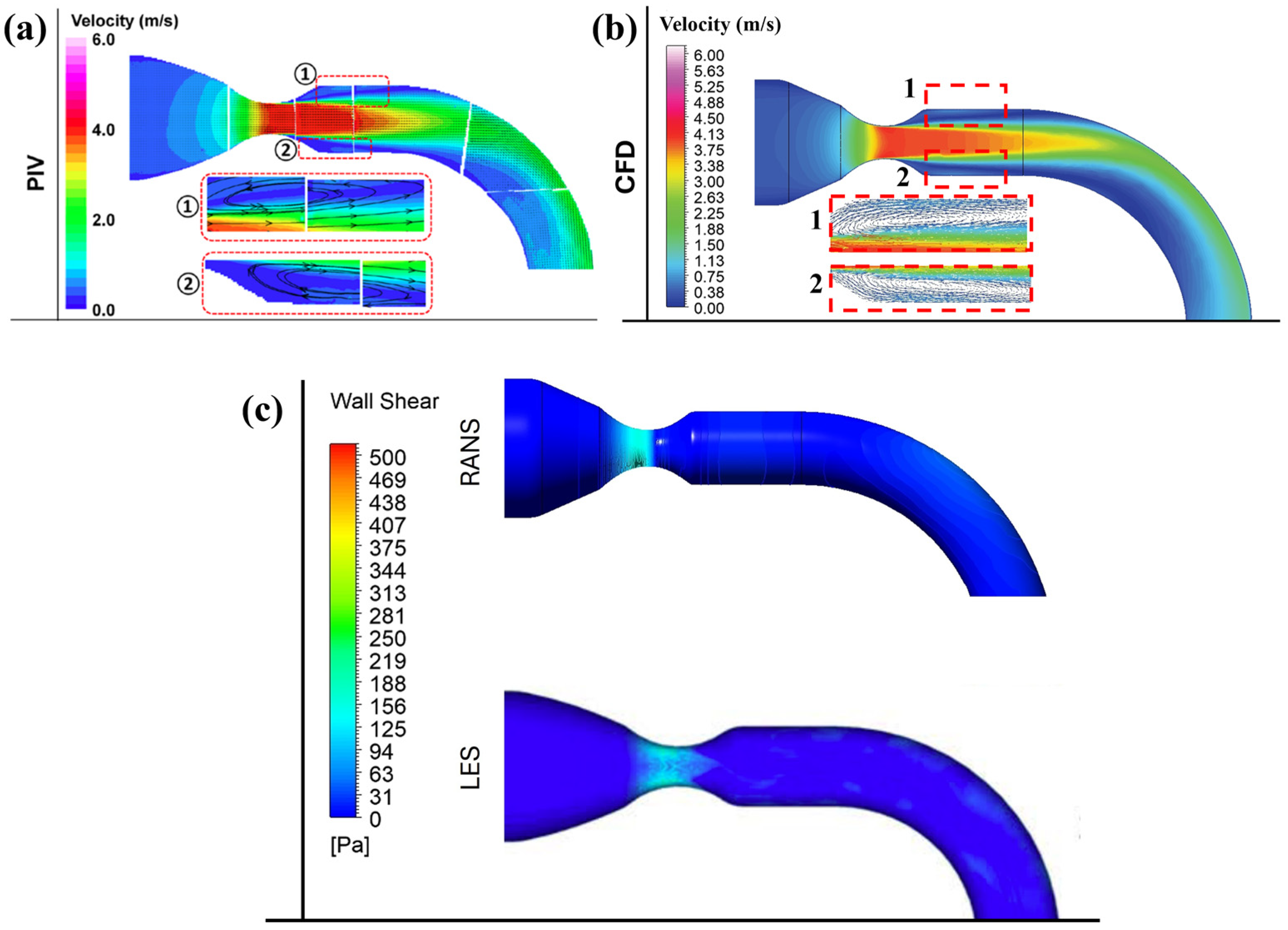
3.1. Validation
3.2. Impact of Aortic Stenosis on Aortic Arch Velocity Profile
3.3. Evolution of Flow Structures Along the Aortic Arch
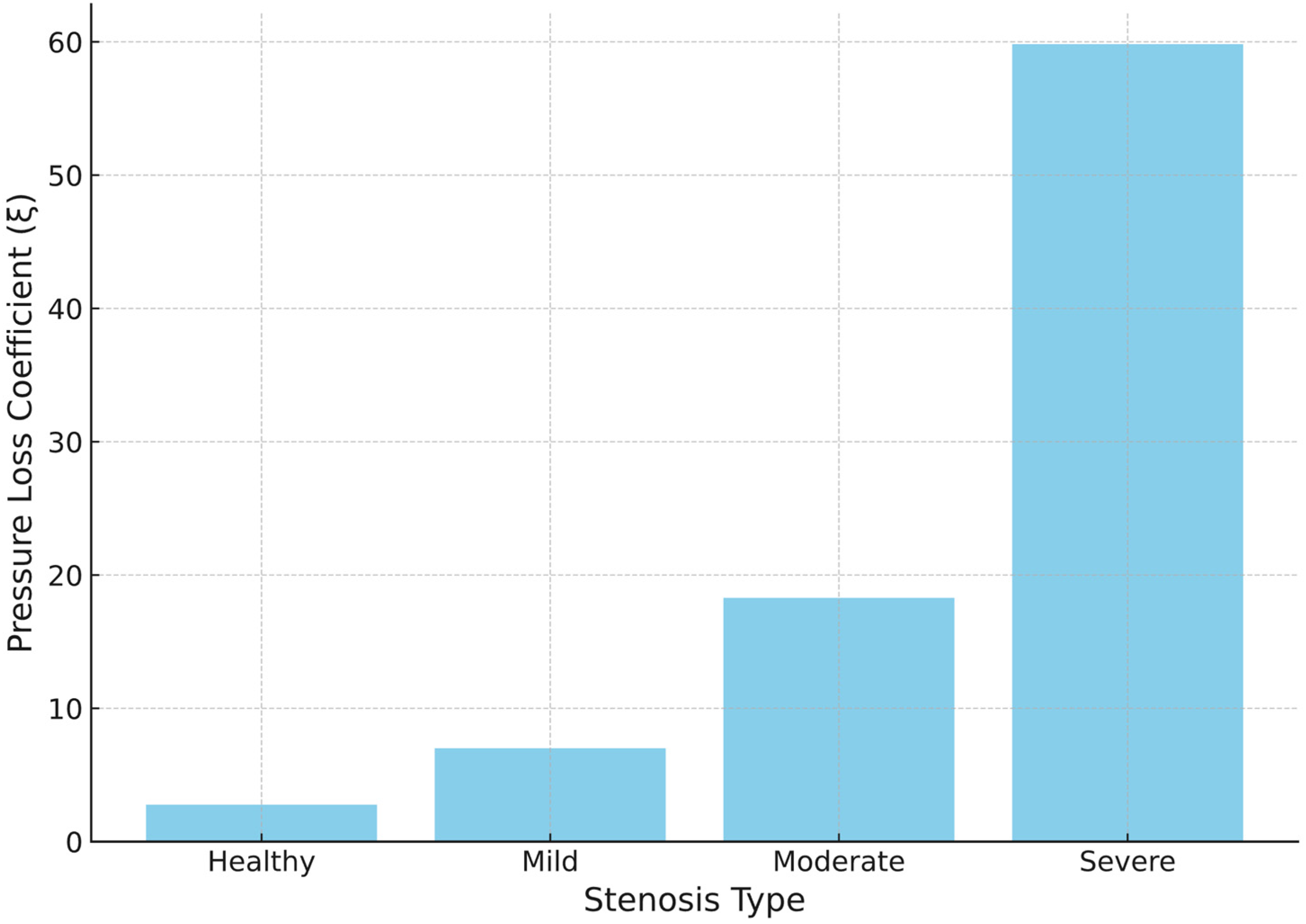
3.4. Variation in Pressure Loss Coefficient
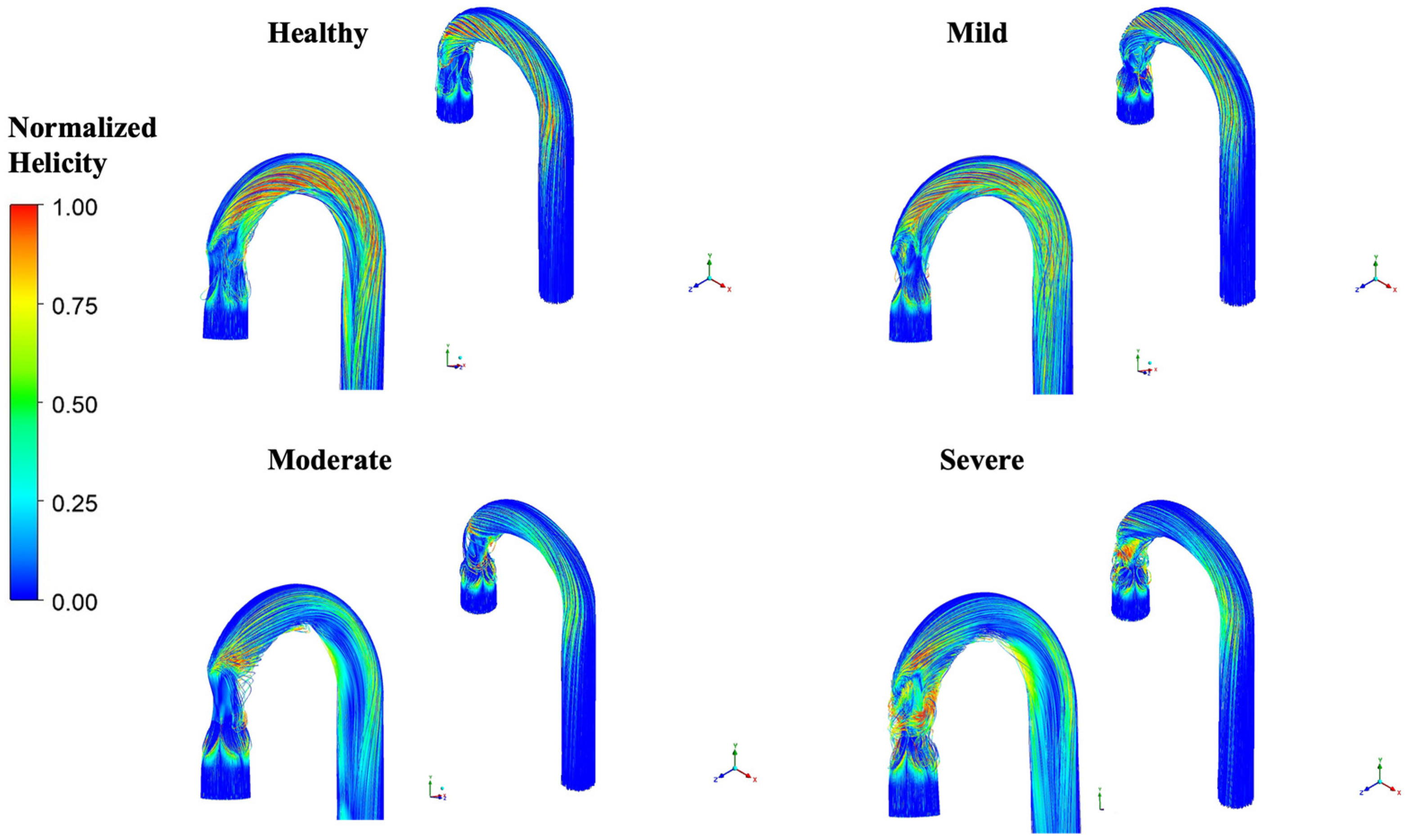
3.5. Changes in Helical Flow with Stenosis
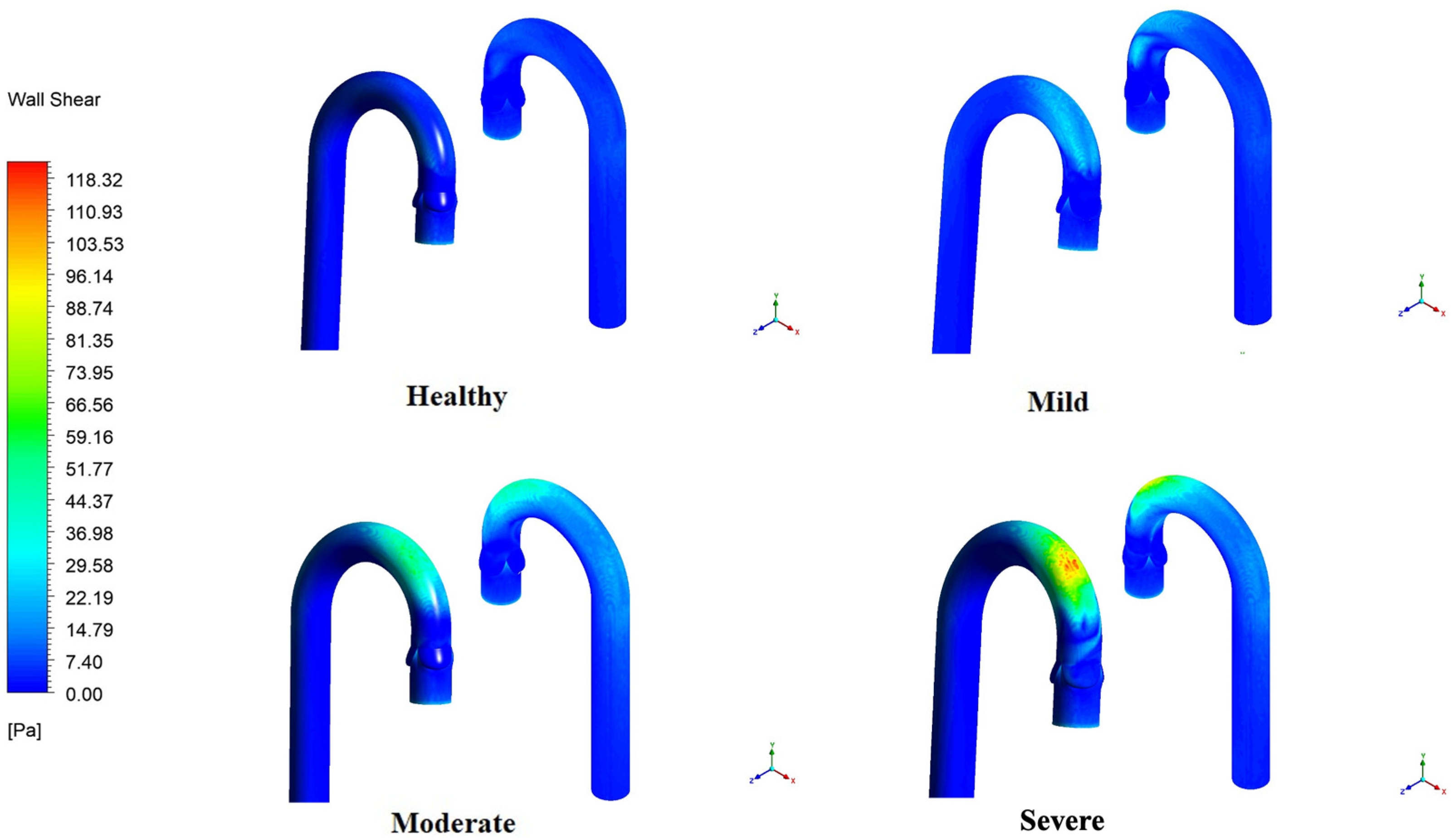
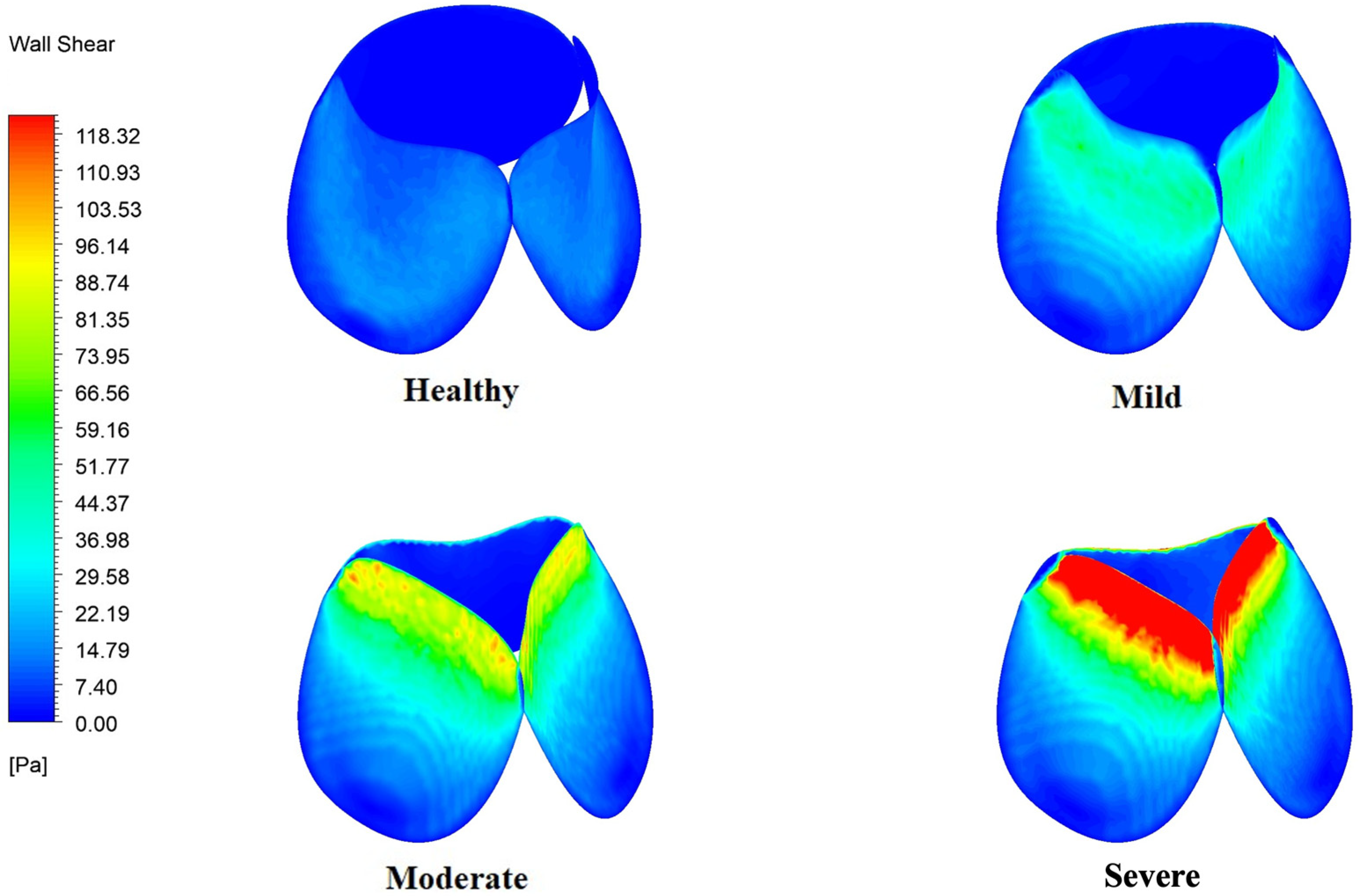
3.6. WSS Variation in the Aortic Arch and Valve Leaflets
4. Discussion
4.1. Velocity Distribution and Maximum Velocity
4.2. Pressure Loss Coefficient
4.3. Helicity
4.4. Wall Shear Stress
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| WSS | Wall shear stress |
| 3D | Three dimensional |
| 4D | Four dimensional |
| MRI | Magnetic resonance imaging |
| PIV | Particle image velocimetry |
| LDV | Laser Doppler velocimetry |
| TKE | Turbulence kinetic energy |
| OSI | Oscillatory shear index |
| RSS | Reynolds shear stress |
| FSI | Fluid–structure interaction |
| 2D | Two dimensional |
References
- Goody, P.R.; Hosen, M.R.; Christmann, D.; Niepmann, S.T.; Zietzer, A.; Adam, M.; Bönner, F.; Zimmer, S.; Nickenig, G.; Jansen, F. Aortic Valve Stenosis: From Basic Mechanisms to Novel Therapeutic Targets. Arterioscler. Thromb. Vasc. Biol. 2020, 40, 885–900. [Google Scholar] [CrossRef]
- Carabello, B.A.; Paulus, W.J.; Blase, P.; Carabello, A. Aortic Stenosis. Lancet 2009, 373, 956–966. [Google Scholar] [CrossRef]
- Yutzey, K.E.; Demer, L.L.; Body, S.C.; Huggins, G.S.; Towler, D.A.; Giachelli, C.M.; Hofmann-Bowman, M.A.; Mortlock, D.P.; Rogers, M.B.; Sadeghi, M.M.; et al. Calcific Aortic Valve Disease: A Consensus Summary from the Alliance of Investigators on Calcific Aortic Valve Disease. Arterioscler. Thromb. Vasc. Biol. 2014, 34, 2387–2393. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, K.D.; Reichenbach, D.D.; Marcovina, S.M.; Kuusisto, J.; Alpers, C.E.; Otto, C.M. Apolipoproteins B, (a), and E Accumulate in the Morphologically Early Lesion of “degenerative” Valvular Aortic Stenosis. Arterioscler. Thromb. Vasc. Biol. 1996, 16, 523–532. [Google Scholar] [CrossRef]
- Rutkovskiy, A.; Malashicheva, A.; Sullivan, G.; Bogdanova, M.; Kostareva, A.; Stensløkken, K.O.; Fiane, A.; Vaage, J. Valve Interstitial Cells: The Key to Understanding the Pathophysiology of Heart Valve Calcification. J. Am. Heart Assoc. 2017, 6, 64–75. [Google Scholar] [CrossRef]
- Torre, M.; Hwang, D.H.; Padera, R.F.; Mitchell, R.N.; Vanderlaan, P.A. Osseous and Chondromatous Metaplasia in Calcific Aortic Valve Stenosis. Cardiovasc. Pathol. 2016, 25, 18–24. [Google Scholar] [CrossRef] [PubMed]
- Sotiropoulos, F.; Le, T.B.; Gilmanov, A. Fluid Mechanics of Heart Valves and Their Replacements. Annu. Rev. Fluid Mech. 2016, 48, 259–283. [Google Scholar] [CrossRef]
- Sacks, M.S.; David Merryman, W.; Schmidt, D.E. On the Biomechanics of Heart Valve Function. J. Biomech. 2009, 42, 1804–1824. [Google Scholar] [CrossRef]
- Sandeep, B.; Liu, X.; Wu, Q.; Gao, K.; Xiao, Z. Recent Updates on Asymptomatic and Symptomatic Aortic Valve Stenosis Its Diagnosis, Pathogenesis, Management and Future Perspectives. Curr. Probl. Cardiol. 2024, 49, 102631. [Google Scholar] [CrossRef]
- Nguyen, V.; Cimadevilla, C.; Estellat, C.; Codogno, I.; Huart, V.; Benessiano, J.; Duval, X.; Pibarot, P.; Clavel, M.A.; Enriquez-Sarano, M.; et al. Haemodynamic and Anatomic Progression of Aortic Stenosis. Heart 2015, 101, 943–947. [Google Scholar] [CrossRef]
- Mittal, T.K.; Marcus, N. Imaging Diagnosis of Aortic Stenosis. Clin. Radiol. 2021, 76, 3–14. [Google Scholar] [CrossRef]
- Manchester, E.L.; Pirola, S.; Salmasi, M.Y.; O’Regan, D.P.; Athanasiou, T.; Xu, X.Y. Analysis of Turbulence Effects in a Patient-Specific Aorta with Aortic Valve Stenosis. Cardiovasc. Eng. Technol. 2021, 12, 438–453. [Google Scholar] [CrossRef] [PubMed]
- Raghav, V.; Sastry, S.; Saikrishnan, N. Experimental Assessment of Flow Fields Associated with Heart Valve Prostheses Using Particle Image Velocimetry (PIV): Recommendations for Best Practices. Cardiovasc. Eng. Technol. 2018, 9, 273–287. [Google Scholar] [CrossRef] [PubMed]
- Yap, C.H.; Saikrishnan, N.; Tamilselvan, G.; Yoganathan, A.P. Experimental Measurement of Dynamic Fluid Shear Stress on the Aortic Surface of the Aortic Valve Leaflet. Biomech. Model Mechanobiol. 2012, 11, 171–182. [Google Scholar] [CrossRef]
- Büsen, M.; Arenz, C.; Neidlin, M.; Liao, S.; Schmitz-Rode, T.; Steinseifer, U.; Sonntag, S.J. Development of an In Vitro PIV Setup for Preliminary Investigation of the Effects of Aortic Compliance on Flow Patterns and Hemodynamics. Cardiovasc. Eng. Technol. 2017, 8, 368–377. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y. An Experimental Study of Pulsatile Flow in a Compliant Aortic Root Model under Varied Cardiac Outputs. Fluids 2018, 3, 71. [Google Scholar] [CrossRef]
- Ding, G.; Choi, K.S.; Ma, B.; Kato, T.; Yuan, W. Transitional Pulsatile Flows with Stenosis in a Two-Dimensional Channel. Phys. Fluids 2021, 33, 034115. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, Y. Experimental Analysis of Pulsatile Flow Characteristics in Prosthetic Aortic Valve Models with Stenosis. Med. Eng. Phys. 2020, 79, 10–18. [Google Scholar] [CrossRef]
- Ong, C.W.; Wee, I.; Syn, N.; Ng, S.; Leo, H.L.; Richards, A.M.; Choong, A.M.T.L. Computational Fluid Dynamics Modeling of Hemodynamic Parameters in the Human Diseased Aorta: A Systematic Review. Ann. Vasc. Surg. 2020, 63, 336–381. [Google Scholar] [CrossRef]
- Shahid, L.; Rice, J.; Berhane, H.; Rigsby, C.; Robinson, J.; Griffin, L.; Markl, M.; Roldán-Alzate, A. Enhanced 4D Flow MRI-Based CFD with Adaptive Mesh Refinement for Flow Dynamics Assessment in Coarctation of the Aorta. Ann. Biomed. Eng. 2022, 50, 1001–1016. [Google Scholar] [CrossRef]
- Youssefi, P.; Gomez, A.; He, T.; Anderson, L.; Bunce, N.; Sharma, R.; Figueroa, C.A.; Jahangiri, M. Patient-Specific Computational Fluid Dynamics—Assessment of Aortic Hemodynamics in a Spectrum of Aortic Valve Pathologies. J. Thorac. Cardiovasc. Surg. 2017, 153, 8–20.e3. [Google Scholar] [CrossRef]
- Qiao, Y.; Luo, K.; Fan, J. Heat Transfer Mechanism in Idealized Healthy and Diseased Aortas Using Fluid-Structure Interaction Method. Biomech. Model Mechanobiol. 2023, 22, 1953–1964. [Google Scholar] [CrossRef]
- Tobin, N.; Good, B.C.; Plasencia, J.D.; Fogel, M.A.; Weiss, W.J.; Manning, K.B. Computational Investigation of Anastomosis Options of a Right-Heart Pump to Patient Specific Pulmonary Arteries. Ann. Biomed. Eng. 2022, 50, 929–940. [Google Scholar] [CrossRef] [PubMed]
- Shahcheranhi, N.; Dwyer, H.A.; Cheer, A.Y.; Barakat, A.I.; Rutaganira, T. Unsteady and Three-Dimensional Simulation of Blood Flow in the Human Aortic Arch. J. Biomech. Eng. 2002, 124, 378–387. [Google Scholar] [CrossRef] [PubMed]
- Marom, G. Numerical Methods for Fluid–Structure Interaction Models of Aortic Valves. Arch. Comput. Methods Eng. 2015, 22, 595–620. [Google Scholar] [CrossRef]
- Amindari, A.; Saltik, L.; Kirkkopru, K.; Yacoub, M.; Yalcin, H.C. Assessment of Calcified Aortic Valve Leaflet Deformations and Blood Flow Dynamics Using Fluid-Structure Interaction Modeling. Inform. Med. Unlocked 2017, 9, 191–199. [Google Scholar] [CrossRef]
- Geronzi, L.; Gasparotti, E.; Capellini, K.; Cella, U.; Groth, C.; Porziani, S.; Chiappa, A.; Celi, S.; Biancolini, M.E. High Fidelity Fluid-Structure Interaction by Radial Basis Functions Mesh Adaption of Moving Walls: A Workflow Applied to an Aortic Valve. J. Comput. Sci. 2021, 51, 101327. [Google Scholar] [CrossRef]
- Capellini, K.; Gasparotti, E.; Cella, U.; Costa, E.; Fanni, B.M.; Groth, C.; Porziani, S.; Biancolini, M.E.; Celi, S. A Novel Formulation for the Study of the Ascending Aortic Fluid Dynamics with in Vivo Data. Med. Eng. Phys. 2021, 91, 68–78. [Google Scholar] [CrossRef]
- Jhun, C.S.; Newswanger, R.; Cysyk, J.P.; Ponnaluri, S.; Good, B.; Manning, K.B.; Rosenberg, G. Dynamics of Blood Flows in Aortic Stenosis: Mild, Moderate, and Severe. ASAIO J. 2021, 67, 666–674. [Google Scholar] [CrossRef]
- Zhu, C.; Seo, J.H.; Mittal, R. Computational Modelling and Analysis of Haemodynamics in a Simple Model of Aortic Stenosis. J. Fluid Mech. 2018, 851, 23–49. [Google Scholar] [CrossRef]
- Yousri, N.; Ibrahim, N.; Roseman, N.A.H.; Taib, I.; Shanta, S. CFD Based on The Visualisation of Aortic Valve Mechanism in Aortic Valve Stenosis for Risk Prediction at The Peak Velocity. J. Adv. Res. Micro Nano Eng. 2024, 17, 56–68. [Google Scholar] [CrossRef]
- Moore, B.L.; Dasi, L.P. Coronary Flow Impacts Aortic Leaflet Mechanics and Aortic Sinus Hemodynamics. Ann. Biomed. Eng. 2015, 43, 2231–2241. [Google Scholar] [CrossRef]
- Cao, K.; Bukač, M.; Sucosky, P. Three-Dimensional Macro-Scale Assessment of Regional and Temporal Wall Shear Stress Characteristics on Aortic Valve Leaflets. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 603–613. [Google Scholar] [CrossRef]
- Cao, K.; Sucosky, P. Aortic Valve Leaflet Wall Shear Stress Characterization Revisited: Impact of Coronary Flow. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 468–470. [Google Scholar] [CrossRef]
- Bonow, R.O.; Carabello, B.A.; Chatterjee, K.; de Leon, A.C.; Faxon, D.P.; Freed, M.D.; Gaasch, W.H.; Lytle, B.W.; Nishimura, R.A.; O’Gara, P.T.; et al. 2008 Focused Update Incorporated into the ACC/AHA 2006 Guidelines for the Management of Patients with Valvular Heart Disease: A Report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines (Writing Committee to Revise the 1998 Guidelines for the Management of Patients With Valvular Heart Disease): Endorsed by the Society of Cardiovascular. Circulation 2008, 118, e523–e661. [Google Scholar] [CrossRef] [PubMed]
- Kannojiya, V.; Das, A.K.; Das, P.K. Simulation of Blood as Fluid: A Review from Rheological Aspects. IEEE Rev. Biomed. Eng. 2021, 14, 327–341. [Google Scholar] [CrossRef] [PubMed]
- Ifraj, N.F.; Akter, F.; Fahad, M.K.; Ahmed, D.H. Thermal-Hydraulic Performance Enhancement with Minimum Entropy Generation of a Heat Exchanger Using Fidget Spinner Vortex Generators. Int. Commun. Heat Mass Transf. 2025, 162, 108610. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, R.; Thomas, N.; Ullah, A.H.; Eichholz, B.; Estevadeordal, J.; Suzen, Y.B. Experimental and Computational Study of Pulsatile Flow Characteristics in Romanesque and Gothic Aortic Arch Models. Med. Eng. Phys. 2022, 102, 103784. [Google Scholar] [CrossRef]
- Zore, K.; Sasanapuri, B.; Parkhi, G.; Varghese, A. Ansys mosaic poly-hexcore mesh for high-lift aircraft configuration. In Proceedings of the 21th Annual CFD Symposium, Bangalore, India, 8–9 August 2019. [Google Scholar]
- Ariff, M.; Salim, S.M.; Cheong, S. Wall y+ Approach for Dealing with Turbulent Flow Over a Surface Mounted Cube: Part 1-Low Reynolds Number. In Proceedings of the Seventh International Conference on CFD in the Minerals and Process Industries CSIRO, Melbourne, Australia, 9–11 December 2009. [Google Scholar]
- Paul, A.K.; Effat, M.; Paquin, J.J.; Banerjee, R.K. Assessment of Aortic Stenosis Severity Using Pressure Drop Coefficient: A Retrospective Study in Humans. In Proceedings of the ASME 2013 Summer Bioengineering Conference (SBC2013), Sunriver, OR, USA, 26–29 June 2013. [Google Scholar] [CrossRef]
- Mansouri, H.; Kemerli, M.; MacIver, R.; Amili, O. Development of Idealized Human Aortic Models for In Vitro and In Silico Hemodynamic Studies. Front. Cardiovasc. Med. 2024, 11, 1358601. [Google Scholar] [CrossRef]
- Kolli, K.K.; Banerjee, R.K.; Peelukhana, S.V.; Helmy, T.A.; Leesar, M.A.; Arif, I.; Schneeberger, E.W.; Hand, D.; Succop, P.; Gottliebson, W.M.; et al. Influence of Heart Rate on Fractional Flow Reserve, Pressure Drop Coefficient, and Lesion Flow Coefficient for Epicardial Coronary Stenosis in a Porcine Model. Am. J. Physiol. Heart Circ. Physiol. 2011, 300, 382–387. [Google Scholar] [CrossRef]
- Kilner, P.J.; Yang, G.Z.; Mohiaddin, R.H.; Firmin, D.N.; Longmore, D.B. Helical and retrograde secondary flow patterns in the aortic arch studied by three-directional magnetic resonance velocity mapping. Circulation 1993, 88, 2235–2247. [Google Scholar] [CrossRef]
- Hope, M.D.; Hope, T.A.; Crook, S.E.S.; Ordovas, K.G.; Urbania, T.H.; Alley, M.T.; Higgins, C.B. 4D Flow CMR in Assessment of Valve-Related Ascending Aortic Disease. JACC Cardiovasc. Imaging 2011, 4, 781–787. [Google Scholar] [CrossRef]
- Hope, M.D.; Meadows, A.K.; Hope, T.A.; Ordovas, K.G.; Saloner, D.; Reddy, G.P.; Alley, M.T.; Higgins, C.B. Clinical evaluation of aortic coarctation with 4D flow MR imaging. J. Magn. Reson. Imaging 2010, 31, 711–718. [Google Scholar] [CrossRef]
- Morbiducci, U.; Ponzini, R.; Grigioni, M.; Redaelli, A. Helical Flow as Fluid Dynamic Signature for Atherogenesis Risk in Aortocoronary Bypass. A Numeric Study. J. Biomech. 2007, 40, 519–534. [Google Scholar] [CrossRef]
- Vincentelli, A.; Susen, S.; Le Tourneau, T.; Six, I.; Fabre, O.; Juthier, F.; Bauters, A.; Decoene, C.; Goudemand, J.; Prat, A.; et al. Acquired von Willebrand Syndrome in Aortic Stenosis. N. Engl. J. Med. 2003, 349, 343–349. [Google Scholar] [CrossRef]
- Jhun, C.S.; Siedlecki, C.; Xu, L.; Lukic, B.; Newswanger, R.; Yeager, E.; Reibson, J.; Cysyk, J.; Weiss, W.; Rosenberg, G. Stress and Exposure Time on von Willebrand Factor Degradation. Artif. Organs 2019, 43, 199–206. [Google Scholar] [CrossRef]
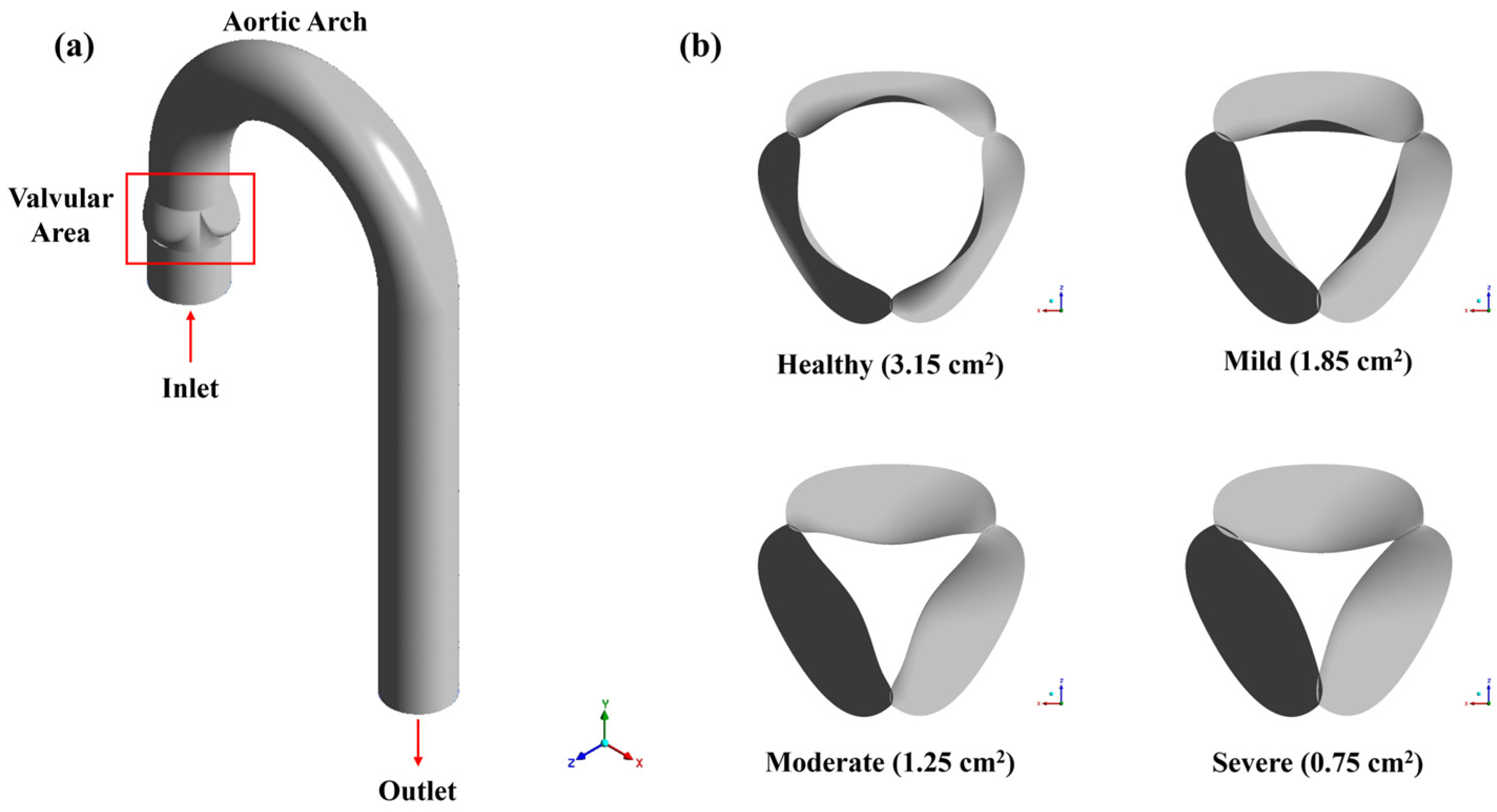



| Parameters | Mild | Moderate | Severe |
|---|---|---|---|
| Jet velocity (m/s) | <3.0 | 3.0–4.0 | >4.0 |
| Mean pressure gradient (mmHg) | <25 | 25–40 | >40 |
| Vascular area (cm2) | >1.5 | 1.0–1.5 | <1.0 |
| Serial No. | Number of Cells (Millions) | WSS (Pa) | % Diff |
|---|---|---|---|
| 1 | 0.7 | 2.55 | 5.73 |
| 2 | 1.2 | 2.411 | 2.15 |
| 3 | 2.5 | 2.361 | 0.59 |
| 4 | 4.4 | 2.347 | - |
| Parameters | Reference (Jhun et al.) [29] | This Study (CFD) | % Diff |
|---|---|---|---|
| Inlet flow rate | 18 LPM | 18 LPM | - |
| Orifice diameter | 10 mm | 10 mm | - |
| Peak centerline jet velocity [m/s] | 4.20 | 4.12 | 1.9 |
| Metrics | Healthy | Mild | Moderate | Severe | %Δ vs. Healthy (Mild/Moderate/Severe) |
|---|---|---|---|---|---|
| Peak velocity in aortic arch [m/s] | 1.08 | 1.82 | 2.73 | 4.70 | +68.5%/+152.8%/+335.2% |
| Pressure-loss coefficient, ξ | 2.78 | 7.02 | 18.33 | 59.96 | +152.5%/+559.6%/+2057.0% |
| Pressure drop ΔP across arch [Pa] | 323 | 815 | 2128 | 6962 | +152.3%/+558.8%/+2055.4% |
| Arch WSS (peak) [Pa] | 11 | 35 | 80 | 122 | +218.2%/+627.3%/+1009.1% |
| Leaflet WSS (peak) [Pa] | 30 | 63 | 122 | 298 | +110.0%/+306.7%/+893.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nuhash, M.M.; Lai, V.K.; Zhang, R. Hemodynamic Alteration in Aortic Valve Stenosis: CFD Insights from Leaflet-Resolved Models. Bioengineering 2025, 12, 1029. https://doi.org/10.3390/bioengineering12101029
Nuhash MM, Lai VK, Zhang R. Hemodynamic Alteration in Aortic Valve Stenosis: CFD Insights from Leaflet-Resolved Models. Bioengineering. 2025; 12(10):1029. https://doi.org/10.3390/bioengineering12101029
Chicago/Turabian StyleNuhash, Mashrur Muntasir, Victor K. Lai, and Ruihang Zhang. 2025. "Hemodynamic Alteration in Aortic Valve Stenosis: CFD Insights from Leaflet-Resolved Models" Bioengineering 12, no. 10: 1029. https://doi.org/10.3390/bioengineering12101029
APA StyleNuhash, M. M., Lai, V. K., & Zhang, R. (2025). Hemodynamic Alteration in Aortic Valve Stenosis: CFD Insights from Leaflet-Resolved Models. Bioengineering, 12(10), 1029. https://doi.org/10.3390/bioengineering12101029








