Machine Learning Approach for Predicting Hypertension Based on Body Composition in South Korean Adults
Abstract
1. Introduction
2. Materials and Methods
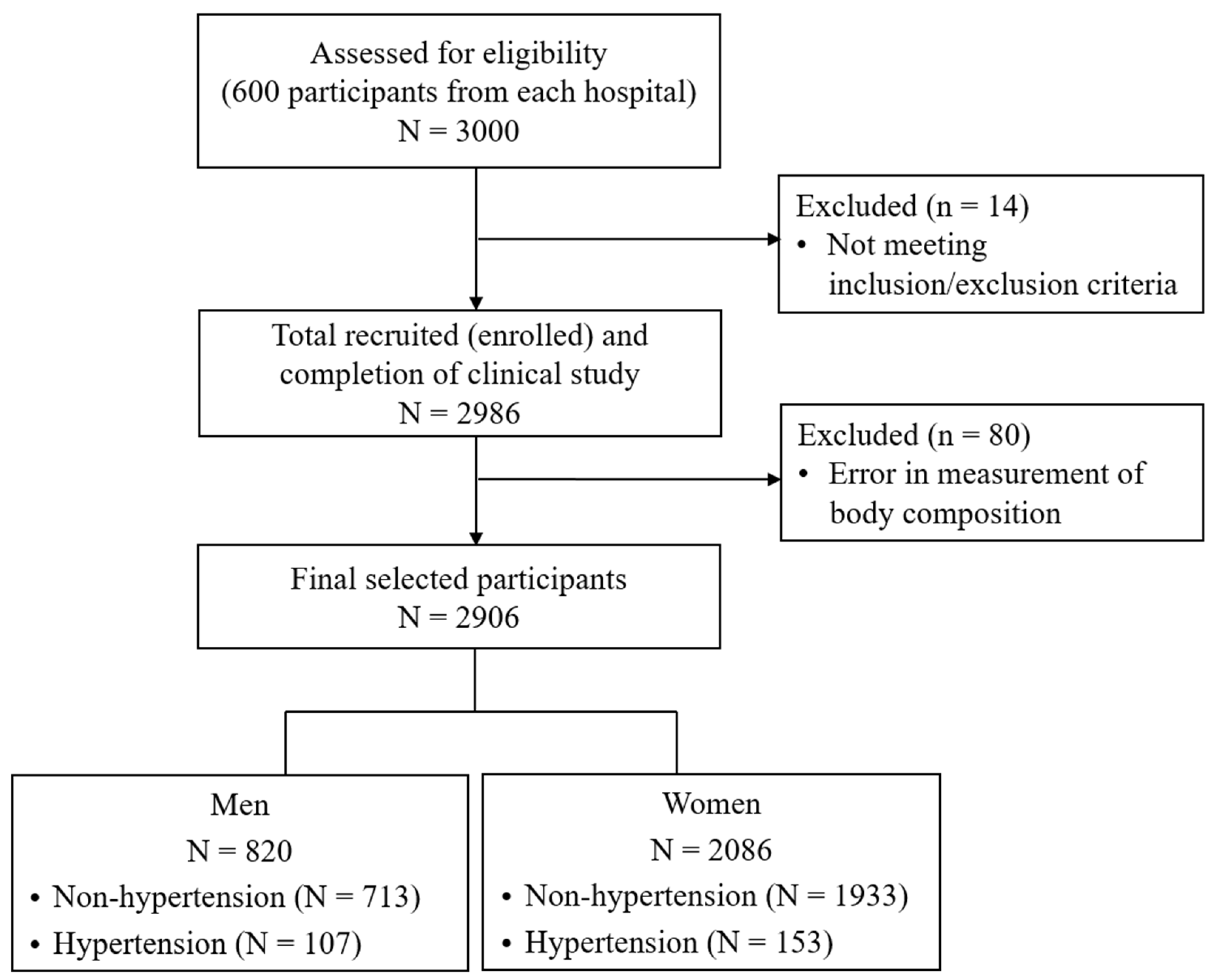
2.1. Data Sources and Participant Selection
2.2. Body Composition Measurement
2.3. Model Development and Assessment
3. Results
3.1. General Characteristics and Body Composition
3.2. Association of Individual Body Composition Variables with Hypertension
3.3. Comparison of Performance of the Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, E.H.; Lee, J.; Lee, S.A.; Jung, Y.W. Impact of Maternal Age on Singleton Pregnancy Outcomes in Primiparous Women in South Korea. J. Clin. Med. 2022, 11, 969. [Google Scholar] [CrossRef] [PubMed]
- Genaro, L.E.; Marconato, J.V.; Tagliaferro, E.P.d.S.; Pinotti, F.E.; Valsecki Júnior, A.; Adas Saliba, T.; Rosell, F.L. Home Care for the Elderly: An Integrated Approach to Perception, Quality of Life, and Cognition. Int. J. Environ. Res. Public Health 2024, 21, 539. [Google Scholar] [CrossRef]
- Heymsfield, S.B.; Ebbeling, C.B.; Zheng, J.; Pietrobelli, A.; Strauss, B.J.; Silva, A.M.; Ludwig, D.S. Multi-Component Molecular-Level Body Composition Reference Methods: Evolving Concepts and Future Directions. Obes. Rev. 2015, 15, 282–294. [Google Scholar] [CrossRef] [PubMed]
- Kyle, U.G.; Bosaeus, I.; De Lorenzo, A.D.; Deurenberg, P.; Elia, M.; Gómez, J.M.; Heitmann, B.L.; Kent-Smith, L.; Melchior, J.C.; Pirlich, M.; et al. Bioelectrical impedance analysis--part I: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef] [PubMed]
- Borga, M.; West, J.; Bell, J.D.; Harvey, N.C.; Romu, T.; Heymsfield, S.B.; Leinhard, O.D. Advanced body composition assessment: From body mass index to body composition profiling. J. Investig. Med. 2018, 66, 5. [Google Scholar] [CrossRef]
- Pi-Sunyer, X. Changes in body composition and metabolic disease risk. Eur. J. Clin. Nutr. 2019, 73, 231–235. [Google Scholar] [CrossRef]
- Li, Z.; Tong, X.; Ma, Y.; Bao, T.; Yue, J. Relationship between Low Skeletal Muscle Mass and Arteriosclerosis in Western China: A Cross-Sectional Study. Front. Cardiovasc. Med. 2021, 8, 735262. [Google Scholar] [CrossRef]
- Cleymaet, R.; D’Hondt, M.; Scheinok, T.; Malbrain, L.; De Laet, I.; Schoonheydt, K.; Dits, H.; Van Regenmortel, N.; Mekeirele, M.; Cordemans, C.; et al. Comparison of Bioelectrical Impedance Analysis (BIA)-Derived Parameters in Healthy Volunteers and Critically Ill Patients. Life 2024, 14, 27. [Google Scholar] [CrossRef]
- Ceniccola, G.D.; Castro, M.G.; Piovacari, S.M.F.; Horie, L.M.; Corrêa, F.G.; Barrere, A.P.N.; Toledo, D.O. Current technologies in body composition assessment: Advantages and disadvantages. Nutrition 2019, 62, 25–31. [Google Scholar] [CrossRef]
- Ye, S.; Zhu, C.; Wei, C.; Yang, M.; Zheng, W.; Gan, D.; Zhu, S. Associations of Body Composition with Blood Pressure and Hypertension. Obesity 2018, 26, 1644–1650. [Google Scholar] [CrossRef]
- Kim, S.T.; Song, Y.-H. Nutrition, Body Composition, and Blood Pressure in Children and Adolescents from the Korea National Health and Nutrition Examination Survey. Int. J. Environ. Res. Public Health 2022, 19, 13272. [Google Scholar] [CrossRef] [PubMed]
- Nematollahi, M.A.; Jahangiri, S.; Asadollahi, A.; Salimi, M.; Dehghan, A.; Mashayekh, M.; Roshanzamir, M.; Gholamabbas, G.; Alizadehsani, R.; Bazrafshan, M.; et al. Body composition predicts hypertension using machine learning methods: A cohort study. Sci. Rep. 2023, 13, 6885. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. 2022. Available online: https://www.R-project.org/ (accessed on 1 April 2024).
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Team, C. Package ‘caret’. R J. 2020, 223, 7. [Google Scholar]
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Benesty, M.; Lescarbeau, R.; Ziem, A.; et al. (The R Core Team) Caret: Classification and Regression Training; R Package Version 6.0-80. Available online: https://cran.r-project.org/web/packages/caret/caret.pdf (accessed on 11 September 2024).
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inform. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Yao, X. Evolving artificial neural networks. Proc. IEEE 1999, 87, 1423–1447. [Google Scholar]
- Stehman, S.V. Selecting and interpreting measures of thematic classification accuracy. Remote Sens. Environ. 1997, 62, 77–89. [Google Scholar] [CrossRef]
- Provost, F.; Kohavi, R. Guest editors’ introduction: On applied research in machine learning. Mach. Learn. 1998, 30, 127–132. [Google Scholar] [CrossRef]
- Huang, J.; Ling, C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005, 17, 299–310. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Hanley, J.A.; McNeil, B.J. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 1983, 148, 839–843. [Google Scholar] [CrossRef]
- Elshawi, R.; Al-Mallah, M.H.; Sakr, S. On the interpretability of machine learning-based model for predicting hypertension. BMC Med. Inform. Decis. Mak. 2019, 19, 146. [Google Scholar] [CrossRef]
- Oh, Y.S. Arterial stiffness and hypertension. Clin. Hypertens. 2018, 24, 17. [Google Scholar] [CrossRef]
- Mahmood, S.S.; Levy, D.; Vasan, R.S.; Wang, T.J. The Framingham Heart Study and the epidemiology of cardiovascular disease: A historical perspective. Lancet 2014, 383, 999–1008. [Google Scholar] [CrossRef]
- Cheng, W.; Du, Y.; Zhang, Q.; Wang, X.; He, C.; He, J.; Jing, F.; Ren, H.; Guo, M.; Tian, J.; et al. Age-related changes in the risk of high blood pressure. Front. Cardiovasc. Med. 2022, 9, 939103. [Google Scholar] [CrossRef]
- Han, T.S.; Al-Gindan, Y.Y.; Govan, L.; Hankey, C.R.; Lean, M.E.J. Associations of body fat and skeletal muscle with hypertension. J. Clin. Hypertens. 2019, 21, 230–238. [Google Scholar] [CrossRef]
- Al-Sendi, A.M.; Shetty, P.; Musaiger, A.O.; Myatt, M. Relationship between body composition and blood pressure in Bahraini adolescents. Br. J. Nutr. 2003, 90, 837–844. [Google Scholar] [CrossRef]
- Gana, R. Ridge Regression and the Elastic Net: How Do They Do as Finders of True Regressors and Their Coefficients? Mathematics 2022, 10, 3057. [Google Scholar] [CrossRef]
- De Mol, C.; De Vito, E.; Rosasco, L. Elastic-net regularization in learning theory. J. Complex. 2009, 25, 201–230. [Google Scholar] [CrossRef]
- George, C.; Goedecke, J.H.; Crowther, N.J.; Jaff, N.G.; Kengne, A.P.; Norris, S.A.; Micklesfield, L.K. The Role of Body Fat and Fat Distribution in Hypertension Risk in Urban Black South African Women. PLoS ONE 2016, 11, e0154894. [Google Scholar] [CrossRef] [PubMed]


| Variables | Description |
|---|---|
| Body fat mass | |
| BFM | Body fat mass |
| PBF | Percentage of body fat mass to weight |
| FMI | Fat mass index |
| BFMp_WB † | Body fat mass (%) of whole body |
| BFM_RA | Body fat mass of right arm |
| BFMp_RA † | Body fat mass (%) of right arm |
| BFM_LA | Body fat mass of left arm |
| BFMp_LA † | Body fat mass (%) of left arm |
| BFM_TR | Body fat mass of trunk |
| BFMp_TR † | Body fat mass (%) of trunk |
| BFM_RL | Body fat mass of right leg |
| BFMp_RL † | Body fat mass (%) of right leg |
| BFM_LL | Body fat mass of left leg |
| BFMp_LL † | Body fat mass (%) of left leg |
| Lean mass | |
| SLM | Soft lean mass |
| SMM | Skeletal muscle mass |
| SMM_WT | Percentage of skeletal muscle mass to weight |
| Body water | |
| TBW | Total body water |
| ICW | Intracellular water |
| ECW | Extracellular water |
| TBW_WT | Percentage of total body water to weight |
| ECW_TBW | Proportion of extracellular water to total body water |
| ECW_TBW_RA | Proportion of extracellular water to total body water of right arm |
| ECW_TBW_LA | Proportion of extracellular water to total body water of left arm |
| ECW_TBW_TR | Proportion of extracellular water to total body water of trunk |
| ECW_TBW_RL | Proportion of extracellular water to total body water of right leg |
| ECW_TBW_LL | Proportion of extracellular water to total body water of left leg |
| Additional data | |
| VFL | Visceral fat level |
| VFA | Visceral fat area |
| Obesity_D | Proportion of weight to ideal weight |
| TBW_FFM | Proportion of total body water to fat-free mass |
| PAngle50_TR | 50 kHz phase angle of trunk |
| Variables | Men | Women | ||||
|---|---|---|---|---|---|---|
| Training Set | Test Set | p | Training Set | Test Set | p | |
| Participants (n) | 575 | 245 | 1462 | 624 | ||
| Hypertension | 1 | 0.961 | ||||
| Yes | 75 (13.04) | 32 (13.06) | 108 (7.39) | 45 (7.21) | ||
| No | 500 (86.96) | 213 (86.94) | 1354 (92.61) | 579 (92.79) | ||
| Age (years) | 44.27 ± 14.39 | 43.65 ± 14.57 | 0.574 | 46.62 ± 12.25 | 46.7 ± 12.45 | 0.887 |
| Temperature (°C) | 36.51 ± 0.33 | 36.51 ± 0.32 | 0.998 | 36.70 ± 0.32 | 36.71 ± 0.33 | 0.726 |
| SBP (mmHg) | 119.59 ± 14.07 | 120.09 ± 14.29 | 0.649 | 108.39 ± 17.15 | 109.24 ± 17.54 | 0.307 |
| DBP (mmHg) | 70.03 ± 10.14 | 70.17 ± 10.35 | 0.864 | 63.22 ± 10.73 | 64.02 ± 10.97 | 0.123 |
| Pulse rate (bmp) | 68.93 ± 10.04 | 67.77 ± 9.77 | 0.123 | 71.54 ± 10.31 | 70.89 ± 9.87 | 0.175 |
| Height (cm) | 172.20 ± 6.33 | 172.19 ± 6.16 | 0.983 | 159.40 ± 5.64 | 159.60 ± 5.62 | 0.450 |
| Weight (kg) | 74.47 ± 11.43 | 74.67 ± 10.61 | 0.804 | 58.74 ± 9.30 | 59.16 ± 9.35 | 0.340 |
| BMI (kg/m2) | 25.07 ± 3.22 | 25.16 ± 3.14 | 0.681 | 23.12 ± 3.51 | 23.24 ± 3.52 | 0.509 |
| Body fat mass | ||||||
| BFM | 17.75 ± 6.43 | 18.02 ± 6.17 | 0.569 | 19.42 ± 6.51 | 19.56 ± 6.29 | 0.643 |
| PBF | 23.39 ± 5.87 | 23.73 ± 5.86 | 0.452 | 32.41 ± 6.31 | 32.45 ± 6.11 | 0.908 |
| FMI | 5.99 ± 2.14 | 6.09 ± 2.11 | 0.533 | 7.67 ± 2.61 | 7.71 ± 2.51 | 0.753 |
| BFMp_WB | 181.46 ± 64.69 | 184.44 ± 64.11 | 0.543 | 190.05 ± 82.71 | 191.23 ± 79.73 | 0.760 |
| BFM_RA | 1.05 ± 0.59 | 1.07 ± 0.56 | 0.677 | 1.37 ± 0.64 | 1.38 ± 0.59 | 0.715 |
| BFMp_RA | 178.93 ± 98.29 | 182.73 ± 96.08 | 0.607 | 153.51 ± 71.42 | 154.20 ± 66.08 | 0.830 |
| BFM_LA | 1.08 ± 0.59 | 1.10 ± 0.56 | 0.648 | 1.40 ± 0.64 | 1.40 ± 0.59 | 0.776 |
| BFMp_LA | 183.72 ± 98.44 | 187.49 ± 96.42 | 0.611 | 156.33 ± 71.81 | 156.68 ± 66.15 | 0.915 |
| BFM_TR | 9.11 ± 3.52 | 9.29 ± 3.43 | 0.495 | 9.42 ± 3.35 | 9.50 ± 3.29 | 0.601 |
| BFMp_TR | 220.63 ± 83.51 | 225.34 ± 83.85 | 0.461 | 188.17 ± 67.78 | 189.44 ± 66.41 | 0.691 |
| BFM_RL | 2.69 ± 0.86 | 2.72 ± 0.8 | 0.697 | 3.10 ± 0.93 | 3.12 ± 0.89 | 0.669 |
| BFMp_RL | 160.18 ± 50.85 | 161.64 ± 48.9 | 0.699 | 136.41 ± 41.79 | 136.89 ± 39.76 | 0.803 |
| BFM_LL | 2.67 ± 0.84 | 2.69 ± 0.8 | 0.729 | 3.09 ± 0.92 | 3.11 ± 0.88 | 0.717 |
| BFMp_LL | 158.72 ± 50.12 | 160.3 ± 48.77 | 0.675 | 135.88 ± 41.39 | 136.33 ± 39.40 | 0.814 |
| Lean mass | ||||||
| SLM | 53.59 ± 6.93 | 53.53 ± 6.54 | 0.905 | 37.02 ± 4.16 | 37.28 ± 4.29 | 0.196 |
| SMM | 31.80 ± 4.47 | 31.74 ± 4.22 | 0.858 | 21.10 ± 2.64 | 21.27 ± 2.73 | 0.194 |
| SMM_WT | 42.90 ± 3.51 | 42.70 ± 3.51 | 0.438 | 36.24 ± 3.46 | 36.24 ± 3.33 | 0.998 |
| Body water | ||||||
| TBW | 41.71 ± 5.36 | 41.66 ± 5.07 | 0.915 | 28.89 ± 3.24 | 29.1 ± 3.33 | 0.188 |
| ICW | 25.92 ± 3.43 | 25.87 ± 3.24 | 0.863 | 17.71 ± 2.03 | 17.84 ± 2.09 | 0.197 |
| ECW | 15.79 ± 1.96 | 15.79 ± 1.87 | 0.992 | 11.18 ± 1.23 | 11.26 ± 1.26 | 0.180 |
| TBW_WT | 56.35 ± 4.32 | 56.10 ± 4.30 | 0.447 | 49.68 ± 4.63 | 49.64 ± 4.49 | 0.880 |
| ECW_TBW † | 378.91 ± 7.56 | 379.29 ± 8.03 | 0.526 | 386.98 ± 6.02 | 386.95 ± 6.27 | 0.918 |
| ECW_TBW_RA † | 375.18 ± 4.3 | 375.39 ± 4.71 | 0.548 | 377.98 ± 3.63 | 378.26 ± 3.58 | 0.103 |
| ECW_TBW_LA † | 375.54 ± 4.55 | 375.59 ± 4.93 | 0.897 | 378.58 ± 3.67 | 378.69 ± 3.60 | 0.525 |
| ECW_TBW_TR † | 378.29 ± 7.46 | 378.65 ± 7.87 | 0.545 | 386.96 ± 5.86 | 386.94 ± 6.10 | 0.944 |
| ECW_TBW_RL † | 379.43 ± 9.38 | 380.06 ± 10.47 | 0.419 | 388.57 ± 7.73 | 388.53 ± 8.34 | 0.911 |
| ECW_TBW_LL † | 382.36 ± 9.74 | 382.61 ± 9.72 | 0.736 | 390.57 ± 7.56 | 390.38 ± 7.65 | 0.604 |
| Additional data | ||||||
| VFL | 7.02 ± 2.96 | 7.22 ± 3.05 | 0.401 | 8.72 ± 3.66 | 8.78 ± 3.59 | 0.732 |
| VFA | 75.34 ± 29.97 | 77.43 ± 30.45 | 0.366 | 92.14 ± 37.16 | 92.68 ± 35.95 | 0.753 |
| Obesity_D | 113.94 ± 14.62 | 114.38 ± 14.24 | 0.688 | 110.12 ± 16.73 | 110.63 ± 16.76 | 0.525 |
| TBW_FFM | 73.55 ± 0.25 | 73.56 ± 0.25 | 0.687 | 73.5 ± 0.21 | 73.49 ± 0.23 | 0.278 |
| PAngle50_TR | 7.38 ± 0.91 | 7.34 ± 0.88 | 0.516 | 5.81 ± 0.52 | 5.79 ± 0.57 | 0.357 |
| Variables | Men | Women | ||||
|---|---|---|---|---|---|---|
| Non-Hypertension | Hypertension | p | Non-Hypertension | Hypertension | p | |
| Participants (n) | 500 | 75 | 1354 | 108 | ||
| General characteristics | ||||||
| Age (years) | 41.96 ± 13.42 | 59.68 ± 10.72 | <0.001 | 45.76 ± 12.09 | 57.36 ± 8.59 | <0.001 |
| Temperature (°C) | 36.51 ± 0.33 | 36.50 ± 0.34 | 0.700 | 36.70 ± 0.32 | 36.70 ± 0.31 | 0.952 |
| SBP (mmHg) | 118.52 ± 13.45 | 126.75 ± 16 | <0.001 | 107.04 ± 16.58 | 125.20 ± 15.24 | <0.001 |
| DBP (mmHg) | 69.50 ± 9.79 | 73.56 ± 11.71 | 0.005 | 62.51 ± 10.55 | 72.03 ± 9.08 | <0.001 |
| Pulse rate (bmp) | 68.96 ± 10.10 | 68.72 ± 9.63 | 0.839 | 71.61 ± 10.22 | 70.58 ± 11.43 | 0.365 |
| Height (cm) | 172.63 ± 6.16 | 169.36 ± 6.76 | <0.001 | 159.56 ± 5.61 | 157.41 ± 5.63 | <0.001 |
| Weight (kg) | 74.29 ± 11.21 | 75.66 ± 12.83 | 0.383 | 58.34 ± 8.99 | 63.65 ± 11.56 | <0.001 |
| BMI (kg/m2) | 24.88 ± 3.16 | 26.29 ± 3.38 | 0.001 | 22.92 ± 3.36 | 25.66 ± 4.33 | <0.001 |
| Body fat mass | ||||||
| BFM | 17.21 ± 6.31 | 21.37 ± 6.08 | <0.001 | 19.06 ± 6.25 | 23.95 ± 7.92 | <0.001 |
| PBF | 22.72 ± 5.75 | 27.89 ± 4.61 | <0.001 | 32.06 ± 6.20 | 36.88 ± 5.97 | <0.001 |
| FMI | 5.78 ± 2.08 | 7.43 ± 1.97 | <0.001 | 7.51 ± 2.49 | 9.67 ± 3.19 | <0.001 |
| BFMp_WB | 174.92 ± 62.93 | 225.05 ± 59.50 | <0.001 | 184.98 ± 78.92 | 253.62 ± 101.20 | <0.001 |
| BFM_RA | 1.00 ± 0.58 | 1.38 ± 0.58 | <0.001 | 1.34 ± 0.60 | 1.81 ± 0.91 | <0.001 |
| BFMp_RA | 169.31 ± 95.04 | 243.1 ± 96.04 | <0.001 | 149.2 ± 66.58 | 207.52 ± 102.03 | <0.001 |
| BFM_LA | 1.03 ± 0.58 | 1.42 ± 0.59 | <0.001 | 1.36 ± 0.60 | 1.84 ± 0.90 | <0.001 |
| BFMp_LA | 173.82 ± 95.16 | 249.72 ± 94.97 | <0.001 | 152.03 ± 67.03 | 210.24 ± 102.11 | <0.001 |
| BFM_TR | 8.83 ± 3.46 | 11.03 ± 3.33 | <0.001 | 9.23 ± 3.24 | 11.79 ± 3.76 | <0.001 |
| BFMp_TR | 212.46 ± 81.49 | 275.12 ± 76.53 | <0.001 | 183.96 ± 65.24 | 240.94 ± 76.61 | <0.001 |
| BFM_RL | 2.62 ± 0.84 | 3.18 ± 0.78 | <0.001 | 3.06 ± 0.89 | 3.70 ± 1.18 | <0.001 |
| BFMp_RL | 154.88 ± 49.50 | 195.51 ± 45.57 | <0.001 | 134.01 ± 39.81 | 166.44 ± 53.14 | <0.001 |
| BFM_LL | 2.60 ± 0.83 | 3.16 ± 0.77 | <0.001 | 3.05 ± 0.89 | 3.68 ± 1.15 | <0.001 |
| BFMp_LL | 153.49 ± 48.80 | 193.6 ± 44.82 | <0.001 | 133.51 ± 39.49 | 165.57 ± 52.09 | <0.001 |
| Lean mass | ||||||
| SLM | 53.93 ± 6.76 | 51.3 ± 7.65 | 0.006 | 36.99 ± 4.12 | 37.43 ± 4.67 | 0.348 |
| SMM | 32.05 ± 4.36 | 30.15 ± 4.88 | 0.002 | 21.09 ± 2.62 | 21.27 ± 2.94 | 0.538 |
| SMM_WT | 43.34 ± 3.41 | 39.99 ± 2.73 | <0.001 | 36.44 ± 3.40 | 33.76 ± 3.21 | <0.001 |
| Body water | ||||||
| TBW | 41.96 ± 5.23 | 39.99 ± 5.94 | 0.008 | 28.87 ± 3.20 | 29.23 ± 3.64 | 0.310 |
| ICW | 26.11 ± 3.35 | 24.65 ± 3.74 | 0.002 | 17.70 ± 2.01 | 17.84 ± 2.25 | 0.536 |
| ECW | 15.86 ± 1.91 | 15.34 ± 2.23 | 0.06 | 11.16 ± 1.22 | 11.39 ± 1.40 | 0.101 |
| TBW_WT | 56.83 ± 4.24 | 53.12 ± 3.39 | <0.001 | 49.93 ± 4.56 | 46.47 ± 4.38 | <0.001 |
| ECW_TBW † | 378.19 ± 7.30 | 383.71 ± 7.58 | <0.001 | 386.77 ± 5.97 | 389.62 ± 6.07 | <0.001 |
| ECW_TBW_RA † | 374.87 ± 4.14 | 377.28 ± 4.75 | <0.001 | 377.92 ± 3.63 | 378.71 ± 3.53 | 0.027 |
| ECW_TBW_LA † | 375.24 ± 4.32 | 377.60 ± 5.47 | 0.001 | 378.54 ± 3.70 | 379.09 ± 3.14 | 0.086 |
| ECW_TBW_TR † | 377.56 ± 7.18 | 383.13 ± 7.48 | <0.001 | 386.75 ± 5.81 | 389.52 ± 6.01 | <0.001 |
| ECW_TBW_RL † | 378.59 ± 9.19 | 385.05 ± 8.74 | <0.001 | 388.30 ± 7.65 | 392.01 ± 7.88 | <0.001 |
| ECW_TBW_LL † | 381.48 ± 9.46 | 388.19 ± 9.67 | <0.001 | 390.28 ± 7.47 | 394.28 ± 7.73 | <0.001 |
| Additional data | ||||||
| VFL | 6.75 ± 2.86 | 8.85 ± 2.98 | <0.001 | 8.49 ± 3.54 | 11.55 ± 4.01 | <0.001 |
| VFA | 72.56 ± 29.00 | 93.85 ± 29.93 | <0.001 | 89.89 ± 35.84 | 120.32 ± 41.72 | <0.001 |
| Obesity_D | 113.10 ± 14.34 | 119.51 ± 15.28 | 0.001 | 109.16 ± 16.00 | 122.19 ± 20.64 | <0.001 |
| TBW_FFM | 73.53 ± 0.24 | 73.67 ± 0.22 | <0.001 | 73.49 ± 0.21 | 73.63 ± 0.19 | <0.001 |
| PAngle50_TR | 7.49 ± 0.87 | 6.67 ± 0.85 | <0.001 | 5.83 ± 0.52 | 5.64 ± 0.47 | <0.001 |
| Variables | Men | Women | ||
|---|---|---|---|---|
| Crude OR (95% CI) | p | Crude OR (95% CI) | p | |
| General characteristics | ||||
| Age (years) | 4.32 (3.09, 6.06) | <0.001 | 3.36 (2.57, 4.4) | <0.001 |
| Height (cm) | 0.58 (0.45, 0.75) | <0.001 | 0.68 (0.56, 0.83) | <0.001 |
| Weight (kg) | 1.12 (0.89, 1.42) | 0.333 | 1.58 (1.34, 1.85) | <0.001 |
| BMI (kg/m2) | 1.50 (1.20, 1.89) | 0.001 | 1.82 (1.55, 2.14) | <0.001 |
| Body fat mass | ||||
| BFM | 1.77 (1.41, 2.22) | <0.001 | 1.78 (1.51, 2.09) | <0.001 |
| PBF | 2.70 (2.02, 3.61) | <0.001 | 2.20 (1.79, 2.71) | <0.001 |
| FMI | 2.03 (1.60, 2.58) | <0.001 | 1.89 (1.60, 2.22) | <0.001 |
| BFMp_WB | 2.03 (1.60, 2.58) | <0.001 | 1.89 (1.60, 2.22) | <0.001 |
| BFM_RA | 1.68 (1.35, 2.09) | <0.001 | 1.63 (1.40, 1.89) | <0.001 |
| BFMp_RA | 1.86 (1.48, 2.33) | <0.001 | 1.70 (1.46, 1.98) | <0.001 |
| BFM_LA | 1.71 (1.37, 2.13) | <0.001 | 1.63 (1.40, 1.89) | <0.001 |
| BFMp_LA | 1.90 (1.51, 2.39) | <0.001 | 1.70 (1.46, 1.97) | <0.001 |
| BFM_TR | 1.78 (1.41, 2.25) | <0.001 | 1.88 (1.58, 2.23) | <0.001 |
| BFMp_TR | 2.04 (1.60, 2.61) | <0.001 | 2.00 (1.68, 2.38) | <0.001 |
| BFM_RL | 1.79 (1.43, 2.25) | <0.001 | 1.69 (1.44, 1.98) | <0.001 |
| BFMp_RL | 2.07 (1.63, 2.63) | <0.001 | 1.79 (1.53, 2.11) | <0.001 |
| BFM_LL | 1.80 (1.44, 2.26) | <0.001 | 1.69 (1.44, 1.98) | <0.001 |
| BFMp_LL | 2.08 (1.64, 2.64) | <0.001 | 1.8 0(1.53, 2.11) | <0.001 |
| Lean mass | ||||
| SLM | 0.67 (0.51, 0.87) | 0.002 | 1.11 (0.91, 1.34) | 0.295 |
| SMM | 0.64 (0.49, 0.83) | 0.001 | 1.07 (0.88, 1.30) | 0.495 |
| SMM_WT | 0.33 (0.24, 0.44) | <0.001 | 0.44 (0.35, 0.54) | <0.001 |
| Body water | ||||
| TBW | 0.68 (0.52, 0.88) | 0.003 | 1.12 (0.92, 1.35) | 0.256 |
| ICW | 0.64 (0.49, 0.83) | 0.001 | 1.07 (0.88, 1.3) | 0.494 |
| ECW | 0.76 (0.59, 0.98) | 0.034 | 1.2 (0.99, 1.44) | 0.063 |
| TBW_WT | 0.38 (0.29, 0.51) | <0.001 | 0.46 (0.37, 0.57) | <0.001 |
| ECW_TBW | 2.08 (1.61, 2.69) | <0.001 | 1.62 (1.33, 1.99) | <0.001 |
| ECW_TBW_RA | 1.74 (1.36, 2.22) | <0.001 | 1.25 (1.02, 1.52) | 0.029 |
| ECW_TBW_LA | 1.66 (1.3, 2.11) | <0.001 | 1.16 (0.95, 1.42) | 0.133 |
| ECW_TBW_TR | 2.09 (1.62, 2.69) | <0.001 | 1.61 (1.32, 1.97) | <0.001 |
| ECW_TBW_RL | 2.01 (1.56, 2.59) | <0.001 | 1.64 (1.34, 2) | <0.001 |
| ECW_TBW_LL | 2.05 (1.58, 2.67) | <0.001 | 1.72 (1.41, 2.11) | <0.001 |
| Additional data | ||||
| VFL | 1.88 (1.5, 2.37) | <0.001 | 2.03 (1.7, 2.42) | <0.001 |
| VFA | 1.86 (1.48, 2.35) | <0.001 | 1.95 (1.65, 2.32) | <0.001 |
| Obesity_D | 1.5 (1.19, 1.9) | 0.001 | 1.82 (1.55, 2.14) | <0.001 |
| TBW_FFM | 1.82 (1.4, 2.37) | <0.001 | 1.9 (1.56, 2.32) | <0.001 |
| PAngle50_TR | 0.36 (0.27, 0.49) | <0.001 | 0.69 (0.56, 0.84) | <0.001 |
| Men’ Models | Training Set AUROC | Test Set AUROC (95% CI) | AUROC Test | p | Kappa (95% CI) | F1 Score (95% CI) | Precision (95% CI) | Accuracy (95% CI) | Sensitivity (95% CI) | Specificity (95% CI) |
|---|---|---|---|---|---|---|---|---|---|---|
| E-net | 0.874 | 0.865 (0.806, 0.914) | 0.335 (0.228, 0.435) | 0.466 (0.348, 0.563) | 0.310 (0.215, 0.400) | 0.718 (0.657, 0.771) | 0.941 (0.833, 1.000) | 0.686 (0.620, 0.742) | ||
| K-NN | 0.876 | 0.81 (0.74, 0.873) | E-net vs. K-NN | 0.075 | 0.264 (0.168, 0.362) | 0.409 (0.301, 0.507) | 0.271 (0.186, 0.355) | 0.682 (0.620, 0.739) | 0.848 (0.707, 0.966) | 0.659 (0.593, 0.718) |
| RF | 1 | 0.793 (0.717, 0.862) | E-net vs. RF | 0.045 | 0.203 (0.132, 0.286) | 0.372 (0.275, 0.459) | 0.231 (0.162, 0.303) | 0.584 (0.522, 0.645) | 0.941 (0.840, 1.000) | 0.530 (0.462, 0.600) |
| SVM | 0.959 | 0.783 (0.697, 0.857) | E-net vs. SVM | 0.018 | 0.243 (0.154, 0.337) | 0.395 (0.292, 0.493) | 0.256 (0.177, 0.340) | 0.653 (0.592, 0.710) | 0.879 (0.750, 0.971) | 0.619 (0.553, 0.682) |
| XGBoost | 0.956 | 0.827 (0.761, 0.883) | E-net vs. XGBoost | 0.433 | 0.261 (0.185, 0.354) | 0.413 (0.312, 0.514) | 0.263 (0.188, 0.345) | 0.645 (0.584, 0.706) | 0.970 (0.893, 1.000) | 0.597 (0.531, 0.659) |
| NN | 0.9 | 0.853 (0.797, 0.904) | E-net vs. NN | 0.757 | 0.365 (0.257, 0.469) | 0.489 (0.37, 0.586) | 0.330 (0.232, 0.424) | 0.743 (0.69, 0.796) | 0.941 (0.833, 1.000) | 0.714 (0.653, 0.771) |
| Women’s Models | Training Set AUROC | Test Set AUROC (95% CI) | AUROC Test | p | Kappa (95% CI) | F1 Score (95% CI) | Precision (95% CI) | Accuracy (95% CI) | Sensitivity (95% CI) | Specificity (95% CI) |
| E-net | 0.833 | 0.831 (0.78, 0.881) | 0.153 (0.111, 0.201) | 0.259 (0.197, 0.322) | 0.149 (0.110, 0.192) | 0.597 (0.558, 0.636) | 0.979 (0.927, 1.000) | 0.568 (0.527, 0.607) | ||
| K-NN | 0.849 | 0.805 (0.747, 0.855) | E-net vs. K-NN | 0.399 | 0.224 (0.142, 0.299) | 0.312 (0.225, 0.391) | 0.198 (0.136, 0.260) | 0.768 (0.732, 0.798) | 0.735 (0.600, 0.857) | 0.770 (0.733, 0.802) |
| RF | 1 | 0.804 (0.745, 0.857) | E-net vs. RF | 0.435 | 0.145 (0.104, 0.190) | 0.251 (0.191, 0.312) | 0.144 (0.107, 0.187) | 0.591 (0.553, 0.628) | 0.957 (0.889, 1.000) | 0.563 (0.524, 0.603) |
| SVM | 1 | 0.774 (0.712, 0.831) | E-net vs. SVM | 0.117 | 0.179 (0.122, 0.242) | 0.276 (0.209, 0.349) | 0.166 (0.12, 0.219) | 0.692 (0.655, 0.728) | 0.829 (0.708, 0.932) | 0.683 (0.644, 0.720) |
| XGBoost | 0.915 | 0.826 (0.772, 0.876) | E-net vs. XGBoost | 0.910 | 0.265 (0.186, 0.345) | 0.347 (0.262, 0.430) | 0.223 (0.162, 0.291) | 0.790 (0.758, 0.821) | 0.780 (0.653, 0.896) | 0.791 (0.758, 0.824) |
| NN | 0.846 | 0.822 (0.771, 0.871) | E-net vs. NN | 0.780 | 0.165 (0.117, 0.220) | 0.268 (0.206, 0.334) | 0.157 (0.116, 0.203) | 0.633 (0.595, 0.671) | 0.938 (0.850, 1.000) | 0.611 (0.569, 0.649) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, J.-W.; Lee, S.; Yim, M.H. Machine Learning Approach for Predicting Hypertension Based on Body Composition in South Korean Adults. Bioengineering 2024, 11, 921. https://doi.org/10.3390/bioengineering11090921
Seo J-W, Lee S, Yim MH. Machine Learning Approach for Predicting Hypertension Based on Body Composition in South Korean Adults. Bioengineering. 2024; 11(9):921. https://doi.org/10.3390/bioengineering11090921
Chicago/Turabian StyleSeo, Jeong-Woo, Sanghun Lee, and Mi Hong Yim. 2024. "Machine Learning Approach for Predicting Hypertension Based on Body Composition in South Korean Adults" Bioengineering 11, no. 9: 921. https://doi.org/10.3390/bioengineering11090921
APA StyleSeo, J.-W., Lee, S., & Yim, M. H. (2024). Machine Learning Approach for Predicting Hypertension Based on Body Composition in South Korean Adults. Bioengineering, 11(9), 921. https://doi.org/10.3390/bioengineering11090921










