Experimental Protocols to Test Aortic Soft Tissues: A Systematic Review
Abstract
1. Introduction
2. Materials and Methods
2.1. Search Strategy
2.2. Inclusion and Exclusion Selection Criteria
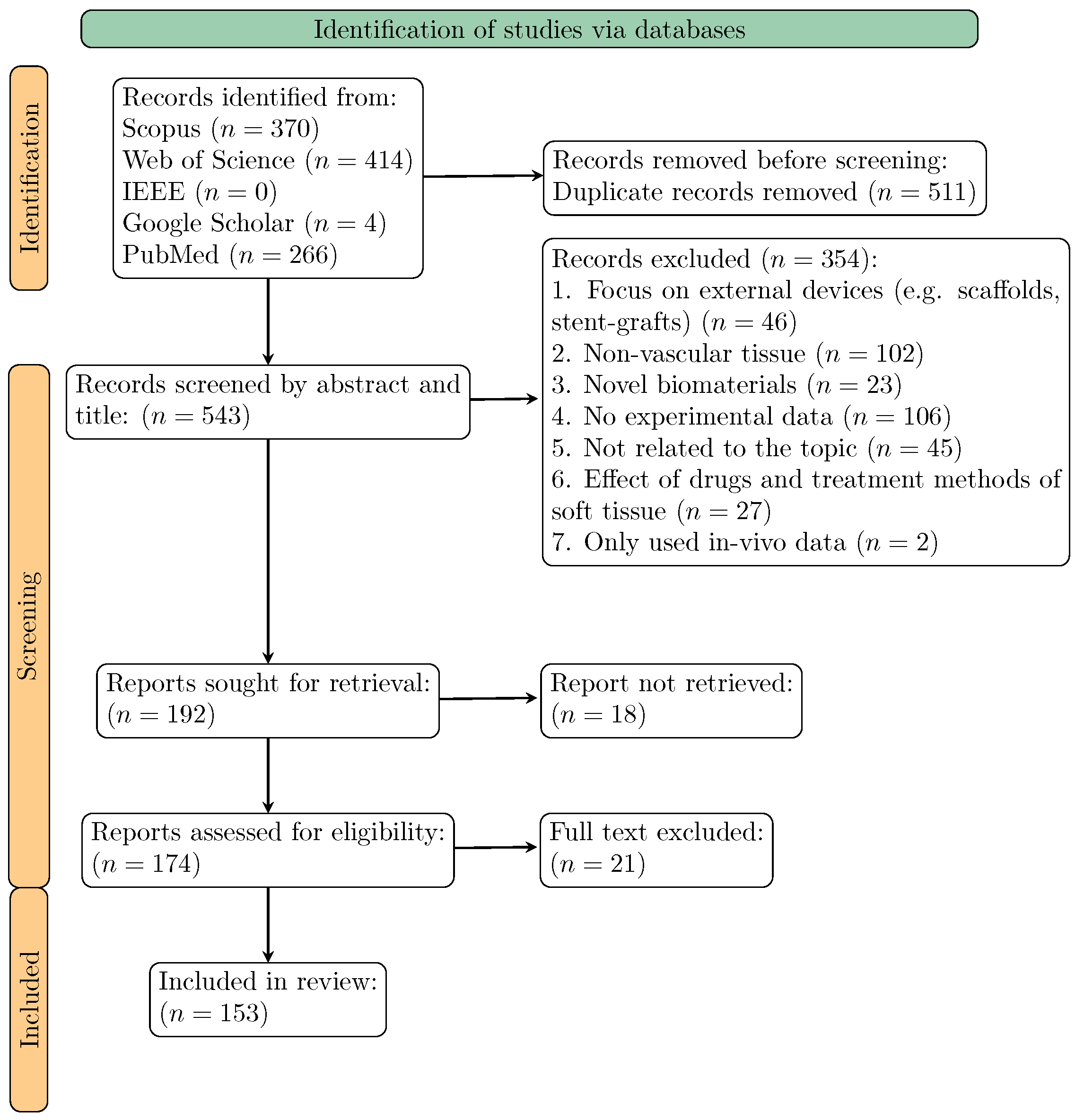
2.3. Study Selection
3. Results
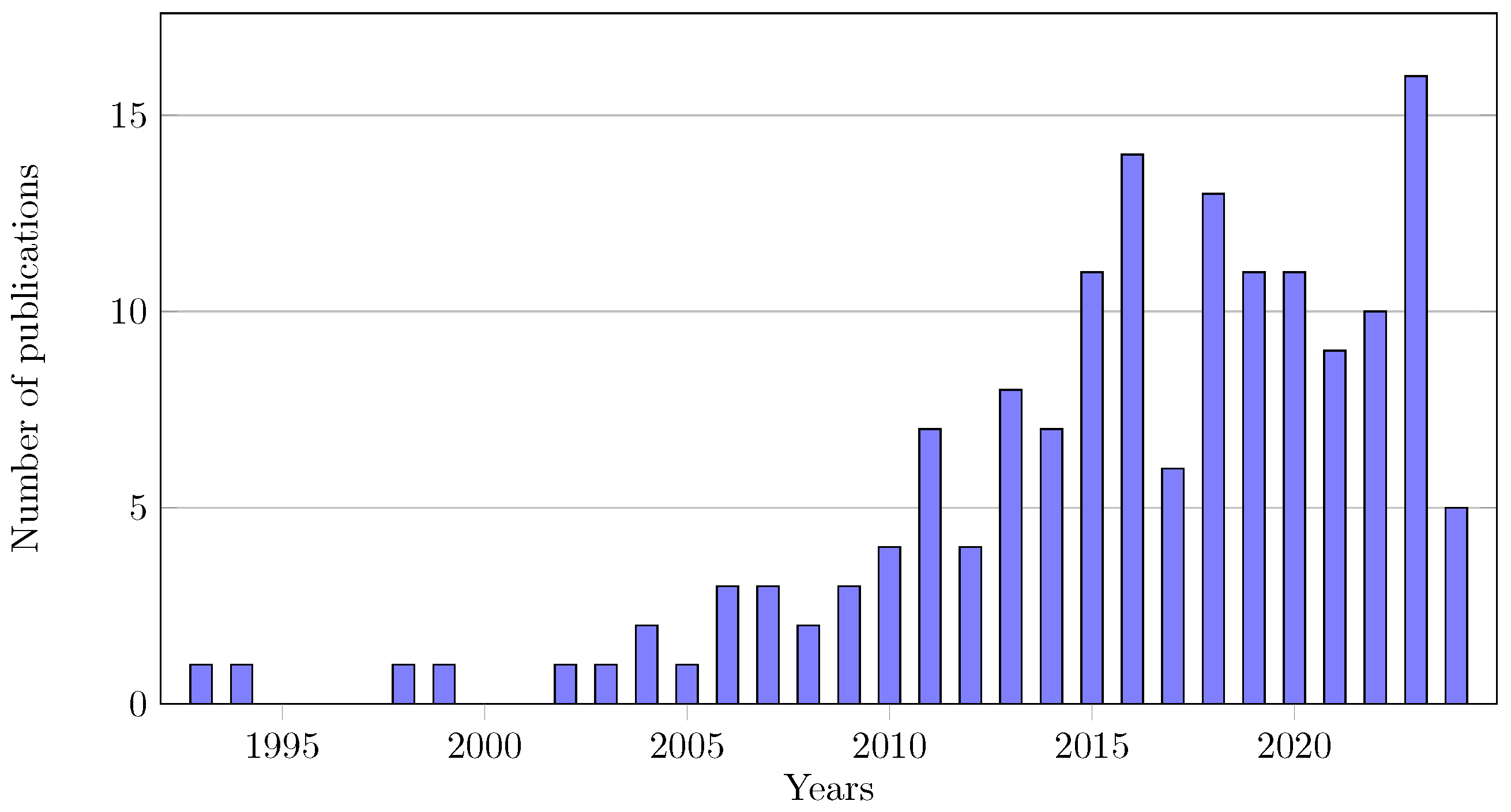
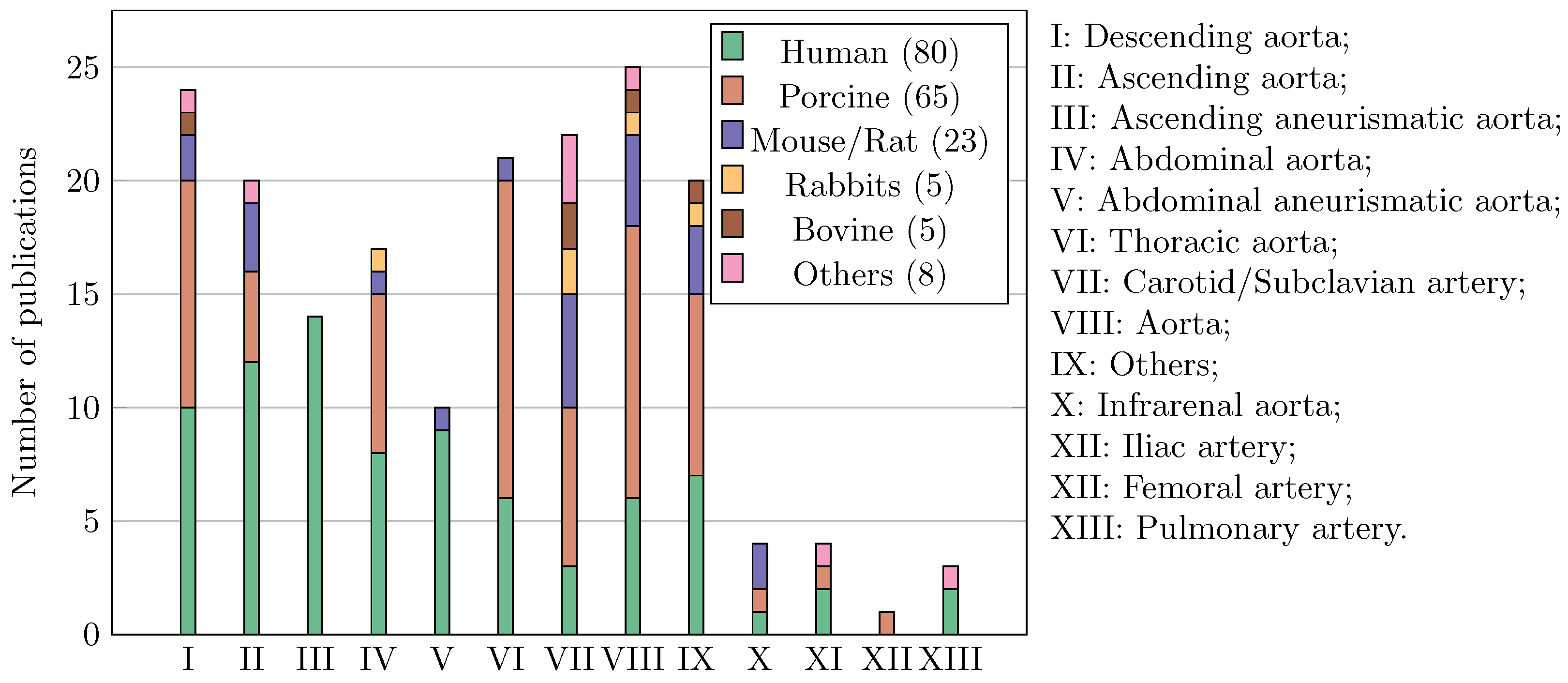
3.1. Publication Overview
3.2. General Practices
3.2.1. Conservation Methods
3.2.2. Bath during Test
3.2.3. Full-Field Measurements
3.3. Mechanical Test Methods
3.3.1. Uniaxial Test
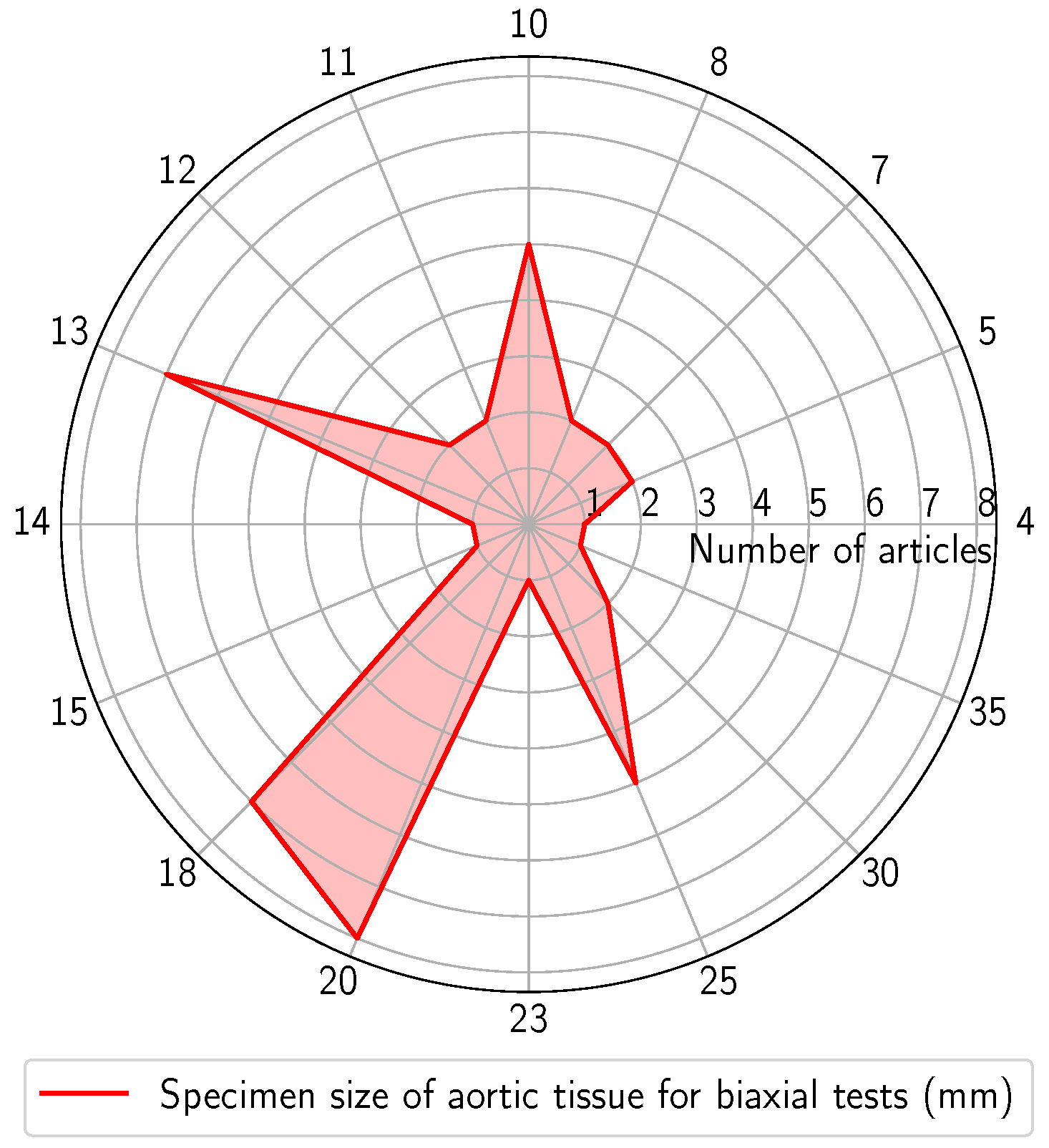
3.3.2. Biaxial Test
3.3.3. Inflation Test
3.3.4. Other Tests
3.4. Experimental Results and Post-Processing
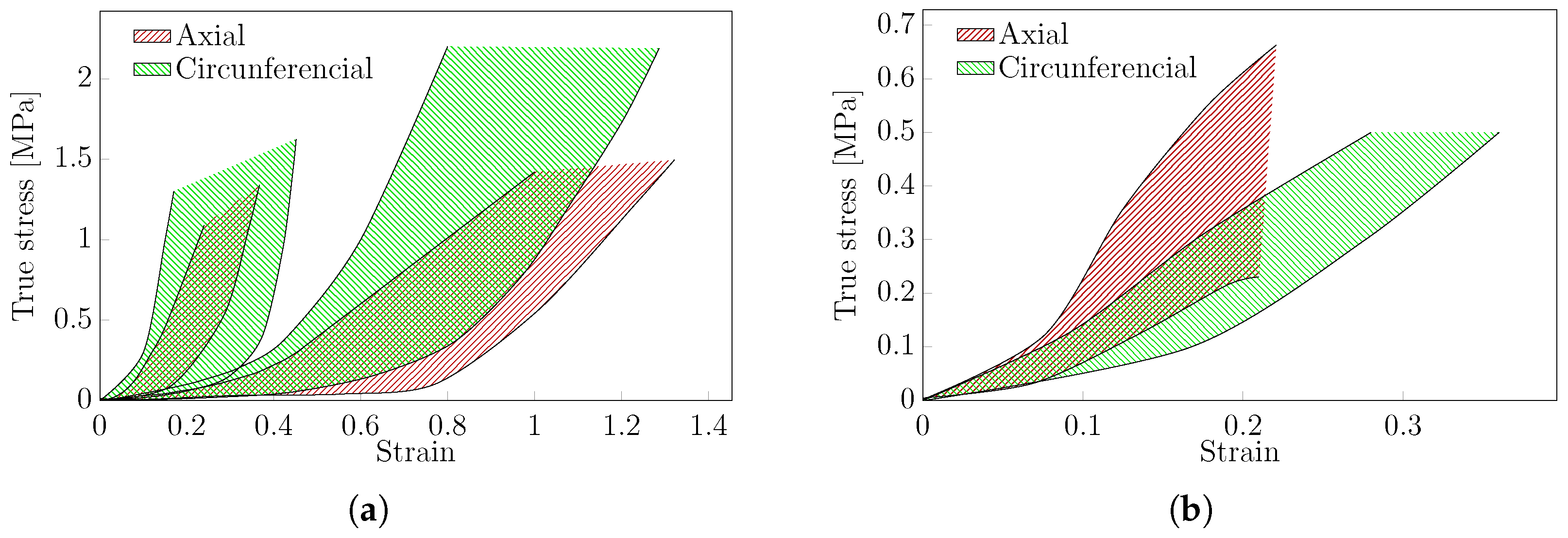
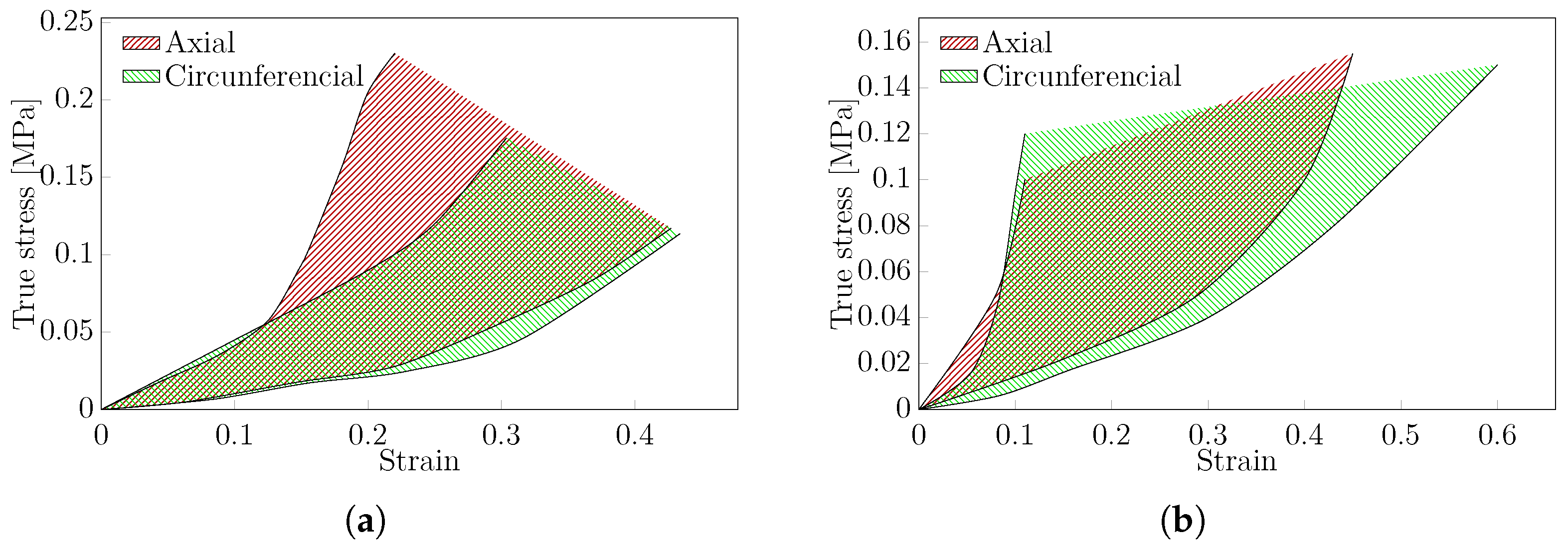
3.4.1. Uniaxial Test
3.4.2. Biaxial Test
3.4.3. Post-Processing
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AAA | Abdominal Aorta Aneurysms |
| DIC | Digital Image Correlation |
| dMEM | Dulbecco’s Modified Eagle Medium |
| dPBS | Dulbecco’s Phosphate-Buffered Saline |
| DVC | Digital Volume Correlation |
| HBSS | Hank’s Balanced Salt Solution |
| HGO | Holzapfel–Gasser–Ogden |
| KHS | Krebs–Henseleit Solution |
| KRS | Krebs–Ringer Solution |
| OCT | Optical Coherence Tomography |
| PBS | Phosphate-Buffered Saline |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-Analyses |
| PSS | Physiologic Saline Solution |
| RS | Ringer Solution |
| SEDF | Strain Energy Density Function |
References
- di Gioia, C.R.T.; Ascione, A.; Carletti, R.; Giordano, C. Thoracic Aorta: Anatomy and Pathology. Diagnostics 2023, 13, 2166. [Google Scholar] [CrossRef]
- Hall, J.E.; Hall, M.E. Guyton and Hall: Textbook of Medical Physiology e-Book; Elsevier Health Sciences: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Giudici, A.; Li, Y.; Cleary, S.; Connolly, K.; McEniery, C.; Wilkinson, I.B.; Khir, A.W. Time-course of the human thoracic aorta ageing process assessed using uniaxial mechanical testing and constitutive modelling. J. Mech. Behav. Biomed. Mater. 2022, 134, 105339. [Google Scholar] [CrossRef] [PubMed]
- Jadidi, M.; Razian, S.A.; Habibnezhad, M.; Anttila, E.; Kamenskiy, A. Mechanical, structural, and physiologic differences in human elastic and muscular arteries of different ages: Comparison of the descending thoracic aorta to the superficial femoral artery. Acta Biomater. 2021, 119, 268–283. [Google Scholar] [CrossRef] [PubMed]
- Giudici, A.; Khir, A.; Szafron, J.; Spronck, B. From Uniaxial Testing of Isolated Layers to a Tri-Layered Arterial Wall: A Novel Constitutive Modelling Framework. Ann. Biomed. Eng. 2021, 49, 2454–2467. [Google Scholar] [CrossRef] [PubMed]
- Peña, J.; Cilla, M.; Martínez, M.; Peña, E. Biomechanical characterization and constitutive modeling of the layer-dissected residual strains and mechanical properties of abdominal porcine aorta. J. Biomech. 2022, 132, 110909. [Google Scholar] [CrossRef] [PubMed]
- Gheysen, L.; Maes, L.; Caenen, A.; Segers, P.; Peirlinck, M.; Famaey, N. Uncertainty quantification of the wall thickness and stiffness in an idealized dissected aorta. J. Mech. Behav. Biomed. Mater. 2024, 151, 106370. [Google Scholar] [CrossRef] [PubMed]
- Sanders, S.N.; Lopata, R.G.P.; van Breemen, L.C.A.; van de Vosse, F.N.; Rutten, M.C.M. A novel technique for the assessment of mechanical properties of vascular tissue. Biomech. Model. Mechanobiol. 2020, 19, 1585–1594. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Cocciolone, A.; Staiculescu, M.; Mecham, R.; Wagenseil, J. Passive biaxial mechanical behavior of newborn mouse aorta with and without elastin. J. Mech. Behav. Biomed. Mater. 2022, 126, 105021. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Sommer, G.; Niestrawska, J.A.; Holzapfel, G.A.; Nordsletten, D. The effects of viscoelasticity on residual strain in aortic soft tissues. Acta Biomater. 2022, 140, 398–411. [Google Scholar] [CrossRef]
- Polzer, S.; Gasser, T.; Novak, K.; Man, V.; Tichy, M.; Skacel, P.; Bursa, J. Structure-based constitutive model can accurately predict planar biaxial properties of aortic wall tissue. Acta Biomater. 2015, 14, 133–145. [Google Scholar] [CrossRef]
- Niestrawska, J.; Regitnig, P.; Viertler, C.; Cohnert, T.; Babu, A.; Holzapfel, G. The role of tissue remodeling in mechanics and pathogenesis of abdominal aortic aneurysms. Acta Biomater. 2019, 88, 149–161. [Google Scholar] [CrossRef]
- Eberth, J.F.; Taucer, A.I.; Wilson, E.; Humphrey, J.D. Mechanics of Carotid Arteries in a Mouse Model of Marfan Syndrome. Ann. Biomed. Eng. 2009, 37, 1093–1104. [Google Scholar] [CrossRef]
- Kobielarz, M. Effect of collagen fibre and elastic lamella content on the mechanical behaviour of abdominal aortic aneurysms. Acta Bioeng. Biomech. 2020, 22, 1–21. [Google Scholar] [CrossRef]
- Forneris, A.; Kennard, J.; Ismaguilova, A.; Shepherd, R.D.; Studer, D.; Bromley, A.; Moore, R.D.; Rinker, K.D.; Di Martino, E.S. Linking Aortic Mechanical Properties, Gene Expression and Microstructure: A New Perspective on Regional Weakening in Abdominal Aortic Aneurysms. Front. Cardiovasc. Med. 2021, 8, 631790. [Google Scholar] [CrossRef]
- Chirila, T.; Suzuki, S. Photocrosslinking of Adventitial Collagen in the Porcine Abdominal Aorta: A Preliminary Approach to a Strategy for Prevention of Aneurysmal Rupture. Designs 2022, 6, 5. [Google Scholar] [CrossRef]
- Chiu, P.; Lee, H.P.; Dalal, A.; Koyano, T.; Nguyen, M.; Connolly, A.; Chaudhuri, O.; Fischbein, M. Relative strain is a novel predictor of aneurysmal degeneration of the thoracic aorta: An ex vivo mechanical study. JVS-Vasc. Sci. 2021, 2, 235–246. [Google Scholar] [CrossRef]
- Maier, A.; Gee, M.; Reeps, C.; Eckstein, H.H.; Wall, W. Impact of calcifications on patient-specific wall stress analysis of abdominal aortic aneurysms. Biomech. Model. Mechanobiol. 2010, 9, 511–521. [Google Scholar] [CrossRef] [PubMed]
- Mourato, A.; Valente, R.; Xavier, J.; Brito, M.; Avril, S.; de Sá, J.C.; Tomás, A.; Fragata, J. Computational Modelling and Simulation of Fluid Structure Interaction in Aortic Aneurysms: A Systematic Review and Discussion of the Clinical Potential. Appl. Sci. 2022, 12, 8049. [Google Scholar] [CrossRef]
- Valente, R.; Mourato, A.; Brito, M.; Xavier, J.; Tomás, A.; Avril, S. Fluid–structure interaction modeling of ascending thoracic aortic aneurysms in simvascular. Biomechanics 2022, 2, 189–204. [Google Scholar] [CrossRef]
- Page, M.J.; Moher, D.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. Br. Med. J. 2021, 372, 1–11. [Google Scholar] [CrossRef]
- Falagas, M.E.; Pitsouni, E.I.; Malietzis, G.A.; Pappas, G. Comparison of PubMed, Scopus, Web of Science, and Google Scholar: Strengths and weaknesses. FASEB J. 2008, 22, 338–342. [Google Scholar] [CrossRef]
- Camasão, D.; Mantovani, D. The mechanical characterization of blood vessels and their substitutes in the continuous quest for physiological-relevant performances. A critical review. Mater. Today Bio 2021, 10, 100106. [Google Scholar] [CrossRef] [PubMed]
- Emmott, A.; Garcia, J.; Chung, J.; Lachapelle, K.; El-Hamamsy, I.; Mongrain, R.; Cartier, R.; Leask, R. Biomechanics of the Ascending Thoracic Aorta: A Clinical Perspective on Engineering Data. Can. J. Cardiol. 2016, 32, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Macrae, R.A.; Miller, K.; Doyle, B.J. Methods in Mechanical Testing of Arterial Tissue: A Review. Strain 2016, 52, 380–399. [Google Scholar] [CrossRef]
- Giudici, A.; Wilkinson, I.; Khir, A. Review of the Techniques Used for Investigating the Role Elastin and Collagen Play in Arterial Wall Mechanics. IEEE Rev. Biomed. Eng. 2021, 14, 256–269. [Google Scholar] [CrossRef] [PubMed]
- Antonova, M.; Antonova, S.; Shikova, L.; Kaneva, M.; Govedarski, V.; Zahariev, T.; Stoytchev, S. A review of the mechanical stresses predisposing abdominal aortic aneurysmal rupture: Uniaxial experimental approach. J. Mech. Med. Biol. 2020, 20, 2030001. [Google Scholar] [CrossRef]
- Tong, J.; Yang, F.; Li, X.; Xu, X.; Wang, G.X. Mechanical Characterization and Material Modeling of Diabetic Aortas in a Rabbit Model. Ann. Biomed. Eng. 2018, 46, 429–442. [Google Scholar] [CrossRef] [PubMed]
- Zeinali-Davarani, S.; Chow, M.J.; Turcotte, R.; Zhang, Y. Characterization of biaxial mechanical behavior of porcine aorta under gradual elastin degradation. Ann. Biomed. Eng. 2013, 41, 1528–1538. [Google Scholar] [CrossRef] [PubMed]
- Gramigna, V.; Fragomeni, G.; Fontanella, C.G.; Stefanini, C.; Carniel, E.L. A coupled experimental and numerical approach to characterize the anisotropic mechanical behavior of aortic tissues. J. Mech. Med. Biol. 2020, 20, 2050027. [Google Scholar] [CrossRef]
- Sokolis, D.P.; Boudoulas, H.; Karayannacos, P.E. Assessment of the Aortic Stress–Strain Relation in Uniaxial Tension. J. Biomech. 2002, 35, 1213–1223. [Google Scholar] [CrossRef]
- Cavinato, C.; Chen, M.; Weiss, D.; Ruiz-Rodriguez, M.J.; Schwartz, M.A.; Humphrey, J.D. Progressive Microstructural Deterioration Dictates Evolving Biomechanical Dysfunction in the Marfan Aorta. Front. Cardiovasc. Med. 2021, 8, 800730. [Google Scholar] [CrossRef]
- Zhou, B.; Rachev, A.; Shazly, T. The Biaxial Active Mechanical Properties of the Porcine Primary Renal Artery. J. Mech. Behav. Biomed. Mater. 2015, 48, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Jadidi, M.; Sherifova, S.; Sommer, G.; Kamenskiy, A.; Holzapfel, G.A. Constitutive Modeling Using Structural Information on Collagen Fiber Direction and Dispersion in Human Superficial Femoral Artery Specimens of Different Ages. Acta Biomater. 2021, 121, 461–474. [Google Scholar] [CrossRef]
- Sokolis, D.P. A Passive Strain-Energy Function for Elastic and Muscular Arteries: Correlation of Material Parameters with Histological Data. Med. Biol. Eng. Comput. 2010, 48, 507–518. [Google Scholar] [CrossRef]
- Polzer, S.; Christian Gasser, T.; Bursa, J.; Staffa, R.; Vlachovsky, R.; Man, V.; Skacel, P. Importance of Material Model in Wall Stress Prediction in Abdominal Aortic Aneurysms. Med. Eng. Phys. 2013, 35, 1282–1289. [Google Scholar] [CrossRef]
- Pandit, A.; Lu, X.; Wang, C.; Kassab, G.S. Biaxial Elastic Material Properties of Porcine Coronary Media and Adventitia. Am. J. Physiol. Heart Circ. Physiol. 2005, 288, H2581–H2587. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Qian, X.; Yan, S.; Lei, J.; Wang, X.; Zhang, H.; Liu, Z. Determination of Material Parameters of the Two-Dimensional Holzapfel–Weizsäcker Type Model Based on Uniaxial Extension Data of Arterial Walls. Comput. Methods Biomech. Biomed. Engin. 2013, 16, 358–367. [Google Scholar] [CrossRef] [PubMed]
- García-Herrera, C.M.; Celentano, D.J.; Cruchaga, M.A. Bending and Pressurisation Test of the Human Aortic Arch: Experiments, Modelling and Simulation of a Patient-Specific Case. Comput. Methods Biomech. Biomed. Engin. 2013, 16, 830–839. [Google Scholar] [CrossRef]
- Linka, K.; Cavinato, C.; Humphrey, J.D.; Cyron, C.J. Predicting and understanding arterial elasticity from key microstructural features by bidirectional deep learning. Acta Biomater. 2022, 147, 63–72. [Google Scholar] [CrossRef]
- Sokolis, D.P.; Sassani, S.; Kritharis, E.P.; Tsangaris, S. Differential Histomechanical Response of Carotid Artery in Relation to Species and Region: Mathematical Description Accounting for Elastin and Collagen Anisotropy. Med. Biol. Eng. Comput. 2011, 49, 867–879. [Google Scholar] [CrossRef]
- Shcherbakova, D.; Papadacci, C.; Swillens, A.; Caenen, A.; De Bock, S.; Saey, V.; Chiers, K.; Tanter, M.; Greenwald, S.; Pernot, M.; et al. Supersonic shear wave imaging to assess arterial nonlinear behavior and anisotropy: Proof of principle via ex vivo testing of the horse Aorta. Adv. Mech. Eng. 2014, 2014, 272586. [Google Scholar] [CrossRef]
- Leng, X.; Deng, X.; Ravindran, S.; Kidane, A.; Lessner, S.M.; Sutton, M.A.; Shazly, T. Viscoelastic Behavior of Porcine Arterial Tissue: Experimental and Numerical Study. Exp. Mech. 2022, 62, 953–967. [Google Scholar] [CrossRef]
- Vignali, E.; Di Bartolo, F.; Gasparotti, E.; Malacarne, A.; Concistré, G.; Chiaramonti, F.; Murzi, M.; Positano, V.; Landini, L.; Celi, S. Correlation between Micro and Macrostructural Biaxial Behavior of Ascending Thoracic Aneurysm: A Novel Experimental Technique. Med. Eng. Phys. 2020, 86, 78–85. [Google Scholar] [CrossRef] [PubMed]
- Durbak, E.; Tarraf, S.; Gillespie, C.; Germano, E.; Cikach, F.; Blackstone, E.; Emerton, K.; Colbrunn, R.; Bellini, C.; Roselli, E.E. Ex vivo biaxial load testing analysis of aortic biomechanics demonstrates variation in elastic energy distribution across the aortic zone zero. J. Thorac. Cardiovasc. Surg. 2023, 166, 701–712. [Google Scholar] [CrossRef] [PubMed]
- Kramer, B.; Thompson, M.A.; Tarraf, S.A.; Vianna, E.; Gillespie, C.; Germano, E.; Gentle, B.; Cikach, F.; Lowry, A.M.; Pande, A.; et al. Longitudinal versus circumferential biomechanical behavior of the aneurysmal ascending aorta. J. Thorac. Cardiovasc. Surg. 2023; in press. [Google Scholar] [CrossRef]
- Thompson, M.A.; Kramer, B.; Tarraf, S.A.; Vianna, E.; Gillespie, C.; Germano, E.; Gentle, B.; Cikach, F.; Lowry, A.M.; Pande, A.; et al. Age Is Superior to Aortopathy Phenotype as a Predictor of Aortic Mechanics in Patients with Bicuspid Valve. J. Thorac. Cardiovasc. Surg. 2023; in press. [Google Scholar] [CrossRef]
- Anttila, E.; Balzani, D.; Desyatova, A.; Deegan, P.; MacTaggart, J.; Kamenskiy, A. Mechanical damage characterization in human femoropopliteal arteries of different ages. Acta Biomater. 2019, 90, 225–240. [Google Scholar] [CrossRef] [PubMed]
- Polzer, S.; Man, V.; Vlachovský, R.; Kubíček, L.; Kracík, J.; Staffa, R.; Novotný, T.; Burša, J.; Raghavan, M. Failure Properties of Abdominal Aortic Aneurysm Tissue Are Orientation Dependent. J. Mech. Behav. Biomed. Mater. 2021, 114, 104181. [Google Scholar] [CrossRef] [PubMed]
- Sokolis, D.P.; Kefaloyannis, E.M.; Kouloukoussa, M.; Marinos, E.; Boudoulas, H.; Karayannacos, P.E. A Structural Basis for the Aortic Stress–Strain Relation in Uniaxial Tension. J. Biomech. 2006, 39, 1651–1662. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, M.; Nolan, D.R.; Lally, C. An Investigation into the Role of Different Constituents in Damage Accumulation in Arterial Tissue and Constitutive Model Development. Biomech. Model. Mechanobiol. 2018, 17, 1757–1769. [Google Scholar] [CrossRef]
- Marra, S.P.; Kennedy, F.E.; Kinkaid, J.N.; Fillinger, M.F. Elastic and Rupture Properties of Porcine Aortic Tissue Measured Using Inflation Testing. Cardiovasc. Eng. 2006, 6, 123–131. [Google Scholar] [CrossRef]
- Zou, Y.; Zhang, Y. The Orthotropic Viscoelastic Behavior of Aortic Elastin. Biomech. Model. Mechanobiol. 2011, 10, 613–625. [Google Scholar] [CrossRef]
- Kamenskiy, A.V.; Dzenis, Y.A.; Kazmi, S.A.J.; Pemberton, M.A.; Pipinos, I.I.; Phillips, N.Y.; Herber, K.; Woodford, T.; Bowen, R.E.; Lomneth, C.S.; et al. Biaxial mechanical properties of the human thoracic and abdominal aorta, common carotid, subclavian, renal and common iliac arteries. Biomech. Model. Mechanobiol. 2014, 13, 1341–1359. [Google Scholar] [CrossRef]
- Ngwangwa, H.; Nemavhola, F.; Pandelani, T.; Msibi, M.; Mabuda, I.; Davies, N.; Franz, T. Determination of Cross-Directional and Cross-Wall Variations of Passive Biaxial Mechanical Properties of Rat Myocardia. Processes 2022, 10, 629. [Google Scholar] [CrossRef]
- Kim, J.H.; Avril, S.; Duprey, A.; Favre, J.P. Experimental Characterization of Rupture in Human Aortic Aneurysms Using a Full-Field Measurement Technique. Biomech. Model. Mechanobiol. 2012, 11, 841–853. [Google Scholar] [CrossRef] [PubMed]
- Pancheri, F.Q.; Peattie, R.A.; Reddy, N.D.; Ahamed, T.; Lin, W.; Ouellette, T.D.; Iafrati, M.D.; Luis Dorfmann, A. Histology and Biaxial Mechanical Behavior of Abdominal Aortic Aneurysm Tissue Samples. J. Biomech. Eng. 2017, 139, 031002. [Google Scholar] [CrossRef]
- García, A.; Peña, E.; Laborda, A.; Lostalé, F.; De Gregorio, M.; Doblaré, M.; Martínez, M. Experimental study and constitutive modelling of the passive mechanical properties of the porcine carotid artery and its relation to histological analysis: Implications in animal cardiovascular device trials. Med. Eng. Phys. 2011, 33, 665–676. [Google Scholar] [CrossRef] [PubMed]
- Sassani, S.G.; Kakisis, J.; Tsangaris, S.; Sokolis, D.P. Layer-dependent wall properties of abdominal aortic aneurysms: Experimental study and material characterization. J. Mech. Behav. Biomed. Mater. 2015, 49, 141–161. [Google Scholar] [CrossRef]
- Sassani, S.G.; Tsangaris, S.; Sokolis, D.P. Layer- and region-specific material characterization of ascending thoracic aortic aneurysms by microstructure-based models. J. Biomech. 2015, 48, 3757–3765. [Google Scholar] [CrossRef]
- Peña, J.; Martínez, M.; Peña, E. Failure damage mechanical properties of thoracic and abdominal porcine aorta layers and related constitutive modeling: Phenomenological and microstructural approach. Biomech. Model. Mechanobiol. 2019, 18, 1709–1730. [Google Scholar] [CrossRef]
- Geest, J.P.V.; Sacks, M.S.; Vorp, D.A. Age Dependency of the Biaxial Biomechanical Behavior of Human Abdominal Aorta. J. Biomech. Eng. 2004, 126, 815–822. [Google Scholar] [CrossRef]
- Sáez, P.; García, A.; Peña, E.; Gasser, T.; Martínez, M. Microstructural quantification of collagen fiber orientations and its integration in constitutive modeling of the porcine carotid artery. Acta Biomater. 2016, 33, 183–193. [Google Scholar] [CrossRef]
- Vande Geest, J.P.; Sacks, M.S.; Vorp, D.A. The effects of aneurysm on the biaxial mechanical behavior of human abdominal aorta. J. Biomech. 2006, 39, 1324–1334. [Google Scholar] [CrossRef] [PubMed]
- Amabili, M.; Balasubramanian, P.; Bozzo, I.; Breslavsky, I.D.; Ferrari, G. Layer-Specific Hyperelastic and Viscoelastic Characterization of Human Descending Thoracic Aortas. J. Mech. Behav. Biomed. Mater. 2019, 99, 27–46. [Google Scholar] [CrossRef] [PubMed]
- Ahuja, A.; Noblet, J.N.; Trudnowski, T.; Patel, B.; Krieger, J.F.; Chambers, S.; Kassab, G.S. Biomechanical Material Characterization of Stanford Type-B Dissected Porcine Aortas. Front. Physiol. 2018, 9, 1317. [Google Scholar] [CrossRef] [PubMed]
- Niestrawska, J.A.; Viertler, C.; Regitnig, P.; Cohnert, T.U.; Sommer, G.; Holzapfel, G.A. Microstructure and Mechanics of Healthy and Aneurysmatic Abdominal Aortas: Experimental Analysis and Modelling. J. R. Soc. Interface 2016, 13, 20160620. [Google Scholar] [CrossRef] [PubMed]
- Labrosse, M.R.; Beller, C.J.; Mesana, T.; Veinot, J.P. Mechanical Behavior of Human Aortas: Experiments, Material Constants and 3-D Finite Element Modeling Including Residual Stress. J. Biomech. 2009, 42, 996–1004. [Google Scholar] [CrossRef]
- Tarraf, S.A.; Kramer, B.; Vianna, E.; Gillespie, C.; Germano, E.; Emerton, K.B.; Amini, R.; Colbrunn, R.; Hargrave, J.; Roselli, E.E.; et al. Lengthwise Regional Mechanics of the Human Aneurysmal Ascending Thoracic Aorta. Acta Biomater. 2023, 162, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Nierenberger, M.; Fargier, G.; Ahzi, S.; Rémond, Y. Evolution of the Three-Dimensional Collagen Structure in Vascular Walls during Deformation: An in Situ Mechanical Testing under Multiphoton Microscopy Observation. Biomech. Model. Mechanobiol. 2015, 14, 693–702. [Google Scholar] [CrossRef] [PubMed]
- Lillie, M.; Gosline, J. Mechanical properties of elastin along the thoracic aorta in the pig. J. Biomech. 2007, 40, 2214–2221. [Google Scholar] [CrossRef]
- Kamenskiy, A.; Seas, A.; Deegan, P.; Poulson, W.; Anttila, E.; Sim, S.; Desyatova, A.; MacTaggart, J. Constitutive Description of Human Femoropopliteal Artery Aging. Biomech. Model. Mechanobiol. 2017, 16, 681–692. [Google Scholar] [CrossRef]
- Noble, C.; Smulders, N.; Green, N.H.; Lewis, R.; Carré, M.J.; Franklin, S.E.; MacNeil, S.; Taylor, Z.A. Creating a Model of Diseased Artery Damage and Failure from Healthy Porcine Aorta. J. Mech. Behav. Biomed. Mater. 2016, 60, 378–393. [Google Scholar] [CrossRef]
- Li, L.; Qian, X.; Yan, S.; Hua, L.; Zhang, H.; Liu, Z. Determination of the Material Parameters of Four-Fibre Family Model Based on Uniaxial Extension Data of Arterial Walls. Comput. Methods Biomech. Biomed. Engin. 2014, 17, 695–703. [Google Scholar] [CrossRef] [PubMed]
- Askari, F.; Shafieian, M.; Solouk, A.; Hashemi, A. A Comparison of the Material Properties of Natural and Synthetic Vascular Walls. J. Mech. Behav. Biomed. Mater. 2017, 71, 209–215. [Google Scholar] [CrossRef] [PubMed]
- Veselý, J.; Horný, L.; Chlup, H.; Adámek, T.; Krajíček, M.; Žitný, R. Constitutive Modeling of Human Saphenous Veins at Overloading Pressures. J. Mech. Behav. Biomed. Mater. 2015, 45, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Chow, M.J.; Zhang, Y. Changes in the mechanical and biochemical properties of aortic tissue due to cold storage. J. Surg. Res. 2011, 171, 434–442. [Google Scholar] [CrossRef]
- Wang, Y.; Zeinali-Davarani, S.; Zhang, Y. Arterial Mechanics Considering the Structural and Mechanical Contributions of ECM Constituents. J. Biomech. 2016, 49, 2358–2365. [Google Scholar] [CrossRef] [PubMed]
- Polzer, S.; Vitásek, R. Low Cycle Fatigue Properties of Porcine Aorta—Pilot Study. J. Mech. Behav. Biomed. Mater. 2023, 140, 105725. [Google Scholar] [CrossRef] [PubMed]
- Schroeder, F.; Polzer, S.; Slazansky, M.; Man, V.; Skacel, P. Predictive capabilities of various constitutive models for arterial tissue. J. Mech. Behav. Biomed. Mater. 2018, 78, 369–380. [Google Scholar] [CrossRef] [PubMed]
- Fischer, J.; Turčanová, M.; Man, V.; Hermanová, M.; Bednařík, Z.; Burša, J. Importance of Experimental Evaluation of Structural Parameters for Constitutive Modelling of Aorta. J. Mech. Behav. Biomed. Mater. 2023, 138, 105615. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Dong, H.; Russell, D.; Litsky, A.; Litsky, A.; Joseph, M.; Mo, X.; White, R.; White, R.; Kolipaka, A.; et al. In Vivo Aortic Magnetic Resonance Elastography in Abdominal Aortic Aneurysm: A Validation in an Animal Model. Investig. Radiol. 2020, 55, 463–472. [Google Scholar] [CrossRef]
- van Disseldorp, E.M.J.; van den Hoven, M.H.M.H.; van de Vosse, F.N.; van Sambeek, M.R.H.M.; Lopata, R.G.P. Reproducibility assessment of ultrasound-based aortic stiffness quantification and verification using Bi-axial tensile testing. J. Mech. Behav. Biomed. Mater. 2020, 103, 103571. [Google Scholar] [CrossRef]
- Santamaría, V.A.A.; García, M.F.; Molimard, J.; Avril, S. Characterization of Chemoelastic Effects in Arteries Using Digital Volume Correlation and Optical Coherence Tomography. Acta Biomater. 2020, 102, 127–137. [Google Scholar] [CrossRef] [PubMed]
- Lisický, O.; Avril, S.; Eydan, B.; Pierrat, B.; Burša, J. Evaluation of image registration for measuring deformation fields in soft tissue mechanics. Strain 2022, 58, e12424. [Google Scholar] [CrossRef]
- Wang, R.; Mattson, J.M.; Zhang, Y. Effect of Aging on the Biaxial Mechanical Behavior of Human Descending Thoracic Aorta: Experiments and Constitutive Modeling Considering Collagen Crosslinking. J. Mech. Behav. Biomed. Mater. 2023, 140, 105705. [Google Scholar] [CrossRef] [PubMed]
- Laffey, M.; Tornifoglio, B.; Lally, C. Development and Initial Characterisation of a Localised Elastin Degradation Ex Vivo Porcine Aortic Aneurysm Model. Appl. Sci. 2023, 13, 9894. [Google Scholar] [CrossRef]
- Pham, T.; Martin, C.; Elefteriades, J.; Sun, W. Biomechanical Characterization of Ascending Aortic Aneurysm with Concomitant Bicuspid Aortic Valve and Bovine Aortic Arch. Acta Biomater. 2013, 9, 7927–7936. [Google Scholar] [CrossRef] [PubMed]
- Tong, T.T.; Nightingale, M.; Scott, M.B.; Sigaeva, T.; Fedak, P.W.M.; Barker, A.J.; Di Martino, E.S. A Classification Approach to Improve out of Sample Predictability of Structure-based Constitutive Models for Ascending Thoracic Aortic Tissue. Int. J. Numer. Meth. Biomed. Eng. 2023, 39, e3708. [Google Scholar] [CrossRef]
- O’Leary, S.A.; Mulvihill, J.J.; Barrett, H.E.; Kavanagh, E.G.; Walsh, M.T.; McGloughlin, T.M.; Doyle, B.J. Determining the influence of calcification on the failure properties of abdominal aortic aneurysm (AAA) tissue. J. Mech. Behav. Biomed. Mater. 2015, 42, 154–167. [Google Scholar] [CrossRef] [PubMed]
- Alloisio, M.; Chatziefraimidou, M.; Roy, J.; Gasser, T.C. Fracture of Porcine Aorta—Part 1: SymconCT Fracture Testing and DIC. Acta Biomater. 2023, 167, 147–157. [Google Scholar] [CrossRef]
- Chen, L.; Gao, Z.; Liu, B.; Lv, Y.; An, M.; Feng, J. Circumferential Variation in Mechanical Characteristics of Porcine Descending Aorta. BIOCELL 2018, 42, 25–34. [Google Scholar] [CrossRef]
- Peña, J.A.; Corral, V.; Martínez, M.A.; Peña, E. Over length quantification of the multiaxial mechanical properties of the ascending, descending and abdominal aorta using Digital Image Correlation. J. Mech. Behav. Biomed. Mater. 2018, 77, 434–445. [Google Scholar] [CrossRef]
- Peña, J.; Martínez, M.; Peña, E. Layer-specific residual deformations and uniaxial and biaxial mechanical properties of thoracic porcine aorta. J. Mech. Behav. Biomed. Mater. 2015, 50, 55–69. [Google Scholar] [CrossRef] [PubMed]
- O’Leary, S.A.; Healey, D.A.; Kavanagh, E.G.; Walsh, M.T.; McGloughlin, T.M.; Doyle, B.J. The Biaxial Biomechanical Behavior of Abdominal Aortic Aneurysm Tissue. Ann. Biomed. Eng. 2014, 42, 2440–2450. [Google Scholar] [CrossRef] [PubMed]
- Cosentino, F.; Sherifova, S.; Sommer, G.; Raffa, G.; Pilato, M.; Pasta, S.; Holzapfel, G.A. Regional Biomechanical Characterization of Human Ascending Aortic Aneurysms: Microstructure and Biaxial Mechanical Response. Acta Biomater. 2023, 169, 107–117. [Google Scholar] [CrossRef] [PubMed]
- García-Herrera, C.M.; Bustos, C.A.; Celentano, D.J.; Ortega, R. Mechanical Analysis of the Ring Opening Test Applied to Human Ascending Aortas. Comput. Methods Biomech. Biomed. Engin. 2016, 19, 1738–1748. [Google Scholar] [CrossRef] [PubMed]
- Brass, M.; Kassab, G.S. Iliac Veins Are More Compressible Than Iliac Arteries: A New Method of Testing. J. Biomech. Eng. 2019, 141, 091005. [Google Scholar] [CrossRef] [PubMed]
- Gundiah, N.; Ratcliffe, M.B.; Pruitt, L.A. The Biomechanics of Arterial Elastin. J. Mech. Behav. Biomed. Mater. 2009, 2, 288–296. [Google Scholar] [CrossRef] [PubMed]
- Gundiah, N.; B Ratcliffe, M.; A Pruitt, L. Determination of Strain Energy Function for Arterial Elastin: Experiments Using Histology and Mechanical Tests. J. Biomech. 2007, 40, 586–594. [Google Scholar] [CrossRef] [PubMed]
- García-Herrera, C.; Celentano, D.; Cruchaga, M.; Rojo, F.; Atienza, J.; Guinea, G.; Goicolea, J. Mechanical characterisation of the human thoracic descending aorta: Experiments and modelling. Comput. Methods Biomech. Biomed. Engin. 2012, 15, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Davis, F.M.; Luo, Y.; Avril, S.; Duprey, A.; Lu, J. Pointwise Characterization of the Elastic Properties of Planar Soft Tissues: Application to Ascending Thoracic Aneurysms. Biomech. Model. Mechanobiol. 2015, 14, 967–978. [Google Scholar] [CrossRef]
- Bernal, M.; Urban, M.W.; Rosario, D.; Aquino, W.; Greenleaf, J.F. Measurement of biaxial mechanical properties of soft tubes and arteries using piezoelectric elements and sonometry. Phys. Med. Biol. 2011, 56, 3371–3386. [Google Scholar] [CrossRef][Green Version]
- Prim, D.A.; Mohamed, M.A.; Lane, B.A.; Poblete, K.; Wierzbicki, M.A.; Lessner, S.M.; Shazly, T.; Eberth, J.F. Comparative mechanics of diverse mammalian carotid arteries. PLoS ONE 2018, 13, e0202123. [Google Scholar] [CrossRef] [PubMed]
- Ayyalasomayajula, V.; Pierrat, B.; Badel, P. Evaluation of a Multi-Scale Discrete Fiber Model for Analyzing Arterial Failure. J. Biomech. 2023, 157, 111700. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Pei, M.; Zhang, J.; Liu, N.; Wang, J.; Zou, D. A Study to Characterize the Mechanical Properties and Material Constitution of Adult Descending Thoracic Aorta Based on Uniaxial Tensile Test and Digital Image Correlation. Front. Bioeng. Biotechnol. 2023, 11, 1178199. [Google Scholar] [CrossRef] [PubMed]
- Laksari, K.; Shahmirzadi, D.; Acosta, C.J.; Konofagou, E. Energy-based constitutive modelling of local material properties of canine aortas. R. Soc. Open Sci. 2016, 3, 160365. [Google Scholar] [CrossRef] [PubMed]
- Kazim, M.; Razian, S.A.; Zamani, E.; Varandani, D.; Shahbad, R.; Desyatova, A.; Jadidi, M. Variability in Structure, Morphology, and Mechanical Properties of the Descending Thoracic and Infrarenal Aorta around Their Circumference. J. Mech. Behav. Biomed. Mater. 2024, 150, 106332. [Google Scholar] [CrossRef] [PubMed]
- Jadidi, M.; Habibnezhad, M.; Anttila, E.; Maleckis, K.; Desyatova, A.; MacTaggart, J.; Kamenskiy, A. Mechanical and structural changes in human thoracic aortas with age. Acta Biomater. 2020, 103, 172–188. [Google Scholar] [CrossRef] [PubMed]
- Gaur, P.; Sharma, S.; Kumar, D.; Chawla, A.; Mukherjee, S.; Jain, M.; Mayer, C.; Chitteti, R.K.; Ghosh, P.; Malhotra, R.; et al. Inverse Material Characterisation of Human Aortic Tissue for Traumatic Injury in Motor Vehicle Crashes. Int. J. Crashworthiness 2022, 27, 347–366. [Google Scholar] [CrossRef]
- Martufi, G.; Forneris, A.; Nobakht, S.; Rinker, K.D.; Moore, R.D.; Di Martino, E.S. Case Study: Intra-Patient Heterogeneity of Aneurysmal Tissue Properties. Front. Cardiovasc. Med. 2018, 5, 82. [Google Scholar] [CrossRef]
- Rastgar Agah, M.; Laksari, K.; Assari, S.; Darvish, K. Mechanical Behavior of Porcine Thoracic Aorta in Physiological and Supra-Physiological Intraluminal Pressures. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2017, 231, 326–336. [Google Scholar] [CrossRef]
- Dwivedi, K.K.; Lakhani, P.; Yadav, A.; Deepak; Kumar, S.; Kumar, N. Location Specific Multi-Scale Characterization and Constitutive Modeling of Pig Aorta. J. Mech. Behav. Biomed. Mater. 2023, 142, 105809. [Google Scholar] [CrossRef]
- Taghizadeh, H.; Tafazzoli-Shadpour, M.; Shadmehr, M.; Fatouraee, N. Evaluation of Biaxial Mechanical Properties of Aortic Media Based on the Lamellar Microstructure. Materials 2015, 8, 302–316. [Google Scholar] [CrossRef] [PubMed]
- Potter, S.; Graves, J.; Drach, B.; Leahy, T.; Hammel, C.; Feng, Y.; Baker, A.; Sacks, M.S. A Novel Small-Specimen Planar Biaxial Testing System With Full In-Plane Deformation Control. J. Biomech. Eng. 2018, 140, 051001. [Google Scholar] [CrossRef] [PubMed]
- Taghizadeh, H.; Tafazzoli-Shadpour, M. Characterization of mechanical properties of lamellar structure of the aortic wall: Effect of aging. J. Mech. Behav. Biomed. Mater. 2017, 65, 20–28. [Google Scholar] [CrossRef] [PubMed]
- Korenczuk, C.E.; Votava, L.E.; Dhume, R.Y.; Kizilski, S.B.; Brown, G.E.; Narain, R.; Barocas, V.H. Isotropic Failure Criteria Are Not Appropriate for Anisotropic Fibrous Biological Tissues. J. Biomech. Eng. 2017, 139, 071008. [Google Scholar] [CrossRef] [PubMed]
- Myneni, M.; Sridhar, R.L.; Rajagopal, K.R.; Benjamin, C.C. Experimental Investigation of the Anisotropic Mechanical Response of the Porcine Thoracic Aorta. Ann. Biomed. Eng. 2022, 50, 452–466. [Google Scholar] [CrossRef] [PubMed]
- Lillie, M.; Shadwick, R.; Gosline, J. Mechanical Anisotropy of Inflated Elastic Tissue from the Pig Aorta. J. Biomech. 2010, 43, 2070–2078. [Google Scholar] [CrossRef] [PubMed]
- Sigaeva, T.; Polzer, S.; Vitásek, R.; Di Martino, E.S. Effect of Testing Conditions on the Mechanical Response of Aortic Tissues from Planar Biaxial Experiments: Loading Protocol and Specimen Side. J. Mech. Behav. Biomed. Mater. 2020, 111, 103882. [Google Scholar] [CrossRef]
- Sigaeva, T.; Sattari, S.; Polzer, S.; Appoo, J.J.; Di Martino, E.S. Biomechanical Properties of Ascending Aortic Aneurysms: Quantification of Inter- and Intra-Patient Variability. J. Biomech. 2021, 125, 110542. [Google Scholar] [CrossRef] [PubMed]
- Nolan, D.R.; McGarry, J.P. On the Compressibility of Arterial Tissue. Ann. Biomed. Eng. 2016, 44, 993–1007. [Google Scholar] [CrossRef]
- Fehervary, H.; Vander Sloten, J.; Famaey, N. Development of an Improved Parameter Fitting Method for Planar Biaxial Testing Using Rakes. Int. J. Numer. Meth. Biomed. Eng. 2019, 35, e3174. [Google Scholar] [CrossRef]
- Smoljkić, M.; Verbrugghe, P.; Larsson, M.; Widman, E.; Fehervary, H.; D’hooge, J.; Vander Sloten, J.; Famaey, N. Comparison of in vivo vs. ex situ obtained material properties of sheep common carotid artery. Med. Eng. Phys. 2018, 55, 16–24. [Google Scholar] [CrossRef]
- Gundiah, N.; Kam, K.; Matthews, P.; Guccione, J.; Dwyer, H.; Saloner, D.; Chuter, T.; Guy, T.; Ratcliffe, M.; Tseng, E. Asymmetric Mechanical Properties of Porcine Aortic Sinuses. Ann. Thorac. Surg. 2008, 85, 1631–1638. [Google Scholar] [CrossRef] [PubMed]
- Veljković, D.Z.; Ranković, V.J.; Pantović, S.B.; Rosić, M.A.; Kojić, M.R. Hyperelastic behavior of porcine aorta segment under extension-inflation tests fitted with various phenomenological models. Acta Bioeng. Biomech. 2014, 16, 37–45. [Google Scholar] [CrossRef]
- Forsell, C.; Swedenborg, J.; Roy, J.; Gasser, T.C. The Quasi-Static Failure Properties of the Abdominal Aortic Aneurysm Wall Estimated by a Mixed Experimental-Numerical Approach. Ann. Biomed. Eng. 2013, 41, 1554–1566. [Google Scholar] [CrossRef] [PubMed]
- Geelhoed, W.J.; Lalai, R.A.; Sinnige, J.H.; Jongeleen, P.J.; Storm, C.; Rotmans, J.I. Indirect Burst Pressure Measurements for the Mechanical Assessment of Biological Vessels. Tissue Eng. Part C Methods 2019, 25, 472–478. [Google Scholar] [CrossRef] [PubMed]
- Vallabhaneni, S.; Gilling-Smith, G.; How, T.; Carter, S.; Brennan, J.; Harris, P. Heterogeneity of tensile strength and matrix metalloproteinase activity in the wall of abdominal aortic aneurysms. J. Endovasc. Ther. 2004, 11, 494–502. [Google Scholar] [CrossRef]
- Zhou, B.; Ravindran, S.; Ferdous, J.; Kidane, A.; Sutton, M.; Shazly, T. Using digital image correlation to characterize local strains on vascular tissue specimens. J. Vis. Exp. 2016, 2016. [Google Scholar] [CrossRef]
- Huh, U.; Lee, C.W.; You, J.H.; Song, C.H.; Lee, C.S.; Ryu, D.M. Determination of the Material Parameters in the Holzapfel-Gasser-Ogden Constitutive Model for Simulation of Age-Dependent Material Nonlinear Behavior for Aortic Wall Tissue under Uniaxial Tension. Appl. Sci. 2019, 9, 2851. [Google Scholar] [CrossRef]
- Guo, X.; Gong, C.; Zhai, Y.; Yu, H.; Li, J.; Sun, H.; Wang, L.; Tang, D. Biomechanical Characterization of Normal and Pathological Human Ascending Aortic Tissues via Biaxial Testing Experiment, Constitutive Modeling and Finite Element Analysis. Comput. Biol. Med. 2023, 166, 107561. [Google Scholar] [CrossRef]
- Ning, J.; Xu, S.; Wang, Y.; Lessner, S.M.; Sutton, M.A.; Anderson, K.; Bischoff, J.E. Deformation Measurements and Material Property Estimation of Mouse Carotid Artery Using a Microstructure-Based Constitutive Model. J. Biomech. Eng. 2010, 132, 121010. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Z.; Qi, H.J.; Wang, T. A Micro-Structure Based Constitutive Model for Anisotropic Stress–Strain Behaviors of Artery Tissues. Int. J. Solids Struct. 2018, 139–140, 55–64. [Google Scholar] [CrossRef]
- Collins, M.; Bersi, M.; Wilson, E.; Humphrey, J. Mechanical Properties of Suprarenal and Infrarenal Abdominal Aorta: Implications for Mouse Models of Aneurysms. Med. Eng. Phys. 2011, 33, 1262–1269. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Salmasi, M.Y.; Sasidharan, S.; Frattolin, J.; Edgar, L.; Stock, U.; Athanasiou, T.; Moore, J., Jr. Regional Variation in Biomechanical Properties of Ascending Thoracic Aortic Aneurysms. Eur. J. Cardiothorac Surg. 2022, 62, ezac392. [Google Scholar] [CrossRef]
- Fonck, E.; Prod’hom, G.; Roy, S.; Augsburger, L.; Rüfenacht, D.A.; Stergiopulos, N. Effect of Elastin Degradation on Carotid Wall Mechanics as Assessed by a Constituent-Based Biomechanical Model. Am. J. Physiol. Heart Circ. Physiol. 2007, 292, H2754–H2763. [Google Scholar] [CrossRef] [PubMed]
- Lillie, M.A.; David, G.J.; Gosline, J.M. Mechanical Role of Elastin-Associated Microfibrils in Pig Aortic Elastic Tissue. Connect. Tissue Res. 1998, 37, 121–141. [Google Scholar] [CrossRef]
- Yu, X.; Turcotte, R.; Seta, F.; Zhang, Y. Micromechanics of elastic lamellae: Unravelling the role of structural inhomogeneity in multi-scale arterial mechanics. J. R. Soc. Interface 2018, 15, 20180492. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Wang, Y.; Zhang, Y. Transmural variation in elastin fiber orientation distribution in the arterial wall. J. Mech. Behav. Biomed. Mater. 2018, 77, 745–753. [Google Scholar] [CrossRef] [PubMed]
- Assoul, N.; Flaud, P.; Chaouat, M.; Letourneur, D.; Bataille, I. Mechanical Properties of Rat Thoracic and Abdominal Aortas. J. Biomech. 2008, 41, 2227–2236. [Google Scholar] [CrossRef] [PubMed]
- Collins, M.; Eberth, J.; Wilson, E.; Humphrey, J. Acute Mechanical Effects of Elastase on the Infrarenal Mouse Aorta: Implications for Models of Aneurysms. J. Biomech. 2012, 45, 660–665. [Google Scholar] [CrossRef]
- Cosentino, F.; Agnese, V.; Raffa, G.M.; Gentile, G.; Bellavia, D.; Zingales, M.; Pilato, M.; Pasta, S. On the Role of Material Properties in Ascending Thoracic Aortic Aneurysms. Comput. Biol. Med. 2019, 109, 70–78. [Google Scholar] [CrossRef]
- Pasta, S.; Phillippi, J.; Tsamis, A.; D’Amore, A.; Raffa, G.; Pilato, M.; Scardulla, C.; Watkins, S.; Wagner, W.; Gleason, T.; et al. Constitutive modeling of ascending thoracic aortic aneurysms using microstructural parameters. Med. Eng. Phys. 2016, 38, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Di Giuseppe, M.; Alotta, G.; Agnese, V.; Bellavia, D.; Raffa, G.; Vetri, V.; Zingales, M.; Pasta, S.; Pilato, M. Identification of circumferential regional heterogeneity of ascending thoracic aneurysmal aorta by biaxial mechanical testing. J. Mol. Cell. Cardiol. 2019, 130, 205–215. [Google Scholar] [CrossRef] [PubMed]
- Martufi, G.; Satriano, A.; Moore, R.D.; Vorp, D.A.; Di Martino, E.S. Local Quantification of Wall Thickness and Intraluminal Thrombus Offer Insight into the Mechanical Properties of the Aneurysmal Aorta. Ann. Biomed. Eng. 2015, 43, 1759–1771. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, V.; Kollimada, S.A.; Byju, A.G.; Gundiah, N. Regional Variations in the Nonlinearity and Anisotropy of Bovine Aortic Elastin. Biomech. Model. Mechanobiol. 2013, 12, 1181–1194. [Google Scholar] [CrossRef]
- Deng, S.X.; Tomioka, J.; Debes, J.C.; Fung, Y.C. New Experiments on Shear Modulus of Elasticity of Arteries. Am. J. Physiol. Heart Circ. Physiol. 1994, 266, H1–H10. [Google Scholar] [CrossRef] [PubMed]
- Ferraresi, C.; Bertetto, A.M.; Mazza, L.; Maffiodo, D.; Franco, W. One-Dimensional Experimental Mechanical Characterisation of Porcine Aortic Root Wall. Med. Biol. Eng. Comput. 1999, 37, 202–207. [Google Scholar] [CrossRef] [PubMed]
- Ramachandra, A.B.; Cavinato, C.; Humphrey, J.D. A Systematic Comparison of Normal Structure and Function of the Greater Thoracic Vessels. Ann. Biomed. Eng. 2024, 52, 958–966. [Google Scholar] [CrossRef]
- Bersi, M.R.; Bellini, C.; Humphrey, J.D.; Avril, S. Local Variations in Material and Structural Properties Characterize Murine Thoracic Aortic Aneurysm Mechanics. Biomech. Model. Mechanobiol. 2019, 18, 203–218. [Google Scholar] [CrossRef]
- Bersi, M.R.; Bellini, C.; Di Achille, P.; Humphrey, J.D.; Genovese, K.; Avril, S. Novel Methodology for Characterizing Regional Variations in the Material Properties of Murine Aortas. J. Biomech. Eng. 2016, 138, 071005. [Google Scholar] [CrossRef]
- Vargas, A.I.; Tarraf, S.A.; Jennings, T.; Bellini, C.; Amini, R. Vascular Remodeling During Late-Gestation Pregnancy: An In-Vitro Assessment of the Murine Ascending Thoracic Aorta. J. Biomech. Eng. 2024, 146, 071004. [Google Scholar] [CrossRef]
- Keyes, J.T.; Haskett, D.G.; Utzinger, U.; Azhar, M.; Vande Geest, J.P. Adaptation of a Planar Microbiaxial Optomechanical Device for the Tubular Biaxial Microstructural and Macroscopic Characterization of Small Vascular Tissues. J. Biomech. Eng. 2011, 133, 075001. [Google Scholar] [CrossRef] [PubMed]
- Vander Linden, K.; Fehervary, H.; Vastmans, J.; Famaey, N. The influence of out-of-plane motion on the deformation measurement of planar biaxial tests on biological soft tissue. Mech. Res. Commun. 2023, 129, 104099. [Google Scholar] [CrossRef]
- de Deus Filho, J.C.A.; da Silva Nunes, L.C.; Xavier, J.M.C. iCorrVision-2D: An integrated python-based open-source Digital Image Correlation software for in-plane measurements (Part 1). SoftwareX 2022, 19, 101131. [Google Scholar] [CrossRef]
- Xavier, J.; Morais, J.; Pereira, F. Non-linear shear behaviour of bovine cortical bone by coupling the Arcan test with digital image correlation. Opt. Lasers Eng. 2018, 110, 462–470. [Google Scholar] [CrossRef]
- Lionello, G.; Sirieix, C.; Baleani, M. An effective procedure to create a speckle pattern on biological soft tissue for digital image correlation measurements. J. Mech. Behav. Biomed. Mater. 2014, 39, 1–8. [Google Scholar] [CrossRef]
- Xavier, J.; de Jesus, A.; Morais, J.; Pinto, J. Stereovision measurements on evaluating the modulus of elasticity of wood by compression tests parallel to the grain. Constr. Build. Mater. 2012, 26, 207–215. [Google Scholar] [CrossRef]
- Pereira, J.; Xavier, J.; Ghiassi, B.; Lousada, J.; Morais, J. On the identification of earlywood and latewood radial elastic modulus of Pinus pinaster by digital image correlation: A parametric analysis. J. Strain Anal. Eng. Des. 2018, 53, 566–574. [Google Scholar] [CrossRef]
- Marco Palanca, G.T.; Cristofolini, L. The use of digital image correlation in the biomechanical area: A review. Int. Biomech. 2016, 3, 1–21. [Google Scholar] [CrossRef]
- Waffenschmidt, T.; Cilla, M.; Sáez, P.; Pérez, M.; Martínez, M.; Menzel, A.; Peña, E. Towards the modelling of ageing and atherosclerosis effects in ApoE-/- mice aortic tissue. J. Biomech. 2016, 49, 2390–2397. [Google Scholar] [CrossRef]
- Xavier, J.; Pereira, J.; de Jesus, A. Characterisation of steel components under monotonic loading by means of image-based methods. Opt. Lasers Eng. 2014, 53, 142–151. [Google Scholar] [CrossRef]
- Ryu, D.; Baek, S.; Kim, J. Region-Dependent Mechanical Characterization of Porcine Thoracic Aorta with a One-to-Many Correspondence Method to Create Virtual Datasets Using Uniaxial Tensile Tests. Front. Bioeng. Biotechnol. 2022, 10, 937326. [Google Scholar] [CrossRef]
- Acosta-Santamaría, V.A.; Flechas García, M.; Molimard, J.; Avril, S. Three-Dimensional Full-Field Strain Measurements across a Whole Porcine Aorta Subjected to Tensile Loading Using Optical Coherence Tomography–Digital Volume Correlation. Front. Mech. Eng. 2018, 4, 3. [Google Scholar] [CrossRef]
- Marini, G.; Maier, A.; Reeps, C.; Eckstein, H.H.; Wall, W.A.; Gee, M.W. A Continuum Description of the Damage Process in the Arterial Wall of Abdominal Aortic Aneurysms. Int. J. Numer. Meth. Biomed. Eng. 2012, 28, 87–99. [Google Scholar] [CrossRef]
- Jiang, M.; Sridhar, R.L.; Robbins, A.B.; Freed, A.D.; Moreno, M.R. A versatile biaxial testing platform for soft tissues. J. Mech. Behav. Biomed. Mater. 2021, 114, 104144. [Google Scholar] [CrossRef]
- Zeinali-Davarani, S.; Wang, Y.; Chow, M.J.; Turcotte, R.; Zhang, Y. Contribution of Collagen Fiber Undulation to Regional Biomechanical Properties Along Porcine Thoracic Aorta. J. Biomech. Eng. 2015, 137, 051001. [Google Scholar] [CrossRef]
- Turčanová, M.; Fischer, J.; Hermanová, M.; Bednařík, Z.; Skácel, P.; Burša, J. Biaxial Stretch Can Overcome Discrepancy between Global and Local Orientations of Wavy Collagen Fibres. J. Biomech. 2023, 161, 111868. [Google Scholar] [CrossRef]
- Schulze-Bauer, C.A.J.; Mo¨rth, C.; Holzapfel, G.A. Passive Biaxial Mechanical Response of Aged Human Iliac Arteries. J. Biomech. Eng. 2003, 125, 395–406. [Google Scholar] [CrossRef]
- Eberth, J.; Popovic, N.; Gresham, V.; Wilson, E.; Humphrey, J. Time course of carotid artery growth and remodeling in response to altered pulsatility. Am. J. Physiol. Heart Circ. Physiol. 2010, 299, H1875–H1883. [Google Scholar] [CrossRef][Green Version]
- Sommer, G.; Benedikt, C.; Niestrawska, J.A.; Hohenberger, G.; Viertler, C.; Regitnig, P.; Cohnert, T.U.; Holzapfel, G.A. Mechanical response of human subclavian and iliac arteries to extension, inflation and torsion. Acta Biomater. 2018, 75, 235–252. [Google Scholar] [CrossRef]
- Voňavková, T.; Horný, L. Effect of Axial Prestretch and Adipose Tissue on the Inflation-Extension Behavior of the Human Abdominal Aorta. Comput. Methods Biomech. Biomed. Engin. 2020, 23, 81–91. [Google Scholar] [CrossRef]
- Famaey, N.; Fehervary, H.; Akyildiz, A.; Bruyère-Garnier, K.; Lafon, Y. C4Bio: Community challenge towards consensus on characterization of biological tissue, Perspective talk on European Society of Biomechanics. In Proceedings of the 27th Congress of the European Society of Biomechanics, Porto, Portugal, 26–29 June 2022; Available online: https://c4bio.eu (accessed on 13 May 2024).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valente, R.; Mourato, A.; Xavier, J.; Sousa, P.; Domingues, T.; Tavares, P.; Avril, S.; Tomás, A.; Fragata, J. Experimental Protocols to Test Aortic Soft Tissues: A Systematic Review. Bioengineering 2024, 11, 745. https://doi.org/10.3390/bioengineering11080745
Valente R, Mourato A, Xavier J, Sousa P, Domingues T, Tavares P, Avril S, Tomás A, Fragata J. Experimental Protocols to Test Aortic Soft Tissues: A Systematic Review. Bioengineering. 2024; 11(8):745. https://doi.org/10.3390/bioengineering11080745
Chicago/Turabian StyleValente, Rodrigo, André Mourato, José Xavier, Pedro Sousa, Tiago Domingues, Paulo Tavares, Stéphane Avril, António Tomás, and José Fragata. 2024. "Experimental Protocols to Test Aortic Soft Tissues: A Systematic Review" Bioengineering 11, no. 8: 745. https://doi.org/10.3390/bioengineering11080745
APA StyleValente, R., Mourato, A., Xavier, J., Sousa, P., Domingues, T., Tavares, P., Avril, S., Tomás, A., & Fragata, J. (2024). Experimental Protocols to Test Aortic Soft Tissues: A Systematic Review. Bioengineering, 11(8), 745. https://doi.org/10.3390/bioengineering11080745









