Evaluation of Denoising Performance of ResNet Deep Learning Model for Ultrasound Images Corresponding to Two Frequency Parameters
Abstract
1. Introduction
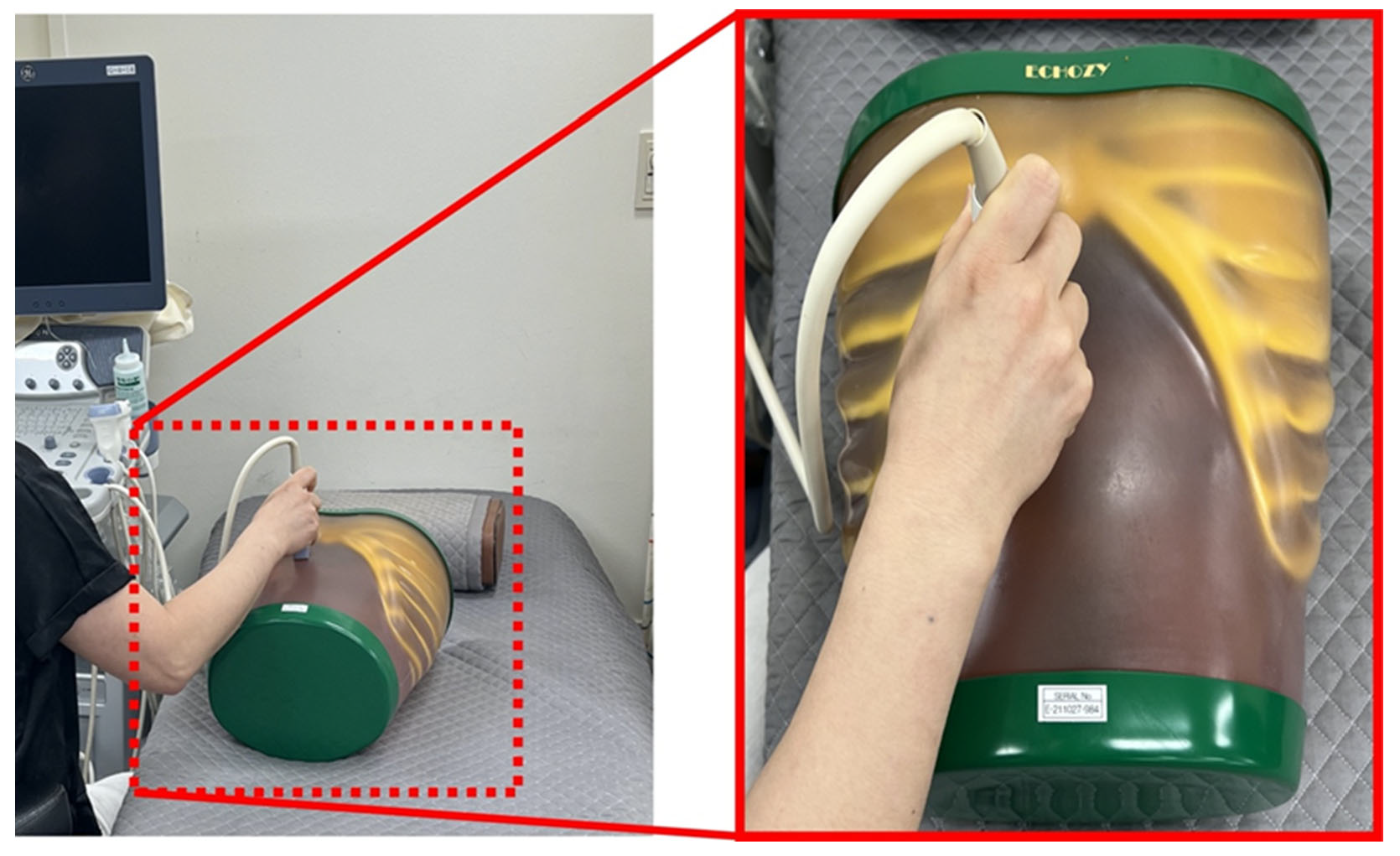
2. Materials and Methods
2.1. Dataset and ResNet Framework
2.2. Quantitative Analysis
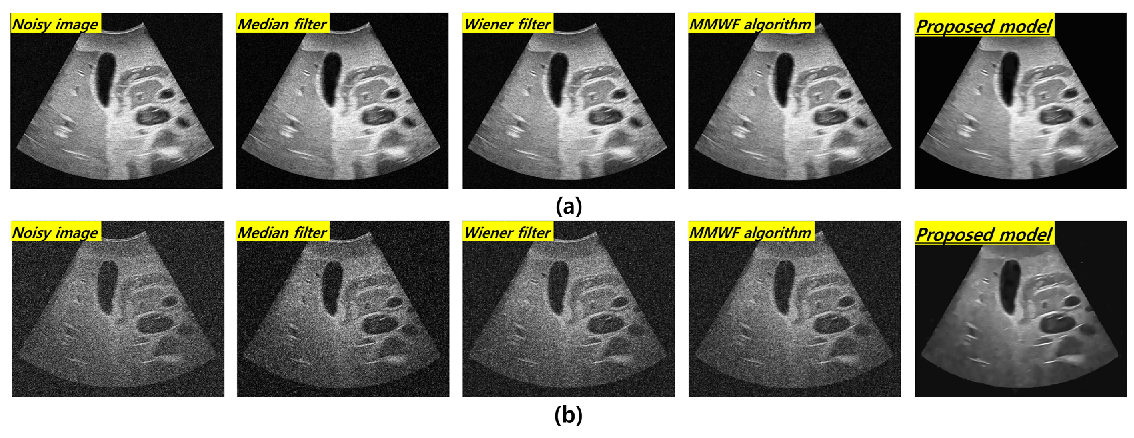
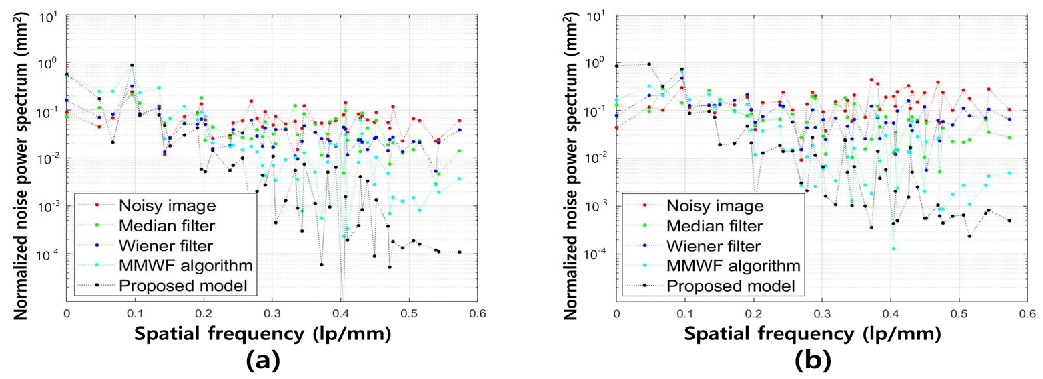
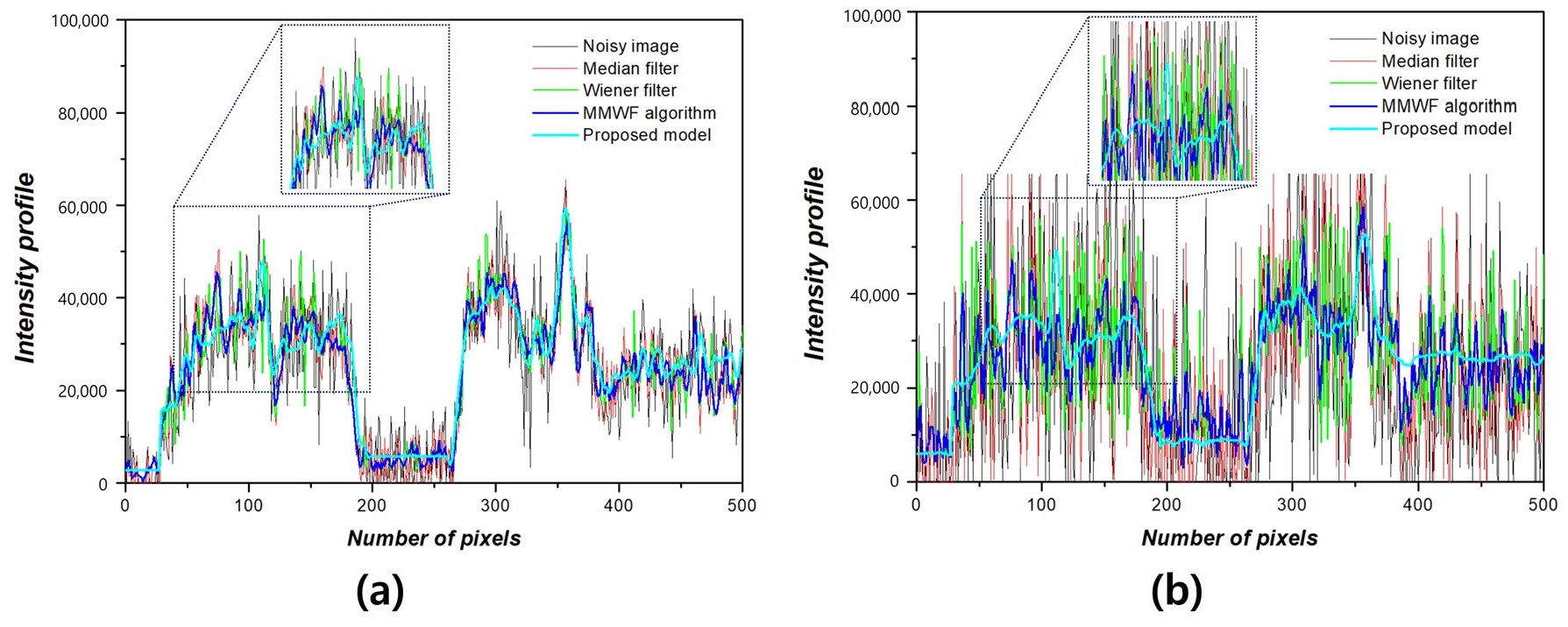
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McCollough, C.H.; Leng, S.; Yu, L.; Fletcher, J.G. Dual- and Multi-Energy CT: Principles, Technical Approaches, and Clinical Applications. Radiology 2015, 276, 637–653. [Google Scholar] [CrossRef] [PubMed]
- Zaidi, H.; Del Guerra, A.D. An outlook on future design of hybrid PET/MRI systems. Med. Phys. 2011, 38, 5667–5689. [Google Scholar] [CrossRef] [PubMed]
- Woods, J.C.; Wild, J.M.; Wielpütz, M.O.; Clancy, J.P.; Hatabu, H.; Kauczor, H.U.; van Beek, E.J.R.; Altes, T.A. Current state of the art MRI for the longitudinal assessment of cystic fibrosis. J. Magn. Reson. Imaging 2020, 52, 1306–1320. [Google Scholar] [CrossRef] [PubMed]
- Ballanger, B.; Jahanshahi, M.; Broussolle, E.; Thobois, S. PET functional imaging of deep brain stimulation in movement disorders and psychiatry. J. Cereb. Blood Flow Metab. 2009, 29, 1743–1754. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Some fundamental properties of speckle. J. Opt. Soc. Am. 1976, 66, 1145–1150. [Google Scholar] [CrossRef]
- Pradeep, S.; Nirmaladevi, P. A Review on Speckle Noise Reduction Techniques in Ultrasound Medical images based on Spatial Domain, Transform Domain and CNN Methods. IOP Conf. Ser. Master. Sci. Eng. 2021, 1055, 012116. [Google Scholar] [CrossRef]
- Liu, W.; Lin, W. Additive white Gaussian noise level estimation in SVD domain for images. IEEE Trans. Image Process. 2013, 22, 872–883. [Google Scholar] [CrossRef]
- Russo, F. A method for estimation and filtering of Gaussian noise in images. IEEE Trans. Instrum. Meas. 2003, 52, 1148–1154. [Google Scholar] [CrossRef]
- Lan, Y.; Zhang, X. Real-Time Ultrasound Image Despeckling Using Mixed-Attention Mechanism Based Residual UNet. IEEE Access 2020, 8, 195327–195340. [Google Scholar] [CrossRef]
- Mafi, M.; Tabarestani, S.; Cabrerizo, M.; Barreto, A.; Adjouadi, M. Denoising of ultrasound images affected by combined speckle and Gaussian noise. IET Image Process. 2018, 12, 2346–2351. [Google Scholar] [CrossRef]
- Singh, M.; Singh, S.; Kansal, S. Comparative Analysis of Spatial filters for Speckle Reduction in Ultrasound Images. In Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering, Los Angeles, CA, USA, 31 March–2 April 2009; Volume 6, pp. 228–232. [Google Scholar]
- Kumar, S.; Kumar, P.; Gupta, M.; Nagawat, A.K. Performance comparison of median and wiener filter in image de-noising. Int. J. Comput. Appl. 2010, 12, 27–31. [Google Scholar]
- Park, J.; Song, S.; Kang, S.H.; Lee, Y. Performance evaluation of improved median-modified Wiener filter with segmentation method to improve resolution in computed tomographic images. J. Korean Phys. Soc. 2024, 84, 573–581. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y. Performance evaluation of median-modified Wiener filter algorithm in high-resolution complementary metal–oxide–semiconductor radio-agnetic X-ray imaging system: An experimental study. Nucl. Instrum. Methods Phys. Res. A 2021, 1010, 165509. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Chen, M.; Fang, H.; Zhong, S. Two-Stage Convolutional Neural Network for Medical Noise Removal via Image Decomposition. IEEE Trans. Instrum. Meas. 2020, 69, 2707–2721. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning log-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. Learn. Syst. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Foster, F.S.; Pavlin, C.J.; Harasiewicz, K.A.; Christopher, D.A.; Turnbull, D.H. Advances in ultrasound biomicroscopy. Ultrasound Med. Biol. 2000, 26, 1–27. [Google Scholar] [CrossRef]
- Huang, Y.M.; Ng, M.K.; Wen, Y.W. A new total variation method for multiplicative noise removal. SIAM J. Imaging Sci. 2009, 2, 20. [Google Scholar] [CrossRef]
- Wang, S.; Huang, T.Z.; Zhao, X.L.; Mei, J.J.; Huang, J. Speckle noise removal in ultrasound images by first- and second-order total variation. Numer. Algorithms 2017, 78, 513–533. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556v6. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Muhtar, Y.; Muhammat, M.; Yadikar, N.; Aysa, A.; Ubul, K. FC-ResNet: A Multilingual Handwritten Signature Verification Model Using an Improved ResNet with CBAM. Appl. Sci. 2023, 13, 8022. [Google Scholar] [CrossRef]
- Mohamed, A.F.; Saba, A.; Hassan, M.K.; Youssef, H.M.; Dahou, A.; Elsheikh, A.H.; El-Bary, A.A.; Elaziz, M.A.; Ibrahim, R.A. Boosted Nutcracker optimizer and Chaos Game Optimization with Cross Vision Transformer for medical image classification. Egypt. Inform. J. 2024, 26, 100457. [Google Scholar] [CrossRef]
- Ukwuoma, C.C.; Qin, Z.; Heyat, M.B.B.; Akhtar, F.; Smahi, A.; Jackson, J.K.; Qadri, S.F.; Muaad, A.Y.; Monday, H.N.; Nneji, G.U. Automated lung-related pneumonia and COVID-19 detection based on novel feature extraction framework and vision transformer approaches using chest X-ray images. Bioengineering 2022, 9, 709. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Kumar, M.; Kumar, A.; Verma, B.K.; Abhishek, K.; Selvarajan, S. Efficient pneumonia detection using Vision Transformers on chest X-rays. Sci. Rep. 2024, 14, 2487. [Google Scholar] [CrossRef]
- Altini, N.; Brunetti, A.; Puro, E.; Taccogna, M.G.; Saponaro, C.; Zito, F.A.; Summa, S.D.; Bevilacqua, V. NDG-CAM:Nuclei detection in histopathology images with semantic segmentation networks and Grad-CAM. Bioengineering 2022, 9, 475. [Google Scholar] [CrossRef] [PubMed]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, H.; Park, C.; Yang, H. Evaluation of Denoising Performance of ResNet Deep Learning Model for Ultrasound Images Corresponding to Two Frequency Parameters. Bioengineering 2024, 11, 723. https://doi.org/10.3390/bioengineering11070723
Kang H, Park C, Yang H. Evaluation of Denoising Performance of ResNet Deep Learning Model for Ultrasound Images Corresponding to Two Frequency Parameters. Bioengineering. 2024; 11(7):723. https://doi.org/10.3390/bioengineering11070723
Chicago/Turabian StyleKang, Hyekyoung, Chanrok Park, and Hyungjin Yang. 2024. "Evaluation of Denoising Performance of ResNet Deep Learning Model for Ultrasound Images Corresponding to Two Frequency Parameters" Bioengineering 11, no. 7: 723. https://doi.org/10.3390/bioengineering11070723
APA StyleKang, H., Park, C., & Yang, H. (2024). Evaluation of Denoising Performance of ResNet Deep Learning Model for Ultrasound Images Corresponding to Two Frequency Parameters. Bioengineering, 11(7), 723. https://doi.org/10.3390/bioengineering11070723





