Investigation of Deconvolution Method with Adaptive Point Spread Function Based on Scintillator Thickness in Wavelet Domain
Abstract
1. Introduction
2. Materials and Methods
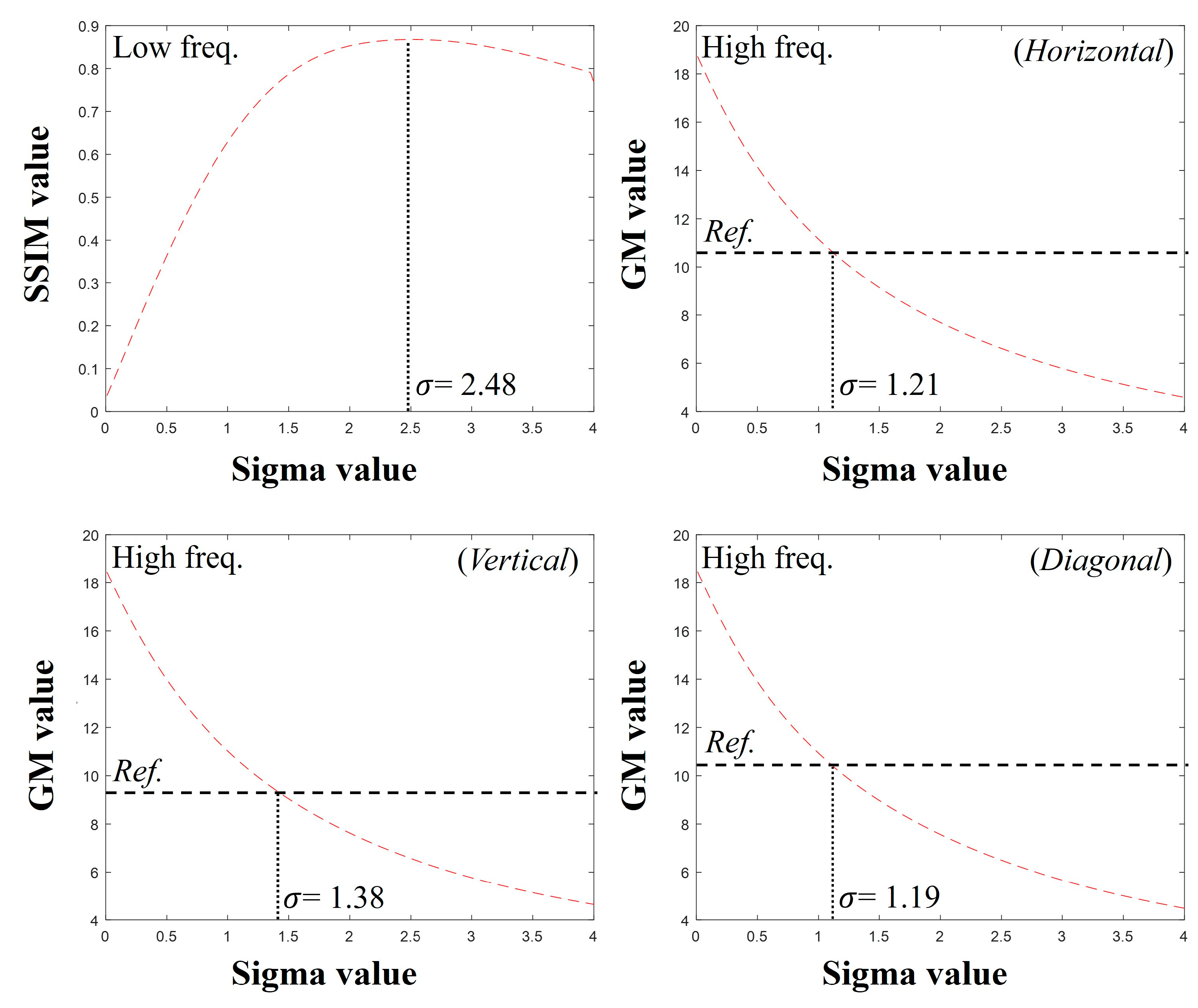
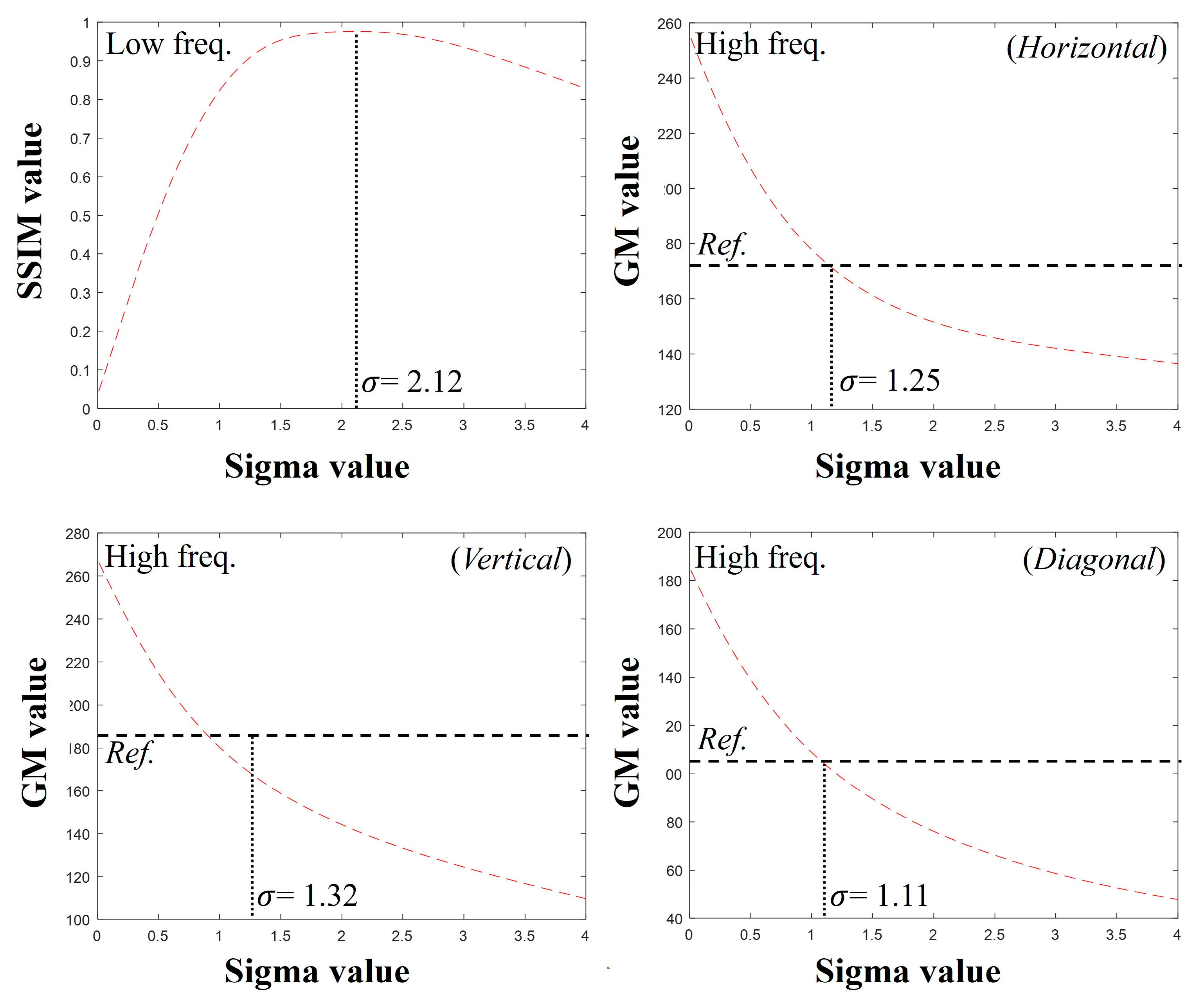
2.1. Proposed Optimal Deblurring Framework
| Algorithm 1 Structure of proposed algorithm framework for predicting optimal PSF |
| 1: Input: Initial 2D matrix IMG1, IMG2 2: Output: Complete 2D matrix PSFL, PSFH, PSFV, PSFD 3: Function Initialize (): 4: Sigmaval = 0.01 to 4 (empirically); 5: Preallocation (SSIMval, GM_Hval, GM_Vval, GM_Dval); 6: END 7: Function Main (): 8: IMG1_L, IMG1_H, IMG1_V, IMG1_D DWT (IMG1); 9: IMG2_L, IMG2_H, IMG2_V, IMG2_D DWT (IMG2); 10: For val = Sigmaval (start): Sigmaval (end) do 11: PSFval Input sigma according to the val; 12: IMG1_Lblur = IMG1_L PSFval; 13: IMG1_Hblur = IMG1_H PSFval; 14: IMG1_Vblur = IMG1_V PSFval; 15: IMG1_Dblur = IMG1_D PSFval; 16: SSIMval (val) Calculate Equation (1) (IMG1_Lblur, IMG2_L); 17: GM_Hval (val) Calculate Equation (2) (IMG1_Hblur); 18: GM_Vval (val) Calculate Equation (2) (IMG1_Vblur); 19: GM_Dval (val) Calculate Equation (2) (IMG1_Dblur); 20: END For 21: PSFL = find the index Sigmaval (max (SSIMval)); 22: GM_HRef Calculate Equation (2) (IMG2_H); 23: GM_VRef Calculate Equation (2) (IMG2_V); 24: GM_DRef Calculate Equation (2) (IMG2_D); 25: PSFH = find the index Sigmaval (GM_Hval ~= GM_HRef); 26: PSFV = find the index Sigmaval (GM_Vval ~= GM_VRef); 27: PSFD = find the index Sigmaval (GM_Dval ~= GM_DRef); 28: Return PSFL, PSFH, PSFV, PSFD 29: END |
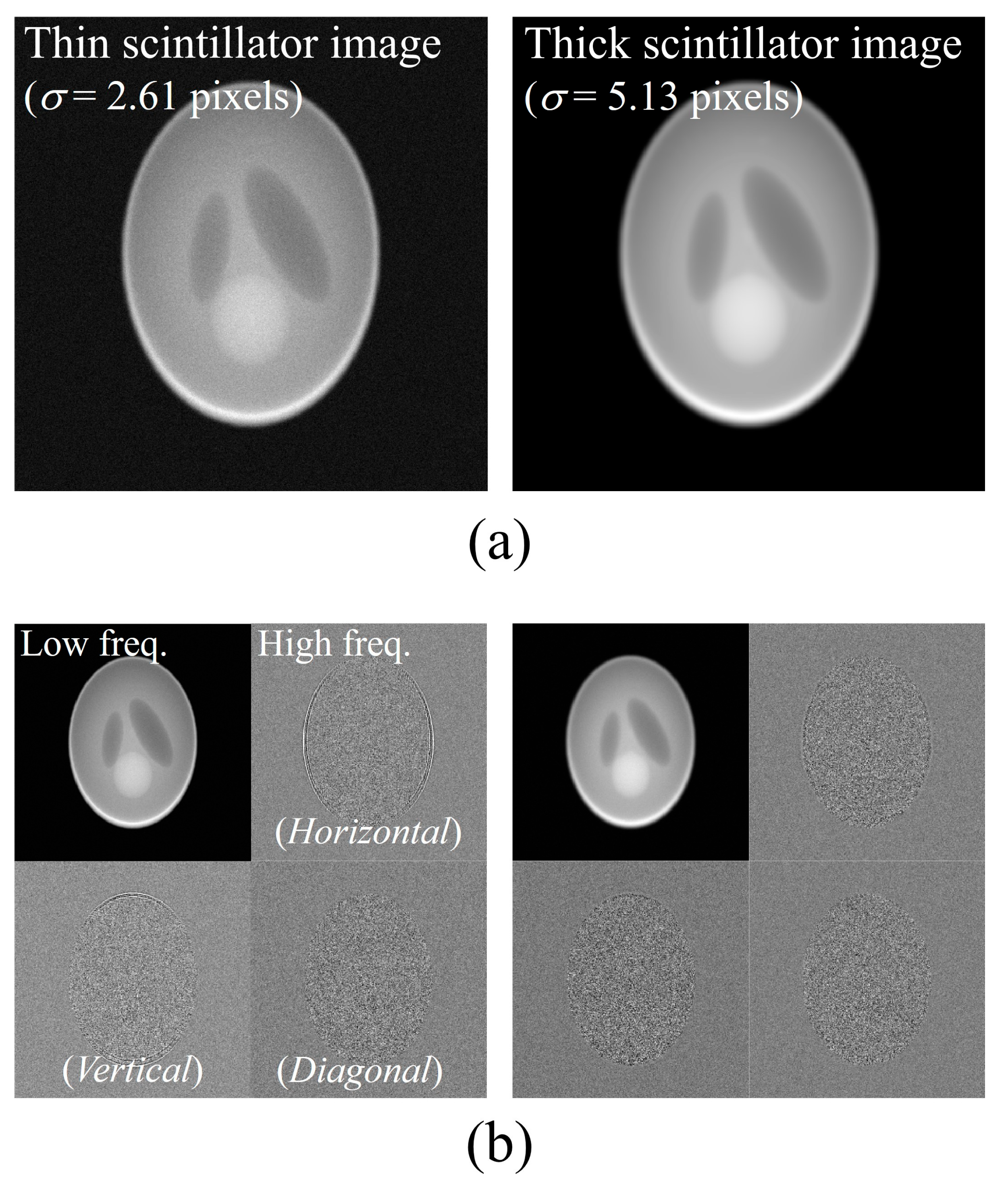
2.2. Simulation and Experiment Conditions
2.3. Quantitative Evaluation for Image Quality
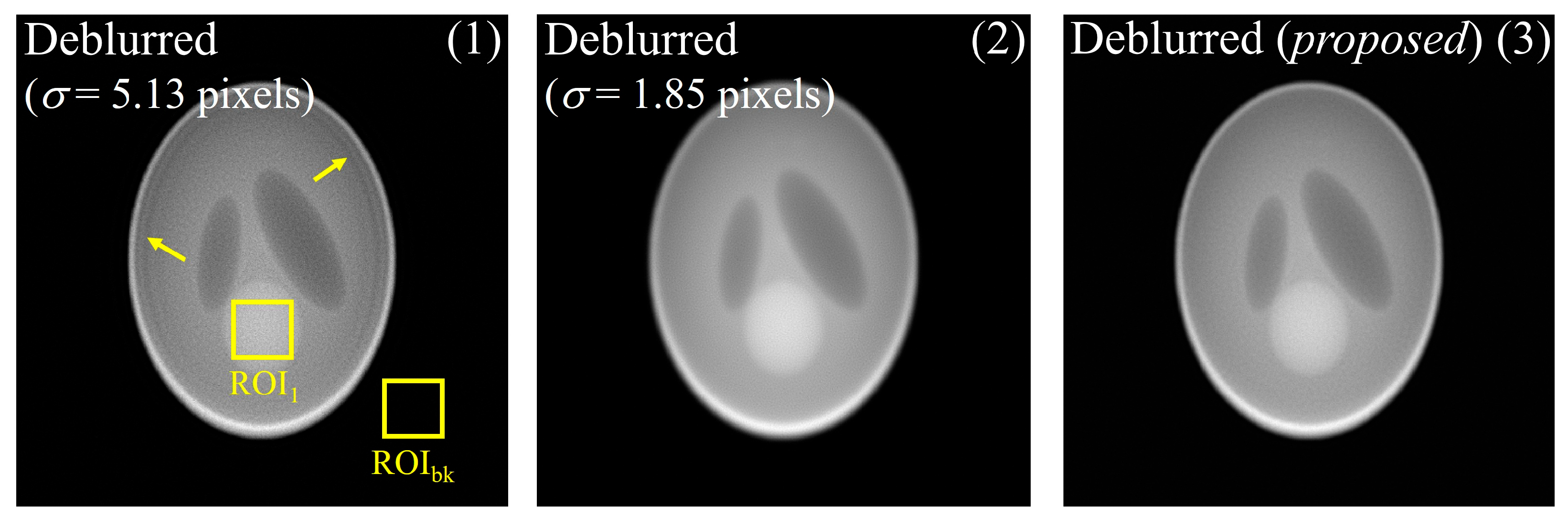
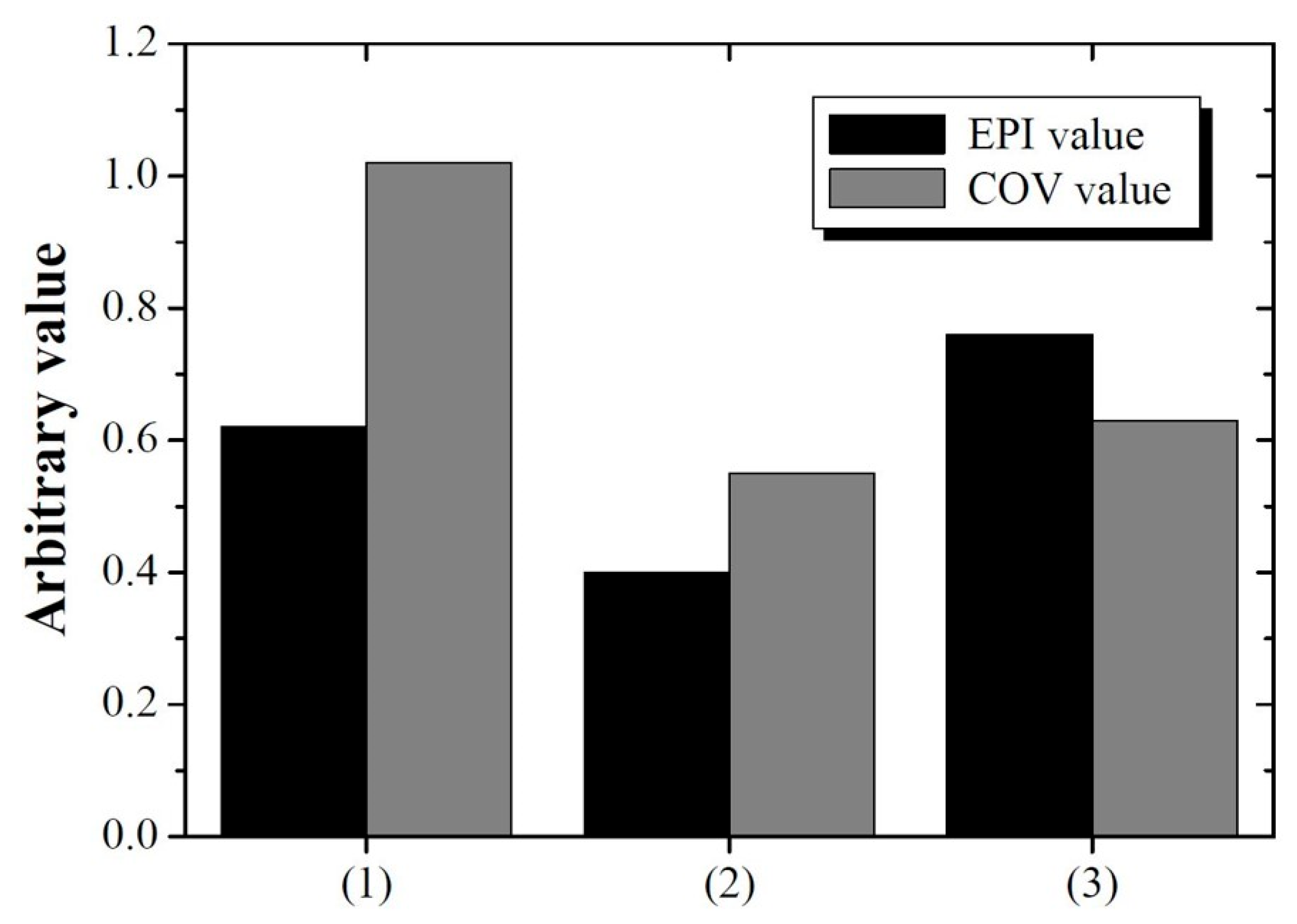
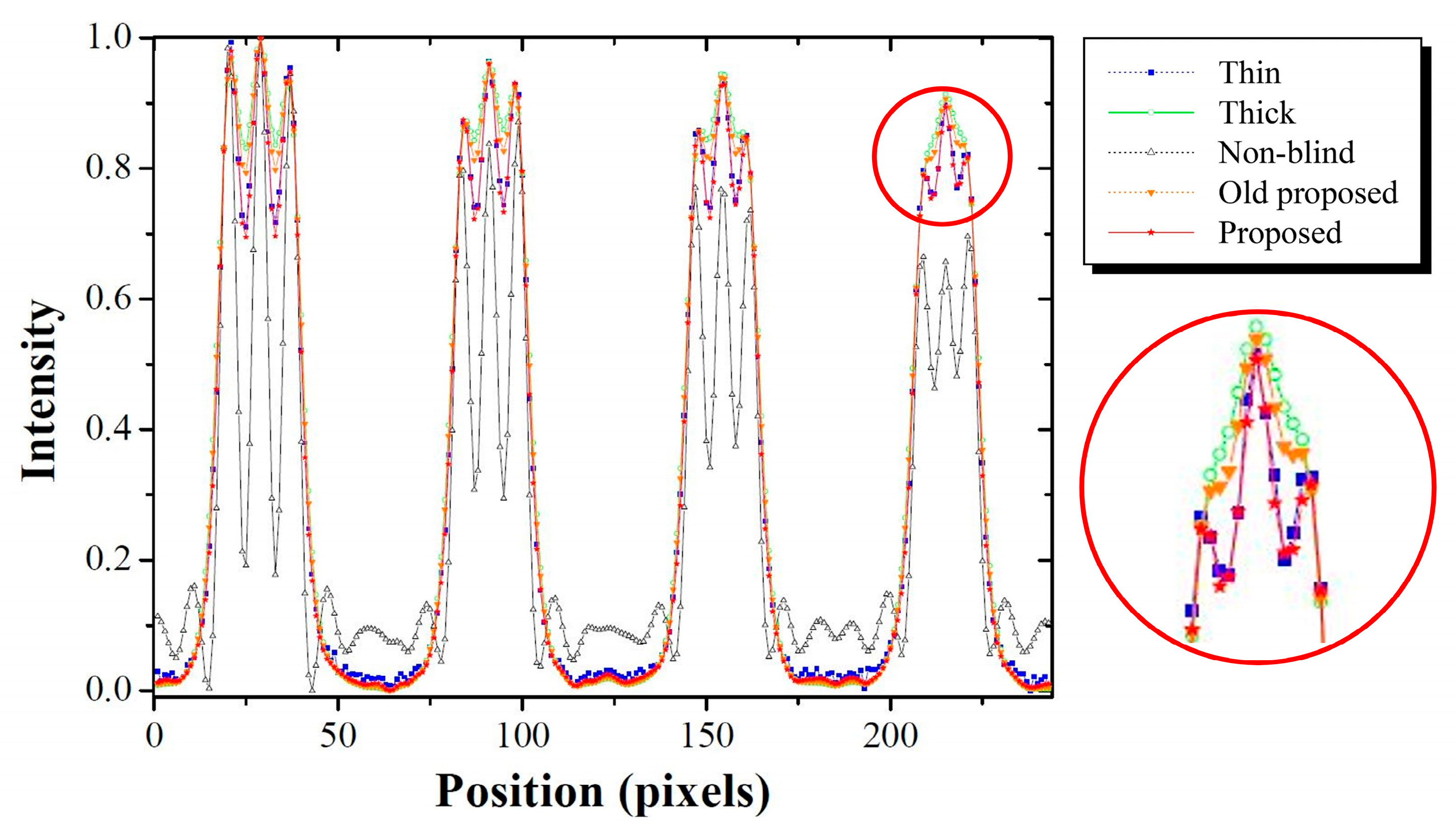
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, J.H.; Kim, Y.J.; Kim, K.G. Bone age estimation using deep learning and hand X-ray images. Biomed. Eng. Lett. 2020, 10, 323. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Choi, J.; Lee, Y. Effectiveness of non-local means algorithm with an industrial 3 MeV LINAC high-energy X-ray system for non-destructive testing. Sensors 2020, 20, 2634. [Google Scholar] [CrossRef] [PubMed]
- Malik, H.; Naeem, A.; Naqvi, R.A.; Loh, W.-K. DMFL_Net: A federated learning-based framework for the classification of COVID-19 from multiple chest diseases using X-rays. Sensors 2023, 23, 743. [Google Scholar] [CrossRef] [PubMed]
- Schaefer-Prokop, C.M.; De Boo, D.W.; Uffmann, M.; Prokop, M. DR and CR. Recent advances in technology. Eur. J. Radiol. 2009, 72, 194–201. [Google Scholar] [CrossRef]
- Cowen, A.R.; Kengyelics, S.M.; Davies, A.G. Solid-state, flat-panel, digital radiography detectors and their physical imaging characteristics. Clin. Radiol. 2008, 63, 487–498. [Google Scholar] [CrossRef] [PubMed]
- Partridge, M.; Hesse, B.-M.; Muller, L. A performance comparison of direct- and indirect-detection flat-panel imagers. Nucl. Instrum. Methods Phys. Res. A 2002, 484, 351–363. [Google Scholar] [CrossRef]
- Fischbach, F.; Freund, T.; Pech, M.; Werk, M.; Bassir, C.; Stoever, B.; Felix, R.; Ricke, J. Comparison of indirect CsI/a:Si and direct a:Se digital radiography. An assessment of contrast and detail visualization. Acta Radiol. 2003, 44, 616–621. [Google Scholar] [CrossRef] [PubMed]
- Gomi, T.; Koshida, K.; Miyati, T.; Miyagawa, J.; Hirano, H. An experimental comparison of flat-panel detector performance for direct and indirect systems (Initial experiences and physical evaluation). J. Digit. Imaging 2006, 19, 362–370. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Park, M.; Kim, K.; Lee, Y. Characterization of flexible amorphous silicon thin-film transistor-based detectors with positive-intrinsic-negative diode in radiography. Diagnostics 2022, 12, 2103. [Google Scholar] [CrossRef]
- Berkhout, A.J. Least-squares inverse filtering and wavelet deconvolution. Geophysics 1977, 42, 1369–1383. [Google Scholar] [CrossRef]
- Treitel, S.; Lines, L.R. Linear inverse theory and deconvolution. Geophysics 1982, 47, 1153–1159. [Google Scholar] [CrossRef]
- De Monvel, J.B.; Le Calvez, S.; Ulfendahl, M. Image restoration for confocal microscopy: Improving the limits of deconvolution, with application to the visualization of the mammalian hearing organ. Biophys. J. 2001, 80, 2455–2470. [Google Scholar] [CrossRef] [PubMed]
- Lin, F.; Jin, C. An improved Wiener deconvolution filter for high-resolution electron microscopy images. Micron 2013, 50, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Levin, A.; Fergus, R.; Durand, F.; Freeman, W.T. Image and Depth from a Conventional Camera with a Coded Aperture. ACM Trans. Graph. (TOG) 2007, 26, 70. [Google Scholar] [CrossRef]
- Javaran, T.A.; Hassanpour, H.; Abolghasemi, V. Non-blind image deconvolution using a regularization based on re-blurring process. CVIU 2017, 154, 16–34. [Google Scholar] [CrossRef]
- Richardson, W.H. Bayesian-based iterative method of image restoration. J. Opt. Soc. Am. 1972, 62, 1972. [Google Scholar] [CrossRef]
- Paris, S.; Durand, F. A fast approximation of the bilateral filter using a signal processing approach. IJCV 2007, 81, 24–52. [Google Scholar] [CrossRef]
- Liu, R.-S.; Mao, C.-S.; Wang, Z.-H.; Li, H.-J. Blind image deblurring via adaptive optimization with flexible sparse structure control. J. Comput. Sci. Tech. 2019, 34, 609–621. [Google Scholar] [CrossRef]
- IEC 62220-1-1:2015; Medical Electrical Equipment—Characteristics of Digital X-ray Imaging Devices-part 1-1: Determination of the Detective Quantum Efficiency—Detectors Used in Radiographic Imaging. International Electrotechnical Commission: Geneva, Switzerland, 2015.
- Nitrosi, A.; Bertolini, M.; Chendi, A.; Trojani, V.; Canovi, L.; Pattacini, P.; Iori, M. Physical characterization of a novel wireless DRX plus 3543C using both a carbon nano tube (CNT) mobile X-ray system and a traditional X-ray system. Phys. Med. Biol. 2020, 65, 11NT02. [Google Scholar] [CrossRef]
- Cha, B.K.; Lee, Y.; Kim, K. Development of adaptive point-spread function estimation method in various scintillation detector thickness for x-ray imaging. Sensors 2023, 23, 8185. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Halidou, A.; Mohamadou, Y.; Ari, A.A.A.; Zacko, E.J.G. Review of wavelet denoising algorithms. Multimed. Tools Appl. 2023, 82, 41539–41569. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, T.; Lim, E.; López-Benítez, M.; Ma, F.; Yu, L. A review of wavelet analysis and its applications: Challenges and opportunities. IEEE Access 2022, 10, 58869–58903. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, L.; Mou, X.; Bovik, A.C. Gradient magnitude similarity deviation: A highly efficient perceptual image quality index. IEEE Trans. Image Process. 2014, 23, 684. [Google Scholar] [CrossRef] [PubMed]
- Kesarwani, A.; Purohit, K.; Dalui, M.; Kisku, D.R. Measuring the degree of suitability of edge detection operators prior to and application. In Proceedings of the 2020 IEEE Applied Signal Processing Conference (ASPCON) 2020, Kolkata, India, 7–9 October 2020. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern. Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Mallat, S. Multiresolution approximations and wavelet orthonormal bases of L2(R). Trans. Amer. Math. Soc. 1989, 315, 69–87. [Google Scholar] [CrossRef]
- Ren, D.; Zuo, W.; Zhang, D.; Xu, J.; Zhang, L. Partial deconvolution with inaccurate blur kernel. IEEE Trans. Image Process. 2018, 27, 511–524. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.-H.; Yun, C.-S.; Kim, K.; Lee, Y. Alzheimer disease neuroimaging initiative. Image restoration algorithm incorporating methods to remove noise and blurring from positron emission tomography imaging for Alzheimer’s disease diagnosis. Phys. Med. 2022, 103, 103–181. [Google Scholar] [CrossRef] [PubMed]
- Chan, S.H.; Khoshabeh, R.; Gibson, K.B.; Gill, P.E.; Nguyen, T.Q. An augmented Lagrangian method for video restoration. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2011, Prague, Czech Republic, 22–27 May 2011. [Google Scholar] [CrossRef]
- Kim, K.; Lee, M.-H.; Lee, Y. Investigation of a blind-deconvolution framework after noise reduction using a gamma camera in nuclear medicine imaging. Nucl. Eng. Technol. 2020, 52, 2594–2600. [Google Scholar] [CrossRef]
- Sattar, F.; Floreby, L.; Salomonsson, G.; Lovstrom, B. Image enhancement based on a nonlinear multiscale method. IEEE Trans. Image Process. 1997, 6, 888–895. [Google Scholar] [CrossRef] [PubMed]
- Qasempour, Y.; Mohammadi, A.; Rezaei, M.; Pouryazadanpanah, P.; Ziaddini, F.; Borbori, A.; Shiri, I.; Hajianfar, G.; Janati, A.; Ghasemirad, S.; et al. Radiographic texture reproducibility: The impact of different materials, their arrangement, and focal spot size. J. Med. Signals Sens. 2020, 10, 275–285. [Google Scholar] [CrossRef] [PubMed]
- Sutour, C.; Deledalle, C.-A.; Aujol, J.-F. Estimation of the noise level function based on a nonparametric detection of homogeneous image regions. SIAM J. Imaging Sci. 2015, 8, 2622–2661. [Google Scholar] [CrossRef]
- Zuo, B.; Hu, X.; Geng, M. Multiscale anisotropic diffusion for ringing artifact suppression in geophysical deconvolution data. Earthq. Sci. 2016, 29, 215–220. [Google Scholar] [CrossRef][Green Version]
- Mosleh, A.; Langlois, J.M.P.; Green, P. Image deconvolution ringing artifact detection and removal via PSF frequency analysis. In ECCV 2014: Computer Vision-ECCV 2014; Springer: Cham, Switzerland, 2014; Volume 8692, pp. 247–268. [Google Scholar] [CrossRef]
- Mori, S. Real-time image-processing algorithm for markerless tumour tracking using X-ray fluoroscopic imaging. Brit. J. Radiol. 2014, 87, 20140001. [Google Scholar] [CrossRef] [PubMed]
- Huda, W.; Abrahams, R.B. Radiographic techniques, contrast, and noise in X-ray imaging. AJR 2015, 204, W126–W131. [Google Scholar] [CrossRef] [PubMed]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Cha, B.K.; Jeong, H.-W.; Lee, Y. Investigation of Deconvolution Method with Adaptive Point Spread Function Based on Scintillator Thickness in Wavelet Domain. Bioengineering 2024, 11, 330. https://doi.org/10.3390/bioengineering11040330
Kim K, Cha BK, Jeong H-W, Lee Y. Investigation of Deconvolution Method with Adaptive Point Spread Function Based on Scintillator Thickness in Wavelet Domain. Bioengineering. 2024; 11(4):330. https://doi.org/10.3390/bioengineering11040330
Chicago/Turabian StyleKim, Kyuseok, Bo Kyung Cha, Hyun-Woo Jeong, and Youngjin Lee. 2024. "Investigation of Deconvolution Method with Adaptive Point Spread Function Based on Scintillator Thickness in Wavelet Domain" Bioengineering 11, no. 4: 330. https://doi.org/10.3390/bioengineering11040330
APA StyleKim, K., Cha, B. K., Jeong, H.-W., & Lee, Y. (2024). Investigation of Deconvolution Method with Adaptive Point Spread Function Based on Scintillator Thickness in Wavelet Domain. Bioengineering, 11(4), 330. https://doi.org/10.3390/bioengineering11040330





