Intuitionistic Fuzzy Biofeedback Control of Implanted Dual-Sensor Cardiac Pacemakers
Abstract
1. Introduction
- Proposing a novel IFLC of implanted pacemakers to regulate heart rates during the daily activities, i.e., at rest, walking, and jogging, of cardiac patients;
- Investigating the robust capabilities of our proposed IFLC to verify the safe health conditions of patients with pacemakers during daily activities;
- Conducting a comparative study among the current state-of-the-art control methods of dual-sensor pacemakers to validate the outperformance of the proposed IFLC.
2. Methods
2.1. Mathematical Pacemaker Model
2.2. Intuitionistic Fuzzy Sets
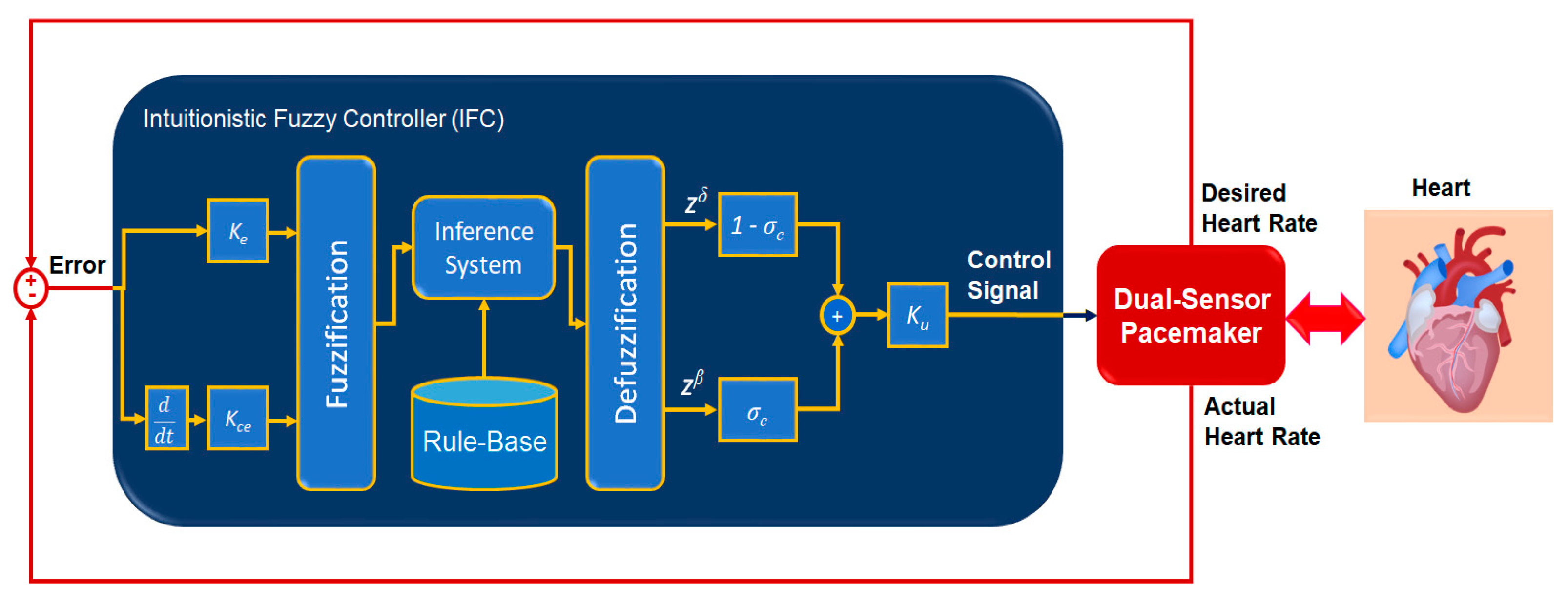
2.3. Developed Controller of Dual-Sensor Pacemakers
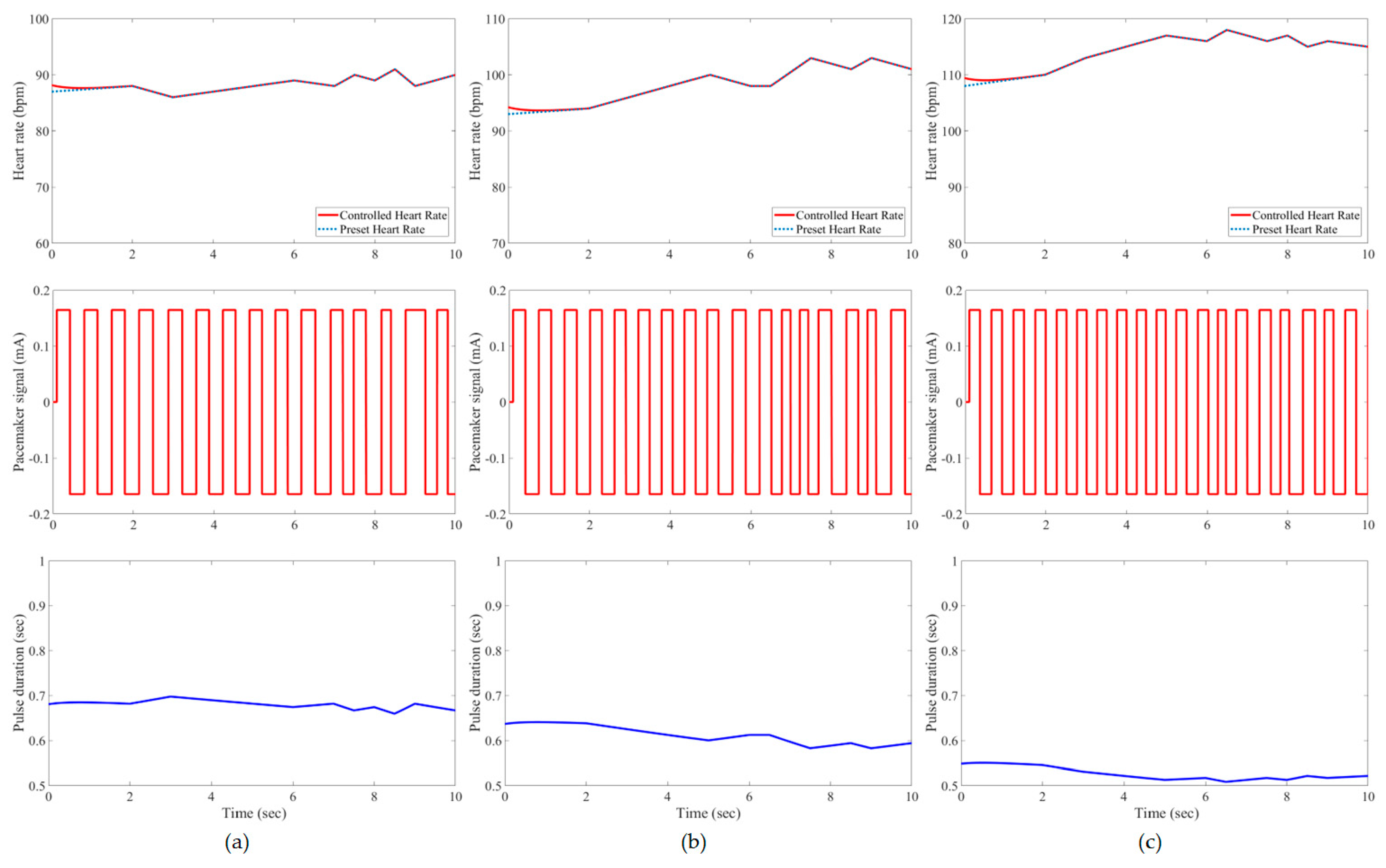
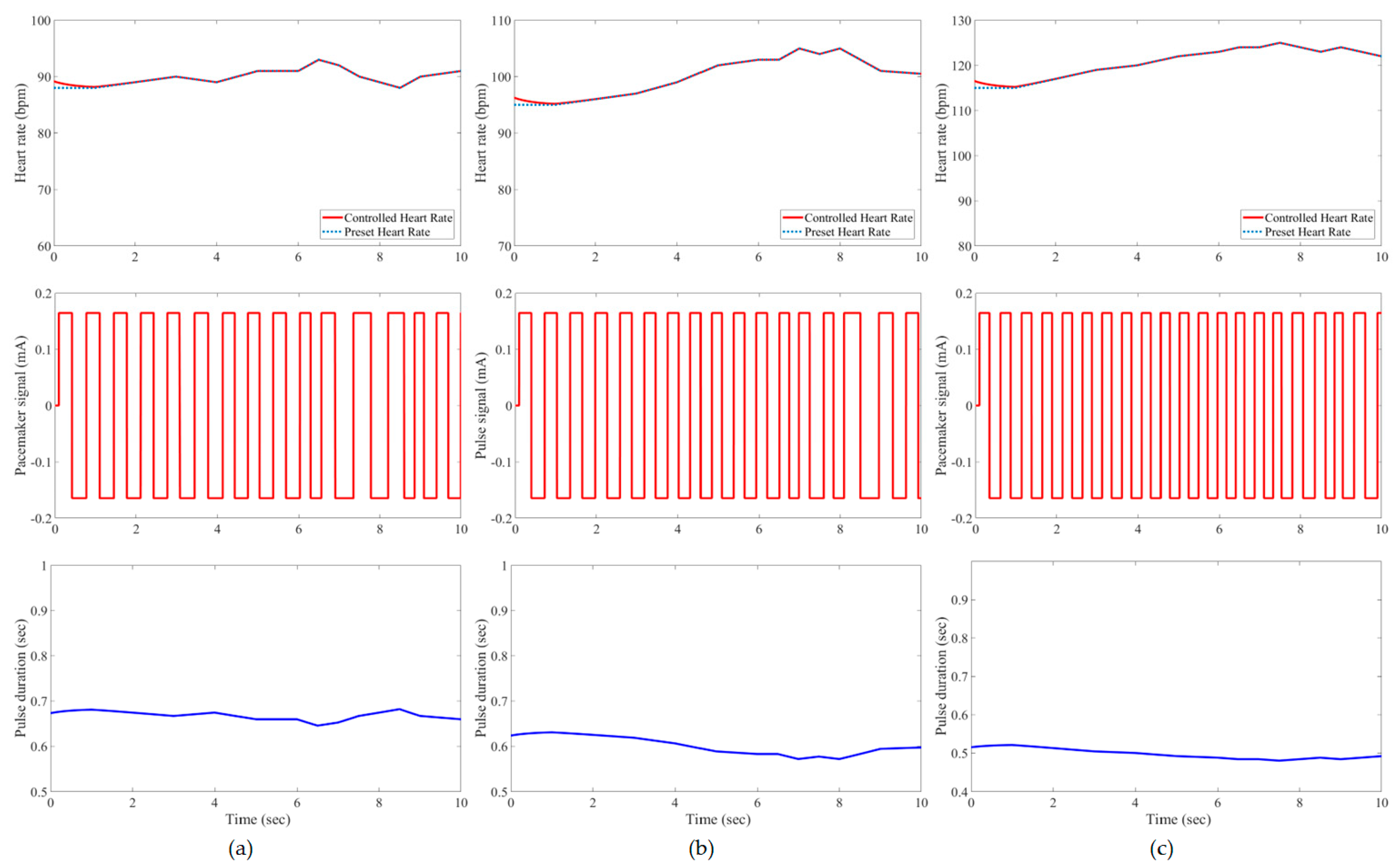
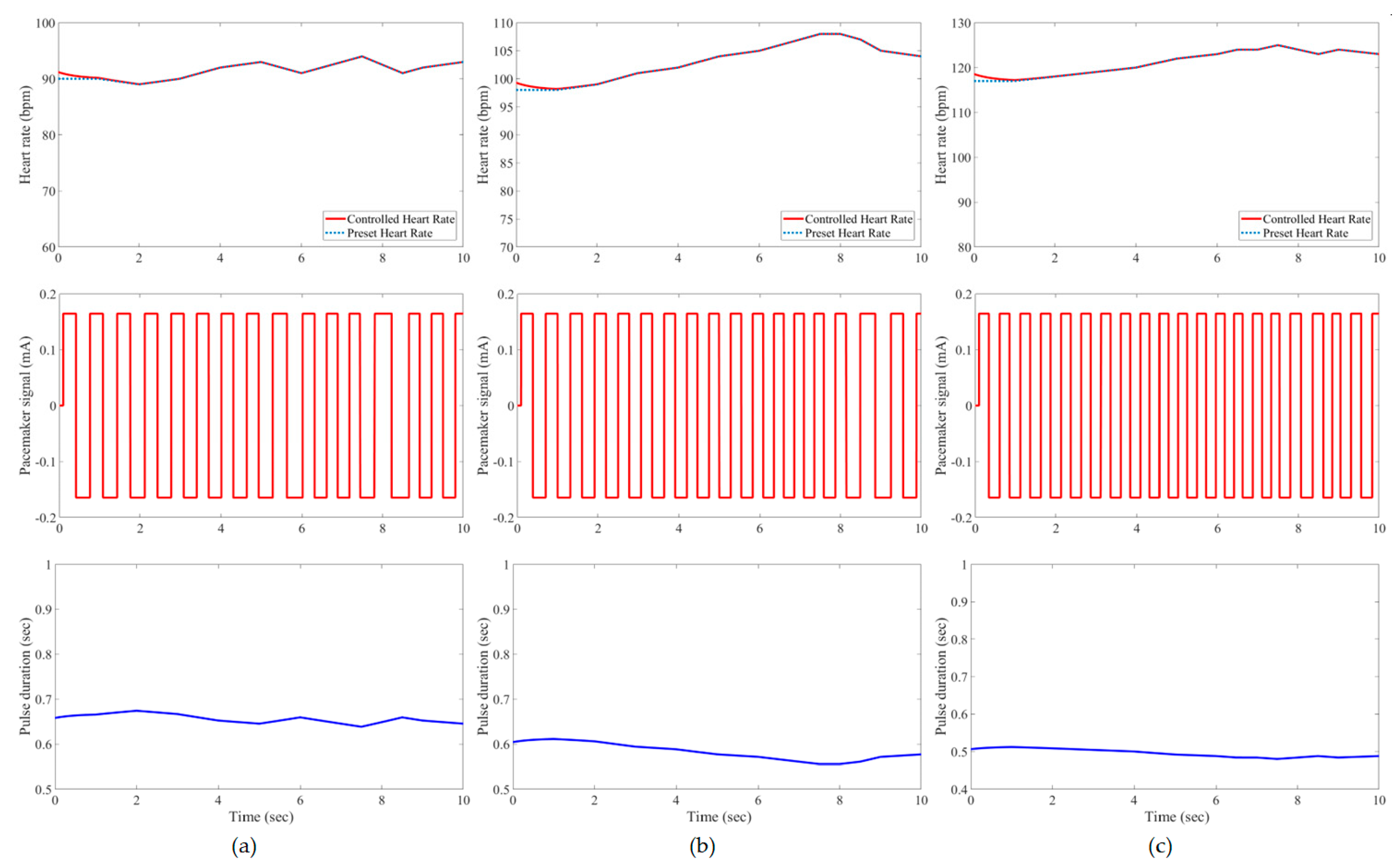
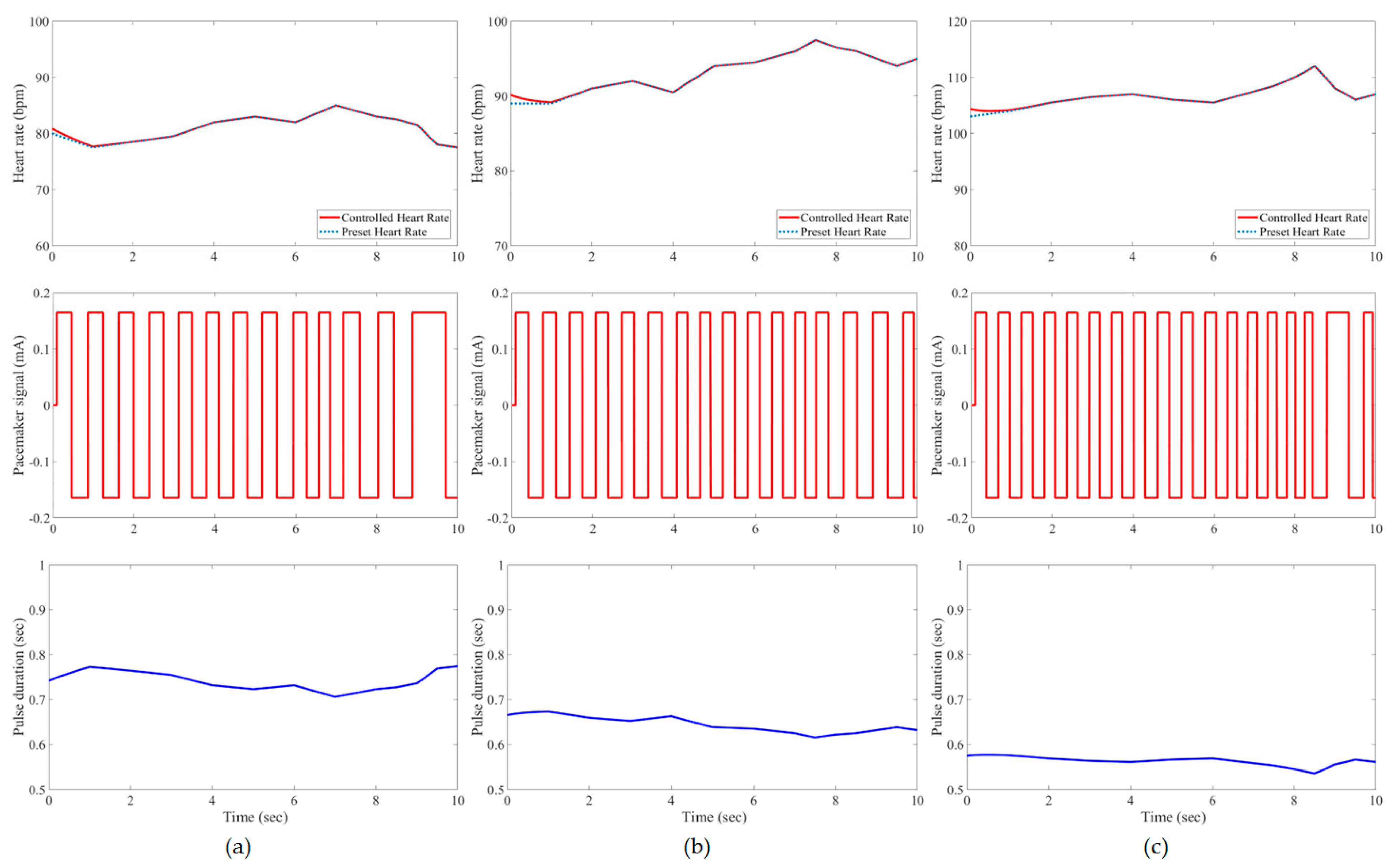
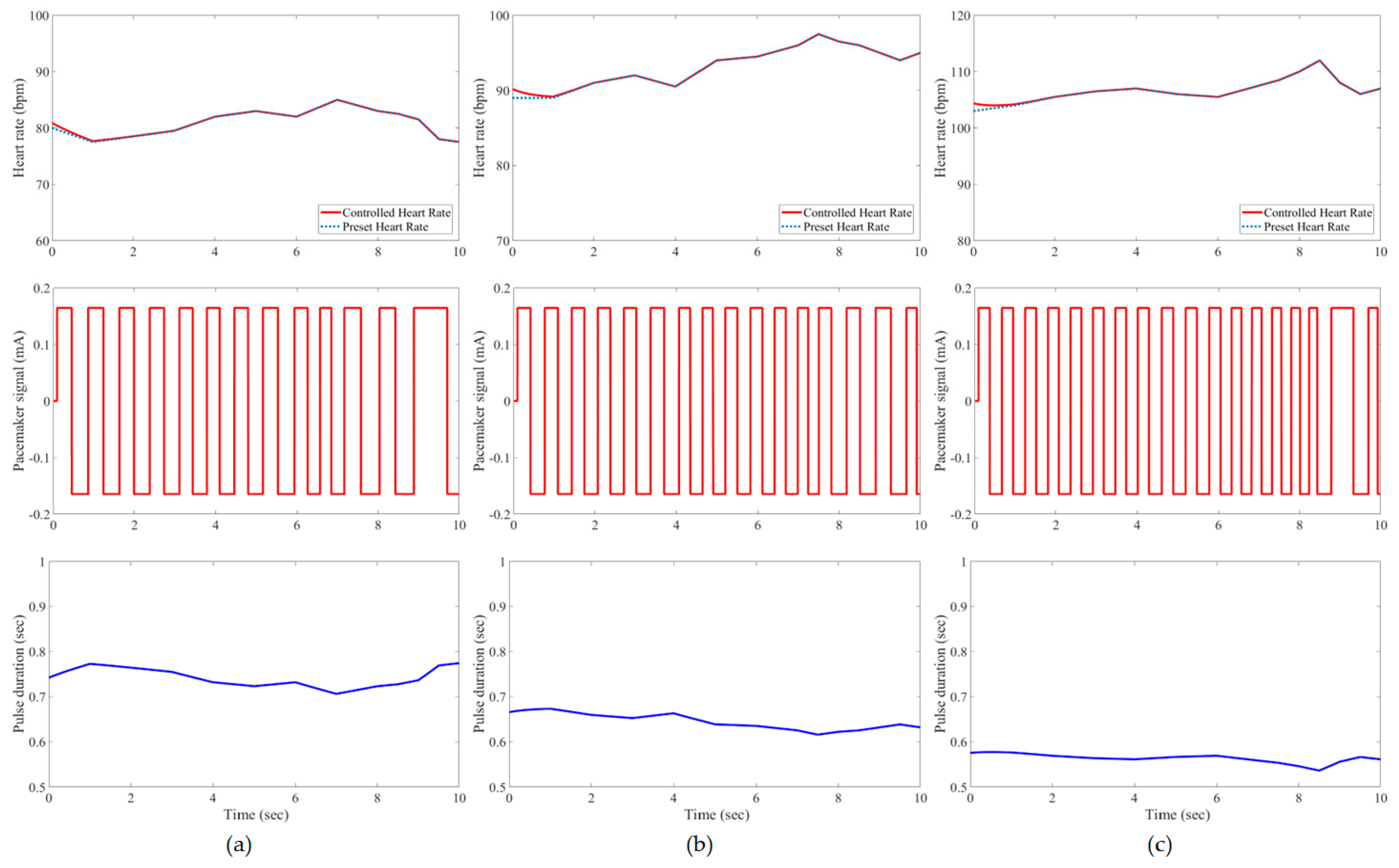
3. Results and Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Awan, M.F.; Cordero, R.; Kansanen, K.; Feuerstein, D. Securing Next Generation Multinodal Leadless Cardiac Pacemaker System: A Proof of Concept in a Single Animal. IEEE Access 2020, 8, 151307–151315. [Google Scholar] [CrossRef]
- Chow, A.W.C.; Buxton, A.E. Implantable Cardiac Pacemakers and Defibrillators: All You Wanted to Know; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Tsao, C.W.; Aday, A.W.; Almarzooq, Z.I.; Alonso, A.; Beaton, A.Z.; Bittencourt, M.S.; Boehme, A.K.; Buxton, A.E.; Carson, A.P.; Commodore-Mensah, Y.; et al. Heart Disease and Stroke Statistics—2022 Update: A Report From the American Heart Association. Circulation 2022, 145, e153–e639. [Google Scholar] [PubMed]
- Sichrovsky, T.; Mittal, S. I Need a Pacemaker—What Are My Options? JAMA Cardiol. 2020, 5, 1456. [Google Scholar] [CrossRef] [PubMed]
- Stewart, C. Global Number of Pacemakers in 2016 and a Forecast for 2023 (in Million Units). Available online: https://www.statista.com/statistics/800794/pacemakers-market-volume-in-units-worldwide/ (accessed on 19 June 2023).
- Mulpuru, S.K.; Madhavan, M.; McLeod, C.J.; Cha, Y.-M.; Friedman, P.A. Cardiac Pacemakers: Function, Troubleshooting, and Management: Part 1 of a 2-Part Series. J. Am. Coll. Cardiol. 2017, 69, 189–210. [Google Scholar] [CrossRef] [PubMed]
- Rezaeiyan, Y.; Zamani, M.; Shoaei, O.; Serdijn, W.A. Mixed-Signal IC With Pulse Width Modulation Wireless Telemetry for Implantable Cardiac Pacemakers in 0.18-μm CMOS. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 589–600. [Google Scholar] [CrossRef] [PubMed]
- Hou, X. Cardiac Pacemaker—A Smart Device. In Biotechnology Products in Everyday Life; Khoobchandani, M., Saxena, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 87–97. [Google Scholar]
- Arunachalam, S.P.; Kapa, S.; Mulpuru, S.K.; Friedman, P.A.; Tolkacheva, E.G. Intelligent Fractional-Order PID (FOPID) Heart Rate Controller for Cardiac Pacemaker. In Proceedings of the 2016 IEEE Healthcare Innovation Point-Of-Care Technologies Conference (HI-POCT), Cancun, Mexico, 9–11 November 2016; pp. 105–108. [Google Scholar]
- Mariello, M. Heart Energy Harvesting and Cardiac Bioelectronics: Technologies and Perspectives. Nanoenergy Adv. 2022, 2, 344–385. [Google Scholar] [CrossRef]
- Mariello, M.; Kim, K.; Wu, K.; Lacour, S.P.; Leterrier, Y. Recent Advances in Encapsulation of Flexible Bioelectronic Implants: Materials, Technologies, and Characterization Methods. Adv. Mater. 2022, 34, 2201129. [Google Scholar] [CrossRef]
- Neogi, B.; Ghosh, R.; Tarafdar, U.; Das, A. Simulation Aspect of an Artificial Pacemaker. Int. J. Inf. Technol. Knowl. Manag. 2010, 3, 723–727. [Google Scholar]
- Nakao, M.; Takizawa, T.; Nakamura, K.; Katayama, N.; Yamamoto, M. An optimal control model of 1/f fluctuations in heart rate variability. IEEE Eng. Med. Biol. Mag. 2001, 20, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Schwartz, F.; Michel, J.; Herve, Y.; Molin, R.D. Implementation Study of an Analog Spiking Neural Network for Assisting Cardiac Delay Prediction in a Cardiac Resynchronization Therapy Device. IEEE Trans. Neural Netw. 2011, 22, 858–869. [Google Scholar] [PubMed]
- Karar, M.E. Robust RBF neural network–based backstepping controller for implantable cardiac pacemakers. Int. J. Adapt. Control Signal Process. 2018, 32, 1040–1051. [Google Scholar] [CrossRef]
- Nawikavatan, A.; Thammarat, C.; Puangdownreong, D. Application of Spiritual Search to Optimal PIDA Controller Design for Cardiac Pacemaker. In Proceedings of the 2019 Joint International Conference on Digital Arts, Media and Technology with ECTI Northern Section Conference on Electrical, Electronics, Computer and Telecommunications Engineering (ECTI DAMT-NCON), Nan, Thailand, 30 January–2 February 2019; pp. 286–289. [Google Scholar]
- Dubljevic, S.; Christofides, P.D. Optimal mechano-electric stabilization of cardiac alternans. Chem. Eng. Sci. 2008, 63, 5425–5433. [Google Scholar] [CrossRef]
- Gupta, N.; Singh, H.; Singla, J. Fuzzy Logic-based Systems for Medical Diagnosis—A Review. In Proceedings of the 2022 3rd International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 17–19 August 2022; pp. 1058–1062. [Google Scholar]
- Karar, M.E.; El-Brawany, M.A. Automated Cardiac Drug Infusion System Using Adaptive Fuzzy Neural Networks Controller. Biomed. Eng. Comput. Biol. 2011, 3, BECB.S6495. [Google Scholar] [CrossRef]
- Yu, Y.-N.; Doctor, F.; Fan, S.-Z.; Shieh, J.-S. An Adaptive Monitoring Scheme for Automatic Control of Anaesthesia in dynamic surgical environments based on Bispectral Index and Blood Pressure. J. Med. Syst. 2018, 42, 95. [Google Scholar] [CrossRef] [PubMed]
- Ngan, R.T.; Son, L.H.; Cuong, B.C.; Ali, M. H-max distance measure of intuitionistic fuzzy sets in decision making. Appl. Soft Comput. 2018, 69, 393–425. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets: Theory and Applications; Physica-Verlag HD: Heidelberg, Germany, 2013. [Google Scholar]
- Nguyen, H. A new interval-valued knowledge measure for interval-valued intuitionistic fuzzy sets and application in decision making. Expert Syst. Appl. 2016, 56, 143–155. [Google Scholar] [CrossRef]
- Karar, M.E.; El-Garawany, A.H.; El-Brawany, M. Optimal adaptive intuitionistic fuzzy logic control of anti-cancer drug delivery systems. Biomed. Signal Process. Control 2020, 58, 101861. [Google Scholar] [CrossRef]
- Nako, J.; Psychalinos, C. Heart Rate Controller Design for Cardiac Pacemaker. In Proceedings of the 2022 Panhellenic Conference on Electronics & Telecommunications (PACET), Tripolis, Greece, 2–3 December 2022; pp. 1–4. [Google Scholar]
- Bacharach, D.W.; Hilden, T.S.; Millerhagen, J.O.; Westrum, B.L.; Kelly, J.M. Activity-Based Pacing: Comparison of a Device Using an Accelerometer Versus a Piezoelectric Crystal. Pacing Clin. Electrophysiol. 1992, 15, 188–196. [Google Scholar] [CrossRef] [PubMed]
- Hexamer, M.P.R.; Meine, M.; Kloppe, A.; Werner, E. Rate-responsive pacing based on the atrio-ventricular conduction time. IEEE Trans. Biomed. Eng. 2002, 49, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Tosato, M.; Yoshida, K.; Toft, E.; Nekrasas, V.; Struijk, J.J. Closed-loop control of the heart rate by electrical stimulation of the vagus nerve. Med. Biol. Eng. Comput. 2006, 44, 161–169. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.Y.; Cheng, C.J.; Liang, M.C. A Low-Power Bidirectional Telemetry Device With a Near-Field Charging Feature for a Cardiac Microstimulator. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 357–367. [Google Scholar] [CrossRef] [PubMed]
- Govind, K.R.A.; Sekhar, R.A. Design of a novel PID controller for cardiac pacemaker. In Proceedings of the 2014 International Conference on Advances in Green Energy (ICAGE), Thiruvananthapuram, India, 17–18 December 2014; pp. 82–87. [Google Scholar]
- Wojtasik, A.; Jaworski, Z.; Kuźmicz, W.; Wielgus, A.; Wałkanis, A.; Sarna, D. Fuzzy logic controller for rate-adaptive heart pacemaker. Appl. Soft Comput. 2004, 4, 259–270. [Google Scholar] [CrossRef]
- Shi, W.V.; Zhou, M. Fuzzy PID controllers for dual-sensor pacing systems in patients with bradycardias at rest. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AK, USA, 9–12 October 2011; pp. 1117–1122. [Google Scholar]
- Momani, S.; Batiha, I.M.; El-Khazali, R. Design of PIλ Dδ-Heart Rate Controllers for Cardiac Pacemaker. In Proceedings of the 2019 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT), Ajman, United Arab Emirates, 10–12 December 2019; pp. 1–5. [Google Scholar]
- Nako, J.; Psychalinos, C.; Elwakil, A.S. Minimum Active Component Count Design of a PIλDμ Controller and Its Application in a Cardiac Pacemaker System. J. Low Power Electron. Appl. 2023, 13, 13. [Google Scholar] [CrossRef]
- Yanagihara, K.; Noma, A.; Irisawa, H. Reconstruction of sino-atrial node pacemaker potential based on the voltage clamp experiments. Jpn. J. Physiol. 1980, 30, 841–857. [Google Scholar] [CrossRef]
- Shi, W.V.; Zhou, M. Optimal Single-Pulse for Pacemakers Based on a Sinoatrial Model. IEEE/ASME Trans. Mechatron. 2013, 18, 348–354. [Google Scholar] [CrossRef]
- Atanassov, K.T. On the Concept of Intuitionistic Fuzzy Sets. In On Intuitionistic Fuzzy Sets Theory; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–16. [Google Scholar]
- Atanassov, K.T. Intuitionistic Fuzzy Predicate Logic. In Intuitionistic Fuzzy Logics; Springer International Publishing: Cham, Switzerland, 2017; pp. 65–77. [Google Scholar]
- Shi, W. Advanced Intelligent Control and Optimization for Cardiac Pacemaker Systems. Ph.D. Thesis, New Jersey Institute of Technology (NJIT), Newark, NJ, USA, 2012. [Google Scholar]
- Shi, W.V. Advanced Intelligent Control of Cardiac Pacemaker Systems Using a Fuzzy PID Controller. Int. J. Intell. Control Systems 2013, 18, 28–34. [Google Scholar]
- Karar, M.-E.; Mahmoud, A.-S.-A. Intelligent Networked Control of Vasoactive Drug Infusion for Patients with Uncertain Sensitivity. Comput. Syst. Sci. Eng. 2023, 47, 721–739. [Google Scholar] [CrossRef]
- Abd-Elhaleem, S.; Hussien, M.A.; Hamdy, M.; Mahmoud, T.A. Event-triggered model-free adaptive control for nonlinear systems using intuitionistic fuzzy neural network: Simulation and experimental validation. Complex Intell. Syst. 2024, 10, 2271–2297. [Google Scholar] [CrossRef]


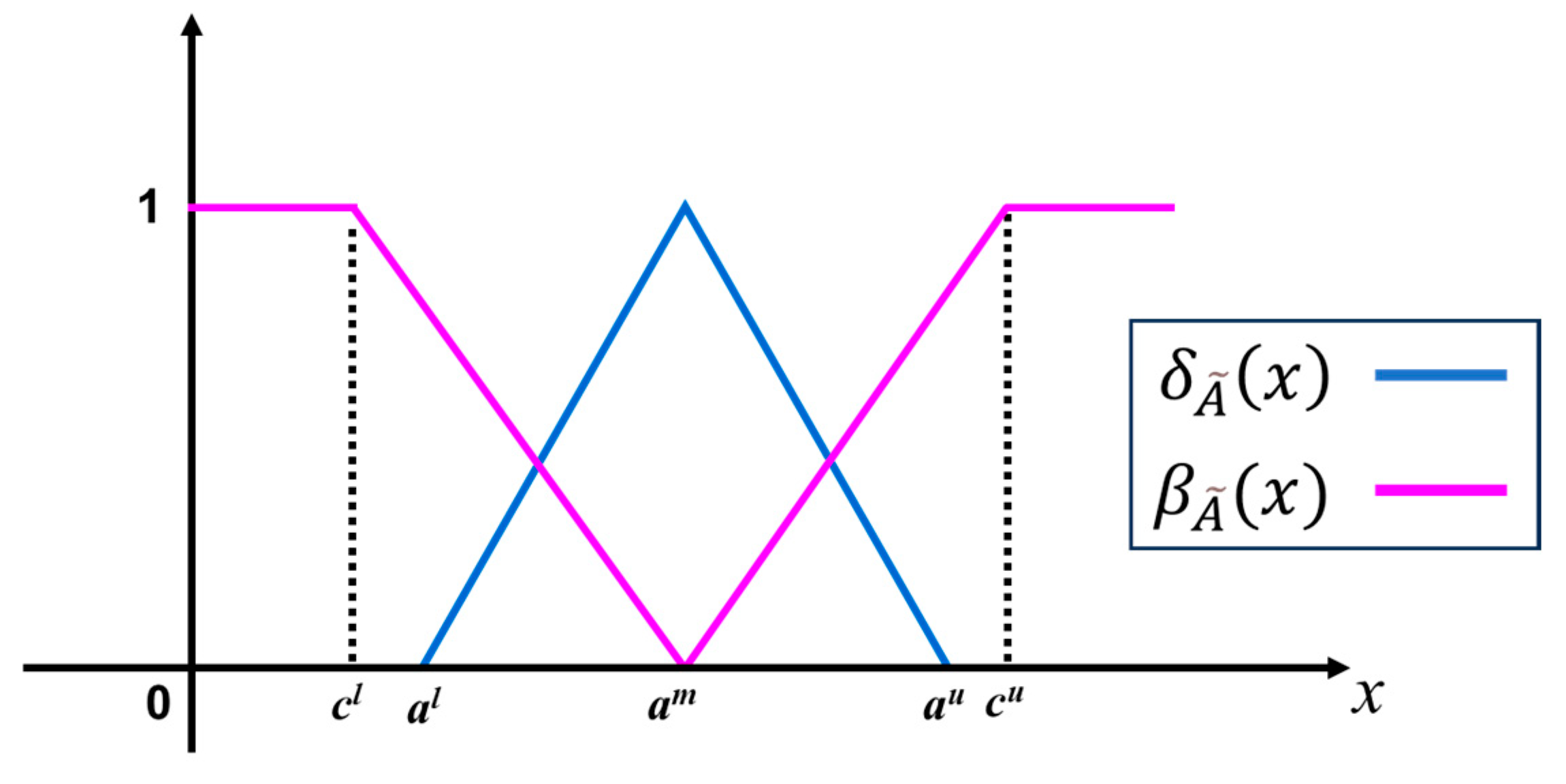

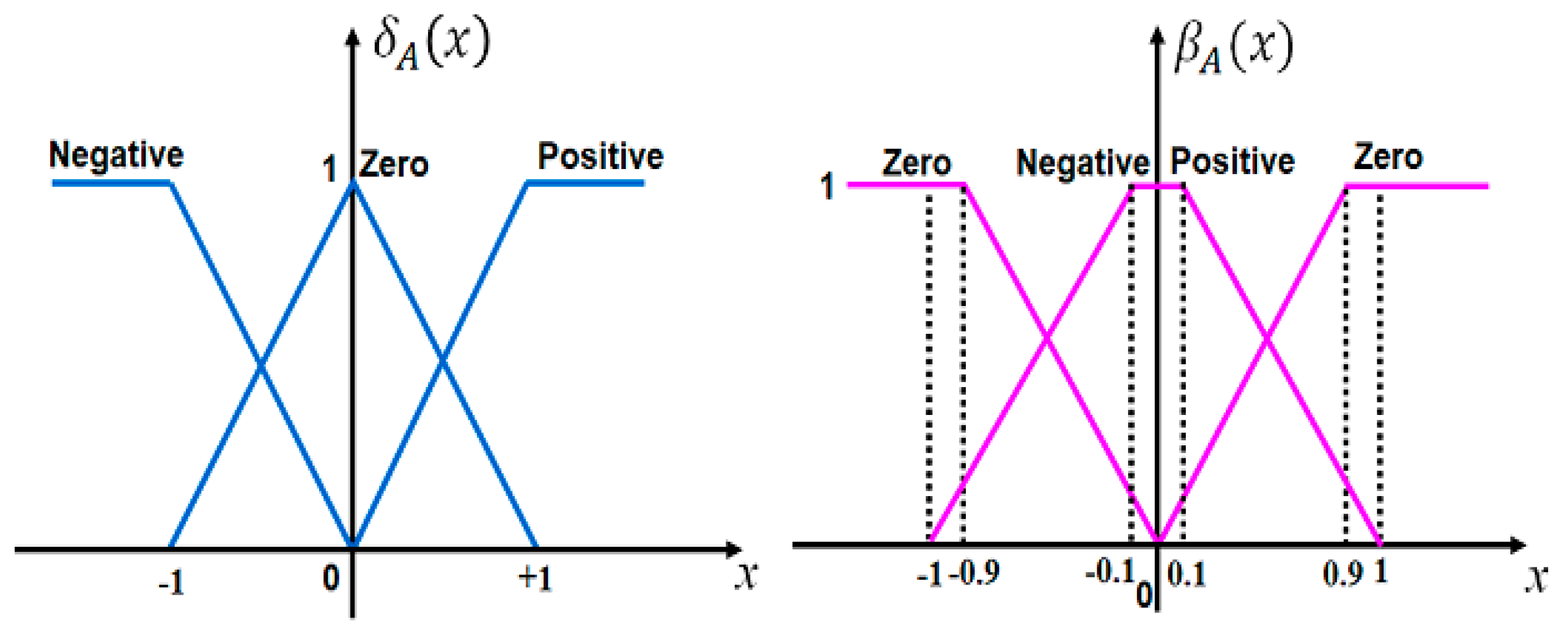

| Change of Error (ce) | Error (e) | ||
|---|---|---|---|
| Negative | Zero | Positive | |
| Negative | Negative | Negative | Zero |
| Zero | Negative | Zero | Positive |
| Positive | Zero | Positive | Positive |
| Cardiac Patient (Sex, Age (Years)) | Desired Heart Rates (bpm) | ||
|---|---|---|---|
| At Rest | Walking | Jogging | |
| Case1 (Female, 66) | 81 ± 5 | 94 ± 5 | 107 ± 5 |
| Case 2 (Male, 54) | 89 ± 5 | 98 ± 5 | 113 ± 5 |
| Case 3 (Male, 48) | 90 ± 5 | 100 ± 5 | 120 ± 5 |
| Case 4 (Female, 45) | 92 ± 5 | 103 ± 5 | 122 ± 5 |
| Case 5 (Female, 58) | 85 ± 6 | 92 ± 4 | 103 ± 3 |
| Case 6 (Male, 62) | 80 ± 5 | 94 ± 5 | 108 ± 4 |
| Control Method | Patient | At Rest | Walking | Jogging | |||
|---|---|---|---|---|---|---|---|
| RMSE | Maximum Error | RMSE | Maximum Error | RMSE | Maximum Error | ||
| Classical Fuzzy [39,40] | Case 1 | 2.38 | 4.88% | 3.72 | 7.29% | 6.40 | 8.26% |
| Case 2 | 2.07 | 3.45% | 4.24 | 6.34% | 3.39 | 5.31% | |
| Case 3 | 3.14 | 5.38% | 4.73 | 6.86% | 2.76 | 4.35% | |
| Case 4 | 3.47 | 6.45% | 3.36 | 4.08% | 2.67 | 4.27% | |
| Case 5 | 1.81 | 2.63% | 2.68 | 2.84% | 2.68 | 5.01% | |
| Case 6 | 2.51 | 4.82% | 2.27 | 3.91% | 2.45 | 3.21% | |
| Fuzzy PID [39,40] | Case 1 | 1.19 | 2.63% | 1.14 | 2.27% | 1.27 | 1.96% |
| Case 2 | 0.91 | 2.30% | 0.95 | 2.15% | 1.23 | 2.77% | |
| Case 3 | 0.89 | 2.63% | 0.87 | 2.08% | 0.62 | 1.71% | |
| Case 4 | 1.09 | 2.13% | 0.76 | 1.47% | 0.64 | 1.71% | |
| Case 5 | 0.89 | 1.72% | 1.35 | 2.27% | 1.44 | 2.51% | |
| Case 6 | 0.82 | 1.92% | 1.15 | 2.23% | 0.66 | 0.94% | |
| RBF Neural Network [15] | Case 1 | 0.64 | 1.68% | 0.54 | 0.57% | 0.90 | 1.13% |
| Case 2 | 0.45 | 1.22% | 0.68 | 0.64% | 0.80 | 0.54% | |
| Case 3 | 0.49 | 1.68% | 0.53 | 1.07% | 0.71 | 0.43% | |
| Case 4 | 0.44 | 0.78% | 0.51 | 0.99% | 0.74 | 0.56% | |
| Case 5 | – | – | – | – | – | – | |
| Case 6 | – | – | – | – | – | – | |
| Developed IFLC | Case 1 | 0.21 * | 1.62% | 0.21 | 1.85% | 0.23 | 2.21% |
| Case 2 | 0.21 | 1.60% | 0.21 | 1.41% | 0.25 | 1.55% | |
| Case 3 | 0.20 | 1.76% | 0.22 | 0.78% | 0.25 | 1.00% | |
| Case 4 | 0.21 | 1.23% | 0.23 | 0.49% | 0.26 | 1.00% | |
| Case 5 | 0.20 | 2.35% | 0.21 | 1.60% | 0.23 | 2.12% | |
| Case 6 | 0.17 | 1.58% | 0.22 | 1.64% | 0.24 | 2.38% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshahrani, H.; Alshahrani, A.; Karar, M.E.; Ramadan, E.A. Intuitionistic Fuzzy Biofeedback Control of Implanted Dual-Sensor Cardiac Pacemakers. Bioengineering 2024, 11, 691. https://doi.org/10.3390/bioengineering11070691
Alshahrani H, Alshahrani A, Karar ME, Ramadan EA. Intuitionistic Fuzzy Biofeedback Control of Implanted Dual-Sensor Cardiac Pacemakers. Bioengineering. 2024; 11(7):691. https://doi.org/10.3390/bioengineering11070691
Chicago/Turabian StyleAlshahrani, Hussain, Amnah Alshahrani, Mohamed Esmail Karar, and Ebrahim A. Ramadan. 2024. "Intuitionistic Fuzzy Biofeedback Control of Implanted Dual-Sensor Cardiac Pacemakers" Bioengineering 11, no. 7: 691. https://doi.org/10.3390/bioengineering11070691
APA StyleAlshahrani, H., Alshahrani, A., Karar, M. E., & Ramadan, E. A. (2024). Intuitionistic Fuzzy Biofeedback Control of Implanted Dual-Sensor Cardiac Pacemakers. Bioengineering, 11(7), 691. https://doi.org/10.3390/bioengineering11070691








