Structural and Organizational Strategies of Locomotor Modules during Landing in Patients with Chronic Ankle Instability
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Protocol and Data Recordings
2.3. Muscle Activation Model
2.4. Non-Negative Matrix Factorization Extracts Muscle Synergies
2.5. K-means Clustering Algorithm for Sorting Muscle Synergies
2.6. Outcome Variables
2.7. Statistical Analysis
3. Results
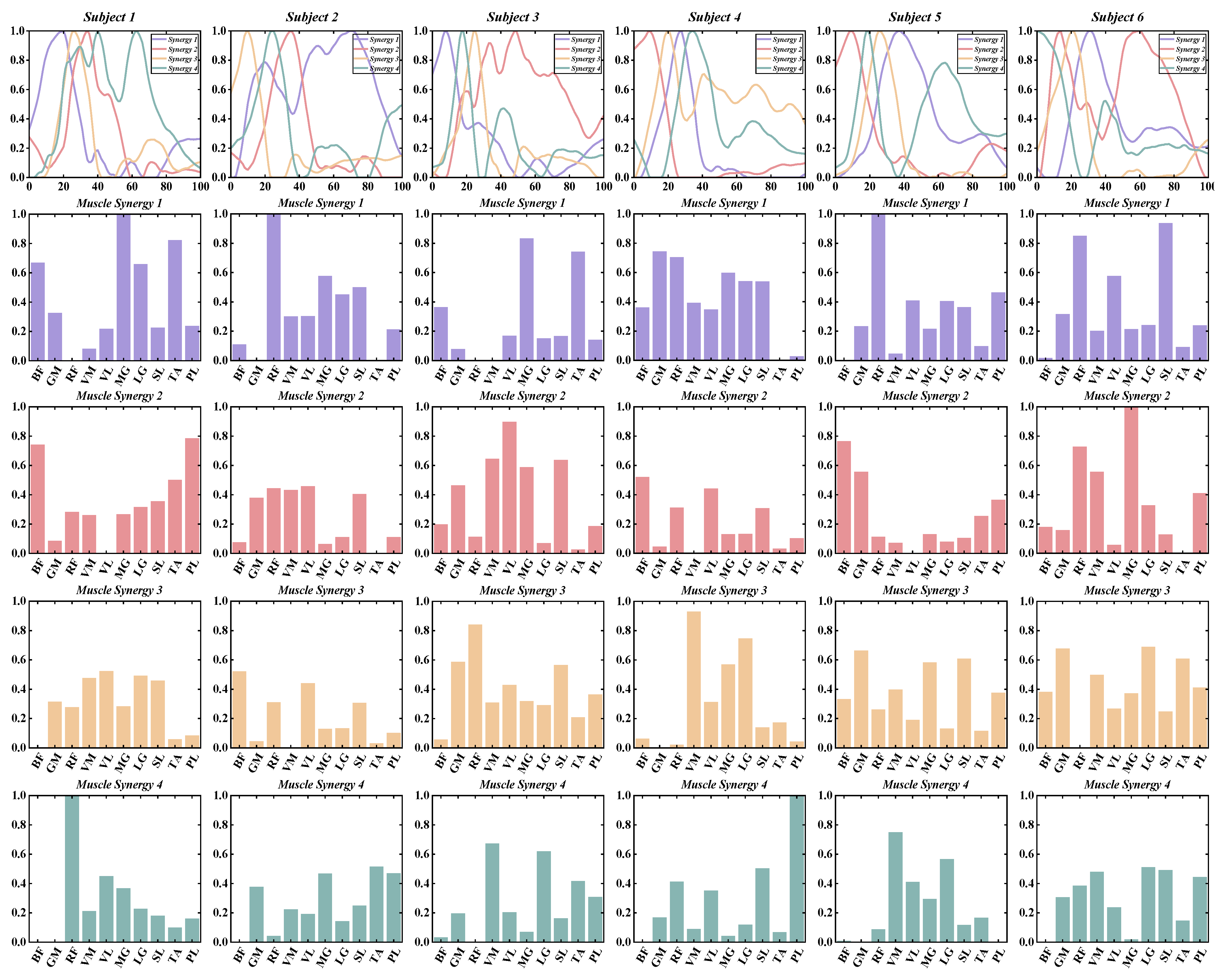
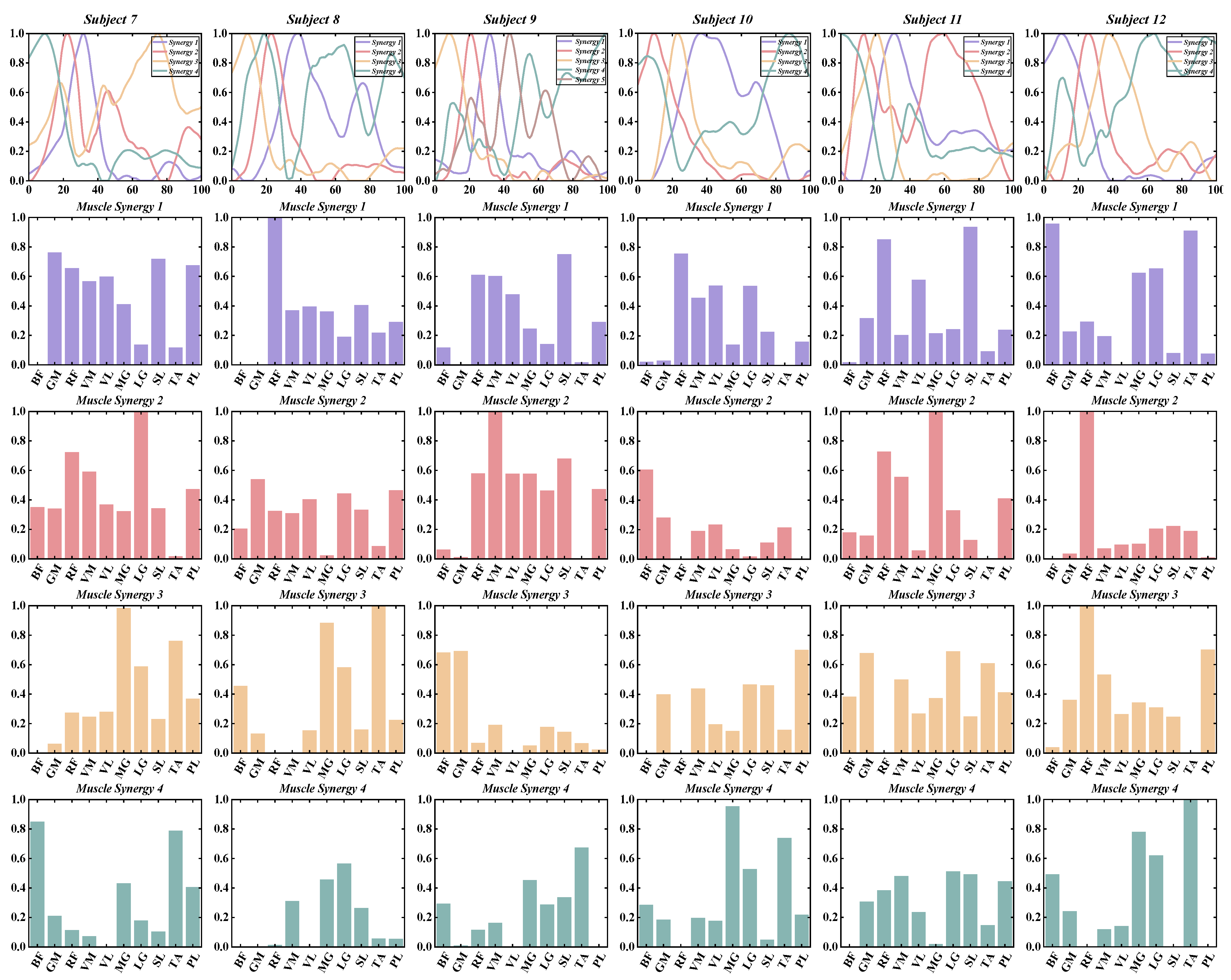
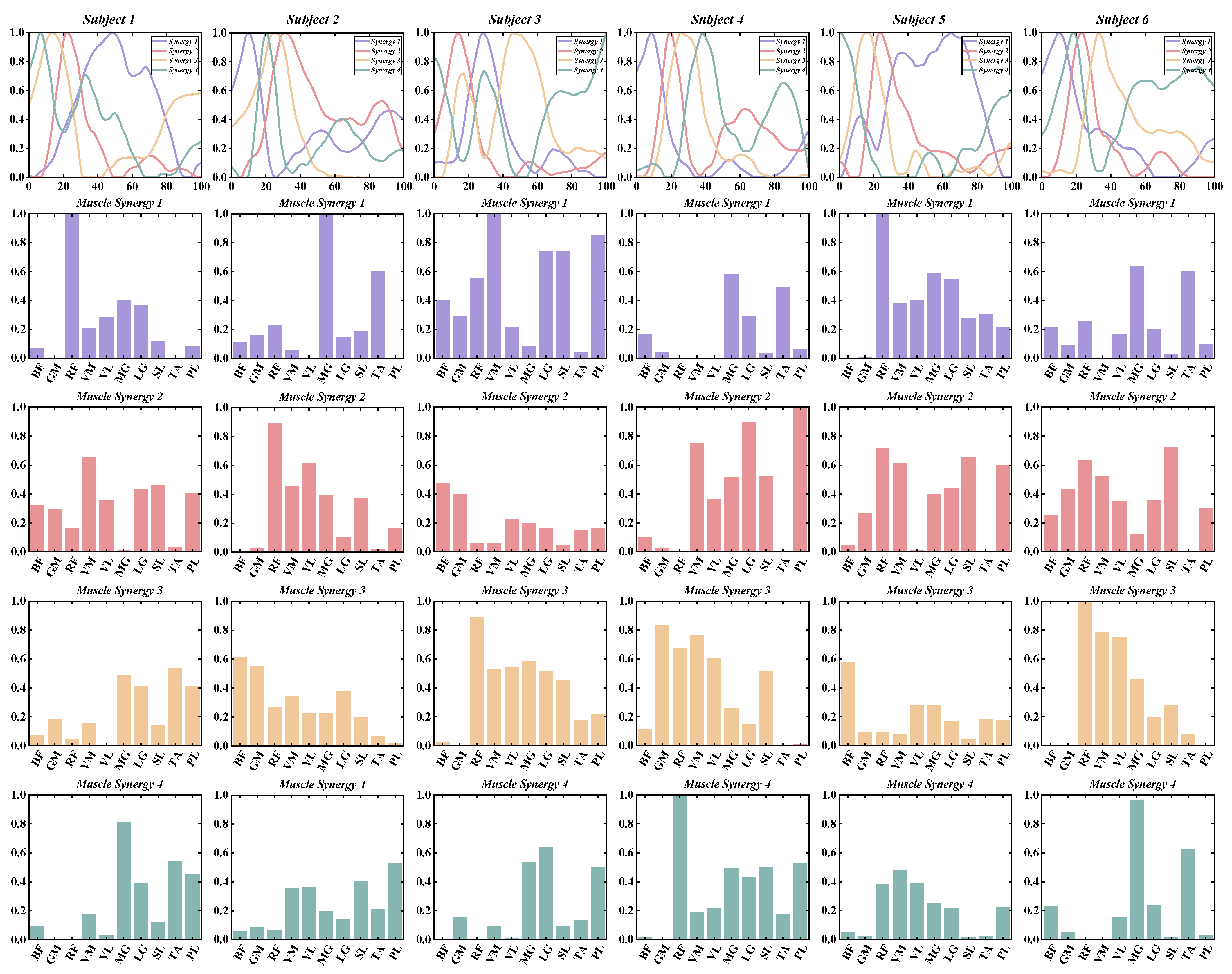
3.1. Number of Muscle Synergy Extraction by NNMF
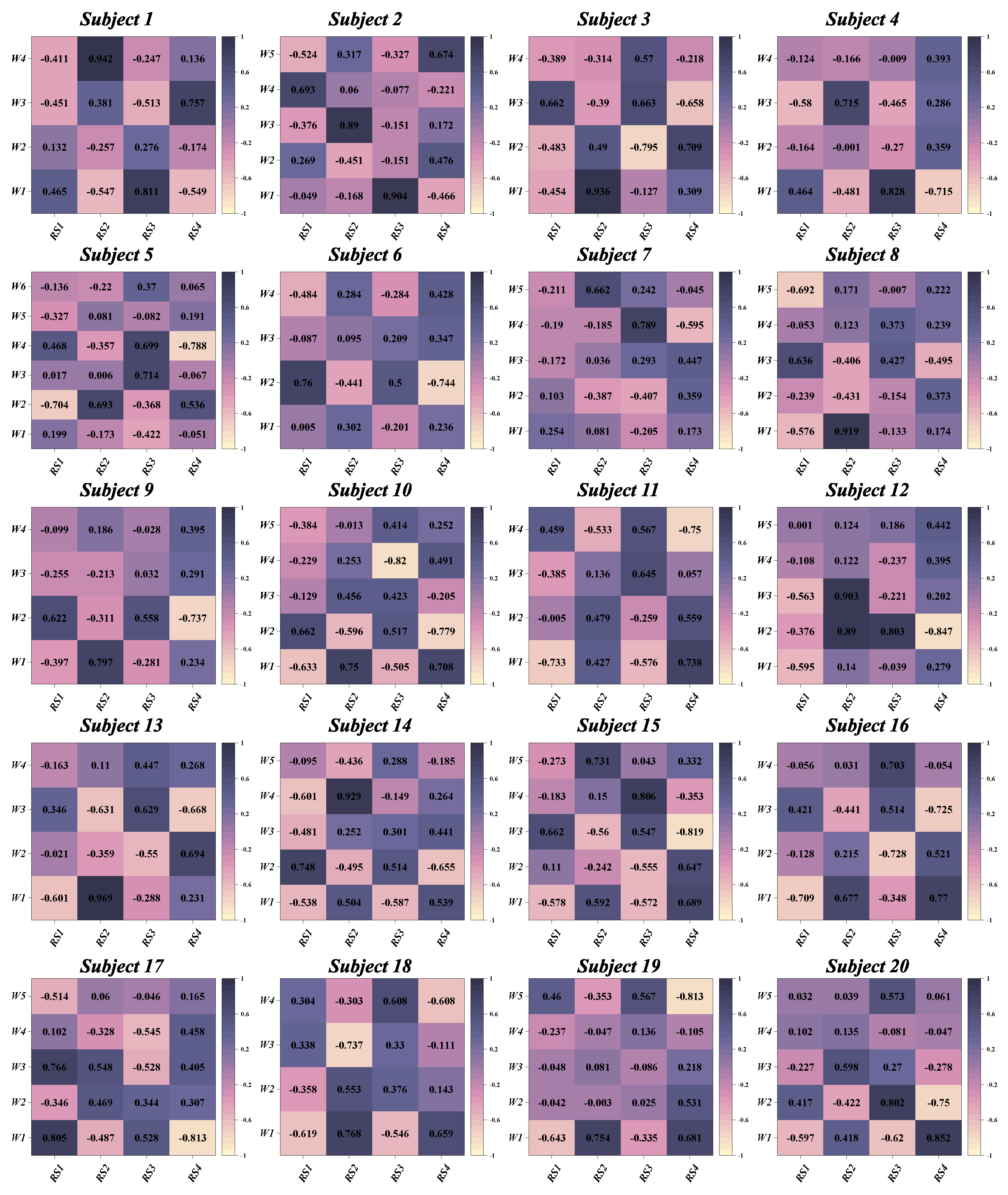
3.2. Similarities between Muscle Synergies
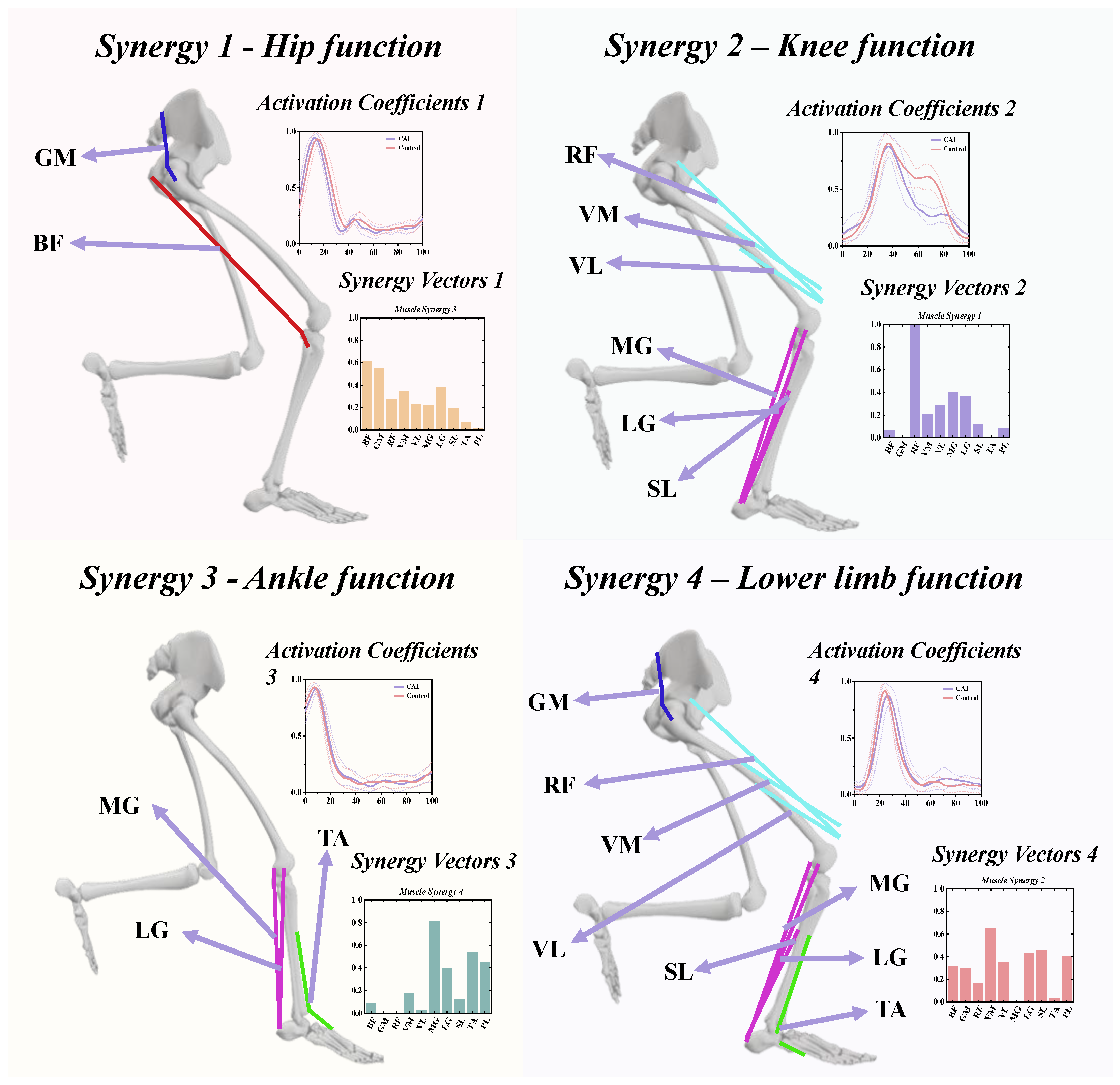
3.3. The Functional Role of Muscle Synergies
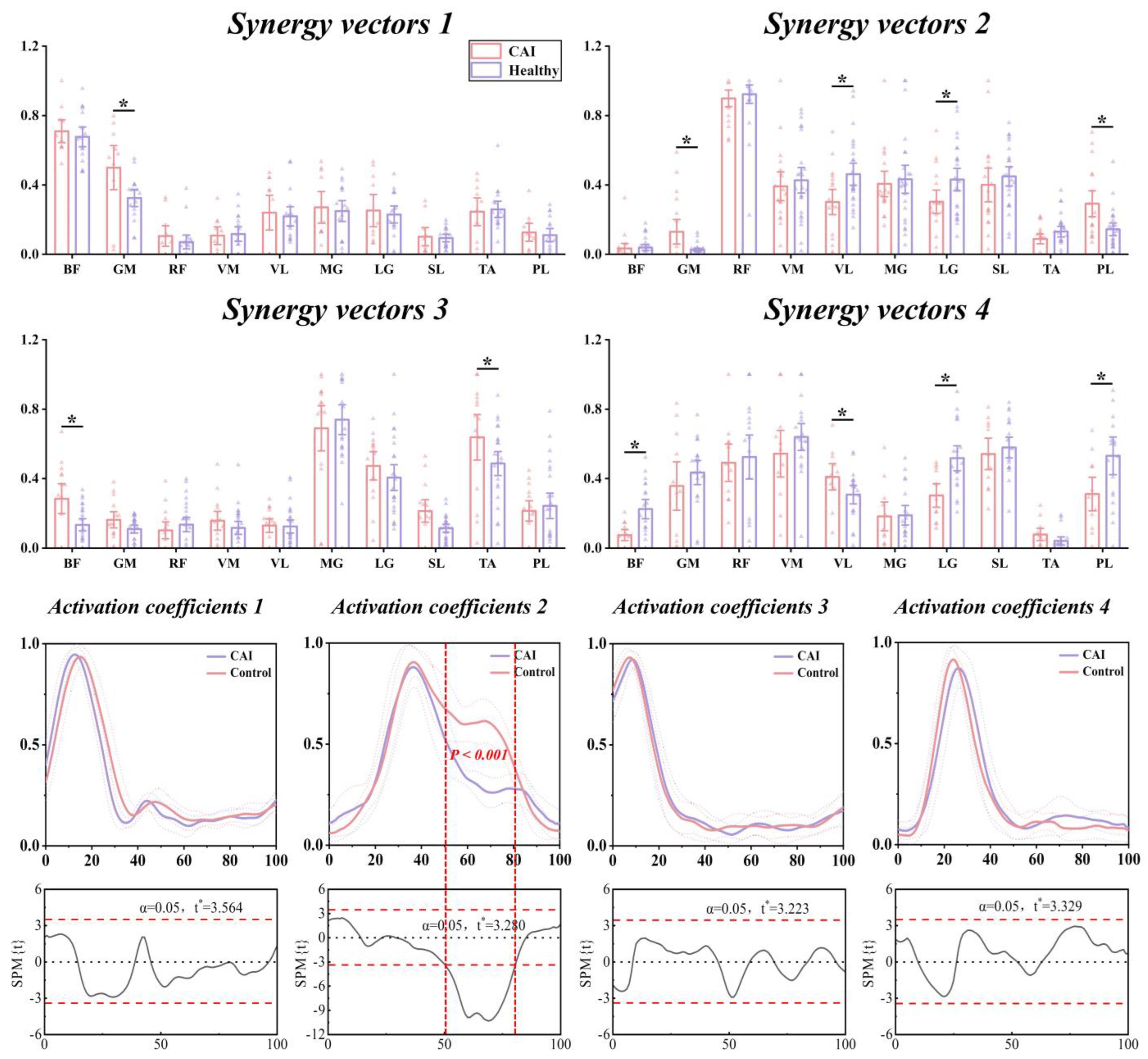
3.4. Characteristics of Temporal and Spatial Modules
4. Discussion
5. Practical Applications
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hølmer, P.; Søndergaard, L.; Konradsen, L.; Nielsen, P.T.; Jørgensen, L.N. Epidemiology of sprains in the lateral ankle and foot. Foot Ankle Int. 1994, 15, 72–74. [Google Scholar] [CrossRef] [PubMed]
- Wikstrom, E.A.; Hubbard-Turner, T.; McKeon, P.O. Understanding and treating lateral ankle sprains and their consequences: A constraints-based approach. Sports Med. 2013, 43, 385–393. [Google Scholar] [CrossRef] [PubMed]
- Gribble, P.A.; Bleakley, C.M.; Caulfield, B.M.; Docherty, C.L.; Fourchet, F.; Fong, D.T.-P.; Hertel, J.; Hiller, C.E.; Kaminski, T.W.; McKeon, P.O. Evidence review for the 2016 International Ankle Consortium consensus statement on the prevalence, impact and long-term consequences of lateral ankle sprains. Br. J. Sports Med. 2016, 50, 1496–1505. [Google Scholar] [CrossRef] [PubMed]
- Yu, P.; Mei, Q.; Xiang, L.; Fernandez, J.; Gu, Y. Differences in the locomotion biomechanics and dynamic postural control between individuals with chronic ankle instability and copers: A systematic review. Sports Biomech. 2022, 21, 531–549. [Google Scholar] [CrossRef] [PubMed]
- Wikstrom, E.A.; Brown, C.N. Minimum reporting standards for copers in chronic ankle instability research. Sports Med. 2014, 44, 251–268. [Google Scholar] [CrossRef] [PubMed]
- Thompson, C.; Schabrun, S.; Romero, R.; Bialocerkowski, A.; van Dieen, J.; Marshall, P. Factors contributing to chronic ankle instability: A systematic review and meta-analysis of systematic reviews. Sports Med. 2018, 48, 189–205. [Google Scholar] [CrossRef] [PubMed]
- Li, H.-Y.; Zheng, J.-J.; Zhang, J.; Cai, Y.-H.; Hua, Y.-H.; Chen, S.-Y. The improvement of postural control in patients with mechanical ankle instability after lateral ankle ligaments reconstruction. Knee Surg. Sports Traumatol. Arthrosc. 2016, 24, 1081–1085. [Google Scholar] [CrossRef] [PubMed]
- Needle, A.R.; Lepley, A.S.; Grooms, D.R. Central nervous system adaptation after ligamentous injury: A summary of theories, evidence, and clinical interpretation. Sports Med. 2017, 47, 1271–1288. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Quan, W.; Zhou, H.; Sun, D.; Baker, J.S.; Gu, Y. Explaining the differences of gait patterns between high and low-mileage runners with machine learning. Sci. Rep. 2022, 12, 2981. [Google Scholar] [CrossRef]
- Tresch, M.C.; Saltiel, P.; Bizzi, E. The construction of movement by the spinal cord. Nat. Neurosci. 1999, 2, 162–167. [Google Scholar] [CrossRef]
- Gao, X.; Xu, D.; Li, F.; Baker, J.S.; Li, J.; Gu, Y. Biomechanical Analysis of Latin Dancers’ Lower Limb during Normal Walking. Bioengineering 2023, 10, 1128. [Google Scholar] [CrossRef] [PubMed]
- Clark, D.J.; Ting, L.H.; Zajac, F.E.; Neptune, R.R.; Kautz, S.A. Merging of healthy motor modules predicts reduced locomotor performance and muscle coordination complexity post-stroke. J. Neurophysiol. 2010, 103, 844–857. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.-Z.; Lin, Y.-A.; Lee, H.-J. Are landing biomechanics altered in elite athletes with chronic ankle instability. J. Sports Sci. Med. 2019, 18, 653. [Google Scholar] [PubMed]
- Son, S.J.; Kim, H.; Seeley, M.K.; Hopkins, J.T. Movement Strategies among Groups of Chronic Ankle Instability, Coper, and Control. Med. Sci. Sports Exerc. 2017, 49, 1649–1661. [Google Scholar] [CrossRef] [PubMed]
- Wright, C.J.; Arnold, B.L.; Ross, S.E. Altered kinematics and time to stabilization during drop-jump landings in individuals with or without functional ankle instability. J. Athl. Train. 2016, 51, 5–15. [Google Scholar] [CrossRef] [PubMed]
- Doherty, C.; Bleakley, C.; Hertel, J.; Caulfield, B.; Ryan, J.; Delahunt, E. Single-leg drop landing movement strategies in participants with chronic ankle instability compared with lateral ankle sprain ‘copers’. Knee Surg. Sports Traumatol. Arthrosc. 2016, 24, 1049–1059. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Han, Y.; Li, Y.; Shen, J.; Tu, J.; Yu, Z.; Zhang, J.; Cheng, H.; Zhu, L.; Dong, F. Autonomous gait switching method and experiments of a hexapod walking robot for Mars environment with multiple terrains. Intell. Serv. Robot. 2024, 1, 1–21. [Google Scholar] [CrossRef]
- Hubbard-Turner, T.; Turner, M.J. Physical activity levels in college students with chronic ankle instability. J. Athl. Train. 2015, 50, 742–747. [Google Scholar] [CrossRef] [PubMed]
- Dorris, H.; Oh, J.; Jacobson, N. Wearable Movement Data as a Potential Digital Biomarker for Chronic Pain: An Investigation Using Deep Learning. Phys. Act. Health 2024, 8, 83–92. [Google Scholar] [CrossRef]
- Saito, H.; Yokoyama, H.; Sasaki, A.; Nakazawa, K. Muscle synergy patterns as altered coordination strategies in individuals with chronic low back pain: A cross-sectional study. J. Neuroeng. Rehabil. 2023, 20, 69. [Google Scholar] [CrossRef]
- Kerkman, J.N.; Daffertshofer, A.; Gollo, L.L.; Breakspear, M.; Boonstra, T.W. Network structure of the human musculoskeletal system shapes neural interactions on multiple time scales. Sci. Adv. 2018, 4, eaat0497. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, A.S.; Silva, P.B.; Lund, M.E.; Kersting, U.G.; Farina, D. Fast changes in direction during human locomotion are executed by impulsive activation of motor modules. Neuroscience 2013, 228, 283–293. [Google Scholar] [CrossRef] [PubMed]
- d’Avella, A.; Saltiel, P.; Bizzi, E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat. Neurosci. 2003, 6, 300–308. [Google Scholar] [CrossRef]
- Cheung, V.C.; d’Avella, A.; Tresch, M.C.; Bizzi, E. Central and sensory contributions to the activation and organization of muscle synergies during natural motor behaviors. J. Neurosci. 2005, 25, 6419–6434. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Rabbi, M.F.; Pizzolato, C.; Lloyd, D.G.; Carty, C.P.; Devaprakash, D.; Diamond, L.E. Non-negative matrix factorisation is the most appropriate method for extraction of muscle synergies in walking and running. Sci. Rep. 2020, 10, 8266. [Google Scholar] [CrossRef]
- Kim, H.; Palmieri-Smith, R.; Kipp, K. Muscle synergies in people with chronic ankle instability during anticipated and unanticipated landing-cutting tasks. J. Athl. Train. 2023, 58, 143–152. [Google Scholar] [CrossRef]
- Fong, D.T.-P.; Hong, Y.; Chan, L.-K.; Yung, P.S.-H.; Chan, K.-M. A systematic review on ankle injury and ankle sprain in sports. Sports Med. 2007, 37, 73–94. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Xu, D.; Zhou, H.; Kovács, B.; Liang, M. The effect of heel height on the Achilles tendon and muscle activity in Latin dancers during a special-landing task. Int. J. Biomed. Eng. Technol. 2024, 44, 303–323. [Google Scholar] [CrossRef]
- Herzog, W.; Sokolosky, J.; Zhang, Y.; Guimarães, A. EMG-force relation in dynamically contracting cat plantaris muscle. J. Electromyogr. Kinesiol. 1998, 8, 147–155. [Google Scholar] [CrossRef]
- Van Ruijven, L.; Weijs, W. A new model for calculating muscle forces from electromyograms. Eur. J. Appl. Physiol. Occup. Physiol. 1990, 61, 479–485. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, T.S.; Lloyd, D.G.; Manal, K.; Besier, T.F. Neuromusculoskeletal modeling: Estimation of muscle forces and joint moments and movements from measurements of neural command. J. Appl. Biomech. 2004, 20, 367–395. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhou, H.; Quan, W.; Gusztav, F.; Baker, J.S.; Gu, Y. Adaptive neuro-fuzzy inference system model driven by the non-negative matrix factorization-extracted muscle synergy patterns to estimate lower limb joint movements. Comput. Methods Programs Biomed. 2023, 242, 107848. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhou, H.; Quan, W.; Gusztav, F.; Wang, M.; Baker, J.S.; Gu, Y. Accurately and effectively predict the ACL force: Utilizing biomechanical landing pattern before and after-fatigue. Comput. Methods Programs Biomed. 2023, 241, 107761. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.W.; Browne, M.; Langville, A.N.; Pauca, V.P.; Plemmons, R.J. Algorithms and applications for approximate nonnegative matrix factorization. Comput. Stat. Data Anal. 2007, 52, 155–173. [Google Scholar] [CrossRef]
- Lee, D.; Seung, H.S. Algorithms for Non-Negative Matrix factorization. Adv. Neural Inf. Process. Syst. 2000, 13. Available online: https://proceedings.neurips.cc/paper_files/paper/2000/file/f9d1152547c0bde01830b7e8bd60024c-Paper.pdf (accessed on 22 April 2024).
- Danion, F.; Latash, M. Motor Control: Theories, Experiments, and Applications; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Li, X.; Zeng, H.; Li, Y.; Song, A. Quantitative Assessment via Multi-Domain Fusion of Muscle Synergy Associated with Upper-Limb Motor Function for Stroke Rehabilitation. IEEE Trans. Biomed. Eng. 2023, 71, 1430–1441. [Google Scholar] [CrossRef]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1999, 29, 433–439. [Google Scholar] [CrossRef]
- Modha, D.S.; Spangler, W.S. Feature weighting in k-means clustering. Mach. Learn. 2003, 52, 217–237. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, Y.; Kim, M.; Yoon, B. Muscle synergies for turning during human walking. J. Mot. Behav. 2019, 51, 1–9. [Google Scholar] [CrossRef]
- Pataky, T.C. One-dimensional statistical parametric mapping in Python. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 295–301. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Palmieri-Smith, R.; Kipp, K. Peak forces and force generating capacities of lower extremity muscles during dynamic tasks in people with and without chronic ankle instability. Sports Biomech. 2022, 21, 487–500. [Google Scholar] [CrossRef] [PubMed]
- McCann, R.S.; Crossett, I.D.; Terada, M.; Kosik, K.B.; Bolding, B.A.; Gribble, P.A. Hip strength and star excursion balance test deficits of patients with chronic ankle instability. J. Sci. Med. Sport 2017, 20, 992–996. [Google Scholar] [CrossRef] [PubMed]
- Yen, S.-C.; Chui, K.K.; Corkery, M.B.; Allen, E.A.; Cloonan, C.M. Hip-ankle coordination during gait in individuals with chronic ankle instability. Gait Posture 2017, 53, 193–200. [Google Scholar] [CrossRef] [PubMed]
- Robbins, S.; Waked, E. Factors associated with ankle injuries: Preventive measures. Sports Med. 1998, 25, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Yeow, C.H.; Lee, P.V.S.; Goh, J.C.H. An investigation of lower extremity energy dissipation strategies during single-leg and double-leg landing based on sagittal and frontal plane biomechanics. Hum. Mov. Sci. 2011, 30, 624–635. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhou, H.; Quan, W.; Jiang, X.; Liang, M.; Li, S.; Ugbolue, U.C.; Baker, J.S.; Gusztav, F.; Ma, X. A new method proposed for realizing human gait pattern recognition: Inspirations for the application of sports and clinical gait analysis. Gait Posture 2024, 107, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhou, H.; Quan, W.; Ma, X.; Chon, T.-E.; Fernandez, J.; Gusztav, F.; Kovács, A.; Baker, J.S.; Gu, Y. New insights optimize landing strategies to reduce lower limb injury risk. Cyborg Bionic Syst. 2024, 5, 0126. [Google Scholar] [CrossRef]
- Kim, H.; Son, S.J.; Seeley, M.K.; Hopkins, J.T. Kinetic Compensations due to Chronic Ankle Instability during Landing and Jumping. Med. Sci. Sports Exerc. 2018, 50, 308–317. [Google Scholar] [CrossRef]
- Gribble, P.; Robinson, R. Differences in spatiotemporal landing variables during a dynamic stability task in subjects with CAI. Scand. J. Med. Sci. Sports 2010, 20, e63–e71. [Google Scholar] [CrossRef]
- Terada, M.; Pfile, K.R.; Pietrosimone, B.G.; Gribble, P.A. Effects of chronic ankle instability on energy dissipation in the lower extremity. Med. Sci. Sports Exerc. 2013, 45, 2120–2128. [Google Scholar] [CrossRef] [PubMed]
- Kramer, L.; Denegar, C.; Buckley, W.; Hertel, J. Factors associated with anterior cruciate ligament injury: History in female athletes. J. Sports Med. Phys. Fit. 2007, 47, 446. [Google Scholar]
- DeMers, M.S.; Hicks, J.L.; Delp, S.L. Preparatory co-activation of the ankle muscles may prevent ankle inversion injuries. J. Biomech. 2017, 52, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Nyska, M.; Shabat, S.; Simkin, A.; Neeb, M.; Matan, Y.; Mann, G. Dynamic force distribution during level walking under the feet of patients with chronic ankle instability. Br. J. Sports Med. 2003, 37, 495–497. [Google Scholar] [CrossRef]
- Madigan, M.L.; Pidcoe, P.E. Changes in landing biomechanics during a fatiguing landing activity. J. Electromyogr. Kinesiol. 2003, 13, 491–498. [Google Scholar] [CrossRef]






| CAI (n = 22) Mean (SD) | Healthy (n = 22) Mean (SD) | p-Value | |
|---|---|---|---|
| Age (year) | 23.5 (1.2) | 22.7 (1.4) | 0.349 |
| Mass (kg) | 80.4 (5.6) | 80.6 (6.1) | 0.864 |
| Height (cm) | 179.7 (4.5) | 178.8 (4.0) | 0.643 |
| CAIT (score) | 20.9 (2.6) | 29.5 (0.5) | <0.001 |
| Ankle sprains (times) | 3.2 (1.1) | 0 | <0.001 |
| CAI Mean (SD) | Healthy Mean (SD) | p-Value | |
|---|---|---|---|
| The number of muscle synergies | 4.55 (0.58) | 4.27 (0.45) | 0.109 |
| Global VAF (%) | |||
| With three synergies | 85.30 (2.13) | 86.24 (1.72) | 0.122 |
| With four synergies | 90.09 (1.61) | 90.64 (1.23) | 0.221 |
| With five synergies | 92.58 (1.10) | 93.37 (1.12) | 0.138 |
| Local VAFs with four synergies (%) | |||
| BF | 88.62 (1.69) | 84.19 (9.42) | 0.297 |
| GM | 84.89 (4.44) | 85.75 (4.33) | 0.730 |
| RF | 90.27 (5.11) | 94.18 (3.21) | 0.128 |
| VM | 91.76 (3.11) | 90.40 (3.47) | 0.471 |
| VL | 89.74 (2.06) | 88.40 (3.67) | 0.426 |
| MG | 92.54 (2.02) | 93.34 (2.58) | 0.543 |
| LG | 90.81 (2.57) | 91.84 (2.13) | 0.452 |
| SL | 89.75 (3.92) | 90.36 (0.90) | 0.713 |
| TA | 88.05 (3.59) | 87.10 (3.95) | 0.658 |
| PL | 90.07 (5.03) | 91.11 (1.83) | 0.639 |
| Synergy Vectors Mean (SD) | Muscle Synergy 1 | Muscle Synergy 2 | Muscle Synergy 3 | Muscle Synergy 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CAI | Healthy | p-Value | CAI | Healthy | p-Value | CAI | Healthy | p-Value | CAI | Healthy | p-Value | |
| 0.71 (0.14) | 0.68 (0.15) | 0.586 | 0.03 (0.07) | 0.04 (0.05) | 0.804 | 0.28 (0.20) | 0.13 (0.11) | 0.026 | 0.08 (0.07) | 0.22 (0.15) | 0.002 | |
| 0.50 (0.25) | 0.32 (0.13) | 0.035 | 0.13 (0.18) | 0.02 (0.03) | 0.042 | 0.16 (0.11) | 0.11 (0.07) | 0.095 | 0.37 (0.29) | 0.43 (0.19) | 0.411 | |
| 0.11 (0.11) | 0.07 (0.10) | 0.698 | 0.90 (0.13) | 0.92 (0.17) | 0.635 | 0.10 (0.10) | 0.13 (0.12) | 0.454 | 0.49 (0.22) | 0.52 (0.35) | 0.766 | |
| 0.11 (0.10) | 0.12 (0.11) | 0.835 | 0.39 (0.22) | 0.43 (0.23) | 0.642 | 0.16 (0.13) | 0.12 (0.11) | 0.335 | 0.54 (0.28) | 0.64 (0.21) | 0.324 | |
| 0.24 (0.20) | 0.22 (0.14) | 0.785 | 0.30 (0.20) | 0.46 (0.20) | 0.018 | 0.13 (0.09) | 0.12 (0.11) | 0.894 | 0.45 (0.17) | 0.31 (0.15) | 0.030 | |
| 0.27 (0.18) | 0.25 (0.15) | 0.763 | 0.41 (0.18) | 0.43 (0.26) | 0.730 | 0.69 (0.31) | 0.74 (0.27) | 0.619 | 0.18 (0.17) | 0.19 (0.15) | 0.922 | |
| 0.25 (0.19) | 0.23 (0.12) | 0.749 | 0.30 (0.18) | 0.43 (0.21) | 0.049 | 0.47 (0.20) | 0.41 (0.23) | 0.383 | 0.30 (0.14) | 0.52 (0.20) | 0.005 | |
| 0.10 (0.10) | 0.09 (0.05) | 0.810 | 0.40 (0.26) | 0.44 (0.18) | 0.482 | 0.20 (0.15) | 0.11 (0.07) | 0.065 | 0.54 (0.14) | 0.58 (0.16) | 0.599 | |
| 0.25 (0.16) | 0.26 (0.12) | 0.813 | 0.09 (0.08) | 0.13 (0.10) | 0.163 | 0.64 (0.31) | 0.48 (0.22) | 0.042 | 0.08 (0.07) | 0.04 (0.06) | 0.186 | |
| 0.13 (0.10) | 0.11 (0.09) | 0.714 | 0.29 (0.20) | 0.14 (0.12) | 0.006 | 0.21 (0.14) | 0.24 (0.23) | 0.645 | 0.31 (0.20) | 0.53 (0.30) | 0.047 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jie, T.; Xu, D.; Zhang, Z.; Teo, E.-C.; Baker, J.S.; Zhou, H.; Gu, Y. Structural and Organizational Strategies of Locomotor Modules during Landing in Patients with Chronic Ankle Instability. Bioengineering 2024, 11, 518. https://doi.org/10.3390/bioengineering11050518
Jie T, Xu D, Zhang Z, Teo E-C, Baker JS, Zhou H, Gu Y. Structural and Organizational Strategies of Locomotor Modules during Landing in Patients with Chronic Ankle Instability. Bioengineering. 2024; 11(5):518. https://doi.org/10.3390/bioengineering11050518
Chicago/Turabian StyleJie, Tianle, Datao Xu, Zanni Zhang, Ee-Chon Teo, Julien S. Baker, Huiyu Zhou, and Yaodong Gu. 2024. "Structural and Organizational Strategies of Locomotor Modules during Landing in Patients with Chronic Ankle Instability" Bioengineering 11, no. 5: 518. https://doi.org/10.3390/bioengineering11050518
APA StyleJie, T., Xu, D., Zhang, Z., Teo, E.-C., Baker, J. S., Zhou, H., & Gu, Y. (2024). Structural and Organizational Strategies of Locomotor Modules during Landing in Patients with Chronic Ankle Instability. Bioengineering, 11(5), 518. https://doi.org/10.3390/bioengineering11050518







