Staging of Liver Fibrosis Based on Energy Valley Optimization Multiple Stacking (EVO-MS) Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
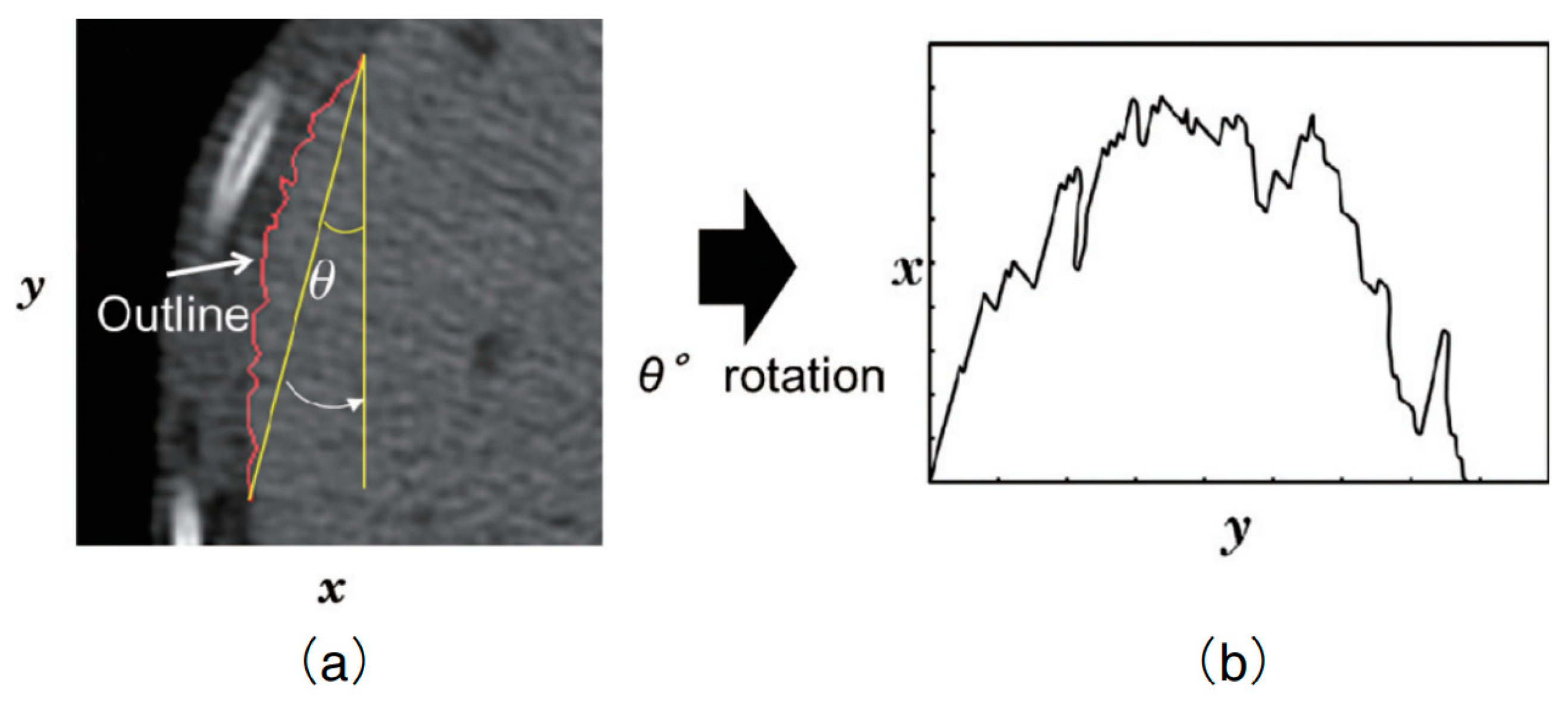
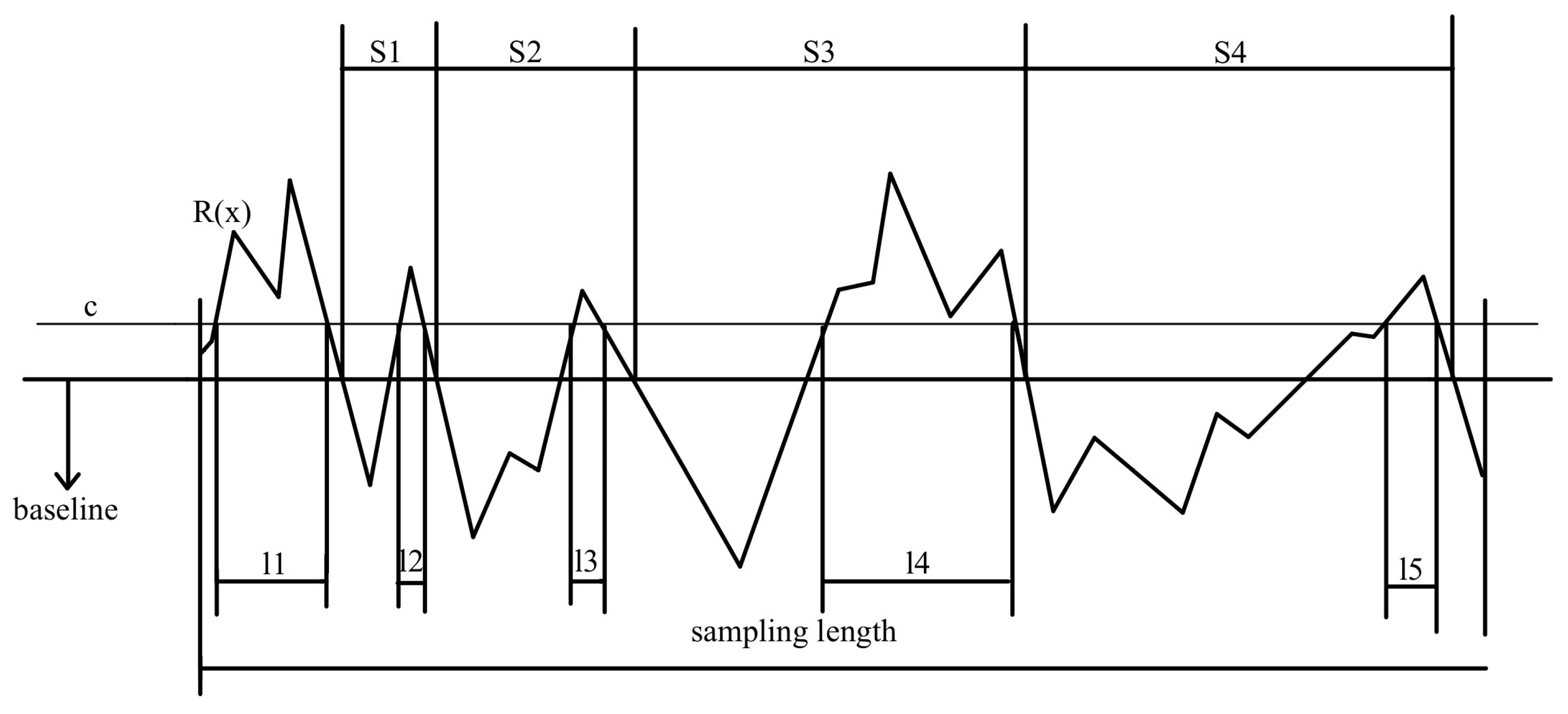
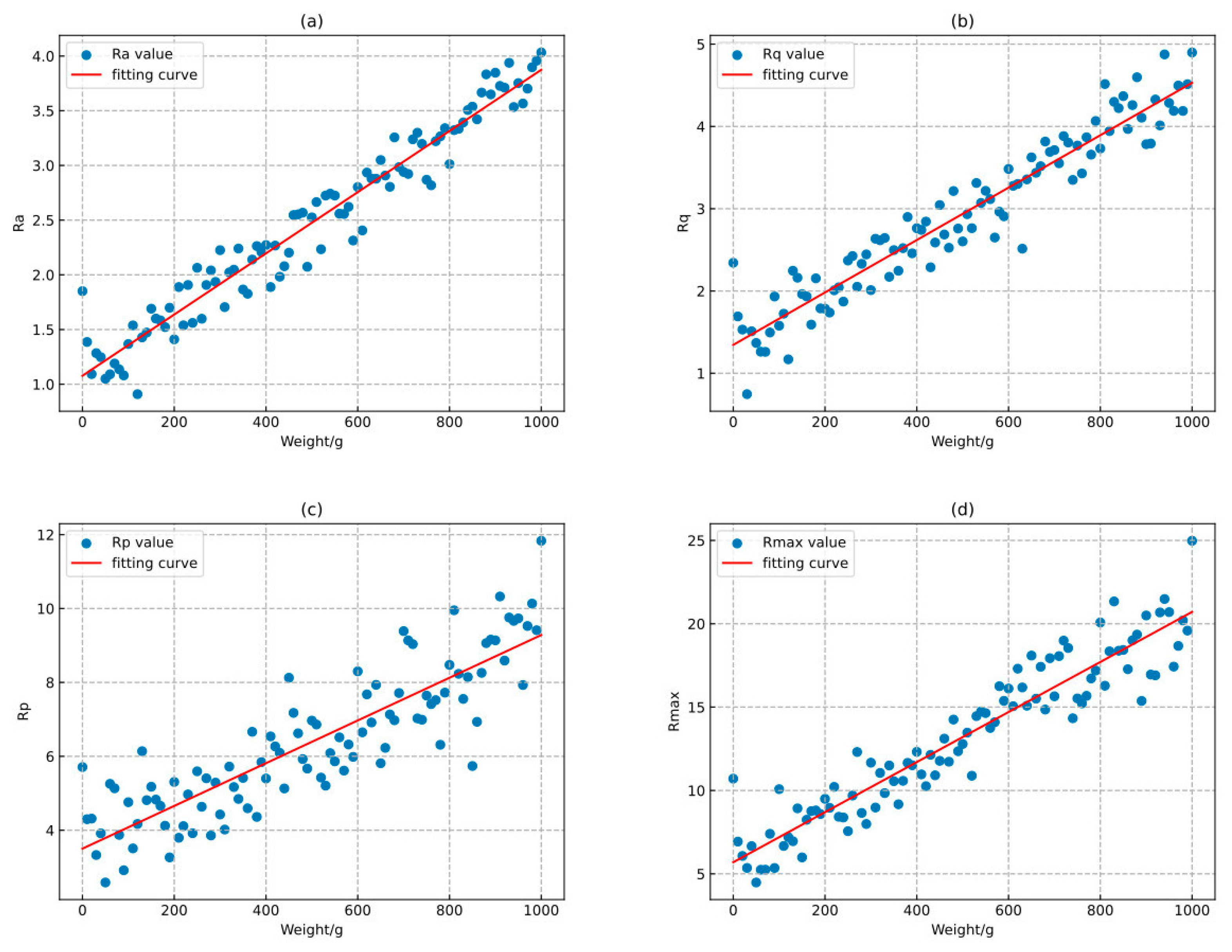
2.2. Microscopic Roughness
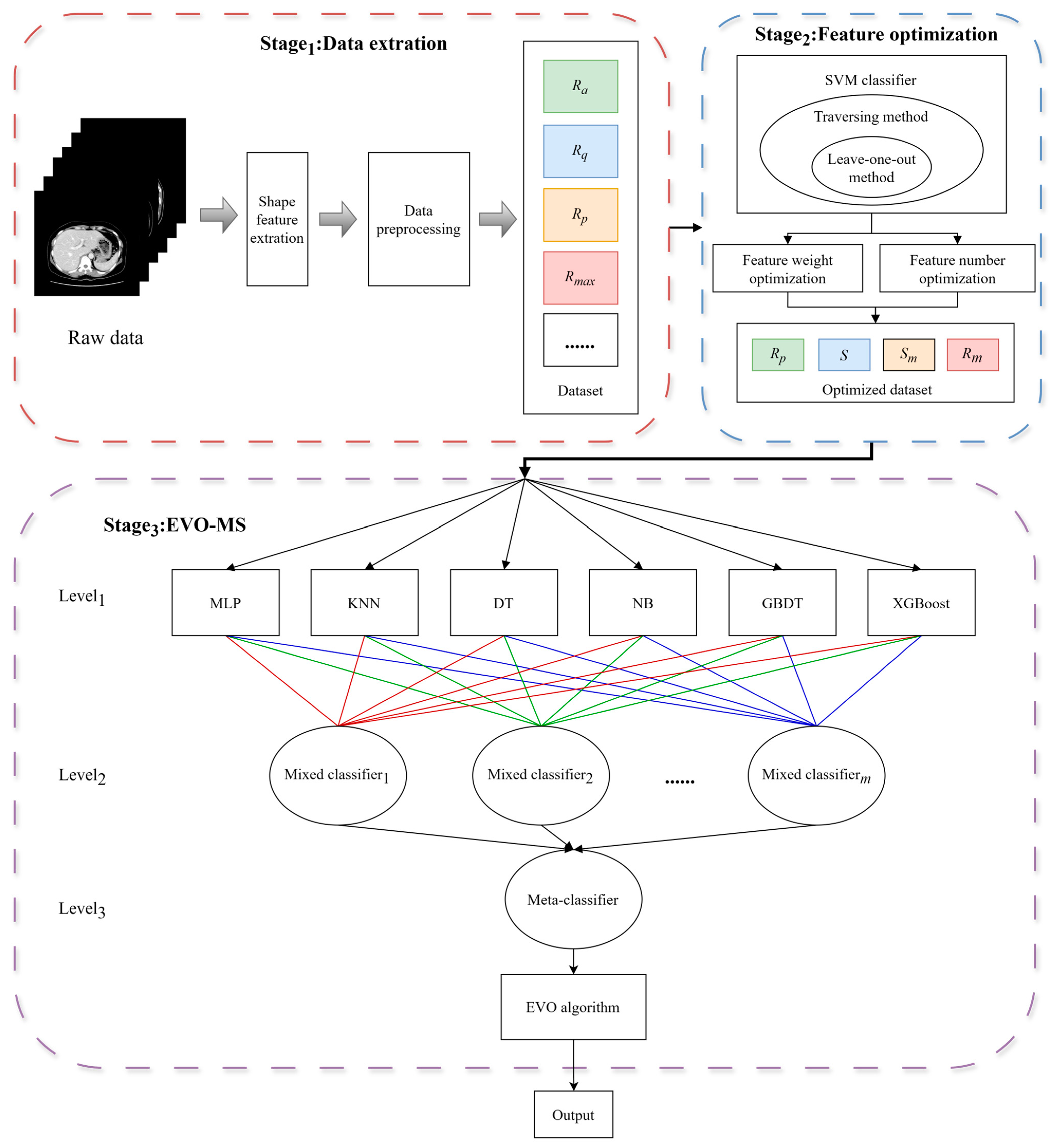
2.3. Overview of the Proposed Method
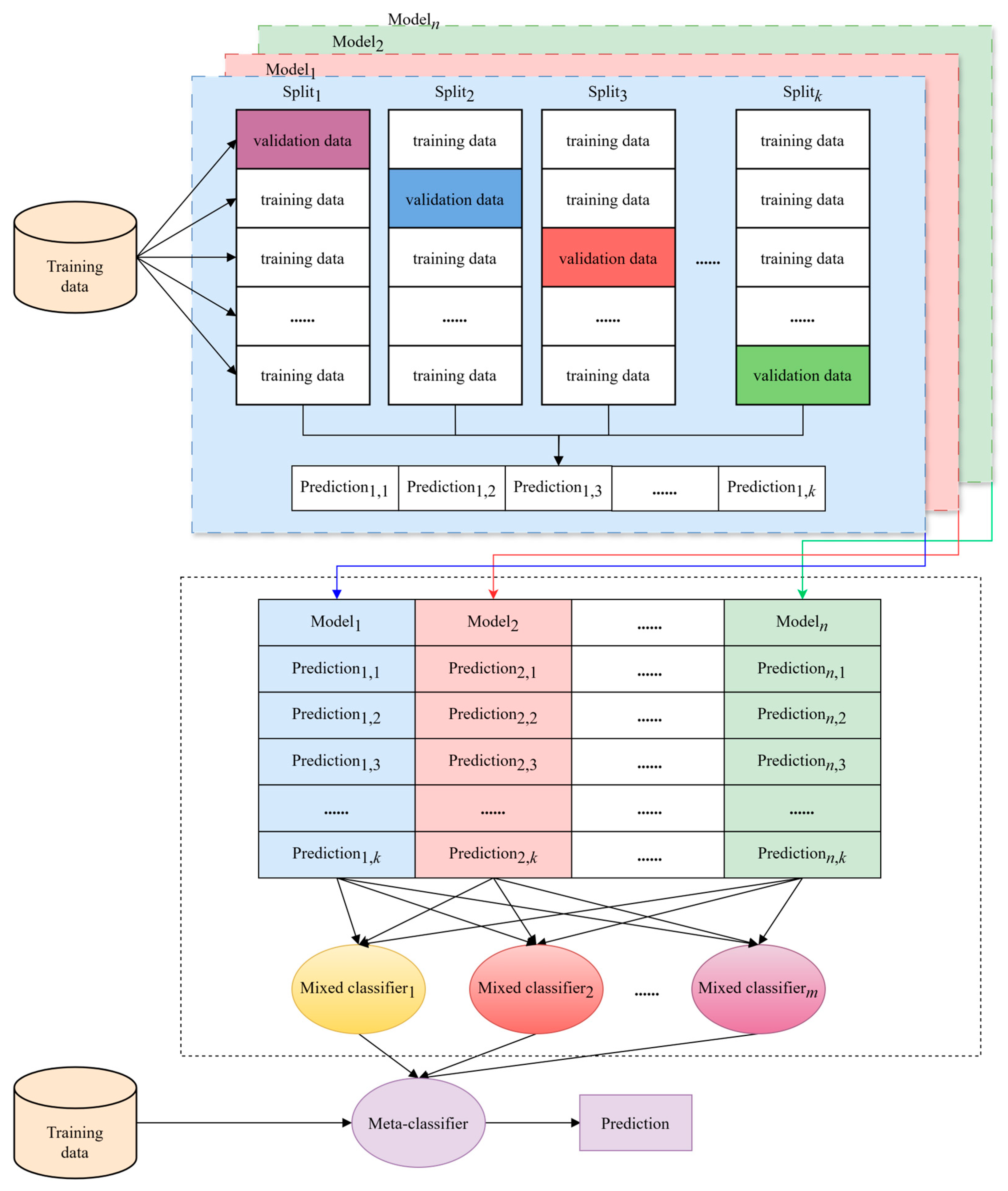
2.4. Multiple Model
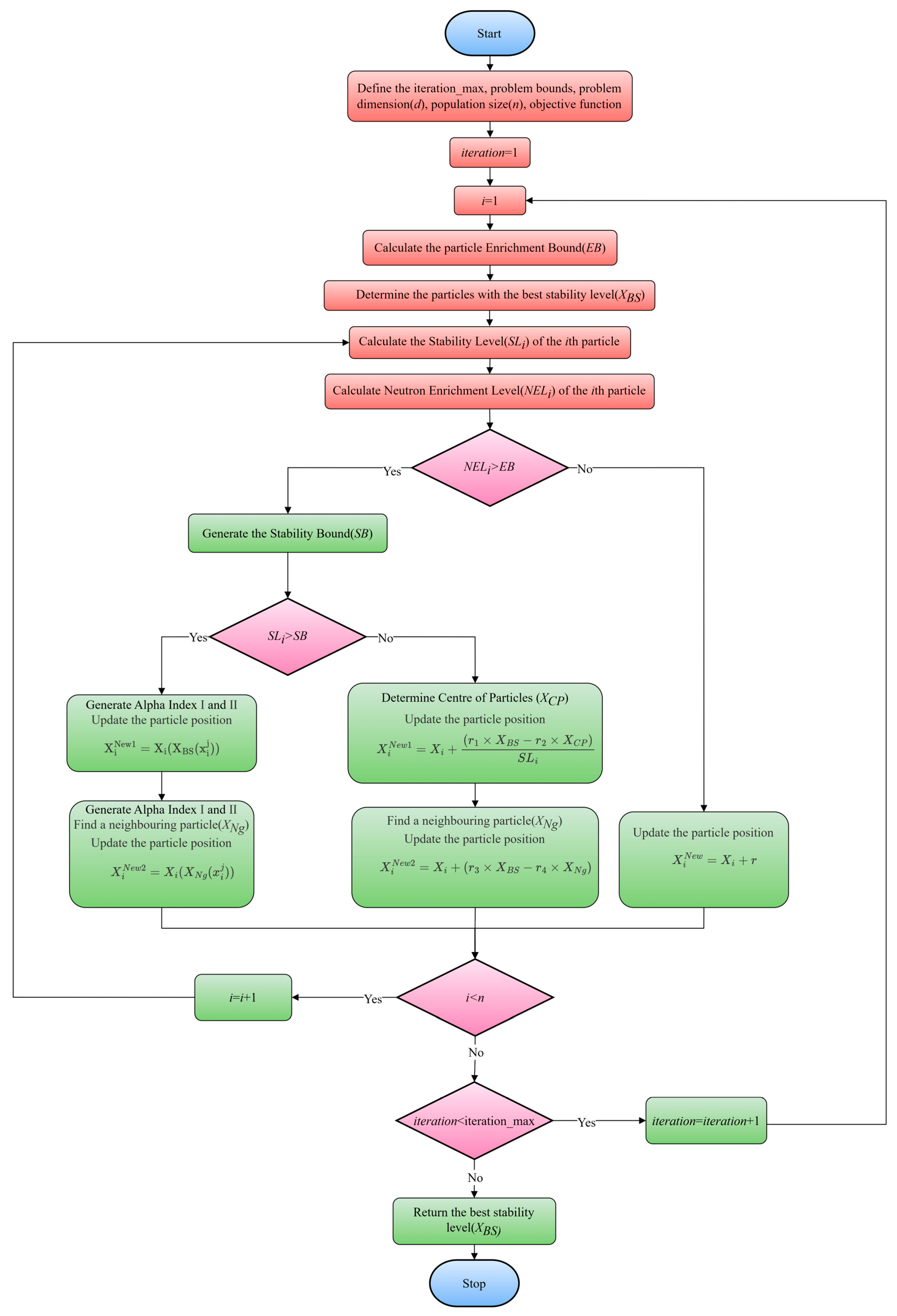
2.5. Energy Valley Optimization
3. Results
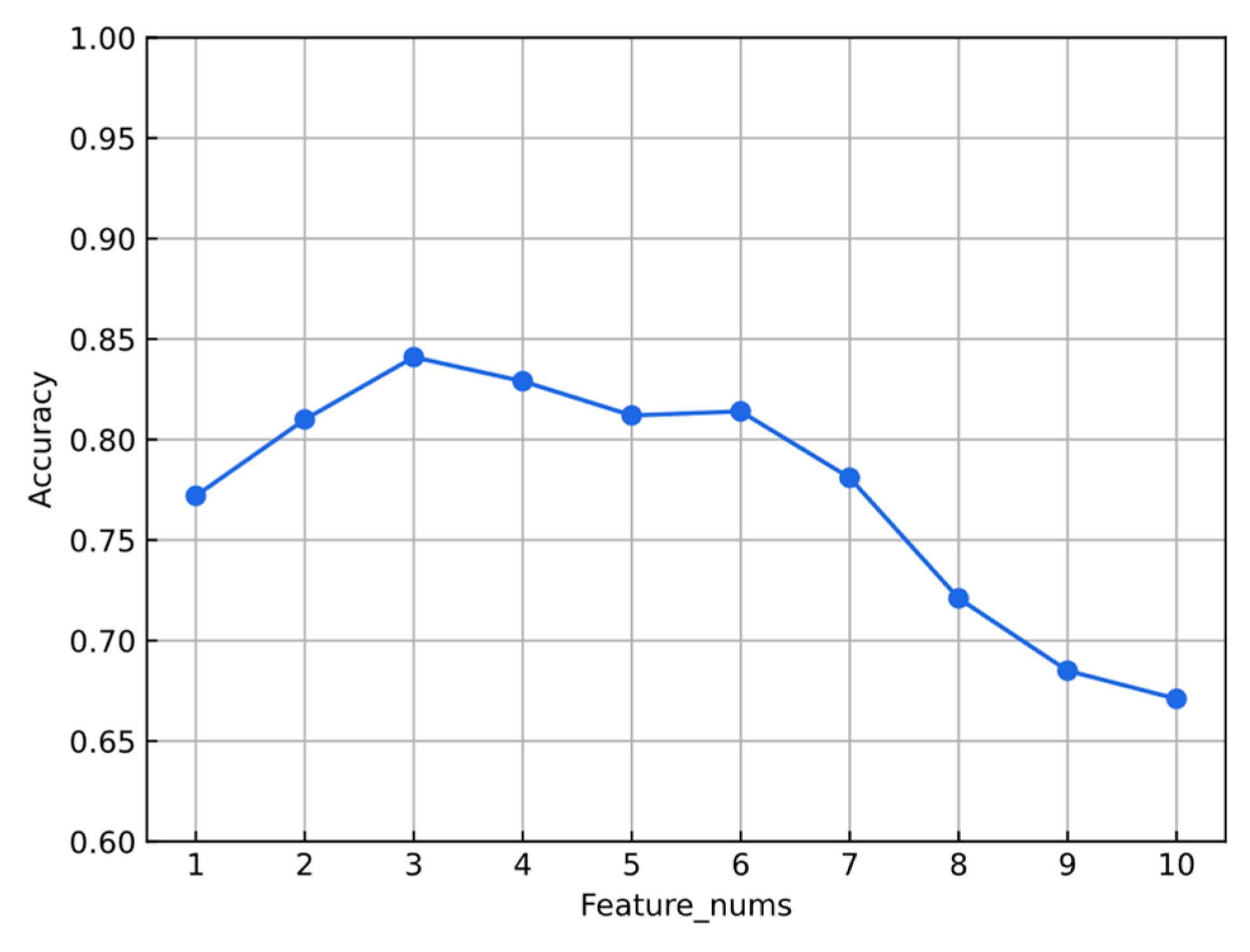
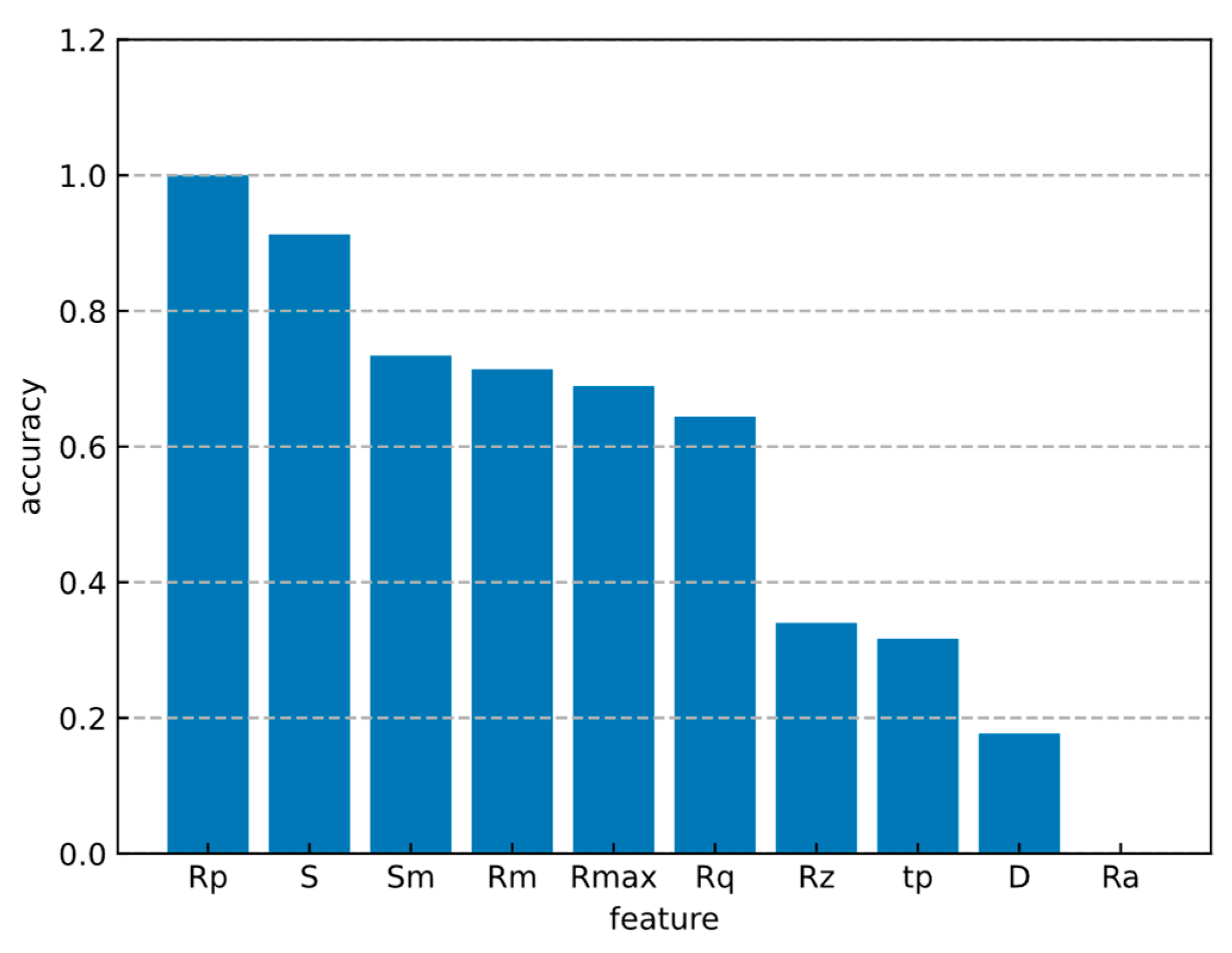
3.1. Feature Optimization
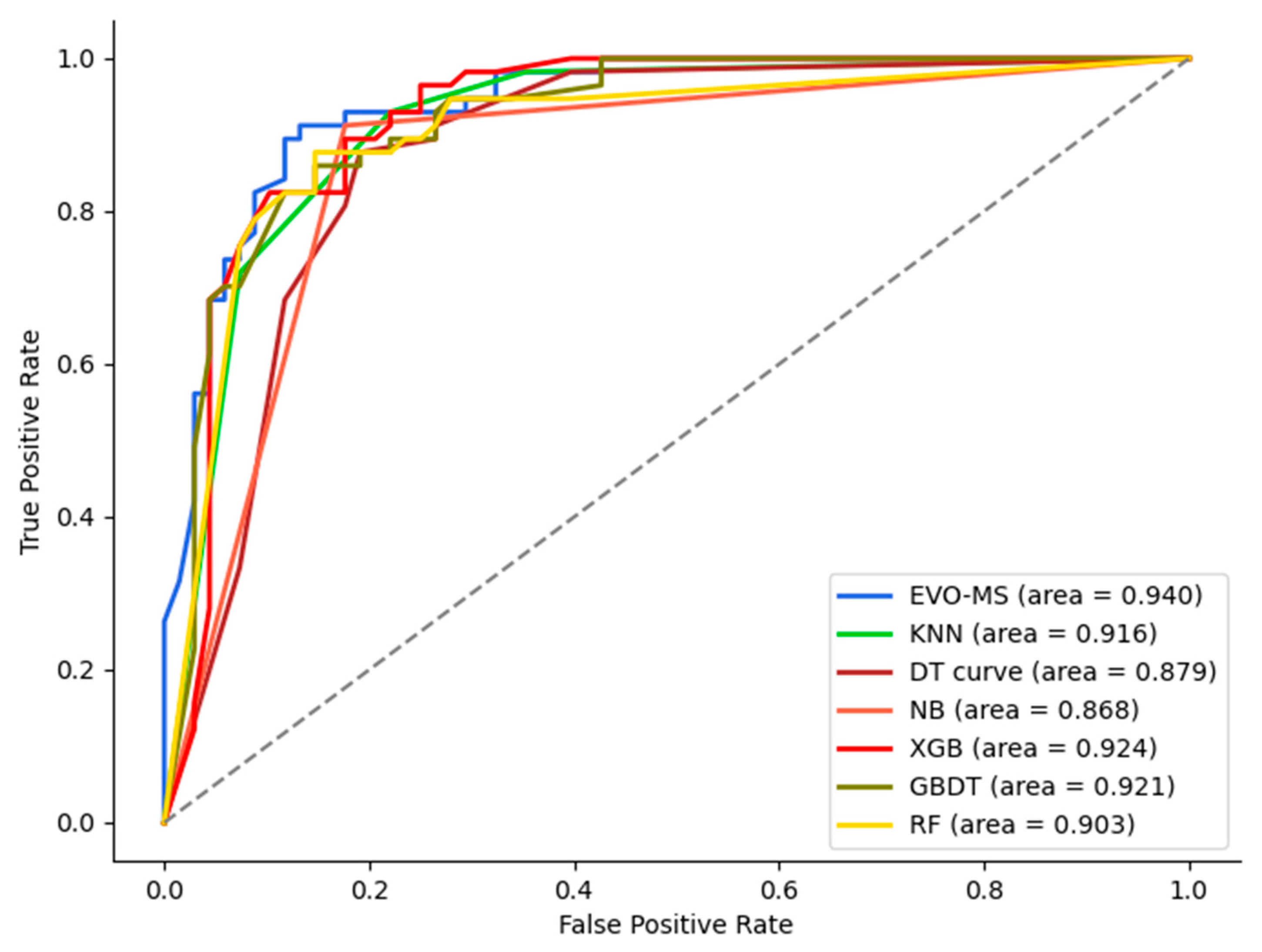
3.2. EVO-MS Model Performance
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Friedman, S.L.; Pinzani, M. Hepatic fibrosis: 2022 Unmet needs and a blueprint for the future. Hepatology 2022, 75, 473–488. [Google Scholar] [CrossRef]
- Rockey, D.C. Hepatic fibrosis and cirrhosis. Yamada’s Textbook of Gastroenterology, John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2022; 2000–2023. [Google Scholar]
- Heyens, L.J.M.; Busschots, D.; Koek, G.H.; Robaeys, G.; Francque, S. Liver fibrosis in non-alcoholic fatty liver disease: From liver biopsy to non-invasive biomarkers in diagnosis and treatment. Front. Med. 2021, 8, 615978. [Google Scholar] [CrossRef] [PubMed]
- Khalifa, A.; Rockey, D.C. The utility of liver biopsy in 2020. Curr. Opin. Gastroenterol. 2020, 36, 184–191. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, A.B.; Mehta, K.J. Liver biopsy for assessment of chronic liver diseases: A synopsis. Clin. Exp. Med. 2022, 23, 273–285. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.J.; Zhou, B.; Ma, K.; Qu, X.H.; Tan, X.M.; Gao, X.; Yan, W.; Long, L.L.; Fujita, H. Selection of optimal shape features for staging hepatic fibrosis on CT image. J. Med. Imaging Health Inform. 2015, 5, 1926–1930. [Google Scholar] [CrossRef]
- Zhou, S.K.; Greenspan, H.; Davatzikos, C.; Duncan, J.S.; Van Ginneken, B.; Madabhushi, A.; Prince, J.L.; Rueckert, D.; Summers, R.M. A review of deep learning in medical imaging: Imaging traits, technology trends, case studies with progress highlights, and future promises. Proc. IEEE 2021, 109, 820–838. [Google Scholar] [CrossRef]
- Liu, X.; Gao, K.; Liu, B.; Pan, C.; Liang, K.; Yan, L.; Ma, J.; He, F.; Zhang, S.; Pan, S.; et al. Advances in deep learning-based medical image analysis. Health Data Sci. 2021, 2021, 8786793. [Google Scholar] [CrossRef]
- Aggarwal, R.; Sounderajah, V.; Martin, G.; Ting, D.S.W.; Karthikesalingam, A.; King, D.; Ashrafian, H.; Darzi, A. Diagnostic accuracy of deep learning in medical imaging: A systematic review and meta-analysis. npj Digit. Med. 2021, 4, 65. [Google Scholar] [CrossRef]
- Singh, S.P.; Wang, L.; Gupta, S.; Goli, H.; Padmanabhan, P.; Gulyás, B. 3D deep learning on medical images: A review. Sensors 2020, 20, 5097. [Google Scholar] [CrossRef]
- Panayides, A.S.; Amini, A.; Filipovic, N.D.; Sharma, A.; Tsaftaris, S.A.; Young, A.A.; Foran, D.J.; Do, N.V.; Golemati, S.; Kurc, T.; et al. AI in medical imaging informatics: Current challenges and future directions. IEEE J. Biomed. Health Inform. 2020, 24, 1837–1857. [Google Scholar] [CrossRef]
- Loomba, R.; Adams, L.A.J.G. Advances in non-invasive assessment of hepatic fibrosis. Gut 2020, 69, 1343–1352. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. Texture feature extraction methods: A survey. IEEE Access 2019, 7, 8975–9000. [Google Scholar] [CrossRef]
- Mayerhoefer, M.E.; Materka, A.; Langs, G.; Häggström, I.; Szczypiński, P.; Gibbs, P.; Cook, G. Introduction to radiomics. J. Nucl. Med. 2020, 61, 488–495. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A survey on ensemble learning. Front. Comput. Sci. 2019, 14, 241–258. [Google Scholar] [CrossRef]
- Binder, H.; Gefeller, O.; Schmid, M.; Mayr, A. The evolution of boosting algorithms. Methods Inf. Med. 2014, 53, 419–427. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Liang, M.; Chang, T.; An, B.; Duan, X.; Du, L.; Wang, X.; Miao, J.; Xu, L.; Gao, X.; Zhang, L.; et al. A stacking ensemble learning framework for genomic prediction. Front. Genet. 2021, 12, 600040. [Google Scholar] [CrossRef]
- Cui, S.; Yin, Y.; Wang, D.; Li, Z.; Wang, Y. A stacking-based ensemble learning method for earthquake casualty prediction. Appl. Soft Comput. 2020, 101, 107038. [Google Scholar] [CrossRef]
- Mota, L.F.M.; Giannuzzi, D.; Bisutti, V.; Pegolo, S.; Trevisi, E.; Schiavon, S.; Gallo, L.; Fineboym, D.; Katz, G.; Cecchinato, A. Real-time milk analysis integrated with stacking ensemble learning as a tool for the daily prediction of cheese-making traits in Holstein cattle. J. Dairy Sci. 2022, 105, 4237–4255. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.-L.; Liu, X.-M.; Dong, C. Multi-dimensional feature fusion and stacking ensemble mechanism for network intrusion detection. Futur. Gener. Comput. Syst. 2021, 122, 130–143. [Google Scholar] [CrossRef]
- Rashid, M.; Kamruzzaman, J.; Imam, T.; Wibowo, S.; Gordon, S. A tree-based stacking ensemble technique with feature selection for network intrusion detection. Appl. Intell. 2022, 52, 9768–9781. [Google Scholar] [CrossRef]
- Kardani, N.; Zhou, A.; Nazem, M.; Shen, S.-L. Improved prediction of slope stability using a hybrid stacking ensemble method based on finite element analysis and field data. J. Rock Mech. Geotech. Eng. 2020, 13, 188–201. [Google Scholar] [CrossRef]
- Azad, A.; Sajid, I.; Lu, S.-D.; Sarwar, A.; Tariq, M.; Ahmad, S.; Liu, H.-D.; Lin, C.-H.; Mahmoud, H.A. Energy Valley Optimizer (EVO) for Tracking the Global Maximum Power Point in a Solar PV System under Shading. Processes 2023, 11, 2986. [Google Scholar] [CrossRef]
- Azizi, M.; Aickelin, U.; Khorshidi, H.A.; Shishehgarkhaneh, M.B. Energy valley optimizer: A novel metaheuristic algorithm for global and engineering optimization. Sci. Rep. 2023, 13, 226. [Google Scholar] [CrossRef] [PubMed]
- Fathy, A. Efficient energy valley optimization approach for reconfiguring thermoelectric generator system under non-uniform heat distribution. Renew. Energy 2023, 217, 119177. [Google Scholar] [CrossRef]
- Rao, M.R.; Sundar, S. Allocation of Resources in LPWAN Using Hybrid Coati-Energy Valley Optimization Algorithm Based on Reinforcement Learning. IEEE Access 2023, 11, 116169–116182. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, X.; Liu, B.J.; Ma, K.; Yan, W.; Long, L.; Huang, Y.; Fujita, H. Effective staging of fibrosis by the selected texture features of liver: Which one is better, CT or MR imaging? Comput. Med. Imaging Graph. 2015, 46 Pt 2, 227–236. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, G.; Zhang, X.; Wu, D. Staging of Hepatic Fibrosis Based on Optimization of Selected Texture Features. Comput. Sci. Appl. 2018, 8, 1089–1101. [Google Scholar]


| Scan Phase | CT Scan Timing | Contrast Agent Diffusion |
|---|---|---|
| N Phase: Non-contrast Phase | <0 s | No contrast agent injected |
| A Phase: Arterial Phase | 25 s | Contrast agent diffused into hepatic arterial vessels |
| V Phase: Venous Phase | 60 s | Contrast agent refluxed into hepatic venous vessels |
| P Phase: Equilibrium Phase | 120 s | Contrast agent diffused into hepatic capillary tissues |
| EVO Pseudo-Code |
|---|
| Define the iteration_max, problem bounds, problem dimension (), population size (), objective function. Calculate the fitness values of all candidate particles based on the neutron enrichment level () while iteration < iteration_max do Calculate the particle enrichment boundary () Determine the particle with the best stability level () for do Calculate the stability level () of the particle Calculate the neutron enrichment level () of the particle if then Generate the stability bound () if then Generate for do end Generate Find a neighboring particle () for do end else if then Determine center of particles () Find a neighboring particle () end else if then end + 1 end iteration = iteration + 1 end Return the best stability level () |
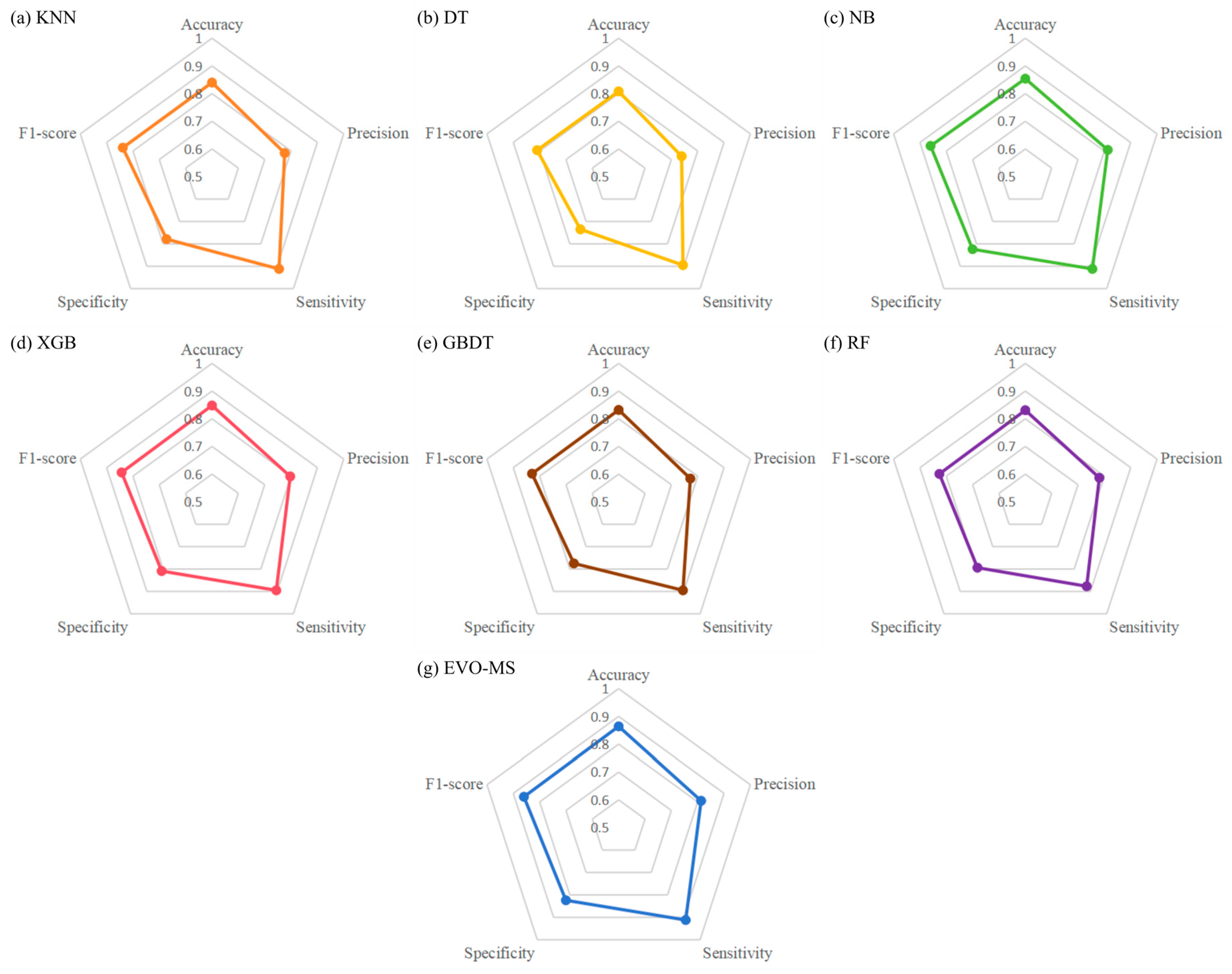
| Accuracy | Precision | Sensitivity | Specificity | F1-Score | |
|---|---|---|---|---|---|
| EVO-MS | 0.864 | 0.813 | 0.912 | 0.824 | 0.860 |
| KNN | 0.840 | 0.776 | 0.912 | 0.779 | 0.839 |
| DT | 0.808 | 0.739 | 0.895 | 0.735 | 0.810 |
| NB | 0.854 | 0.813 | 0.912 | 0.824 | 0.860 |
| XGB | 0.848 | 0.797 | 0.895 | 0.809 | 0.843 |
| GBDT | 0.832 | 0.772 | 0.895 | 0.775 | 0.829 |
| RF | 0.831 | 0.781 | 0.877 | 0.794 | 0.826 |
| Pair Comparison | Value |
|---|---|
| EVO-MS vs. KNN | 0.041 |
| EVO-MS vs. DT | 0.040 |
| EVO-MS vs. NB | 0.039 |
| EVO-MS vs. XGB | 0.000 |
| EVO-MS vs. GBDT | 0.045 |
| EVO-MS vs. RF | 0.037 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, S.; Zhang, P.; Wang, C.; Wang, Q.; Zhou, X. Staging of Liver Fibrosis Based on Energy Valley Optimization Multiple Stacking (EVO-MS) Model. Bioengineering 2024, 11, 485. https://doi.org/10.3390/bioengineering11050485
Zhang X, Chen S, Zhang P, Wang C, Wang Q, Zhou X. Staging of Liver Fibrosis Based on Energy Valley Optimization Multiple Stacking (EVO-MS) Model. Bioengineering. 2024; 11(5):485. https://doi.org/10.3390/bioengineering11050485
Chicago/Turabian StyleZhang, Xuejun, Shengxiang Chen, Pengfei Zhang, Chun Wang, Qibo Wang, and Xiangrong Zhou. 2024. "Staging of Liver Fibrosis Based on Energy Valley Optimization Multiple Stacking (EVO-MS) Model" Bioengineering 11, no. 5: 485. https://doi.org/10.3390/bioengineering11050485
APA StyleZhang, X., Chen, S., Zhang, P., Wang, C., Wang, Q., & Zhou, X. (2024). Staging of Liver Fibrosis Based on Energy Valley Optimization Multiple Stacking (EVO-MS) Model. Bioengineering, 11(5), 485. https://doi.org/10.3390/bioengineering11050485







