Neural Network Model Based on Branch Architecture for the Quality Assurance of Volumetric Modulated Arc Therapy
Abstract
1. Introduction
- By designing different branches to build the multi-branch network, it adopts different branches to learn different complexity metrics to predict the GPR. This brings two benefits: on the one hand, each branch focuses on learning intra-class features, and on the other hand, each branch needs to focus on fewer features. The branching design enhances the feature extraction capability of the model: each branch extracts different category complexity metric features, and these features are fused as a more comprehensive feature to the predictor for GPR prediction.
- The prediction results contribute to improved clinical application. Samples with large errors between model predictions and clinical evaluations are revalidated. The results show that the model predictions of two-thirds of the validation samples outperform the clinical evaluation results, suggesting that the proposed model can assist physicists in the clinic.
- A QA dataset of VMAT containing 850 samples with more than 10 cancers was constructed.
2. Related Work
3. Materials and Methods
3.1. Dataset
- *
- SASX mm: the percentage of small aperture score < X mm
- *
- leaf gap X–Y mm: the percentage of leaf gap X mm < Y mm
- *
- mean jawX gap: the average gap of jawX
- *
- mean jawY gap: the average gap of jawY
- *
- jawY gap 0–X mm: the percentage of jawY gap < X mm
- *
- jawX gap 0–X mm: the percentage of jawX gap < X mm
3.2. The Neural Network Model Based on Branch Architecture
| Algorithm 1 Framework of multi-branch neural networks model |
Input: The complexity metrics () Output: The prediction of input ()
|
4. Experiments
4.1. The Experimental Setup
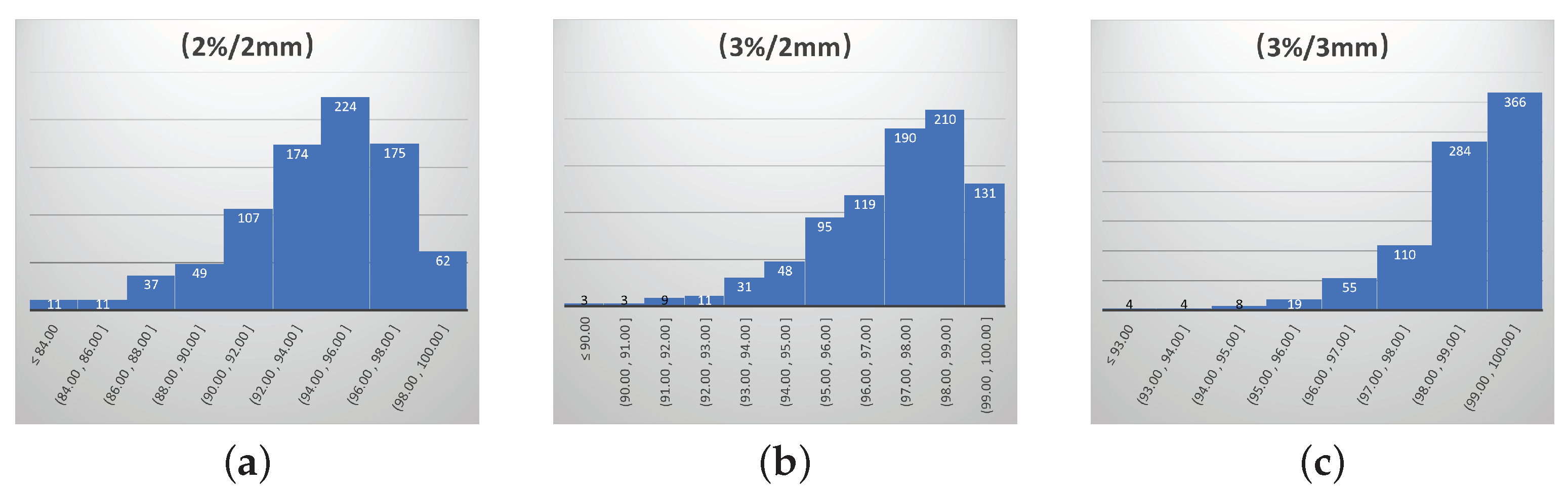
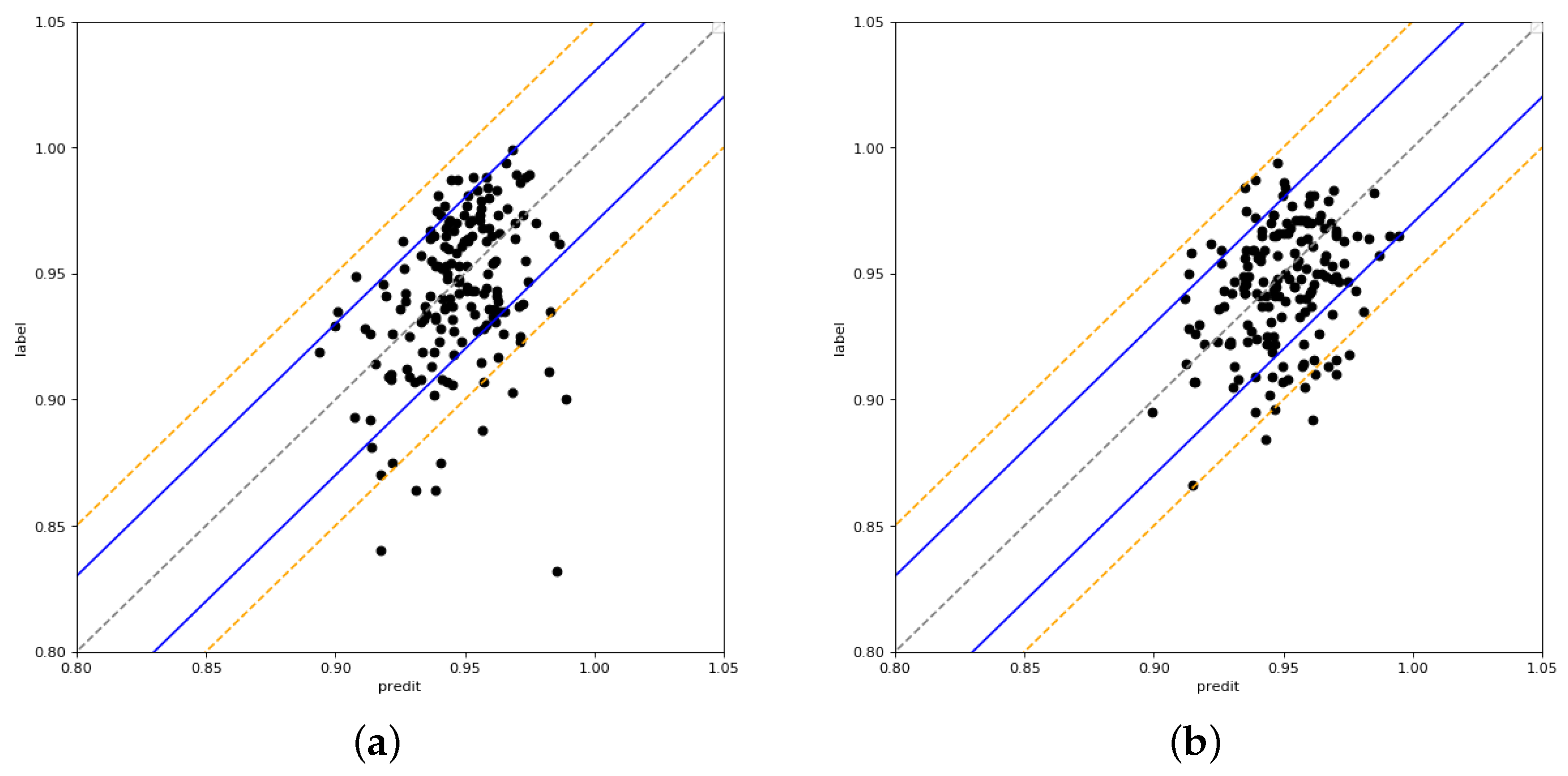
4.2. Results
4.3. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khanfari, H.; Mehranfar, S.; Cheki, M.; Sadr, M.M.; Moniri, S.; Heydarheydari, S.; Rezaeijo, S.M. Exploring the efficacy of multi-flavored feature extraction with radiomics and deep features for prostate cancer grading on mpmri. BMC Med. Imaging 2023, 23, 1. [Google Scholar] [CrossRef] [PubMed]
- Teoh, M.; Clark, C.H.; Wood, K.; Whitaker, S.N. Volumetric modulated arc therapy: A review of current literature and clinical use in practice. Br. J. Radiol. 2011, 84, 967–996. [Google Scholar] [CrossRef] [PubMed]
- Low, D.A.; Dempsey, J.F. Evaluation of the gamma dose distribution comparison method. Med. Phys. 2003, 30, 2455–2464. [Google Scholar] [CrossRef] [PubMed]
- Low, D.A.; Harms, W.B.; Mutic, S.; Purdy, J.A. A technique for the quantitative evaluation of dose distributions. Med. Phys. 1998, 25, 656–661. [Google Scholar] [CrossRef]
- Granville, D.A.; Sutherland, J.G.; Belec, J.G.; La Russa, D.J. Predicting VMAT patient-specific QA results using a support vector classifier trained on treatment plan characteristics and linac QC metrics. Phys. Med. Biol. 2019, 64, 095017. [Google Scholar] [CrossRef]
- Valdes, G.; Scheuermann, R.; Hung, C.Y.; Olszanski, A.; Bellerive, M.; Solberg, T. A mathematical framework for virtual IMRT QA using machine learning. Med. Phys. 2016, 43, 4323–4334. [Google Scholar] [CrossRef]
- Li, J.; Wang, L.; Zhang, X.; Liu, L.; Li, J.; Chan, M.; Sui, J.; Yang, R. Machine Learning for Patient-Specific Quality Assurance of VMAT: Prediction and Classification Accuracy. Int. J. Radiat. Oncol. Biol. Phys. 2019, 105, 893–902. [Google Scholar] [CrossRef]
- Otto, K. Volumetric modulated arc therapy: IMRT in a single gantry arc. Med. Phys. 2007, 35, 310–317. [Google Scholar] [CrossRef]
- Interian, Y.; Rideout, V.; Kearney, V.; Gennatas, E.D.; Morin, O.; Cheung, J.; Solberg, T.; Valdes, G. Deep nets vs expert designed features in medical physics: An IMRT QA case study. Med. Phys. 2018, 45, 2672–2680. [Google Scholar] [CrossRef]
- Ono, T.; Hirashima, H.; Iramina, H.; Mukumoto, N.; Miyabe, Y.; Nakamura, M.; Mizowaki, T. Prediction of dosimetric accuracy for VMAT plans using plan complexity parameters via machine learning. Med. Phys. 2019, 46, 3823–3832. [Google Scholar] [CrossRef]
- Tomori, S.; Kadoya, N.; Takayama, Y.; Kajikawa, T.; Shima, K.; Narazaki, K.; Jingu, K. A deep learning-based prediction model for gamma evaluation in patient-specific quality assurance. Med. Phys. 2018, 45, 4055–4065. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Cui, Q.; Wei, X.-S.; Chen, Z.-M. BBN: Bilateral-branch network with cumulative learning for long-tailed visual recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 9716–9725. [Google Scholar]
- Poudel, R.P.K.; Liwicki, S.; Cipolla, R. Fast-SCNN: Fast semantic segmentation network. arXiv 2019, arXiv:1902.04502. [Google Scholar]
- Yu, C.; Gao, C.; Wang, J.; Yu, G.; Shen, C.; Sang, N. Bisenet v2: Bilateral Network with Guided Aggregation for Real-Time Semantic Segmentation. Int. J. Comput. Vis. 2021, 129, 3051–3068. [Google Scholar] [CrossRef]
- Tsai, T.H.; Tseng, Y.W. Bisenet v3: Bilateral segmentation network with coordinate attention for real-time semantic segmentation. Neurocomputing 2023, 532, 33–42. [Google Scholar] [CrossRef]
- Zhang, L.; Yi, Z. Dynamical properties of background neural networks with uniform firing rate and background input. Chaos Solitons Fractals 2007, 33, 979–985. [Google Scholar] [CrossRef]
- Xie, L.; Zhang, L.; Hu, T.; Huang, H.; Yi, Z. Neural networks model based on an automated multi-scale method for mammogram classification. Knowl.-Based Syst. 2020, 208, 106465. [Google Scholar] [CrossRef]
- Camps, S.; Antico, M. Artificial intelligence applications in ultrasound-guided radiotherapy. In Modern Applications of 3D/4D Ultrasound Imaging in Radiotherapy; IOP: Bristol, UK, 2021. [Google Scholar]
- Chow, J.C.L. Artificial intelligence in radiotherapy and patient care. In Artificial Intelligence in Medicine; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–13. [Google Scholar]
- Robertson, S.P.; Quon, H.; Kiess, A.P.; Moore, J.A.; Yang, W.; Cheng, Z.; Afonso, S.; Allen, M.; Richardson, M.; Choflet, A.; et al. A data-mining framework for large scale analysis of dose-outcome relationships in a database of irradiated head and neck cancer patients. Med. Phys. 2015, 42, 4329–4337. [Google Scholar] [CrossRef] [PubMed]
- Stanhope, C.; Wu, Q.J.; Yuan, L.; Liu, J.; Hood, R.; Yin, F.F.; Adamson, J. Utilizing knowledge from prior plans in the evaluation of quality assurance. Phys. Med. Biol. 2015, 60, 4873. [Google Scholar] [CrossRef] [PubMed]
- Schreibmann, E.; Fox, T. Prior-knowledge treatment planning for volumetric arc therapy using feature-based database mining. J. Appl. Clin. Med. Phys. 2014, 15, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Valdes, G.; Chan, M.; Lim, S.; Scheuermann, R.; Deasy, J.O.; Solberg, T. IMRT QA using machine learning: A multi-institutional validation. J. Appl. Clin. Med. Phys. 2017, 18, 279–284. [Google Scholar] [CrossRef]
- Hu, T.; Xie, L.; Zhang, L.; Li, G.; Yi, Z. Deep multimodal neural network based on data-feature fusion for patient-specific quality assurance. Int. J. Neural Syst. 2022, 32, 2150055. [Google Scholar] [CrossRef]
- Chiavassa, S.; Bessieres, I.; Edouard, M.; Mathot, M.; Moignier, A. Complexity metrics for IMRT and VMAT plans: A review of current literature and applications. Br. J. Radiol. 2019, 92, 20190270. [Google Scholar] [CrossRef] [PubMed]
- Miften, M.; Olch, A.J.; Mihailidis, D.; Moran, J.M.; Pawlicki, T.; Molineu, A.; Li, H.; Wijesooriya, K.; Shi, J.; Xia, P.; et al. Tolerance limits and methodologies for IMRT measurement-based verification QA: Recommendations of AAPM Task Group No. 218. Med. Phys. 2018, 45, e53–e83. [Google Scholar] [CrossRef] [PubMed]



| Cancer | Sample Number |
|---|---|
| Abdomen | 80 |
| Brain | 28 |
| Breast | 4 |
| H&N | 117 |
| Npc | 127 |
| Pelvis | 162 |
| Prostate | 56 |
| Rectum | 186 |
| Stomach | 42 |
| Other | 48 |
| Total | 850 |
| Category | Complexity Metrics |
|---|---|
| SASX mm | SAS2 mm, SAS5 mm, SAS10 mm, SAS15 mm, SAS20 mm, SAS30 mm |
| leaf gap X-Y mm | leaf gap 2–5 mm, leaf gap 5–10 mm, leaf gap 10–15 mm, leaf gap 15–20 mm, leaf gap 20–30 mm |
| mean jawi gap | mean jawY gap, mean jawX gap |
| jawY gap 0–X mm | jawY gap 0–2 mm, jawY gap 0–5 mm, jawY gap 0–10 mm, jawY gap 0–15 mm, jawY gap 0–20 mm, jawY gap 0–30 mm |
| jawX gap 0–X mm | jawX gap 0–2 mm, jawX gap 0–5 mm, jawX gap 0–10 mm, jawX gap 0–15 mm, jawX gap 0–20 mm, jawX gap 0–30 mm |
| Complexity Metrics | Definition |
|---|---|
| Fraction dose | The fraction dose |
| Mean CP number | Mean control point number |
| Mean CP MU | Mean control point monitor |
| PMU | Plan normalized MU |
| Beam number | The beam number |
| Linac | Linear accelerator |
| CAS | Cross-axis score |
| CIAO | Complete irradiated area outline |
| MAD | Mean asymmetry distance |
| PA | Plan area |
| PI | Plan averaged beam irregularity |
| PM | Plan averaged beam modulation |
| PALG | Plan average leaf gap |
| ALT X1 | Averaged leaf gap of xl |
| ALT X2 | Averaged leaf gap of x2 |
| ALG | Averaged leaf gap |
| MCS | Modulation complex score |
| Doctor | The treating physicist |
| Positions | The treating position |
| MU1 | MU value in first arc |
| MU2 | MU value in second arc |
| TMU | Total MU |
| Gamma Criterion | Action Limit | Tolerability Limit |
|---|---|---|
| (2%/2 mm) | 90% | 84% |
| (3%/2 mm) | 95% | 90% |
| (3%/3 mm) | 97% | 93% |
| Method | MAE | ||
|---|---|---|---|
| (2%/2 mm) | (3%/2 mm) | (3%/3 mm) | |
| The proposed MBNN | 2.12% | 1.69% | 1.30% |
| SVM [5] | 2.49% | 1.95% | 1.33% |
| RF | 2.56% | 1.90% | 1.35% |
| KNN | 2.78% | 1.87% | 1.34% |
| lasso regression [7] | 2.60% | 1.89% | 1.36% |
| ONO-Net [10] | 2.30% | 1.77% | 1.30% |
| 3D-MResNet [24] | 2.20% | 1.73% | 1.30% |
| Hidden Layers | MAE of 2%/2 mm |
|---|---|
| 128-512-1024-512-128 | 2.31% |
| 128-1024-256-64 | 2.26% |
| 128-512-128 | 2.23% |
| 128-1024-128 | 2.31% |
| 64-256-64 | 2.25% |
| 32-128-32 | 2.39% |
| 512-64 | 2.28% |
| 256-64 | 2.27% |
| Method | MAE | ||
|---|---|---|---|
| (2%/2 mm) | (3%/2 mm) | (3%/3 mm) | |
| Our method | 2.12% | 1.69% | 1.30% |
| FM-Net | 2.23% | 1.70% | 1.32% |
| LM-Net | 2.67% | 1.72% | 1.52% |
| PM-Net | 2.36% | 1.90% | 1.37% |
| ONO-Net | 2.30% | 1.77% | 1.30% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Zhang, L.; Hu, T.; Li, G.; Yi, Z. Neural Network Model Based on Branch Architecture for the Quality Assurance of Volumetric Modulated Arc Therapy. Bioengineering 2024, 11, 362. https://doi.org/10.3390/bioengineering11040362
Xie L, Zhang L, Hu T, Li G, Yi Z. Neural Network Model Based on Branch Architecture for the Quality Assurance of Volumetric Modulated Arc Therapy. Bioengineering. 2024; 11(4):362. https://doi.org/10.3390/bioengineering11040362
Chicago/Turabian StyleXie, Lizhang, Lei Zhang, Ting Hu, Guangjun Li, and Zhang Yi. 2024. "Neural Network Model Based on Branch Architecture for the Quality Assurance of Volumetric Modulated Arc Therapy" Bioengineering 11, no. 4: 362. https://doi.org/10.3390/bioengineering11040362
APA StyleXie, L., Zhang, L., Hu, T., Li, G., & Yi, Z. (2024). Neural Network Model Based on Branch Architecture for the Quality Assurance of Volumetric Modulated Arc Therapy. Bioengineering, 11(4), 362. https://doi.org/10.3390/bioengineering11040362






