SpineHRformer: A Transformer-Based Deep Learning Model for Automatic Spine Deformity Assessment with Prospective Validation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset and Image Pre-Processing
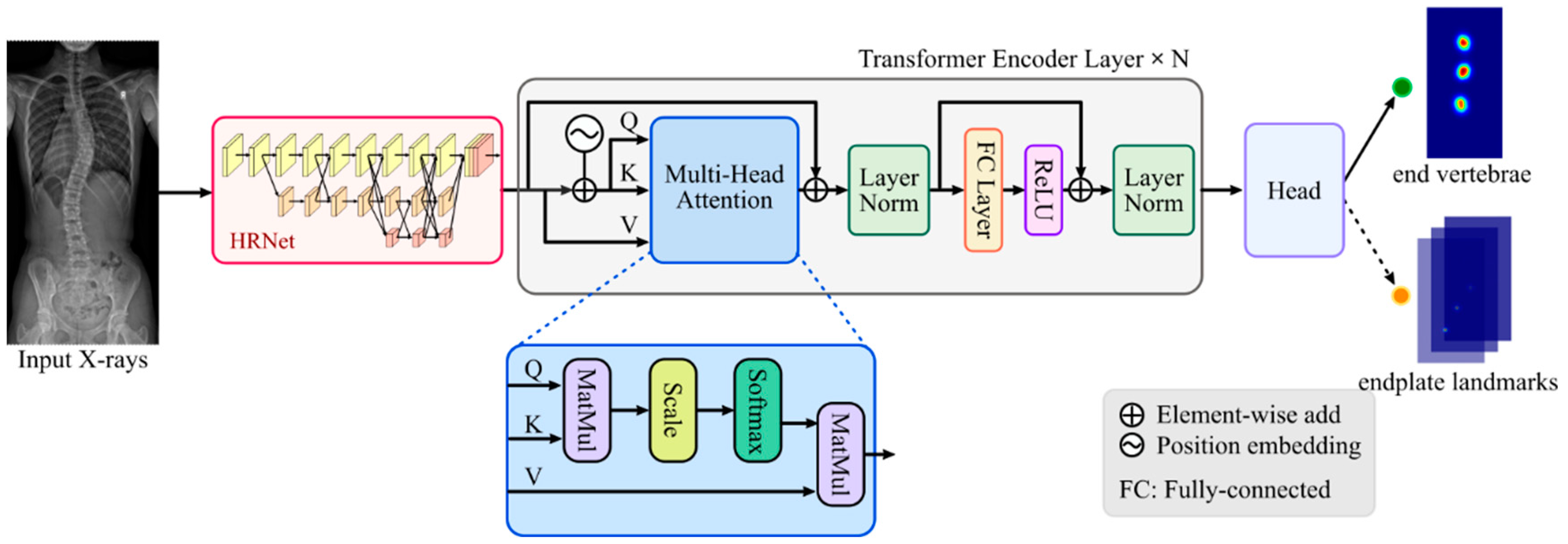
2.2. SpineHRformer
2.2.1. HRNet
2.2.2. Transformer Encoder
 in Figure 1) is generated by position encoder, which is formed by:
in Figure 1) is generated by position encoder, which is formed by:2.2.3. Output Head
2.3. Performance Evaluation and Statistical Analysis
3. Experiments and Results
3.1. Training
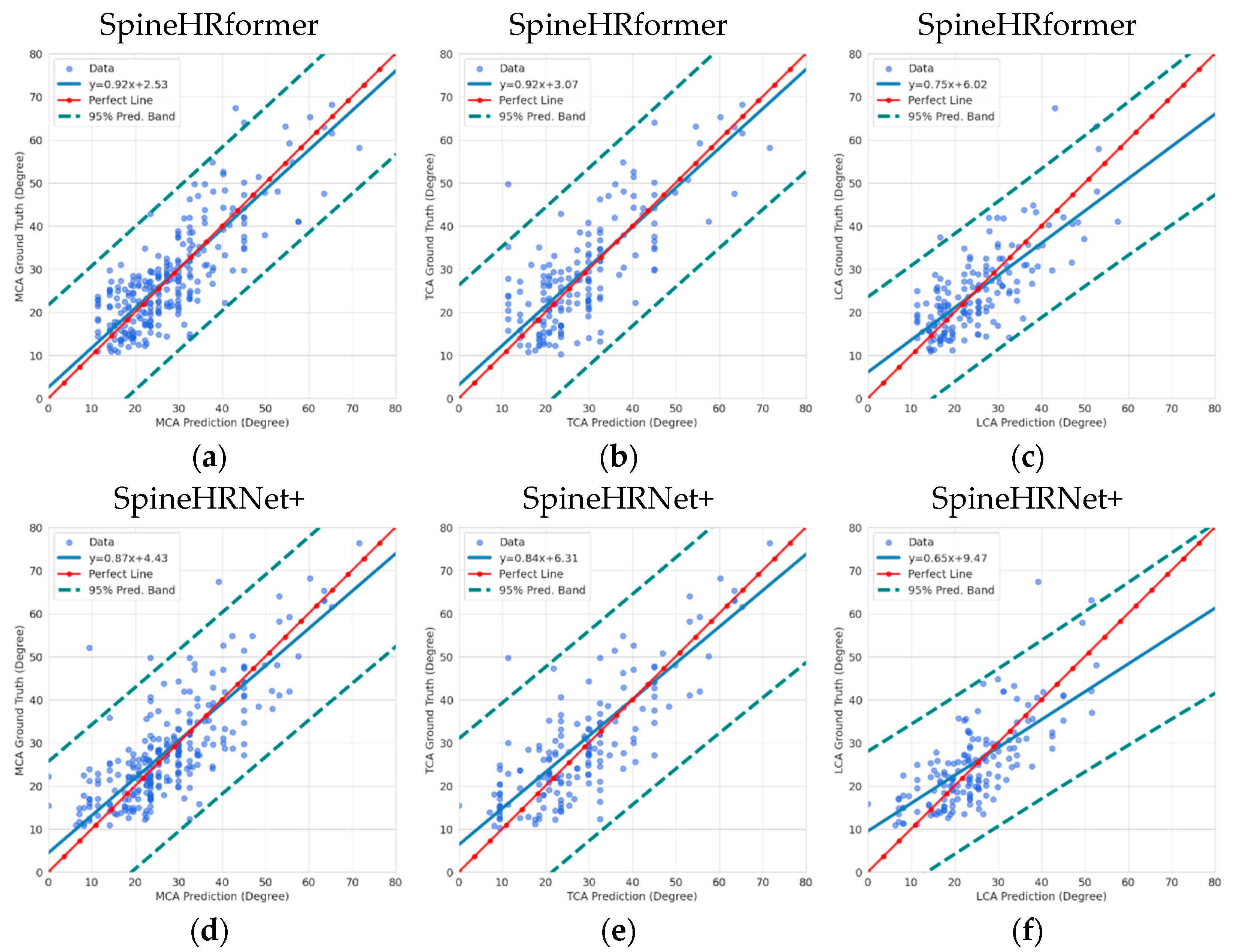
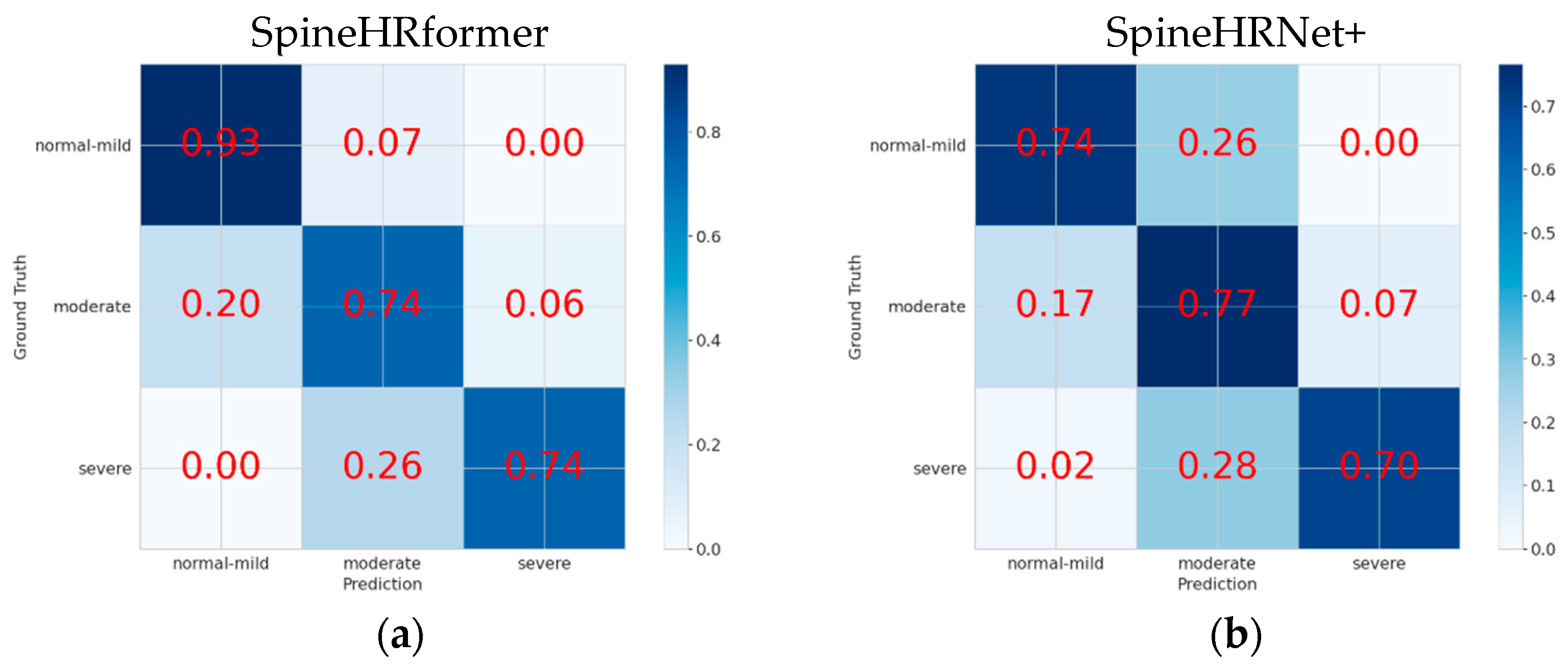
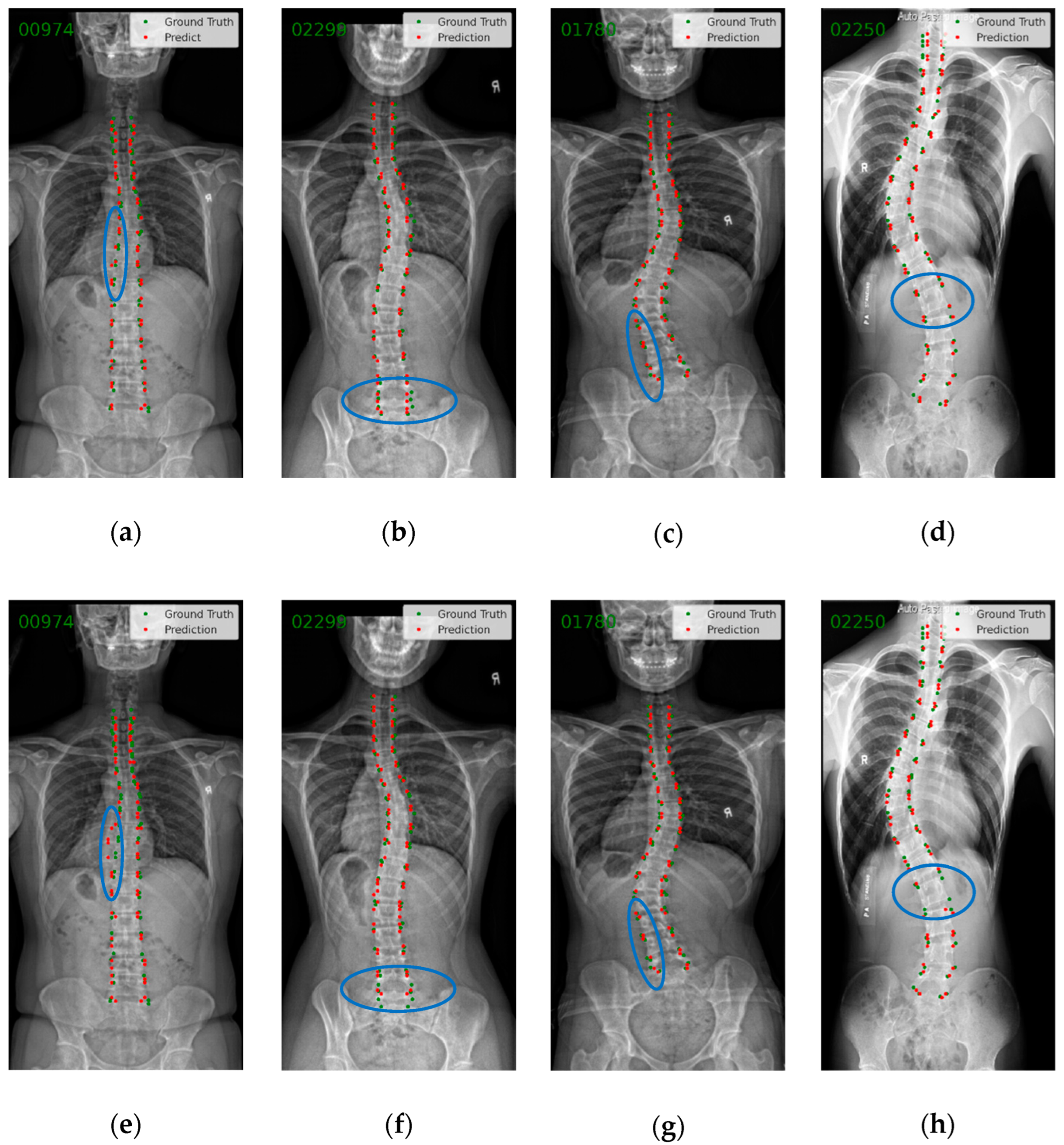
3.2. Endplate Landmark Detection and CA Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fong, D.Y.; Cheung, K.M.; Wong, Y.-W.; Wan, Y.-Y.; Lee, C.-F.; Lam, T.-P.; Cheng, J.C.; Ng, B.K.; Luk, K.D. A population-based cohort study of 394,401 children followed for 10 years exhibits sustained effectiveness of scoliosis screening. Spine J. 2015, 15, 825–833. [Google Scholar] [CrossRef] [PubMed]
- Weinstein, S.L.; Dolan, L.A.; Cheng, J.C.; Danielsson, A.; Morcuende, J.A. Adolescent idiopathic scoliosis. Lancet 2008, 371, 1527–1537. [Google Scholar] [CrossRef] [PubMed]
- Chung, N.; Cheng, Y.-H.; Po, H.-L.; Ng, W.-K.; Cheung, K.-C.; Yung, H.-Y.; Lai, Y.-M. Spinal phantom comparability study of Cobb angle measurement of scoliosis using digital radiographic imaging. J. Orthop. Transl. 2018, 15, 81–90. [Google Scholar] [CrossRef] [PubMed]
- De Sèze, M.; Cugy, E. Pathogenesis of idiopathic scoliosis: A review. Ann. Phys. Rehabil. Med. 2012, 55, 128–138. [Google Scholar] [CrossRef]
- Kikanloo, S.R.; Tarpada, S.P.; Cho, W. Etiology of Adolescent Idiopathic Scoliosis: A Literature Review. Asian Spine J. 2019, 13, 519–526. [Google Scholar] [CrossRef]
- Cheung, J.P.Y.; Cheung, P.W.H.; Samartzis, D.; Luk, K.D.-K. Curve Progression in Adolescent Idiopathic Scoliosis Does Not Match Skeletal Growth. Clin. Orthop. Relat. Res. 2018, 476, 429–436. [Google Scholar] [CrossRef]
- Hresko, M.T.; Talwalkar, V.; Schwend, R. Early detection of idiopathic scoliosis in adolescents. JBJS 2016, 98, e67. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, C.; Zhao, Y.; Zhao, M.; Wang, Z.; Song, R.; Meng, N.; Sial, A.; Diwan, A.; Liu, J. Deep Learning Model to Classify and Monitor Idiopathic Scoliosis in Adolescents Using a Single Smartphone Photograph. JAMA Netw. Open 2023, 6, e2330617. [Google Scholar] [CrossRef]
- Langensiepen, S.; Semler, O.; Sobottke, R.; Fricke, O.; Franklin, J.; Schönau, E.; Eysel, P. Measuring procedures to determine the Cobb angle in idiopathic scoliosis: A systematic review. Eur. Spine J. 2013, 22, 2360–2371. [Google Scholar] [CrossRef]
- Gstoettner, M.; Sekyra, K.; Walochnik, N.; Winter, P.; Wachter, R.; Bach, C.M. Inter-and intraobserver reliability assessment of the Cobb angle: Manual versus digital measurement tools. Eur. Spine J. 2007, 16, 1587–1592. [Google Scholar] [CrossRef]
- Chen, C.; Namdar, K.; Wu, Y.; Hosseinpour, S.; Shroff, M.; Doria, A.S.; Khalvati, F. Automating Cobb Angle Measurement for Adolescent Idiopathic Scoliosis using Instance Segmentation. arXiv 2022, arXiv:2211.14122. [Google Scholar]
- Kim, K.C.; Yun, H.S.; Kim, S.; Seo, J.K. Automation of Spine Curve Assessment in Frontal Radiographs Using Deep Learning of Vertebral-Tilt Vector. IEEE Access 2020, 8, 84618–84630. [Google Scholar] [CrossRef]
- Anitha, H.; Prabhu, G.K. Automatic Quantification of Spinal Curvature in Scoliotic Radiograph using Image Processing. J. Med. Syst. 2012, 36, 1943–1951. [Google Scholar]
- Anitha, H.; Karunakar, A.; Dinesh, K. Automatic extraction of vertebral endplates from scoliotic radiographs using customized filter. Biomed. Eng. Lett. 2014, 4, 158–165. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, J.H.; Li, H.J.; Gu, X.Y.; Li, Z.G.; Zhang, S. Automatic Cobb angle measurement method based on vertebra segmentation by deep learning. Med. Biol. Eng. Comput. 2022, 60, 2257–2269. [Google Scholar] [CrossRef] [PubMed]
- Horng, M.-H.; Kuok, C.-P.; Fu, M.-J.; Lin, C.-J.; Sun, Y.-N. Cobb angle measurement of spine from X-ray images using convolutional neural network. Comput. Math. Methods Med. 2019, 2019, 6357171. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.S.; Li, J.; Zhang, Z.X.; Jiao, Z.C.; Gao, X.B. A Coarse-to-Fine Deep Heatmap Regression Method for Adolescent Idiopathic Scoliosis Assessment. In Computational Methods and Clinical Applications for Spine Imaging: 6th International Workshop and Challenge, CSI 2019, Shenzhen, China, 17 October 2019; Springer: Cham, Switzerland, 2020; Volume 11963, pp. 101–106. [Google Scholar]
- Zhang, K.L.; Xu, N.F.; Yang, G.S.; Wu, J.; Fu, X.L. An Automated Cobb Angle Estimation Method Using Convolutional Neural Network with Area Limitation. In Medical Image Computing and Computer Assisted Intervention—Miccai 2019, Pt Vi; Springer: Cham, Switzerland, 2019; Volume 11769, pp. 775–783. [Google Scholar]
- Kuang, X.; Cheung, J.P.Y.; Ding, X.; Zhang, T. SpineGEM: A Hybrid-Supervised Model Generation Strategy Enabling Accurate Spine Disease Classification with a Small Training Dataset; Springer International Publishing: Cham, Switzerland, 2021; pp. 145–154. [Google Scholar]
- Wu, C.; Meng, G.D.; Lian, J.; Xu, J.X.; Gao, M.J.; Huang, C.C.; Zhang, S.; Zhang, Y.F.; Yu, Y.Z.; Wang, H.Y.; et al. A multi-stage ensemble network system to diagnose adolescent idiopathic scoliosis. Eur. Radiol. 2022, 32, 5880–5889. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Bailey, C.; Rasoulinejad, P.; Li, S. Automated comprehensive adolescent idiopathic scoliosis assessment using MVC-Net. Med. Image Anal. 2018, 48, 1–11. [Google Scholar] [CrossRef]
- Wang, L.S.; Xu, Q.H.; Leung, S.; Chung, J.; Chen, B.; Li, S. Accurate automated Cobb angles estimation using multi-view extrapolation net. Med. Image Anal. 2019, 58, 101542. [Google Scholar] [CrossRef]
- Zhang, K.L.; Xu, N.F.; Guo, C.Y.; Wu, J. MPF-net: An effective framework for automated cobb angle estimation. Med. Image Anal. 2022, 75, 102277. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Cheung, J.P.Y.; Dokos, S.; Wong, K.Y.-K. Learning-based coronal spine alignment prediction using smartphone-acquired scoliosis radiograph images. IEEE Access 2021, 9, 38287–38295. [Google Scholar] [CrossRef]
- Meng, N.; Cheung, J.P.Y.; Wong, K.K.; Dokos, S.; Li, S.; Choy, R.W.; To, S.; Li, R.J.; Zhang, T. An artificial intelligence powered platform for auto-analyses of spine alignment irrespective of image quality with prospective validation. EClinicalMedicine 2022, 43, 101252. [Google Scholar] [CrossRef] [PubMed]
- Meng, N.; Wong, K.-Y.K.; Zhao, M.; Cheung, J.P.; Zhang, T. Radiograph-comparable image synthesis for spine alignment analysis using deep learning with prospective clinical validation. eClinicalMedicine 2023, 61, 102050. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sun, K.; Cheng, T.; Jiang, B.; Deng, C.; Zhao, Y.; Liu, D.; Mu, Y.; Tan, M.; Wang, X. Deep high-resolution representation learning for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3349–3364. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Sun, K.; Xiao, B.; Liu, D.; Wang, J. Deep high-resolution representation learning for human pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in vision: A survey. ACM Comput. Surv. (CSUR) 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Steiner, A.; Kolesnikov, A.; Zhai, X.; Wightman, R.; Uszkoreit, J.; Beyer, L. How to train your vit? Data, augmentation, and regularization in vision transformers. arXiv 2021, arXiv:2106.10270. [Google Scholar]

| Severity Level | Cobb Angle | Clinical Intervention |
|---|---|---|
| Normal-mild | No intervention required. | |
| Moderate | May require bracing to prevent curve progression. | |
| Severe | Surgical intervention may be required |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Meng, N.; Cheung, J.P.Y.; Yu, C.; Lu, P.; Zhang, T. SpineHRformer: A Transformer-Based Deep Learning Model for Automatic Spine Deformity Assessment with Prospective Validation. Bioengineering 2023, 10, 1333. https://doi.org/10.3390/bioengineering10111333
Zhao M, Meng N, Cheung JPY, Yu C, Lu P, Zhang T. SpineHRformer: A Transformer-Based Deep Learning Model for Automatic Spine Deformity Assessment with Prospective Validation. Bioengineering. 2023; 10(11):1333. https://doi.org/10.3390/bioengineering10111333
Chicago/Turabian StyleZhao, Moxin, Nan Meng, Jason Pui Yin Cheung, Chenxi Yu, Pengyu Lu, and Teng Zhang. 2023. "SpineHRformer: A Transformer-Based Deep Learning Model for Automatic Spine Deformity Assessment with Prospective Validation" Bioengineering 10, no. 11: 1333. https://doi.org/10.3390/bioengineering10111333
APA StyleZhao, M., Meng, N., Cheung, J. P. Y., Yu, C., Lu, P., & Zhang, T. (2023). SpineHRformer: A Transformer-Based Deep Learning Model for Automatic Spine Deformity Assessment with Prospective Validation. Bioengineering, 10(11), 1333. https://doi.org/10.3390/bioengineering10111333









