Using Fused Data from Perimetry and Optical Coherence Tomography to Improve the Detection of Visual Field Progression in Glaucoma
Abstract
1. Introduction
2. Materials and Methods:
2.1. VF and OCT Data
2.2. Data Fusion Models for Function-Structure Measurements
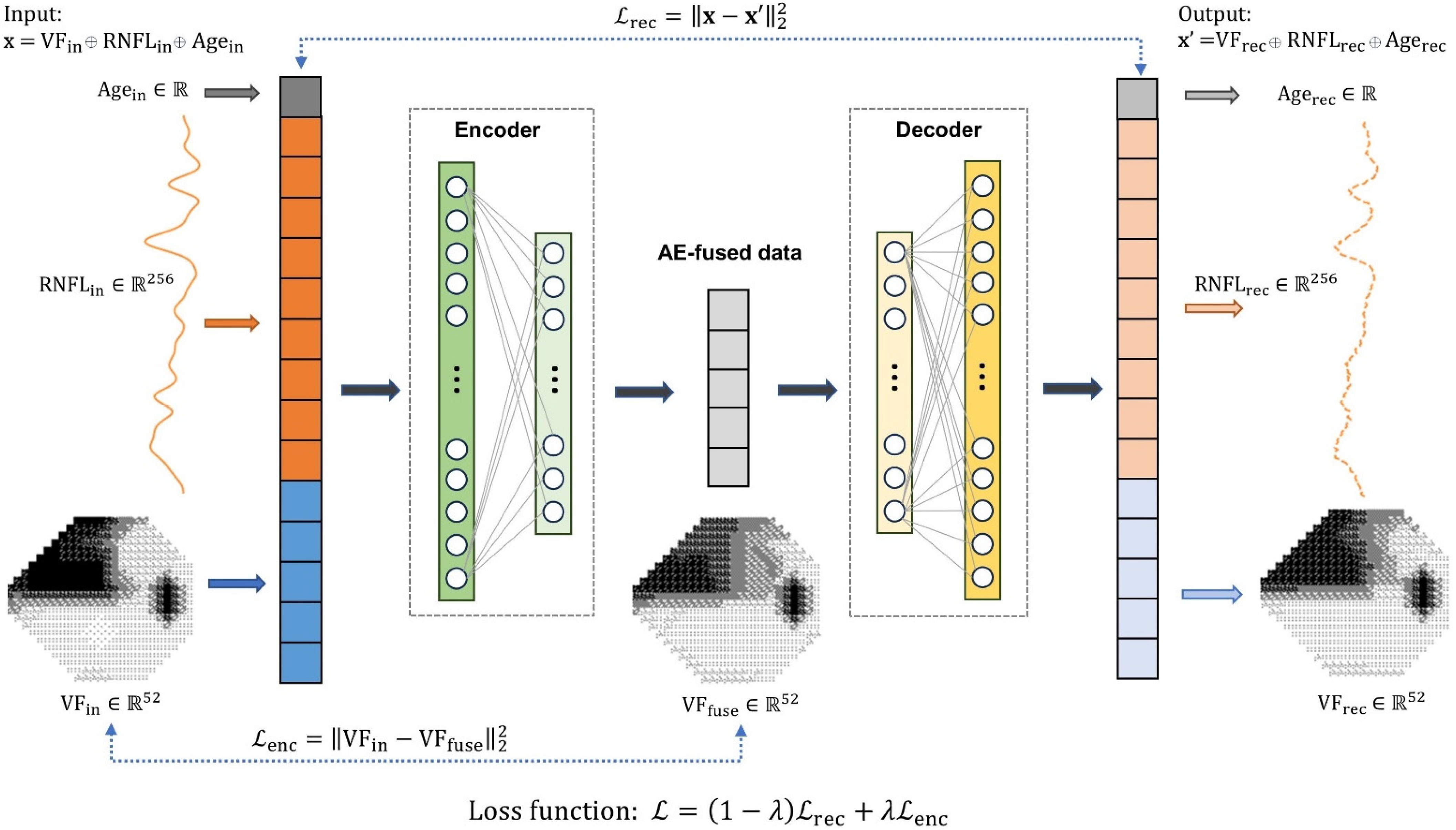
2.2.1. Autoencoder Data Fusion Model
2.2.2. Bayesian Linear Regression Model
2.3. Performance Evaluation
3. Results
3.1. Data Characteristics
3.2. Autoencoder Data Fusion Model
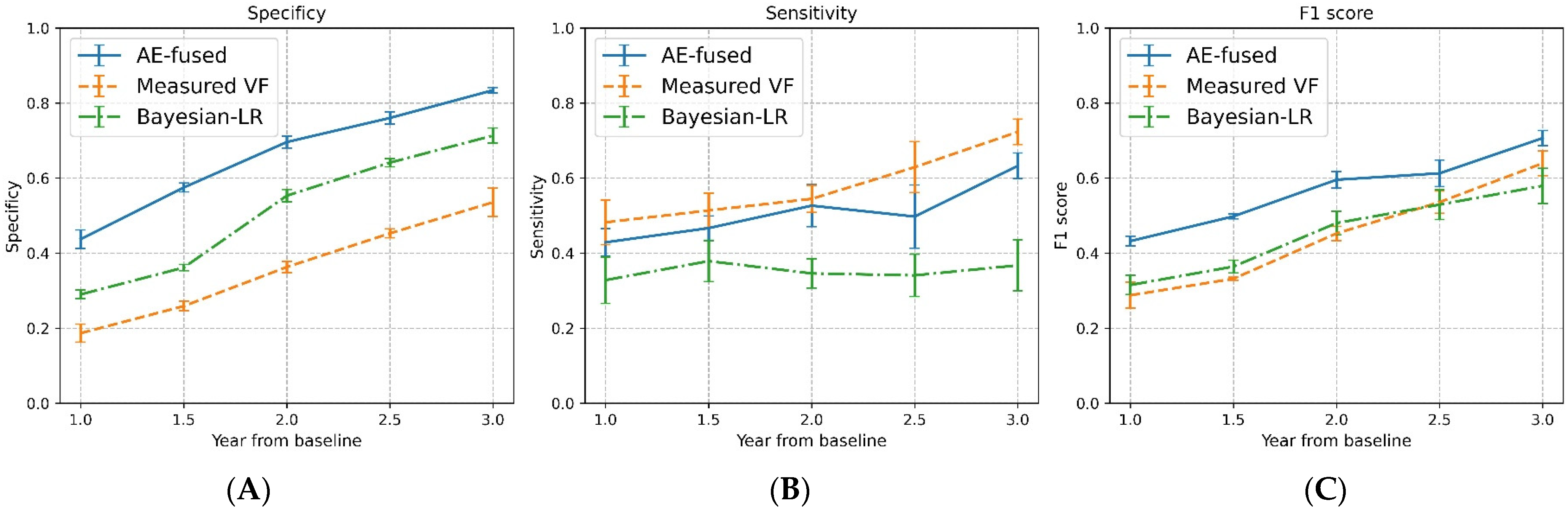
3.3. Detecting VF Progression
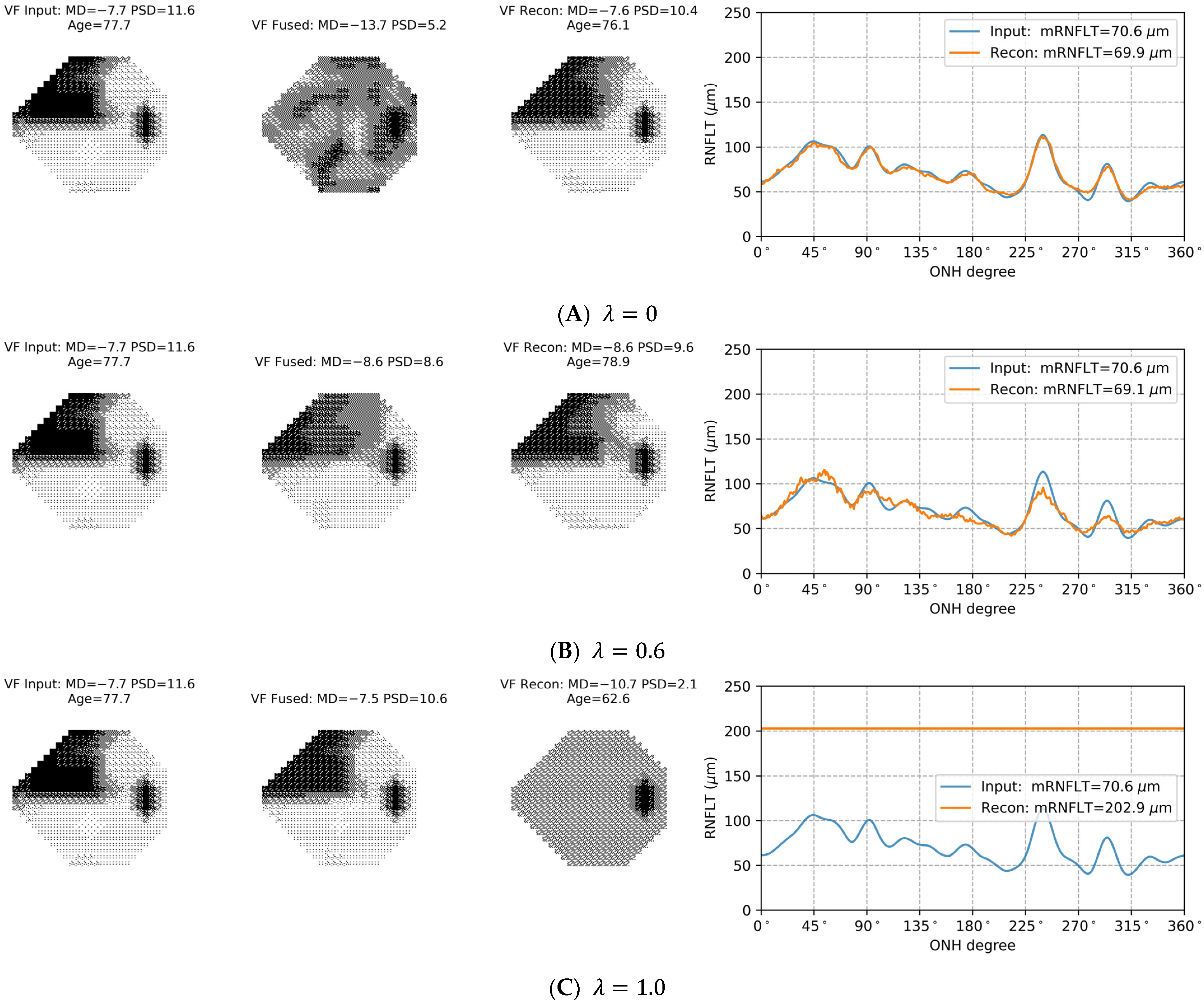
3.4. Selection of in the Loss Function
3.5. Sensitivity to Input Parameters
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Stein, J.D.; Khawaja, A.P.; Weizer, J.S. Glaucoma in adults—Screening, diagnosis, and management: A review. JAMA 2021, 325, 164–174. [Google Scholar] [CrossRef] [PubMed]
- Heijl, A.; Lindgren, A.; Lindgren, G. Test-retest variability in glaucomatous visual fields. Am. J. Ophthalmol. 1989, 108, 130–135. [Google Scholar] [CrossRef] [PubMed]
- Hood, D.C.; Kardon, R.H. A framework for comparing structural and functional measures of glaucomatous damage. Prog. Retin. Eye Res. 2007, 26, 688–710. [Google Scholar] [CrossRef] [PubMed]
- Malik, R.; Swanson, W.H.; Garway-Heath, D.F. Structure–function relationship in glaucoma: Past thinking and current concepts. Clin. Exp. Ophthalmol. 2012, 40, 369–380. [Google Scholar] [CrossRef] [PubMed]
- Denniss, J.; Turpin, A.; McKendrick, A.M. Relating optical coherence tomography to visual fields in glaucoma: Structure–function mapping, limitations and future applications. Clin. Exp. Optom. 2019, 102, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Bizios, D.; Heijl, A.; Bengtsson, B. Integration and fusion of standard automated perimetry and optical coherence tomography data for improved automated glaucoma diagnostics. BMC Ophthalmol. 2011, 11, 20. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Fu, B.; Li, F.; Xiong, J.; He, J.; Zhang, X.; Qiao, Y. Deep relation transformer for diagnosing glaucoma with optical coherence tomography and visual field function. IEEE Trans. Med. Imaging 2021, 40, 2392–2402. [Google Scholar] [CrossRef]
- Wu, Z.; Medeiros, F.A. A simplified combined index of structure and function for detecting and staging glaucomatous damage. Sci. Rep. 2021, 11, 3172. [Google Scholar] [CrossRef]
- Chauhan, B.C.; Malik, R.; Shuba, L.M.; Rafuse, P.E.; Nicolela, M.T.; Artes, P.H. Rates of glaucomatous visual field change in a large clinical population. Investig. Ophthalmol. Vis. Sci. 2014, 55, 4135–4143. [Google Scholar] [CrossRef]
- Heijl, A.; Buchholz, P.; Norrgren, G.; Bengtsson, B. Rates of visual field progression in clinical glaucoma care. Acta Ophthalmol. 2013, 91, 406–412. [Google Scholar] [CrossRef] [PubMed]
- Medeiros, F.A.; Leite, M.T.; Zangwill, L.M.; Weinreb, R.N. Combining structural and functional measurements to improve detection of glaucoma progression using Bayesian hierarchical models. Investig. Ophthalmol. Vis. Sci. 2011, 52, 5794–5803. [Google Scholar] [CrossRef]
- Russell, R.A.; Malik, R.; Chauhan, B.C.; Crabb, D.P.; Garway-Heath, D.F. Improved estimates of visual field progression using Bayesian linear regression to integrate structural information in patients with ocular hypertension. Investig. Ophthalmol. Vis. Sci. 2012, 53, 2760–2769. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Chapter 14 Autoencoder. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Ma, M.; Sun, C.; Chen, X. Deep coupling autoencoder for fault diagnosis with multimodal sensory data. IEEE Trans. Ind. Inform. 2018, 14, 1137–1145. [Google Scholar] [CrossRef]
- Chaudhary, K.; Poirion, O.B.; Lu, L.; Garmire, L.X. Deep learning–based multi-omics integration robustly predicts survival in liver cancer. Clin. Cancer Res. 2018, 24, 1248–1259. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Zhang, H.; Wu, Z.; Wang, F.; Wang, L.; Smith, J.K.; Lin, W.; Li, G.; Shen, D. Disentangled-multimodal adversarial autoencoder: Application to infant age prediction with incomplete multimodal neuroimages. IEEE Trans. Med. Imaging 2020, 39, 4137–4149. [Google Scholar] [CrossRef]
- Rao, H.L.; Kumar, A.U.; Babu, J.G.; Senthil, S.; Garudadri, C.S. Relationship between severity of visual field loss at presentation and rate of visual field progression in glaucoma. Ophthalmology 2011, 118, 249–253. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Gimelshein, A.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Curran Associates, Inc.: Nice, France, 2019; pp. 8024–8035. Available online: http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf (accessed on 10 January 2023).
- Medeiros, F.A.; Zangwill, L.M.; Bowd, C.; Mansouri, K.; Weinreb, R.N. The structure and function relationship in glaucoma: Implications for detection of progression and measurement of rates of change. Investig. Ophthalmol. Vis. Sci. 2012, 53, 6939–6946. [Google Scholar] [CrossRef]
- Otarola, F.; Chen, A.; Morales, E.; Yu, F.; Afifi, A.; Caprioli, J. Course of glaucomatous visual field loss across the entire perimetric range. JAMA Ophthalmol. 2016, 134, 496–502. [Google Scholar] [CrossRef]
- Chauhan, B.C.; Garway-Heath, D.F.; Goñi, F.J.; Rossetti, L.; Bengtsson, B.; Viswanathan, A.; Heijl, A. Practical recommendations for measuring rates of visual field change in glaucoma. Br. J. Ophthalmol. 2008, 92, 569–573. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Available online: https://www.zeiss.com/content/dam/Meditec/us/brochures/cirrus_how_to_read.pdf (accessed on 1 November 2023).
- Garway-Heath, D.F.; Poinoosawmy, D.; Fitzke, F.W.; Hitchings, R.A. Mapping the visual field to the optic disc in normal tension glaucoma eyes. Ophthalmology 2000, 107, 1809–1815. [Google Scholar] [CrossRef] [PubMed]
- Coleman, A.L.; Miglior, S. Risk factors for glaucoma onset and progression. Surv. Ophthalmol. 2008, 53, S3–S10. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial autoencoders. arXiv 2015, arXiv:1511.05644. [Google Scholar]
- Passing, H.; Bablok, W. A new biometrical procedure for testing the equality of measurements from two different analytical methods. Application of linear regression procedures for method comparison studies in clinical chemistry, Part I. Clin. Chem. Lab. Med. 1983, 21, 709–720. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.P. Conjugate Bayesian analysis of the Gaussian distribution. def 2007, 1, 16. [Google Scholar]

| Measurements | Mean (Standard Deviation) | Median (Interquartile Range) |
|---|---|---|
| Age (years) | 63.7 (11.8) | 65.7 (56.4 to 71.8) |
| Follow-up years | 7.7 (1.7) | 8.1 (6.8 to 8.8) |
| Number of visits | 9.9 (3.7) | 10.0 (7.0 to 13.0) |
| Initial mean deviation 1 (dB) | −3.2 (5.8) | −1.4 (−4.2 to 0.4) |
| Initial mRNFLT 2 (µm) | 78.7 (14.4) | 78.3 (66.9 to 89.8) |
| MD slope 3 (dB/year) | −0.21 (0.44) | −0.15 (−0.33 to 0.02) |
| mRNFLT slope 4 (µm/year) | −0.24 (0.97) | −0.24 (−0.58 to 0.10) |
| Criteria 1 | Metrics | AE-Fused Data 2 | Measured Data | BLR Data |
|---|---|---|---|---|
| <−0.2 dB/year | Specificity | 0.67 ± 0.01 | 0.34 ± 0.01 | 0.50 ± 0.01 |
| Sensitivity | 0.53 ± 0.01 | 0.56 ± 0.01 | 0.51 ± 0.02 | |
| F1 score | 0.62 ± 0.01 | 0.50 ± 0.01 | 0.52 ± 0.02 | |
| <−0.5 dB/year | Specificity | 0.70 ± 0.01 | 0.36 ± 0.01 | 0.55 ± 0.01 |
| Sensitivity | 0.53 ± 0.03 | 0.54 ± 0.02 | 0.35 ± 0.02 | |
| F1 score | 0.60 ± 0.01 | 0.45 ± 0.01 | 0.48 ± 0.02 | |
| <−1.0 dB/year | Specificity | 0.70 ± 0.01 | 0.36 ± 0.02 | 0.55 ± 0.01 |
| Sensitivity | 0.41 ± 0.07 | 0.49 ± 0.06 | 0.27 ± 0.04 | |
| F1 score | 0.50 ± 0.03 | 0.37 ± 0.02 | 0.44 ± 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li-Han, L.Y.; Eizenman, M.; Shi, R.B.; Buys, Y.M.; Trope, G.E.; Wong, W. Using Fused Data from Perimetry and Optical Coherence Tomography to Improve the Detection of Visual Field Progression in Glaucoma. Bioengineering 2024, 11, 250. https://doi.org/10.3390/bioengineering11030250
Li-Han LY, Eizenman M, Shi RB, Buys YM, Trope GE, Wong W. Using Fused Data from Perimetry and Optical Coherence Tomography to Improve the Detection of Visual Field Progression in Glaucoma. Bioengineering. 2024; 11(3):250. https://doi.org/10.3390/bioengineering11030250
Chicago/Turabian StyleLi-Han, Leo Yan, Moshe Eizenman, Runjie Bill Shi, Yvonne M. Buys, Graham E. Trope, and Willy Wong. 2024. "Using Fused Data from Perimetry and Optical Coherence Tomography to Improve the Detection of Visual Field Progression in Glaucoma" Bioengineering 11, no. 3: 250. https://doi.org/10.3390/bioengineering11030250
APA StyleLi-Han, L. Y., Eizenman, M., Shi, R. B., Buys, Y. M., Trope, G. E., & Wong, W. (2024). Using Fused Data from Perimetry and Optical Coherence Tomography to Improve the Detection of Visual Field Progression in Glaucoma. Bioengineering, 11(3), 250. https://doi.org/10.3390/bioengineering11030250





