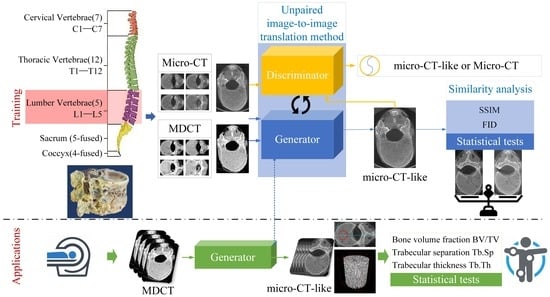
Exploring the Possibility of Measuring Vertebrae Bone Structure Metrics Using MDCT Images: An Unpaired Image-to-Image Translation Method
Abstract
1. Introduction
2. Literature Reviews
3. Methodology
3.1. Specimens
3.2. Imaging Techniques
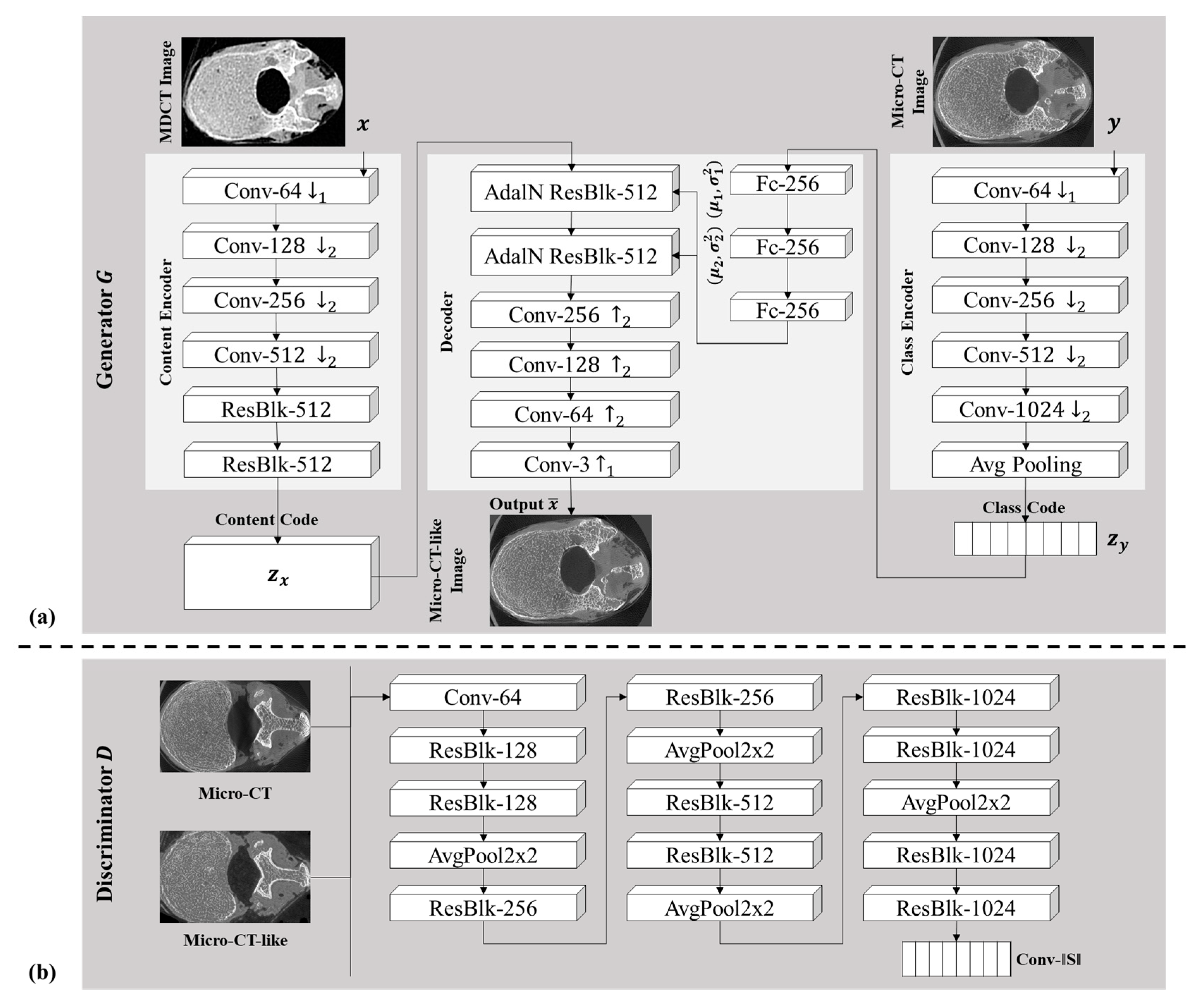
3.3. Few-Shot Unpaired-Image-Based Translation Model for Generating Micro-CT-like Images
3.4. Training and Testing
3.4.1. Training Process
3.4.2. Image Pairing Method for Testing
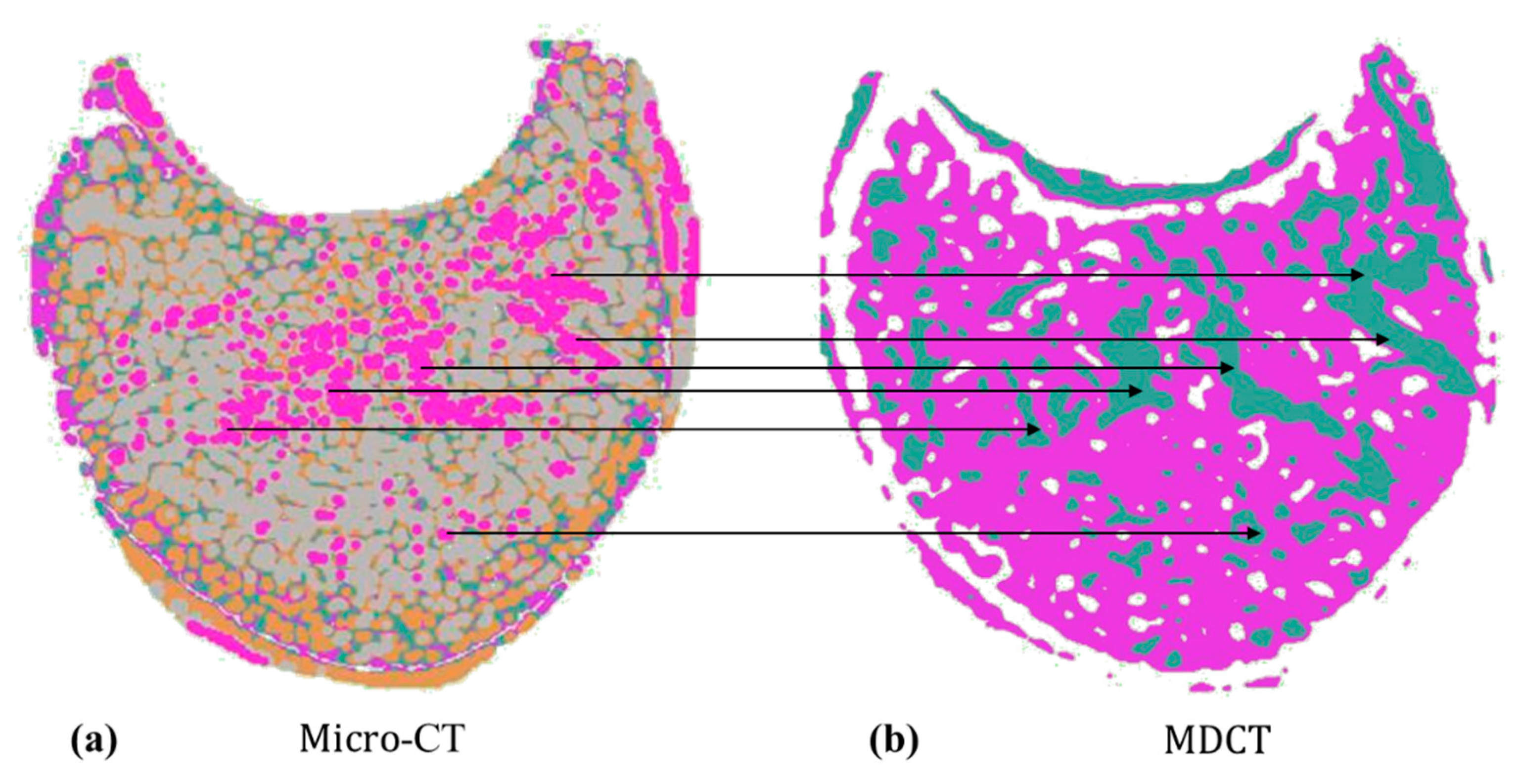
- Image matching: The scale invariant feature transform (SIFT) algorithm [78] was used to find coupling key points in MDCT and micro-CT images. We calculated the Euclidean distance between key points and set the mean value to be the distance between MDCT and micro-CT images (Figure 4). Based on this, we compared MDCT and micro-CT images one by one and constructed the matrix of distances between all MDCT and micro-CT images. The best matched image pair could be obtained via the dynamic time warping (DTW) algorithm [79].
- MDCT image amplification and image pair generation: Due to the different layer spacing between the two scanning methods, MDCT images and micro-CT images of the same specimen are not equal in overall number, and approximately two layers of micro-CT images correspond to one layer of MDCT images. Therefore, the MDCT images of each vertebra needed to be replicated () according to the matching relationship to obtain one-to-one paired-image pairs of MDCT and micro-CT images, i.e., 500 image pairs were generated for each vertebral specimen. Applying the above method to all 25 vertebrae in the test set, a total of image pairs could be obtained.
3.5. Assessment Methods
3.5.1. Similarity Metrics
3.5.2. Born Structure Metrics
4. Results
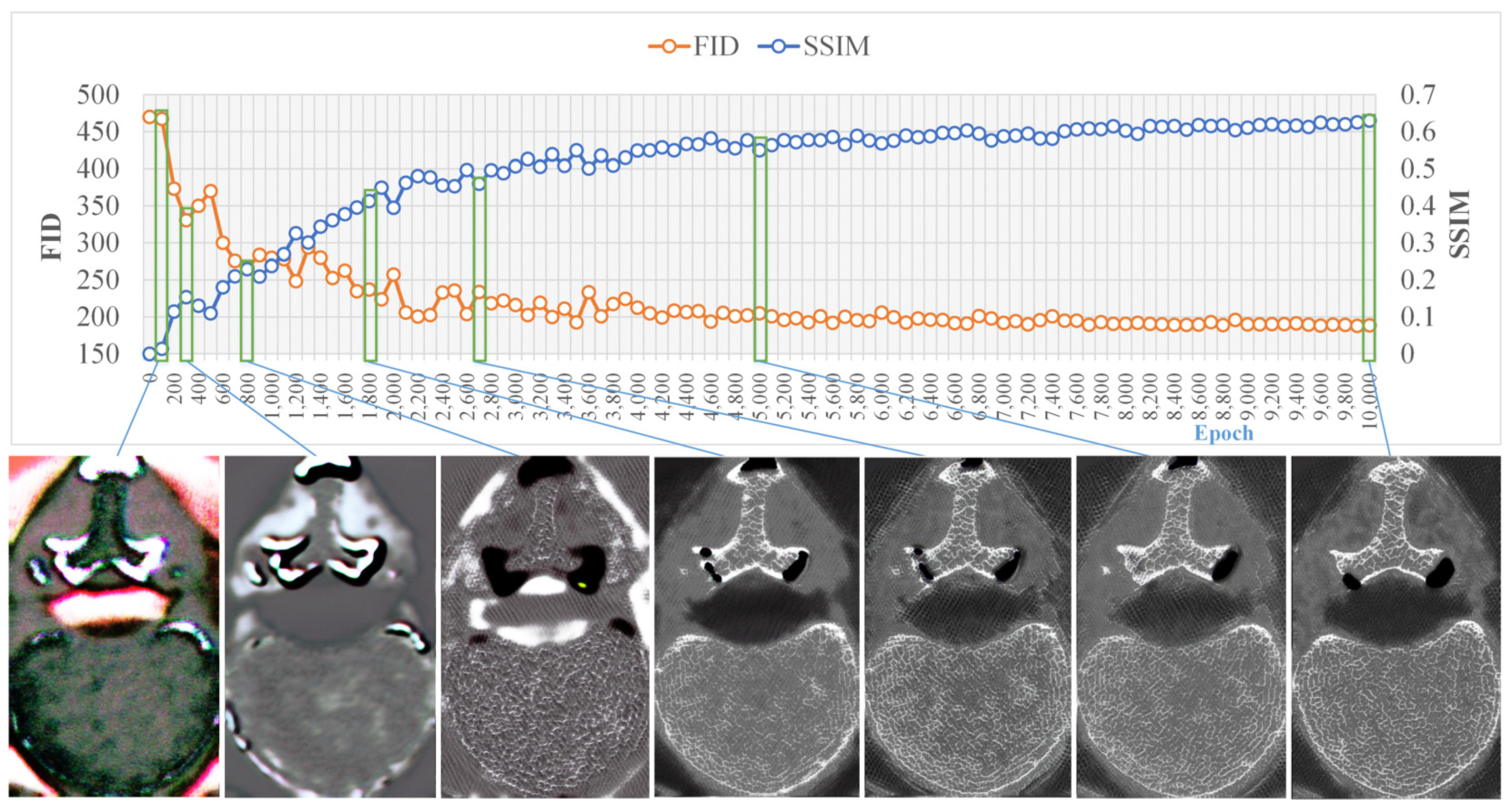
4.1. Training Results
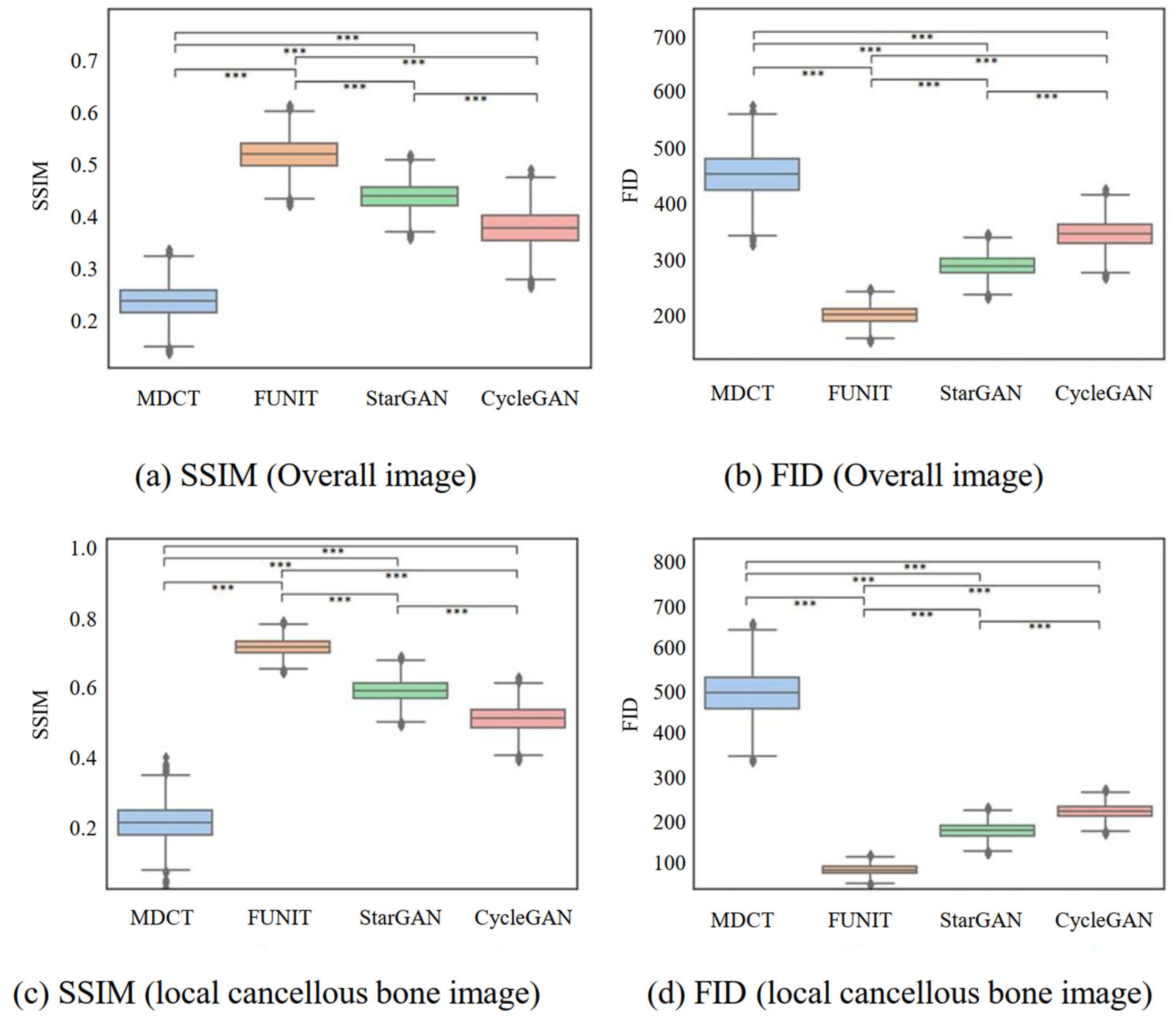
4.2. Comparison of SSIMs and FIDs for Generated Images
4.2.1. Comparing Generated Micro-CT-like Images with MDCT Images
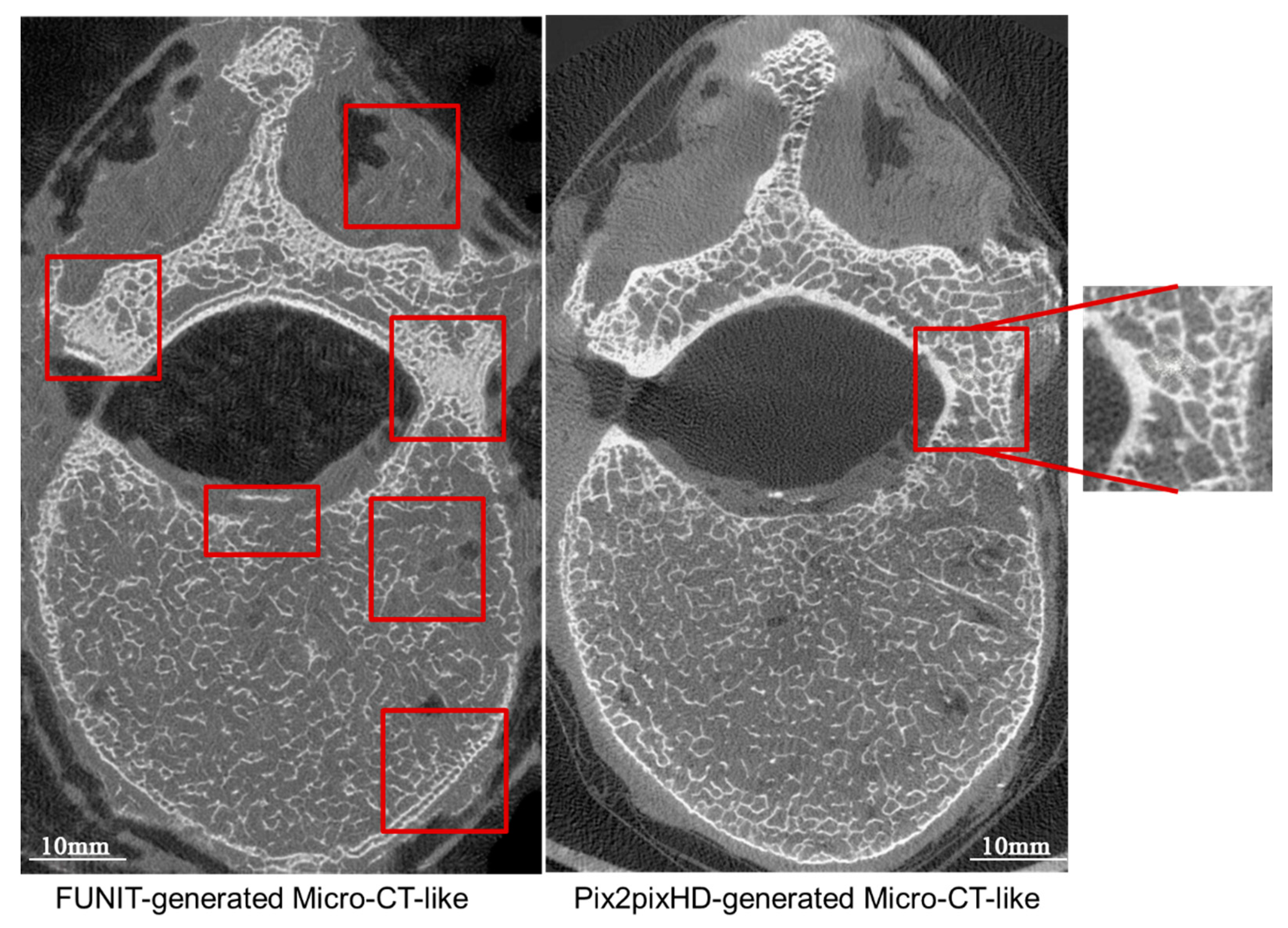
4.2.2. Comparison of Micro-CT-like Images Generated Using Unpaired-Image-Based FUNIT Model and Paired-Image-Based pix2pixHD Model
4.3. Correlation and Consistency of Bone Structure Metrics between Generated Micro-CT-like and Gold-Standard Micro-CT Images
4.3.1. Correlation of Bone Structure between FUNIT-Generated Micro-CT-like and Gold-Standard Micro-CT Images
4.3.2. Consistency between Bone Structure Metrics of FUNIT Micro-CT-like and Gold-Standard Micro-CT Images
4.4. Discussion
4.4.1. Characterization of the Proposed Method
4.4.2. Paired-Image-Based pix2pixHD Model versus Unpaired-Image-Based FUNIT Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cosman, F.; de Beur, S.J.; LeBoff, M.S.; Lewiecki, E.M.; Tanner, B.; Randall, S.; Lindsay, R. Clinician’s guide to prevention and treatment of osteoporosis. Osteoporos. Int. 2014, 25, 2359–2381. [Google Scholar] [CrossRef]
- Ammann, P.; Rizzoli, R. Bone strength and its determinants. Osteoporos. Int. 2003, 14 (Suppl. 3), S13–S18. [Google Scholar] [CrossRef]
- Delmas, P.D.; van de Langerijt, L.; Watts, N.B.; Eastell, R.; Genant, H.; Grauer, A.; Cahall, D.L. Underdiagnosis of vertebral fractures is a worldwide problem: The impact study. J. Bone Miner. Res. Off. J. Am. Soc. Bone Miner. Res. 2005, 20, 557–563. [Google Scholar] [CrossRef] [PubMed]
- Schuit, S.C.E.; van der Klift, M.; Weel, A.E.A.M.; de Laet, C.E.D.H.; Burger, H.; Seeman, E.; Hofman, A.; Uitterlinden, A.G.; van Leeuwen, J.P.T.M.; Pols, H.A.P. Fracture incidence and association with bone mineral density in elderly men and women: The rotterdam study. Bone 2004, 34, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Cranney, A.; Jamal, S.A.; Tsang, J.F.; Josse, R.G.; Leslie, W.D. Low bone mineral density and fracture burden in postmenopausal women. CMAJ 2007, 177, 575–580. [Google Scholar] [CrossRef] [PubMed]
- Pasco, J.A.; Seeman, E.; Henry, M.J.; Merriman, E.N.; Nicholson, G.C.; Kotowicz, M.A. The population burden of fractures originates in women with osteopenia, not osteoporosis. Osteoporos. Int. 2006, 17, 1404–1409. [Google Scholar] [CrossRef]
- Stone, K.L.; Seeley, D.G.; Lui, L.-Y.; Cauley, J.A.; Ensrud, K.; Browner, W.S.; Nevitt, M.C.; Cummings, S.R. Bmd at multiple sites and risk of fracture of multiple types: Long-term results from the study of osteoporotic fractures. J. Bone Miner. Res. Off. J. Am. Soc. Bone Miner. Res. 2003, 18, 1947–1954. [Google Scholar] [CrossRef]
- Wainwright, S.A.; Marshall, L.M.; Ensrud, K.E.; Cauley, J.A.; Black, D.M.; Hillier, T.A.; Hochberg, M.C.; Vogt, M.T.; Orwoll, E.S. Hip fracture in women without osteoporosis. J. Clin. Endocrinol. Metab. 2005, 90, 2787–2793. [Google Scholar] [CrossRef]
- Wehrli, F.W.; Saha, P.K.; Gomberg, B.R.; Song, H.K.; Snyder, P.J.; Benito, M.; Wright, A.; Weening, R. Role of magnetic resonance for assessing structure and function of trabecular bone. Top Magn. Reason. Imaging 2002, 13, 335–355. [Google Scholar] [CrossRef]
- McCoy, S.; Tundo, F.; Chidambaram, S.; Baaj, A.A. Clinical considerations for spinal surgery in the osteoporotic patient: A comprehensive review. Clin. Neurol. Neurosurg. 2019, 180, 40–47. [Google Scholar] [CrossRef]
- Koester, K.J.; Barth, H.D.; Ritchie, R.O. Effect of aging on the transverse toughness of human cortical bone: Evaluation by r-curves. J. Mech. Behav. Biomed. Mater. 2011, 4, 1504–1513. [Google Scholar] [CrossRef] [PubMed]
- Morgan, E.F.; Bayraktar, H.H.; Keaveny, T.M. Trabecular bone modulus-density relationships depend on anatomic site. J. Biomech. 2003, 36, 897–904. [Google Scholar] [CrossRef] [PubMed]
- Cummings, S.R.; Black, D.M.; Rubin, S.M. Lifetime risks of hip, colles’, or vertebral fracture and coronary heart disease among white postmenopausal women. Arch. Intern. Med. 1989, 149, 2445–2448. [Google Scholar] [CrossRef] [PubMed]
- Taes, Y.; Lapauw, B.; Griet, V.; De Bacquer, D.; Goemaere, S.; Zmierczak, H.; Kaufman, J.-M. Prevalent fractures are related to cortical bone geometry in young healthy men at age of peak bone mass. J. Bone Miner. Res. Off. J. Am. Soc. Bone Miner. Res. 2010, 25, 1433–1440. [Google Scholar] [CrossRef]
- Wehrli, F.W.; Rajapakse, C.S.; Magland, J.F.; Snyder, P.J. Mechanical implications of estrogen supplementation in early postmenopausal women. J. Bone Miner. Res. 2010, 25. [Google Scholar] [CrossRef]
- Currey, J.D. Mechanical properties of bone tissues with greatly differing functions. J. Biomech. 1979, 12, 313–319. [Google Scholar] [CrossRef]
- Pang, Y.; Lin, J.; Qin, T.; Chen, Z. Image-to-image translation: Methods and applications. arXiv 2021, arXiv:2101.08629. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein gan. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2016; pp. 1125–1134. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Jin, D.; Zheng, H.; Zhao, Q.; Wang, C.; Zhang, M.; Yuan, H. Generation of vertebra micro-ct-like image from mdct: A deep-learning-based image enhancement approach. Tomography 2021, 7, 767–782. [Google Scholar] [CrossRef]
- Liu, M.-Y.; Huang, X.; Mallya, A.; Karras, T.; Aila, T.; Lehtinen, J.; Kautz, J. Few-shot unsupervised image-to-image translation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October—2 November 2019. [Google Scholar]
- Van Tulder, G.; De Bruijne, M. Why does synthesized data improve multi-sequence classification? In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 531–538. [Google Scholar]
- Ye, D.H.; Zikic, D.; Glocker, B.; Criminisi, A.; Konukoglu, E. Modality propagation: Coherent synthesis of subject-specific scans with data-driven regularization. Med. Image Comput. Comput. Assist. Interv. 2013, 16, 606–613. [Google Scholar]
- Huang, Y.; Shao, L.; Frangi, A.F. Simultaneous super-resolution and cross-modality synthesis of 3d medical images using weakly-supervised joint convolutional sparse coding. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5787–5796. [Google Scholar]
- Costa, P.; Galdran, A.; Meyer, M.I.; Niemeijer, M.; Abramoff, M.; Mendonca, A.M.; Campilho, A. End-to-end adversarial retinal image synthesis. IEEE Trans. Med. Imaging 2018, 37, 781–791. [Google Scholar] [CrossRef] [PubMed]
- Reeth, E.V.; Tham, I.; Tan, C.H.; Poh, C.L. Super-resolution in magnetic resonance imaging: A review. Concepts Magn. Reson. Part A 2012, 40A, 306–325. [Google Scholar] [CrossRef]
- Peleg, I.S. Motion analysis for image enhancement: Resolution, occlusion, and transparency. J. Vis. Commun. Image Represent. 1993, 4, 324–335. [Google Scholar]
- Hayit, G. Super-resolution in medical imaging. Comput. J. 2009, 1, 43–63. [Google Scholar]
- Wang, Z.; Chen, J.; Hoi, S.C.H. Deep learning for image super-resolution: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3365–3387. [Google Scholar] [CrossRef]
- Ashikaga, H.; Estner, H.L.; Herzka, D.A.; McVeigh, E.R.; Halperin, H.R. Quantitative assessment of single-image super-resolution in myocardial scar imaging. IEEE J. Transl. Eng. Health Med. 2014, 2, 1–12. [Google Scholar] [CrossRef]
- Bernstein, M.A.; Fain, S.B.; Riederer, S.J. Effect of windowing and zero-filled reconstruction of mri data on spatial resolution and acquisition strategy. J. Magn. Reason. Imaging 2001, 14, 270–280. [Google Scholar] [CrossRef]
- Robinson, M.; Toth, C.; Lo, J.; Farsiu, S. Efficient fourier-wavelet super-resolution. IEEE Trans. Image Process. A Publ. IEEE Signal Process. Soc. 2010, 19, 2669–2681. [Google Scholar] [CrossRef]
- Robinson, M.D.; Farsiu, S.; Lo, J.Y.; Toth, C.A. Efficient restoration and enhancement of super-resolved X-ray images. In Proceedings of the 2008 15th IEEE International Conference on Image Processing, San Diego, CA, USA, 12–15 October 2008; pp. 629–632. [Google Scholar]
- Salvador, J. Example-Based Super Resolution; Academic Press: Cambridge, MA, USA, 2016; pp. 1–141. [Google Scholar]
- Wang, Y.; Ma, G.; An, L.; Shi, F.; Zhang, P.; Lalush, D.S.; Wu, X.; Pu, Y.; Zhou, J.; Shen, D. Semisupervised tripled dictionary learning for standard-dose pet image prediction using low-dose pet and multimodal mri. IEEE Trans. Biomed. Eng. 2017, 64, 569–579. [Google Scholar] [CrossRef]
- Jog, A.; Carass, A.; Roy, S.; Pham, D.L.; Prince, J.L. Random forest regression for magnetic resonance image synthesis. Med. Image Anal. 2017, 35, 475–488. [Google Scholar] [CrossRef] [PubMed]
- Semmlow, J.L.; Griffel, B. Biosignal and Medical Image Processing; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Sahiner, B.; Pezeshk, A.; Hadjiiski, L.M.; Wang, X.; Drukker, K.; Cha, K.H.; Summers, R.M.; Giger, M.L. Deep learning in medical imaging and radiation therapy. Med. Phys. 2019, 46, e1–e36. [Google Scholar] [CrossRef]
- Yi, X.; Walia, E.; Babyn, P. Generative adversarial network in medical imaging: A review. Med. Image Anal. 2019, 58, 101552. [Google Scholar] [CrossRef] [PubMed]
- Fleet, D.; Pajdla, T.; Schiele, B.; Tuytelaars, T. Learning a deep convolutional network for image super-resolution. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Volume 8692, pp. 184–199. [Google Scholar]
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Van Nguyen, H.; Zhou, K.; Vemulapalli, R. Cross-domain synthesis of medical images using efficient location-sensitive deep network. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 677–684. [Google Scholar]
- Chen, H.; Zhang, Y.; Zhang, W.; Liao, P.; Li, K.; Zhou, J.; Wang, G. Low-dose ct via convolutional neural network. Biomed. Opt. Express 2017, 8, 679–694. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y.; Kalra, M.K.; Lin, F.; Chen, Y.; Liao, P.; Zhou, J.; Wang, G. Low-dose ct with a residual encoder-decoder convolutional neural network. IEEE Trans. Med. Imaging 2017, 36, 2524–2535. [Google Scholar] [CrossRef] [PubMed]
- Zeng, K.; Zheng, H.; Cai, C.; Yang, Y.; Zhang, K.; Chen, Z. Simultaneous single-and multi-contrast super-resolution for brain mri images based on a convolutional neural network. Comput. Biol. Med. 2018, 99, 133–141. [Google Scholar] [CrossRef]
- Chaudhari, A.S.; Fang, Z.; Kogan, F.; Wood, J.; Stevens, K.J.; Gibbons, E.K.; Lee, J.H.; Gold, G.E.; Hargreaves, B.A. Super-resolution musculoskeletal mri using deep learning. Magn. Reson. Med. 2018, 80, 2139–2154. [Google Scholar] [CrossRef]
- Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 1962, 160, 106–154. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Chen, Q.; Koltun, V. Photographic image synthesis with cascaded refinement networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Chartsias, A.; Joyce, T.; Giuffrida, M.V.; Tsaftaris, S.A. Multimodal mr synthesis via modality-invariant latent representation. IEEE Trans. Med. Imaging 2018, 37, 803–814. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, Q.; Nie, D.; Zhang, L.; Jin, X.; Qiao, Y.; Shen, D. Deep embedding convolutional neural network for synthesizing ct image from t1-weighted mr image. Med. Image Anal. 2018, 47, 31–44. [Google Scholar] [CrossRef]
- Wang, T.C.; Liu, M.Y.; Zhu, J.Y.; Tao, A.; Kautz, J.; Catanzaro, B. High-resolution image synthesis and semantic manipulation with conditional gans. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8798–8807. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. Comput. Sci. 2014. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. arXiv 2014, arXiv:1411.1784. [Google Scholar]
- Ben-Cohen, A.; Klang, E.; Raskin, S.P.; Amitai, M.M.; Greenspan, H. Virtual pet images from ct data using deep convolutional networks: Initial results. In Proceedings of the International Workshop on Simulation and Synthesis in Medical Imaging, Québec City, QC, Canada, 10 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 49–57. [Google Scholar]
- Bi, L.; Kim, J.; Kumar, A.; Feng, D.; Fulham, M. Synthesis of positron emission tomography (pet) images via multi-channel generative adversarial networks (gans). In Molecular Imaging, Reconstruction and Analysis of Moving Body Organs, and Stroke Imaging and Treatment; Springer: Berlin/Heidelberg, Germany, 2017; pp. 43–51. [Google Scholar]
- Chartsias, A.; Joyce, T.; Dharmakumar, R.; Tsaftaris, S.A. Adversarial image synthesis for unpaired multi-modal cardiac data. In Proceedings of the International Workshop on Simulation and Synthesis in Medical Imaging, Québec City, QC, Canada, 10 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 3–13. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.; Smolley, S.P. Least squares generative adversarial networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Yu, S.; Dong, H.; Yang, G.; Slabaugh, G.; Dragotti, P.; Ye, X.; Liu, F.; Arridge, S.; Keegan, J.; Firmin, D.; et al. Deep de-aliasing for fast compressive sensing mri. arXiv 2017, arXiv:1705.07137. [Google Scholar]
- Gupta, R.; Sharma, A.; Kumar, A. Super-resolution using gans for medical imaging. Procedia Comput. Sci. 2020, 173, 28–35. [Google Scholar] [CrossRef]
- Nie, D.; Trullo, R.; Lian, J.; Wang, L.; Petitjean, C.; Ruan, S.; Wang, Q.; Shen, D. Medical image synthesis with deep convolutional adversarial networks. IEEE Trans. Biomed. Eng. 2018, 65, 2720–2730. [Google Scholar] [CrossRef]
- Hiasa, Y.; Otake, Y.; Takao, M.; Matsuoka, T.; Takashima, K.; Carass, A.; Prince, J.L.; Sugano, N.; Sato, Y. Cross-modality image synthesis from unpaired data using cyclegan. In Proceedings of the International Workshop on Simulation and Synthesis in Medical Imaging, Granada, Spain, 16 September 2018; Springer: Berlin/Heidelberg, Germany; pp. 31–41. [Google Scholar]
- Dar, S.U.; Yurt, M.; Karacan, L.; Erdem, A.; Erdem, E.; Çukur, T. Image synthesis in multi-contrast mri with conditional generative adversarial networks. IEEE Trans. Med. Imaging 2019, 38, 2375–2388. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Uh, Y.; Yoo, J.; Ha, J.W. Stargan v2: Diverse image synthesis for multiple domains. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Liu, X.S.; Stein, E.M.; Zhou, B.; Zhang, C.A.; Nickolas, T.L.; Cohen, A.; Thomas, V.; McMahon, D.J.; Cosman, F.; Nieves, J.; et al. Individual trabecula segmentation (its)-based morphological analyses and microfinite element analysis of hr-pqct images discriminate postmenopausal fragility fractures independent of dxa measurements. J. Bone Miner. Res. Off. J. Am. Soc. Bone Miner. Res. 2012, 27, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Shuai, B.; Shen, L.; Yang, Y.; Ma, C.; Zhu, R.; Xu, X. Assessment of the impact of zoledronic acid on ovariectomized osteoporosis model using micro-ct scanning. PLoS ONE 2015, 10, e0132104. [Google Scholar] [CrossRef]
- Gomes, C.C.; Freitas, D.Q.; Medeiros Araújo, A.M.; Ramírez-Sotelo, L.R.; Yamamoto-Silva, F.P.; de Freitas Silva, B.S.; de Melo Távora, D.; Almeida, S.M. Effect of alendronate on bone microarchitecture in irradiated rats with osteoporosis: Micro-ct and histomorphometric analysis. J. Oral Maxillofac. Surg. 2018, 76, 972–981. [Google Scholar] [CrossRef]
- Xie, F.; Zhou, B.; Wang, J.; Liu, T.; Wu, X.; Fang, R.; Kang, Y.; Dai, R. Microstructural properties of trabecular bone autografts: Comparison of men and women with and without osteoporosis. Arch. Osteoporos. 2018, 13, 18. [Google Scholar] [CrossRef]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Huang, X.; Liu, M.Y.; Belongie, S.; Kautz, J. Multimodal Unsupervised Image-to-Image Translation; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Mescheder, L.; Geiger, A.; Nowozin, S. Which training methods for gans do actually converge? In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018.
- Bradski, G. The opencv library. Dr. Dobb’s J. Softw. Tools 2000, 25, 120–123. [Google Scholar]
- Keogh, E.; Ratanamahatana, C.A. Exact indexing of dynamic time warping. Knowl. Inf. Syst. 2005, 7, 358–386. [Google Scholar] [CrossRef]
- Zhou, W.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans Image Process 2004, 13, 600–612. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. Adv. Neural Inf. Process. Syst. 2017, 30, 6629–6640. [Google Scholar]
- Domander, R.; Felder, A.; Doube, M. Bonej2—Refactoring established research software. Wellcome Open Res. 2021, 6, 37. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. Imagej2: Imagej for the next generation of scientific image data. BMC Bioinform. 2017, 18, 1–26. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. Nih image to imagej: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Ridler, T.W.; Calvard, S. Picture thresholding using an iterative selection method. IEEE Trans. Syst. Man Cybern. 1978, 8, 630–632. [Google Scholar]
- Dougherty, R.; Kunzelmann, K.H. Computing local thickness of 3d structures with imagej. Microsc. Microanal. 2007, 13, 1678–1679. [Google Scholar] [CrossRef]




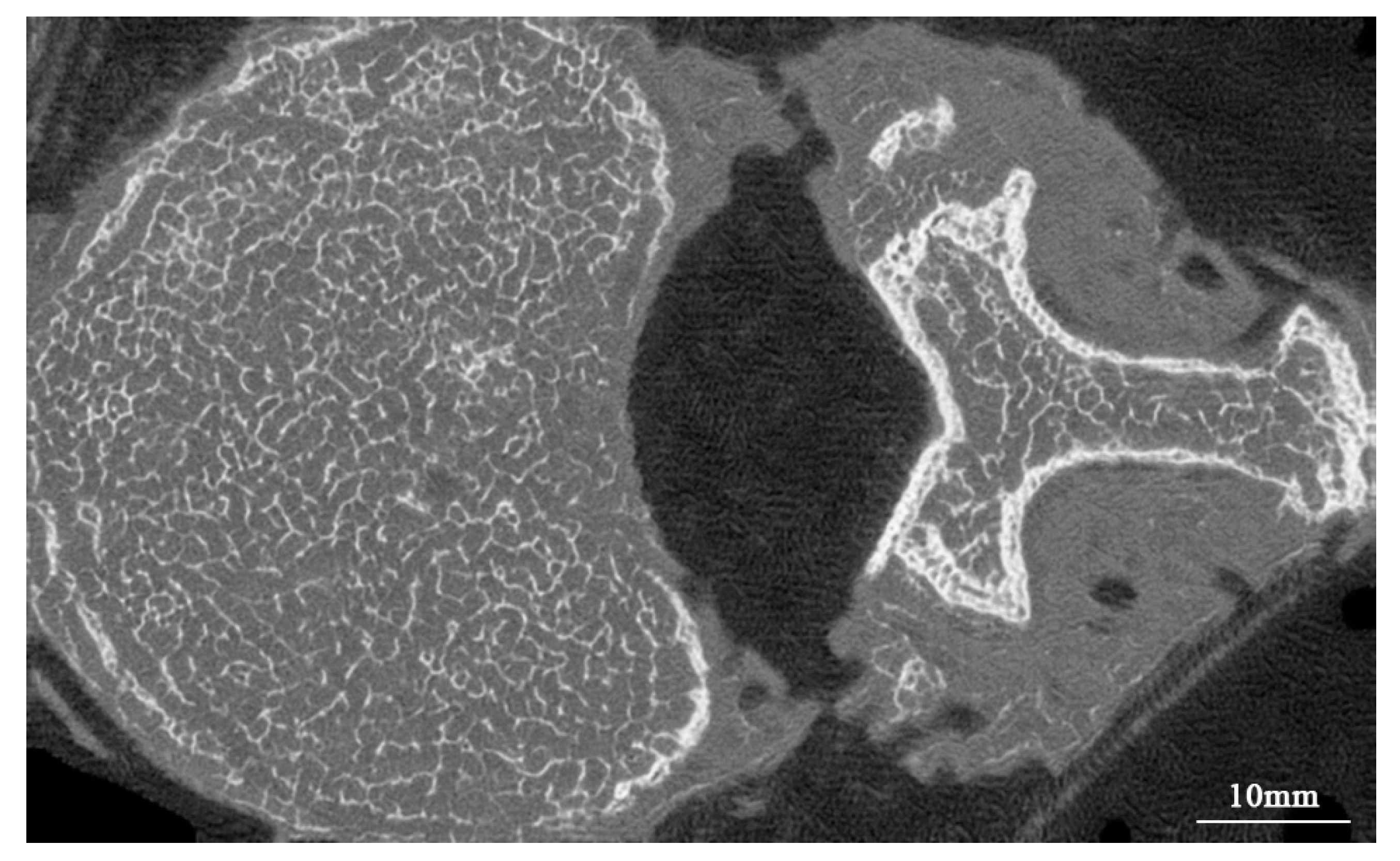



| Scale | Metrics | MDCT | FUNIT | StarGAN | CycleGAN | p-Value † |
|---|---|---|---|---|---|---|
| Overall image | SSIM | 0.238 ± 0.031 | 0.519 ± 0.030 | 0.437 ± 0.025 | 0.377 ± 0.035 | <0.001 *** |
| FID | 453.425 ± 39.081 | 201.737 ± 15.031 | 289.503 ± 18.037 | 347.311 ± 25.051 | <0.001 *** | |
| Localized cancellous bone images | SSIM | 0.213 ± 0.052 | 0.714 ± 0.023 | 0.589 ± 0.031 | 0.508 ± 0.037 | <0.001 *** |
| FID | 495.024 ± 54.435 | 83.696 ± 11.022 | 175.531 ± 17.035 | 219.559 ± 16.033 | <0.001 *** |
| Scale | Metrics | FUNIT | pix2pixHD [22] | p-Value † |
|---|---|---|---|---|
| Overall image | SSIM | 0.519 ± 0.030 | 0.804 ± 0.037 | <0.001 *** |
| FID | 201.737 ± 15.031 | 43.598 ± 9.108 | <0.001 *** | |
| Localized cancellous bone images | SSIM | 0.714 ± 0.023 | 0.849 ± 0.021 | <0.001 *** |
| FID | 83.696 ± 11.022 | 31.724 ± 10.021 | <0.001 *** |
| FUNIT Micro-CT-like | Micro-CT | p-Value † | F-Value | p-Value ‡ | ||
|---|---|---|---|---|---|---|
| BV/TV (%) | 0.143 ± 0.018 | 0.180 ± 0.016 | <0.001 *** | 0.667 | 96.102 | <0.001 *** |
| Tb.Th (mm) | 0.158 ± 0.021 | 0.218 ± 0.015 | <0.001 *** | 0.613 | 78.69 | <0.001 *** |
| Tb.Sp (mm) | 1.144 ± 0.166 | 0.934 ± 0.126 | <0.001 *** | 0.603 | 75.573 | <0.001 *** |
| Bone Structure Metrics | ICC | 95% CI | p-Value | |
|---|---|---|---|---|
| micro-CT-like (FUNIT). vs. micro-CT | BV/TV | 0.809 | 0.887~0.686 | <0.001 |
| Tb.Th | 0.752 | 0.852~0.601 | <0.001 | |
| Tb.Sp | 0.753 | 0.852~0.603 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, D.; Zheng, H.; Yuan, H. Exploring the Possibility of Measuring Vertebrae Bone Structure Metrics Using MDCT Images: An Unpaired Image-to-Image Translation Method. Bioengineering 2023, 10, 716. https://doi.org/10.3390/bioengineering10060716
Jin D, Zheng H, Yuan H. Exploring the Possibility of Measuring Vertebrae Bone Structure Metrics Using MDCT Images: An Unpaired Image-to-Image Translation Method. Bioengineering. 2023; 10(6):716. https://doi.org/10.3390/bioengineering10060716
Chicago/Turabian StyleJin, Dan, Han Zheng, and Huishu Yuan. 2023. "Exploring the Possibility of Measuring Vertebrae Bone Structure Metrics Using MDCT Images: An Unpaired Image-to-Image Translation Method" Bioengineering 10, no. 6: 716. https://doi.org/10.3390/bioengineering10060716
APA StyleJin, D., Zheng, H., & Yuan, H. (2023). Exploring the Possibility of Measuring Vertebrae Bone Structure Metrics Using MDCT Images: An Unpaired Image-to-Image Translation Method. Bioengineering, 10(6), 716. https://doi.org/10.3390/bioengineering10060716