A Disentangled VAE-BiLSTM Model for Heart Rate Anomaly Detection
Abstract
1. Introduction
- (1)
- We propose a combination of multiple unsupervised machine learning algorithms and a sliding-window-based dynamic outlier detection approach to label the data, taking into consideration both contextual and global anomalies.
- (2)
- We develop an anomaly detection algorithm based on disentangled variational autoencoder (β-VAE) and bidirectional long short-term memory network (BiLSTM), and validate its effectiveness on HR wearables data by comparing its performance with well-known and state-of-the-art anomaly detection algorithms. Adding a BiLSTM backend to the VAE model allows us to capture contextual relationships in VAE-processed HR sequences by analyzing both forward and backward directions of the information flow. Ultimately, this leads the algorithm to better model the considered time series and to learn more accurate patterns.
- (3)
- We explore the latent space of our proposed algorithm and compare it with that of a standard VAE, giving consideration to how tuning the β parameter helps with anomaly detection and with encoding temporal sequences.
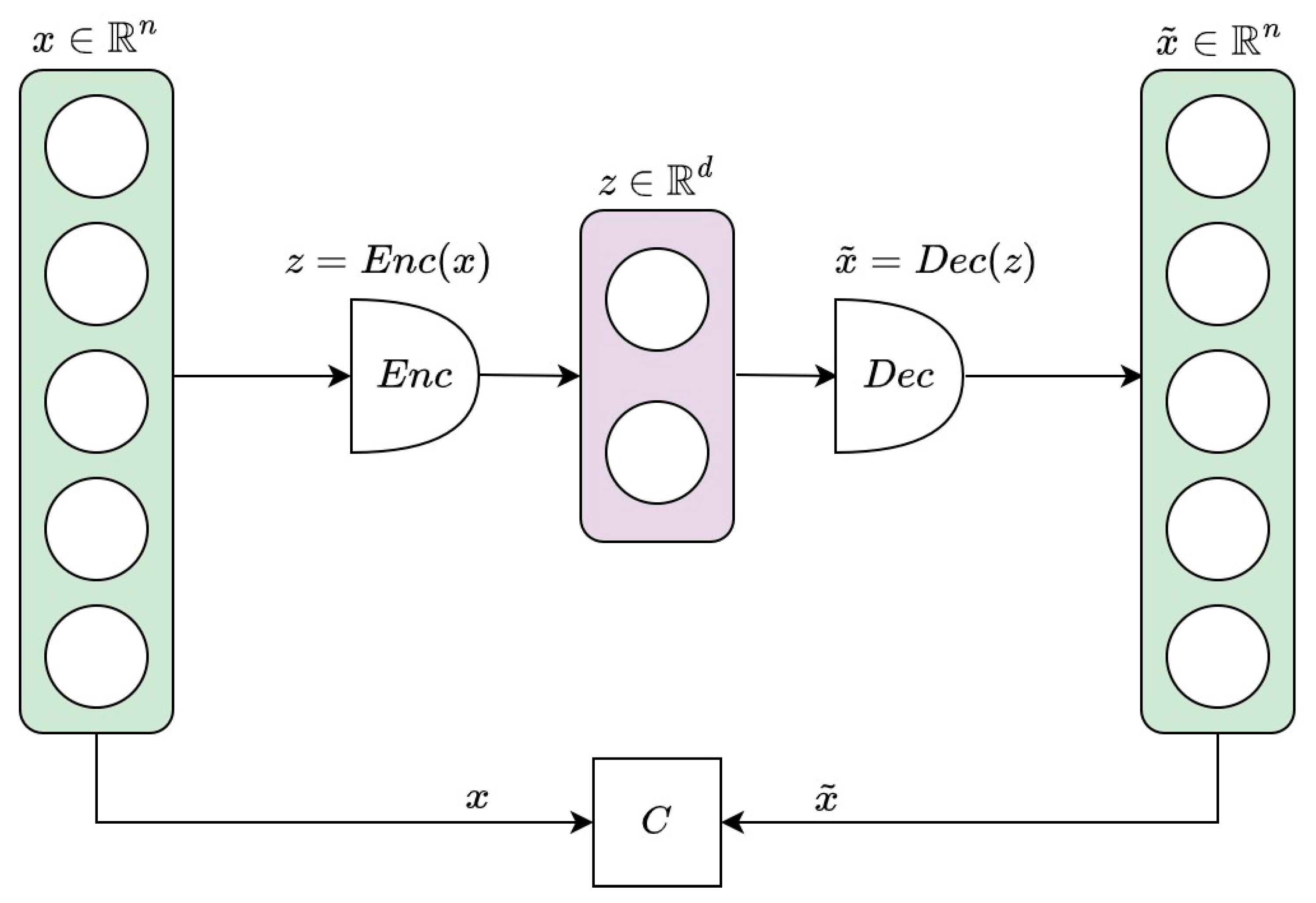
2. Materials and Methods
2.1. Study Participants and Wearable Device
2.2. Data Labeling and Preprocessing
| Algorithm 1: Data Labeling |
| Input HR data of the participant (), set of participants Output: set of anomalies for the participants () Models: Isolation Forest (), One-Class Support Vector Machine (), Kernel Density Estimation (), Sliding-Window () for 1,2,…, do { } end for [; ;…; ] return |
2.3. Anomaly Detection Models
2.3.1. ARIMA
2.3.2. LSTM
2.3.3. CAE-LSTM
2.3.4. BiLSTM
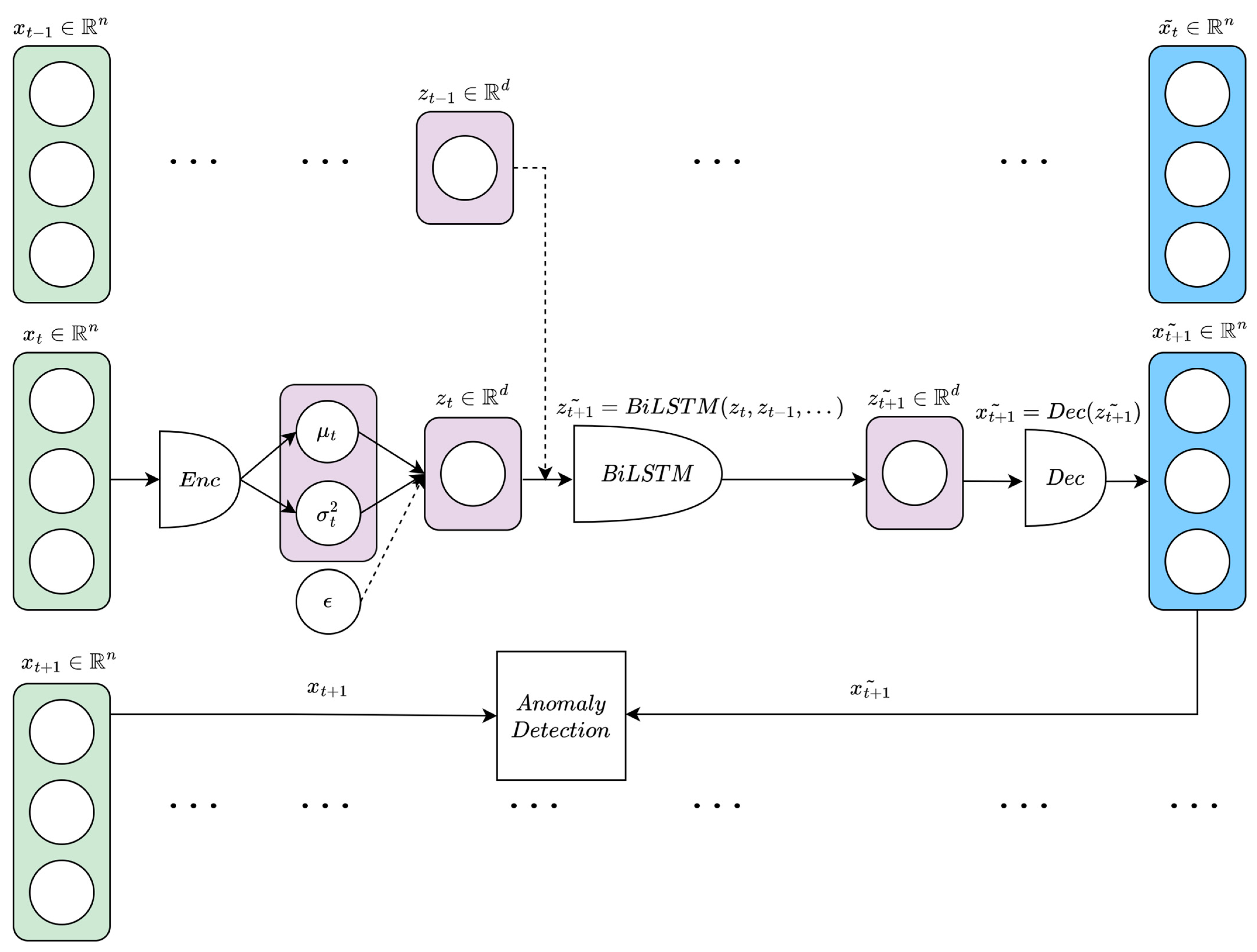
2.3.5. β-VAE-BiLSTM
3. Results and Discussion
Temporal Embeddings in the VAE Latent Space
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Cardiovascular Diseases. Available online: https://www.who.int/health-topics/cardiovascular-diseases#tab=tab_1 (accessed on 20 January 2023).
- American Heart Association. 2022 Heart Disease & Stroke Statistical Update Fact Sheet Global Burden of Disease. Available online: https://professional.heart.org/-/media/PHD-Files-2/Science-News/2/2022-Heart-and-Stroke-Stat-Update/2022-Stat-Update-factsheet-GIobal-Burden-of-Disease.pdf (accessed on 20 January 2023).
- Centers for Disease Control and Prevention; National Center for Health Statistics. About Multiple Cause of Death, 1999–2020; CDC WONDER Online Database Website; Centers for Disease Control and Prevention: Atlanta, GA, USA, 2022. Available online: https://wonder.cdc.gov/mcd-icd10.html (accessed on 21 February 2022).
- Tsao, C.W.; Aday, A.W.; Almarzooq, Z.I.; Alonso, A.; Beaton, A.Z.; Bittencourt, M.S.; Boehme, A.K.; Buxton, A.E.; Carson, A.P.; Commodore-Mensah, Y.; et al. Heart Disease and Stroke Statistics—2022 Update: A Report From the American Heart Association. Circulation 2022, 145, e153–e639. [Google Scholar] [CrossRef]
- Mensah, G.A.; Roth, G.A.; Fuster, V. The Global Burden of Cardiovascular Diseases and Risk Factors: 2020 and Beyond. J. Am. Coll. Cardiol. 2019, 74, 2529–2532. [Google Scholar] [CrossRef]
- Allarakha, S.; Yadav, J.; Yadav, A.K. Financial Burden and financing strategies for treating the cardiovascular diseases in India. Soc. Sci. Humanit. Open 2022, 6, 100275. [Google Scholar] [CrossRef]
- Agliari, E.; Barra, A.; Barra, O.A.; Fachechi, A.; Vento, L.F.; Moretti, L. Detecting cardiac pathologies via machine learning on heart-rate variability time series and related markers. Sci. Rep. 2020, 10, 8845. [Google Scholar] [CrossRef]
- Sajadieh, A.; Rasmussen, V.; Hein, H.O.; Hansen, J.F. Familial predisposition to premature heart attack and reduced heart rate variability. Am. J. Cardiol. 2003, 92, 234–236. [Google Scholar] [CrossRef] [PubMed]
- Melillo, P.; Izzo, R.; Orrico, A.; Scala, P.; Attanasio, M.; Mirra, M.; DE Luca, N.; Pecchia, L. Automatic Prediction of Cardiovascular and Cerebrovascular Events Using Heart Rate Variability Analysis. PLoS ONE 2015, 10, e0118504. [Google Scholar] [CrossRef] [PubMed]
- Neubeck, L.; Coorey, G.; Peiris, D.; Mulley, J.; Heeley, E.; Hersch, F.; Redfern, J. Development of an integrated e-health tool for people with, or at high risk of, cardiovascular disease: The Consumer Navigation of Electronic Cardiovascular Tools (CONNECT) web application. Int. J. Med. Inform. 2016, 96, 24–37. [Google Scholar] [CrossRef] [PubMed]
- Chatellier, G.; Blinowska, A.; Menard, J.; Degoulet, P. Do physicians estimate reliably the cardiovascular risk of hypertensive patients? Medinfo 1995, 8 Pt 2, 876–879. [Google Scholar]
- Zhang, Y.; Diao, L.; Ma, L. Logistic Regression Models in Predicting Heart Disease. J. Phys. Conf. Ser. 2021, 1769, 012024. [Google Scholar] [CrossRef]
- Ciu, T.; Oetama, R.S. Logistic Regression Prediction Model for Cardiovascular Disease. IJNMT (Int. J. New Media Technol.) 2020, 7, 33–38. [Google Scholar] [CrossRef]
- Jia, X.; Baig, M.M.; Mirza, F.; GholamHosseini, H. A Cox-Based Risk Prediction Model for Early Detection of Cardiovascular Disease: Identification of Key Risk Factors for the Development of a 10-Year CVD Risk Prediction. Adv. Prev. Med. 2019, 2019, 8392348. [Google Scholar] [CrossRef]
- Brophy, J.M.; Dagenais, G.R.; McSherry, F.; Williford, W.; Yusuf, S. A multivariate model for predicting mortality in patients with heart failure and systolic dysfunction. Am. J. Med. 2004, 116, 300–304. [Google Scholar] [CrossRef]
- Liu, E.; Lim, K. Using the Weibull accelerated failure time regression model to predict time to health events. bioRxiv 2018. [Google Scholar] [CrossRef]
- Damen, J.A.A.G.; Hooft, L.; Schuit, E.; Debray, T.P.A.; Collins, G.S.; Tzoulaki, I.; Lassale, C.M.; Siontis, G.C.M.; Chiocchia, V.; Roberts, C.; et al. Prediction models for cardiovascular disease risk in the general population: Systematic review. BMJ 2016, 353, i2416. [Google Scholar] [CrossRef]
- Hsich, E.; Gorodeski, E.Z.; Blackstone, E.H.; Ishwaran, H.; Lauer, M.S. Identifying Important Risk Factors for Survival in Patient With Systolic Heart Failure Using Random Survival Forests. Circ. Cardiovasc. Qual. Outcomes 2011, 4, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Pal, M.; Parija, S.; Panda, G.; Dhama, K.; Mohapatra, R.K. Risk prediction of cardiovascular disease using machine learning classifiers. Open Med. 2022, 17, 1100–1113. [Google Scholar] [CrossRef]
- Gopal, D.P.; Usher-Smith, J.A. Cardiovascular risk models for South Asian populations: A systematic review. Int. J. Public Health 2016, 61, 525–534. [Google Scholar] [CrossRef] [PubMed]
- Zhiting, G.; Jiaying, T.; Haiying, H.; Yuping, Z.; Qunfei, Y.; Jingfen, J. Cardiovascular disease risk prediction models in the Chinese population- a systematic review and meta-analysis. BMC Public Health 2022, 22, 1608. [Google Scholar] [CrossRef] [PubMed]
- Fuller, D.; Colwell, E.; Low, J.; Orychock, K.; Tobin, M.A.; Simango, B.; Buote, R.; Van Heerden, D.; Luan, H.; Cullen, K.; et al. Reliability and Validity of Commercially Available Wearable Devices for Measuring Steps, Energy Expenditure, and Heart Rate: Systematic Review. JMIR mHealth uHealth 2020, 8, e18694. [Google Scholar] [CrossRef] [PubMed]
- Benedetto, S.; Caldato, C.; Bazzan, E.; Greenwood, D.C.; Pensabene, V.; Actis, P. Assessment of the Fitbit Charge 2 for monitoring heart rate. PLoS ONE 2018, 13, e0192691. [Google Scholar] [CrossRef]
- Sunny, J.S.; Patro, C.P.K.; Karnani, K.; Pingle, S.C.; Lin, F.; Anekoji, M.; Jones, L.D.; Kesari, S.; Ashili, S. Anomaly Detection Framework for Wearables Data: A Perspective Review on Data Concepts, Data Analysis Algorithms and Prospects. Sensors 2022, 22, 756. [Google Scholar] [CrossRef] [PubMed]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41, 15. [Google Scholar] [CrossRef]
- Wang, P.; Han, Y.; Qin, J.; Wang, B.; Yang, X. Anomaly Detection for Streaming Data from Wearable Sensor Network. In Proceedings of the 2017 IEEE 15th Intl Conf on Dependable, Autonomic and Secure Computing, 15th Intl Conf on Pervasive Intelligence and Computing, 3rd Intl Conf on Big Data Intelligence and Computing and Cyber Science and Technology Congress (DASC/PiCom/DataCom/CyberSciTech), Orlando, FL, USA, 6–10 November 2017; pp. 263–268. [Google Scholar] [CrossRef]
- Zhu, G.; Li, J.; Meng, Z.; Yu, Y.; Li, Y.; Tang, X.; Dong, Y.; Sun, G.; Zhou, R.; Wang, H.; et al. Learning from Large-Scale Wearable Device Data for Predicting the Epidemic Trend of COVID-19. Discret. Dyn. Nat. Soc. 2020, 2020, 6152041. [Google Scholar] [CrossRef]
- Perez, M.V.; Mahaffey, K.W.; Hedlin, H.; Rumsfeld, J.S.; Garcia, A.; Ferris, T.; Balasubramanian, V.; Russo, A.M.; Rajmane, A.; Cheung, L.; et al. Large-Scale Assessment of a Smartwatch to Identify Atrial Fibrillation. N. Engl. J. Med. 2019, 381, 1909–1917. [Google Scholar] [CrossRef] [PubMed]
- Staffini, A.; Svensson, T.; Chung, U.-I.; Svensson, A.K. Heart Rate Modeling and Prediction Using Autoregressive Models and Deep Learning. Sensors 2022, 22, 34. [Google Scholar] [CrossRef] [PubMed]
- Fox, K.; Borer, J.S.; Camm, A.J.; Danchin, N.; Ferrari, R.; Sendon, J.L.L.; Steg, P.G.; Tardif, J.-C.; Tavazzi, L.; Tendera, M. Resting Heart Rate in Cardiovascular Disease. J. Am. Coll. Cardiol. 2007, 50, 823–830. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Han, C.; Wang, C.; Wang, J.; Li, L.; Zhang, L.; Wang, B.; Ren, Y.; Zhang, H.; Yang, X.; et al. Association of resting heart rate and cardiovascular disease mortality in hypertensive and normotensive rural Chinese. J. Cardiol. 2017, 69, 779–784. [Google Scholar] [CrossRef] [PubMed]
- Larsson, S.C.; Drca, N.; Mason, A.M.; Burgess, S. Resting Heart Rate and Cardiovascular Disease. Circ. Genom. Precis. Med. 2019, 12, e002459. [Google Scholar] [CrossRef]
- Lee, J.; Lim, H.; Chung, K.S. CLC: Noisy Label Correction via Curriculum Learning. In Proceedings of the 2021 IEEE Symposium Series on Computational Intelligence (SSCI), Orlando, FL, USA, 5–7 December 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Priyanto, C.Y.; Hendry; Purnomo, H.D. Combination of Isolation Forest and LSTM Autoencoder for Anomaly Detection. In Proceedings of the 2021 2nd International Conference on Innovative and Creative Information Technology (ICITech), Salatiga, Indonesia, 23–25 September 2021; pp. 35–38. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar] [CrossRef]
- Lamrini, B.; Gjini, A.; Daudin, S.; Pratmarty, P.; Armando, F.; Travé-Massuyès, L. Anomaly Detection Using Similarity-based One-Class SVM for Network Traffic Characterization. In Proceedings of the 29th International Workshop on Principles of Diagnosis, Warsaw, Poland, 27–30 August 2018. [Google Scholar]
- Schölkopf, B.; Williamson, R.C.; Smola, A.; Shawe-Taylor, J.; Platt, J. Support vector method for novelty detection. Adv. Neural Inf. Process. Syst 1999, 12, 582–588. [Google Scholar]
- Henriques, J.; Caldeira, F.; Cruz, T.; Simões, P. Combining K-Means and XGBoost Models for Anomaly Detection Using Log Datasets. Electronics 2020, 9, 1164. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Xu, H.; Pang, G.; Wang, Y.; Wang, Y. Deep Isolation Forest for Anomaly Detection. arXiv 2022, arXiv:2206.06602. [Google Scholar] [CrossRef]
- Tian, Y.; Mirzabagheri, M.; Bamakan, S.M.H.; Wang, H.; Qu, Q. Ramp loss one-class support vector machine; A robust and effective approach to anomaly detection problems. Neurocomputing 2018, 310, 223–235. [Google Scholar] [CrossRef]
- Rosenberger, J.; Müller, K.; Selig, A.; Bühren, M.; Schramm, D. Extended kernel density estimation for anomaly detection in streaming data. Procedia CIRP 2022, 112, 156–161. [Google Scholar] [CrossRef]
- Sato, R.C. Disease management with ARIMA model in time series. Einstein 2013, 11, 128–131. [Google Scholar] [CrossRef]
- Zhang, R.; Song, H.; Chen, Q.; Wang, Y.; Wang, S.; Li, Y. Comparison of ARIMA and LSTM for prediction of hemorrhagic fever at different time scales in China. PLoS ONE 2022, 17, e0262009. [Google Scholar] [CrossRef]
- Kazmi, S.; Bozanta, A.; Cevik, M. Time series forecasting for patient arrivals in online health services. In Proceedings of the CASCON ‘21: Proceedings of the 31st Annual International Conference on Computer Science and Software Engineering, Toronto, ON, Canada, 22–25 November 2021; pp. 43–52.
- Moayedi, H.Z.; Masnadi-Shirazi, M.A. Arima model for network traffic prediction and anomaly detection. In Proceedings of the 2008 International Symposium on Information Technology, Kuala Lumpur, Malaysia, 26–29 August 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Pincombe, B. Anomaly detection in time series of graphs using arma processes. Asor Bull. 2005, 24, 2. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory as an Extension of the Maximum Likelihood Principle. In Second International Symposium on Information Theory; Petrov, B.N., Csaki, F., Eds.; Akademiai Kiado: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long short-term memory networks for anomaly detection in time series. In Proceedings: ESANN; Presses Universitaires de Louvain: Louvain-la-Neuve, Belgium, 2015; Volume 89, pp. 89–94. [Google Scholar]
- Nguyen, H.; Tran, K.; Thomassey, S.; Hamad, M. Forecasting and Anomaly Detection approaches using LSTM and LSTM Autoencoder techniques with the applications in supply chain management. Int. J. Inf. Manag. 2021, 57, 102282. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Morgan, N.; Nelson; Bourlard, H. Generalization and parameter estimation in feedforward nets: Some experiments. Adv. Neural Inf. Process. Syst. 1990, 2, 630–637. [Google Scholar]
- Wang, J.; He, H.; Prokhorov, D.V. A Folded Neural Network Autoencoder for Dimensionality Reduction. Procedia Comput. Sci. 2012, 13, 120–127. [Google Scholar] [CrossRef]
- Arai, H.; Chayama, Y.; Iyatomi, H.; Oishi, K. Significant Dimension Reduction of 3D Brain MRI using 3D Convolutional Autoencoders. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 5162–5165. [Google Scholar] [CrossRef]
- Shinde, K.; Itier, V.; Mennesson, J.; Vasiukov, D.; Shakoor, M. Dimensionality reduction through convolutional autoencoders for fracture patterns prediction. Appl. Math. Model. 2023, 114, 94–113. [Google Scholar] [CrossRef]
- Gogoi, M.; Begum, S.A. Image Classification Using Deep Autoencoders. In Proceedings of the 2017 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Coimbatore, India, 14–16 December 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Briciu, A.; Czibula, G.; Lupea, M. AutoAt: A deep autoencoder-based classification model for supervised authorship attribution. Procedia Comput. Sci. 2021, 192, 397–406. [Google Scholar] [CrossRef]
- Toma, R.N.; Piltan, F.; Kim, J.-M. A Deep Autoencoder-Based Convolution Neural Network Framework for Bearing Fault Classification in Induction Motors. Sensors 2021, 21, 8453. [Google Scholar] [CrossRef]
- Chen, Z.; Yeo, C.K.; Lee, B.S.; Lau, C.T. Autoencoder-based network anomaly detection. In Proceedings of the 2018 Wireless Telecommunications Symposium (WTS), Phoenix, AZ, USA, 17–20 April 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Tziolas, T.; Papageorgiou, K.; Theodosiou, T.; Papageorgiou, E.; Mastos, T.; Papadopoulos, A. Autoencoders for Anomaly Detection in an Industrial Multivariate Time Series Dataset. Eng. Proc. 2022, 18, 23. [Google Scholar] [CrossRef]
- Wei, W.; Wu, H.; Ma, H. An AutoEncoder and LSTM-Based Traffic Flow Prediction Method. Sensors 2019, 19, 2946. [Google Scholar] [CrossRef] [PubMed]
- Michelucci, U. An Introduction to Autoencoders. arXiv 2022, arXiv:2201.03898. [Google Scholar]
- Graves, A.H.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM networks. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks, Montreal, QC, Canada, 31 July–4 August 2005; Volume 4, pp. 2047–2052. [Google Scholar]
- Liu, G.; Guo, J. Bidirectional LSTM with attention mechanism and convolutional layer for text classification. Neurocomputing 2019, 337, 325–338. [Google Scholar] [CrossRef]
- Sundermeyer, M.; Alkhouli, T.; Wuebker, J.; Ney, H. Translation Modeling with Bidirectional Recurrent Neural Networks. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014; pp. 14–25. [Google Scholar] [CrossRef]
- Aljbali, S.; Roy, K. Anomaly Detection Using Bidirectional LSTM. In Intelligent Systems and Applications; Springer: Cham, Switzerland, 2021; pp. 612–619. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. Beta-vae: Learning basic visual concepts with a constrained variational framework. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Shao, H.; Yao, S.; Sun, D.; Zhang, A.; Liu, S.; Liu, D.; Wang, J.; Abdelzaher, T. ControlVAE: Controllable Variational Autoencoder. arXiv 2020, arXiv:2004.05988. [Google Scholar]
- Wan, Z.; Zhang, T.; He, H. Variational Autoencoder Based Synthetic Data Generation for Imbalanced Learning. In Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence (SSCI), Honolulu, HI, USA, 27 November–1 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Saldanha, J.; Chakraborty, S.; Patil, S.; Kotecha, K.; Kumar, S.; Nayyar, A. Data augmentation using Variational Autoencoders for improvement of respiratory disease classification. PLoS ONE 2022, 17, e0266467. [Google Scholar] [CrossRef]
- Nishizaki, H. Data augmentation and feature extraction using variational autoencoder for acoustic modelling. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur, Malaysia, 12–15 December 2017; pp. 1222–1227. [Google Scholar] [CrossRef]
- Lin, S.; Clark, R.; Birke, R.; Schonborn, S.; Trigoni, N.; Roberts, S. Anomaly Detection for Time Series Using VAE-LSTM Hybrid Model. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 4322–4326. [Google Scholar] [CrossRef]
- Zhou, L.; Deng, W.; Wu, X. Unsupervised anomaly localization using VAE and beta-VAE. arXiv 2020, arXiv:2005.10686. [Google Scholar]
- Ulger, F.; Yuksel, S.E.; Yilmaz, A. Anomaly Detection for Solder Joints Using β-VAE. IEEE Trans. Components, Packag. Manuf. Technol. 2021, 11, 2214–2221. [Google Scholar] [CrossRef]
- Chen, R.Q.; Shi, G.H.; Zhao, W.L.; Liang, C.H. Sequential VAE-LSTM for Anomaly Detection on Time Series. arXiv 2021, arXiv:1910.03818v5. [Google Scholar]
- Xu, H.; Feng, Y.; Chen, J.; Wang, Z.; Qiao, H.; Chen, W.; Zhao, N.; Li, Z.; Bu, J.; Li, Z.; et al. Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in Web Applications. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 187–196. [Google Scholar] [CrossRef]
- Palmer, C.; Harrison, G.; Hiorns, R. Association between smoking and drinking and sleep duration. Ann. Hum. Biol. 1980, 7, 103–107. [Google Scholar] [CrossRef]
- Pietilä, J.; Helander, E.; Korhonen, I.; Myllymäki, T.; Kujala, U.M.; Lindholm, H. Acute Effect of Alcohol Intake on Cardiovascular Autonomic Regulation During the First Hours of Sleep in a Large Real-World Sample of Finnish Employees: Observational Study. JMIR Ment. Health 2018, 5, e23. [Google Scholar] [CrossRef]
- Colrain, I.M.; Nicholas, C.L.; Baker, F.C. Alcohol and the sleeping brain. In Handbook of Clinical Neurology; Elsevier: Amsterdam, The Netherlands, 2014; Volume 125, pp. 415–431. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G.E. Visualizing data using t-SNE. Journal of Machine Learning Research. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Li, X.; Kiringa, I.; Yeap, T.; Zhu, X.; Li, Y. Anomaly Detection Based on Unsupervised Disentangled Representation Learning in Combination with Manifold Learning. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–10. [Google Scholar] [CrossRef]

| Participant | Age(Decade) | Sex | PastDiseases | Present Diseases | Smoking/Drinking Habits | Exercise Habits |
|---|---|---|---|---|---|---|
| Participant 1 | 40s | Male | No diseases | No diseases | Past smoker; consumes alcohol 2–4 times per month | Exercises 3 or more days per week |
| Participant 2 | 50s | Male | 2 diseases | 1 disease | Smoker; consumes alcohol 2–4 times per month | Exercises 1–2 days per week |
| Participant 3 | 30s | Male | 3 diseases | 3 diseases | Smoker; consumes alcohol 4 or more times per week | No exercise |
| Participant 4 | 30s | Female | No diseases | No diseases | Non–smoker; consumes alcohol 2–3 times per week | Exercises 1–2 days per week |
| Participant 5 | 40s | Female | 1 disease | No diseases | Non–smoker; consumes alcohol 2–4 times per month | No exercise |
| Participant 6 | 50s | Female | 1 disease | 1 disease | Non–smoker; consumes alcohol 4 or more times per week | Exercises 3 or more days per week |
| Participant 7 | 50s | Male | 3 diseases | 1 disease | Non–smoker; consumes alcohol 2–3 times per week | Exercises 1–2 days per week |
| Participant 8 | 50s | Female | 2 diseases | No diseases | Non–smoker; consumes alcohol 1 time or less per month | No exercise |
| Participant | Number of Anomalies (30 s) | Number of Anomalies (1 min) |
|---|---|---|
| Participant 1 | 33 | 17 |
| Participant 2 | 10 | 5 |
| Participant 3 | 6 | 5 |
| Participant 4 | 20 | 4 |
| Participant 5 | 21 | 18 |
| Participant 6 | 12 | 4 |
| Participant 7 | 12 | 5 |
| Participant 8 | 8 | 3 |
| Participant | Metrics | ARIMA | LSTM | CAE-LSTM | BiLSTM | β-VAE-BiLSTM |
|---|---|---|---|---|---|---|
| Participant 1 | Precision | 0.372 | 0.689 (0.073) | 0.671 (0.048) | 0.908 (0.032) | 0.949 (0.065) |
| Recall | 0.970 | 0.628 (0.013) | 0.688 (0.027) | 0.656 (0.045) | 0.715 (0.015) | |
| F1-score | 0.538 | 0.655 (0.034) | 0.678 (0.023) | 0.761 (0.031) | 0.815 (0.029) | |
| Participant 2 | Precision | 0.162 | 0.800 (0.163) | 0.812 (0.108) | 0.732 (0.080) | 0.950 (0.068) |
| Recall | 0.600 | 0.585 (0.036) | 0.575 (0.043) | 0.595 (0.022) | 0.611 (0.016) | |
| F1-score | 0.255 | 0.669 (0.063) | 0.668 (0.034) | 0.653 (0.045) | 0.742 (0.022) | |
| Participant 3 | Precision | 0.111 | 0.441 (0.199) | 0.408 (0.083) | 0.517 (0.318) | 0.625 (0.252) |
| Recall | 0.167 | 0.208 (0.072) | 0.275 (0.079) | 0.300 (0.145) | 0.400 (0.111) | |
| F1-score | 0.133 | 0.265 (0.052) | 0.315 (0.059) | 0.319 (0.105) | 0.460 (0.115) | |
| Participant 4 | Precision | 0.351 | 0.708 (0.239) | 0.875 (0.153) | 0.933 (0.220) | 0.966 (0.073) |
| Recall | 0.650 | 0.175 (0.097) | 0.200 (0.100) | 0.160 (0.110) | 0.590 (0.080) | |
| F1-score | 0.456 | 0.258 (0.156) | 0.312 (0.114) | 0.238 (0.181) | 0.727 (0.065) | |
| Participant 5 | Precision | 0.348 | 0.676 (0.120) | 0.860 (0.043) | 0.778 (0.041) | 0.915 (0.024) |
| Recall | 0.762 | 0.829 (0.038) | 0.769 (0.077) | 0.765 (0.077) | 0.817 (0.017) | |
| F1-score | 0.478 | 0.738 (0.078) | 0.809 (0.042) | 0.768 (0.044) | 0.863 (0.014) | |
| Participant 6 | Precision | 0.174 | 0.712 (0.065) | 0.760 (0.196) | 0.745 (0.160) | 0.888 (0.124) |
| Recall | 0.333 | 0.250 (0.000) | 0.250 (0.000) | 0.250 (0.000) | 0.250 (0.000) | |
| F1-score | 0.229 | 0.369 (0.010) | 0.372 (0.023) | 0.371 (0.019) | 0.389 (0.012) | |
| Participant 7 | Precision | 0.188 | 0.438 (0.006) | 0.491 (0.032) | 0.403 (0.047) | 0.747 (0.212) |
| Recall | 0.500 | 0.658 (0.069) | 0.754 (0.104) | 0.667 (0.053) | 0.767 (0.081) | |
| F1-score | 0.273 | 0.525 (0.023) | 0.591 (0.043) | 0.500 (0.036) | 0.736 (0.105) | |
| Participant 8 | Precision | 0.219 | 0.694 (0.350) | 0.843 (0.313) | 1.000 (0.000) | 1.000 (0.000) |
| Recall | 0.875 | 0.550 (0.061) | 0.462 (0.057) | 0.462 (0.057) | 0.581 (0.006) | |
| F1-score | 0.350 | 0.561 (0.180) | 0.562 (0.142) | 0.630 (0.056) | 0.733 (0.049) |
| Participant | Metrics | ARIMA | LSTM | CAE-LSTM | BiLSTM | β-VAE-BiLSTM |
|---|---|---|---|---|---|---|
| Participant 1 | Precision | 0.448 | 0.722 (0.065) | 0.610 (0.043) | 0.792 (0.166) | 0.919 (0.069) |
| Recall | 0.765 | 0.753 (0.024) | 0.741 (0.073) | 0.671 (0.073) | 0.806 (0.035) | |
| F1-score | 0.565 | 0.735 (0.035) | 0.666 (0.038) | 0.714 (0.081) | 0.857 (0.038) | |
| Participant 2 | Precision | 0.231 | 0.660 (0.073) | 0.705 (0.069) | 0.738 (0.054) | 0.938 (0.108) |
| Recall | 0.600 | 0.600 (0.000) | 0.600 (0.000) | 0.600 (0.000) | 0.600 (0.000) | |
| F1-score | 0.333 | 0.627 (0.033) | 0.647 (0.031) | 0.661 (0.026) | 0.729 (0.036) | |
| Participant 3 | Precision | 0.333 | 0.466 (0.371) | 0.268 (0.133) | 0.548 (0.303) | 0.731 (0.203) |
| Recall | 0.200 | 0.230 (0.145) | 0.400 (0.000) | 0.560 (0.332) | 0.610 (0.325) | |
| F1-score | 0.250 | 0.224 (0.186) | 0.300 (0.106) | 0.466 (0.174) | 0.611 (0.219) | |
| Participant 4 | Precision | 0.143 | 0.600 (0.184) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| Recall | 0.750 | 0.675 (0.225) | 0.540 (0.049) | 0.538 (0.089) | 0.682 (0.075) | |
| F1-score | 0.240 | 0.570 (0.249) | 0.700 (0.041) | 0.695 (0.068) | 0.809 (0.053) | |
| Participant 5 | Precision | 0.478 | 0.800 (0.200) | 0.813 (0.184) | 0.922 (0.073) | 0.933 (0.037) |
| Recall | 0.611 | 0.903 (0.133) | 0.853 (0.174) | 0.825 (0.194) | 0.872 (0.090) | |
| F1-score | 0.537 | 0.829 (0.124) | 0.805 (0.116) | 0.857 (0.116) | 0.898 (0.045) | |
| Participant 6 | Precision | 0.667 | 0.340 (0.143) | 0.850 (0.166) | 0.940 (0.092) | 0.990 (0.044) |
| Recall | 0.500 | 0.660 (0.358) | 0.500 (0.000) | 0.700 (0.245) | 0.775 (0.249) | |
| F1-score | 0.571 | 0.406 (0.216) | 0.624 (0.047) | 0.776 (0.154) | 0.847 (0.169) | |
| Participant 7 | Precision | 0.278 | 0.748 (0.042) | 0.825 (0.238) | 0.736 (0.037) | 0.980 (0.060) |
| Recall | 1.000 | 0.890 (0.099) | 0.970 (0.071) | 0.930 (0.095) | 0.960 (0.080) | |
| F1-score | 0.435 | 0.811 (0.054) | 0.870 (0.158) | 0.818 (0.038) | 0.968 (0.059) | |
| Participant 8 | Precision | 0.200 | 0.404 (0.344) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| Recall | 1.000 | 0.667 (0.000) | 0.500 (0.167) | 0.467 (0.164) | 0.667 (0.000) | |
| F1-score | 0.333 | 0.436 (0.211) | 0.650 (0.150) | 0.620 (0.147) | 0.800 (0.000) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staffini, A.; Svensson, T.; Chung, U.-i.; Svensson, A.K. A Disentangled VAE-BiLSTM Model for Heart Rate Anomaly Detection. Bioengineering 2023, 10, 683. https://doi.org/10.3390/bioengineering10060683
Staffini A, Svensson T, Chung U-i, Svensson AK. A Disentangled VAE-BiLSTM Model for Heart Rate Anomaly Detection. Bioengineering. 2023; 10(6):683. https://doi.org/10.3390/bioengineering10060683
Chicago/Turabian StyleStaffini, Alessio, Thomas Svensson, Ung-il Chung, and Akiko Kishi Svensson. 2023. "A Disentangled VAE-BiLSTM Model for Heart Rate Anomaly Detection" Bioengineering 10, no. 6: 683. https://doi.org/10.3390/bioengineering10060683
APA StyleStaffini, A., Svensson, T., Chung, U.-i., & Svensson, A. K. (2023). A Disentangled VAE-BiLSTM Model for Heart Rate Anomaly Detection. Bioengineering, 10(6), 683. https://doi.org/10.3390/bioengineering10060683








