Prediction of Metabolic Flux Distribution by Flux Sampling: As a Case Study, Acetate Production from Glucose in Escherichia coli
Abstract
1. Introduction
2. Materials and Methods
2.1. Metabolic Model
2.2. Flux Sampling
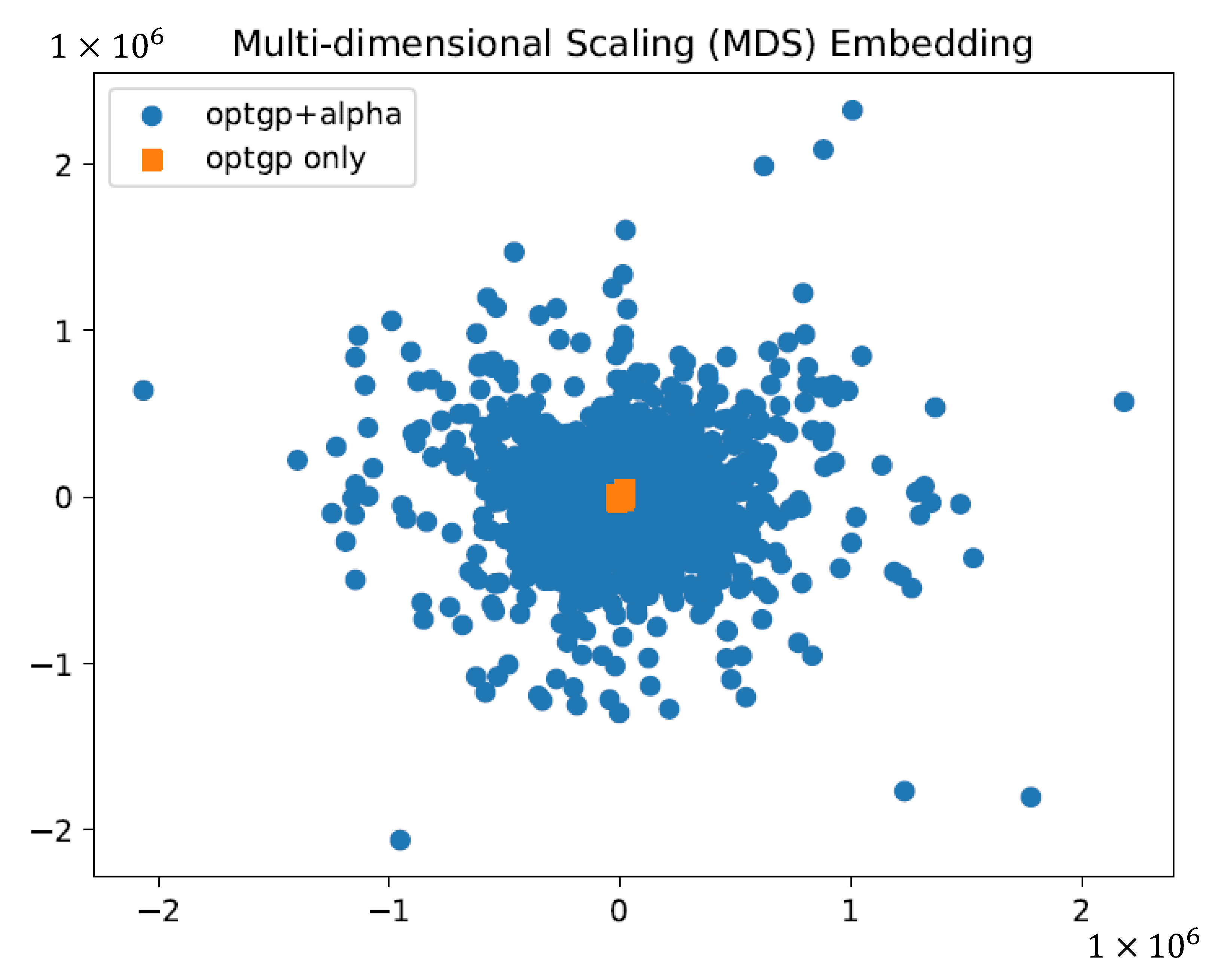
2.3. Verification of the Effect of Using Constraints on Sampling by Dimensional Compression
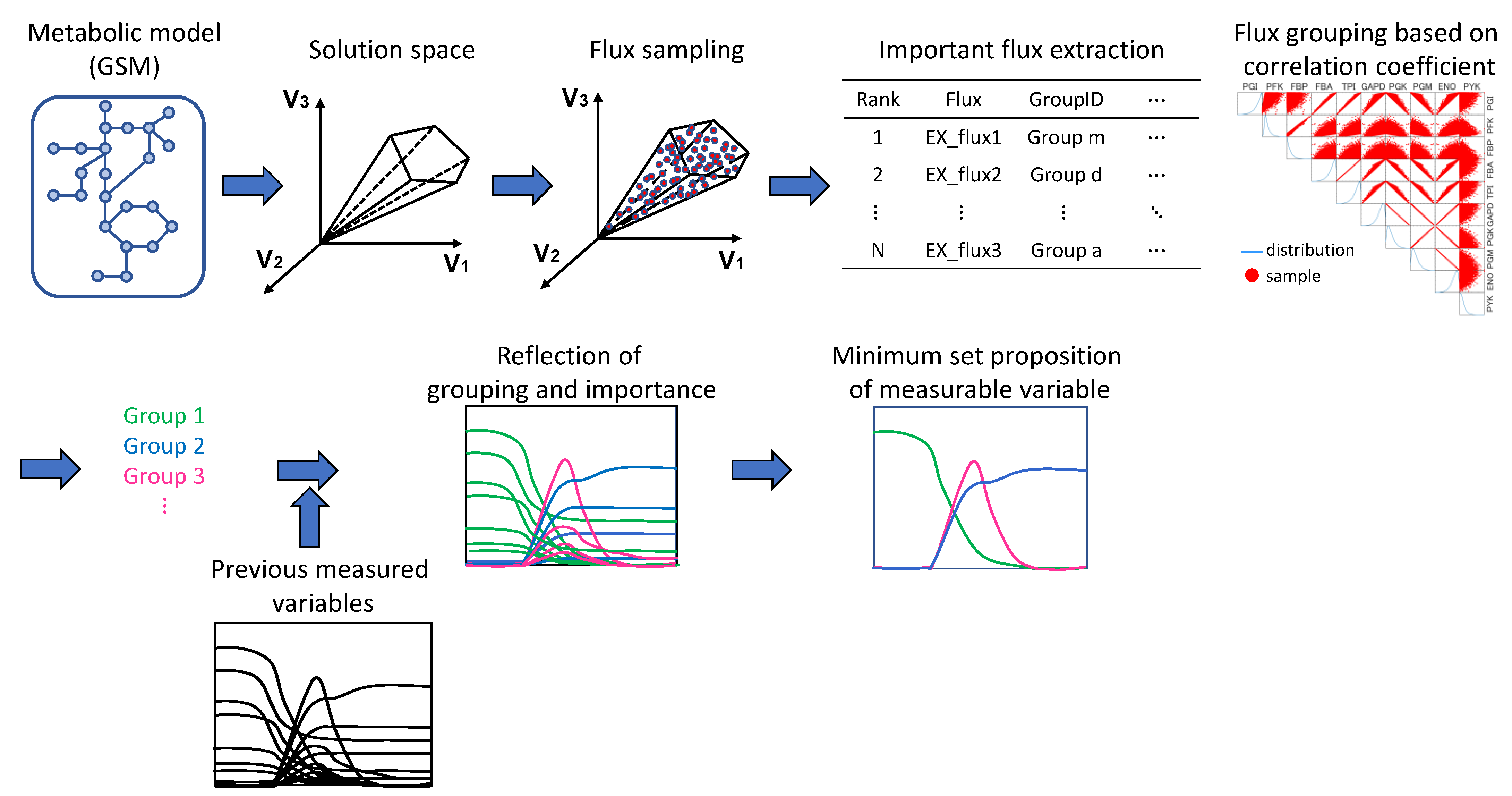
2.4. Search and Evaluation of Fluxes and Combinations of Fluxes Important for Metabolic Flux Distribution Prediction
2.5. Validation of Important Flux
2.6. Computer Code and Software
3. Results
3.1. Creating Constraints for Flux Sampling
3.2. Flux Sampling
3.3. Exploration and Evaluation of Fluxes and Combinations of Fluxes Important for Flux Distribution Prediction
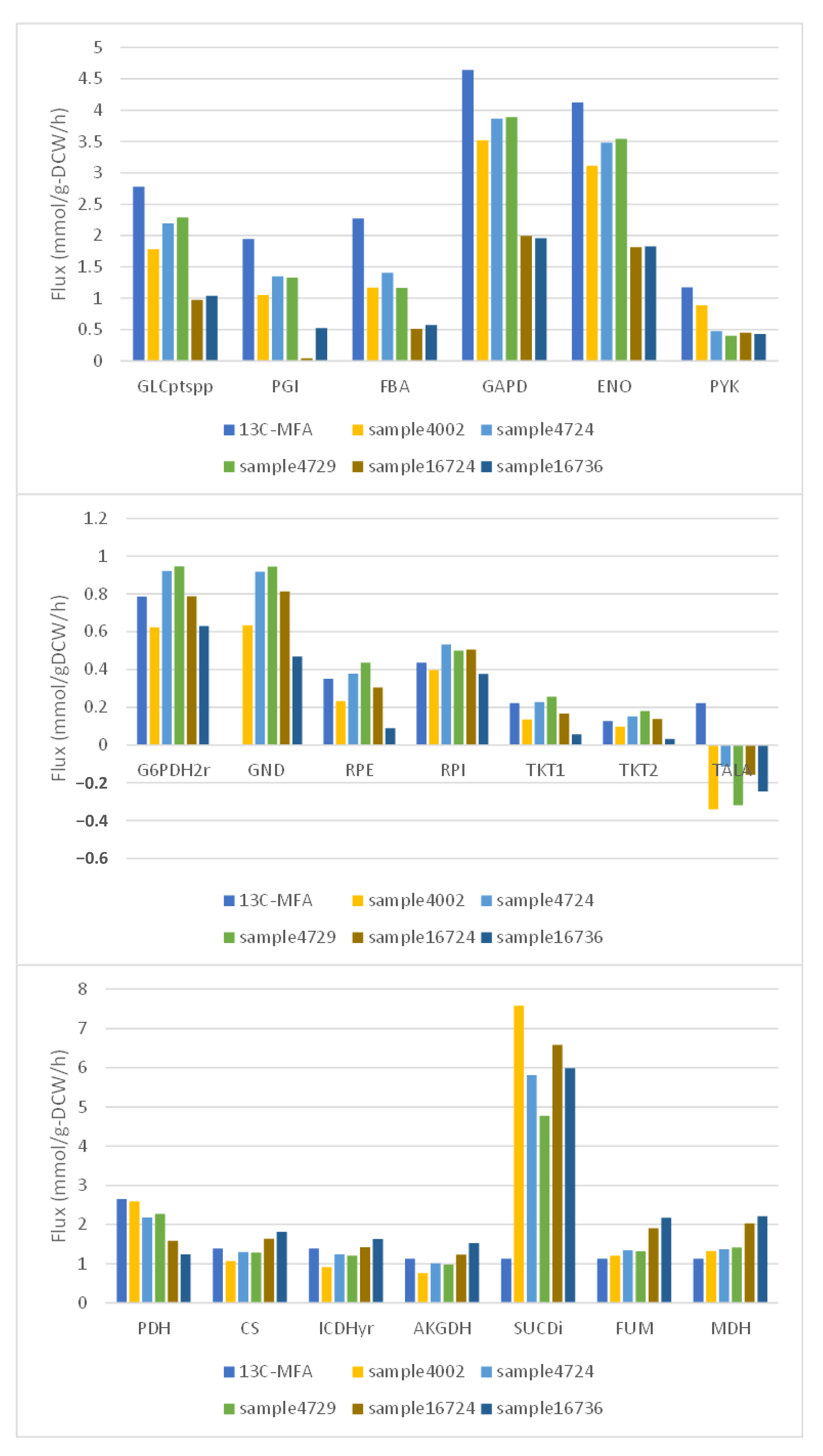
3.4. Validation of Important Flux
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bordbar, A.; Yurkovich, J.T.; Paglia, G.; Rolfsson, O.; Sigurjónsson, Ó.E.; Palsson, B.O. Elucidating dynamic metabolic physiology through network integration of quantitative time-course metabolomics. Sci. Rep. 2017, 7, 46249. [Google Scholar] [CrossRef]
- Beal, L.D.R.; Hill, D.C.; Martin, R.A.; Hedengren, J.D. GEKKO Optimization Suite. Processes 2018, 6, 106. [Google Scholar] [CrossRef]
- Kamsen, R.; Kalapanulak, S.; Chiewchankaset, P.; Saithong, T. Transcriptome integrated metabolic modeling of carbon assimilation underlying storage root development in cassava. Sci. Rep. 2021, 11, 8758. [Google Scholar] [CrossRef]
- Di Filippo, M.; Pescini, D.; Galuzzi, B.G.; Bonanomi, M.; Gaglio, D.; Mangano, E.; Consolandi, C.; Alberghina, L.; Vanoni, M.; Damiani, C. INTEGRATE: Model-based multi-omics data integration to characterize multi-level metabolic regulation. PLoS Comput. Biol. 2022, 18, e1009337. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Shimizu, K. Metabolic flux analysis of Escherichia coli K12 grown on 13C-labeled acetate and glucose using GC-MS and powerful flux calculation method. J. Biotechnol. 2003, 101, 101–117. [Google Scholar] [CrossRef] [PubMed]
- Ishii, N.; Nakahigashi, K.; Baba, T.; Robert, M.; Soga, T.; Kanai, A.; Hirasawa, T.; Naba, M.; Hirai, K.; Hoque, A.; et al. Multiple high-throughput analyses monitor the response of E. coli to perturbations. Science 2007, 316, 593–597. [Google Scholar] [CrossRef] [PubMed]
- Toya, Y.; Ishii, N.; Nakahigashi, K.; Hirasawa, T.; Soga, T.; Tomita, M.; Shimizu, K. 13C-metabolic flux analysis for batch culture of Escherichia coli and its Pyk and Pgi gene knockout mutants based on mass isotopomer distribution of intracellular metabolites. Biotechnol. Prog. 2010, 26, 975–992. [Google Scholar] [CrossRef]
- Maeda, K.; Okahashi, N.; Toya, Y.; Matsuda, F.; Shimizu, H. Investigation of useful carbon tracers for 13C-metabolic flux analysis of Escherichia coli by considering five experimentally determined flux distributions. Metab. Eng. Commun. 2016, 3, 187–195. [Google Scholar] [CrossRef]
- Okahashi, N.; Kajihata, S.; Furusawa, C.; Shimizu, H. Reliable Metabolic Flux Estimation in Escherichia coli Central Carbon Metabolism Using Intracellular Free Amino Acids. Metabolites 2014, 4, 408–420. [Google Scholar] [CrossRef]
- Crown, S.B.; Long, C.P.; Antoniewicz, M.R. Integrated 13C-metabolic flux analysis of 14 parallel labeling experiments in Escherichia coli. Metab. Eng. 2015, 28, 151–158. [Google Scholar] [CrossRef]
- Van Dien, S.; Iwatani, S.; Usuda, Y.; Matsui, K.; Ueda, T.; Tsuji, Y. Method for Determining Metabolic Flux Affecting Substance Production. U.S. Patent 7,809,511 B2, 5 October 2010. [Google Scholar]
- Klamt, S.; Schuster, S. Calculating as many fluxes as possible in underdetermined metabolic networks. Mol. Biol. Rep. 2002, 29, 243–248. [Google Scholar] [CrossRef]
- Bogaerts, P.; Vande Wouwer, A. How to Tackle Underdeterminacy in Metabolic Flux Analysis? A Tutorial and Critical Review. Processes 2021, 9, 1577. [Google Scholar] [CrossRef]
- Fallahi, S.; Skaug, H.J.; Alendal, G. A comparison of Monte Carlo sampling methods for metabolic network models. PLoS ONE 2020, 15, e0235393. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, D.E.; Smith, R.L. Direction choice for accelerated convergence in hit-and-run sampling. Oper. Res. 1998, 46, 84–95. [Google Scholar] [CrossRef]
- Haraldsdottir, H.S.; Cousins, B.; Thiele, I.; Fleming, R.M.T.; Vempala, S. CHRR: Coordinate hit-and-run with rounding for uniform sampling of constraint-based models. Bioinformatics 2017, 33, 1741–1743. [Google Scholar] [CrossRef] [PubMed]
- Megchelenbrink, W.; Huynen, M.; Marchiori, E. optGpSampler: An improved tool for uniformly sampling the solution-space of genome-scale metabolic networks. PLoS ONE 2014, 9, e86587. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Burgard, A.P.; Vaidyaraman, S.; Maranas, C.D. Minimal reaction sets for Escherichia coli metabolism under different growth requirements and uptake environments. Biotechnol. Prog. 2001, 17, 791–797. [Google Scholar] [CrossRef]
- Herrmann, H.A.; Dyson, B.C.; Vass, L.; Johnson, G.N.; Schwartz, J.M. Flux sampling is a powerful tool to study metabolism under changing environmental conditions. npj Syst. Biol. Appl. 2019, 5, 32. [Google Scholar] [CrossRef]
- Scott, W.T.; Smid, E.J.; Block, D.E.; Notebaart, R.A. Metabolic flux sampling predicts strain-dependent differences related to aroma production among commercial wine yeasts. Microb. Cell Fact. 2021, 20, 204. [Google Scholar] [CrossRef]
- Orth, J.D.; Conrad, T.M.; Na, J.; Lerman, J.A.; Nam, H.; Feist, A.M.; Palsson, B.Ø. A comprehensive genome-scale reconstruction of Escherichia coli metabolism—2011. Mol. Syst. Biol. 2011, 7, 535. [Google Scholar] [CrossRef]
- Ebrahim, A.; Lerman, J.A.; Palsson, B.Ø.; Hyduke, D.R. COBRApy: COnstraints-Based Reconstruction and Analysis for Python. BMC Syst. Biol. 2013, 7, 74. [Google Scholar] [CrossRef]
- Mugavin, M.E. Multidimensional scaling: A brief overview. Nurs. Res. 2008, 57, 64–68. [Google Scholar] [CrossRef] [PubMed]
- Beyß, M.; Azzouzi, S.; Weitzel, M.; Wiechert, W.; Nöh, K. The Design of FluxML: A Universal Modeling Language for 13C Metabolic Flux Analysis. Front. Microbiol. 2019, 10, 1022. [Google Scholar] [CrossRef] [PubMed]
- Chalkis, A.; Fisikopoulos, V. Volesti: Volume Approximation and Sampling for Convex Polytopes in R. arXiv 2020, arXiv:2007.01578. [Google Scholar] [CrossRef]
- Chevallier, A.; Cazals, F.; Fearnhead, P. Efficient Computation of the Volume of a Polytope in High-Dimensions Using Piecewise Deterministic Markov Processes. In Proceedings of the 25th International Conference on Artificial Intelligence and Statistics, Virtual, 28–30 March 2022; Volume 151, pp. 10146–10160. Available online: https://proceedings.mlr.press/v151/chevallier22a.html (accessed on 12 April 2023).
- Hubbard, J.A.; Lewandowska, K.B.; Hughes, M.N.; Poole, R.K. Effects of iron-limitation of Escherichia coli on growth, the respiratory chains and gallium uptake. Arch. Microbiol. 1986, 146, 80–86. [Google Scholar] [CrossRef]
- Pourciau, C.; Pannuri, A.; Potts, A.; Yakhnin, H.; Babitzke, P.; Romeo, T. Regulation of Iron Storage by CsrA Supports Ex-ponential Growth of Escherichia coli. mBio 2019, 10, e01034-19. [Google Scholar] [CrossRef] [PubMed]
- Gerken, H.; Vuong, P.; Soparkar, K.; Misra, R. Roles of the EnvZ/OmpR Two-Component System and Porins in Iron Acquisition in Escherichia coli. mBio 2020, 11, e01192-20. [Google Scholar] [CrossRef] [PubMed]

| Rank | Flux Name | Group ID | Flux ID | Sol. Num. (Ave.) 1 | Sol. Num. (Med.) 2 |
|---|---|---|---|---|---|
| 1 | EX_fe2_e | 11 | 127 | 1.3685 | 1 |
| 2 | EX_fe3_e | 11 | 128 | 1.3763 | 1 |
| 3 | EX_h_e | 11 | 185 | 1.3768 | 1 |
| 4 | EX_h2o_e | 11 | 187 | 1.742 | 2 |
| 5 | EX_o2_e | 11 | 252 | 2.4766 | 2 |
| 6 | EX_co2_e | 30 | 85 | 11.355 | 10 |
| 7 | EX_nh4_e | 2 | 244 | 33.095 | 32 |
| 8 | EX_glc__D_e | 457 | 164 | 40.319 | 40 |
| 9 | EX_ac_e | 452 | 36 | 49.47 | 40 |
| 10 | EX_pi_e | 2 | 263 | 364.97 | 337 |
| Sample ID | Sample4002 | Sample4724 | Sample4729 | Sample16724 | Sample16736 |
|---|---|---|---|---|---|
| MAPE 1 | 83.8828 | 54.1644 | 57.1455 | 77.5504 | 88.2746 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuriya, Y.; Murata, M.; Yamamoto, M.; Watanabe, N.; Araki, M. Prediction of Metabolic Flux Distribution by Flux Sampling: As a Case Study, Acetate Production from Glucose in Escherichia coli. Bioengineering 2023, 10, 636. https://doi.org/10.3390/bioengineering10060636
Kuriya Y, Murata M, Yamamoto M, Watanabe N, Araki M. Prediction of Metabolic Flux Distribution by Flux Sampling: As a Case Study, Acetate Production from Glucose in Escherichia coli. Bioengineering. 2023; 10(6):636. https://doi.org/10.3390/bioengineering10060636
Chicago/Turabian StyleKuriya, Yuki, Masahiro Murata, Masaki Yamamoto, Naoki Watanabe, and Michihiro Araki. 2023. "Prediction of Metabolic Flux Distribution by Flux Sampling: As a Case Study, Acetate Production from Glucose in Escherichia coli" Bioengineering 10, no. 6: 636. https://doi.org/10.3390/bioengineering10060636
APA StyleKuriya, Y., Murata, M., Yamamoto, M., Watanabe, N., & Araki, M. (2023). Prediction of Metabolic Flux Distribution by Flux Sampling: As a Case Study, Acetate Production from Glucose in Escherichia coli. Bioengineering, 10(6), 636. https://doi.org/10.3390/bioengineering10060636





