Pre-Planning the Surgical Target for Optimal Implant Positioning in Robotic-Assisted Total Knee Arthroplasty
Abstract
1. Introduction
2. Materials and Methods
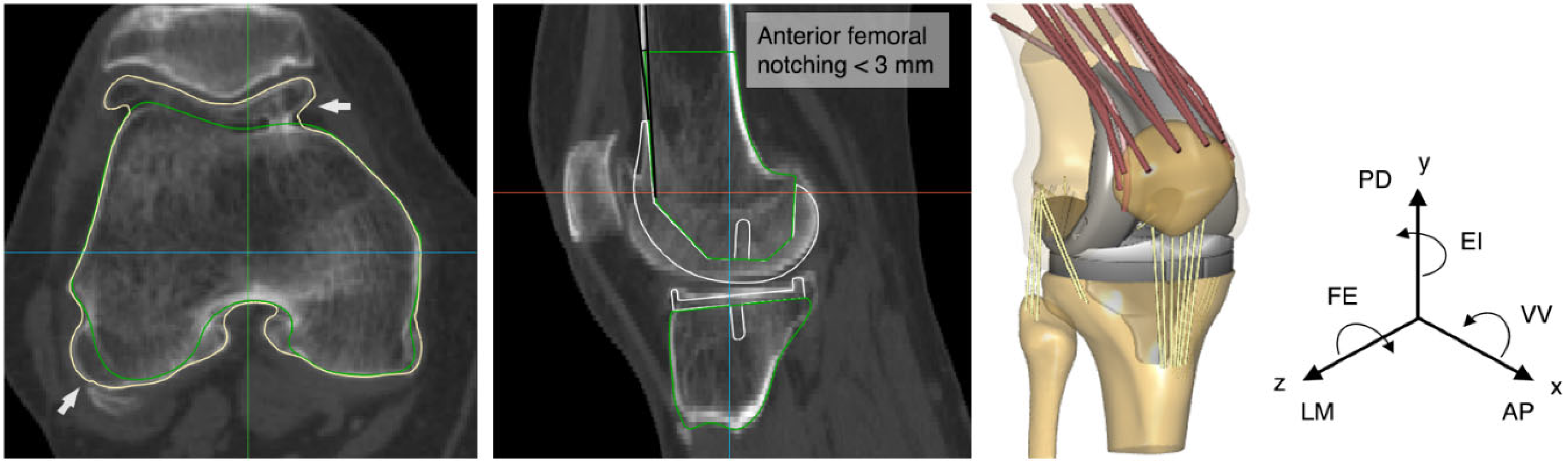
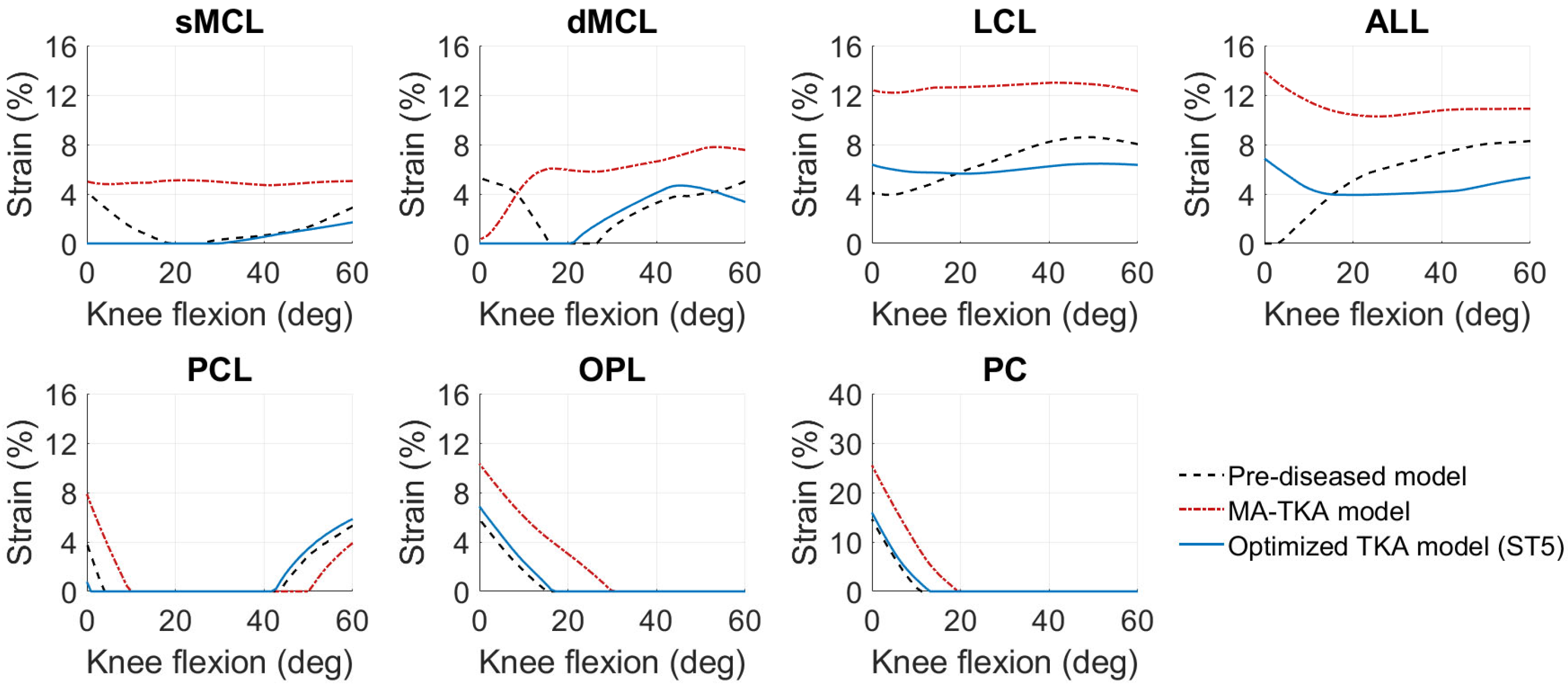
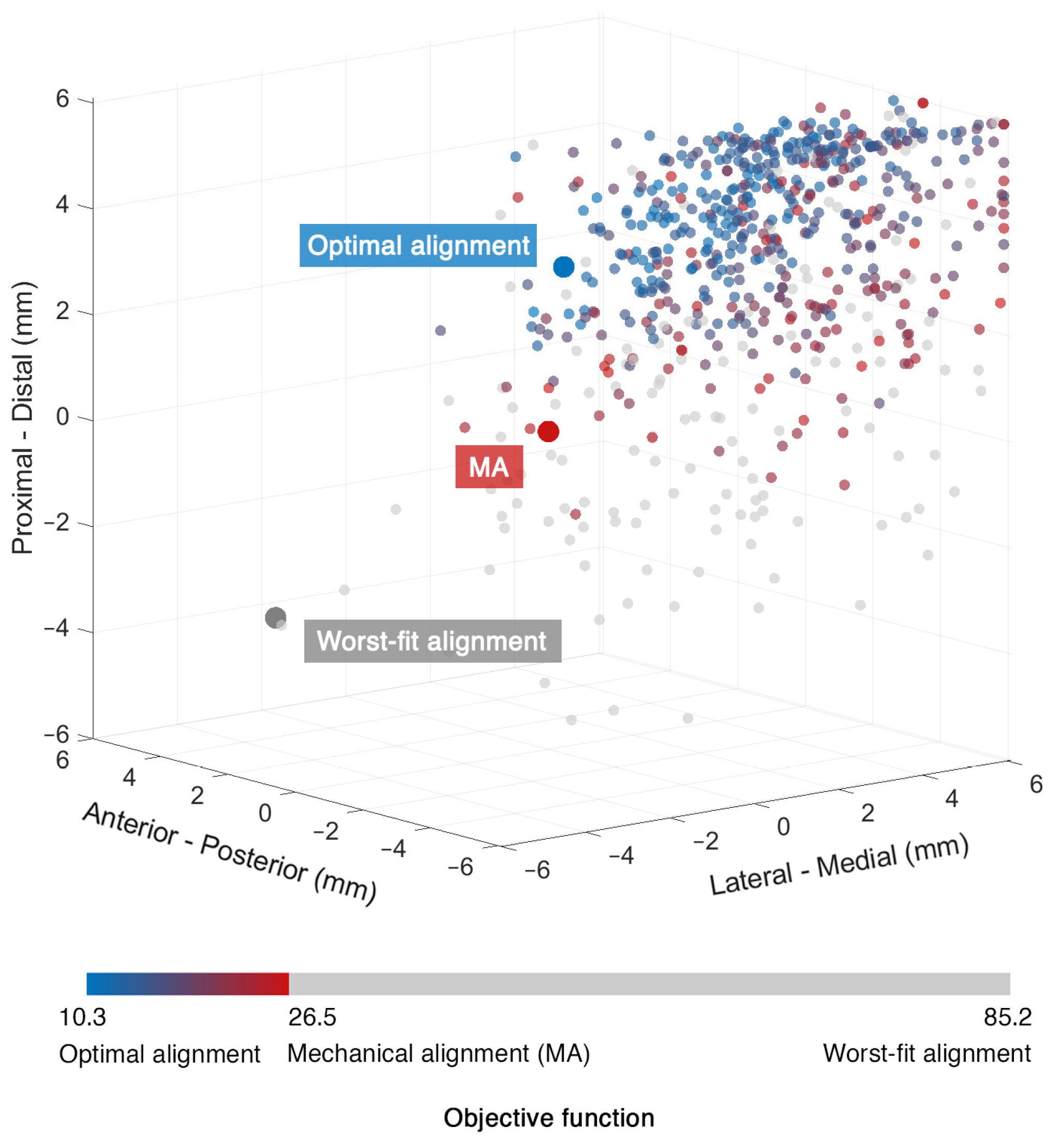
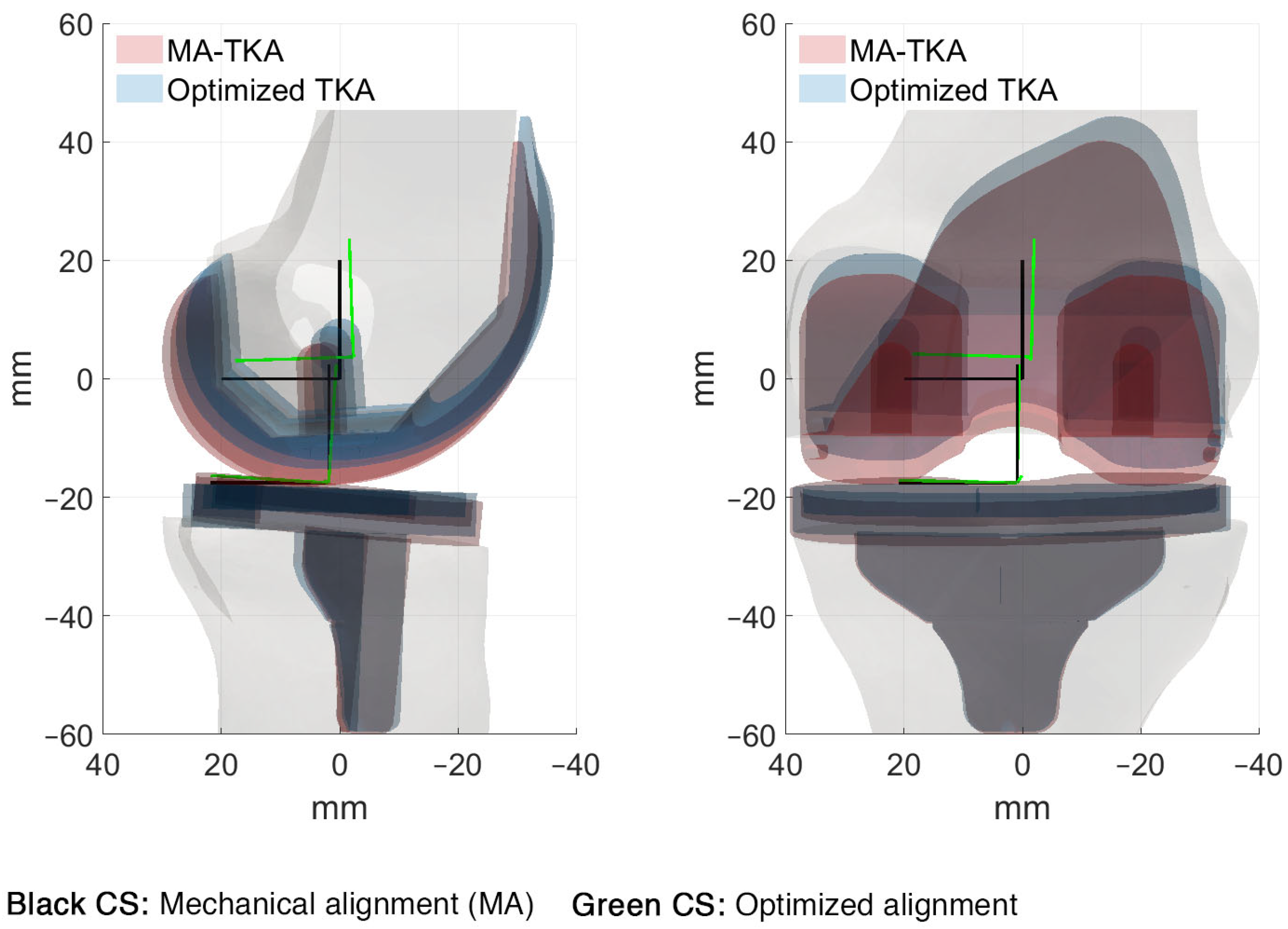
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sikorski, J.M. Alignment in total knee replacement. J. Bone Jt. Surg. Br. 2008, 90, 1121–1127. [Google Scholar] [CrossRef] [PubMed]
- Thompson, J.A.; Hast, M.W.; Granger, J.F.; Piazza, S.J.; Siston, R.A. Biomechanical effects of total knee arthroplasty component malrotation: A computational simulation. J. Orthop. Res. 2011, 29, 969–975. [Google Scholar] [CrossRef] [PubMed]
- Fehring, T.K. Rotational malalignment of the femoral component in total knee arthroplasty. Clin. Orthop. Relat. Res. 2000, 380, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Kuriyama, S.; Ishikawa, M.; Furu, M.; Ito, H.; Matsuda, S. Malrotated tibial component increases medial collateral ligament tension in total knee arthroplasty. J. Orthop. Res. 2014, 32, 1658–1666. [Google Scholar] [CrossRef] [PubMed]
- Steinbrück, A.; Fottner, A.; Schröder, C.; Woiczinski, M.; Schmitt-Sody, M.; Müller, T.; Müller, P.E.; Jansson, V. Influence of mediolateral tibial baseplate position in TKA on knee kinematics and retropatellar pressure. Knee Surg. Sports Traumatol. Arthrosc. 2017, 25, 2602–2608. [Google Scholar] [CrossRef]
- Kayani, B.; Konan, S.; Ayuob, A.; Onochie, E.; Al-Jabri, T.; Haddad, F.S. Robotic technology in total knee arthroplasty: A systematic review. EFORT Open Rev. 2019, 4, 611–617. [Google Scholar] [CrossRef]
- Song, E.K.; Seon, J.K.; Yim, J.H.; Netravali, N.A.; Bargar, W.L. Robotic-assisted TKA reduces postoperative alignment outliers and improves gap balance compared to conventional TKA knee. Clin. Orthop. Relat. Res. 2013, 471, 118–126. [Google Scholar] [CrossRef]
- Kayani, B.; Konan, S.; Pietrzak, J.R.T.; Haddad, F.S. Iatrogenic bone and soft tissue trauma in robotic-arm assisted total knee arthroplasty compared with conventional jig-based total knee arthroplasty: A prospective cohort study and validation of a new classification system. J. Arthroplast. 2018, 33, 2496–2501. [Google Scholar] [CrossRef]
- Khlopas, A.; Chughtai, M.; Hampp, E.L.; Scholl, L.Y.; Prieto, M.; Chang, T.-C.; Abbas, A.; Bhowmik-Stoker, M.; Otto, J.; Jacofsky, D.J.; et al. Robotic-arm assisted total knee arthroplasty demonstrated soft tissue protection. Surg. Technol. Int. 2017, 30, 441–446. [Google Scholar] [PubMed]
- Hampp, E.L.; Chughtai, M.; Scholl, L.Y.; Sodhi, N.; Bhowmik-Stoker, M.; Jacofsky, D.J.; Mont, M.A. Robotic-arm assisted total knee arthroplasty demonstrated greater accuracy and precision to plan compared with manual techniques. J. Knee Surg. 2019, 32, 239–250. [Google Scholar] [CrossRef]
- Sires, J.D.; Craik, J.D.; Wilson, C.J. Accuracy of bone resection in MAKO total knee robotic-assisted surgery. J. Knee Surg. 2021, 34, 745–748. [Google Scholar] [CrossRef] [PubMed]
- Ollivier, M.; Parratte, S.; Lino, L.; Flecher, X.; Pesenti, S.; Argenson, J.N. No benefit of computer-assisted TKA: 10-year results of a prospective randomized study. Clin. Orthop. Relat. Res. 2018, 476, 126–134. [Google Scholar] [CrossRef] [PubMed]
- Cherian, J.J.; Kapadia, B.H.; Banerjee, S.; Jauregui, J.J.; Issa, K.; Mont, M.A. Mechanical, anatomical, and kinematic axis in TKA: Concepts and practical applications. Curr. Rev. Musculoskelet. Med. 2014, 7, 89–95. [Google Scholar] [CrossRef] [PubMed]
- Berend, M.E.; Ritter, M.A.; Meding, J.B.; Faris, P.M.; Keating, E.M.; Redelman, R.; Faris, G.W.; Davis, K.E. Tibial component failure mechanisms in total knee arthroplasty. Clin. Orthop. Relat. Res. 2004, 428, 26–34. [Google Scholar] [CrossRef]
- Bellemans, J.; Colyn, W.; Vandenneucker, H.; Victor, J. The Chitranjan Ranawat Award: Is neutral mechanical alignment normal for all patients?: The concept of constitutional varus. Clin. Orthop. Relat. Res. 2012, 470, 45–53. [Google Scholar] [CrossRef]
- Rivière, C.; Villet, L.; Jeremic, D.; Vendittoli, P.A. What you need to know about kinematic alignment for total knee arthroplasty. Orthop. Traumatol. Surg. Res. 2021, 107, 4–6. [Google Scholar] [CrossRef]
- Shatrov, J.; Batailler, C.; Sappey-Marinier, E.; Gunst, S.; Servien, E.; Lustig, S. Kinematic alignment fails to achieve balancing in 50% of varus knees and resects more bone compared to functional alignment. Knee Surg. Sports Traumatol. Arthrosc. 2022, 30, 2991–2999. [Google Scholar] [CrossRef]
- Lee, G.C.; Wakelin, E.; Plaskos, C. What is the alignment and balance of a total knee arthroplasty performed using a calipered kinematic alignment technique? J. Arthroplast. 2022, 37, 176–181. [Google Scholar] [CrossRef]
- Chang, J.S.; Kayani, B.; Haddad, F.S.; Wallace, C. Functional alignment achieves soft-tissue balance in total knee arthroplasty as measured with quantitative sensor-guided technology. Bone Jt. J. 2021, 103-B, 507–514. [Google Scholar] [CrossRef]
- Clark, G.; Steer, R.; Wood, D. Functional alignment achieves a more balanced total knee arthroplasty than either mechanical alignment or kinematic alignment prior to soft tissue releases. Knee Surg. Sports Traumatol. Arthrosc. 2022, 31, 1420–1426. [Google Scholar] [CrossRef]
- Tzanetis, P.; De Souza, K.; Robertson, S.; Fluit, R.; Koopman, B.; Verdonschot, N. Numerical study of osteophyte effects on pre-operative knee functionality in patients undergoing robotic-assisted total knee arthroplasty. J. Orthop. Res. 2022; submitted. [Google Scholar]
- Marra, M.A.; Vanheule, V.; Fluit, R.; Koopman, B.H.F.J.M.; Rasmussen, J.; Verdonschot, N.; Andersen, M.S. A subject-specific musculoskeletal modeling framework to predict in vivo mechanics of total knee arthroplasty. J. Biomech. Eng. 2015, 137, 020904. [Google Scholar] [CrossRef]
- Oussedik, S.; Scholes, C.; Ferguson, D.; Roe, J.; Parker, D. Is femoral component rotation in a TKA reliably guided by the functional flexion axis? Clin. Orthop. Relat. Res. 2012, 470, 3227–3232. [Google Scholar] [CrossRef]
- Bowes, M.A.; Kacena, K.; Alabas, O.A.; Brett, A.D.; Dube, B.; Bodick, N.; Conaghan, P.G. Machine-learning, MRI bone shape and important clinical outcomes in osteoarthritis: Data from the Osteoarthritis Initiative. Ann. Rheum. Dis. 2021, 80, 502–508. [Google Scholar] [CrossRef]
- Motesharei, A.; Batailler, C.; De Massari, D.; Vincent, G.; Chen, A.F.; Lustig, S.; Batailler, C. Predicting robotic-assisted total knee arthroplasty operating time: Benefits of machine-learning and 3D patient-specific data. Bone Jt. Open 2022, 3, 383–389. [Google Scholar] [CrossRef]
- Brett, A.; Bowes, M.A.; Conaghan, P.G. Comparison of 3D quantitative osteoarthritis imaging biomarkers from paired CT and MR images: Data from the IMI-APPROACH study. BMC Musculoskelet. Disord. 2023, 24, 76. [Google Scholar] [CrossRef]
- Carbone, V.; Fluit, R.; Pellikaan, P.; van der Krogt, M.M.; Janssen, D.; Damsgaard, M.; Vigneron, L.; Feilkas, T.; Koopman, H.F.J.M.; Verdonschot, N. TLEM 2.0—A comprehensive musculoskeletal geometry dataset for subject-specific modeling of lower extremity. J. Biomech. 2015, 48, 734–741. [Google Scholar] [CrossRef]
- Hunter, D.J.; Bowes, M.A.; Eaton, C.B.; Holmes, A.P.; Mann, H.; Kwoh, C.K.; Maciewicz, R.A.; Samuels, J.; Waterton, J.C. Can cartilage loss be detected in knee osteoarthritis (OA) patients with 3–6 months’ observation using advanced image analysis of 3T MRI? Osteoarthr. Cartil. 2010, 18, 677–683. [Google Scholar] [CrossRef]
- Tzanetis, P.; Marra, M.A.; Fluit, R.; Koopman, B.; Verdonschot, N. Biomechanical consequences of tibial insert thickness after total knee arthroplasty: A musculoskeletal simulation study. Appl. Sci. 2021, 11, 2423. [Google Scholar] [CrossRef]
- Grood, E.S.; Suntay, W.J. A joint coordinate system for the clinical description of three-dimensional motions: Application to the knee. J. Biomech. Eng. 1983, 105, 136–144. [Google Scholar] [CrossRef]
- Dejtiar, D.L.; Bartsoen, L.; Wesseling, M.; Wirix-Speetjens, R.; Sloten, J.V.; Perez, M.A. Standard cruciate-retaining total knee arthroplasy implants can reproduce native kinematics. EPiC Ser. Health Sci. 2020, 4, 61–64. [Google Scholar] [CrossRef]
- Bartsoen, L.; Faes, M.G.R.; Wirix-Speetjens, R.; Moens, D.; Jonkers, I.; Sloten, J.V. Probabilistic planning for ligament-balanced TKA—Identification of critical ligament properties. Front. Bioeng. Biotechnol. 2022, 10, 930724. [Google Scholar] [CrossRef] [PubMed]
- Quilez, M.P.; Delport, H.P.; Wirix-Speetjens, R.; Wesseling, M.; Perez, M.A.; Jonkers, I.; Sloten, J.V. Can standard implants reproduce the native kinematics of a TKA patient? EPiC Ser. Health Sci. 2019, 3, 311–314. [Google Scholar] [CrossRef]
- Zalzal, P.; Backstein, D.; Gross, A.E.; Papini, M. Notching of the anterior femoral cortex during total knee arthroplasty. Characteristics that increase local stresses. J. Arthroplast. 2006, 21, 737–743. [Google Scholar] [CrossRef]
- Stamiris, D.; Gkekas, N.K.; Asteriadis, K.; Stamiris, S.; Anagnostis, P.; Poultsides, L.; Sarris, I.; Potoupnis, M.; Kenanidis, E.; Tsiridis, E. Anterior femoral notching ≥ 3 mm is associated with increased risk for supracondylar periprosthetic femoral fracture after total knee arthroplasty: A systematic review and meta-analysis. Eur. J. Orthop. Surg. Traumatol. 2022, 32, 383–393. [Google Scholar] [CrossRef]
- Andersen, M.S.; De Zee, M.; Damsgaard, M.; Nolte, D.; Rasmussen, J. Introduction to force-dependent kinematics: Theory and application to mandible modeling. J. Biomech. Eng. 2017, 139, 091001. [Google Scholar] [CrossRef]
- Cavaignac, E.; Carpentier, K.; Pailhé, R.; Luyckx, T.; Bellemans, J. The role of the deep medial collateral ligament in controlling rotational stability of the knee. Knee Surg. Sports Traumatol. Arthrosc. 2015, 23, 3101–3107. [Google Scholar] [CrossRef]
- Völlner, F.; Herl, F.; Greimel, F.; Benditz, A.; Renkawitz, T.; Grifka, J.; Craiovan, B.; Weber, M. The effects of soft tissue lateral release on the stability of the ligament complex of the knee. Arch. Orthop. Trauma Surg. 2020, 140, 933–940. [Google Scholar] [CrossRef]
- Provenzano, P.P.; Heisey, D.; Hayashi, K.; Lakesand, R.; Vanderby, R. Subfailure damage in ligament: A structural and cellular evaluation. J. Appl. Physiol. 2002, 92, 362–371. [Google Scholar] [CrossRef]
- Hansen, N. The CMA evolution strategy: A comparing review. Stud. Fuzziness Soft Comput. 2006, 192, 75–102. [Google Scholar] [CrossRef]
- Schelker, B.L.; Nowakowski, A.M.; Hirschmann, M.T. What is the “safe zone” for transition of coronal alignment from systematic to a more personalised one in total knee arthroplasty? A systematic review. Knee Surg. Sports Traumatol. Arthrosc. 2022, 30, 419–427. [Google Scholar] [CrossRef]
- Delport, H.; Labey, L.; Innocenti, B.; De Corte, R.; Sloten, J.V.; Bellemans, J. Restoration of constitutional alignment in TKA leads to more physiological strains in the collateral ligaments. Knee Surg. Sports Traumatol. Arthrosc. 2015, 23, 2159–2169. [Google Scholar] [CrossRef]
- Vincent, J.P.; Magnussen, R.A.; Gezmez, F.; Uguen, A.; Jacobi, M.; Weppe, F.; Al-Saati, M.F.; Lustig, S.; Demey, G.; Servien, E.; et al. The anterolateral ligament of the human knee: An anatomic and histologic study. Knee Surg. Sports Traumatol. Arthrosc. 2012, 20, 147–152. [Google Scholar] [CrossRef]
- Willinger, L.; Shinohara, S.; Athwal, K.K.; Ball, S.; Williams, A.; Amis, A.A. Length-change patterns of the medial collateral ligament and posterior oblique ligament in relation to their function and surgery. Knee Surg. Sports Traumatol. Arthrosc. 2020, 28, 3720–3732. [Google Scholar] [CrossRef]
- Su, E.P. Fixed flexion deformity and total knee arthroplasty. J. Bone Jt. Surg. Br. 2012, 94, 112–115. [Google Scholar] [CrossRef]
- Butler, D.; Kay, M.; Stouffer, D. Fascicle-bone units from human patellar tendon and knee ligaments. J. Biomech. 1986, 19, 425–432. [Google Scholar] [CrossRef]
- Rachmat, H.H.; Janssen, D.; Verkerke, G.J.; Diercks, R.L.; Verdonschot, N. Material properties of the human posterior knee capsule. Biomed. Mater. Eng. 2015, 25, 177–187. [Google Scholar] [CrossRef]
- Marra, M.A.; Strzelczak, M.; Heesterbeek, P.J.C.; van de Groes, S.A.W.; Janssen, D.W.; Koopman, B.F.J.M.; Wymenga, A.B.; Verdonschot, N.J.J. Anterior referencing of tibial slope in total knee arthroplasty considerably influences knee kinematics: A musculoskeletal simulation study. Knee Surg. Sports Traumatol. Arthrosc. 2018, 26, 1540–1548. [Google Scholar] [CrossRef]
- Abdel, M.P.; Ollivier, M.; Parratte, S.; Trousdale, R.T.; Berry, D.J.; Pagnano, M.W. Effect of postoperativemechanical axis alignment on survival and functional outcomes of modern total knee arthroplasties with cement: A concise follow-up at 20 years. J. Bone Jt. Surg. 2018, 100, 472–478. [Google Scholar] [CrossRef]
- Guo, Z.; Freeman, J.W.; Barrett, J.G.; De Vita, R. Quantification of strain induced damage in medial collateral ligaments. J. Biomech. Eng. 2015, 137, 071011. [Google Scholar] [CrossRef]
- Hu, J.; Xin, H.; Chen, Z.; Zhang, Q.; Peng, Y.; Jin, Z. The role of menisci in knee contact mechanics and secondary kinematics during human walking. Clin. Biomech. 2019, 61, 58–63. [Google Scholar] [CrossRef] [PubMed]
- Petersen, W.; Rembitzki, I.V.; Brüggemann, G.P.; Ellermann, A.; Best, R.; Koppenburg, A.G.; Liebau, C. Anterior knee pain after total knee arthroplasty: A narrative review. Int. Orthop. 2014, 38, 319–328. [Google Scholar] [CrossRef] [PubMed]


| Implant Positional Parameters | Boundary Conditions Relative to MA | Components | |
|---|---|---|---|
| Upper Bound | Lower Bound | ||
| Translations (mm) | |||
| AP | −6 | +6 | Femoral |
| LM | −6 | +6 | Femoral |
| PD | −6 | +6 | Femoral |
| Rotations (°) | |||
| FE | −3 | +3 | Femoral, Tibial 1 |
| EI | −6 | +6 | Femoral, Tibial |
| VV | −6 | +6 | Femoral, Tibial |
| Surgical Target/ Components | Translations (mm) | Rotations (°) | ||||
|---|---|---|---|---|---|---|
| AP | LM | PD | FE | EI | VV | |
| Surgical target 1 | ||||||
| Femoral | −2.8 | −0.2 | 3.9 | −1.4 | −0.2 | −1.2 |
| Tibial | - | - | - | 5.2 | 2.8 | 2.2 |
| Surgical target 2 | ||||||
| Femoral | −1.7 | −1.8 | 3.6 | −1.5 | −1.6 | −1.5 |
| Tibial | - | - | - | 0.9 | 2.8 | −1.9 |
| Surgical target 3 | ||||||
| Femoral | −1.1 | 0.1 | 2.3 | 0.9 | −1.8 | −0.4 |
| Tibial | - | - | - | −1.8 | −1.5 | 3.2 |
| Surgical target 4 | ||||||
| Femoral | −2.4 | −0.8 | 3.6 | −0.6 | −0.3 | 1.6 |
| Tibial | - | - | - | −2.8 | −0.2 | 2.6 |
| Surgical target 5 | ||||||
| Femoral | −2.3 | −1.5 | 3.7 | −1.9 | −0.5 | −1.4 |
| Tibial | - | - | - | 3.6 | 2.3 | −1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzanetis, P.; Fluit, R.; de Souza, K.; Robertson, S.; Koopman, B.; Verdonschot, N. Pre-Planning the Surgical Target for Optimal Implant Positioning in Robotic-Assisted Total Knee Arthroplasty. Bioengineering 2023, 10, 543. https://doi.org/10.3390/bioengineering10050543
Tzanetis P, Fluit R, de Souza K, Robertson S, Koopman B, Verdonschot N. Pre-Planning the Surgical Target for Optimal Implant Positioning in Robotic-Assisted Total Knee Arthroplasty. Bioengineering. 2023; 10(5):543. https://doi.org/10.3390/bioengineering10050543
Chicago/Turabian StyleTzanetis, Periklis, René Fluit, Kevin de Souza, Seonaid Robertson, Bart Koopman, and Nico Verdonschot. 2023. "Pre-Planning the Surgical Target for Optimal Implant Positioning in Robotic-Assisted Total Knee Arthroplasty" Bioengineering 10, no. 5: 543. https://doi.org/10.3390/bioengineering10050543
APA StyleTzanetis, P., Fluit, R., de Souza, K., Robertson, S., Koopman, B., & Verdonschot, N. (2023). Pre-Planning the Surgical Target for Optimal Implant Positioning in Robotic-Assisted Total Knee Arthroplasty. Bioengineering, 10(5), 543. https://doi.org/10.3390/bioengineering10050543







