The Impact of Left Ventricular Performance and Afterload on the Evaluation of Aortic Valve Stenosis: A 1D Mathematical Modeling Approach
Abstract
1. Introduction
2. Materials and Methods
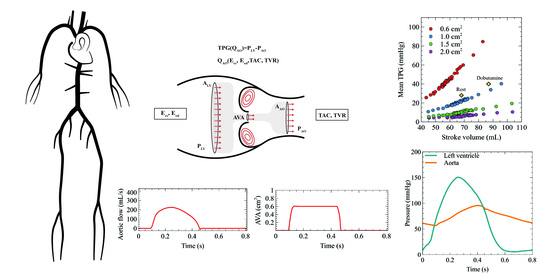
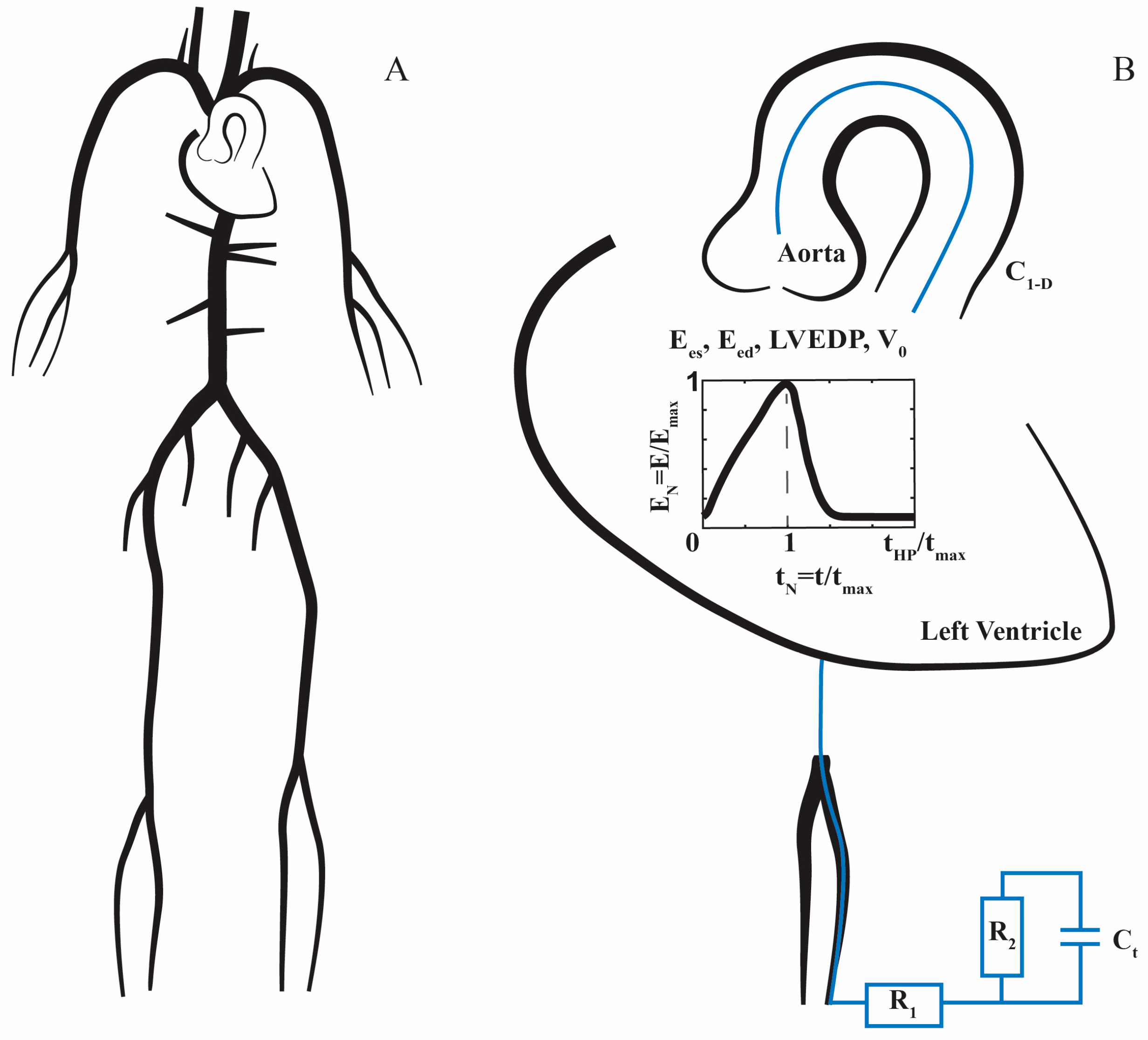
2.1. 1D Mathematical Model of the Cardiovascular System
2.2. Boundary Conditions
2.3. Stenotic Aortic Valve Model
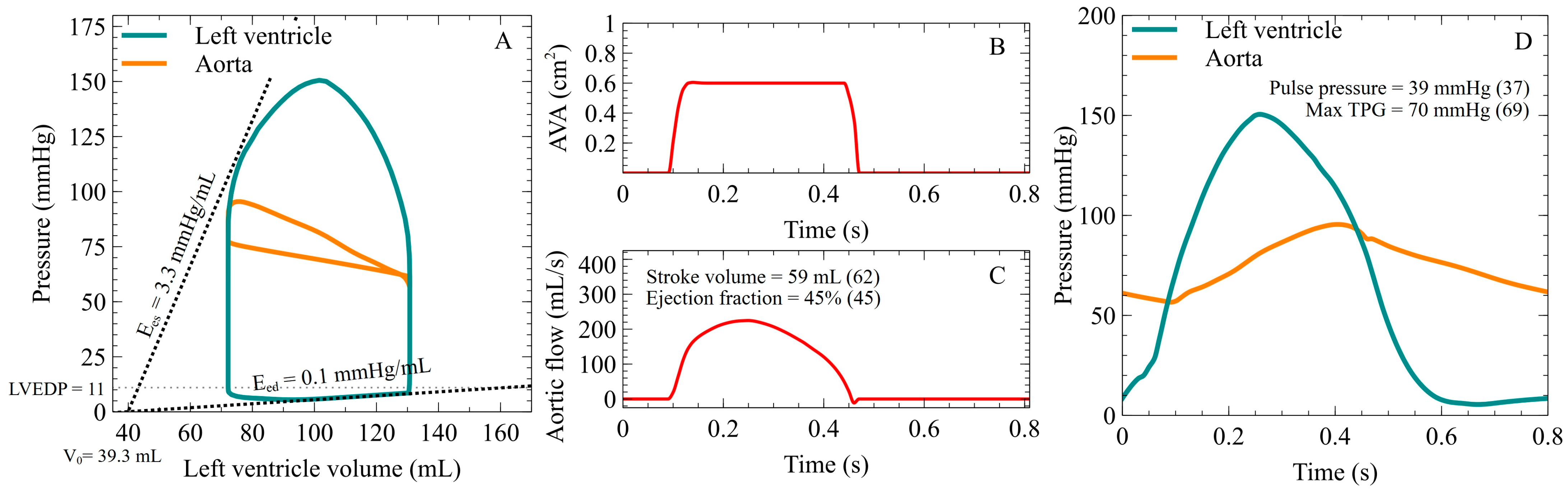
2.4. Validation of the Coupled Model
2.5. Simulation Strategy of the Aortic Stenosis Cases
2.6. Echocardiography
2.7. Statistical Analysis
3. Results
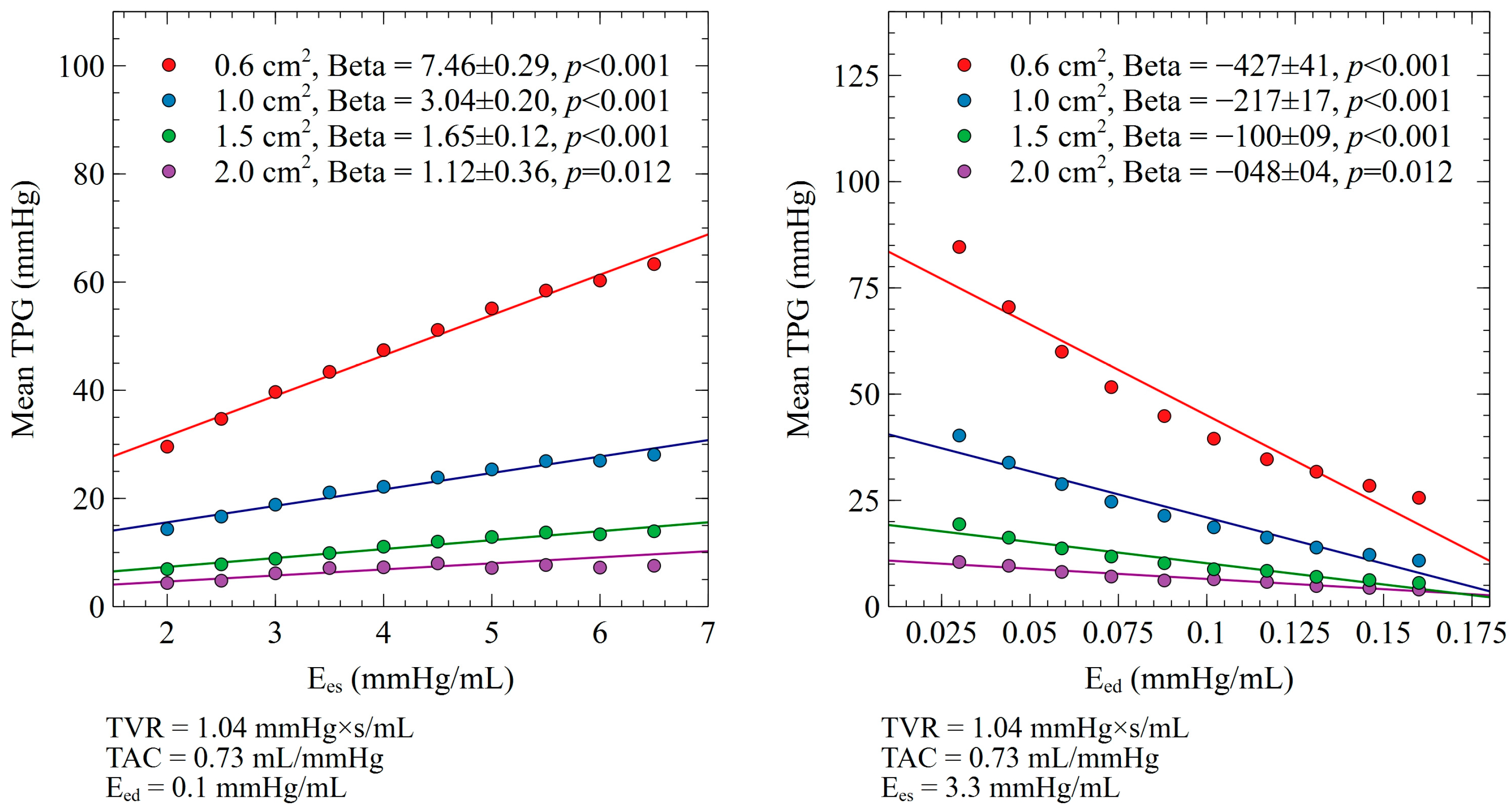
3.1. Ees and Eed Impact on Mean TPG
3.2. TVR and TAC Impact on Mean TPG
3.3. Relative Contribution of Ees, Eed, TVR, and TAC on Mean TPG
3.4. SV and Mean TPG Relationship for a Given AVA
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, J.; Wang, Z.; Bao, Q.; Lei, S.; You, Y.; Yin, Z.; Xie, X. Global Burden of Calcific Aortic Valve Disease and Attributable Risk Factors from 1990 to 2019. Front. Cardiovasc. Med. 2022, 9, 1003233. [Google Scholar] [CrossRef] [PubMed]
- Yadgir, S.; Johnson, C.O.; Aboyans, V.; Adebayo, O.M.; Adedoyin, R.A.; Afarideh, M.; Alahdab, F.; Alashi, A.; Alipour, V.; Arabloo, J.; et al. Global, Regional, and National Burden of Calcific Aortic Valve and Degenerative Mitral Valve Diseases, 1990–2017. Circulation 2020, 141, 1670–1680. [Google Scholar] [CrossRef] [PubMed]
- Go, A.S.; Mozaffarian, D.; Roger, V.L.; Benjamin, E.J.; Berry, J.D.; Borden, W.B.; Bravata, D.M.; Dai, S.; Ford, E.S.; Fox, C.S.; et al. Executive Summary: Heart Disease and Stroke Statistics—2013 Update: A Report From the American Heart Association. Circulation 2013, 127, 143–152. [Google Scholar] [CrossRef]
- Lindman, B.R.; Clavel, M.-A.; Mathieu, P.; Iung, B.; Lancellotti, P.; Otto, C.M.; Pibarot, P. Calcific Aortic Stenosis. Nat. Rev. Dis. Primers 2016, 2, 16006. [Google Scholar] [CrossRef] [PubMed]
- Roth, G.A.; Mensah, G.A.; Johnson, C.O.; Addolorato, G.; Ammirati, E.; Baddour, L.M.; Barengo, N.C.; Beaton, A.Z.; Benjamin, E.J.; Benziger, C.P.; et al. Global Burden of Cardiovascular Diseases and Risk Factors 1990–2019. J. Am. Coll. Cardiol. 2020, 76, 2982–3021. [Google Scholar] [CrossRef]
- Pibarot, P.; Clavel, M.-A. Live Longer and Better without Aortic Valve Stenosis. Lancet Healthy Longev. 2022, 3, e573–e574. [Google Scholar] [CrossRef]
- Vahanian, A.; Beyersdorf, F.; Praz, F.; Milojevic, M.; Baldus, S.; Bauersachs, J.; Capodanno, D.; Conradi, L.; De Bonis, M.; De Paulis, R.; et al. 2021 ESC/EACTS Guidelines for the Management of Valvular Heart Disease. Eur. Heart J. 2022, 43, 561–632. [Google Scholar] [CrossRef]
- Baumgartner, H.; Hung, J.; Bermejo, J.; Chambers, J.B.; Edvardsen, T.; Goldstein, S.; Lancellotti, P.; LeFevre, M.; Miller, F.; Otto, C.M. Recommendations on the Echocardiographic Assessment of Aortic Valve Stenosis: A Focused Update from the European Association of Cardiovascular Imaging and the American Society of Echocardiography. J. Am. Soc. Echocardiogr. 2017, 30, 372–392. [Google Scholar] [CrossRef]
- Otto, C.M.; Nishimura, R.A.; Bonow, R.O.; Carabello, B.A.; Erwin, J.P.; Gentile, F.; Jneid, H.; Krieger, E.V.; Mack, M.; McLeod, C.; et al. 2020 ACC/AHA Guideline for the Management of Patients With Valvular Heart Disease: A Report of the American College of Cardiology/American Heart Association Joint Committee on Clinical Practice Guidelines. Circulation 2021, 143, e72–e227. [Google Scholar] [CrossRef]
- Reymond, P.; Bohraus, Y.; Perren, F.; Lazeyras, F.; Stergiopulos, N. Validation of a Patient-Specific One-Dimensional Model of the Systemic Arterial Tree. Am. J. Physiol.-Heart Circ. Physiol. 2011, 301, H1173–H1182. [Google Scholar] [CrossRef]
- Kondiboyina, A.; Harrington, H.A.; Smolich, J.J.; Cheung, M.M.H.; Mynard, J.P. Optimized Design of an Arterial Network Model Reproduces Characteristic Central and Peripheral Haemodynamic Waveform Features of Young Adults. J. Physiol. 2022, 600, 3725–3747. [Google Scholar] [CrossRef]
- Charlton, P.H.; Mariscal Harana, J.; Vennin, S.; Li, Y.; Chowienczyk, P.; Alastruey, J. Modeling Arterial Pulse Waves in Healthy Aging: A Database for in Silico Evaluation of Hemodynamics and Pulse Wave Indexes. Am. J. Physiol-Heart Circ. Physiol. 2019, 317, H1062–H1085. [Google Scholar] [CrossRef]
- Blanco, P.J.; Watanabe, S.M.; Passos, M.A.R.F.; Lemos, P.A.; Feijoo, R.A. An Anatomically Detailed Arterial Network Model for One-Dimensional Computational Hemodynamics. IEEE Trans. Biomed. Eng. 2015, 62, 736–753. [Google Scholar] [CrossRef] [PubMed]
- Bikia, V.; Adamopoulos, D.; Pagoulatou, S.; Rovas, G.; Stergiopulos, N. AI-Based Estimation of End-Systolic Elastance from Arm-Pressure and Systolic Time Intervals. Front. Artif. Intell. 2021, 4, 579541. [Google Scholar] [CrossRef]
- Pagoulatou, S.; Rommel, K.-P.; Kresoja, K.-P.; von Roeder, M.; Lurz, P.; Thiele, H.; Bikia, V.; Rovas, G.; Adamopoulos, D.; Stergiopulos, N. In Vivo Application and Validation of a Novel Noninvasive Method to Estimate the End-Systolic Elastance. Am. J. Physiol. Heart Circ. Physiol. 2021, 320, H1554–H1564. [Google Scholar] [CrossRef]
- Bikia, V.; Pagoulatou, S.; Trachet, B.; Soulis, D.; Protogerou, A.D.; Papaioannou, T.G.; Stergiopulos, N. Noninvasive Cardiac Output and Central Systolic Pressure From Cuff-Pressure and Pulse Wave Velocity. IEEE J. Biomed. Health Inform. 2020, 24, 1968–1981. [Google Scholar] [CrossRef]
- Clark, C. Relation between Pressure Difference across the Aortic Valve and Left Ventricular Outflow. Cardiovasc. Res. 1978, 12, 276–287. [Google Scholar] [CrossRef] [PubMed]
- Garcia, D.; Pibarot, P.; Durand, L.-G. Analytical Modeling of the Instantaneous Pressure Gradient across the Aortic Valve. J. Biomech. 2005, 38, 1303–1311. [Google Scholar] [CrossRef] [PubMed]
- Garcia, D.; Kadem, L.; Savéry, D.; Pibarot, P.; Durand, L.-G. Analytical Modeling of the Instantaneous Maximal Transvalvular Pressure Gradient in Aortic Stenosis. J. Biomech. 2006, 39, 3036–3044. [Google Scholar] [CrossRef]
- Hatoum, H.; Mo, X.-M.; Crestanello, J.A.; Dasi, L.P. Modeling of the Instantaneous Transvalvular Pressure Gradient in Aortic Stenosis. Ann. Biomed. Eng. 2019, 47, 1748–1763. [Google Scholar] [CrossRef]
- Ringle Griguer, A.; Tribouilloy, C.; Truffier, A.; Castel, A.-L.; Delelis, F.; Levy, F.; Vincentelli, A.; Bohbot, Y.; Maréchaux, S. Clinical Significance of Ejection Dynamics Parameters in Patients with Aortic Stenosis: An Outcome Study. J. Am. Soc. Echocardiogr. 2018, 31, 551–560.e2. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.H.; Kim, J.S.; Kim, B.S.; Choi, J.; Lee, S.-C.; Oh, J.K.; Park, S.W. Time to Peak Velocity of Aortic Flow Is Useful in Predicting Severe Aortic Stenosis. Int. J. Cardiol. 2014, 172, e443–e446. [Google Scholar] [CrossRef] [PubMed]
- Altes, A.; Thellier, N.; Bohbot, Y.; Ringle Griguer, A.; Verdun, S.; Levy, F.; Castel, A.L.; Delelis, F.; Mailliet, A.; Tribouilloy, C.; et al. Relationship Between the Ratio of Acceleration Time/Ejection Time and Mortality in Patients With High-Gradient Severe Aortic Stenosis. JAHA 2021, 10, e021873. [Google Scholar] [CrossRef] [PubMed]
- Virag, Z.; Lulić, F. Modeling of Aortic Valve Dynamics in a Lumped Parameter Model of Left Ventricular-Arterial Coupling. Ann. Univ. Ferrara 2008, 54, 335–347. [Google Scholar] [CrossRef]
- Aboelkassem, Y.; Savic, D.; Campbell, S.G. Mathematical Modeling of Aortic Valve Dynamics during Systole. J. Theor. Biol. 2015, 365, 280–288. [Google Scholar] [CrossRef] [PubMed]
- Laubscher, R.; van der Merwe, J.; Liebenberg, J.; Herbst, P. Dynamic Simulation of Aortic Valve Stenosis Using a Lumped Parameter Cardiovascular System Model with Flow Regime Dependent Valve Pressure Loss Characteristics. Med. Eng. Phys. 2022, 106, 103838. [Google Scholar] [CrossRef]
- Korakianitis, T.; Shi, Y. A Concentrated Parameter Model for the Human Cardiovascular System Including Heart Valve Dynamics and Atrioventricular Interaction. Med. Eng. Phys. 2006, 28, 613–628. [Google Scholar] [CrossRef]
- Korakianitis, T.; Shi, Y. Numerical Simulation of Cardiovascular Dynamics with Healthy and Diseased Heart Valves. J. Biomech. 2006, 39, 1964–1982. [Google Scholar] [CrossRef]
- Mynard, J.P.; Davidson, M.R.; Penny, D.J.; Smolich, J.J. A Simple, Versatile Valve Model for Use in Lumped Parameter and One-Dimensional Cardiovascular Models. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 626–641. [Google Scholar] [CrossRef]
- Mynard, J.P.; Smolich, J.J. One-Dimensional Haemodynamic Modeling and Wave Dynamics in the Entire Adult Circulation. Ann. Biomed. Eng. 2015, 43, 1443–1460. [Google Scholar] [CrossRef]
- Briand, M.; Dumesnil, J.G.; Kadem, L.; Tongue, A.G.; Rieu, R.; Garcia, D.; Pibarot, P. Reduced Systemic Arterial Compliance Impacts Significantly on Left Ventricular Afterload and Function in Aortic Stenosis. J. Am. Coll. Cardiol. 2005, 46, 291–298. [Google Scholar] [CrossRef] [PubMed]
- Hachicha, Z.; Dumesnil, J.G.; Pibarot, P. Usefulness of the Valvuloarterial Impedance to Predict Adverse Outcome in Asymptomatic Aortic Stenosis. J. Am. Coll. Cardiol. 2009, 54, 1003–1011. [Google Scholar] [CrossRef]
- Côté, N.; Simard, L.; Zenses, A.; Tastet, L.; Shen, M.; Clisson, M.; Clavel, M. Impact of Vascular Hemodynamics on Aortic Stenosis Evaluation: New Insights Into the Pathophysiology of Normal Flow—Small Aortic Valve Area—Low Gradient Pattern. JAHA 2017, 6, e006276. [Google Scholar] [CrossRef] [PubMed]
- Gardikioti, V.; Terentes-Printzios, D.; Iliopoulos, D.; Aznaouridis, K.; Sigala, E.; Tsioufis, K.; Vlachopoulos, C. Arterial Biomarkers in the Evaluation, Management and Prognosis of Aortic Stenosis. Atherosclerosis 2021, 332, 1–15. [Google Scholar] [CrossRef]
- Gholampour, S.; Yamini, B.; Droessler, J.; Frim, D. A New Definition for Intracranial Compliance to Evaluate Adult Hydrocephalus After Shunting. Front. Bioeng. Biotechnol. 2022, 10, 900644. [Google Scholar] [CrossRef]
- Gholampour, S.; Frim, D.; Yamini, B. Long-Term Recovery Behavior of Brain Tissue in Hydrocephalus Patients after Shunting. Commun. Biol. 2022, 5, 1198. [Google Scholar] [CrossRef]
- Lancellotti, P.; Donal, E.; Magne, J.; Moonen, M.; O’Connor, K.; Daubert, J.-C.; Pierard, L.A. Risk Stratification in Asymptomatic Moderate to Severe Aortic Stenosis: The Importance of the Valvular, Arterial and Ventricular Interplay. Heart 2010, 96, 1364–1371. [Google Scholar] [CrossRef]
- Mancusi, C.; de Simone, G.; Brguljan Hitij, J.; Sudano, I.; Mahfoud, F.; Parati, G.; Kahan, T.; Barbato, E.; Pierard, L.A.; Garbi, M.; et al. Management of Patients with Combined Arterial Hypertension and Aortic Valve Stenosis: A Consensus Document from the Council on Hypertension and Council on Valvular Heart Disease of the European Society of Cardiology, the European Association of Cardiovascular Imaging (EACVI), and the European Association of Percutaneous Cardiovascular Interventions (EAPCI). Eur. Heart J.—Cardiovasc. Pharmacother. 2021, 7, 242–250. [Google Scholar] [CrossRef]
- Gotzmann, M.; Hauptmann, S.; Hogeweg, M.; Choudhury, D.S.; Schiedat, F.; Dietrich, J.W.; Westhoff, T.H.; Bergbauer, M.; Mügge, A. Hemodynamics of Paradoxical Severe Aortic Stenosis: Insight from a Pressure–Volume Loop Analysis. Clin. Res. Cardiol. 2019, 108, 931–939. [Google Scholar] [CrossRef]
- Awtry, E.H.; Davidoff, R. Low-Flow Low-Gradient Aortic Stenosis. Circ. Cardiovasc. Imaging 2012, 5, 6–8. [Google Scholar] [CrossRef] [PubMed]
- Burwash, I.G.; Pearlman, A.S.; Kraft, C.D.; Miyake-Hull, C.; Healy, N.L.; Otto, C.M. Flow Dependence of Measures of Aortic Stenosis Severity during Exercise. J. Am. Coll. Cardiol. 1994, 24, 1342–1350. [Google Scholar] [CrossRef] [PubMed]
- Burwash, I.G.; Thomas, D.D.; Sadahiro, M.; Pearlman, A.S.; Verrier, E.D.; Thomas, R.; Kraft, C.D.; Otto, C.M. Dependence of Gorlin Formula and Continuity Equation Valve Areas on Transvalvular Volume Flow Rate in Valvular Aortic Stenosis. Circulation 1994, 89, 827–835. [Google Scholar] [CrossRef]
- Hayek, A.; Derimay, F.; Green, L.; Rosset, M.; Thibault, H.; Rioufol, G.; Finet, G. Impact of Arterial Blood Pressure on Ultrasound Hemodynamic Assessment of Aortic Valve Stenosis Severity. J. Am. Soc. Echocardiogr. 2020, 33, 1324–1333. [Google Scholar] [CrossRef] [PubMed]
- Kadem, L.; Dumesnil, J.G.; Rieu, R.; Durand, L.-G.; Garcia, D.; Pibarot, P. Impact of Systemic Hypertension on the Assessment of Aortic Stenosis. Heart 2005, 91, 354–361. [Google Scholar] [CrossRef] [PubMed]
- Pagoulatou, S.; Adamopoulos, D.; Rovas, G.; Bikia, V.; Müller, H.; Giannakopoulos, G.; Mauler-Wittwer, S.; Licker, M.-J.; Stergiopulos, N.; Noble, S. Arterial Wave Reflection and Aortic Valve Stenosis: Diagnostic Challenges and Prognostic Significance. Front. Cardiovasc. Med. 2022, 9, 863968. [Google Scholar] [CrossRef]
- deFilippi, C.R.; Willett, D.L.; Brickner, M.E.; Appleton, C.P.; Yancy, C.W.; Eichhorn, E.J.; Grayburn, P.A. Usefulness of Dobutamine Echocardiography in Distinguishing Severe from Nonsevere Valvular Aortic Stenosis in Patients with Depressed Left Ventricular Function and Low Transvalvular Gradients. Am. J. Cardiol. 1995, 75, 191–194. [Google Scholar] [CrossRef]
- Eleid, M.F.; Nishimura, R.A.; Sorajja, P.; Borlaug, B.A. Systemic Hypertension in Low-Gradient Severe Aortic Stenosis With Preserved Ejection Fraction. Circulation 2013, 128, 1349–1353. [Google Scholar] [CrossRef]
- Reymond, P.; Merenda, F.; Perren, F.; Rüfenacht, D.; Stergiopulos, N. Validation of a One-Dimensional Model of the Systemic Arterial Tree. Am. J. Physiol. Heart Circ. Physiol. 2009, 297, H208–H222. [Google Scholar] [CrossRef]
- Langewouters, G.J.; Wesseling, K.H.; Goedhard, W.J. The Static Elastic Properties of 45 Human Thoracic and 20 Abdominal Aortas in Vitro and the Parameters of a New Model. J. Biomech. 1984, 17, 425–435. [Google Scholar] [CrossRef]
- Holenstein, R.; Niederer, P.; Anliker, M. A Viscoelastic Model for Use in Predicting Arterial Pulse Waves. J. Biomech. Eng. 1980, 102, 318–325. [Google Scholar] [CrossRef]
- Womersley, J.R. An Elastic Tube Theory of Pulse Transmission and Oscillatory Flow in Mammalian Arteries; WADC Technical Report; Wright Air Development Center, Air Research and Development Command, Wright-Patterson Air Force Base: Dayton, OH, USA, 1957. [Google Scholar]
- Sagawa, K.; Maughan, L.; Suga, H.; Sunagawa, K. Cardiac Contraction and the Pressure-Volume Relationship, 1st ed.; Oxford University Press: New York, NY, USA, 1988; ISBN 978-0-19-504320-4. [Google Scholar]
- Senzaki, H.; Chen, C.-H.; Kass, D.A. Single-Beat Estimation of End-Systolic Pressure-Volume Relation in Humans. Circulation 1996, 94, 2497–2506. [Google Scholar] [CrossRef] [PubMed]
- Segers, P.; Stergiopulos, N.; Schreuder, J.J.; Westerhof, B.E.; Westerhof, N. Left Ventricular Wall Stress Normalization in Chronic Pressure-Overloaded Heart: A Mathematical Model Study. Am. J. Physiol-Heart Circ. Physiol. 2000, 279, H1120–H1127. [Google Scholar] [CrossRef] [PubMed]
- Young, D.F.; Tsai, F.Y. Flow Characteristics in Models of Arterial Stenoses—I. Steady Flow. J. Biomech. 1973, 6, 395–410. [Google Scholar] [CrossRef] [PubMed]
- Young, D.F.; Tsai, F.Y. Flow Characteristics in Models of Arterial Stenoses—II. Unsteady Flow. J. Biomech. 1973, 6, 547–559. [Google Scholar] [CrossRef]
- Dekker, A.L.A.J. Pressure-Volume Loops in Cardiac Surgery; Maastricht University: Maastricht, The Netherlands, 2003. [Google Scholar]
- Feldman, M.D.; Pak, P.H.; Wu, C.C.; Haber, H.L.; Heesch, C.M.; Bergin, J.D.; Powers, E.R.; Cowart, T.D.; Johnson, W.; Feldman, A.M.; et al. Acute Cardiovascular Effects of OPC-18790 in Patients with Congestive Heart Failure. Time- and Dose-Dependence Analysis Based on Pressure-Volume Relations. Circulation 1996, 93, 474–483. [Google Scholar] [CrossRef]
- Chen, C.H.; Nakayama, M.; Nevo, E.; Fetics, B.J.; Maughan, W.L.; Kass, D.A. Coupled Systolic-Ventricular and Vascular Stiffening with Age: Implications for Pressure Regulation and Cardiac Reserve in the Elderly. J. Am. Coll. Cardiol. 1998, 32, 1221–1227. [Google Scholar] [CrossRef] [PubMed]
- Segers, P.; Stergiopulos, N.; Westerhof, N. Relation of Effective Arterial Elastance to Arterial System Properties. Am. J. Physiol. Heart Circ. Physiol. 2002, 282, H1041–H1046. [Google Scholar] [CrossRef]
- Wohlfahrt, P.; Redfield, M.M.; Melenovsky, V.; Lopez-Jimenez, F.; Rodeheffer, R.J.; Borlaug, B.A. Impact of Chronic Changes in Arterial Compliance and Resistance on Left Ventricular Ageing in Humans. Eur. J. Heart Fail. 2015, 17, 27–34. [Google Scholar] [CrossRef]
- Baumgartner, H.; Hung, J.; Bermejo, J.; Chambers, J.B.; Evangelista, A.; Griffin, B.P.; Iung, B.; Otto, C.M.; Pellikka, P.A.; Quiñones, M.; et al. Echocardiographic Assessment of Valve Stenosis: EAE/ASE Recommendations for Clinical Practice. J. Am. Soc. Echocardiogr. 2009, 22, 1–23. [Google Scholar] [CrossRef]
- Pibarot, P.; Dumesnil, J.G. Paradoxical Low-Flow, Low-Gradient Aortic Stenosis: New Evidence, More Questions. Circulation 2013, 128, 1729–1732. [Google Scholar] [CrossRef]
- Osnabrugge, R.L.J.; Mylotte, D.; Head, S.J.; Van Mieghem, N.M.; Nkomo, V.T.; LeReun, C.M.; Bogers, A.J.J.C.; Piazza, N.; Kappetein, A.P. Aortic Stenosis in the Elderly: Disease Prevalence and Number of Candidates for Transcatheter Aortic Valve Replacement: A Meta-Analysis and Modeling Study. J. Am. Coll. Cardiol. 2013, 62, 1002–1012. [Google Scholar] [CrossRef]
- Salmasi, A.-M.; Alimo, A.; Jepson, E.; Dancy, M. Age-Associated Changes in Left Ventricular Diastolic Function Are Related to Increasing Left Ventricular Mass. Am. J. Hypertens. 2003, 16, 473–477. [Google Scholar] [CrossRef]
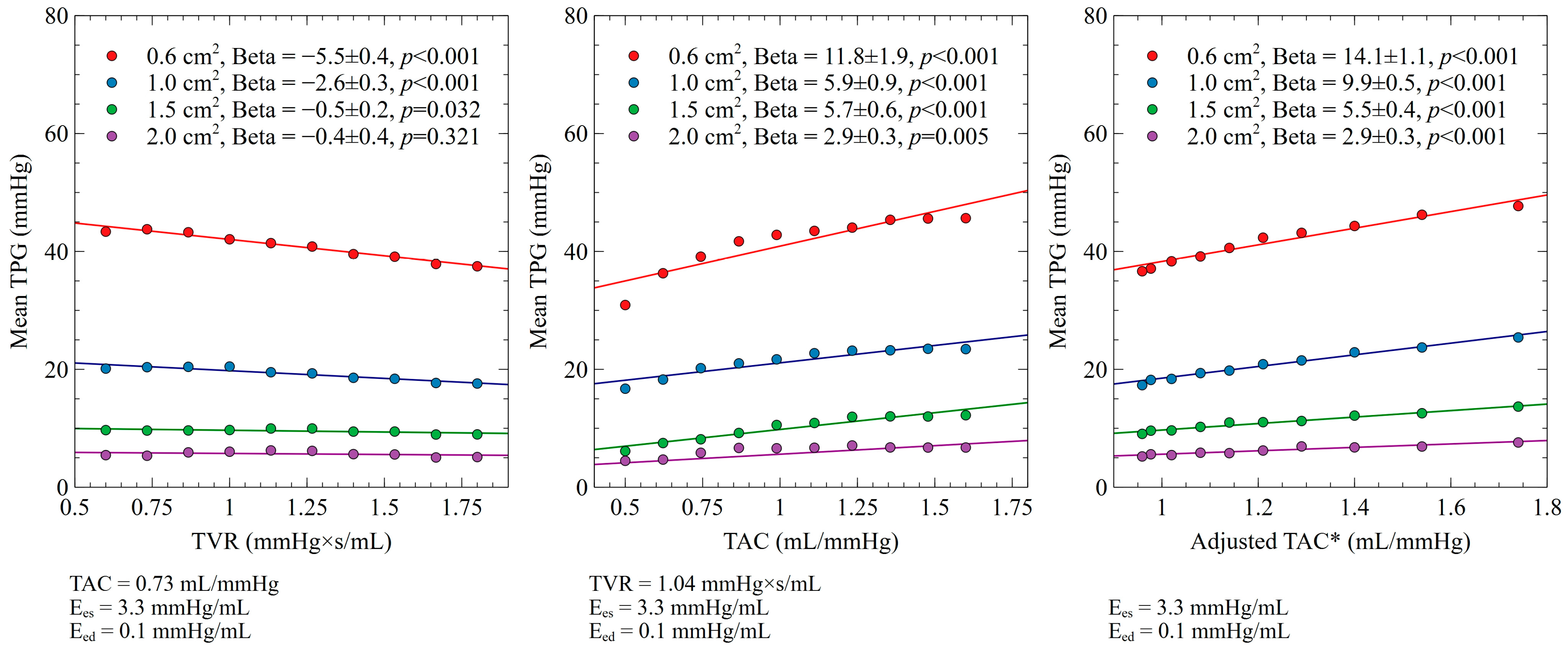

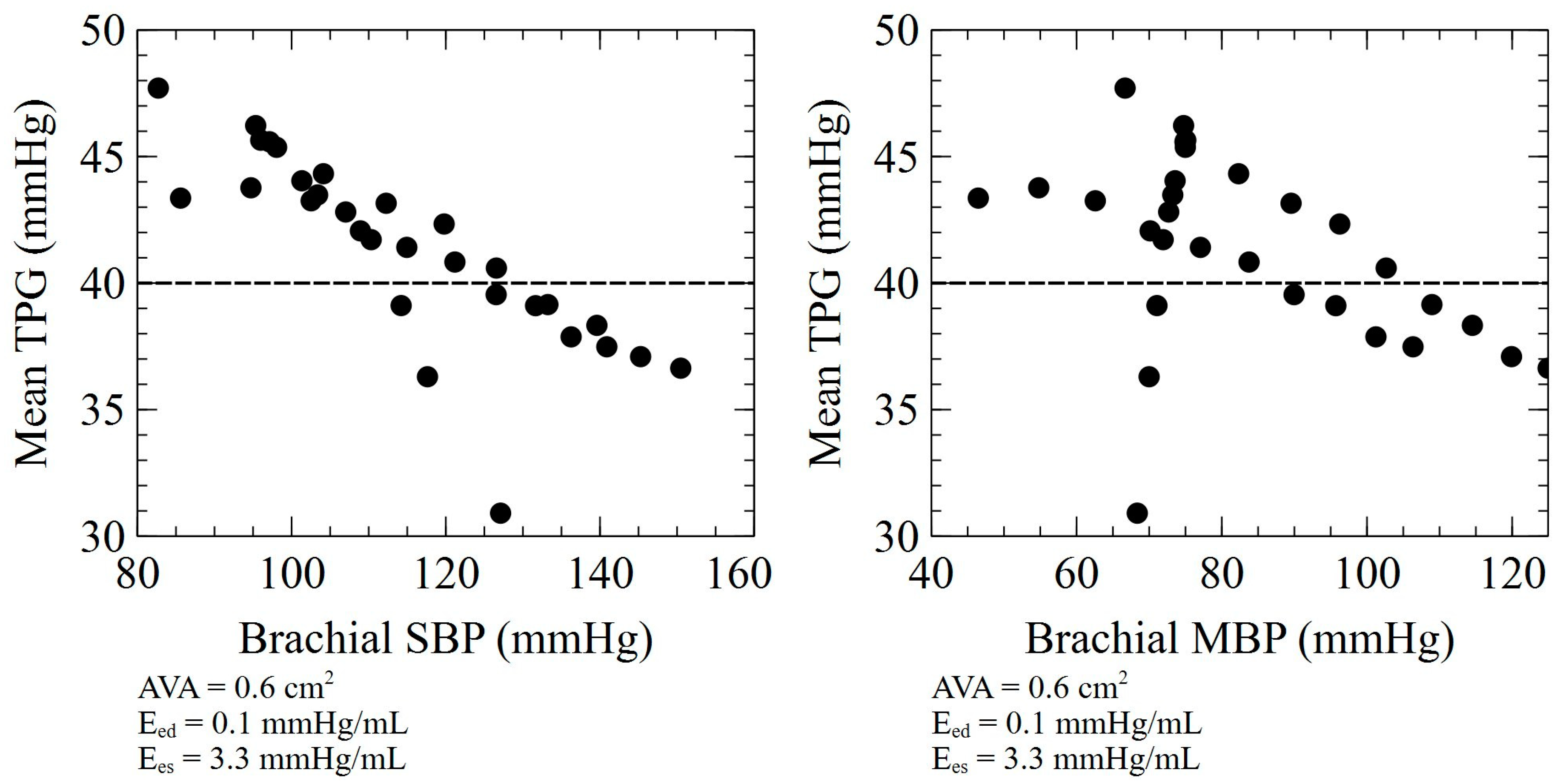
| Aortic Valve Area | 0.6 cm2 | 1.0 cm2 | 1.5 cm2 | 2.0 cm2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beta | S.E. | p Value | Beta | S.E. | p Value | Beta | S.E. | p Value | Beta | S.E. | p Value | |
| Ees (mmHg/mL) | 3.4 | 0.1 | <0.001 | 1.4 | 0.1 | <0.001 | 0.7 | 0.1 | <0.001 | 0.3 | 0.1 | 0.005 |
| Eed (mmHg/mL) | −5.6 | 0.5 | <0.001 | −2.8 | 0.2 | <0.001 | −1.3 | 0.1 | <0.001 | −0.6 | 0.1 | <0.001 |
| TAC (mL/mmHg) | 1.3 | 0.2 | <0.001 | 0.7 | 0.1 | <0.001 | 0.6 | 0.1 | <0.001 | 0.2 | 0.1 | 0.05 |
| TVR (mmHg×s/mL) | −0.7 | 0.04 | <0.001 | −0.3 | 0.04 | <0.001 | −0.1 | 0.03 | 0.032 | −0.04 | 0.04 | 0.321 |
| Adjusted TVR * (mmHg×s/mL) | −1.1 | 0.04 | <0.001 | −0.8 | 0.1 | <0.001 | −0.4 | 0.03 | <0.001 | −0.2 | 0.02 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çelikbudak Orhon, C.; Stergiopulos, N.; Noble, S.; Giannakopoulos, G.; Müller, H.; Adamopoulos, D. The Impact of Left Ventricular Performance and Afterload on the Evaluation of Aortic Valve Stenosis: A 1D Mathematical Modeling Approach. Bioengineering 2023, 10, 425. https://doi.org/10.3390/bioengineering10040425
Çelikbudak Orhon C, Stergiopulos N, Noble S, Giannakopoulos G, Müller H, Adamopoulos D. The Impact of Left Ventricular Performance and Afterload on the Evaluation of Aortic Valve Stenosis: A 1D Mathematical Modeling Approach. Bioengineering. 2023; 10(4):425. https://doi.org/10.3390/bioengineering10040425
Chicago/Turabian StyleÇelikbudak Orhon, Cemre, Nikolaos Stergiopulos, Stéphane Noble, Georgios Giannakopoulos, Hajo Müller, and Dionysios Adamopoulos. 2023. "The Impact of Left Ventricular Performance and Afterload on the Evaluation of Aortic Valve Stenosis: A 1D Mathematical Modeling Approach" Bioengineering 10, no. 4: 425. https://doi.org/10.3390/bioengineering10040425
APA StyleÇelikbudak Orhon, C., Stergiopulos, N., Noble, S., Giannakopoulos, G., Müller, H., & Adamopoulos, D. (2023). The Impact of Left Ventricular Performance and Afterload on the Evaluation of Aortic Valve Stenosis: A 1D Mathematical Modeling Approach. Bioengineering, 10(4), 425. https://doi.org/10.3390/bioengineering10040425