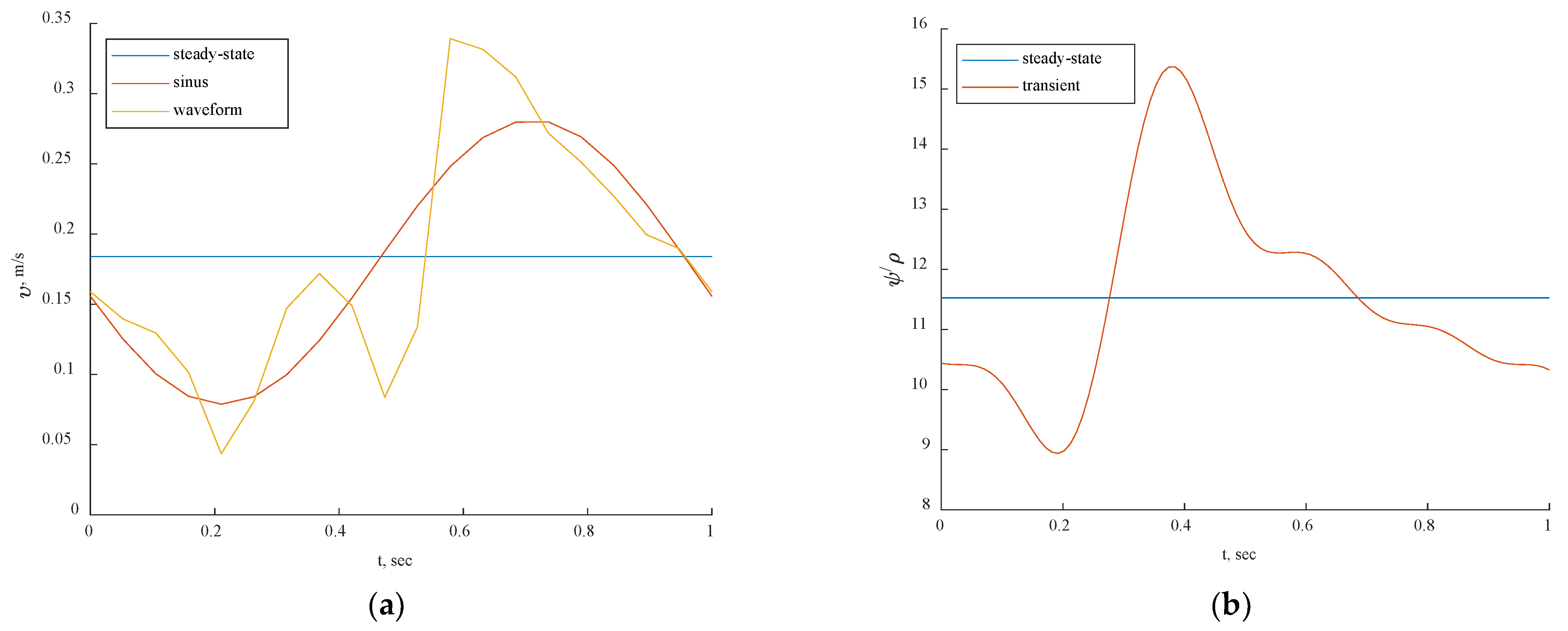1. Introduction
The coronary artery is one of the essential blood arteries that ensure the heart receives steady blood flow. The heart muscle (myocardium) receives oxygenated blood via the coronary arteries; when these are clogged or obstructed, the myocardium starts to deteriorate, a condition known as ischemia. The most significant cause of death worldwide is coronary artery disease (CAD), also known as ischemic heart disease. According to a report by the World Health Organization, CAD causes nearly 50% of disease-related deaths in Kazakhstan [
1]. An American experience a coronary episode roughly every 25 s; statistically, the pass-away rate is approximately one individual every minute [
2].
Coronary angiography may offer information on anatomical stenosis, the gold standard for diagnosing coronary heart disease. Evaluations of fractional flow reserve (FFR) from CT in Europe and the United States suggest that it has the potential to decrease false diagnoses before patients are referred for invasive testing [
3].
Coronary artery computerized tomography (CT) imaging is preferred over coronary angiography for prescreening asymptomatic individuals due to its noninvasive nature, ease of use, low cost, and excellent repeatability. Since FFR from CT is based on high-quality coronary artery CT angiography (CTA) image data, it does not need extra loading, scanning, or dosage. Although there is a grey area that necessitates additional functional measures for diagnosis, the diagnostic accuracy and specificity are greater than those of coronary artery CT imaging. The quantitative coronary artery CT-imaging index may objectively identify functional coronary stenosis [
4].
Compared to angiography alone, FFR is one of the few diagnostic tools that can effectively lead to therapeutic approaches, improve safety and efficacy, and reduce costs. Angio-FFR, a noninvasive estimate of FFR generated from computed tomography coronary angiography, employs specialized software to model three-dimensional coronary blood flow. The DISCOVER-FLOW research revealed an 84.3 percent diagnosis accuracy for lesions contextually assessed using FFR. Similarly, the HEARTFLOW-NXT research found an 86 percent per vessel diagnosis accuracy [
5].
As an optional tool for hemodynamic evaluation in patients with single-vessel CAD, the excellent diagnostic accuracy of SPECT CFR for diagnosing functionally significant stenosis justifies its usage. SPECT CFR is supported by superior diagnostic accuracy for identifying functionally significant stenosis. An aberrant CFR may suggest microvascular dysfunction in individuals whose FFR and CFR differ, which needs more research [
6].
CT scans may be used to construct three-dimensional (3D) solid models that can be seen on display, printed on film or by a 3D printer, or used by a computational fluid dynamics (CFD) approach that enables doctors to quantify the coronary physiology inside an artery. Current CFD programs that have undergone clinical examination in significant clinical investigations include Discover Flow, HeartFlow—NXT, and other platforms for the physiologic study of coronary artery function [
7]. Additionally, using CFD to estimate FFR was offered as a potential noninvasive alternative to fractional flow reserve invasive coronary angiography measurement [
8].
Consequently, computational analysis of FFR utilizing CCTA imaging data enables noninvasive, lesion-specific decline assessment. This anatomical and functional assessment may identify people with lesion-causing coronary pressure decreases. This noninvasive approach may be superior to invasive ICA with FFR for patient treatment. We need more information on incorporating this new strategy into “real-world” clinical practice to influence future patient care decisions [
9].
Instead of simulating maximum hyperemia, boundary conditions are specified to create a pressure–flow curve for stenosis. Then, stenosis is functionally diagnosed using pressure–flow curve characteristics. The suggested strategy is verified with invasive FFR in six individuals using idealized and patient-specific models. According to the results, stenosis flow resistances cannot be directly acquired from anatomy. Simulated pressure–flow parameters correlate linearly and significantly with invasive FFR. The suggested technique may estimate flow resistances using pressure flow from curve-derived parameters. Furthermore, flow resistances can be assessed without modeling maximum hyperemia [
10].
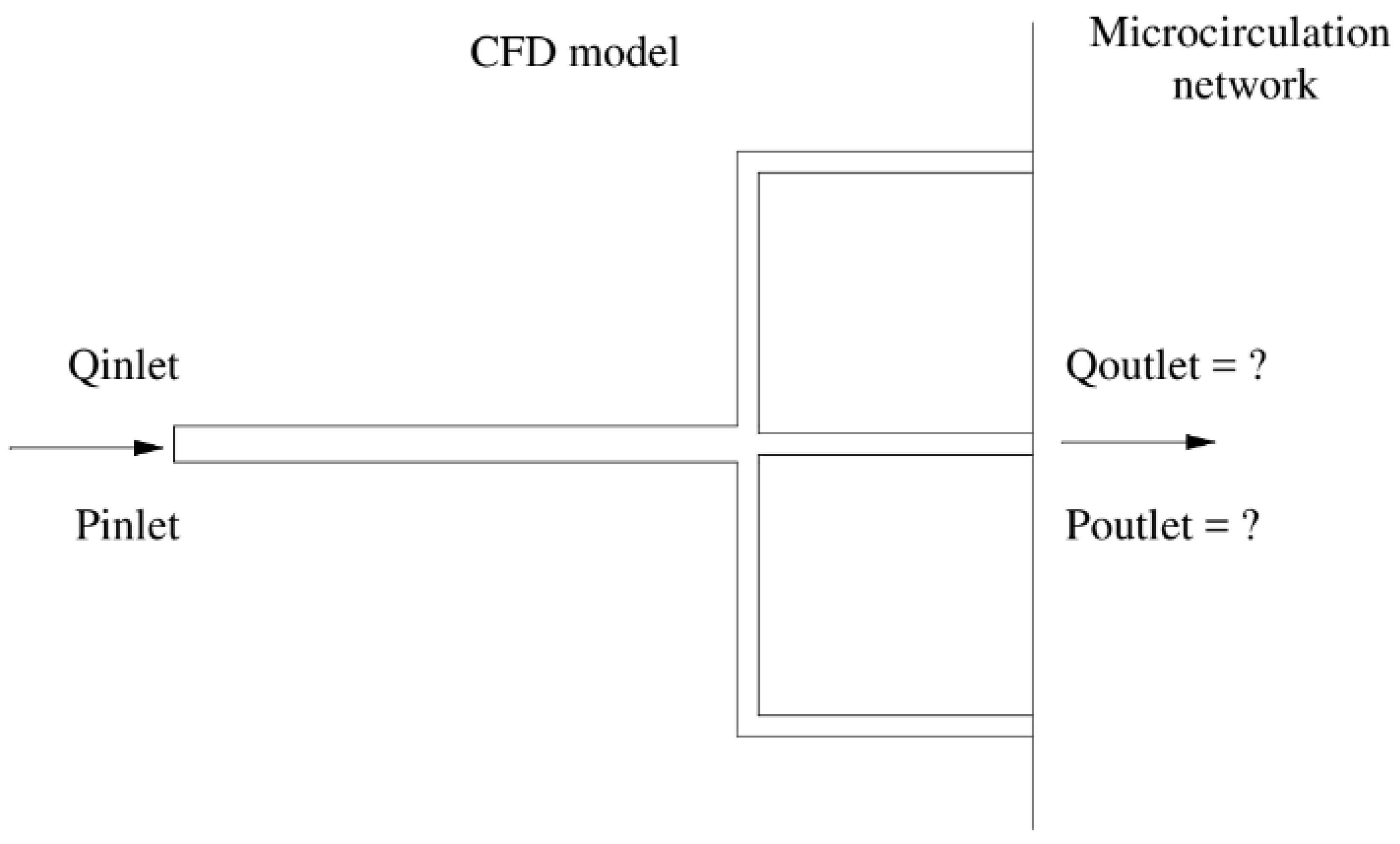
However, since a cardiac tree often includes multiple capillary branches connecting with downstream microcirculation, it is almost impossible to measure the outflow border conditions experimentally owing to their tiny branch diameters. Consequently, the Windkessel-type boundary conditions are based on the so-called lumped parameter model (LPM) and the more complex lumped parameter network model (LPNM). Both methods are typically adopted for approximating the outflow boundary conditions that represent the highly complex dynamic interactions between a tree and its downstream microvasculature. These approaches are based on the circuit analogy theory, which necessitates the measurement of resistances, capacitances, and empirical correlations, which are sometimes challenging to compute without patient-specific data and are not physiologically grounded. The connection of the generated ordinary differential equations (ODEs) from these approaches with the CFD solver also creates unclear boundary conditions, which may often result in slow convergence or even divergence of numerical solutions [
11].
One of the recent works conducted by Chakshu et al [
12] represented a new technique for decreasing invasive, catheter-based assessments consisting of a quick approach for calculating FFR from CT images without operator input that was powered by unsupervised learning and combined with computational fluid dynamics.
The problem addressed in this work is the diagnosis of stenosis (obstruction or narrowing) in the coronary arteries of individual patients. Traditional methods for diagnosing stenosis, such as coronary angiography, have limitations and can be invasive and costly and can carry risks for patients. There is a need for more effective and noninvasive diagnostic methods for stenosis.
The PBA method proposed in this work is based on an extension of Murray’s law and different inlet criteria [
13] and is designed to be used alternately and iteratively to compute the outflow boundary conditions of coronary trees for individual patients. The PBA method is validated using FFR measurements in actual patient arteries and benchmarking with an FDA nozzle. It is intended to provide realistic and tailored outflow boundary conditions for the diagnosis of stenosis without requiring measurable data. The unique contribution of the PBA method to the field is its use of Murray’s law to establish initial boundary conditions that are then modified through the addition of new inlet boundary conditions and iterations, resulting in numerical convergence. This approach may provide a more effective and noninvasive method for diagnosing stenosis in the coronary arteries of individual patients.
In the cardiovascular system, agreements between experiments and the Murray diameter model have been found only in small arteries [
14] and arterioles [
15,
16], as present in our CAD case. The final conditions at the outlets are ultimately decided by a tree’s geometry, the conservation laws built into CFD, the numerical iterations, and the additional inlet patient-specific parameters; we only utilize Murray’s formula to estimate their initial conditions. The third law may not accurately predict the outcome since we use it as a preliminary approximation.
Unlike machine-learning-based data-driven simulation models, which depend on a significant quantity of data for verification, this PBA model is entirely based on physiology and physics. We are currently in the conceptual model-proof stage. It is undoubtedly desirable to undertake large-scale clinical testing, which we hope to accomplish in the next step for possible commercialization and future clinical uses. Because of this, we perform model validation using experimental benchmark data and outputs from other simulations.
The IREC approved the study related to patient data collection and ethical approval.
3. Results and Discussion
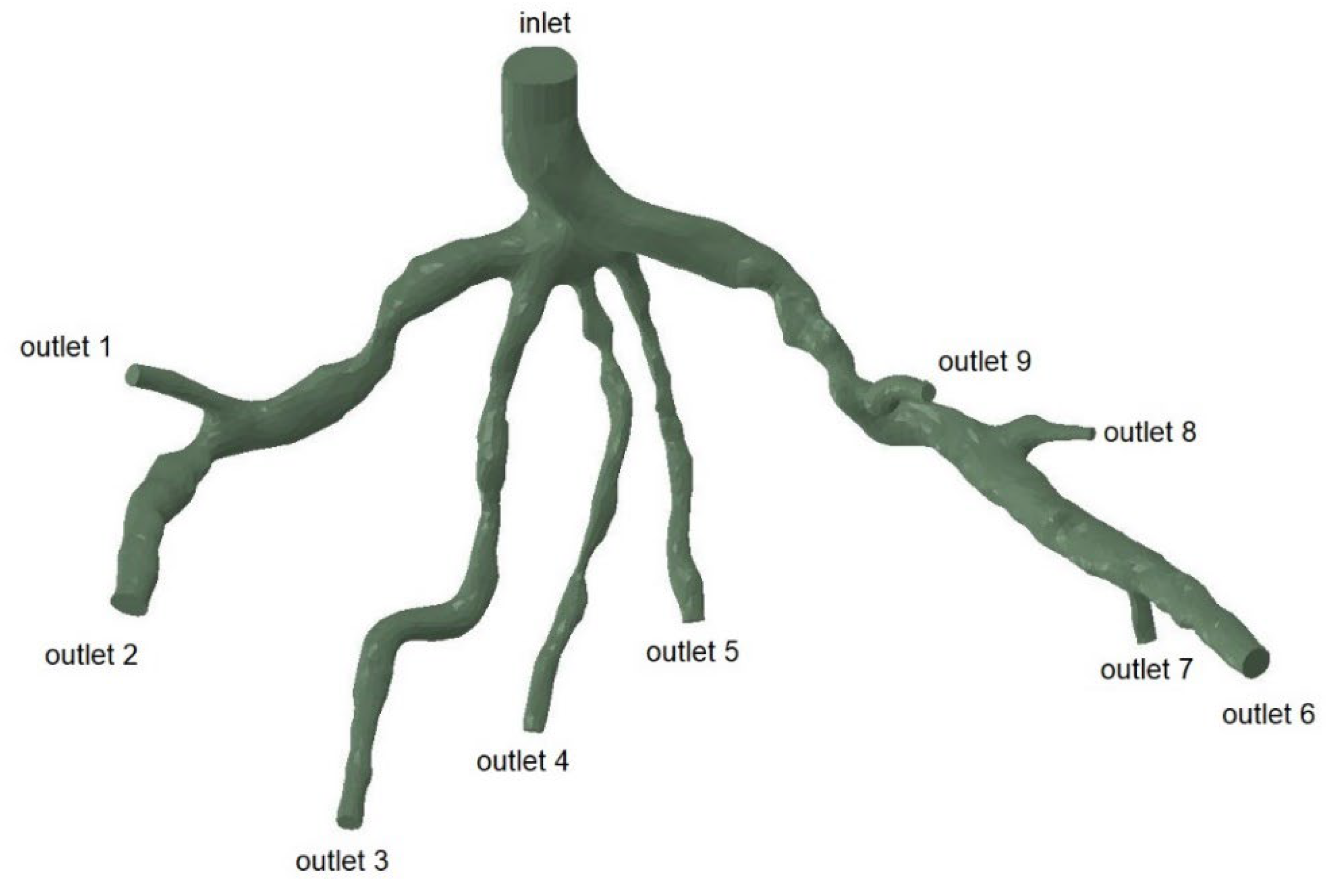
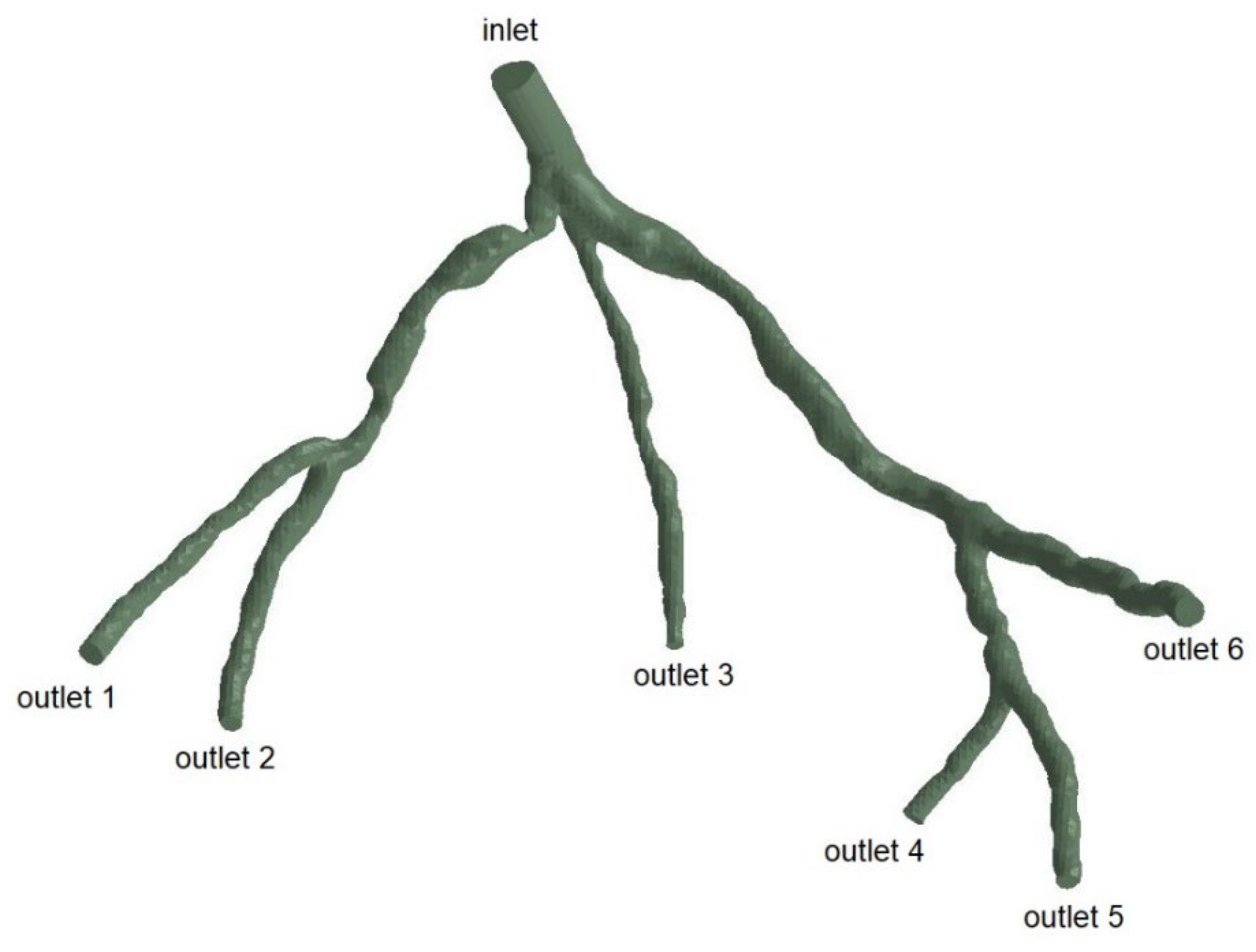
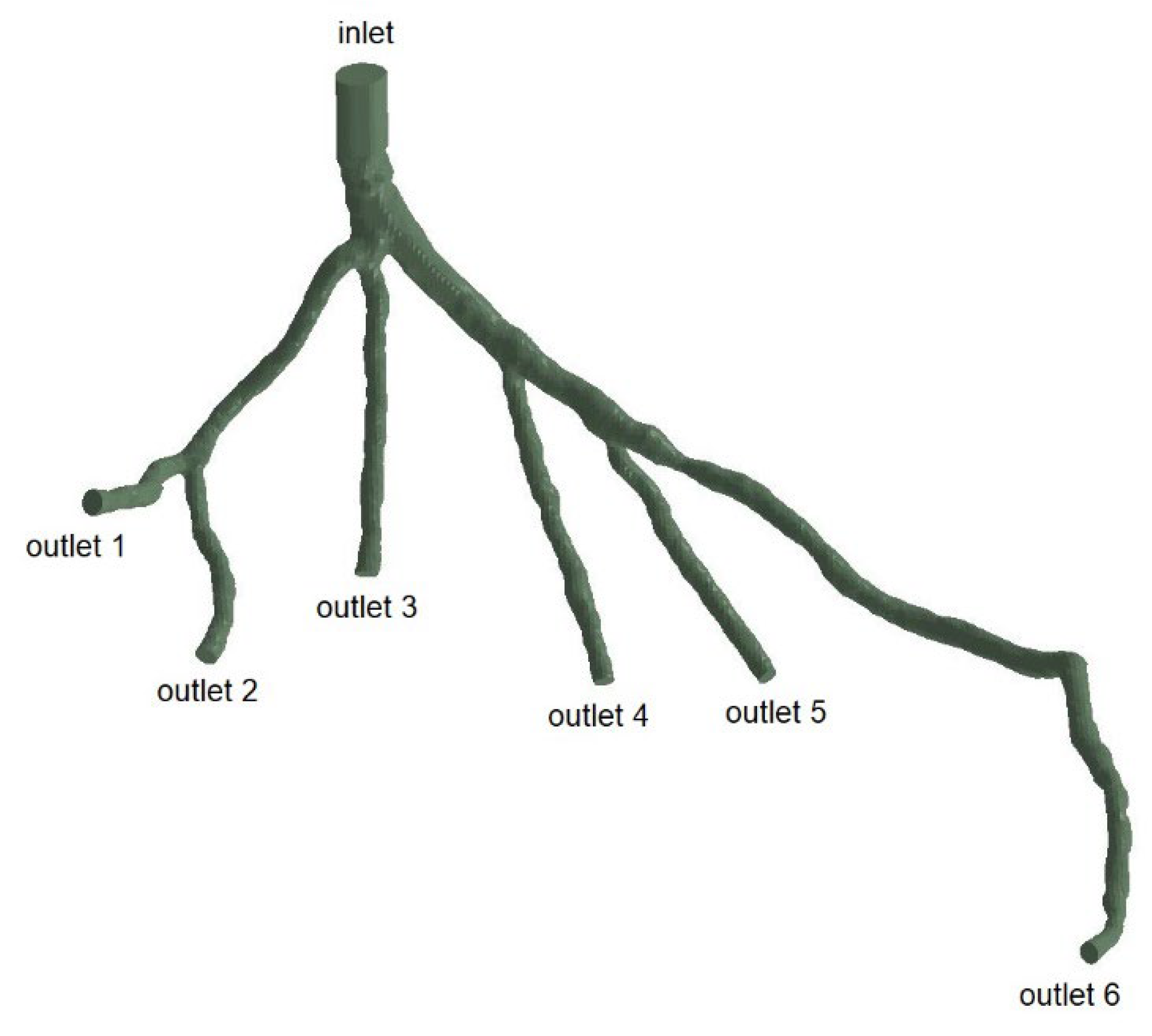
The mesh generation for the blood vessels was performed using the open-source cfMesh utility, which is part of OpenFOAM and generates volumetric meshes of unstructured Cartesian types. cfMesh is also able to automatically generate tetrahedral meshes for a variety of geometries, as shown in
Figure 9. A mesh sensitivity analysis was conducted [
19], and the same models were used in this study. For the CT209, CHN13, and CHN03 arteries, our research group [
19] calculated mesh sizes and numbers of grid cells based on the results of the mesh sensitivity analysis.
The minimum mesh size was half the radius of the model’s smallest artery (inlet or outlet). CT209’s mesh size was 0.1702 mm, whereas CHN13’s was 0.2262 mm. Mesh refinement resulted in a larger number of mesh elements without expansion layers along the vessel walls, which increased simulation computational time. Decreased mesh size from 0.20 mm to 0.1702 mm resulted in 1.7 times increase in computational time.
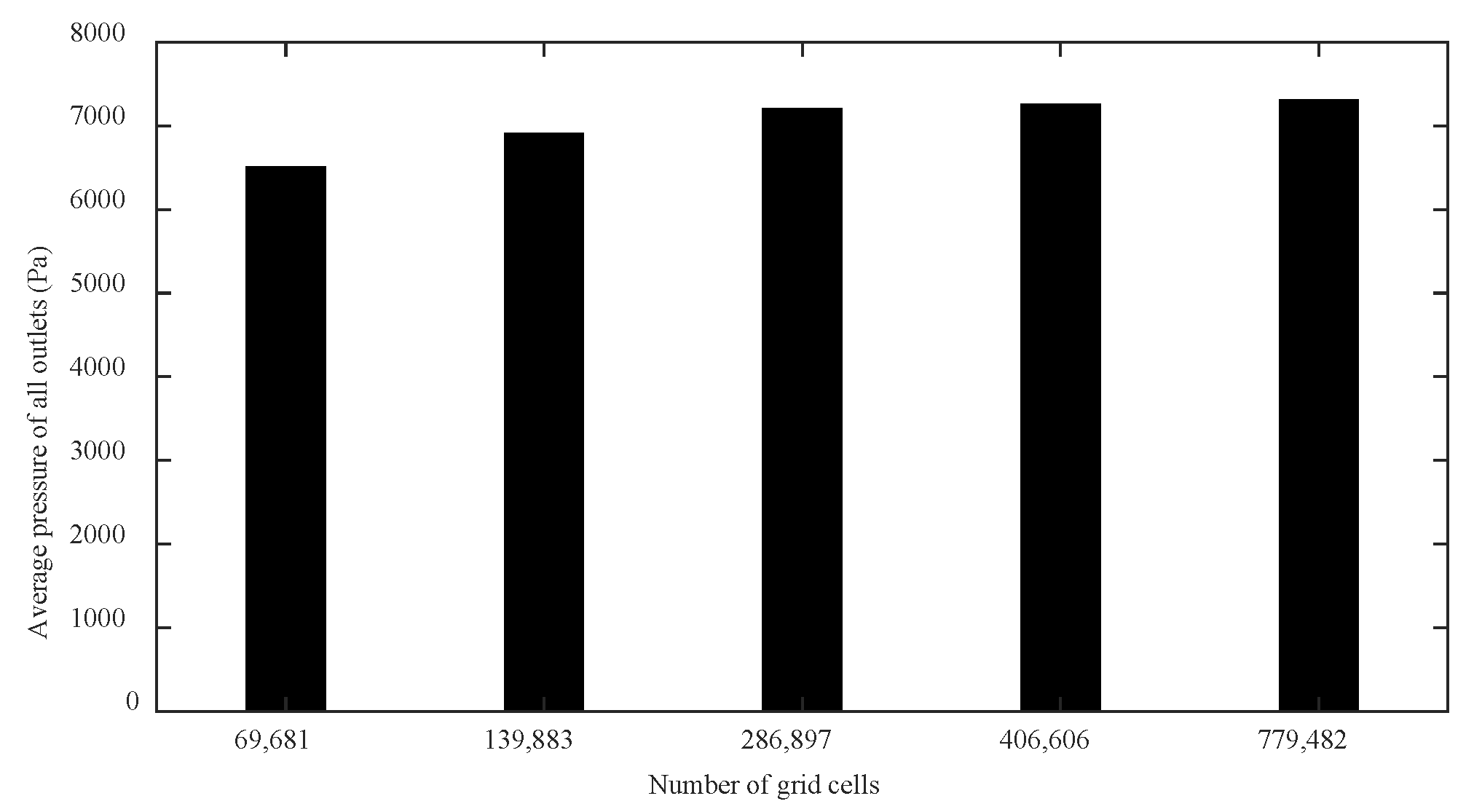
CHN03 had five meshes (69,681; 139,833; 286,897; 406,606; and 779,482) to examine mesh convergence. Increasing the grid number from 100,000 to 1.05 million decreased distal pressure by 2.2%. The model was discretized with 0.5 million volume cells after mesh dependency testing. At 0.4 million volume cells, the CHN03 mesh converged. In
Table 9 and
Table 10, respectively, mesh details for the CT209 and CHN13 artery models are shown.
There were five sets of meshes for CHN03 (with mesh element numbers of 69,681; 139,833; 286,897; 406,606; and 779,482) to study mesh convergence.
Figure 10 shows that, when the grid number was increased from 100,000 to about 1.05 million, the change value of the distal pressure was less than 5% (about 2.2%). After mesh dependency test, the model was discretized with a total of about 0.5 million volume cells. Further grid refinement led to <1% relative error. For CHN03, the mesh convergence results are shown in
Figure 10. The number of volume cells was finally set to 0.4 million.
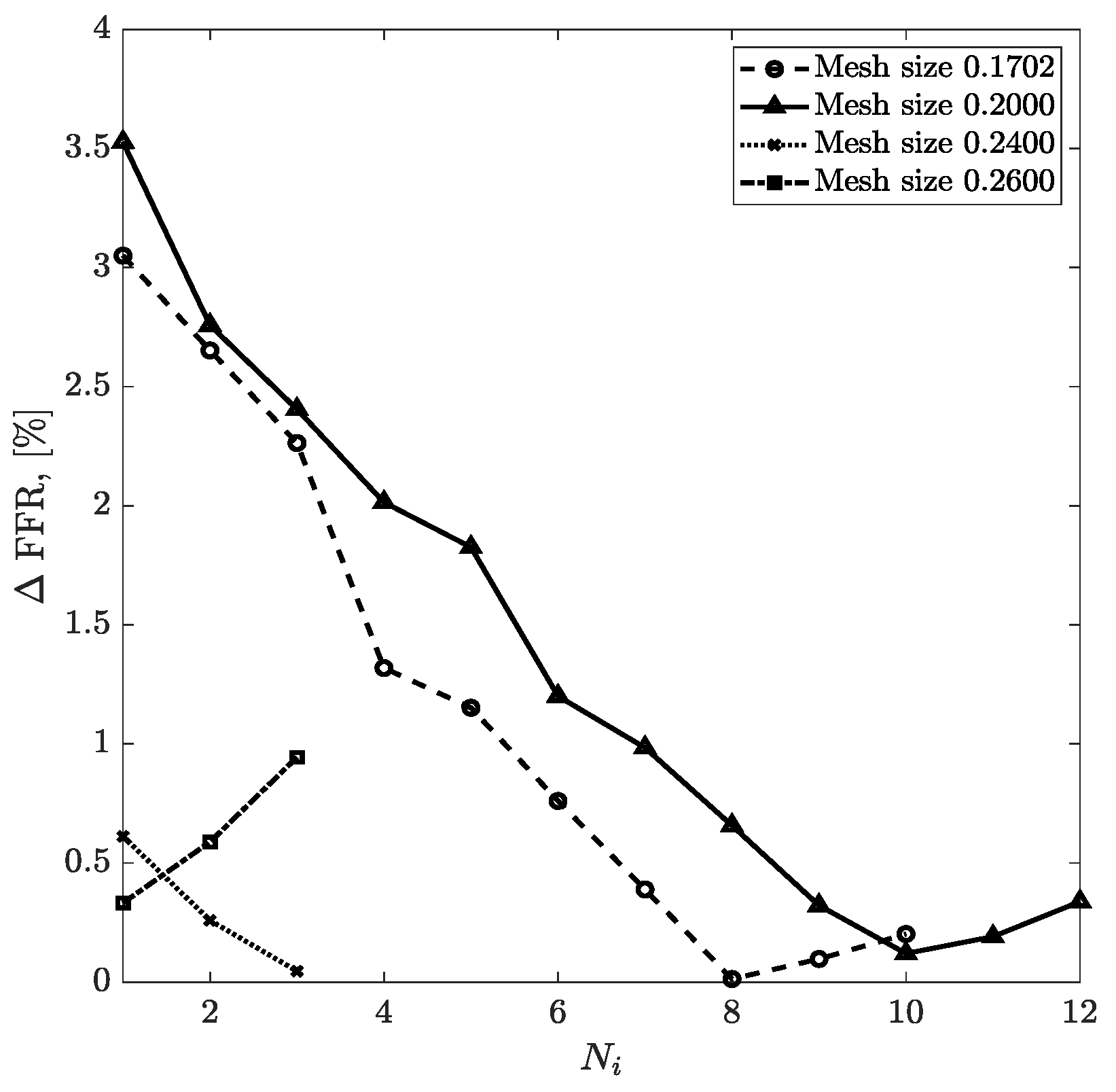
Figure 11 and
Figure 12 show the obtained values of FFR at each round of iteration and the percentage relative difference of the calculated and experimental FFR (degree of deviation from experimentally obtained FFR). The results obtained for mesh sizes of 0.1702 and 0.20 were very close to the experimental value of FFR = 0.76 at the end of the eighth and the tenth rounds of iteration, respectively. At the same time, the results obtained for mesh sizes from 0.24 to 0.26 mesh demonstrated a constant decrease, as shown in
Figure 11, which yielded a constant negative slope. FFR values for mesh sizes between 0.1702 and 0.20 converged when they reached the experimental FFR value. The percentage relative differences of 0.20% and 0.34% for FFR values were recorded for the mesh sizes of 0.1702 and 0.20, respectively.
The simulations of blood flow in the CHN13 model were performed using three mesh sizes (coarse, fine, and very fine). Initially, the number of iterations was set to ten; however, since the relative errors for some mesh sizes showed systematic increases, the simulations with 0.53 and 0.22 mesh sizes were stopped at the fifth and sixth rounds of iterations, respectively. The experimental FFR for the CHN13 model was 0.68. The results showed that the finest mesh size of 0.22 mm produced the closest amount to this value. The FFR obtained from the simulations with the finest mesh size was equal to 0.691, as shown in
Figure 13. The final values of FFR obtained using the 0.35 and 0.53 mesh sizes were 0.619 and 0.531, respectively. Additionally, the results in
Figure 14 show that the accuracy of the FFR obtained from simulations with the 0.35 mesh size decreased with the number of iterations. Consequently, the maximum error was observed in the tenth round of iterations.
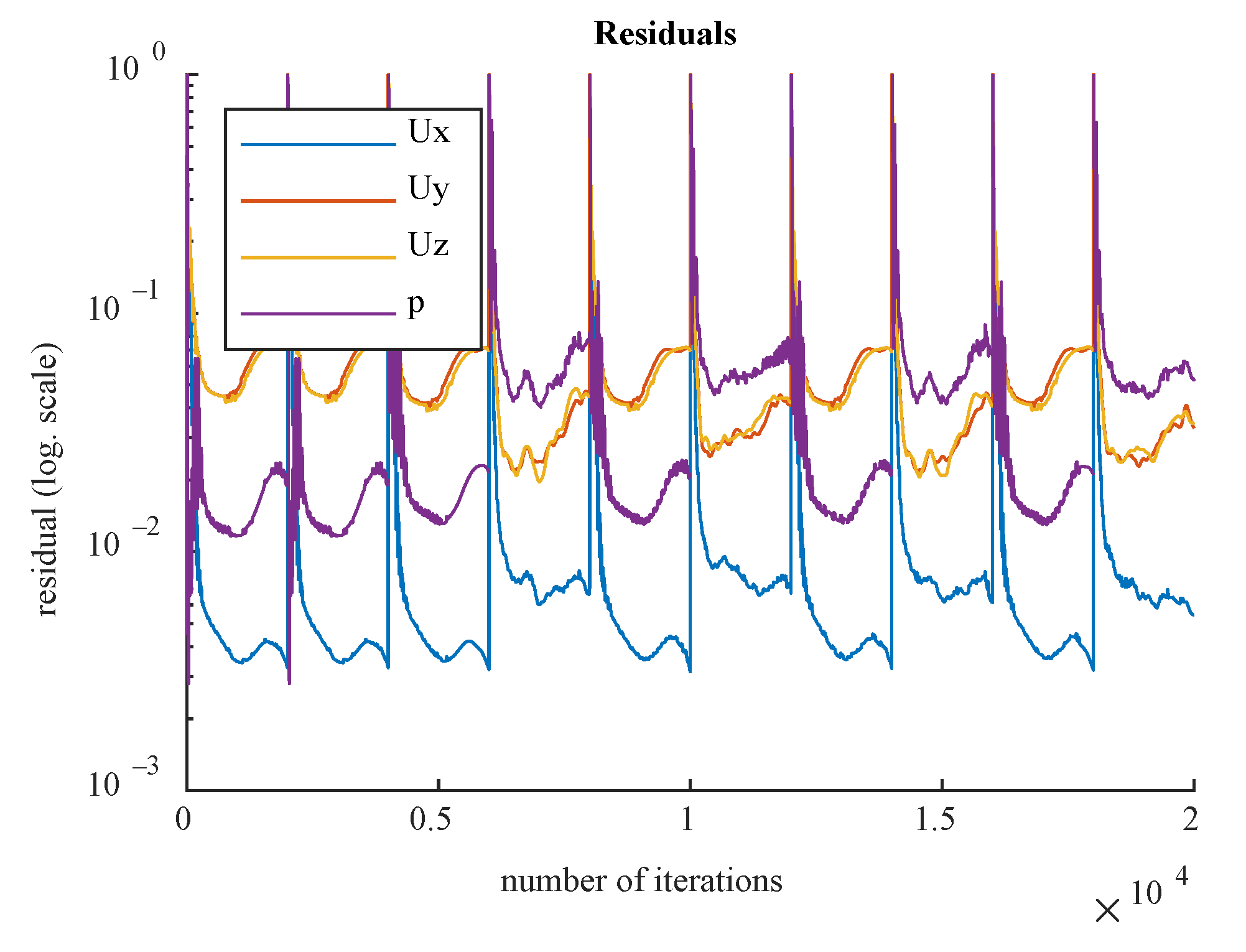
The pressure and flow rate residuals at all the outlets were defined as the averages of relative percentage differences in consecutive iterations. The convergence of the CFD simulation could be monitored by examining the reduction in the values of pressure and velocity/momentum equation residuals at the outlets as well.
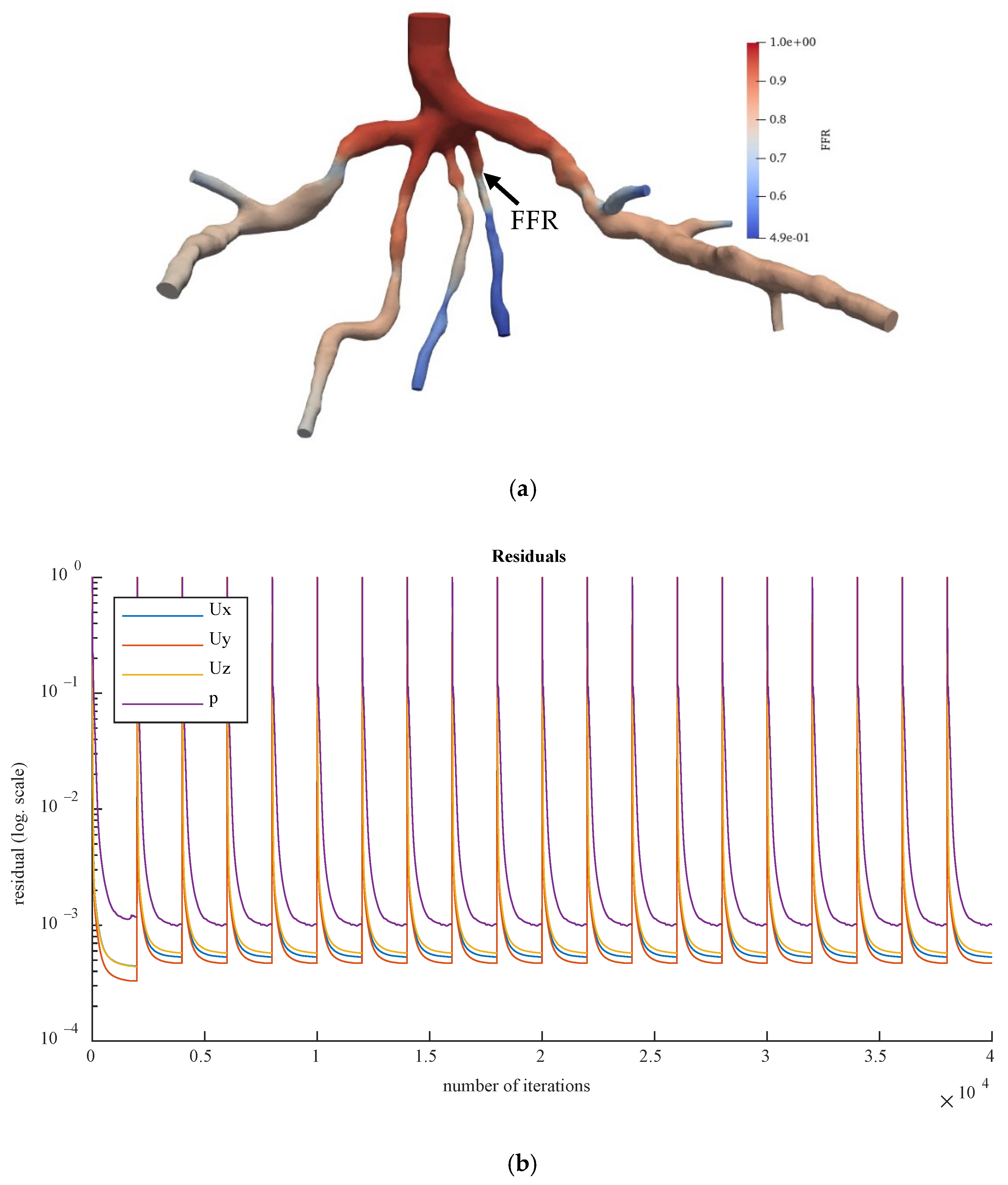
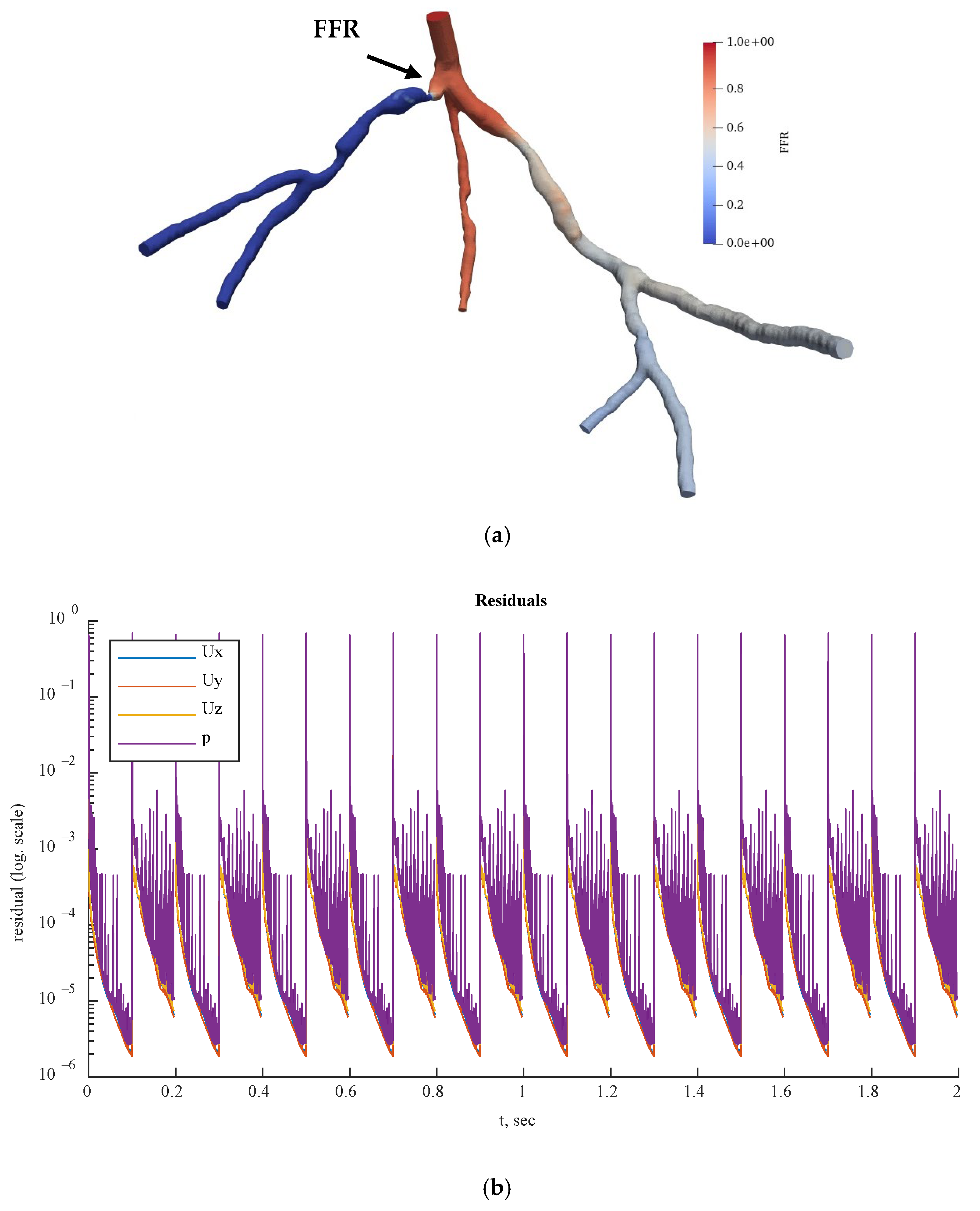
Figure 15 reveals the pressure and flow velocity residuals at the outlets of CT209 for all the iterations, where residual values are plotted in logarithmic scale.
FFR was calculated using Equation (13), and for the CT209 model, it had an experimental value of 0.76 [
23].
Figure 15 shows the derived FFR values from the most recent iteration, along with the relative percentage difference between the computed and experimental FFR (the degree of deviation from the experimentally obtained FFR). The calculated noninvasive FFR value of 0.73 by Zhang et al. [
23] is different from the experimental (ICA) FFR value of approximately 0.76 for the CT209 model. After conducting a mesh sensitivity analysis, Sumbekova et al. [
19] from our research group obtained a final FFR value of FFR = 0.757, which was very close to the ICA FFR. The same algorithm implemented in OpenFOAM produced results that were similar to the ICA measurement, with a final FFR value of FFR = 0.762.
According to Zhang et al. [
23], the left anterior descending (LAD) proximal artery was the site of arterial stenosis in the CT209 model [
23]. In
Figure 15, the LAD proximal region is the dark blue area of the blood artery, and it was observed that the artery stenosis was in the same location as that identified by Zhang et al. [
23].
Figure 15a includes the visualized FFR findings from the tenth iteration of the steady-state PBA.
We compared the steady-state results obtained by the PBA method in OpenFOAM with those obtained using a traditional lumped parameter method and the current approach used by our research group [
19], as well as with the ICA measurement results. It was found that the PBA method demonstrated good accuracy and efficiency, similar to the traditional methods.
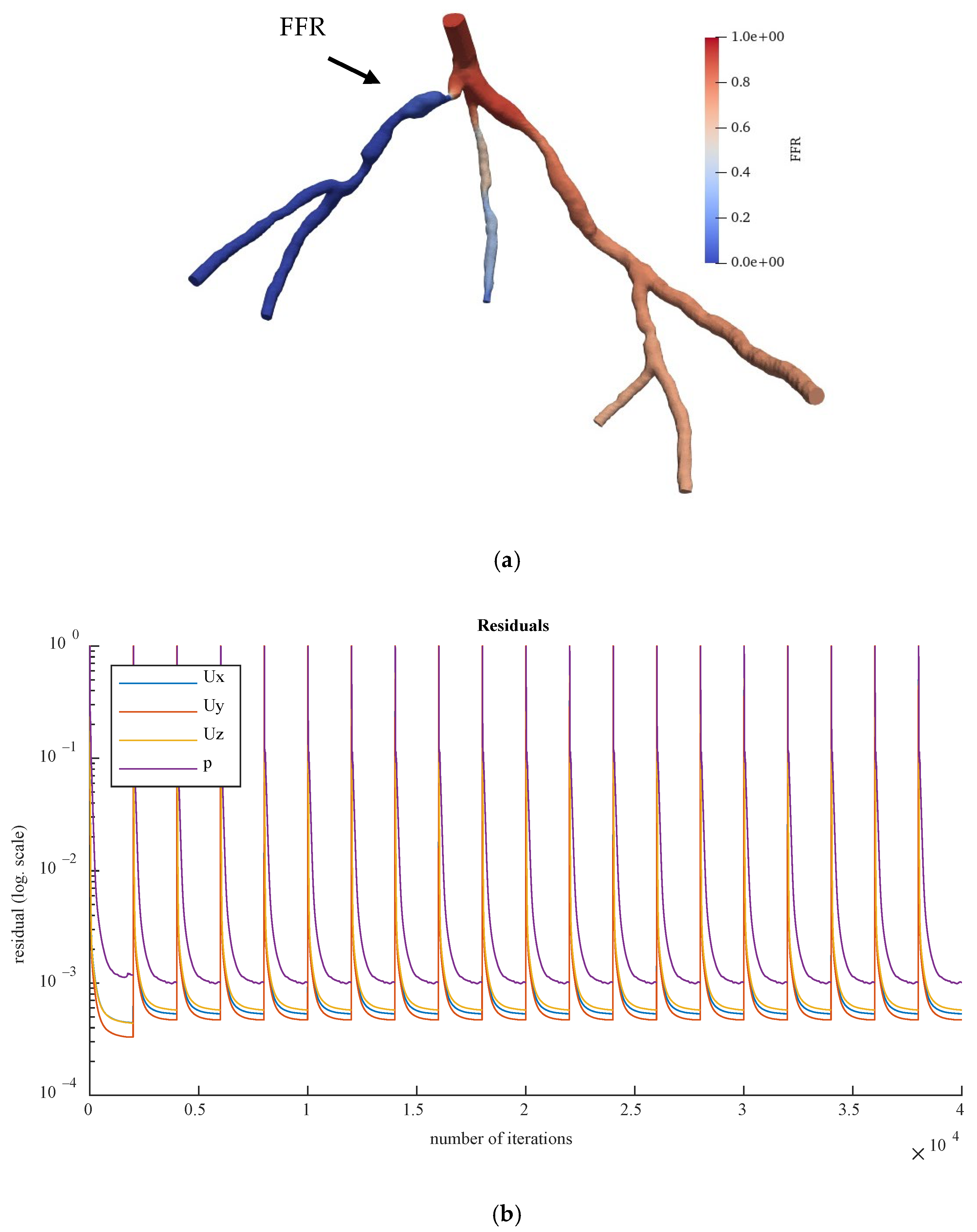
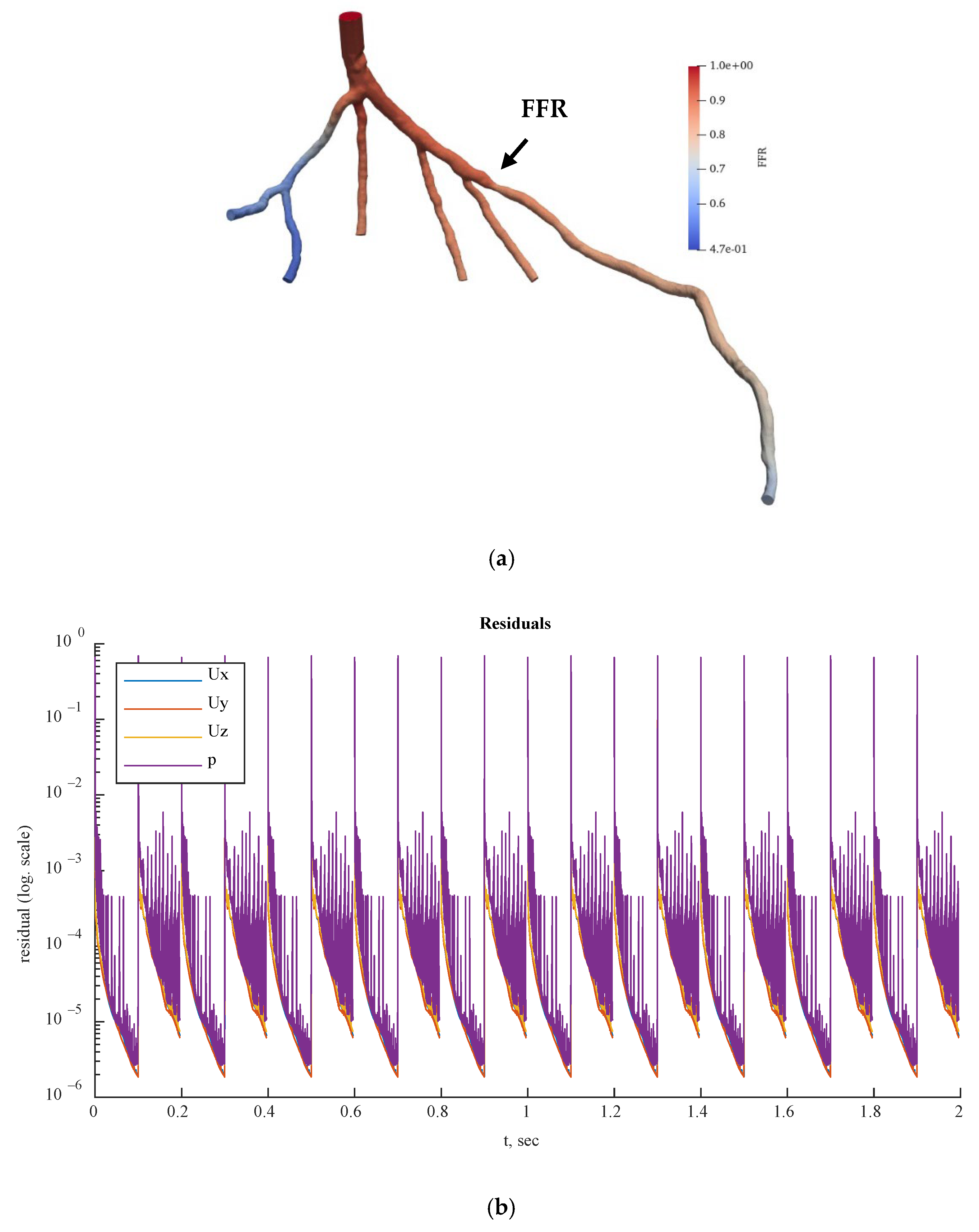
Figure 16 and
Figure 17 show the visualized FFR distributions for the CHN13 and CHN03 models, respectively. The calculated FFRs for CHN03 and CHN13 by the OpenFOAM PBA were 0.88 and 0.683, respectively, which are in excellent agreement with the corresponding experimental values of 0.86 and 0.68.
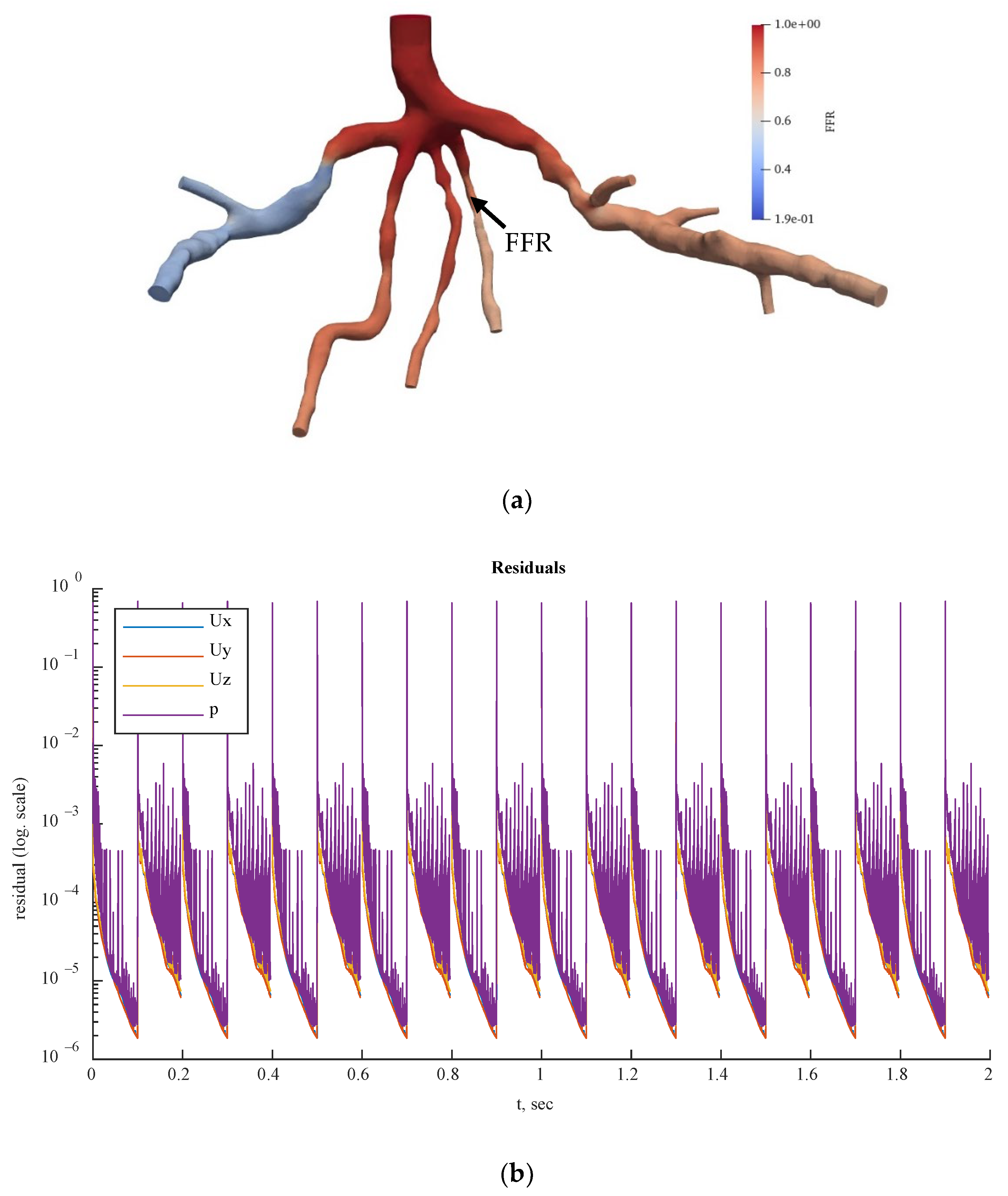
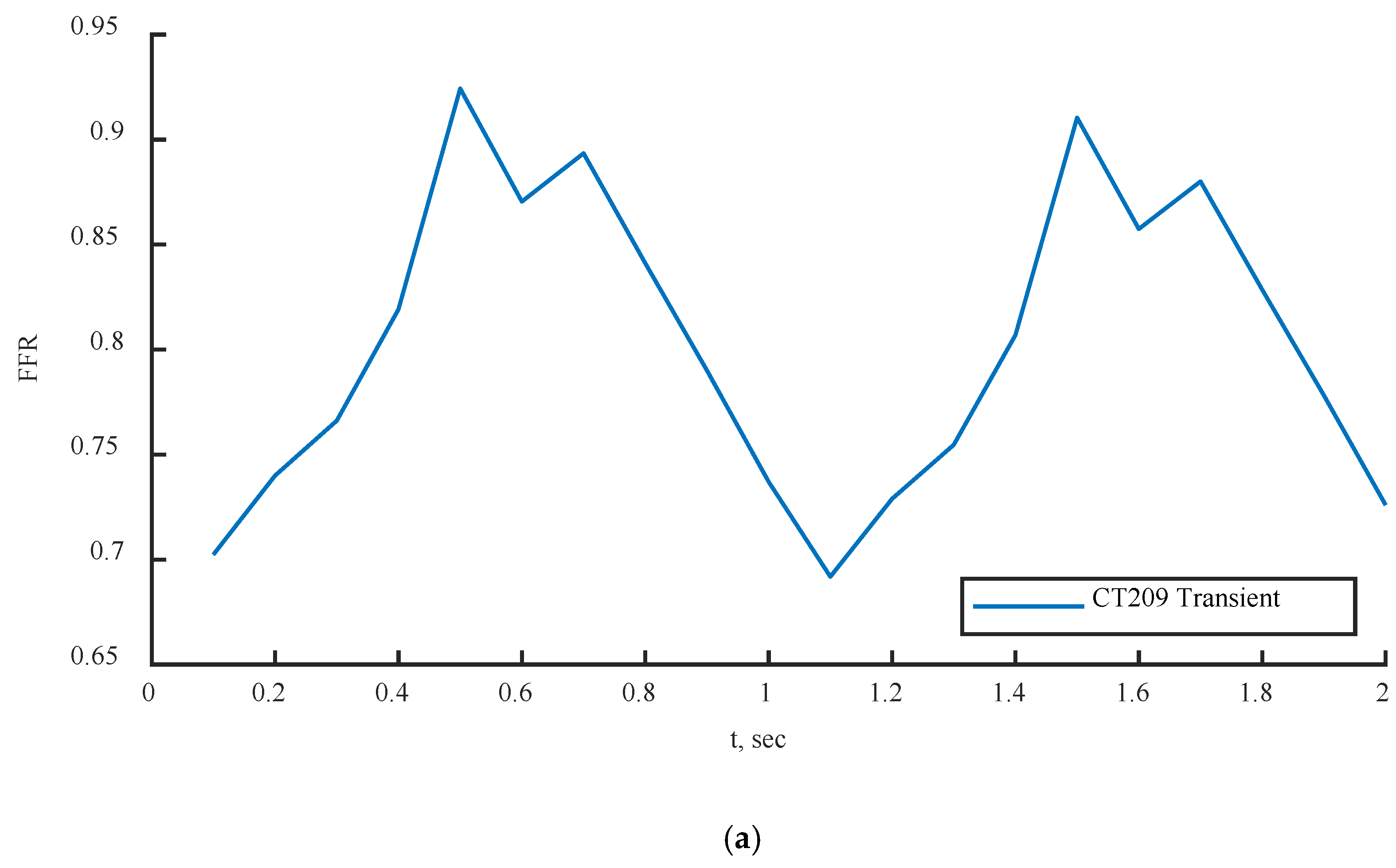
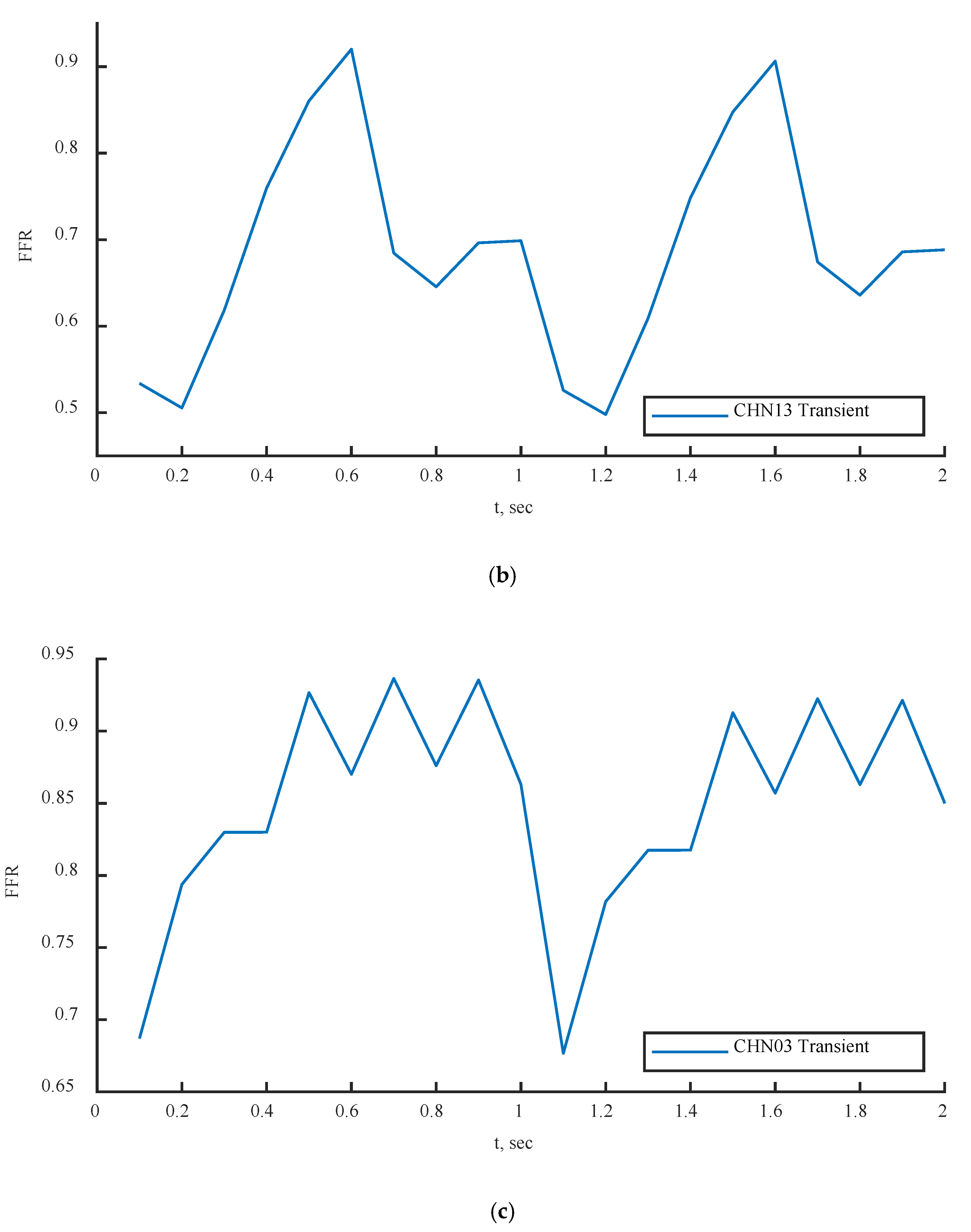
Figure 18,
Figure 19 and
Figure 20 show the FFR distributions in transient simulations for the CT209, CHN13, and CHN03 models, respectively. The PBA residuals also demonstrated convergence in the velocity and pressure equations.
Preliminary steady-state simulations were conducted to achieve convergence of the model before performing OpenFOAM transient PBA simulations using the mapFields package. The mapFields utility converts one or more fields that are specific to a geometry into their equivalents, and it is universal because there is no requirement for the geometries to be similar [
17].
In
Figure 18b,
Figure 19b and
Figure 20b, during iterations, the PBA method switched the boundary conditions, which could lead to high-frequency oscillations. For transient simulations, it was necessary to drive the solution to convergence at each timestep, which resulted in fluctuations that appeared to have high frequencies. The solution could exhibit wave reflections resembling high-frequency oscillations due to the complex geometry.
Figure 16 compares the FFR values between steady-state and transient simulations at the locations indicated by the FFR arrows in
Figure 16,
Figure 17,
Figure 18,
Figure 19 and
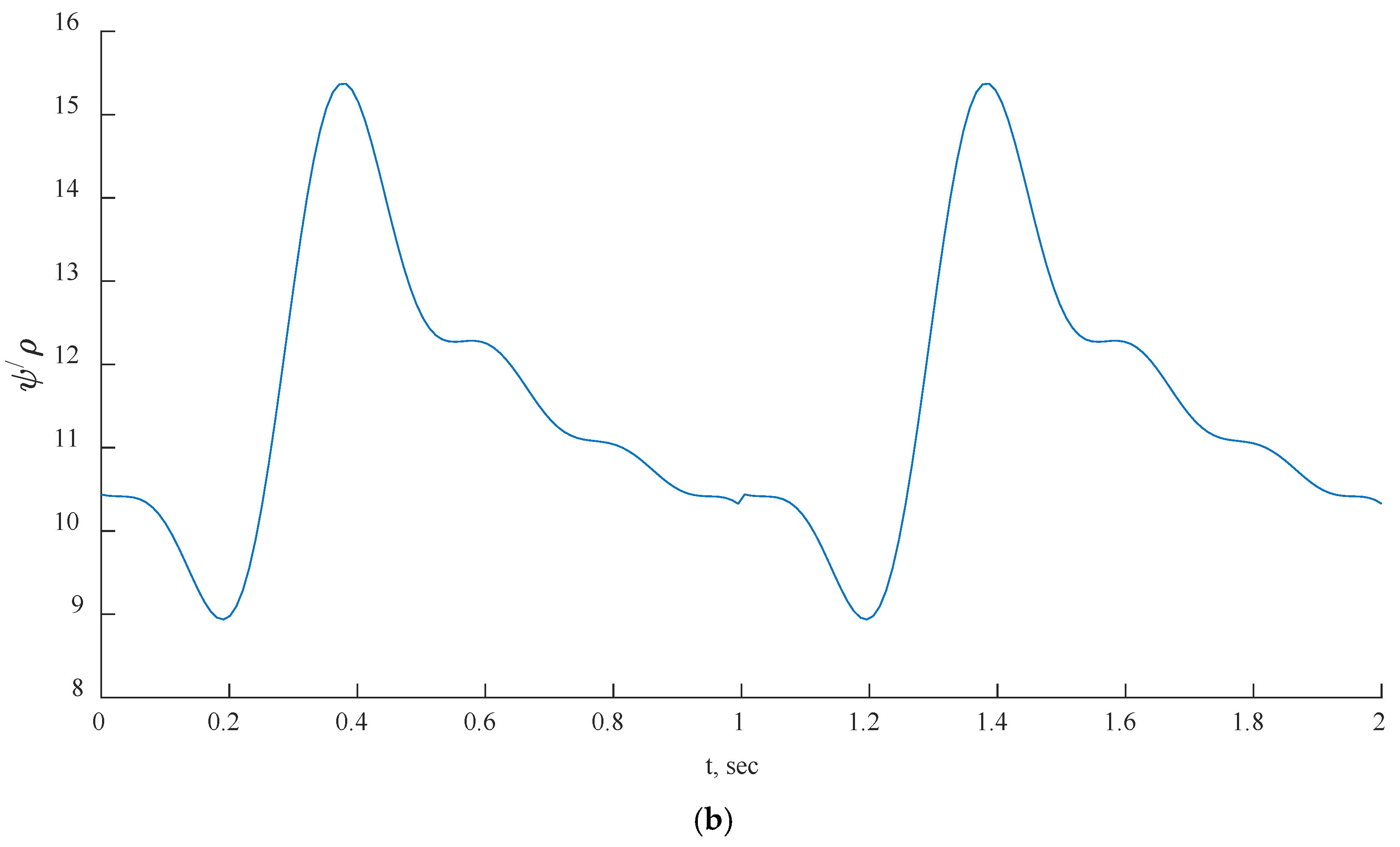
Figure 20. The FFR values increased in all three scenarios and tended to decrease due to alignment with the flow rate waveform.
The mean FFR values are included in
Table 11 as the outcome values for the transient simulations. As shown in
Figure 21c, the second half of the transient instance exhibited rapid fluctuations in FFR due to changes in the PBA boundary conditions. In
Figure 21a,b, the models show good agreement with the flow rate inputs, indicating that the PBA method could converge over several flow rate cycles.
Three artery models were analyzed using both methods: the standard LPM technique was used in ANSYS [
23], while the suggested PBA was implemented in Simvascular [
19] and OpenFOAM for steady-state and transient cases, respectively, as described in
Appendix A and
Appendix B. Additionally, all abbreviations in this work are provided in
Appendix C.
Table 9 provides a summary of the comparison between the computed and experimental ICA FFRs [
19]. This table shows that the recommended PBA produced results that were independent of the solver. Simvascular and OpenFOAM were used for the suggested PBA, while ANSYS was used for the conventional LPM approach.
The findings indicate that the relative errors or discrepancies across steady-state simulations in ANSYS CFX, Simvascular, and OpenFOAM did not exceed 3.24%. The results also show that the relative error disparities in transient simulations in OpenFOAM did not exceed 5.26%. The smallest inaccuracy was observed between the Simvascular and OpenFOAM steady-state PBA for CT209 at 0.26%. The largest inaccuracy for CT209 was in the OpenFOAM transient PBA at 5.26%. This may be due to the highest flow rate values, which could increase the overall FFR readings in the tested artery. The error in the OpenFOAM transient PBA for CHN03 was the smallest recorded at 0.02%, while the largest inaccuracy for CHN03 was in the OpenFOAM steady-state PBA at 2.33%. The error in the OpenFOAM steady-state PBA for CHN13 was the lowest at 0.44%, while the highest error was in ANSYS CFX at 3.24%. Despite the error peaks associated with various methods, the PBA approach showed a promising performance.
The classic LPM and LPNM techniques, which involve the calculation of capacitance, resistance, and inductance and the creation of a fictitious downstream capillary vessel network using fractal techniques, are fundamentally different from the PBA approach. The LPM and LPNM techniques require the calculation of resistance at the outlets and the use of additional inlet measurement conditions and numerical iterations, which are not based purely on physiology. In contrast, the PBA technique is patient-specific and physiologically based. It estimates the initial conditions at the outlets using Murray’s law and then uses the geometry of the arterial tree, the conservation laws incorporated into CFD, the suggested numerical iteration scheme, and the additional measured inlet patient-specific conditions to determine the final conditions at the outlets. The suggested PBA strategy, which is completely based on physics and physiology and is patient-specific, was also shown to be computationally effective. It was integrated into the standard CFD pressure correction iterations as an iterative boundary-switching system that did not require two simulation rounds.
The PBA approach was further validated using the standard LPM method published by Zhang et al. [
23] for real-patient arteries. The LPM method employs a reference pressure, resistances at every outlet representing the flow resistance from the downstream microvasculature, and an overall resistance for the entire CAT that is related to outlet resistances through a population-averaged empirical scaling law [
23]. The LPM is an iterative procedure that calculates the resistances and reference pressure to determine the outlet pressures in each branch outlet. It has been found that the LPM does not always ensure convergence to a unique solution for every situation. In contrast, the suggested PBA also achieved convergence to precise answers for all three analyzed scenarios. The PBA approach was found to be more reliable than the LPM because it is physiologically based and patient-specific, while the LPM does not consider these characteristics.
Additionally, the PBA approach was verified using the benchmark model of an FDA nozzle. The goal was to replicate the study by Stiehm et al. [
18] using the PBA approach. The computational results for axial velocity along the centerline of the nozzle geometry were compared to the CFD data from the FDA’s round-robin study [
18] for validation. The inlet conditions shown in
Figure 7 and
Figure 8 were the same as those in the Stiehm et al. [
18] study. The FFR distribution along the profile of the FDA nozzle can be seen in
Figure 22, but we used the velocity results along the centerline for validation.
Residual values for the steady-state and transient simulations are shown in
Figure 23 and
Figure 24, respectively. Based on the appropriate convergence of the residual values, the findings could be considered acceptable.
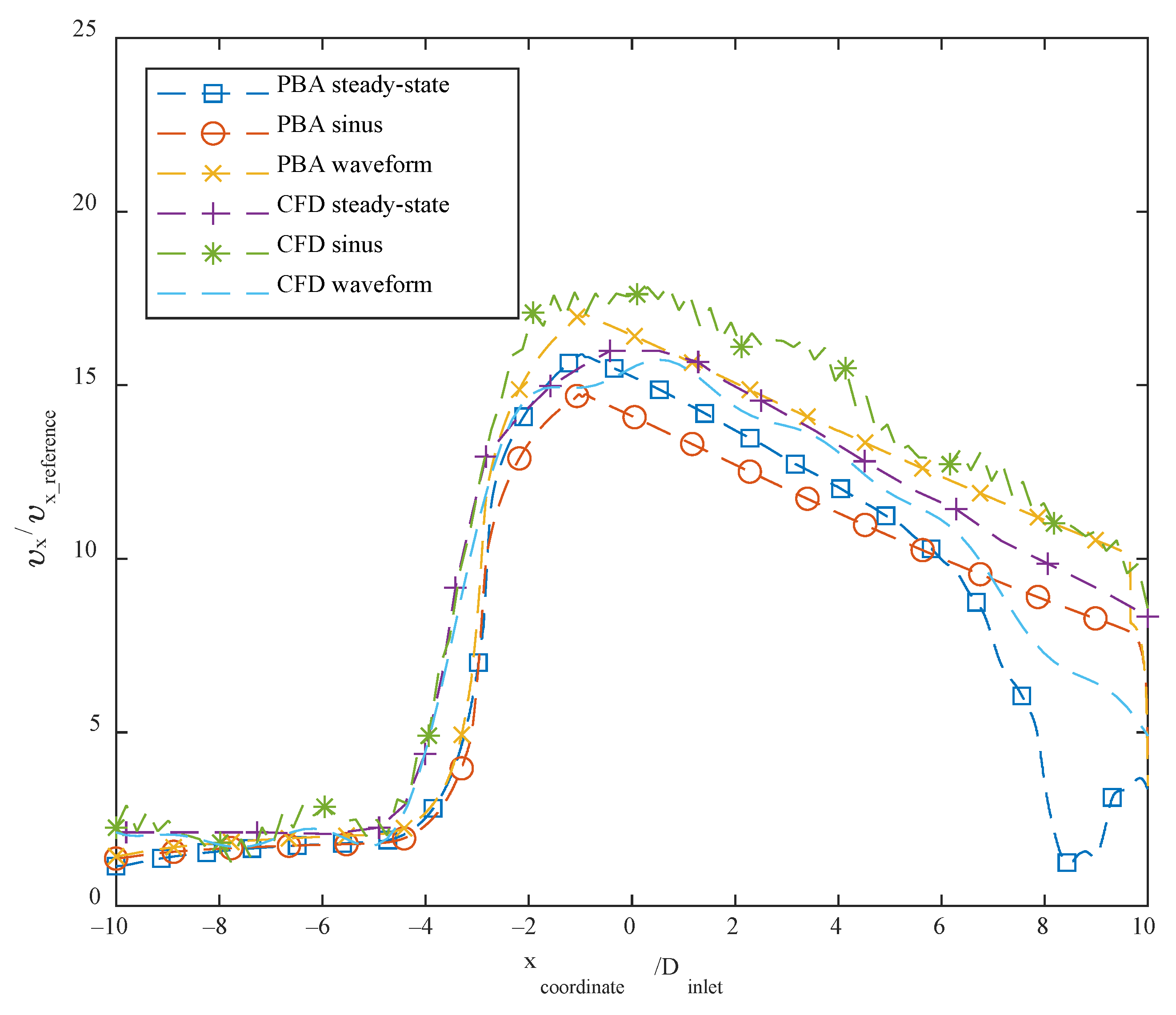
The axial velocity results for the CFD steady-state and CFDPBA databases for the idealized FDA nozzle matched closely, as shown in
Figure 25. Additionally, the time-averaged axial velocity obtained from the transient CFD simulation with waveform inlet conditions agreed well with the steady-state PBA velocity data. However, there were minor differences downstream of the nozzle between 5D and 10D (
Figure 7). The inclusion of wave pressure in the PBA algorithm caused the PBA sinus and waveform deviation. Since the pressure was constant in the steady-state example, the findings were not affected, but the waveform pressure caused a slight fluctuation in the centerline velocity values.