Connectivity Analysis in EEG Data: A Tutorial Review of the State of the Art and Emerging Trends
Abstract
1. Introduction
2. Brain Connectivity: An Overview of Key Topics
3. Functional Connectivity: A Classification of Data-Driven Methods
- Linear time series analysis methods, typically based on the autoregressive (AR) linear model representation of the interactions, which are thus referred to as model-based, or non-linear methods, typically based on probabilistic descriptions of the observed dynamics and thus referred to as model-free.
- Methods developed in the time, frequency, or information-theoretic domain, based on the features of the investigated signals one is interested in (respectively, temporal evolution, oscillatory content, and probabilistic structure);
- Methods treating the time series that represent the neuronal activity of (groups of) brain units as realizations of independent identically distributed (i.i.d.) random variables or identically distributed (i.d.) random processes, respectively, studied in terms of their zero-lag (i.e., static) or time-lagged (i.e., dynamic) correlation structure.
- Approaches that face the analysis of brain connectivity looking at pairs (pairwise analysis) or groups (multivariate analysis) of time series representative of the observed brain dynamics.
3.1. Model-Based vs. Model-Free Connectivity Estimators
3.2. Time-Domain vs. Frequency-Domain Connectivity Estimators
4. Functional Connectivity Estimation Approaches
4.1. Time-Domain Approaches
4.1.1. Non-Directed Connectivity Measures
Pairwise Measures
Multivariate Measures
4.1.2. Directed Connectivity Measures
Pairwise Measures
Multivariate Measures
4.1.3. Applications of Time-Domain Approaches to EEG Data
4.2. Frequency-Domain Approaches
4.2.1. Non-Directed Connectivity Measures
Pairwise Measures
Multivariate Measures
4.2.2. Directed Connectivity Measures
Pairwise Measures
Multivariate Measures
4.2.3. Applications of Frequency-Domain Approaches to EEG Data
4.3. Information-Domain Approaches
4.3.1. Non-Directed Connectivity Measures
Pairwise Measures
Multivariate Measures
4.3.2. Directed Connectivity Measures
Pairwise Measures
Multivariate Measures
4.3.3. Applications of Information-Domain Approaches to EEG Data
4.4. Other Connectivity Estimators
4.4.1. Phase Synchronization
4.4.2. High-Order Interactions
4.4.3. Complex Network Measures
- Functional integration, based on the concept of path [248,254] and estimating the ease of communication between brain areas. These measures have been found useful in studies related to obsessive-compulsive disorders, since their alterations seem to be correlated with the severity of the illness [255,256]. Networks which are simultaneously highly segregated and integrated are referred to as small-world networks; a measure of small-worldness was proposed to describe this property [248,257].
- Network motifs, which are subgraphs showing patterns of local connectivity.
- Network resilience, based on the evidence that anatomical connectivity influences the ability of neuropathological lesions to affect brain activity.
4.5. Statistical Validation Approaches
- Randomly shuffled surrogates [277], which are realizations of i.i.d. stochastic processes with the same mean, variance, and probability distribution as the original series, generated by randomly permuting in temporal order the samples of the original series; this procedure destroys the autocorrelation function.
- Fourier transform (FT) or phase-randomized surrogates [274], which are realizations of linear stochastic processes with the same power spectra as the original series, obtained by a phase randomization procedure applied independently to each series.
- Iterative amplitude adjusted FT (iAAFT) surrogates [275], which are realizations of linear stochastic processes with the same autocorrelations and probability distributions as the original series, and the power spectra are the best approximations of the original ones according to the number of iterations.
- AR surrogates [13], which are realizations of linear stochastic processes with the same power spectra as the original series, constructed by fitting an AR model to each of the original series, using independent white noises as model inputs.
5. EEG Acquisition and Pre-Processing
5.1. Resampling
5.2. Filtering and Artifact Rejection
5.3. Bad Channel Identification, Rejection, and Interpolation
5.4. Re-Referencing
6. Source Connectivity Analysis
- Forward problem—definition of a set of sources and their characteristics and simulation of the signal that would be measured (i.e., the potential on the scalp) knowing the physical characteristics of the medium that makes it diffuse;
- Inverse problem—comparison of the signal generated by the head model with the actual measured EEG and adjustment of the parameters of the source model to make them as similar as possible.
6.1. Forward Problem and Head Models
6.2. Inverse Problem
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AR | Autoregressive |
| bCoh | Block Coherence |
| bDC | Block Directed Coherence |
| BEM | Boundary Element Models |
| bPDC | Block Partial Directed Coherence |
| BSS | Blind Source Separation |
| CAR | Average Reference |
| cGC | Conditional Granger Causality |
| cIC | Conditional Instantaneous Causality |
| cMI | Conditional Mutual Information |
| Coh | Coherence |
| Corr | Correlation |
| cTD | Conditional Total Dependence |
| cTE | Conditional Transfer Entropy |
| DC | Directed Coherence |
| DFT | Discrete Fourier Transform |
| DTF | Directed Transfer Function |
| EC | Effective Connectivity |
| ECD | Equivalent Current Dipole |
| ECoG | Electrocorticography |
| EEG | Electroencephalogram |
| EOG | Electrooculogram |
| FC | Functional Connectivity |
| FEM | Finite Element Models |
| FIR | Finite Impulse Response |
| fMRI | Functional Magnetic Resonance Imaging |
| GC | Granger Causality |
| HOIs | High-Order Interactions |
| IC | Instantaneous Causality |
| ICA | Independent Component Analysis |
| II | Interaction Information |
| i.i.d | Independent Identically Distributed |
| IIR | Infinite Impulse Response |
| i.d | Identically Distributed |
| ITE | Interaction Transfer Entropy |
| jTD | Joint Total Dependence |
| jTE | Joint Transfer Entropy |
| LDD | Linear Distributed Dipole |
| MI | Mutual Information |
| MIR | Mutual Information Rate |
| PCA | Principal Component Analysis |
| PCC | Pearson Correlation Coefficient |
| PCoh | Partial Coherence |
| PCorr | Partial Correlation |
| PDC | Partial Directed Coherence |
| PLV | Phase Locking Value |
| PRho | Partial Correlation Coefficient |
| PSD | Power Spectral Density |
| PSI | Phase Slope Index |
| R | Redundancy |
| REST | Reference Electrode Standardization Technique |
| Rho | Correlation Coefficient |
| S | Synergy |
| SC | Structural Connectivity |
| SNR | Signal-to-Noise Ratio |
| SR | Sampling Rate |
| TD | Total Dependence |
| TE | Transfer Entropy |
| VAR | Vector Autoregressive |
| WSS | Wide-Sense Stationary |
References
- Sporns, O. Structure and function of complex brain networks. Dialogues Clin. Neurosci. 2013, 15, 247–262. [Google Scholar] [CrossRef]
- Craddock, R.; Tungaraza, R.; Milham, M. Connectomics and new approaches for analyzing human brain functional connectivity. Gigascience 2015, 4, 13. [Google Scholar] [CrossRef]
- Sporns, O.; Bassett, D. Editorial: New Trends in Connectomics. Netw. Neurosci. 2018, 2, 125–127. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.E.; Bénar, C.G.; Quilichini, P.P.; Friston, K.J.; Jirsa, V.K.; Bernard, C. A systematic framework for functional connectivity measures. Front. Neurosci. 2014, 8, 405. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Astolfi, L.; Valdés-Sosa, P.A.; Marinazzo, D.; Palva, S.O.; Bénar, C.G.; Michel, C.M.; Koenig, T. Electrophysiological Brain Connectivity: Theory and Implementation. IEEE Trans. Biomed. Eng. 2019, 66, 2115–2137. [Google Scholar] [CrossRef] [PubMed]
- Bastos, A.M.; Schoffelen, J.M. A tutorial review of functional connectivity analysis methods and their interpretational pitfalls. Front. Syst. Neurosci. 2016, 9, 175. [Google Scholar] [CrossRef]
- Cao, J.; Zhao, Y.; Shan, X.; Wei, H.L.; Guo, Y.; Chen, L.; Erkoyuncu, J.A.; Sarrigiannis, P.G. Brain functional and effective connectivity based on electroencephalography recordings: A review. Hum. Brain Mapp. 2022, 43, 860–879. [Google Scholar] [CrossRef]
- Goodfellow, M.; Andrzejak, R.; Masoller, C.; Lehnertz, K. What Models and Tools can Contribute to a Better Understanding of Brain Activity? Front. Netw. Physiol. 2022, 2, 907995. [Google Scholar] [CrossRef]
- McIntosh, A.; Gonzalez-Lima, F. Network interactions among limbic cortices, basal forebrain, and cerebellum differentiate a tone conditioned as a Pavlovian excitor or inhibitor: Fluorodeoxyglucose mapping and covariance structural modeling. J. Neurophysiol. 1994, 72, 1717–1733. [Google Scholar] [CrossRef]
- Friston, K.J.; Harrison, L.; Penny, W. Dynamic causal modelling. Neuroimage 2003, 19, 1273–1302. [Google Scholar] [CrossRef]
- David, O.; Kiebel, S.J.; Harrison, L.M.; Mattout, J.; Kilner, J.M.; Friston, K.J. Dynamic causal modeling of evoked responses in EEG and MEG. NeuroImage 2006, 30, 1255–1272. [Google Scholar] [CrossRef] [PubMed]
- Geweke, J. Measurement of linear dependence and feedback between multiple time series. J. Am. Stat. Assoc. 1982, 77, 304–313. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed]
- Saito, Y.; Harashima, H. Tracking of information within multichannel EEG record causal analysis in eeg. In Recent Advances in {EEG} and {EMG} Data Processing; Yamaguchi, N., Fujisawa, K., Eds.; Elsevier: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Baccalá, L.A.; Sameshima, K.; Ballester, G.; Valle, A.C.d.; Yoshimoto, C.E.; Timo-Iaria, C. Studying the interaction between brain via direct coherence and Granger causality. Appl. Signal Process 1998, 5, 40–48. [Google Scholar] [CrossRef]
- Baccalá, L.A.; Sameshima, K. Partial directed coherence: A new concept in neural structure determination. Biol. Cybern. 2001, 84, 463–474. [Google Scholar] [CrossRef] [PubMed]
- Sameshima, K.; Baccalá, L.A. Using partial directed coherence to describe neuronal ensemble interactions. J. Neurosci. Methods 1999, 94, 93–103. [Google Scholar] [CrossRef]
- Kaminski, M.J.; Blinowska, K.J. A new method of the description of the information flow in the brain structures. Biol. Cybern. 1991, 65, 203–210. [Google Scholar] [CrossRef]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef]
- Barrett, A.B.; Barnett, L.; Seth, A.K. Multivariate Granger causality and generalized variance. Phys. Rev. E 2010, 81, 041907. [Google Scholar] [CrossRef]
- Faes, L.; Erla, S.; Nollo, G. Measuring connectivity in linear multivariate processes: Definitions, interpretation, and practical analysis. Comput. Math. Methods Med. 2012, 2012, 140513. [Google Scholar] [CrossRef]
- Gelfand, I.M.; IAglom, A. Calculation of the Amount of Information about a Random Function Contained in Another Such Function; American Mathematical Society Providence: Providence, RI, USA, 1959. [Google Scholar]
- Duncan, T.E. On the calculation of mutual information. SIAM J. Appl. Math. 1970, 19, 215–220. [Google Scholar] [CrossRef]
- Chicharro, D. On the spectral formulation of Granger causality. Biol. Cybern. 2011, 105, 331–347. [Google Scholar] [CrossRef] [PubMed]
- Rosas, F.E.; Mediano, P.A.; Gastpar, M.; Jensen, H.J. Quantifying high-order interdependencies via multivariate extensions of the mutual information. Phys. Rev. E 2019, 100, 032305. [Google Scholar] [CrossRef] [PubMed]
- Stramaglia, S.; Scagliarini, T.; Daniels, B.C.; Marinazzo, D. Quantifying dynamical high-order interdependencies from the o-information: An application to neural spiking dynamics. Front. Physiol. 2021, 11, 595736. [Google Scholar] [CrossRef]
- Faes, L.; Mijatovic, G.; Antonacci, Y.; Pernice, R.; Barà, C.; Sparacino, L.; Sammartino, M.; Porta, A.; Marinazzo, D.; Stramaglia, S. A New Framework for the Time-and Frequency-Domain Assessment of High-Order Interactions in Networks of Random Processes. IEEE Trans. Signal Process. 2022, 70, 5766–5777. [Google Scholar] [CrossRef]
- Scagliarini, T.; Nuzzi, D.; Antonacci, Y.; Faes, L.; Rosas, F.E.; Marinazzo, D.; Stramaglia, S. Gradients of O-information: Low-order descriptors of high-order dependencies. Phys. Rev. Res. 2023, 5, 013025. [Google Scholar] [CrossRef]
- Bassett, D.S.; Bullmore, E. Small-World Brain Networks. Neuroscientist 2006, 12, 512–523. [Google Scholar] [CrossRef]
- Stam, C.J.; Reijneveld, J.C. Graph theoretical analysis of complex networks in the brain. Nonlinear Biomed. Phys. 2007, 1, 3. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Toga, A.W.; Mazziotta, J.C. Brain Mapping: The Systems; Gulf Professional Publishing: Houston, TX, USA, 2000; Volume 2. [Google Scholar]
- Toga, A.W.; Mazziotta, J.C.; Mazziotta, J.C. Brain Mapping: The Methods; Academic Press: Cambridge, MA, USA, 2002; Volume 1. [Google Scholar]
- Dale, A.M.; Halgren, E. Spatiotemporal mapping of brain activity by integration of multiple imaging modalities. Curr. Opin. Neurobiol. 2001, 11, 202–208. [Google Scholar] [CrossRef]
- Achard, S.; Bullmore, E. Efficiency and cost of economical brain functional networks. PLoS Comput. Biol. 2007, 3, 0174–0183. [Google Scholar] [CrossRef] [PubMed]
- Park, C.H.; Chang, W.H.; Ohn, S.H.; Kim, S.T.; Bang, O.Y.; Pascual-Leone, A.; Kim, Y.H. Longitudinal changes of resting-state functional connectivity during motor recovery after stroke. Stroke 2011, 42, 1357–1362. [Google Scholar] [CrossRef] [PubMed]
- Ding, L.; Shou, G.; Cha, Y.H.; Sweeney, J.A.; Yuan, H. Brain-wide neural co-activations in resting human. NeuroImage 2022, 260, 119461. [Google Scholar] [CrossRef] [PubMed]
- Rizkallah, J.; Amoud, H.; Fraschini, M.; Wendling, F.; Hassan, M. Exploring the Correlation Between M/EEG Source–Space and fMRI Networks at Rest. Brain Topogr. 2020, 33, 151–160. [Google Scholar] [CrossRef] [PubMed]
- Astolfi, L.; Cincotti, F.; Mattia, D.; Marciani, M.G.; Baccala, L.A.; de Vico Fallani, F.; Salinari, S.; Ursino, M.; Zavaglia, M.; Ding, L.; et al. Comparison of different cortical connectivity estimators for high-resolution EEG recordings. Hum. Brain Mapp. 2007, 28, 143–157. [Google Scholar] [CrossRef]
- Rolle, C.E.; Narayan, M.; Wu, W.; Toll, R.; Johnson, N.; Caudle, T.; Yan, M.; El-Said, D.; Watts, M.; Eisenberg, M.; et al. Functional connectivity using high density EEG shows competitive reliability and agreement across test/retest sessions. J. Neurosci. Methods 2022, 367, 109424. [Google Scholar] [CrossRef]
- Gore, J.C. Principles and practice of functional MRI of the human brain. J. Clin. Investig. 2003, 112, 4–9. [Google Scholar] [CrossRef]
- Friston, K.J.; Frith, C.D. Schizophrenia: A disconnection syndrome. Clin. Neurosci. 1995, 3, 89–97. [Google Scholar]
- Frantzidis, C.A.; Vivas, A.B.; Tsolaki, A.; Klados, M.A.; Tsolaki, M.; Bamidis, P.D. Functional disorganization of small-world brain networks in mild Alzheimer’s Disease and amnestic Mild Cognitive Impairment: An EEG study using Relative Wavelet Entropy (RWE). Front. Aging Neurosci. 2014, 6, 224. [Google Scholar] [CrossRef]
- Fogelson, N.; Li, L.; Li, Y.; Fernandez-del Olmo, M.; Santos-Garcia, D.; Peled, A. Functional connectivity abnormalities during contextual processing in schizophrenia and in Parkinson’s disease. Brain Cogn. 2013, 82, 243–253. [Google Scholar] [CrossRef]
- Holmes, M.D. Dense array EEG: Methodology and new hypothesis on epilepsy syndromes. Epilepsia 2008, 49, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Kleffner-Canucci, K.; Luu, P.; Naleway, J.; Tucker, D.M. A novel hydrogel electrolyte extender for rapid application of EEG sensors and extended recordings. J. Neurosci. Methods 2012, 206, 83–87. [Google Scholar] [CrossRef]
- Lebedev, M.A.; Nicolelis, M.A. Brain–machine interfaces: Past, present and future. Trends Neurosci. 2006, 29, 536–546. [Google Scholar] [CrossRef] [PubMed]
- Debener, S.; Ullsperger, M.; Siegel, M.; Engel, A.K. Single-trial EEG–fMRI reveals the dynamics of cognitive function. Trends Cogn. Sci. 2006, 10, 558–563. [Google Scholar] [CrossRef] [PubMed]
- Wolpaw, J.R.; Wolpaw, E.W. Brain-computer interfaces: Something new under the sun. In Brain-Computer Interfaces: Principles and Practice; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Bestmann, S.; Feredoes, E. Combined neurostimulation and neuroimaging in cognitive neuroscience: Past, present, and future. Ann. N. Y. Acad. Sci. 2013, 1296, 11–30. [Google Scholar] [CrossRef]
- Quyen, M.L.V.; Staba, R.; Bragin, A.; Dickson, C.; Valderrama, M.; Fried, I.; Engel, J. Large-Scale Microelectrode Recordings of High-Frequency Gamma Oscillations in Human Cortex during Sleep. J. Neurosci. 2010, 30, 7770–7782. [Google Scholar] [CrossRef]
- Jacobs, J.; Staba, R.; Asano, E.; Otsubo, H.; Wu, J.; Zijlmans, M.; Mohamed, I.; Kahane, P.; Dubeau, F.; Navarro, V.; et al. High-Frequency Oscillations (HFOs) in Clinical Epilepsy. Prog. Neurobiol. 2012, 98, 302–315. [Google Scholar] [CrossRef]
- Grosmark, A.D.; Buzsáki, G. Diversity in Neural Firing Dynamics Supports Both Rigid and Learned Hippocampal Sequences. Science 2016, 351, 1440–1443. [Google Scholar] [CrossRef]
- Gliske, S.V.; Irwin, Z.T.; Chestek, C.; Stacey, W.C. Effect of Sampling Rate and Filter Settings on High Frequency Oscillation Detections. Clin. Neurophysiol. Off. J. Int. Fed. Clin. Neurophysiol. 2016, 127, 3042–3050. [Google Scholar] [CrossRef]
- Bolea, J.; Pueyo, E.; Orini, M.; Bailón, R. Influence of Heart Rate in Non-linear HRV Indices as a Sampling Rate Effect Evaluated on Supine and Standing. Front. Physiol. 2016, 7, 501. [Google Scholar] [CrossRef]
- Jing, H.; Takigawa, M. Low Sampling Rate Induces High Correlation Dimension on Electroencephalograms from Healthy Subjects. Psychiatry Clin. Neurosci. 2000, 54, 407–412. [Google Scholar] [CrossRef] [PubMed]
- Geselowitz, D. The zero of potential. IEEE Eng. Med. Biol. Mag. 1998, 17, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.M.; Murray, M.M.; Lantz, G.; Gonzalez, S.; Spinelli, L.; De Peralta, R.G. EEG source imaging. Clin. Neurophysiol. 2004, 115, 2195–2222. [Google Scholar] [CrossRef] [PubMed]
- Michel, C.M.; Brunet, D. EEG source imaging: A practical review of the analysis steps. Front. Neurol. 2019, 10, 325. [Google Scholar] [CrossRef] [PubMed]
- Koutlis, C.; Kimiskidis, V.K.; Kugiumtzis, D. Comparison of Causality Network Estimation in the Sensor and Source Space: Simulation and Application on EEG. Front. Netw. Physiol. 2021, 1, 706487. [Google Scholar] [CrossRef]
- Nunez, P.L.; Srinivasan, R. Electric Fields of the Brain: The Neurophysics of EEG; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Haufe, S.; Nikulin, V.V.; Müller, K.R.; Nolte, G. A critical assessment of connectivity measures for EEG data: A simulation study. Neuroimage 2013, 64, 120–133. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulou, M.; Friston, K.; Marinazzo, D. Estimating directed connectivity from cortical recordings and reconstructed sources. Brain Topogr. 2019, 32, 741–752. [Google Scholar] [CrossRef]
- Van de Steen, F.; Faes, L.; Karahan, E.; Songsiri, J.; Valdes-Sosa, P.A.; Marinazzo, D. Critical comments on EEG sensor space dynamical connectivity analysis. Brain Topogr. 2019, 32, 643–654. [Google Scholar] [CrossRef]
- Cea-Cañas, B.; Gomez-Pilar, J.; Nùñez, P.; Rodríguez-Vàzquez, E.; de Uribe, N.; Dìez, A.; Pèrez-Escudero, A.; Molina, V. Connectivity strength of the EEG functional network in schizophrenia and bipolar disorder. Prog. Neuropsychopharmacol. Biol. Psychiatry 2020, 98, 109801. [Google Scholar] [CrossRef]
- Jin, L.; Shi, W.; Zhang, C.; Yeh, C.H. Frequency nesting interactions in the subthalamic nucleus correlate with the step phases for Parkinson’s disease. Front. Physiol. 2022, 13, 890753. [Google Scholar] [CrossRef]
- Liang, Y.; Chen, C.; Li, F.; Yao, D.; Xu, P.; Yu, L. Altered Functional Connectivity after Epileptic Seizure Revealed by Scalp EEG. Neural Plast. 2020, 2020, 8851415. [Google Scholar] [CrossRef]
- Pichiorri, F.; Morone, G.; Petti, M.; Toppi, J.; Pisotta, I.; Molinari, M.; Paolucci, S.; Inghilleri, M.; Astolfi, L.; Cincotti, F.; et al. Brain–computer interface boosts motor imagery practice during stroke recovery. Ann. Neurol. 2015, 77, 851–865. [Google Scholar] [CrossRef]
- Chiarion, G.; Mesin, L. Functional connectivity of eeg in encephalitis during slow biphasic complexes. Electronics 2021, 10, 2978. [Google Scholar] [CrossRef]
- Khare, S.K.; Acharya, U.R. An explainable and interpretable model for attention deficit hyperactivity disorder in children using EEG signals. Comput. Biol. Med. 2023, 155, 106676. [Google Scholar] [CrossRef] [PubMed]
- Gena, C.; Hilviu, D.; Chiarion, G.; Roatta, S.; Bosco, F.M.; Calvo, A.; Mattutino, C.; Vincenzi, S. The BciAi4SLA Project: Towards a User-Centered BCI. Electronics 2023, 12, 1234. [Google Scholar] [CrossRef]
- Friston, K.; Moran, R.; Seth, A.K. Analysing connectivity with Granger causality and dynamic causal modelling. Curr. Opin. Neurobiol. 2013, 23, 172–178. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J. Modalities, modes, and models in functional neuroimaging. Science 2009, 326, 399–403. [Google Scholar] [CrossRef] [PubMed]
- Koch, M.A.; Norris, D.G.; Hund-Georgiadis, M. An investigation of functional and anatomical connectivity using magnetic resonance imaging. Neuroimage 2002, 16, 241–250. [Google Scholar] [CrossRef]
- Friston, K.J. Functional and effective connectivity in neuroimaging: A synthesis. Hum. Brain Mapp. 1994, 2, 56–78. [Google Scholar] [CrossRef]
- Damoiseaux, J.S.; Rombouts, S.; Barkhof, F.; Scheltens, P.; Stam, C.J.; Smith, S.M.; Beckmann, C.F. Consistent resting-state networks across healthy subjects. Proc. Natl. Acad. Sci. USA 2006, 103, 13848–13853. [Google Scholar] [CrossRef]
- Passingham, R.E.; Stephan, K.E.; Kötter, R. The anatomical basis of functional localization in the cortex. Nat. Rev. Neurosci. 2002, 3, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Mantini, D.; Perrucci, M.G.; Del Gratta, C.; Romani, G.L.; Corbetta, M. Electrophysiological signatures of resting state networks in the human brain. Proc. Natl. Acad. Sci. USA 2007, 104, 13170–13175. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.L.; Fair, D.A.; Dosenbach, N.U.; Miezin, F.M.; Dierker, D.; Van Essen, D.C.; Schlaggar, B.L.; Petersen, S.E. Defining functional areas in individual human brains using resting functional connectivity MRI. Neuroimage 2008, 41, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Rykhlevskaia, E.; Gratton, G.; Fabiani, M. Combining structural and functional neuroimaging data for studying brain connectivity: A review. Psychophysiology 2008, 45, 173–187. [Google Scholar] [CrossRef]
- Hagmann, P.; Cammoun, L.; Gigandet, X.; Meuli, R.; Honey, C.J.; Wedeen, V.J.; Sporns, O. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008, 6, e159. [Google Scholar] [CrossRef] [PubMed]
- Honey, C.J.; Sporns, O.; Cammoun, L.; Gigandet, X.; Thiran, J.P.; Meuli, R.; Hagmann, P. Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl. Acad. Sci. USA 2009, 106, 2035–2040. [Google Scholar] [CrossRef]
- Friston, K.J. Functional and Effective Connectivity: A Review. Brain Connect. 2011, 1, 13–36. [Google Scholar] [CrossRef]
- Sakkalis, V. Review of advanced techniques for the estimation of brain connectivity measured with EEG/MEG. Comput. Biol. Med. 2011, 41, 1110–1117. [Google Scholar] [CrossRef]
- Goldenberg, D.; Galván, A. The use of functional and effective connectivity techniques to understand the developing brain. Dev. Cogn. Neurosci. 2015, 12, 155–164. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Tononi, G.; Sporns, O. Measuring information integration. BMC Neurosci. 2003, 4, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Garrido, M.I.; Kilner, J.M.; Kiebel, S.J.; Friston, K.J. Evoked brain responses are generated by feedback loops. Proc. Natl. Acad. Sci. USA 2007, 104, 20961–20966. [Google Scholar] [CrossRef]
- Garrido, M.I.; Kilner, J.M.; Kiebel, S.J.; Stephan, K.E.; Baldeweg, T.; Friston, K.J. Repetition suppression and plasticity in the human brain. Neuroimage 2009, 48, 269–279. [Google Scholar] [CrossRef]
- Kiebel, S.J.; Garrido, M.I.; Friston, K.J. Dynamic causal modelling of evoked responses: The role of intrinsic connections. Neuroimage 2007, 36, 332–345. [Google Scholar] [CrossRef]
- Seth, A.K.; Barrett, A.B.; Barnett, L. Granger causality analysis in neuroscience and neuroimaging. J. Neurosci. 2015, 35, 3293–3297. [Google Scholar] [CrossRef] [PubMed]
- Bressler, S.L.; Seth, A.K. Wiener–Granger causality: A well established methodology. Neuroimage 2011, 58, 323–329. [Google Scholar] [CrossRef] [PubMed]
- Geweke, J.F. Measures of conditional linear dependence and feedback between time series. J. Am. Stat. Assoc. 1984, 79, 907–915. [Google Scholar] [CrossRef]
- Brillinger, D.R.; Bryant, H.L.; Segundo, J.P. Identification of synaptic interactions. Biol. Cybern. 1976, 22, 213–228. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wibral, M.; Vicente, R.; Lizier, J.T. Directed Information Measures in Neuroscience; Springer: Berlin/Heidelberg, Germany, 2014; Volume 724. [Google Scholar]
- Muresan, R.C.; Jurjut, O.F.; Moca, V.V.; Singer, W.; Nikolic, D. The oscillation score: An efficient method for estimating oscillation strength in neuronal activity. J. Neurophysiol. 2008, 99, 1333–1353. [Google Scholar] [CrossRef]
- Atyabi, A.; Shic, F.; Naples, A. Mixture of autoregressive modeling orders and its implication on single trial EEG classification. Expert Syst. Appl. 2016, 65, 164–180. [Google Scholar] [CrossRef]
- Sakkalis, V.; Giurcaneanu, C.D.; Xanthopoulos, P.; Zervakis, M.E.; Tsiaras, V.; Yang, Y.; Karakonstantaki, E.; Micheloyannis, S. Assessment of linear and nonlinear synchronization measures for analyzing EEG in a mild epileptic paradigm. IEEE Trans. Inf. Technol. Biomed. 2008, 13, 433–441. [Google Scholar] [CrossRef] [PubMed]
- von Sachs, R. Nonparametric spectral analysis of multivariate time series. Annu. Rev. Stat. Its Appl. 2020, 7, 361–386. [Google Scholar] [CrossRef]
- Sankari, Z.; Adeli, H.; Adeli, A. Wavelet coherence model for diagnosis of Alzheimer disease. Clin. EEG Neurosci. 2012, 43, 268–278. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.L.; Ros, T.; Gruzelier, J.H. Dynamic changes of ICA-derived EEG functional connectivity in the resting state. Hum. Brain Mapp. 2013, 34, 852–868. [Google Scholar] [CrossRef] [PubMed]
- Ieracitano, C.; Duun-Henriksen, J.; Mammone, N.; La Foresta, F.; Morabito, F.C. Wavelet coherence-based clustering of EEG signals to estimate the brain connectivity in absence epileptic patients. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1297–1304. [Google Scholar]
- Lachaux, J.P.; Lutz, A.; Rudrauf, D.; Cosmelli, D.; Le Van Quyen, M.; Martinerie, J.; Varela, F. Estimating the time-course of coherence between single-trial brain signals: An introduction to wavelet coherence. Neurophysiol. Clin. Neurophysiol. 2002, 32, 157–174. [Google Scholar] [CrossRef] [PubMed]
- Khare, S.K.; Bajaj, V.; Acharya, U.R. SchizoNET: A robust and accurate Margenau-Hill time-frequency distribution based deep neural network model for schizophrenia detection using EEG signals. Physiol. Meas. 2023, 44, 035005. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Asgharzadeh-Bonab, A.; Ranjbarzadeh, R. Time-frequency analysis of EEG signals and GLCM features for depth of anesthesia monitoring. Comput. Intell. Neurosci. 2021, 2021, 8430565. [Google Scholar] [CrossRef]
- Lachaux, J.P.; Rodriguez, E.; Martinerie, J.; Varela, F.J. Measuring phase synchrony in brain signals. Hum. Brain Mapp. 1999, 8, 194–208. [Google Scholar] [CrossRef]
- Pereda, E.; Quiroga, R.Q.; Bhattacharya, J. Nonlinear multivariate analysis of neurophysiological signals. Prog. Neurobiol. 2005, 77, 1–37. [Google Scholar] [CrossRef]
- Xu, B.G.; Song, A.G. Pattern recognition of motor imagery EEG using wavelet transform. J. Biomed. Sci. Eng. 2008, 1, 64. [Google Scholar] [CrossRef]
- Akaike, H. A new look at statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Sanchez-Romero, R.; Cole, M.W. Combining multiple functional connectivity methods to improve causal inferences. J. Cogn. Neurosci. 2021, 33, 180–194. [Google Scholar] [CrossRef] [PubMed]
- Ding, M.; Chen, Y.; Bressler, S.L. Granger causality: Basic theory and application to neuroscience. In Handbook of Time Series Analysis: Recent Theoretical Developments and Applications; Wiley: Weinheim, Germany, 2006; pp. 437–460. [Google Scholar]
- Faes, L.; Nollo, G. Measuring frequency domain Granger causality for multiple blocks of interacting time series. Biol. Cybern. 2013, 107, 217–232. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Pernice, R.; Antonacci, Y.; Zanetti, M.; Busacca, A.; Marinazzo, D.; Faes, L.; Nollo, G. Multivariate correlation measures reveal structure and strength of brain–body physiological networks at rest and during mental stress. Front. Neurosci. 2021, 14, 602584. [Google Scholar] [CrossRef]
- Battiston, F.; Cencetti, G.; Iacopini, I.; Latora, V.; Lucas, M.; Patania, A.; Young, J.G.; Petri, G. Networks beyond pairwise interactions: Structure and dynamics. Phys. Rep. 2020, 874, 1–92. [Google Scholar] [CrossRef]
- Faes, L.; Pernice, R.; Mijatovic, G.; Antonacci, Y.; Krohova, J.C.; Javorka, M.; Porta, A. Information decomposition in the frequency domain: A new framework to study cardiovascular and cardiorespiratory oscillations. Philos. Trans. R. Soc. A 2021, 379, 20200250. [Google Scholar] [CrossRef]
- Wiener, N. The theory of prediction. In Modern Mathematics for Engineers; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Porta, A.; Faes, L. Wiener–Granger causality in network physiology with applications to cardiovascular control and neuroscience. Proc. IEEE 2015, 104, 282–309. [Google Scholar] [CrossRef]
- Pernice, R.; Sparacino, L.; Bari, V.; Gelpi, F.; Cairo, B.; Mijatovic, G.; Antonacci, Y.; Tonon, D.; Rossato, G.; Javorka, M.; et al. Spectral decomposition of cerebrovascular and cardiovascular interactions in patients prone to postural syncope and healthy controls. Auton. Neurosci. 2022, 242, 103021. [Google Scholar] [CrossRef]
- Faes, L.; Sameshima, K. Assessing connectivity in the presence of instantaneous causality. In Methods in Brain Connectivity Inference through Multivariate Time Series Analysis; CRC Press: Boca Raton, FL, USA, 2014; Volume 20145078, pp. 87–112. [Google Scholar]
- Schiatti, L.; Nollo, G.; Rossato, G.; Faes, L. Extended Granger causality: A new tool to identify the structure of physiological networks. Physiol. Meas. 2015, 36, 827. [Google Scholar] [CrossRef] [PubMed]
- Šverko, Z.; Vrankić, M.; Vlahinić, S.; Rogelj, P. Complex Pearson correlation coefficient for EEG connectivity analysis. Sensors 2022, 22, 1477. [Google Scholar] [CrossRef]
- Vrankic, M.; Vlahinić, S.; Šverko, Z.; Markovinović, I. EEG-Validated Photobiomodulation Treatment of Dementia—Case Study. Sensors 2022, 22, 7555. [Google Scholar] [CrossRef] [PubMed]
- Dhiman, R. Electroencephalogram channel selection based on pearson correlation coefficient for motor imagery-brain–computer interface. Meas. Sens. 2023, 25, 100616. [Google Scholar]
- Harold, H. Relations between two sets of variates. Biometrika 1936, 28, 321. [Google Scholar]
- Spüler, M.; Walter, A.; Rosenstiel, W.; Bogdan, M. Spatial filtering based on canonical correlation analysis for classification of evoked or event-related potentials in EEG data. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 22, 1097–1103. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W. Multichannel EEG-based emotion recognition via group sparse canonical correlation analysis. IEEE Trans. Cogn. Dev. Syst. 2016, 9, 281–290. [Google Scholar] [CrossRef]
- Al-Shargie, F.; Tang, T.B.; Kiguchi, M. Assessment of mental stress effects on prefrontal cortical activities using canonical correlation analysis: An fNIRS-EEG study. Biomed. Opt. Express 2017, 8, 2583–2598. [Google Scholar] [CrossRef]
- Schindler, K.; Leung, H.; Elger, C.E.; Lehnertz, K. Assessing seizure dynamics by analysing the correlation structure of multichannel intracranial EEG. Brain 2007, 130, 65–77. [Google Scholar] [CrossRef]
- Rummel, C.; Baier, G.; Müller, M. The influence of static correlations on multivariate correlation analysis of the EEG. J. Neurosci. Methods 2007, 166, 138–157. [Google Scholar] [CrossRef] [PubMed]
- Stokes, P.A.; Purdon, P.L. A study of problems encountered in Granger causality analysis from a neuroscience perspective. Proc. Natl. Acad. Sci. USA 2017, 114, E7063–E7072. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Stramaglia, S.; Marinazzo, D. On the interpretability and computational reliability of frequency-domain Granger causality. arXiv 2017, arXiv:1708.06990. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Misunderstandings regarding the application of Granger causality in neuroscience. Proc. Natl. Acad. Sci. USA 2018, 115, E6676–E6677. [Google Scholar] [CrossRef] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Solved problems for Granger causality in neuroscience: A response to Stokes and Purdon. NeuroImage 2018, 178, 744–748. [Google Scholar] [CrossRef] [PubMed]
- Stokes, P.A.; Purdon, P.L. Reply to Barnett et al.: Regarding interpretation of Granger causality analyses. Proc. Natl. Acad. Sci. USA 2018, 115, E6678–E6679. [Google Scholar] [CrossRef] [PubMed]
- Freiwald, W.A.; Valdes, P.; Bosch, J.; Biscay, R.; Jimenez, J.C.; Rodriguez, L.M.; Rodriguez, V.; Kreiter, A.K.; Singer, W. Testing non-linearity and directedness of interactions between neural groups in the macaque inferotemporal cortex. J. Neurosci. Methods 1999, 94, 105–119. [Google Scholar] [CrossRef] [PubMed]
- Marinazzo, D.; Pellicoro, M.; Stramaglia, S. Kernel method for nonlinear Granger causality. Phys. Rev. Lett. 2008, 100, 144103. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wei, H.L.; Billings, S.A.; Liao, X.F. Time-varying linear and nonlinear parametric model for Granger causality analysis. Phys. Rev. E 2012, 85, 041906. [Google Scholar] [CrossRef] [PubMed]
- Dhamala, M.; Rangarajan, G.; Ding, M. Analyzing information flow in brain networks with nonparametric Granger causality. Neuroimage 2008, 41, 354–362. [Google Scholar] [CrossRef]
- Sheikhattar, A.; Miran, S.; Liu, J.; Fritz, J.B.; Shamma, S.A.; Kanold, P.O.; Babadi, B. Extracting neuronal functional network dynamics via adaptive Granger causality analysis. Proc. Natl. Acad. Sci. USA 2018, 115, E3869–E3878. [Google Scholar] [CrossRef]
- Hesse, W.; Möller, E.; Arnold, M.; Schack, B. The use of time-variant EEG Granger causality for inspecting directed interdependencies of neural assemblies. J. Neurosci. Methods 2003, 124, 27–44. [Google Scholar] [CrossRef] [PubMed]
- Bernasconi, C.; KoÈnig, P. On the directionality of cortical interactions studied by structural analysis of electrophysiological recordings. Biol. Cybern. 1999, 81, 199–210. [Google Scholar] [CrossRef]
- Bernasconi, C.; von Stein, A.; Chiang, C.; KoÈnig, P. Bi-directional interactions between visual areas in the awake behaving cat. Neuroreport 2000, 11, 689–692. [Google Scholar] [CrossRef]
- Barrett, A.B.; Murphy, M.; Bruno, M.A.; Noirhomme, Q.; Boly, M.; Laureys, S.; Seth, A.K. Granger causality analysis of steady-state electroencephalographic signals during propofol-induced anaesthesia. PLoS ONE 2012, 7, e29072. [Google Scholar] [CrossRef] [PubMed]
- Kaminski, M.; Brzezicka, A.; Kaminski, J.; Blinowska, K.J. Measures of coupling between neural populations based on Granger causality principle. Front. Comput. Neurosci. 2016, 10, 114. [Google Scholar] [CrossRef] [PubMed]
- Rajagovindan, R.; Ding, M. Decomposing neural synchrony: Toward an explanation for near-zero phase-lag in cortical oscillatory networks. PLoS ONE 2008, 3, e3649. [Google Scholar] [CrossRef]
- Brovelli, A.; Ding, M.; Ledberg, A.; Chen, Y.; Nakamura, R.; Bressler, S.L. Beta oscillations in a large-scale sensorimotor cortical network: Directional influences revealed by Granger causality. Proc. Natl. Acad. Sci. USA 2004, 101, 9849–9854. [Google Scholar] [CrossRef]
- Roelfsema, P.R.; Engel, A.K.; König, P.; Singer, W. Visuomotor integration is associated with zero time-lag synchronization among cortical areas. Nature 1997, 385, 157–161. [Google Scholar] [CrossRef]
- Nuzzi, D.; Stramaglia, S.; Javorka, M.; Marinazzo, D.; Porta, A.; Faes, L. Extending the spectral decomposition of Granger causality to include instantaneous influences: Application to the control mechanisms of heart rate variability. Philos. Trans. R. Soc. A 2021, 379, 20200263. [Google Scholar] [CrossRef]
- Barnett, L.; Seth, A.K. Behaviour of Granger Causality under Filtering: Theoretical Invariance and Practical Application. J. Neurosci. Methods 2011, 201, 404–419. [Google Scholar] [CrossRef] [PubMed]
- Sakkalis, V.; Cassar, T.; Zervakis, M.; Camilleri, K.P.; Fabri, S.G.; Bigan, C.; Karakonstantaki, E.; Micheloyannis, S. Parametric and nonparametric EEG analysis for the evaluation of EEG activity in young children with controlled epilepsy. Comput. Intell. Neurosci. 2008, 2008, 462593. [Google Scholar] [CrossRef] [PubMed]
- Baccalá, L.A.; Sameshima, K. Partial Directed Coherence and the Vector Autoregressive Modelling Myth and a Caveat. Front. Netw. Physiol. 2022, 2, 13. [Google Scholar] [CrossRef]
- Nedungadi, A.G.; Ding, M.; Rangarajan, G. Block coherence: A method for measuring the interdependence between two blocks of neurobiological time series. Biol. Cybern. 2011, 104, 197–207. [Google Scholar] [CrossRef]
- Gevers, M.; Anderson, B. Representations of jointly stationary stochastic feedback processes. Int. J. Control 1981, 33, 777–809. [Google Scholar] [CrossRef]
- Porta, A.; Furlan, R.; Rimoldi, O.; Pagani, M.; Malliani, A.; Van De Borne, P. Quantifying the strength of the linear causal coupling in closed loop interacting cardiovascular variability signals. Biol. Cybern. 2002, 86, 241–251. [Google Scholar] [CrossRef]
- Korhonen, I.; Mainardi, L.; Loula, P.; Carrault, G.; Baselli, G.; Bianchi, A. Linear multivariate models for physiological signal analysis: Theory. Comput. Methods Programs Biomed. 1996, 51, 85–94. [Google Scholar] [CrossRef]
- Faes, L.; Porta, A.; Nollo, G. Testing frequency-domain causality in multivariate time series. IEEE Trans. Biomed. Eng. 2010, 57, 1897–1906. [Google Scholar] [CrossRef]
- Astolfi, L.; Cincotti, F.; Mattia, D.; Marciani, M.G.; Baccala, L.A.; Fallani, F.D.V.; Salinari, S.; Ursino, M.; Zavaglia, M.; Babiloni, F. Assessing cortical functional connectivity by partial directed coherence: Simulations and application to real data. IEEE Trans. Biomed. Eng. 2006, 53, 1802–1812. [Google Scholar] [CrossRef]
- Plomp, G.; Quairiaux, C.; Michel, C.M.; Astolfi, L. The physiological plausibility of time-varying Granger-causal modeling: Normalization and weighting by spectral power. NeuroImage 2014, 97, 206–216. [Google Scholar] [CrossRef]
- Baccala, L.A.; Sameshima, K.; Takahashi, D.Y. Generalized partial directed coherence. In Proceedings of the 2007 15th International Conference on Digital Signal Processing, London, UK, 23–25 August 2017; IEEE: Piscataway, NJ, USA, 2007; pp. 163–166. [Google Scholar]
- Takahashi, D.Y.; Baccalá, L.A.; Sameshima, K. Information theoretic interpretation of frequency domain connectivity measures. Biol. Cybern. 2010, 103, 463–469. [Google Scholar] [CrossRef]
- Baccalá, L.A.; Takahashi, D.Y.; Sameshima, K. Directed transfer function: Unified asymptotic theory and some of its implications. IEEE Trans. Biomed. Eng. 2016, 63, 2450–2460. [Google Scholar] [CrossRef]
- Kamiński, M. Determination of transmission patterns in multichannel data. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 947–952. [Google Scholar] [CrossRef] [PubMed]
- Eichler, M. On the evaluation of information flow in multivariate systems by the directed transfer function. Biol. Cybern. 2006, 94, 469–482. [Google Scholar] [CrossRef] [PubMed]
- Kamiński, M.; Ding, M.; Truccolo, W.A.; Bressler, S.L. Evaluating causal relations in neural systems: Granger causality, directed transfer function and statistical assessment of significance. Biol. Cybern. 2001, 85, 145–157. [Google Scholar] [CrossRef] [PubMed]
- Muroni, A.; Barbar, D.; Fraschini, M.; Monticone, M.; Defazio, G.; Marrosu, F. Case Report: Modulation of Effective Connectivity in Brain Networks after Prosthodontic Tooth Loss Repair. Signals 2022, 3, 550–558. [Google Scholar] [CrossRef]
- Pirovano, I.; Mastropietro, A.; Antonacci, Y.; Barà, C.; Guanziroli, E.; Molteni, F.; Faes, L.; Rizzo, G. Resting State EEG Directed Functional Connectivity Unveils Changes in Motor Network Organization in Subacute Stroke Patients After Rehabilitation. Front. Physiol. 2022, 13, 591. [Google Scholar] [CrossRef]
- Antonacci, Y.; Toppi, J.; Mattia, D.; Pietrabissa, A.; Astolfi, L. Single-trial connectivity estimation through the least absolute shrinkage and selection operator. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 6422–6425. [Google Scholar]
- Schelter, B.; Winterhalder, M.; Eichler, M.; Peifer, M.; Hellwig, B.; Guschlbauer, B.; Lücking, C.H.; Dahlhaus, R.; Timmer, J. Testing for directed influences among neural signals using partial directed coherence. J. Neurosci. Methods 2006, 152, 210–219. [Google Scholar] [CrossRef]
- Vlachos, I.; Krishnan, B.; Treiman, D.M.; Tsakalis, K.; Kugiumtzis, D.; Iasemidis, L.D. The concept of effective inflow: Application to interictal localization of the epileptogenic focus from iEEG. IEEE Trans. Biomed. Eng. 2016, 64, 2241–2252. [Google Scholar] [CrossRef] [PubMed]
- Milde, T.; Leistritz, L.; Astolfi, L.; Miltner, W.H.; Weiss, T.; Babiloni, F.; Witte, H. A new Kalman filter approach for the estimation of high-dimensional time-variant multivariate AR models and its application in analysis of laser-evoked brain potentials. Neuroimage 2010, 50, 960–969. [Google Scholar] [CrossRef] [PubMed]
- Möller, E.; Schack, B.; Arnold, M.; Witte, H. Instantaneous multivariate EEG coherence analysis by means of adaptive high-dimensional autoregressive models. J. Neurosci. Methods 2001, 105, 143–158. [Google Scholar] [CrossRef]
- Chen, Y.; Bressler, S.L.; Ding, M. Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. J. Neurosci. Methods 2006, 150, 228–237. [Google Scholar] [CrossRef]
- Wen, X.; Rangarajan, G.; Ding, M. Multivariate Granger causality: An estimation framework based on factorization of the spectral density matrix. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20110610. [Google Scholar] [CrossRef]
- Guo, S.; Seth, A.K.; Kendrick, K.M.; Zhou, C.; Feng, J. Partial Granger causality—Eliminating exogenous inputs and latent variables. J. Neurosci. Methods 2008, 172, 79–93. [Google Scholar] [CrossRef]
- Seth, A.K. A MATLAB toolbox for Granger causal connectivity analysis. J. Neurosci. Methods 2010, 186, 262–273. [Google Scholar] [CrossRef] [PubMed]
- Ash, R.B. Information Theory; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Faes, L.; Marinazzo, D.; Jurysta, F.; Nollo, G. Linear and non-linear brain–heart and brain–brain interactions during sleep. Physiol. Meas. 2015, 36, 683. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Takahashi, D.Y.; Baccalá, L.A.; Sameshima, K. Canonical information flow decomposition among neural structure subsets. Front. Neuroinformatics 2014, 8, 49. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Entropy, relative entropy and mutual information. Elem. Inf. Theory 1991, 2, 12–13. [Google Scholar]
- Erramuzpe, A.; Ortega, G.J.; Pastor, J.; De Sola, R.G.; Marinazzo, D.; Stramaglia, S.; Cortes, J.M. Identification of redundant and synergetic circuits in triplets of electrophysiological data. J. Neural Eng. 2015, 12, 066007. [Google Scholar] [CrossRef]
- McGill, W. Multivariate information transmission. Trans. IRE Prof. Group Inf. Theory 1954, 4, 93–111. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. In Guided Self-Organization: Inception; Springer: Berlin/Heidelberg, Germany, 2014; pp. 159–190. [Google Scholar]
- Wibral, M.; Finn, C.; Wollstadt, P.; Lizier, J.T.; Priesemann, V. Quantifying information modification in developing neural networks via partial information decomposition. Entropy 2017, 19, 494. [Google Scholar] [CrossRef]
- Lizier, J.T.; Flecker, B.; Williams, P.L. Towards a synergy-based approach to measuring information modification. In Proceedings of the 2013 IEEE Symposium on Artificial Life (ALIFE), Singapore, 15–19 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 43–51. [Google Scholar]
- Faes, L.; Nollo, G.; Porta, A. Information decomposition: A tool to dissect cardiovascular and cardiorespiratory complexity. In Complexity and Nonlinearity in Cardiovascular Signals; Springer: Berlin/Heidelberg, Germany, 2017; pp. 87–113. [Google Scholar]
- Faes, L.; Marinazzo, D.; Stramaglia, S. Multiscale information decomposition: Exact computation for multivariate Gaussian processes. Entropy 2017, 19, 408. [Google Scholar] [CrossRef]
- Mijatovic, G.; Antonacci, Y.; Loncar-Turukalo, T.; Minati, L.; Faes, L. An information-theoretic framework to measure the dynamic interaction between neural spike trains. IEEE Trans. Biomed. Eng. 2021, 68, 3471–3481. [Google Scholar] [CrossRef]
- Faes, L.; Marinazzo, D.; Nollo, G.; Porta, A. An information-theoretic framework to map the spatiotemporal dynamics of the scalp electroencephalogram. IEEE Trans. Biomed. Eng. 2016, 63, 2488–2496. [Google Scholar] [CrossRef]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy—A model-free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef] [PubMed]
- Sabesan, S.; Good, L.B.; Tsakalis, K.S.; Spanias, A.; Treiman, D.M.; Iasemidis, L.D. Information flow and application to epileptogenic focus localization from intracranial EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 17, 244–253. [Google Scholar] [CrossRef]
- Gourévitch, B.; Eggermont, J.J. Evaluating information transfer between auditory cortical neurons. J. Neurophysiol. 2007, 97, 2533–2543. [Google Scholar] [CrossRef]
- Kotiuchyi, I.; Pernice, R.; Popov, A.; Faes, L.; Kharytonov, V. A framework to assess the information dynamics of source EEG activity and its application to epileptic brain networks. Brain Sci. 2020, 10, 657. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Jeannès, R.L.B.; Bellanger, J.J.; Shu, H. A new strategy for model order identification and its application to transfer entropy for EEG signals analysis. IEEE Trans. Biomed. Eng. 2012, 60, 1318–1327. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Frith, C. Abnormal inter-hemispheric integration in schizophrenia: An analysis of neuroimaging data. Neuropsychopharmacology 1994, 10, 719S. [Google Scholar]
- Melia, U.; Guaita, M.; Vallverdú, M.; Embid, C.; Vilaseca, I.; Salamero, M.; Santamaria, J. Mutual information measures applied to EEG signals for sleepiness characterization. Med. Eng. Phys. 2015, 37, 297–308. [Google Scholar] [CrossRef] [PubMed]
- Antonacci, Y.; Minati, L.; Nuzzi, D.; Mijatovic, G.; Pernice, R.; Marinazzo, D.; Stramaglia, S.; Faes, L. Measuring High-Order Interactions in Rhythmic Processes through Multivariate Spectral Information Decomposition. IEEE Access 2021, 9, 149486–149505. [Google Scholar] [CrossRef]
- Antonopoulos, C.G. Network inference combining mutual information rate and statistical tests. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106896. [Google Scholar] [CrossRef]
- Brenner, N.; Strong, S.P.; Koberle, R.; Bialek, W.; Steveninck, R.R.d.R.v. Synergy in a neural code. Neural Comput. 2000, 12, 1531–1552. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Stephens, G.J.; Ham, M.I.; Gross, G.W. Functional structure of cortical neuronal networks grown in vitro. Phys. Rev. E 2007, 75, 021915. [Google Scholar] [CrossRef]
- Bettencourt, L.M.; Gintautas, V.; Ham, M.I. Identification of functional information subgraphs in complex networks. Phys. Rev. Lett. 2008, 100, 238701. [Google Scholar] [CrossRef]
- Gaucher, Q.; Huetz, C.; Gourévitch, B.; Edeline, J.M. Cortical inhibition reduces information redundancy at presentation of communication sounds in the primary auditory cortex. J. Neurosci. 2013, 33, 10713–10728. [Google Scholar] [CrossRef]
- Marinazzo, D.; Gosseries, O.; Boly, M.; Ledoux, D.; Rosanova, M.; Massimini, M.; Noirhomme, Q.; Laureys, S. Directed information transfer in scalp electroencephalographic recordings: Insights on disorders of consciousness. Clin. EEG Neurosci. 2014, 45, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Pernice, R.; Kotiuchyi, I.; Popov, A.; Kharytonov, V.; Busacca, A.; Marinazzo, D.; Faes, L. Synergistic and redundant brain-heart information in patients with focal epilepsy. In Proceedings of the 2020 11th Conference of the European Study Group on Cardiovascular Oscillations (ESGCO), Pisa, Italy, 15 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–2. [Google Scholar]
- Timme, N.M.; Ito, S.; Myroshnychenko, M.; Nigam, S.; Shimono, M.; Yeh, F.C.; Hottowy, P.; Litke, A.M.; Beggs, J.M. High-degree neurons feed cortical computations. PLoS Comput. Biol. 2016, 12, e1004858. [Google Scholar] [CrossRef] [PubMed]
- Stramaglia, S.; Wu, G.R.; Pellicoro, M.; Marinazzo, D. Expanding the transfer entropy to identify information circuits in complex systems. Phys. Rev. E 2012, 86, 066211. [Google Scholar] [CrossRef]
- Stramaglia, S.; Cortes, J.M.; Marinazzo, D. Synergy and redundancy in the Granger causal analysis of dynamical networks. New J. Phys. 2014, 16, 105003. [Google Scholar] [CrossRef]
- Wibral, M.; Lizier, J.T.; Vögler, S.; Priesemann, V.; Galuske, R. Local active information storage as a tool to understand distributed neural information processing. Front. Neuroinformatics 2014, 8, 1. [Google Scholar] [CrossRef]
- Faes, L.; Porta, A.; Nollo, G.; Javorka, M. Information decomposition in multivariate systems: Definitions, implementation and application to cardiovascular networks. Entropy 2016, 19, 5. [Google Scholar] [CrossRef]
- Stam, C.J. Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field. Clin. Neurophysiol. 2005, 116, 2266–2301. [Google Scholar] [CrossRef] [PubMed]
- Leistritz, L.; Schiecke, K.; Astolfi, L.; Witte, H. Time-variant modeling of brain processes. Proc. IEEE 2015, 104, 262–281. [Google Scholar] [CrossRef]
- Wilke, C.; Ding, L.; He, B. Estimation of time-varying connectivity patterns through the use of an adaptive directed transfer function. IEEE Trans. Biomed. Eng. 2008, 55, 2557–2564. [Google Scholar] [CrossRef]
- Astolfi, L.; Cincotti, F.; Mattia, D.; Fallani, F.D.V.; Tocci, A.; Colosimo, A.; Salinari, S.; Marciani, M.G.; Hesse, W.; Witte, H.; et al. Tracking the time-varying cortical connectivity patterns by adaptive multivariate estimators. IEEE Trans. Biomed. Eng. 2008, 55, 902–913. [Google Scholar] [CrossRef]
- Palva, J.M.; Palva, S.; Kaila, K. Phase synchrony among neuronal oscillations in the human cortex. J. Neurosci. 2005, 25, 3962–3972. [Google Scholar] [CrossRef] [PubMed]
- Siegel, M.; Donner, T.H.; Engel, A.K. Spectral fingerprints of large-scale neuronal interactions. Nat. Rev. Neurosci. 2012, 13, 121–134. [Google Scholar] [CrossRef] [PubMed]
- Siems, M.; Siegel, M. Dissociated neuronal phase- and amplitude-coupling patterns in the human brain. NeuroImage 2020, 209, 116538. [Google Scholar] [CrossRef]
- Gotman, J. Measurement of small time differences between EEG channels: Method and application to epileptic seizure propagation. Electroencephalogr. Clin. Neurophysiol. 1983, 56, 501–514. [Google Scholar] [CrossRef]
- Cassidy, M.; Brown, P. Spectral phase estimates in the setting of multidirectional coupling. J. Neurosci. Methods 2003, 127, 95–103. [Google Scholar] [CrossRef]
- Alonso, J.M.; Usrey, W.M.; Reid, R.C. Precisely correlated firing in cells of the lateral geniculate nucleus. Nature 1996, 383, 815–819. [Google Scholar] [CrossRef] [PubMed]
- Nolte, G.; Ziehe, A.; Nikulin, V.V.; Schlögl, A.; Krämer, N.; Brismar, T.; Müller, K.R. Robustly estimating the flow direction of information in complex physical systems. Phys. Rev. Lett. 2008, 100, 234101. [Google Scholar] [CrossRef]
- Lau, T.M.; Gwin, J.T.; McDowell, K.G.; Ferris, D.P. Weighted phase lag index stability as an artifact resistant measure to detect cognitive EEG activity during locomotion. J. NeuroEngineering Rehabil. 2012, 9, 47. [Google Scholar] [CrossRef]
- Nolte, G.; Bai, O.; Wheaton, L.; Mari, Z.; Vorbach, S.; Hallett, M. Identifying true brain interaction from EEG data using the imaginary part of coherency. Clin. Neurophysiol. 2004, 115, 2292–2307. [Google Scholar] [CrossRef]
- Bosman, C.A.; Schoffelen, J.M.; Brunet, N.; Oostenveld, R.; Bastos, A.M.; Womelsdorf, T.; Rubehn, B.; Stieglitz, T.; De Weerd, P.; Fries, P. Attentional stimulus selection through selective synchronization between monkey visual areas. Neuron 2012, 75, 875–888. [Google Scholar] [CrossRef]
- Buschman, T.J.; Miller, E.K. Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. Science 2007, 315, 1860–1862. [Google Scholar] [CrossRef] [PubMed]
- Gregoriou, G.G.; Gotts, S.J.; Zhou, H.; Desimone, R. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science 2009, 324, 1207–1210. [Google Scholar] [CrossRef] [PubMed]
- Hipp, J.F.; Engel, A.K.; Siegel, M. Oscillatory synchronization in large-scale cortical networks predicts perception. Neuron 2011, 69, 387–396. [Google Scholar] [CrossRef]
- Palva, J.M.; Monto, S.; Kulashekhar, S.; Palva, S. Neuronal synchrony reveals working memory networks and predicts individual memory capacity. Proc. Natl. Acad. Sci. USA 2010, 107, 7580–7585. [Google Scholar] [CrossRef]
- Buschman, T.J.; Denovellis, E.L.; Diogo, C.; Bullock, D.; Miller, E.K. Synchronous oscillatory neural ensembles for rules in the prefrontal cortex. Neuron 2012, 76, 838–846. [Google Scholar] [CrossRef] [PubMed]
- Bruns, A.; Eckhorn, R.; Jokeit, H.; Ebner, A. Amplitude envelope correlation detects coupling among incoherent brain signals. Neuroreport 2000, 11, 1509–1514. [Google Scholar] [CrossRef]
- Engel, A.K.; Gerloff, C.; Hilgetag, C.C.; Nolte, G. Intrinsic coupling modes: Multiscale interactions in ongoing brain activity. Neuron 2013, 80, 867–886. [Google Scholar] [CrossRef]
- Bassett, D.S.; Sporns, O. Network neuroscience. Nat. Neurosci. 2017, 20, 353–364. [Google Scholar] [CrossRef]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010, 52, 1059–1069. [Google Scholar] [CrossRef]
- Lizier, J.T.; Bertschinger, N.; Jost, J.; Wibral, M. Information decomposition of target effects from multi-source interactions: Perspectives on previous, current and future work. Entropy 2018, 20, 307. [Google Scholar] [CrossRef]
- Sparacino, L.; Antonacci, Y.; Marinazzo, D.; Stramaglia, S.; Faes, L. Quantifying High-Order Interactions in Complex Physiological Networks: A Frequency-Specific Approach. In Complex Networks and Their Applications XI: Proceedings of the Eleventh International Conference on Complex Networks and Their Applications: COMPLEX NETWORKS 2022—Volume 1; Springer: Berlin/Heidelberg, Germany, 2023; pp. 301–309. [Google Scholar]
- Horwitz, B. The elusive concept of brain connectivity. Neuroimage 2003, 19, 466–470. [Google Scholar] [CrossRef] [PubMed]
- Butts, C.T. Revisiting the foundations of network analysis. Science 2009, 325, 414–416. [Google Scholar] [CrossRef] [PubMed]
- Gallos, L.K.; Makse, H.A.; Sigman, M. A small world of weak ties provides optimal global integration of self-similar modules in functional brain networks. Proc. Natl. Acad. Sci. USA 2012, 109, 2825–2830. [Google Scholar] [CrossRef] [PubMed]
- Alexander-Bloch, A.F.; Gogtay, N.; Meunier, D.; Birn, R.; Clasen, L.; Lalonde, F.; Lenroot, R.; Giedd, J.; Bullmore, E.T. Disrupted modularity and local connectivity of brain functional networks in childhood-onset schizophrenia. Front. Syst. Neurosci. 2010, 4, 147. [Google Scholar] [CrossRef]
- Boschi, A.; Brofiga, M.; Massobrio, P. Thresholding functional connectivity matrices to recover the topological properties of large-scale neuronal networks. Front. Neurosci. 2021, 15, 705103. [Google Scholar] [CrossRef]
- Ismail, L.E.; Karwowski, W. A Graph Theory-Based Modeling of Functional Brain Connectivity Based on EEG: A Systematic Review in the Context of Neuroergonomics. IEEE Access 2020, 8, 155103–155135. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Choi, S.I.; Kim, J.B. Altered Brain Networks in Chronic Obstructive Pulmonary Disease: An Electroencephalography Analysis. Clin. EEG Neurosci. 2022, 53, 160–164. [Google Scholar] [CrossRef]
- Song, Y.; Wang, K.; Wei, Y.; Zhu, Y.; Wen, J.; Luo, Y. Graph Theory Analysis of the Cortical Functional Network During Sleep in Patients With Depression. Front. Physiol. 2022, 13, 899. [Google Scholar] [CrossRef]
- Albano, L.; Agosta, F.; Basaia, S.; Cividini, C.; Stojkovic, T.; Sarasso, E.; Stankovic, I.; Tomic, A.; Markovic, V.; Stefanova, E.; et al. Functional Connectivity in Parkinson’s Disease Candidates for Deep Brain Stimulation. NPJ Park. Dis. 2022, 8, 4. [Google Scholar] [CrossRef]
- Schwedt, T.J.; Nikolova, S.; Dumkrieger, G.; Li, J.; Wu, T.; Chong, C.D. Longitudinal Changes in Functional Connectivity and Pain-Induced Brain Activations in Patients with Migraine: A Functional MRI Study Pre- and Post- Treatment with Erenumab. J. Headache Pain 2022, 23, 159. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Fast Algorithm for Detecting Community Structure in Networks. Phys. Review. E, Stat. Nonlinear, Soft Matter Phys. 2004, 69, 066133. [Google Scholar] [CrossRef] [PubMed]
- Latora, V.; Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001, 87, 198701-1–198701-4. [Google Scholar] [CrossRef]
- Luo, L.; Li, Q.; You, W.; Wang, Y.; Tang, W.; Li, B.; Yang, Y.; Sweeney, J.A.; Li, F.; Gong, Q. Altered brain functional network dynamics in obsessive–compulsive disorder. Hum. Brain Mapp. 2021, 42, 2061–2076. [Google Scholar] [CrossRef]
- Tan, B.; Yan, J.; Zhang, J.; Jin, Z.; Li, L. Aberrant Whole-Brain Resting-State Functional Connectivity Architecture in Obsessive-Compulsive Disorder: An EEG Study. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 1887–1897. [Google Scholar] [CrossRef] [PubMed]
- Humphries, M.D.; Gurney, K. Network ‘small-world-ness’: A quantitative method for determining canonical network equivalence. PLoS ONE 2008, 3, e0002051. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, T.; Shi, Z.; Tan, S.; Suo, D.; Dai, C.; Wang, L.; Wu, J.; Funahashi, S.; Liu, M. Impaired Self-Referential Cognitive Processing in Bipolar Disorder: A Functional Connectivity Analysis. Front. Aging Neurosci. 2022, 14, 754600. [Google Scholar] [CrossRef] [PubMed]
- Ocay, D.D.; Teel, E.F.; Luo, O.D.; Savignac, C.; Mahdid, Y.; Blain, S.; Ferland, C.E. Electroencephalographic characteristics of children and adolescents with chronic musculoskeletal pain. Pain Rep. 2022, 7, e1054. [Google Scholar] [CrossRef]
- Desowska, A.; Berde, C.B.; Cornelissen, L. Emerging functional connectivity patterns during sevoflurane anaesthesia in the developing human brain. Br. J. Anaesth. 2023, 130, e381–e390. [Google Scholar] [CrossRef]
- Tomagra, G.; Franchino, C.; Cesano, F.; Chiarion, G.; de lure, A.; Carbone, E.; Calabresi, P.; Mesin, L.; Picconi, B.; Marcantoni, A.; et al. Alpha-synuclein oligomers alter the spontaneous firing discharge of cultured midbrain neurons. Front. Cell. Neurosci. 2023, 17, 107855. [Google Scholar] [CrossRef]
- Hassan, M.; Shamas, M.; Khalil, M.; El Falou, W.; Wendling, F. EEGNET: An open source tool for analyzing and visualizing M/EEG connectome. PLoS ONE 2015, 10, e0138297. [Google Scholar] [CrossRef] [PubMed]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Maslov, S.; Sneppen, K. Specificity and stability in topology of protein networks. Science 2002, 296, 910–913. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.J.; Jones, B.; Manshanden, I.; Van Walsum, A.v.C.; Montez, T.; Verbunt, J.P.; de Munck, J.C.; van Dijk, B.W.; Berendse, H.W.; Scheltens, P. Magnetoencephalographic evaluation of resting-state functional connectivity in Alzheimer’s disease. Neuroimage 2006, 32, 1335–1344. [Google Scholar] [CrossRef]
- Rubinov, M.; Knock, S.A.; Stam, C.J.; Micheloyannis, S.; Harris, A.W.; Williams, L.M.; Breakspear, M. Small-world properties of nonlinear brain activity in schizophrenia. Hum. Brain Mapp. 2009, 30, 403–416. [Google Scholar] [CrossRef] [PubMed]
- Micheloyannis, S.; Pachou, E.; Stam, C.J.; Breakspear, M.; Bitsios, P.; Vourkas, M.; Erimaki, S.; Zervakis, M. Small-world networks and disturbed functional connectivity in schizophrenia. Schizophr. Res. 2006, 87, 60–66. [Google Scholar] [CrossRef]
- Tufa, U.; Gravitis, A.; Zukotynski, K.; Chinvarun, Y.; Devinsky, O.; Wennberg, R.; Carlen, P.L.; Bardakjian, B.L. A peri-ictal EEG-based biomarker for sudden unexpected death in epilepsy (SUDEP) derived from brain network analysis. Front. Netw. Physiol. 2022, 2, 866540. [Google Scholar] [CrossRef]
- Bartolomei, F.; Bosma, I.; Klein, M.; Baayen, J.C.; Reijneveld, J.C.; Postma, T.J.; Heimans, J.J.; van Dijk, B.W.; de Munck, J.C.; de Jongh, A.; et al. Disturbed functional connectivity in brain tumour patients: Evaluation by graph analysis of synchronization matrices. Clin. Neurophysiol. 2006, 117, 2039–2049. [Google Scholar] [CrossRef]
- Koopmans, L.H. The Spectral Analysis of Time Series; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Baccalá, L.A.; De Brito, C.S.; Takahashi, D.Y.; Sameshima, K. Unified asymptotic theory for all partial directed coherence forms. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120158. [Google Scholar] [CrossRef]
- Toppi, J.; Mattia, D.; Risetti, M.; Formisano, R.; Babiloni, F.; Astolfi, L. Testing the significance of connectivity networks: Comparison of different assessing procedures. IEEE Trans. Biomed. Eng. 2016, 63, 2461–2473. [Google Scholar]
- Challis, R.; Kitney, R. Biomedical signal processing (in four parts) Part 3 The power spectrum and coherence function. Med. Biol. Eng. Comput. 1991, 29, 225–241. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635. [Google Scholar] [CrossRef] [PubMed]
- Faes, L.; Pinna, G.D.; Porta, A.; Maestri, R.; Nollo, G. Surrogate data analysis for assessing the significance of the coherence function. IEEE Trans. Biomed. Eng. 2004, 51, 1156–1166. [Google Scholar] [CrossRef] [PubMed]
- Palus, M. Detecting phase synchronization in noisy systems. Phys. Lett. A 1997, 235, 341–351. [Google Scholar] [CrossRef]
- Chávez, M.; Martinerie, J.; Le Van Quyen, M. Statistical assessment of nonlinear causality: Application to epileptic EEG signals. J. Neurosci. Methods 2003, 124, 113–128. [Google Scholar] [CrossRef] [PubMed]
- Lizier, J.T.; Heinzle, J.; Horstmann, A.; Haynes, J.D.; Prokopenko, M. Multivariate information-theoretic measures reveal directed information structure and task relevant changes in fMRI connectivity. J. Comput. Neurosci. 2011, 30, 85–107. [Google Scholar] [CrossRef]
- Vejmelka, M.; Paluš, M. Inferring the directionality of coupling with conditional mutual information. Phys. Rev. E 2008, 77, 026214. [Google Scholar] [CrossRef]
- Musizza, B.; Stefanovska, A.; McClintock, P.V.; Paluš, M.; Petrovčič, J.; Ribarič, S.; Bajrović, F.F. Interactions between cardiac, respiratory and EEG-δ oscillations in rats during anaesthesia. J. Physiol. 2007, 580, 315–326. [Google Scholar] [CrossRef]
- Faes, L.; Nollo, G.; Chon, K.H. Assessment of Granger causality by nonlinear model identification: Application to short-term cardiovascular variability. Ann. Biomed. Eng. 2008, 36, 381–395. [Google Scholar] [CrossRef]
- Faes, L.; Porta, A.; Nollo, G. Mutual nonlinear prediction as a tool to evaluate coupling strength and directionality in bivariate time series: Comparison among different strategies based on k nearest neighbors. Phys. Rev. E 2008, 78, 026201. [Google Scholar] [CrossRef]
- Muthuraman, M.; Hellriegel, H.; Hoogenboom, N.; Anwar, A.R.; Mideksa, K.G.; Krause, H.; Schnitzler, A.; Deuschl, G.; Raethjen, J. Beamformer source analysis and connectivity on concurrent EEG and MEG data during voluntary movements. PLoS ONE 2014, 9, e91441. [Google Scholar] [CrossRef]
- Tamás, G.; Chirumamilla, V.C.; Anwar, A.R.; Raethjen, J.; Deuschl, G.; Groppa, S.; Muthuraman, M. Primary sensorimotor cortex drives the common cortical network for gamma synchronization in voluntary hand movements. Front. Hum. Neurosci. 2018, 12, 130. [Google Scholar] [CrossRef]
- Anwar, A.R.; Muthalib, M.; Perrey, S.; Galka, A.; Granert, O.; Wolff, S.; Heute, U.; Deuschl, G.; Raethjen, J.; Muthuraman, M. Effective connectivity of cortical sensorimotor networks during finger movement tasks: A simultaneous fNIRS, fMRI, EEG study. Brain Topogr. 2016, 29, 645–660. [Google Scholar] [CrossRef]
- Babiloni, F.; Cincotti, F.; Babiloni, C.; Carducci, F.; Mattia, D.; Astolfi, L.; Basilisco, A.; Rossini, P.M.; Ding, L.; Ni, Y.; et al. Estimation of the cortical functional connectivity with the multimodal integration of high-resolution EEG and fMRI data by directed transfer function. Neuroimage 2005, 24, 118–131. [Google Scholar] [CrossRef] [PubMed]
- Coito, A.; Michel, C.M.; Vulliemoz, S.; Plomp, G. Directed functional connections underlying spontaneous brain activity. Hum. Brain Mapp. 2019, 40, 879–888. [Google Scholar] [CrossRef] [PubMed]
- Astolfi, L.; Cincotti, F.; Mattia, D.; Babiloni, C.; Carducci, F.; Basilisco, A.; Rossini, P.; Salinari, S.; Ding, L.; Ni, Y.; et al. Assessing cortical functional connectivity by linear inverse estimation and directed transfer function: Simulations and application to real data. Clin. Neurophysiol. 2005, 116, 920–932. [Google Scholar] [CrossRef]
- Haufe, S.; Ewald, A. A simulation framework for benchmarking EEG-based brain connectivity estimation methodologies. Brain Topogr. 2019, 32, 625–642. [Google Scholar] [CrossRef] [PubMed]
- García, A.O.M.; Müller, M.F.; Schindler, K.; Rummel, C. Genuine cross-correlations: Which surrogate based measure reproduces analytical results best? Neural Netw. 2013, 46, 154–164. [Google Scholar] [CrossRef] [PubMed]
- Prichard, D.; Theiler, J. Generating surrogate data for time series with several simultaneously measured variables. Phys. Rev. Lett. 1994, 73, 951. [Google Scholar] [CrossRef] [PubMed]
- Dolan, K.T.; Neiman, A. Surrogate analysis of coherent multichannel data. Phys. Rev. E 2002, 65, 026108. [Google Scholar] [CrossRef]
- Breakspear, M.; Brammer, M.; Robinson, P.A. Construction of multivariate surrogate sets from nonlinear data using the wavelet transform. Phys. D Nonlinear Phenom. 2003, 182, 1–22. [Google Scholar] [CrossRef]
- Breakspear, M.; Brammer, M.J.; Bullmore, E.T.; Das, P.; Williams, L.M. Spatiotemporal wavelet resampling for functional neuroimaging data. Hum. Brain Mapp. 2004, 23, 1–25. [Google Scholar] [CrossRef]
- Shannon, C. Communication in the Presence of Noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Kayser, J.; Tenke, C.E. In Search of the Rosetta Stone for Scalp EEG: Converging on Reference-Free Techniques. Clin. Neurophysiol. 2010, 121, 1973–1975. [Google Scholar] [CrossRef] [PubMed]
- Berger, H. Über das elektroenkephalogramm des menschen. Arch. Für Psychiatr. Und Nervenkrankh. 1929, 87, 527–570. [Google Scholar] [CrossRef]
- Yao, D.; Qin, Y.; Hu, S.; Dong, L.; Bringas Vega, M.L.; Valdés Sosa, P.A. Which Reference Should We Use for EEG and ERP Practice? Brain Topogr. 2019, 32, 530–549. [Google Scholar] [CrossRef]
- Niedermeyer, E.; da Silva, F.L. Electroencephalography: Basic Principles, Clinical Applications, and Related Fields; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2005. [Google Scholar]
- Widmann, A.; Schröger, E.; Maess, B. Digital Filter Design for Electrophysiological Data–a Practical Approach. J. Neurosci. Methods 2015, 250, 34–46. [Google Scholar] [CrossRef]
- Mullen, T. Cleanline Tool. 2012. Available online: https://www.nitrc.org/projects/cleanline/ (accessed on 10 December 2022).
- Bigdely-Shamlo, N.; Mullen, T.; Kothe, C.; Su, K.M.; Robbins, K.A. The PREP Pipeline: Standardized Preprocessing for Large-Scale EEG Analysis. Front. Neuroinform. 2015, 9, 16. [Google Scholar] [CrossRef] [PubMed]
- Leske, S.; Dalal, S.S. Reducing Power Line Noise in EEG and MEG Data via Spectrum Interpolation. NeuroImage 2019, 189, 763–776. [Google Scholar] [CrossRef] [PubMed]
- Phadikar, S.; Sinha, N.; Ghosh, R.; Ghaderpour, E. Automatic muscle artifacts identification and removal from single-channel eeg using wavelet transform with meta-heuristically optimized non-local means filter. Sensors 2022, 22, 2948. [Google Scholar] [CrossRef]
- Ghosh, R.; Phadikar, S.; Deb, N.; Sinha Sr, N.; Das, P.; Ghaderpour, E. Automatic Eye-blink and Muscular Artifact Detection and Removal from EEG Signals using k-Nearest Neighbour Classifier and Long Short-Term Memory Networks. IEEE Sens. J. 2023, 23, 5422–5436. [Google Scholar] [CrossRef]
- da Cruz, J.R.; Chicherov, V.; Herzog, M.H.; Figueiredo, P. An Automatic Pre-Processing Pipeline for EEG Analysis (APP) Based on Robust Statistics. Clin. Neurophysiol. Off. J. Int. Fed. Clin. Neurophysiol. 2018, 129, 1427–1437. [Google Scholar] [CrossRef] [PubMed]
- Miljevic, A.; Bailey, N.W.; Vila-Rodriguez, F.; Herring, S.E.; Fitzgerald, P.B. Electroencephalographic Connectivity: A Fundamental Guide and Checklist for Optimal Study Design and Evaluation. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2022, 7, 546–554. [Google Scholar] [CrossRef] [PubMed]
- Zaveri, H.P.; Duckrow, R.B.; Spencer, S.S. The effect of a scalp reference signal on coherence measurements of intracranial electroencephalograms. Clin. Neurophysiol. 2000, 111, 1293–1299. [Google Scholar] [CrossRef]
- Urigüen, J.A.; Garcia-Zapirain, B. EEG Artifact Removal—State-of-the-Art and Guidelines. J. Neural Eng. 2015, 12, 031001. [Google Scholar] [CrossRef]
- Barlow, J.S. Artifact Processing (Rejection and Minimization) in EEG Data Processing. Handb. Electroencephalogr. Clin. Neurophysiology. Revis. Ser. 1986, 2, 15–62. [Google Scholar]
- Croft, R.; Barry, R. Removal of Ocular Artifact from the EEG: A Review. Neurophysiol. Clin. Neurophysiol. 2000, 30, 5–19. [Google Scholar] [CrossRef]
- Wallstrom, G.L.; Kass, R.E.; Miller, A.; Cohn, J.F.; Fox, N.A. Automatic Correction of Ocular Artifacts in the EEG: A Comparison of Regression-Based and Component-Based Methods. Int. J. Psychophysiol. 2004, 53, 105–119. [Google Scholar] [CrossRef]
- Romero, S.; Mañanas, M.A.; Barbanoj, M.J. A Comparative Study of Automatic Techniques for Ocular Artifact Reduction in Spontaneous EEG Signals Based on Clinical Target Variables: A Simulation Case. Comput. Biol. Med. 2008, 38, 348–360. [Google Scholar] [CrossRef]
- Anderer, P.; Roberts, S.; Schlögl, A.; Gruber, G.; Klösch, G.; Herrmann, W.; Rappelsberger, P.; Filz, O.; Barbanoj, M.J.; Dorffner, G.; et al. Artifact Processing in Computerized Analysis of Sleep EEG—A Review. Neuropsychobiology 1999, 40, 150–157. [Google Scholar] [CrossRef]
- Sörnmo, L.; Laguna, P. Bioelectrical Signal Processing in Cardiac and Neurological Applications; Elsevier: Amsterdam, The Netherlands; Academic Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Makeig, S.; Bell, A.; Jung, T.P.; Sejnowski, T.J. Independent Component Analysis of Electroencephalographic Data. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1995; Volume 8. [Google Scholar]
- Lee, T.W.; Girolami, M.; Sejnowski, T.J. Independent Component Analysis Using an Extended Infomax Algorithm for Mixed Subgaussian and Supergaussian Sources. Neural Comput. 1999, 11, 417–441. [Google Scholar] [CrossRef]
- Albera, L.; Kachenoura, A.; Comon, P.; Karfoul, A.; Wendling, F.; Senhadji, L.; Merlet, I. ICA-Based EEG Denoising: A Comparative Analysis of Fifteen Methods. Bull. Pol. Acad. Sci. Tech. Sci. 2012, 60, 407–418. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. A Fast Fixed-Point Algorithm for Independent Component Analysis. Neural Comput. 1997, 9, 1483–1492. [Google Scholar] [CrossRef]
- Hyvarinen, A. Fast and Robust Fixed-Point Algorithms for Independent Component Analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [PubMed]
- Belouchrani, A.; Abed-Meraim, K.; Cardoso, J.F.; Moulines, É. A blind source separation technique using second-order statistics. IEEE Trans. Signal Process. 1997, 45, 434–444. [Google Scholar] [CrossRef]
- Mesin, L.; Holobar, A.; Merletti, R. Blind Source Separation. Application to Biomedical Signals. In Advanced Methods of Biomedical Signal Processing; Cerutti, S., Marchesi, C., Eds.; IEEE Press Series in Biomedical Engineering; John Wiley &Sons: Hoboken, NJ, USA, 2011; pp. 379–409. [Google Scholar]
- Jung, T.P.; Makeig, S.; Humphries, C.; Lee, T.W.; McKeown, M.J.; Iragui, V.; Sejnowski, T.J. Removing Electroencephalographic Artifacts by Blind Source Separation. Psychophysiology 2000, 37, 163–178. [Google Scholar] [CrossRef]
- Weber, I.; Florin, E.; von Papen, M.; Timmermann, L. The influence of filtering and downsampling on the estimation of transfer entropy. PLoS ONE 2017, 12, e0188210. [Google Scholar] [CrossRef]
- Vinck, M.; Oostenveld, R.; van Wingerden, M.; Battaglia, F.; Pennartz, C.M. An improved index of phase-synchronization for electrophysiological data in the presence of volume-conduction, noise and sample-size bias. NeuroImage 2011, 55, 1548–1565. [Google Scholar] [CrossRef]
- Montefusco-Siegmund, R.; Maldonado, P.E.; Devia, C. Effects of ocular artifact removal through ICA decomposition on EEG phase. In Proceedings of the 2013 6th International IEEE/EMBS Conference on Neural Engineering (NER), San Diego, CA, USA, 6–8 November 2013; IEEE: Piscataway, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Florin, E.; Gross, J.; Pfeifer, J.; Fink, G.R.; Timmermann, L. The Effect of Filtering on Granger Causality Based Multivariate Causality Measures. NeuroImage 2010, 50, 577–588. [Google Scholar] [CrossRef]
- Picton, T.; Bentin, S.; Berg, P.; Donchin, E.; Hillyard, S.; Johnson JR., R.; Miller, G.; Ritter, W.; Ruchkin, D.; Rugg, M.; et al. Guidelines for Using Human Event-Related Potentials to Study Cognition: Recording Standards and Publication Criteria. Psychophysiology 2000, 37, 127–152. [Google Scholar] [CrossRef]
- Van der Meer, M.; Tewarie, P.; Schoonheim, M.; Douw, L.; Barkhof, F.; Polman, C.; Stam, C.; Hillebrand, A. Cognition in MS Correlates with Resting-State Oscillatory Brain Activity: An Explorative MEG Source-Space Study. NeuroImage Clin. 2013, 2, 727–734. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, L.G.; Radhu, N.; Farzan, F.; Daskalakis, Z.J. Characterizing Long Interval Cortical Inhibition over the Time-Frequency Domain. PLoS ONE 2014, 9, e92354. [Google Scholar] [CrossRef]
- Perrin, F.; Pernier, J.; Bertrand, O.; Echallier, J. Spherical Splines for Scalp Potential and Current Density Mapping. Electroencephalogr. Clin. Neurophysiol. 1989, 72, 184–187. [Google Scholar] [CrossRef]
- Re-Referencing. Available online: https://eeglab.org/tutorials/ConceptsGuide/rereferencing_background.html (accessed on 10 December 2022).
- Schiff, S.J. Dangerous Phase. Neuroinformatics 2005, 3, 315–318. [Google Scholar] [CrossRef]
- Hjorth, B. An on-line transformation of EEG scalp potentials into orthogonal source derivations. Electroencephalogr. Clin. Neurophysiol. 1975, 39, 526–530. [Google Scholar] [CrossRef]
- Yao, D. A Method to Standardize a Reference of Scalp EEG Recordings to a Point at Infinity. Physiol. Meas. 2001, 22, 693. [Google Scholar] [CrossRef]
- Zhai, Y.; Yao, D. A Study on the Reference Electrode Standardization Technique for a Realistic Head Model. Comput. Methods Programs Biomed. 2004, 76, 229–238. [Google Scholar] [CrossRef]
- Marzetti, L.; Nolte, G.; Perrucci, M.; Romani, G.; Del Gratta, C. The Use of Standardized Infinity Reference in EEG Coherency Studies. NeuroImage 2007, 36, 48–63. [Google Scholar] [CrossRef]
- Yao, D. Is the Surface Potential Integral of a Dipole in a Volume Conductor Always Zero? A Cloud Over the Average Reference of EEG and ERP. Brain Topogr. 2017, 30, 161–171. [Google Scholar] [CrossRef]
- Liu, Q.; Balsters, J.H.; Baechinger, M.; van der Groen, O.; Wenderoth, N.; Mantini, D. Estimating a Neutral Reference for Electroencephalographic Recordings: The Importance of Using a High-Density Montage and a Realistic Head Model. J. Neural Eng. 2015, 12, 056012. [Google Scholar] [CrossRef]
- Chella, F.; Pizzella, V.; Zappasodi, F.; Marzetti, L. Impact of the Reference Choice on Scalp EEG Connectivity Estimation. J. Neural Eng. 2016, 13, 036016. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, J.; Cui, Y.; Yang, G.; He, L.; Liu, Q.; Yin, G. How Different EEG References Influence Sensor Level Functional Connectivity Graphs. Front. Neurosci. 2017, 11, 368. [Google Scholar] [CrossRef] [PubMed]
- Lepage, K.Q.; Kramer, M.A.; Chu, C.J. A statistically robust EEG re-referencing procedure to mitigate reference effect. J. Neurosci. Methods 2014, 235, 101–116. [Google Scholar] [CrossRef]
- Yao, D.; Wang, L.; Oostenveld, R.; Nielsen, K.D.; Arendt-Nielsen, L.; Chen, A.C.N. A comparative study of different references for EEG spectral mapping: The issue of the neutral reference and the use of the infinity reference. Physiol. Meas. 2005, 26, 173–184. [Google Scholar] [CrossRef] [PubMed]
- Nunez, P.L.; Srinivasan, R.; Westdorp, A.F.; Wijesinghe, R.S.; Tucker, D.M.; Silberstein, R.B.; Cadusch, P.J. EEG Coherency: I: Statistics, Reference Electrode, Volume Conduction, Laplacians, Cortical Imaging, and Interpretation at Multiple Scales. Electroencephalogr. Clin. Neurophysiol. 1997, 103, 499–515. [Google Scholar] [CrossRef]
- Qin, Y.; Xu, P.; Yao, D. A comparative study of different references for EEG default mode network: The use of the infinity reference. Clin. Neurophysiol. 2010, 121, 1981–1991. [Google Scholar] [CrossRef]
- Lai, M.; Demuru, M.; Hillebrand, A.; Fraschini, M. A comparison between scalp-and source-reconstructed EEG networks. Sci. Rep. 2018, 8, 12269. [Google Scholar] [CrossRef] [PubMed]
- Jatoi, M.A.; Kamel, N.; Malik, A.S.; Faye, I.; Begum, T. A Survey of Methods Used for Source Localization Using EEG Signals. Biomed. Signal Process. Control 2014, 11, 42–52. [Google Scholar] [CrossRef]
- Snieder, R.; Trampert, J. Inverse Problems in Geophysics. In Wavefield Inversion; Wirgin, A., Ed.; Springer: Vienna, Austria, 1999; pp. 119–190. [Google Scholar] [CrossRef]
- Lai, Y.; van Drongelen, W.; Ding, L.; Hecox, K.; Towle, V.; Frim, D.; He, B. Estimation of in vivo human brain-to-skull conductivity ratio from simultaneous extra- and intra-cranial electrical potential recordings. Clin. Neurophysiol. 2005, 116, 456–465. [Google Scholar] [CrossRef]
- He, B.; Musha, T.; Okamoto, Y.; Homma, S.; Nakajima, Y.; Sato, T. Electric Dipole Tracing in the Brain by Means of the Boundary Element Method and Its Accuracy. IEEE Trans. Biomed. Eng. 1987, BME-34, 406–414. [Google Scholar] [CrossRef]
- Lee, W.H.; Liu, Z.; Mueller, B.A.; Lim, K.; He, B. Influence of white matter anisotropic conductivity on EEG source localization: Comparison to fMRI in human primary visual cortex. Clin. Neurophysiol. 2009, 120, 2071–2081. [Google Scholar] [CrossRef]
- Scherg, M.; Von Cramon, D. A New Interpretation of the Generators of BAEP Waves I–V: Results of a Spatio-Temporal Dipole Model. Electroencephalogr. Clin. Neurophysiol. Potentials Sect. 1985, 62, 290–299. [Google Scholar] [CrossRef]
- Hämäläinen, M.; Ilmoniemi, R. Interpreting Measured Magnetic Fields of the Brain: Estimates of Current Distributions; The University of Helsinki: Helsinki, Finland, 1984; Volume 32. [Google Scholar]
- Hämäläinen, M.S.; Ilmoniemi, R.J. Interpreting magnetic fields of the brain: Minimum norm estimates. Med. Biol. Eng. Comput. 1994, 32, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Pascual-Marqui, R.D.; Michel, C.M.; Lehmann, D. Low resolution electromagnetic tomography: A new method for localizing electrical activity in the brain. Int. J. Psychophysiol. 1994, 18, 49–65. [Google Scholar] [CrossRef] [PubMed]
- Pascual-Marqui, R.D. Standardized low-resolution brain electromagnetic tomography (sLORETA): Technical details. Methods Find Exp. Clin. Pharmacol. 2002, 24, 5–12. [Google Scholar] [PubMed]
- Pascual-Marqui, R.D.; Lehmann, D.; Koukkou, M.; Kochi, K.; Anderer, P.; Saletu, B.; Tanaka, H.; Hirata, K.; John, E.R.; Prichep, L.; et al. Assessing Interactions in the Brain with Exact Low-Resolution Electromagnetic Tomography. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 3768–3784. [Google Scholar] [CrossRef]
- Pascual-Marqui, R.D. Discrete, 3D distributed, linear imaging methods of electric neuronal activity. Part 1: Exact, zero error localization. arXiv 2007, arXiv:0710.3341. [Google Scholar]
- Blinowska, K.J. Review of the methods of determination of directed connectivity from multichannel data. Med. Biol. Eng. Comput. 2011, 49, 521–529. [Google Scholar] [CrossRef]
- Brunner, C.; Billinger, M.; Seeber, M.; Mullen, T.R.; Makeig, S. Volume Conduction Influences Scalp-Based Connectivity Estimates. Front. Comput. Neurosci. 2016, 10, 121. [Google Scholar] [CrossRef]
- Kaminski, M.; Blinowska, K.J. The Influence of Volume Conduction on DTF Estimate and the Problem of Its Mitigation. Front. Comput. Neurosci. 2017, 11, 36. [Google Scholar] [CrossRef]
- Schoffelen, J.M.; Gross, J. Source connectivity analysis with MEG and EEG. Hum. Brain Mapp. 2009, 30, 1857–1865. [Google Scholar] [CrossRef] [PubMed]
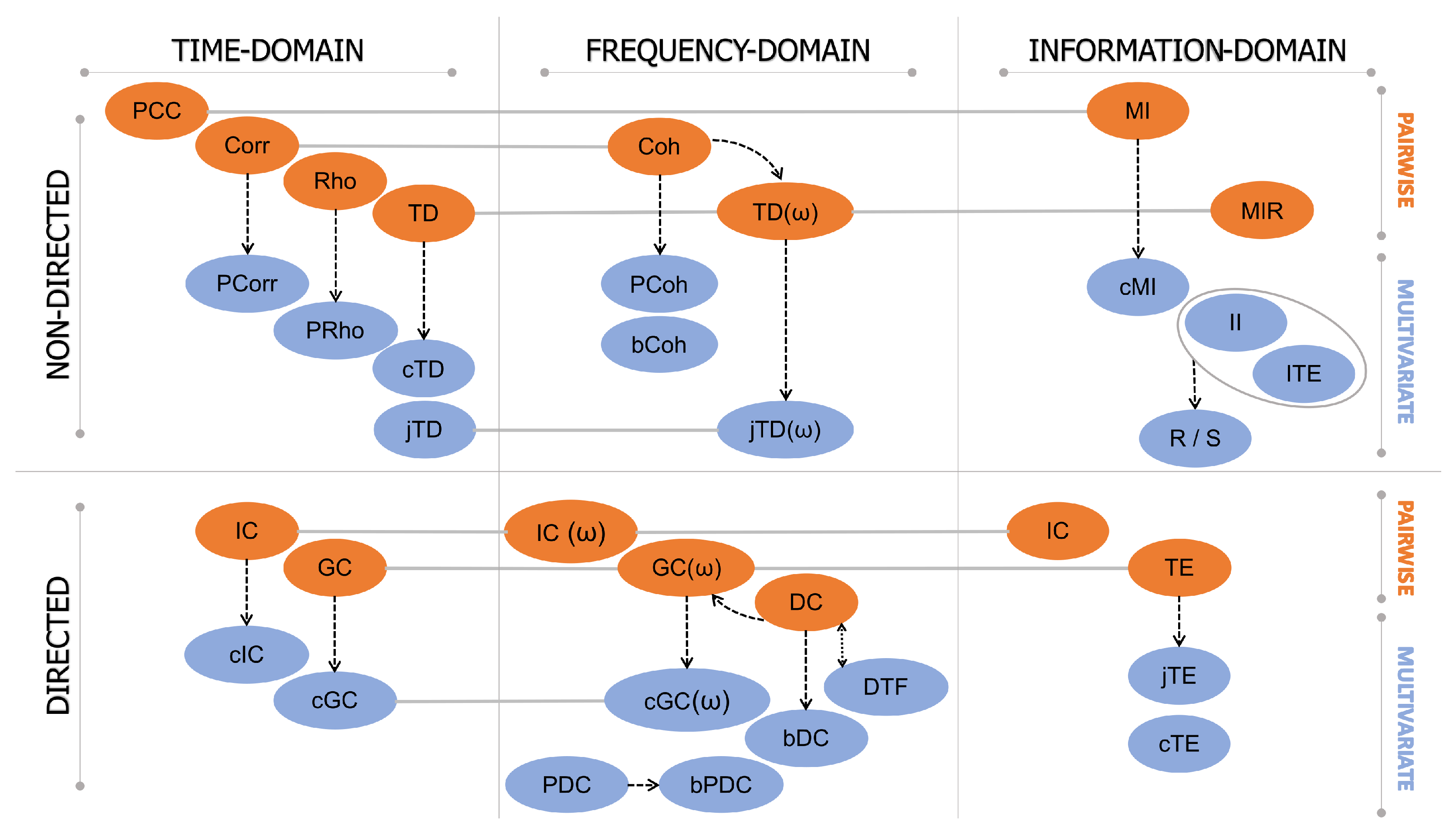
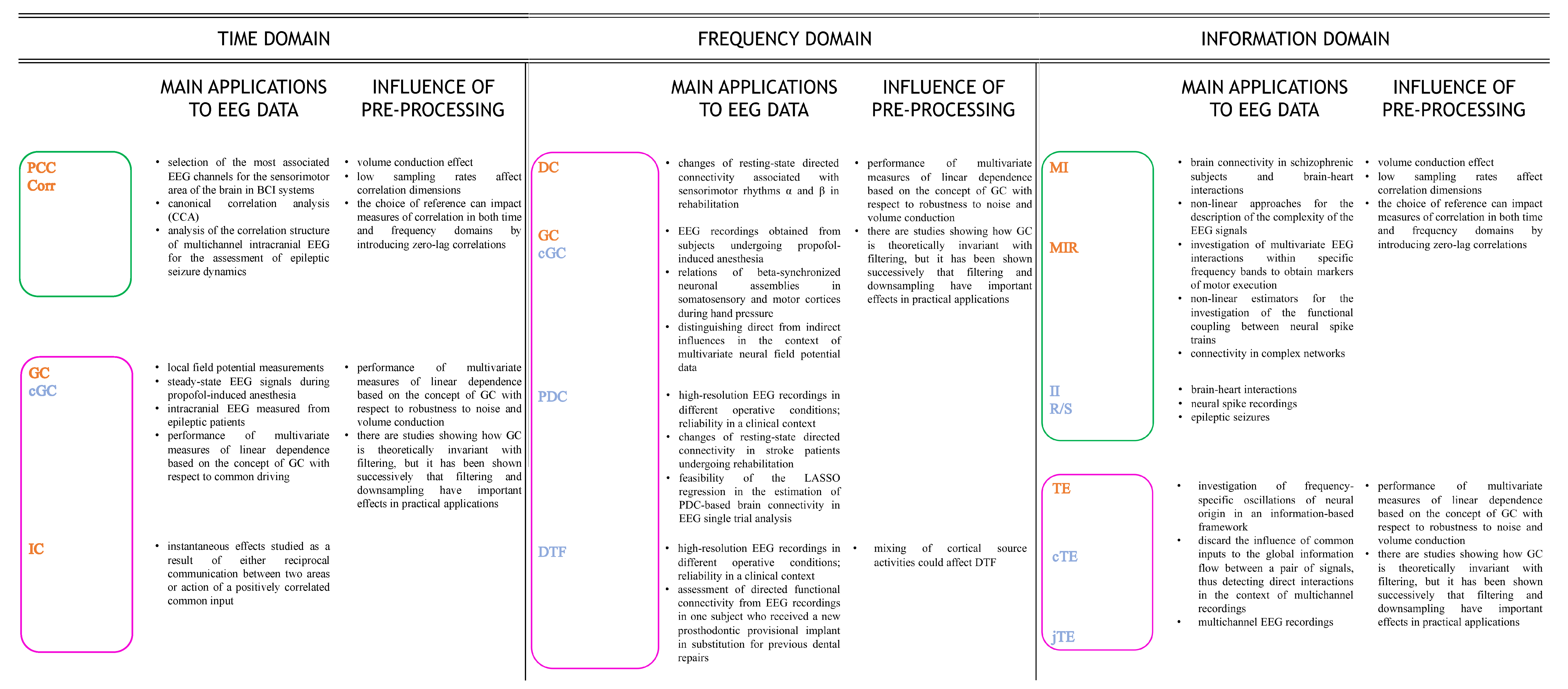


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiarion, G.; Sparacino, L.; Antonacci, Y.; Faes, L.; Mesin, L. Connectivity Analysis in EEG Data: A Tutorial Review of the State of the Art and Emerging Trends. Bioengineering 2023, 10, 372. https://doi.org/10.3390/bioengineering10030372
Chiarion G, Sparacino L, Antonacci Y, Faes L, Mesin L. Connectivity Analysis in EEG Data: A Tutorial Review of the State of the Art and Emerging Trends. Bioengineering. 2023; 10(3):372. https://doi.org/10.3390/bioengineering10030372
Chicago/Turabian StyleChiarion, Giovanni, Laura Sparacino, Yuri Antonacci, Luca Faes, and Luca Mesin. 2023. "Connectivity Analysis in EEG Data: A Tutorial Review of the State of the Art and Emerging Trends" Bioengineering 10, no. 3: 372. https://doi.org/10.3390/bioengineering10030372
APA StyleChiarion, G., Sparacino, L., Antonacci, Y., Faes, L., & Mesin, L. (2023). Connectivity Analysis in EEG Data: A Tutorial Review of the State of the Art and Emerging Trends. Bioengineering, 10(3), 372. https://doi.org/10.3390/bioengineering10030372







