Investigation of Biomaterial Ink Viscosity Properties and Optimization of the Printing Process Based on Pattern Path Planning
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Biomaterial Ink
2.2. Fourier-Transform Infrared (FTIR)
2.3. Design of Experiments
2.4. Rheological Measurements
2.5. Mechanical Testing
2.6. Latin Hypercube Sampling
2.7. Modeling and Simulations
2.8. Neural Network Prediction Model
2.9. 3D Bioprinting
2.10. Characterization of Microstructures and Printing Processes
3. Results and Discussion
3.1. Preparation and Characterization of Biomaterial Ink
3.2. Analysis of the RSM Model
3.3. Analysis of the Mechanical Property
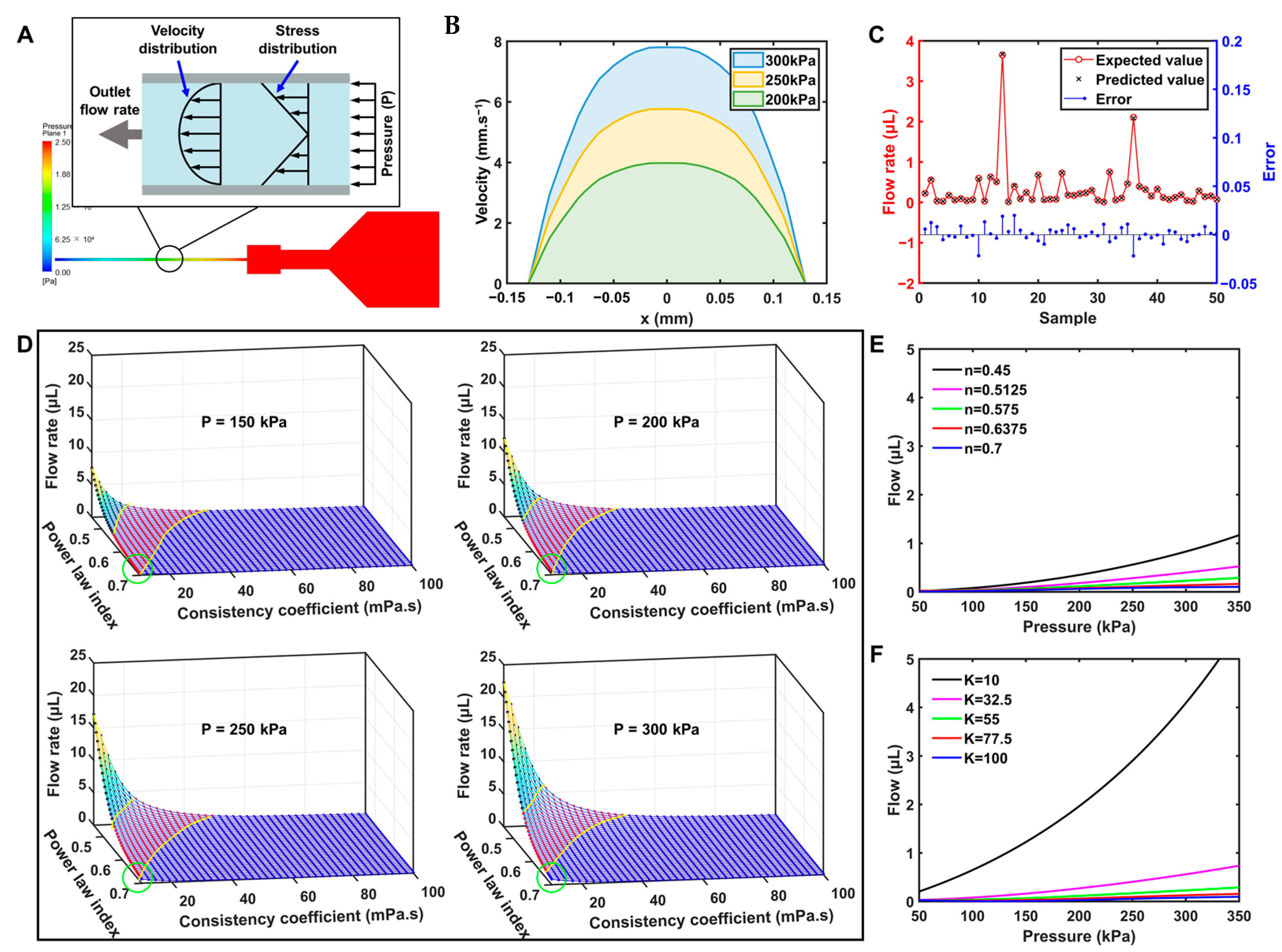
3.4. Analysis of Simulation Results
3.5. Analysis of the Prediction Model
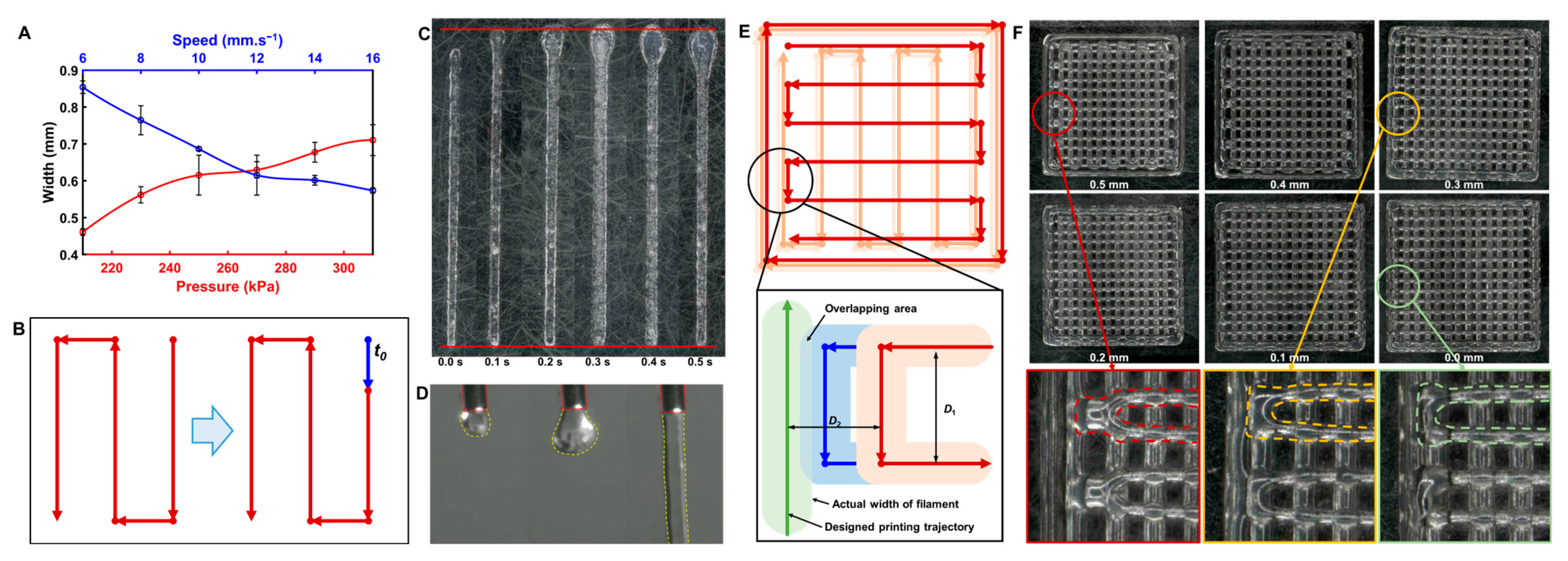
3.6. Analysis of the Printing Process
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hsieh, H.B.; Fitch, J.; White, D.; Torres, F.; Roy, J.; Matusiak, R.; Krivacic, B.; Kowalski, B.; Bruce, R.; Elrod, S. Ultra-High-Throughput Microarray Generation and Liquid Dispensing Using Multiple Disposable Piezoelectric Ejectors. SLAS Discov. 2004, 9, 85–94. [Google Scholar] [CrossRef][Green Version]
- Guillemot, F.; Mironov, V.; Nakamura, M. Bioprinting Is Coming of Age: Report from the International Conference on Bioprinting and Biofabrication in Bordeaux (3B’09). Biofabrication 2010, 2, 010201. [Google Scholar] [CrossRef]
- Bishop, E.S.; Mostafa, S.; Pakvasa, M.; Luu, H.H.; Lee, M.J.; Wolf, J.M.; Ameer, G.A.; He, T.-C.; Reid, R.R. 3-D Bioprinting Technologies in Tissue Engineering and Regenerative Medicine: Current and Future Trends. Genes Dis. 2017, 4, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Decante, G.; Costa, J.B.; Silva-Correia, J.; Collins, M.N.; Reis, R.L.; Oliveira, J.M. Engineering Bioinks for 3D Bioprinting. Biofabrication 2021, 13, 032001. [Google Scholar] [CrossRef] [PubMed]
- Vijayavenkataraman, S.; Yan, W.-C.; Lu, W.F.; Wang, C.-H.; Fuh, J.Y.H. 3D Bioprinting of Tissues and Organs for Regenerative Medicine. Adv. Drug Deliv. Rev. 2018, 132, 296–332. [Google Scholar] [CrossRef] [PubMed]
- Mironov, V.; Boland, T.; Trusk, T.; Forgacs, G.; Markwald, R.R. Organ Printing: Computer-Aided Jet-Based 3D Tissue Engineering. Trends Biotechnol. 2003, 21, 157–161. [Google Scholar] [CrossRef] [PubMed]
- Afanasenkau, D.; Kalinina, D.; Lyakhovetskii, V.; Tondera, C.; Gorsky, O.; Moosavi, S.; Pavlova, N.; Merkulyeva, N.; Kalueff, A.V.; Minev, I.R.; et al. Rapid Prototyping of Soft Bioelectronic Implants for Use as Neuromuscular Interfaces. Nat. Biomed. Eng. 2020, 4, 1010–1022. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, X.; Pan, Y.; Liu, H.; Cheng, J.; Xiong, Z.; Lin, F.; Wu, R.; Zhang, R.; Lu, Q. Fabrication of Viable Tissue-Engineered Constructs with 3D Cell-Assembly Technique. Biomaterials 2005, 26, 5864–5871. [Google Scholar] [CrossRef]
- Lawlor, K.T.; Vanslambrouck, J.M.; Higgins, J.W.; Chambon, A.; Bishard, K.; Arndt, D.; Er, P.X.; Wilson, S.B.; Howden, S.E.; Tan, K.S.; et al. Cellular Extrusion Bioprinting Improves Kidney Organoid Reproducibility and Conformation. Nat. Mater. 2021, 20, 260–271. [Google Scholar] [CrossRef]
- Dhariwala, B.; Hunt, E.; Boland, T. Rapid Prototyping of Tissue-Engineering Constructs, Using Photopolymerizable Hydrogels and Stereolithography. Tissue Eng. 2004, 10, 1316–1322. [Google Scholar] [CrossRef]
- Naghieh, S.; Chen, X. Printability—A Key Issue in Extrusion-Based Bioprinting. J. Pharm. Anal. 2021, 11, 564–579. [Google Scholar] [CrossRef]
- Placone, J.K.; Engler, A.J. Recent Advances in Extrusion-Based 3D Printing for Biomedical Applications. Adv. Healthc. Mater. 2018, 7, 1701161. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Zhao, W.; Xiahou, Z.; Wang, X.; Zhang, K.; Yin, J. Bioink Design for Extrusion-Based Bioprinting. Appl. Mater. Today 2021, 25, 101227. [Google Scholar] [CrossRef]
- Ning, L.; Mehta, R.; Cao, C.; Theus, A.; Tomov, M.; Zhu, N.; Weeks, E.R.; Bauser-Heaton, H.; Serpooshan, V. Embedded 3D Bioprinting of Gelatin Methacryloyl-Based Constructs with Highly Tunable Structural Fidelity. ACS Appl. Mater. Interfaces 2020, 12, 44563–44577. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, L.; Armstrong, J.P.K.; Lin, Y.; Wojciechowski, J.P.; Lee-Reeves, C.; Hachim, D.; Zhou, K.; Burdick, J.A.; Stevens, M.M. Expanding and Optimizing 3D Bioprinting Capabilities Using Complementary Network Bioinks. Sci. Adv. 2020, 6, eabc5529. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, A.; Blokzijl, M.M.; Levato, R.; Visser, C.W.; Castilho, M.; Hennink, W.E.; Vermonden, T.; Malda, J. Assessing Bioink Shape Fidelity to Aid Material Development in 3D Bioprinting. Biofabrication 2017, 10, 014102. [Google Scholar] [CrossRef]
- Yi, S.; Liu, Q.; Luo, Z.; He, J.J.; Ma, H.; Li, W.; Wang, D.; Zhou, C.; Garciamendez, C.E.; Hou, L.; et al. Micropore-Forming Gelatin Methacryloyl (GelMA) Bioink Toolbox 2.0: Designable Tunability and Adaptability for 3D Bioprinting Applications. Small 2022, 18, 2106357. [Google Scholar] [CrossRef] [PubMed]
- Hay, E.D. (Ed.) Cell Biology of Extracellular Matrix, 2nd ed.; Springer: Boston, MA, USA, 1991; ISBN 978-1-4613-6680-5. [Google Scholar]
- Echave, M.C.; del Burgo, L.S.; Pedraz, J.L.; Orive, G. Gelatin as Biomaterial for Tissue Engineering. Curr. Pharm. Des. 2017, 23, 3567–3584. [Google Scholar] [CrossRef]
- Kozlov, P.V.; Burdygina, G.I. The Structure and Properties of Solid Gelatin and the Principles of Their Modification. Polymer 1983, 24, 651–666. [Google Scholar] [CrossRef]
- Yue, K.; Trujillo-de Santiago, G.; Alvarez, M.M.; Tamayol, A.; Annabi, N.; Khademhosseini, A. Synthesis, Properties, and Biomedical Applications of Gelatin Methacryloyl (GelMA) Hydrogels. Biomaterials 2015, 73, 254–271. [Google Scholar] [CrossRef]
- Leuenberger, B.H. Investigation of Viscosity and Gelation Properties of Different Mammalian and Fish Gelatins. Food Hydrocoll. 1991, 5, 353–361. [Google Scholar] [CrossRef]
- Van Den Bulcke, A.I.; Bogdanov, B.; De Rooze, N.; Schacht, E.H.; Cornelissen, M.; Berghmans, H. Structural and Rheological Properties of Methacrylamide Modified Gelatin Hydrogels. Biomacromolecules 2000, 1, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.Y.; Mooney, D.J. Alginate: Properties and Biomedical Applications. Prog. Polym. Sci. 2012, 37, 106–126. [Google Scholar] [CrossRef] [PubMed]
- Rowley, J.A.; Madlambayan, G.; Mooney, D.J. Alginate Hydrogels as Synthetic Extracellular Matrix Materials. Biomaterials 1999, 20, 45–53. [Google Scholar] [CrossRef]
- Nasatto, P.; Pignon, F.; Silveira, J.; Duarte, M.; Noseda, M.; Rinaudo, M. Methylcellulose, a Cellulose Derivative with Original Physical Properties and Extended Applications. Polymers 2015, 7, 777–803. [Google Scholar] [CrossRef]
- Sarkar, N. Thermal Gelation Properties of Methyl and Hydroxypropyl Methylcellulose. J. Appl. Polym. Sci. 1979, 24, 1073–1087. [Google Scholar] [CrossRef]
- Bonetti, L.; De Nardo, L.; Farè, S. Thermo-Responsive Methylcellulose Hydrogels: From Design to Applications as Smart Biomaterials. Tissue Eng. Part B Rev. 2021, 27, 486–513. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y.; Wang, C. Investigation of Collagen-Incorporated Sodium Alginate Bioprinting Hydrogel for Tissue Engineering. J. Compos. Sci. 2022, 6, 227. [Google Scholar] [CrossRef]
- Choi, D.J.; Park, S.J.; Gu, B.K.; Kim, Y.-J.; Chung, S.; Kim, C.-H. Effect of the Pore Size in a 3D Bioprinted Gelatin Scaffold on Fibroblast Proliferation. J. Ind. Eng. Chem. 2018, 67, 388–395. [Google Scholar] [CrossRef]
- Delkash, Y.; Gouin, M.; Rimbeault, T.; Mohabatpour, F.; Papagerakis, P.; Maw, S.; Chen, X. Bioprinting and In Vitro Characterization of an Eggwhite-Based Cell-Laden Patch for Endothelialized Tissue Engineering Applications. J. Funct. Biomater. 2021, 12, 45. [Google Scholar] [CrossRef]
- Duin, S.; Schütz, K.; Ahlfeld, T.; Lehmann, S.; Lode, A.; Ludwig, B.; Gelinsky, M. 3D Bioprinting of Functional Islets of Langerhans in an Alginate/Methylcellulose Hydrogel Blend. Adv. Healthc. Mater. 2019, 8, 1801631. [Google Scholar] [CrossRef] [PubMed]
- Schütz, K.; Placht, A.-M.; Paul, B.; Brüggemeier, S.; Gelinsky, M.; Lode, A. Three-Dimensional Plotting of a Cell-Laden Alginate/Methylcellulose Blend: Towards Biofabrication of Tissue Engineering Constructs with Clinically Relevant Dimensions: 3D Plotting of a Cell-Laden Alginate/Methylcellulose Blend. J. Tissue Eng. Regen. Med. 2017, 11, 1574–1587. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Ao, Q.; Tian, X.; Fan, J.; Tong, H.; Hou, W.; Bai, S. Gelatin-Based Hydrogels for Organ 3D Bioprinting. Polymers 2017, 9, 401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.M. Synergistic Blends from Aqueous Solutions of Two Cellulose Derivatives. Colloid Polym. Sci. 1999, 277, 886–890. [Google Scholar] [CrossRef]
- Kumari, M.; Gupta, S.K. Response Surface Methodological (RSM) Approach for Optimizing the Removal of Trihalomethanes (THMs) and Its Precursor’s by Surfactant Modified Magnetic Nanoadsorbents (sMNP)—An Endeavor to Diminish Probable Cancer Risk. Sci. Rep. 2019, 9, 18339. [Google Scholar] [CrossRef]
- Dean, A.; Voss, D.; Draguljić, D. Response Surface Methodology. In Design and Analysis of Experiments; Dean, A., Voss, D., Draguljić, D., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 565–614. ISBN 978-3-319-52250-0. [Google Scholar]
- Andriotis, E.G.; Eleftheriadis, G.K.; Karavasili, C.; Fatouros, D.G. Development of Bio-Active Patches Based on Pectin for the Treatment of Ulcers and Wounds Using 3D-Bioprinting Technology. Pharmaceutics 2020, 12, 56. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, X.; Bao, Z.; Lang, X.; Zhou, Z.; Li, Y.; Feng, C.; Chen, X. Reinforcement of Thermoplastic Chitosan Hydrogel Using Chitin Whiskers Optimized with Response Surface Methodology. Carbohydr. Polym. 2018, 189, 280–288. [Google Scholar] [CrossRef]
- Zhou, N.; Liu, C.; Lv, S.; Sun, D.; Qiao, Q.; Zhang, R.; Liu, Y.; Xiao, J.; Sun, G. Degradation Prediction Model and Stem Cell Growth of Gelatin-PEG Composite Hydrogel: Stem cell growth of gelatin-peg composite hydrogel. J. Biomed. Mater. Res. A 2016, 104, 3149–3156. [Google Scholar] [CrossRef]
- Bicudo, E.; Faulkner, A.; Li, P. Digital Readiness in 3D Bioprinting: Software, Governance and Hospitals’ Proto-Clinical Interfaces. Regen. Med. 2021, 16, 237–252. [Google Scholar] [CrossRef]
- Cano-Vicent, A.; Tambuwala, M.M.; Hassan, S.S.; Barh, D.; Aljabali, A.A.A.; Birkett, M.; Arjunan, A.; Serrano-Aroca, Á. Fused Deposition Modelling: Current Status, Methodology, Applications and Future Prospects. Addit. Manuf. 2021, 47, 102378. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, J.; Zhao, H.; Huang, F. Prediction of the Fiber Diameter of Melt Electrospinning Writing by Kriging Model. J. Appl. Polym. Sci. 2022, 139, 52212. [Google Scholar] [CrossRef]
- Chhabra, R.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: Woburn, MA, USA, 2008. [Google Scholar]
- Tang, T.; Yang, G.; Zhang, D.; Lei, L.; Li, B.; Gao, L. A Hydrodynamic Prediction Model of Throttle Orifice Plate Using Space Filling and Adaptive Sampling Method. Struct. Multidiscip. Optim. 2020, 62, 1563–1578. [Google Scholar] [CrossRef]
- Fu, Z.; Naghieh, S.; Xu, C.; Wang, C.; Sun, W.; Chen, X. Printability in Extrusion Bioprinting. Biofabrication 2021, 13, 033001. [Google Scholar] [CrossRef]
- Tian, X.Y.; Li, M.G.; Chen, X.B. Bio-Rapid-Prototyping of Tissue Engineering Scaffolds and the Process-Induced Cell Damage. J. Biomim. Biomater. Tissue Eng. 2013, 17, 1–23. [Google Scholar] [CrossRef]
- Muyonga, J.H.; Cole, C.G.B.; Duodu, K.G. Fourier Transform Infrared (FTIR) Spectroscopic Study of Acid Soluble Collagen and Gelatin from Skins and Bones of Young and Adult Nile Perch (Lates niloticus). Food Chem. 2004, 86, 325–332. [Google Scholar] [CrossRef]
- Papageorgiou, S.K.; Kouvelos, E.P.; Favvas, E.P.; Sapalidis, A.A.; Romanos, G.E.; Katsaros, F.K. Metal–Carboxylate Interactions in Metal–Alginate Complexes Studied with FTIR Spectroscopy. Carbohydr. Res. 2010, 345, 469–473. [Google Scholar] [CrossRef]
- Kondo, T.; Sawatari, C. A Fourier Transform Infra-Red Spectroscopic Analysis of the Character of Hydrogen Bonds in Amorphous Cellulose. Polymer 1996, 37, 393–399. [Google Scholar] [CrossRef]
- Nazmi, N.N.; Isa, M.I.N.; Sarbon, N.M. Preparation and Characterization of Chicken Skin Gelatin/CMC Composite Film as Compared to Bovine Gelatin Film. Food Biosci. 2017, 19, 149–155. [Google Scholar] [CrossRef]
- Arrese-Igor, S.; Alegria, A.; Colmenero, J. Multimodal Character of Shear Viscosity Response in Hydrogen Bonded Liquids. Phys. Chem. Chem. Phys. 2018, 20, 27758–27765. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, H.; Guo, J.; Wang, L.; Zhang, J. Effect of Hydrogen Bond on the Viscosity of Ionic Liquid Studied by Combination of Molecular Dynamics and Quantum Chemistry. Theor. Chem. Acc. 2017, 136, 110. [Google Scholar] [CrossRef]
- Zandi, N.; Sani, E.S.; Mostafavi, E.; Ibrahim, D.M.; Saleh, B.; Shokrgozar, M.A.; Tamjid, E.; Weiss, P.S.; Simchi, A.; Annabi, N. Nanoengineered Shear-Thinning and Bioprintable Hydrogel as a Versatile Platform for Biomedical Applications. Biomaterials 2021, 267, 120476. [Google Scholar] [CrossRef] [PubMed]
- Ho, L.; Hsu, S. Cell Reprogramming by 3D Bioprinting of Human Fibroblasts in Polyurethane Hydrogel for Fabrication of Neural-like Constructs. Acta Biomater. 2018, 70, 57–70. [Google Scholar] [CrossRef]
- Raveendran, N.; Ivanovski, S.; Vaquette, C. The Effect of Culture Conditions on the Bone Regeneration Potential of Osteoblast-Laden 3D Bioprinted Constructs. Acta Biomater. 2023, 156, 190–201. [Google Scholar] [CrossRef] [PubMed]
- Yipeng, J.; Yongde, X.; Yuanyi, W.; Jilei, S.; Jiaxiang, G.; Jiangping, G.; Yong, Y. Microtissues Enhance Smooth Muscle Differentiation and Cell Viability of hADSCs for Three Dimensional Bioprinting. Front. Physiol. 2017, 8, 534. [Google Scholar] [CrossRef] [PubMed]
- Niu, J.; Zheng, L.; Zhang, X. Unsteady Convective Heat Transfer of Power-Law Fluid with Variable Fluid Properties in a Concentric Annulus Originating from a Polymer Flooding Process. Numer. Heat Transf. Part Appl. 2015, 68, 761–776. [Google Scholar] [CrossRef]
- Wang, Y.; Yong, H.; He, X. The Unusual Rheological Behaviors of Poly(Acrylamide-Co-Acrylonitrile)s with UCST Features in Aqueous Solutions. J. Mol. Liq. 2022, 364, 120013. [Google Scholar] [CrossRef]
- Thombare, N.; Jha, U.; Mishra, S.; Siddiqui, M.Z. Guar Gum as a Promising Starting Material for Diverse Applications: A Review. Int. J. Biol. Macromol. 2016, 88, 361–372. [Google Scholar] [CrossRef]
- Benwood, C.; Chrenek, J.; Kirsch, R.L.; Masri, N.Z.; Richards, H.; Teetzen, K.; Willerth, S.M. Natural Biomaterials and Their Use as Bioinks for Printing Tissues. Bioengineering 2021, 8, 27. [Google Scholar] [CrossRef]
- Sharma, R.; Kirsch, R.; Valente, K.P.; Perez, M.R.; Willerth, S.M. Physical and Mechanical Characterization of Fibrin-Based Bioprinted Constructs Containing Drug-Releasing Microspheres for Neural Tissue Engineering Applications. Processes 2021, 9, 1205. [Google Scholar] [CrossRef]
- Isobe, N.; Komamiya, T.; Kimura, S.; Kim, U.-J.; Wada, M. Cellulose Hydrogel with Tunable Shape and Mechanical Properties: From Rigid Cylinder to Soft Scaffold. Int. J. Biol. Macromol. 2018, 117, 625–631. [Google Scholar] [CrossRef]
- Hu, J.; Lu, Y.; Cai, L.; Owusu-Ansah, K.G.; Xu, G.; Han, F.; Bao, J.; Lin, X.; Huang, Y. Functional Compressive Mechanics and Tissue Biocompatibility of an Injectable SF/PU Hydrogel for Nucleus Pulposus Replacement. Sci. Rep. 2017, 7, 2347. [Google Scholar] [CrossRef] [PubMed]
- Wingate, K.; Bonani, W.; Tan, Y.; Bryant, S.J.; Tan, W. Compressive Elasticity of Three-Dimensional Nanofiber Matrix Directs Mesenchymal Stem Cell Differentiation to Vascular Cells with Endothelial or Smooth Muscle Cell Markers. Acta Biomater. 2012, 8, 1440–1449. [Google Scholar] [CrossRef] [PubMed]
- Baker, B.M.; Chen, C.S. Deconstructing the Third Dimension—How 3D Culture Microenvironments Alter Cellular Cues. J. Cell Sci. 2012, 125, 3015–3024. [Google Scholar] [CrossRef] [PubMed]
- Hospodiuk, M.; Dey, M.; Sosnoski, D.; Ozbolat, I.T. The Bioink: A Comprehensive Review on Bioprintable Materials. Biotechnol. Adv. 2017, 35, 217–239. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Yao, B.; Hu, T.; Cui, X.; Shu, X.; Tang, S.; Wang, R.; Wang, Y.; Liu, Y.; Song, W.; et al. Properties of an Alginate-Gelatin-Based Bioink and Its Potential Impact on Cell Migration, Proliferation, and Differentiation. Int. J. Biol. Macromol. 2019, 135, 1107–1113. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Huang, S.; Liu, Y.; Yao, B.; Hu, T.; Shi, H.; Xie, J.; Fu, X. Tuning Alginate-Gelatin Bioink Properties by Varying Solvent and Their Impact on Stem Cell Behavior. Sci. Rep. 2018, 8, 8020. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, S.; Lin, L. Rheological Study on 3D Printability of Alginate Hydrogel and Effect of Graphene Oxide. Int. J. Bioprint. 2016, 2, 163–175. [Google Scholar] [CrossRef]
- Li, X.; Deng, Q.; Wang, S.; Li, Q.; Zhao, W.; Lin, B.; Luo, Y.; Zhang, X. Hydroxyethyl Cellulose As a Rheological Additive for Tuning the Extrusion Printability and Scaffold Properties. 3D Print. Addit. Manuf. 2021, 8, 87–98. [Google Scholar] [CrossRef]
- Sacks, J.; Schiller, S.; Welch, W. Designs for Computer Experiments. Technometrics 1989, 31, 41–47. [Google Scholar] [CrossRef]
- Lin, L.; He, Z.; Peeta, S. Predicting Station-Level Hourly Demand in a Large-Scale Bike-Sharing Network: A Graph Convolutional Neural Network Approach. Transp. Res. Part C Emerg. Technol. 2018, 97, 258–276. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Mouser, V.H.M.; Melchels, F.P.W.; Visser, J.; Dhert, W.J.A.; Gawlitta, D.; Malda, J. Yield Stress Determines Bioprintability of Hydrogels Based on Gelatin-Methacryloyl and Gellan Gum for Cartilage Bioprinting. Biofabrication 2016, 8, 035003. [Google Scholar] [CrossRef] [PubMed]
- Sikora, R. The Barus Complex Effect and Its Dimensional and Forming Results. Polimery 1997, 42, 50–54. [Google Scholar] [CrossRef]
- Liu, W.; Heinrich, M.A.; Zhou, Y.; Akpek, A.; Hu, N.; Liu, X.; Guan, X.; Zhong, Z.; Jin, X.; Khademhosseini, A.; et al. Extrusion Bioprinting of Shear-Thinning Gelatin Methacryloyl Bioinks. Adv. Healthc. Mater. 2017, 6, 1601451. [Google Scholar] [CrossRef] [PubMed]
- Malda, J.; Visser, J.; Melchels, F.P.; Jüngst, T.; Hennink, W.E.; Dhert, W.J.A.; Groll, J.; Hutmacher, D.W. 25th Anniversary Article: Engineering Hydrogels for Biofabrication. Adv. Mater. 2013, 25, 5011–5028. [Google Scholar] [CrossRef]
- Kim, G.-J.; Kim, L.; Kwon, O.S. Application of 3D Bioprinting Technology for Tissue Regeneration, Drug Evaluation, and Drug Delivery. Appl. Sci. Converg. Technol. 2023, 32, 1–6. [Google Scholar] [CrossRef]



| Variables Xi | Levels | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| Gel (wt%) | 6 | 8 | 10 |
| SA (wt%) | 3 | 4 | 5 |
| MC (wt%) | 2 | 3 | 4 |
| nPrediction | nReality | nAccuracy | KPrediction | KReality | KAccuracy | |
|---|---|---|---|---|---|---|
| 10:4:3 | 0.45 | 0.44 | 97.06% | 161.44 | 146.02 | 90.44% |
| 6:5:4 | 0.55 | 0.55 | 99.47% | 81.57 | 80.98 | 99.28% |
| 7:4:4 | 0.59 | 0.58 | 98.59% | 62.85 | 60.52 | 96.30% |
| 7.5:3:2 | 0.67 | 0.65 | 96.85% | 12.80 | 15.41 | 79.62% |
| 9:5:3 | 0.46 | 0.46 | 99.32% | 184.07 | 147.79 | 80.29% |
| Printing Speed (mm/s) | Length of Filament (Design Values: 15 mm) | Accuracy | |
|---|---|---|---|
| Unoptimized | 8 | 14.12 ± 0.05 | 94.20% |
| 12 | 14.07 ± 0.03 | 93.81% | |
| 16 | 13.98 ± 0.07 | 93.23% | |
| Optimized (t0 = 0.1 s) | 8 | 14.92 ± 0.02 | 99.47% |
| 12 | 14.86 ± 0.01 | 99.13% | |
| 16 | 14.98 ± 0.03 | 99.89% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Wu, C.; Zou, S.; Li, X.; Ho, B.; Sun, R.; Liu, C.; Chen, M. Investigation of Biomaterial Ink Viscosity Properties and Optimization of the Printing Process Based on Pattern Path Planning. Bioengineering 2023, 10, 1358. https://doi.org/10.3390/bioengineering10121358
Wu J, Wu C, Zou S, Li X, Ho B, Sun R, Liu C, Chen M. Investigation of Biomaterial Ink Viscosity Properties and Optimization of the Printing Process Based on Pattern Path Planning. Bioengineering. 2023; 10(12):1358. https://doi.org/10.3390/bioengineering10121358
Chicago/Turabian StyleWu, Jiahao, Chunya Wu, Siyang Zou, Xiguang Li, Bo Ho, Ruijiang Sun, Chang Liu, and Mingjun Chen. 2023. "Investigation of Biomaterial Ink Viscosity Properties and Optimization of the Printing Process Based on Pattern Path Planning" Bioengineering 10, no. 12: 1358. https://doi.org/10.3390/bioengineering10121358
APA StyleWu, J., Wu, C., Zou, S., Li, X., Ho, B., Sun, R., Liu, C., & Chen, M. (2023). Investigation of Biomaterial Ink Viscosity Properties and Optimization of the Printing Process Based on Pattern Path Planning. Bioengineering, 10(12), 1358. https://doi.org/10.3390/bioengineering10121358








