Mathematical and Machine Learning Models of Renal Cell Carcinoma: A Review
Abstract
:1. Introduction
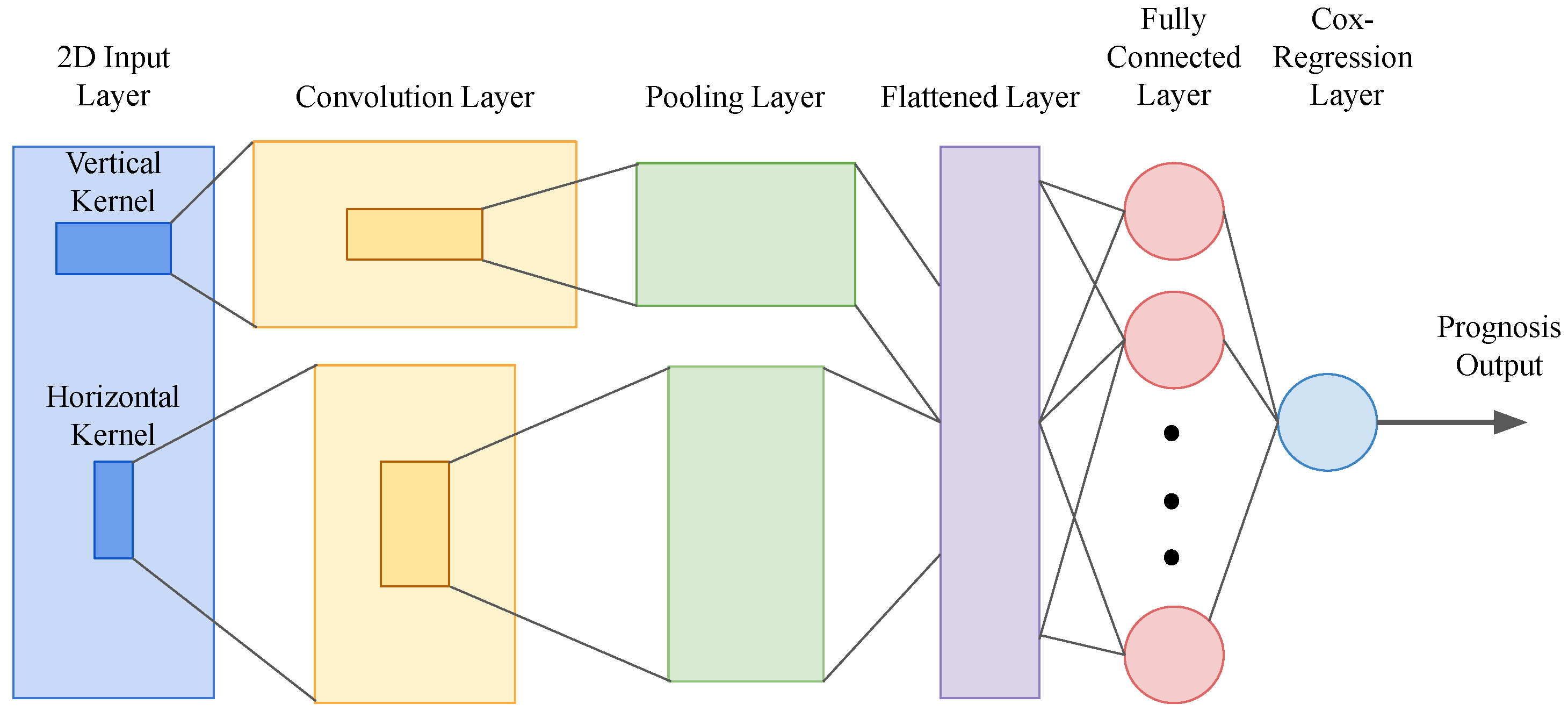
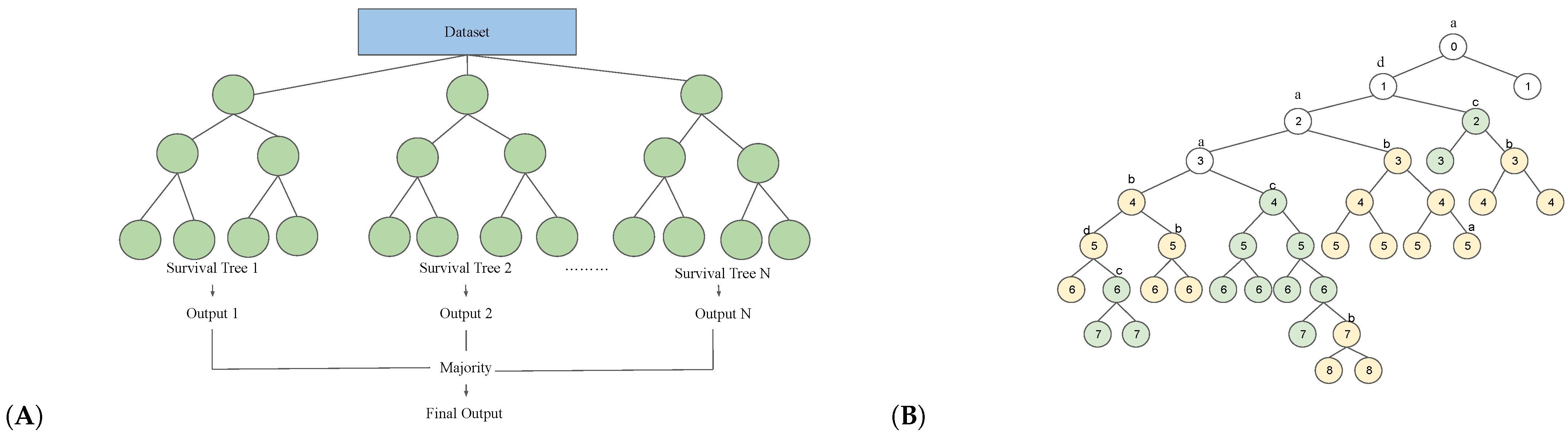
2. Machine Learning Models
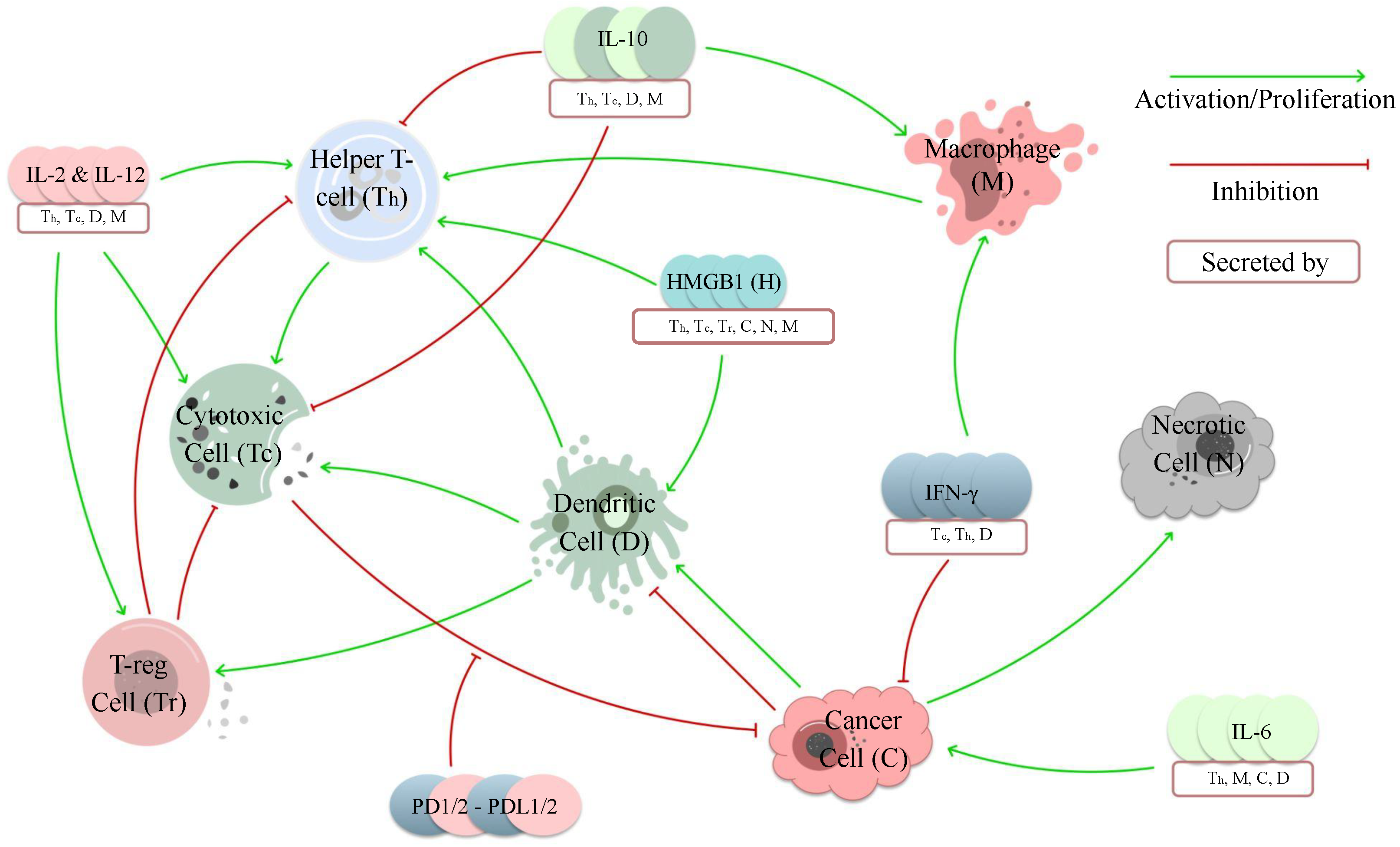
3. Mechanistic Models
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RCC | Renal Cell Carcinoma |
| GSEA | Gene Set Enrichment Analysis |
| TCGA | The Cancer Genome Atlas |
| VHL | Von Hippel–Lindau |
| HIF | Hypoxia-Inducible Factor |
| ODE | Ordinary Differential Equation |
| GFP | Green Fluorescent Protein |
| MRI | Magnetic Resonance Imaging |
| PDE | Partial Differential Equation |
| UMAP | Uniform Manifold Approximation and Projection |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| RSF-VH | Random Survival Forests-Variable Hunting |
| FDE | Fractional Differential Equation |
References
- National Cancer Institute. Clear Cell Renal Cell Carcinoma. Available online: https://www.cancer.gov/pediatric-adult-rare-tumor/rare-tumors/rare-kidney-tumors/clear-cell-renal-cell-carcinoma (accessed on 12 August 2020).
- Barata, P.C.; Rini, B.I. Treatment of renal cell carcinoma: Current status and future directions. CA Cancer J. Clin. 2017, 67, 507–524. [Google Scholar] [CrossRef] [PubMed]
- Rini, B.I.; Atkins, M.B.; Choueiri, T.K.; Teresi, R.E.; Rosbrook, B.; Thakur, M.; Hutson, T.E. Plain language summary looking at how long side effects last after treatment with axitinib is stopped in people with advanced renal cell carcinoma? Future Oncol. 2023. [Google Scholar] [CrossRef] [PubMed]
- Su, S.; Akbarinejad, S.; Shahriyari, L. Immune classification of clear cell renal cell carcinoma. Sci. Rep. 2021, 11, 4338. [Google Scholar] [CrossRef] [PubMed]
- Ljungberg, B.; Campbell, S.C.; Cho, H.Y.; Jacqmin, D.; Lee, J.E.; Weikert, S.; Kiemeney, L.A. The epidemiology of renal cell carcinoma. Eur. Urol. 2011, 60, 615–621. [Google Scholar] [CrossRef]
- World Cancer Research Fund International. Kidney Cancer Statistics. 2023. Available online: https://www.wcrf.org/cancer-trends/kidney-cancer-statistics/ (accessed on 20 August 2023).
- He, T.; Zhang, Q.; Xu, P.; Tao, W.; Lin, F.; Liu, R.; Li, M.; Duan, X.; Cai, C.; Gu, D.; et al. Extracellular vesicle-circEHD2 promotes the progression of renal cell carcinoma by activating cancer-associated fibroblasts. Mol. Cancer 2023, 22, 117. [Google Scholar] [CrossRef]
- Santoni, M.; Buti, S.; Myint, Z.W.; Maruzzo, M.; Iacovelli, R.; Pichler, M.; Kopecky, J.; Kucharz, J.; Rizzo, M.; Galli, L.; et al. Real-world Outcome of Patients with Advanced Renal Cell Carcinoma and Intermediate- or Poor-risk International Metastatic Renal Cell Carcinoma Database Consortium Criteria Treated by Immune-oncology Combinations: Differential Effectiveness by Risk Group? Eur. Urol. Oncol. 2023, in press. [Google Scholar] [CrossRef]
- Chung, E.M.; Lattin, G.E.; Fagen, K.E.; Kim, A.M.; Pavio, M.A.; Fehringer, A.J.; Conran, R.M. Renal Tumors of Childhood: Radiologic-Pathologic Correlation Part 2. The 2nd Decade: From the Radiologic Pathology Archives. Radiographics 2017, 37, 1538–1558. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention (CDC). United States Cancer Statistics: Data Visualizations. Available online: https://gis.cdc.gov/Cancer/USCS/#/Trends/ (accessed on 7 November 2023).
- Cancer.Net. Kidney Cancer: Statistics. 2023. Available online: https://www.cancer.net/cancer-types/kidney-cancer/statistics (accessed on 1 November 2023).
- Society, A.C. What Is Kidney Cancer? Available online: https://www.cancer.org/cancer/kidney-cancer/about/what-is-kidney-cancer.html (accessed on 12 August 2020).
- Padala, S.A.; Barsouk, A.; Thandra, K.C.; Saginala, K.; Mohammed, A.; Vakiti, A.; Rawla, P.; Barsouk, A. Epidemiology of Renal Cell Carcinoma. World J. Oncol. 2020, 11, 79–87. [Google Scholar] [CrossRef]
- Nabi, S.; Kessler, E.R.; Bernard, B.; Flaig, T.W.; Lam, E.T. Renal cell carcinoma: A review of biology and pathophysiology. F1000Research 2018, 7, 307. [Google Scholar] [CrossRef]
- Kondo, K.; Kim, W.Y.; Lechpammer, M.; Kaelin, W.G. Inhibition of HIF2α Is Sufficient to Suppress pVHL-Defective Tumor Growth. PLoS Biol. 2003, 1, e83. [Google Scholar] [CrossRef]
- Bajaj, S.; Gandhi, D.; Nayar, D.; Serhal, A. Von Hippel-Lindau Disease (VHL): Characteristic Lesions with Classic Imaging Findings. J. Kidney Cancer VHL 2023, 10, 23–31. [Google Scholar] [CrossRef]
- Huang, J.J.; Hsieh, J.J. The therapeutic landscape of renal cell carcinoma: From the dark age to the golden age. Proc. Semin. Nephrol. 2020, 40, 28–41. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, D.D.; Virumbrales-Muñoz, M.; Beebe, D.J.; Abel, E.J. Models of Renal Cell Carcinoma Used to Investigate Molecular Mechanisms and Develop New Therapeutics. Front. Oncol. 2022, 12, 871252. [Google Scholar] [CrossRef]
- Hsieh, J.J.; Purdue, M.P.; Signoretti, S.; Swanton, C.; Albiges, L.; Schmidinger, M.; Heng, D.Y.; Larkin, J.; Ficarra, V. Renal cell carcinoma. Nat. Rev. Dis. Primers 2017, 3, 17009. [Google Scholar] [CrossRef] [PubMed]
- Dionese, M.; Pierantoni, F.; Bezzon, E.; Cumerlato, E.; Bimbatti, D.; Basso, U.; Maruzzo, M.; Zagonel, V. Role of enhancement modifications in evaluating tumor response to immunotherapy in metastatic renal cell carcinoma. Tumori 2023. [Google Scholar] [CrossRef]
- Liu, H.; Luo, Y.; Zhao, S.; Tan, J.; Chen, M.; Liu, X.; Ye, J.; Cai, S.; Deng, Y.; Li, J.; et al. A reactive oxygen species-related signature to predict prognosis and aid immunotherapy in clear cell renal cell carcinoma. Front. Oncol. 2023, 13, 1202151. [Google Scholar] [CrossRef]
- Considine, B.; Hurwitz, M.E. Current Status and Future Directions of Immunotherapy in Renal Cell Carcinoma. Curr. Oncol. Rep. 2019, 21, 34. [Google Scholar] [CrossRef]
- Escudier, B. Emerging immunotherapies for renal cell carcinoma. Ann. Oncol. 2012, 23, viii35–viii40. [Google Scholar] [CrossRef]
- Chevrier, S.; Levine, J.H.; Zanotelli, V.R.T.; Silina, K.; Schulz, D.; Bacac, M.; Ries, C.H.; Ailles, L.; Jewett, M.A.S.; Moch, H.; et al. An Immune Atlas of Clear Cell Renal Cell Carcinoma. Cell 2017, 169, 736–749.e18. [Google Scholar] [CrossRef]
- Dine, J.; Gordon, R.; Shames, Y.; Kasler, M.K.; Barton-Burke, M. Immune checkpoint inhibitors: An innovation in immunotherapy for the treatment and management of patients with cancer. Asia-Pac. J. Oncol. Nurs. 2017, 4, 127–135. [Google Scholar] [CrossRef]
- Kitamura, T.; Qian, B.Z.; Pollard, J.W. Immune cell promotion of metastasis. Nat. Rev. Immunol. 2015, 15, 73–86. [Google Scholar] [CrossRef]
- Krüger, T.; Schoor, O.; Lemmel, C.; Kraemer, B.; Reichle, C.; Dengjel, J.; Weinschenk, T.; Müller, M.; Hennenlotter, J.; Stenzl, A.; et al. Lessons to be learned from primary renal cell carcinomas: Novel tumor antigens and HLA ligands for immunotherapy. Cancer Immunol. Immunother. 2005, 54, 826–836. [Google Scholar] [CrossRef]
- Ni, L.; Lu, J. Interferon gamma in cancer immunotherapy. Cancer Med. 2018, 7, 4509–4516. [Google Scholar] [CrossRef] [PubMed]
- Peng, W.; Liu, C.; Xu, C.; Lou, Y.; Chen, J.; Yang, Y.; Yagita, H.; Overwijk, W.W.; Lizée, G.; Radvanyi, L.; et al. PD-1 Blockade Enhances T-cell Migration to Tumors by Elevating IFN-γ Inducible Chemokines. Cancer Res. 2012, 72, 5209–5218. [Google Scholar] [CrossRef] [PubMed]
- Rambhia, A.; Patel, R.D.; Okhawere, K.E.; Korn, T.G.; Badani, K.K. Immunotherapy for metastatic renal cell carcinoma: A brief history, current trends, and future directions. Urol. Oncol. Semin. Orig. Investig. 2021, 39, 664–677. [Google Scholar] [CrossRef]
- Wu, X.; Gu, Z.; Chen, Y.; Chen, B.; Chen, W.; Weng, L.; Liu, X. Application of PD-1 Blockade in Cancer Immunotherapy. Comput. Struct. Biotechnol. J. 2019, 17, 661–674. [Google Scholar] [CrossRef]
- Harada, M.; Iida, Y.; Kotani, H.; Minami, T.; Komohara, Y.; Eto, M.; Yoshikawa, K.; Uemura, H. T-cell responses and combined immunotherapy against human carbonic anhydrase 9-expressing mouse renal cell carcinoma. Cancer Immunol. Immunother. 2022, 71, 339–352. [Google Scholar] [CrossRef] [PubMed]
- Popovic, M.; Matovina-Brko, G.; Jovic, M.; Popovic, L.S. Immunotherapy: A new standard in the treatment of metastatic clear cell renal cell carcinoma. World J. Clin. Oncol. 2022, 13, 28–38. [Google Scholar] [CrossRef]
- Zitvogel, L.; Kroemer, G. Targeting PD-1/PD-L1 interactions for cancer immunotherapy. Oncoimmunology 2012, 1, 1223–1225. [Google Scholar] [CrossRef]
- Rosenberg, S.A. IL-2: The first effective immunotherapy for human cancer. J. Immunol. 2014, 192, 5451–5458. [Google Scholar] [CrossRef]
- Gudbrandsdottir, G.; Aarstad, H.H.; Bostad, L.; Hjelle, K.M.; Aarstad, H.J.; Bruserud, Ø.; Tvedt, T.H.A.; Beisland, C. Serum levels of the IL-6 family of cytokines predict prognosis in renal cell carcinoma (RCC). Cancer Immunol. Immunother. 2021, 70, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Lalani, A.K.A.; McGregor, B.A.; Albiges, L.; Choueiri, T.K.; Motzer, R.; Powles, T.; Wood, C.; Bex, A. Systemic treatment of metastatic clear cell renal cell carcinoma in 2018: Current paradigms, use of immunotherapy, and future directions. Eur. Urol. 2019, 75, 100–110. [Google Scholar] [CrossRef]
- Wang, J.; Wei, W.S.; Jiang, L.J.; Zhang, Z.L.; Guo, S.J.; Han, H.; Zhou, F.J.; Dong, P. [Efficacy and safety evaluation of immunotherapy combined with targeted therapy as second-line treatment in patients with metastatic non-clear cell renal cell carcinoma]. Zhonghua Zhong Liu Za Zhi 2023, 45, 704–708. [Google Scholar] [PubMed]
- Wang, H.; Borlongan, M.; Hemminki, A.; Basnet, S.; Kaufman, H.; Rabkin, S.; Saha, D. Viral vectors expressing interleukin 2 for cancer immunotherapy. Hum. Gene Ther. 2023, 34, 878–895. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, S.; Lu, Y.; Xia, D.; Liu, Y. TLR4 predicts patient prognosis and immunotherapy efficacy in clear cell renal cell carcinoma. J. Cancer 2023, 14, 2181–2197. [Google Scholar] [CrossRef]
- Kaur, J.; Patil, G.; Geynisman, D.M.; Ghatalia, P. Role of perioperative immunotherapy in localized renal cell carcinoma. Ther. Adv. Med. Oncol. 2023, 15, 17588359231181497. [Google Scholar] [CrossRef] [PubMed]
- Fukumoto, W.; Yoshino, H.; Horike, S.I.; Kawakami, I.; Tamai, M.; Arima, J.; Kawahara, I.; Mitsuke, A.; Sakaguchi, T.; Inoguchi, S.; et al. in sunitinib-resistant renal cell carcinoma. Cancer Sci. 2023, 114, 3946–3956. [Google Scholar] [CrossRef]
- Pilskog, M.; Bostad, L.; Edelmann, R.J.; Akslen, L.A.; Beisland, C.; Straume, O. Tumour cell expression of interleukin 6 receptor α is associated with response rates in patients treated with sunitinib for metastatic clear cell renal cell carcinoma: Interleukin 6 receptor α in renal cancer. J. Path Clin. Res. 2018, 4, 114–123. [Google Scholar] [CrossRef]
- Pilskog, M.; Nilsen, G.H.; Beisland, C.; Straume, O. Elevated plasma interleukin 6 predicts poor response in patients treated with sunitinib for metastatic clear cell renal cell carcinoma. Cancer Treat. Res. Commun. 2019, 19, 100127. [Google Scholar] [CrossRef]
- Climent, M.A.; Muñoz-Langa, J.; Basterretxea-Badiola, L.; Santander-Lobera, C. Systematic review and survival meta-analysis of real world evidence on first-line pazopanib for metastatic renal cell carcinoma. Crit. Rev. Oncol. 2018, 121, 45–50. [Google Scholar] [CrossRef]
- Tesarova, T.; Koucka, K.; Vaclavikova, R.; Seborova, K.; Hora, M.; Hes, O.; Pivovarcikova, K.; Soucek, P.; Fiala, O. Association of lncRNA and transcriptome intersections with response to targeted therapy in metastatic renal cell carcinoma. Oncol. Lett. 2023, 26, 365. [Google Scholar] [CrossRef]
- Li, L.; Tan, H.; Zhou, J.; Hu, F. Predicting response of immunotherapy and targeted therapy and prognosis characteristics for renal clear cell carcinoma based on m1A methylation regulators. Sci. Rep. 2023, 13, 12645. [Google Scholar] [CrossRef] [PubMed]
- Rini, B.I. Vascular endothelial growth factor-targeted therapy in renal cell carcinoma: Current status and future directions. Clin. Cancer Res. 2007, 13, 1098–1106. [Google Scholar] [CrossRef] [PubMed]
- Pillis, L.D.; Caldwell, T.; Sarapata, E.; Williams, H. Mathematical Modeling of the Regulatory T Cell Effects on Renal Cell Carcinoma Treatment. Discret. Contin. Dyn. Syst. Ser. 2013, 18, 915–943. [Google Scholar] [CrossRef]
- Hanin, L.; Jandrig, B.; Pavlova, L.; Seidel, K. The natural history of renal cell carcinoma with pulmonary metastases illuminated through mathematical modeling. Math. Biosci. 2019, 309, 118–130. [Google Scholar] [CrossRef]
- Puchalski, T.; Prabhakar, U.; Jiao, Q.; Berns, B.; Davis, H.M. Pharmacokinetic and pharmacodynamic modeling of an anti-interleukin-6 chimeric monoclonal antibody (siltuximab) in patients with metastatic renal cell carcinoma. Clin. Cancer Res. 2010, 16, 1652–1661. [Google Scholar] [CrossRef]
- Sharma, K.; Patidar, K.; Ali, M.A.; Patil, P.; Goud, H.; Hussain, T.; Nayarisseri, A.; Singh, S.K. Structure-Based Virtual Screening for the Identification of High Affinity Compounds as Potent VEGFR2 Inhibitors for the Treatment of Renal Cell Carcinoma. Curr. Top. Med. Chem. 2018, 18, 2174–2185. [Google Scholar] [CrossRef] [PubMed]
- Pili, R.; Quinn, D.I.; Hammers, H.J.; Monk, P.; George, S.; Dorff, T.B.; Olencki, T.; Shen, L.; Orillion, A.; Lamonica, D.; et al. Immunomodulation by Entinostat in Renal Cell Carcinoma Patients Receiving High-Dose Interleukin 2: A Multicenter, Single-Arm, Phase I/II Trial (NCI-CTEP#7870). Clin. Cancer Res. 2017, 23, 7199–7208. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Xu, L.; Lu, X.; Fu, D.; Su, J.; Geng, H.; Qin, G.; Chen, R.; Quan, C.; et al. CD4 + T cells promote renal cell carcinoma proliferation via modulating YBX1. Exp. Cell Res. 2018, 363, 95–101. [Google Scholar] [CrossRef]
- Hsieh, J.J.; Manley, B.J.; Khan, N.; Gao, J.; Carlo, M.I.; Cheng, E.H. Overcome tumor heterogeneity-imposed therapeutic barriers through convergent genomic biomarker discovery: A braided cancer river model of kidney cancer. Semin. Cell Dev. Biol. 2017, 64, 98–106. [Google Scholar] [CrossRef]
- Orton, M.R.; Hann, E.; Doran, S.J.; Shepherd, S.T.C.; Ap Dafydd, D.; Spencer, C.E.; López, J.I.; Albarrán-Artahona, V.; Comito, F.; Warren, H.; et al. Interpretability of radiomics models is improved when using feature group selection strategies for predicting molecular and clinical targets in clear-cell renal cell carcinoma: Insights from the TRACERx Renal study. Cancer Imaging 2023, 23, 76. [Google Scholar] [CrossRef]
- Guer, M.; Janitzky, A.; Schostak, M. On-treatment risk model for predicting treatment response in advanced renal cell carcinoma. World J. Urol. 2023, 41, 2735–2742. [Google Scholar] [CrossRef]
- Cooley, L.S.; Rudewicz, J.; Souleyreau, W.; Emanuelli, A.; Alvarez-Arenas, A.; Clarke, K.; Falciani, F.; Dufies, M.; Lambrechts, D.; Modave, E.; et al. Experimental and computational modeling for signature and biomarker discovery of renal cell carcinoma progression. Mol. Cancer 2021, 20, 136. [Google Scholar] [CrossRef] [PubMed]
- Stein, A.; Wang, W.; Carter, A.A.; Chiparus, O.; Hollaender, N.; Kim, H.; Motzer, R.J.; Sarr, C. Dynamic tumor modeling of the dose-response relationship for everolimus in metastatic renal cell carcinoma using data from the phase 3 RECORD-1 trial. BMC Cancer 2012, 12, 311. [Google Scholar] [CrossRef]
- Zhan, Y.; Guo, W.; Zhang, Y.; Wang, Q.; Xu, X.J.; Zhu, L. A Five-Gene Signature Predicts Prognosis in Patients with Kidney Renal Clear Cell Carcinoma. Comput. Math. Methods Med. 2015, 2015, 842784. [Google Scholar] [CrossRef] [PubMed]
- Yin, Q.; Chen, W.; Zhang, C.; Wei, Z. A convolutional neural network model for survival prediction based on prognosis-related cascaded Wx feature selection. Lab. Investig. 2022, 102, 1064–1074. [Google Scholar] [CrossRef]
- Cherdantseva, T.M.; Bobrov, I.P.; Avdalyan, A.M.; Klimachev, V.V.; Kazartsev, A.V.; Kryuchkova, N.G.; Klimachev, I.V.; Myadelets, M.N.; Lepilov, A.V.; Lushnikova, E.L.; et al. Mast Cells in Renal Cancer: Clinical Morphological Correlations and Prognosis. Bull. Exp. Biol. Med. 2017, 163, 801–804. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, H.; Miyata, Y.; Mochizuki, Y.; Yasuda, T.; Nakamura, Y.; Araki, K.; Sagara, Y.; Matsuo, T.; Ohba, K.; Sakai, H. Pathological significance and prognostic roles of densities of CD57+ cells, CD68+ cells, and mast cells, and their ratios in clear cell renal cell carcinoma. Hum. Pathol. 2018, 79, 102–108. [Google Scholar] [CrossRef] [PubMed]
- Pagès, F.; Kirilovsky, A.; Mlecnik, B.; Asslaber, M.; Tosolini, M.; Bindea, G.; Lagorce, C.; Wind, P.; Marliot, F.; Bruneval, P.; et al. In Situ Cytotoxic and Memory T Cells Predict Outcome in Patients with Early-Stage Colorectal Cancer. JCO 2009, 27, 5944–5951. [Google Scholar] [CrossRef]
- Chen, Z.; Lv, Y.; He, L.; Wu, S.; Wu, Z. Expression in Clear Cell Renal Cell Carcinoma Predicts Worse Overall Survival. Front. Mol. Biosci. 2021, 8, 657672. [Google Scholar] [CrossRef]
- Situ, Y.; Xu, Q.; Deng, L.; Zhu, Y.; Gao, R.; Lei, L.; Shao, Z. System analysis of VEGFA renal cell carcinoma: The expression, prognosis, gene regulation network and regulation targets. Int. J. Biol. Markers 2021. [Google Scholar] [CrossRef]
- Patil, S.; Ishill, N.; Deluca, J.; Motzer, R.J. Stage migration and increasing proportion of favorable-prognosis metastatic renal cell carcinoma patients: Implications for clinical trial design and interpretation. Cancer 2010, 116, 347–354. [Google Scholar] [CrossRef]
- Le, T.; Su, S.; Shahriyari, L. Immune classification of osteosarcoma. Math. Biosci. Eng. 2021, 18, 1879–1897. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, R.; Jiang, M.; Hu, B.; Zheng, P.; Chen, G. Comprehensive analysis of the expression, prognosis and biological significance of FSCN family in clear cell renal cell carcinoma. Oncol. Lett. 2023, 26, 379. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Zhang, E.; Guo, T.; Wang, T.; Chen, J.; Zhang, N.; Wang, X.; Zheng, J. Development and verification of a deep learning-based m6A modification model for clinical prognosis prediction of renal cell carcinoma. J. Cancer Res. Clin. Oncol. 2023, 149, 14283–14296. [Google Scholar] [CrossRef]
- Lian, M.; Feng, Y.; Wu, Z.; Zheng, Z.; Liu, H.; Li, J.; Yu, H.; Lian, C. Identification and validation of a genetic risk signature associated with prognosis in clear-cell renal cell carcinoma patients. Medicine 2023, 102, e34582. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, Z.; Zhao, L.; Zhang, P.; Xu, Y.; Xia, Q. High C1QTNF1 expression mediated by potential ncRNAs is associated with poor prognosis and tumor immunity in kidney renal clear cell carcinoma. Front. Mol. Biosci. 2023, 10, 1201155. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; He, Z.; Wang, H.; Ding, M.; Huang, Y.; Li, H.; Shi, H.; Mao, L.; Hu, C.; Wang, J. Identification of potential biomarkers for progression and prognosis of renal clear cell carcinoma by comprehensive bioinformatics analysis. Technol. Health Care 2023. [Google Scholar] [CrossRef]
- Terrematte, P.; Andrade, D.S.; Justino, J.; Stransky, B.; de Araújo, D.S.A.; Dória Neto, A.D. A Novel Machine Learning 13-Gene Signature: Improving Risk Analysis and Survival Prediction for Clear Cell Renal Cell Carcinoma Patients. Cancers 2022, 14, 2111. [Google Scholar] [CrossRef] [PubMed]
- Satter, K.B.; Tran, P.M.H.; Tran, L.K.H.; Ramsey, Z.; Pinkerton, K.; Bai, S.; Savage, N.M.; Kavuri, S.; Terris, M.K.; She, J.X.; et al. Oncocytoma-Related Gene Signature to Differentiate Chromophobe Renal Cancer and Oncocytoma Using Machine Learning. Cells 2022, 11, 287. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Hwang, S.I.; Lee, H.J. The Classification of Renal Cancer in 3-Phase CT Images Using a Deep Learning Method. J. Digit. Imaging 2019, 32, 638–643. [Google Scholar] [CrossRef] [PubMed]
- Eraslan, G.; Avsec, Z.; Gagneur, J.; Theis, F.J. Deep learning: New computational modelling techniques for genomics. Nat. Rev. Genet. 2019, 20, 389–403. [Google Scholar] [CrossRef] [PubMed]
- Kirshtein, A.; Akbarinejad, S.; Hao, W.; Le, T.; Su, S.; Aronow, R.A.; Shahriyari, L. Data driven mathematical model of colon cancer progression. J. Clin. Med. 2020, 9, 3947. [Google Scholar] [CrossRef]
- Le, T.; Su, S.; Kirshtein, A.; Shahriyari, L. Data-Driven Mathematical Model of Osteosarcoma. Cancers 2021, 13, 2367. [Google Scholar] [CrossRef]
- Mohammad Mirzaei, N.; Su, S.; Sofia, D.; Hegarty, M.; Abdel-Rahman, M.H.; Asadpoure, A.; Cebulla, C.M.; Chang, Y.H.; Hao, W.; Jackson, P.R.; et al. A Mathematical Model of Breast Tumor Progression Based on Immune Infiltration. J. Pers. Med. 2021, 11, 1031. [Google Scholar] [CrossRef]
- Mohammad Mirzaei, N.; Changizi, N.; Asadpoure, A.; Su, S.; Sofia, D.; Tatarova, Z.; Zervantonakis, I.K.; Chang, Y.H.; Shahriyari, L. Investigating key cell types and molecules dynamics in PyMT mice model of breast cancer through a mathematical model. PLoS Comput. Biol. 2022, 18, e1009953. [Google Scholar] [CrossRef]
- Mohammad Mirzaei, N.; Tatarova, Z.; Hao, W.; Changizi, N.; Asadpoure, A.; Zervantonakis, I.K.; Hu, Y.; Chang, Y.H.; Shahriyari, L. A PDE Model of Breast Tumor Progression in MMTV-PyMT Mice. J. Pers. Med. 2022, 12, 807. [Google Scholar] [CrossRef]
- Hu, Y.; Mirzaei, N.M.; Shahriyari, L. Bio-Mechanical Model of Osteosarcoma Tumor Microenvironment: A Porous Media Approach. Cancers 2022, 14, 6143. [Google Scholar] [CrossRef]
- Mirzaei, N.M.; Hao, W.; Shahriyari, L. Investigating the spatial interaction of immune cells in colon cancer. iScience 2023, 26, 106596. [Google Scholar] [CrossRef]
- Lee, M.H.; Theodoropoulos, J.; Huuhtanen, J.; Bhattacharya, D.; Järvinen, P.; Tornberg, S.; Sen, H.; Mirtti, T.; Uski, I.; Kumari, A.; et al. Immunologic Characterization and T cell Receptor Repertoires of Expanded Tumor-infiltrating Lymphocytes in Patients with Renal Cell Carcinoma. Cancer Res. Commun. 2023, 3, 1260–1276. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.D.; Zhang, Y.T.; McGrail, D.J.; Zhang, X.; Lam, T.; Hoang, A.; Hasanov, E.; Manyam, G.; Peterson, C.B.; Zhu, H.; et al. SETD2 loss and ATR inhibition synergize to promote cGAS signaling and immunotherapy response in renal cell carcinoma. Clin. Cancer Res. 2023, 29, 4002–4015. [Google Scholar] [CrossRef] [PubMed]
- Le, T.; Su, S.; Shahriyari, L. Investigating Optimal Chemotherapy Options for Osteosarcoma Patients through a Mathematical Model. Cells 2021, 10, 2009. [Google Scholar] [CrossRef] [PubMed]
- Budithi, A.; Su, S.; Kirshtein, A.; Shahriyari, L. Data Driven Mathematical Model of FOLFIRI Treatment for Colon Cancer. Cancers 2021, 13, 2632. [Google Scholar] [CrossRef]
- Galfano, A.; Novara, G.; Iafrate, M.; Cavalleri, S.; Martignoni, G.; Gardiman, M.; D’Elia, C.; Patard, J.J.; Artibani, W.; Ficarra, V. Mathematical models for prognostic prediction in patients with renal cell carcinoma. Urol. Int. 2008, 80, 113–123. [Google Scholar] [CrossRef]
- Zisman, A.; Pantuck, A.J.; Dorey, F.; Chao, D.H.; Gitlitz, B.J.; Moldawer, N.; Lazarovici, D.; deKernion, J.B.; Figlin, R.A.; Belldegrun, A.S. Mathematical model to predict individual survival for patients with renal cell carcinoma. J. Clin. Oncol. 2002, 20, 1368–1374. [Google Scholar] [CrossRef]
- Gatenby, R.A.; Gawlinski, E.T.; Tangen, C.M.; Flanigan, R.C.; Crawford, E.D. The possible role of postoperative azotemia in enhanced survival of patients with metastatic renal cancer after cytoreductive nephrectomy. Cancer Res. 2002, 62, 5218–5222. [Google Scholar]
- Sofia, D.; Mohammad Mirzaei, N.; Shahriyari, L. Patient-Specific Mathematical Model of the Clear Cell Renal Cell Carcinoma Microenvironment. J. Pers. Med. 2022, 12, 1681. [Google Scholar] [CrossRef]
- Baratchart, E.; Benzekry, S.; Bikfalvi, A.; Colin, T.; Cooley, L.S.; Pineau, R.; Ribot, E.J.; Saut, O.; Souleyreau, W. Computational Modelling of Metastasis Development in Renal Cell Carcinoma. PLoS Comput. Biol. 2015, 11, e1004626. [Google Scholar] [CrossRef]
- Iwata, K.; Kawasaki, K.; Shigesada, N. A dynamical model for the growth and size distribution of multiple metastatic tumors. J. Theor. Biol. 2000, 203, 177–186. [Google Scholar] [CrossRef]
- Goldman, M.J.; Craft, B.; Hastie, M.; Repečka, K.; McDade, F.; Kamath, A.; Banerjee, A.; Luo, Y.; Rogers, D.; Brooks, A.N.; et al. Visualizing and interpreting cancer genomics data via the Xena platform. Nat. Biotechnol. 2020, 38, 675–678. [Google Scholar] [CrossRef] [PubMed]
- Weinstein, J.N.; Collisson, E.A.; Mills, G.B.; Shaw, K.R.; Ozenberger, B.A.; Ellrott, K.; Shmulevich, I.; Sander, C.; Stuart, J.M.; Chang, K.; et al. The Cancer Genome Atlas Pan-Cancer analysis project. Nat. Genet. 2013, 45, 1113–1120. [Google Scholar] [CrossRef] [PubMed]
- Shin, B.; Park, S.; Hong, J.H.; An, H.J.; Chun, S.H.; Kang, K.; Ahn, Y.H.; Ko, Y.H.; Kang, K. Cascaded Wx: A Novel Prognosis-Related Feature Selection Framework in Human Lung Adenocarcinoma Transcriptomes. Front. Genet. 2019, 10, 662. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.; Gorodeski, E.; Minn, A.; Lauer, M. High-Dimensional Variable Selection for Survival Data. J. Am. Stat. Assoc. 2010, 105, 205–217. [Google Scholar] [CrossRef]
- Sun, C.M.; Geng, J.; Yan, Y.; Yao, X.; Liu, M. Overexpression of CKAP4 is Associated with Poor Prognosis in Clear Cell Renal Cell Carcinoma and Functions via Cyclin B Signaling. J. Cancer 2017, 8, 4018–4026. [Google Scholar] [CrossRef]
- Miller, M.R.; Ma, D.; Schappet, J.; Breheny, P.; Mott, S.L.; Bannick, N.; Askeland, E.; Brown, J.; Henry, M.D. Downregulation of dystroglycan glycosyltransferases LARGE2 and ISPD associate with increased mortality in clear cell renal cell carcinoma. Mol. Cancer 2015, 14, 141. [Google Scholar] [CrossRef]
- Cox, A.; Tolkach, Y.; Stein, J.; Kristiansen, G.; Ritter, M.; Ellinger, J. Otoferlin is a prognostic biomarker in patients with clear cell renal cell carcinoma: A systematic expression analysis. Int. J. Urol. 2021, 28, 424–431. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Ma, Y.; Gao, C.; Zhang, Y.; Yang, X.; Zhao, X.; Wang, W.; Wang, L. Tumor-associated M2 macrophages in the immune microenvironment influence the progression of renal clear cell carcinoma by regulating M2 macrophage-associated genes. Front. Oncol. 2023, 13, 1157861. [Google Scholar] [CrossRef]
- Creighton, C.J.; Morgan, M.; Gunaratne, P.H.; Wheeler, D.A.; Gibbs, R.A.; Robertson, A.; Chu, A.; Beroukhim, R.; Cibulskis, K.; Signoretti, S.; et al. Comprehensive molecular characterization of clear cell renal cell carcinoma. Nature 2013, 499, 43–49. [Google Scholar]
- Le, T.; Aronow, R.A.; Kirshtein, A.; Shahriyari, L. A review of digital cytometry methods: Estimating the relative abundance of cell types in a bulk of cells. Briefings Bioinform. 2021, 22, bbaa219. [Google Scholar] [CrossRef]
- Aronow, R.A.; Akbarinejad, S.; Le, T.; Su, S.; Shahriyari, L. TumorDecon: A digital cytometry software. SoftwareX 2022, 18, 101072. [Google Scholar] [CrossRef] [PubMed]
- Jee, B.; Seo, E.; Park, K.; Kim, Y.R.; Byeon, S.J.; Lee, S.M.; Chung, J.H.; Song, W.; Sung, H.H.; Jeon, H.G.; et al. Molecular Subtypes Based on Genomic and Transcriptomic Features Correlate with the Responsiveness to Immune Checkpoint Inhibitors in Metastatic Clear Cell Renal Cell Carcinoma. Cancers 2022, 14, 2354. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, D.; Chen, Y.; Su, J.; Wang, Y.; Li, X.; Zhai, W.; Niu, Y.; Yue, D.; Geng, H. G3BP1 promotes tumor progression and metastasis through IL-6/G3BP1/STAT3 signaling axis in renal cell carcinomas. Cell Death Dis. 2018, 9, 501. [Google Scholar] [CrossRef] [PubMed]
- Thiounn, N.; Pages, F.; Flam, T.; Tartour, E.; Mosseri, V.; Zerbib, M.; Beuzeboc, P.; Deneux, L.; Fridman, W.H.; Debré, B. IL-6 is a survival prognostic factor in renal cell carcinoma. Immunol. Lett. 1997, 58, 121–124. [Google Scholar] [CrossRef] [PubMed]
- Walther, M.M.; Johnson, B.; Culley, D.; Shah, R.; Weber, J.; Venzon, D.; Yang, J.C.; Linehan, W.M.; Rosenberg, S.A. Serum interleukin-6 levels in metastatic renal cell carcinoma before treatment with interleukin-2 correlates with paraneoplastic syndromes but not patient survival. J. Urol. 1998, 159, 718–722. [Google Scholar] [CrossRef]
- Apetoh, L.; Ghiringhelli, F.; Tesniere, A.; Criollo, A.; Ortiz, C.; Lidereau, R.; Mariette, C.; Chaput, N.; Mira, J.P.; Delaloge, S.; et al. The interaction between HMGB1 and TLR4 dictates the outcome of anticancer chemotherapy and radiotherapy. Immunol. Rev. 2007, 220, 47–59. [Google Scholar] [CrossRef]
- Iyiola, O.S.; Zaman, F. A fractional diffusion equation model for cancer tumor. AIP Adv. 2014, 4, 107121. [Google Scholar] [CrossRef]
- Ghanbari, B. On the modeling of the interaction between tumor growth and the immune system using some new fractional and fractional-fractal operators. Adv. Differ. Equ. 2020, 2020, 585. [Google Scholar] [CrossRef]
- Baleanu, D.; Arshad, S.; Jajarmi, A.; Shokat, W.; Ghassabzade, F.A.; Wali, M. Dynamical behaviours and stability analysis of a generalized fractional model with a real case study. J. Adv. Res. 2023, 48, 157–173. [Google Scholar] [CrossRef]
- Baleanu, D.; Hasanabadi, M.; Mahmoudzadeh Vaziri, A.; Jajarmi, A. A new intervention strategy for an HIV/AIDS transmission by a general fractional modeling and an optimal control approach. Chaos Solitons Fractals 2023, 167, 113078. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sofia, D.; Zhou, Q.; Shahriyari, L. Mathematical and Machine Learning Models of Renal Cell Carcinoma: A Review. Bioengineering 2023, 10, 1320. https://doi.org/10.3390/bioengineering10111320
Sofia D, Zhou Q, Shahriyari L. Mathematical and Machine Learning Models of Renal Cell Carcinoma: A Review. Bioengineering. 2023; 10(11):1320. https://doi.org/10.3390/bioengineering10111320
Chicago/Turabian StyleSofia, Dilruba, Qilu Zhou, and Leili Shahriyari. 2023. "Mathematical and Machine Learning Models of Renal Cell Carcinoma: A Review" Bioengineering 10, no. 11: 1320. https://doi.org/10.3390/bioengineering10111320
APA StyleSofia, D., Zhou, Q., & Shahriyari, L. (2023). Mathematical and Machine Learning Models of Renal Cell Carcinoma: A Review. Bioengineering, 10(11), 1320. https://doi.org/10.3390/bioengineering10111320







